Figure it Out (Page 219)
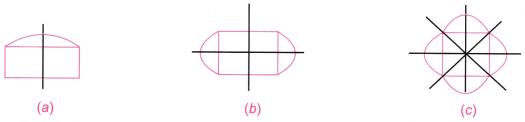
1. Do you see any Line of symmetry in the figures at the start of the chapter? What about in the picture of the cloud?
Solution:
Flower has 6 lines of symmetry.
Butterfly has 1 line of symmetry.
Rangoli has 4 lines of symmetry.
Pinwheel has no line of symmetry.
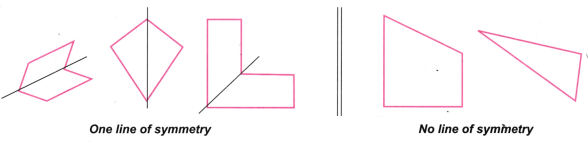
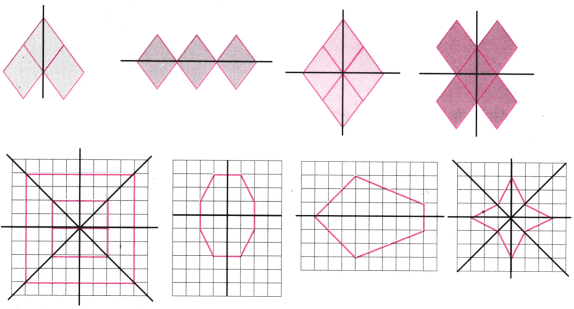
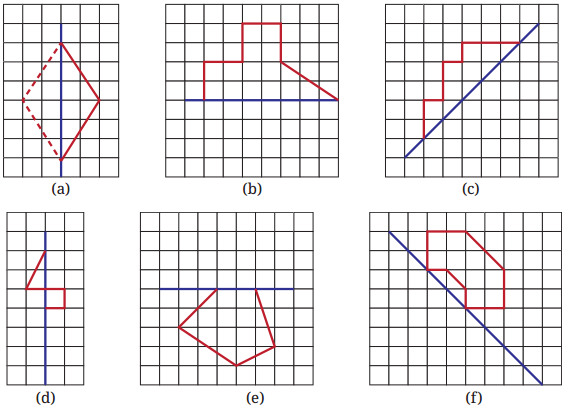
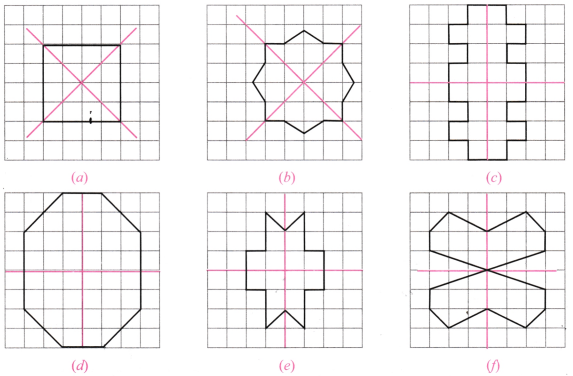
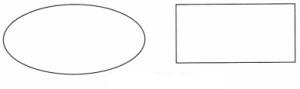
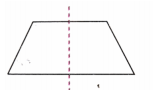
2. For each of the following figures, identify the line(s) of symmetry if it exists.
Solution:
Figure it Out (Page 223)
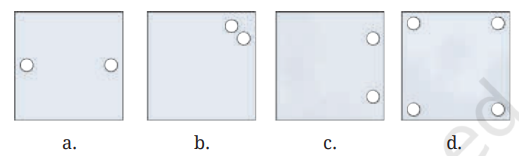
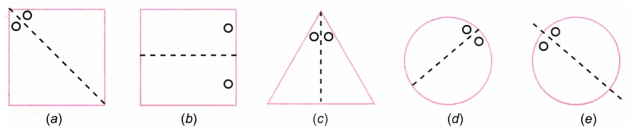
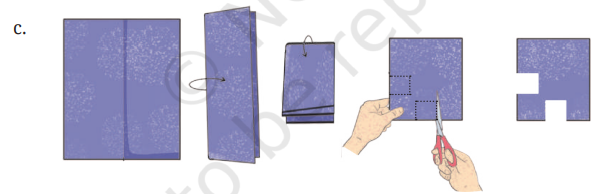
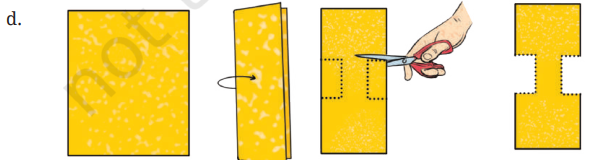
1. In each of the following figures, a hole was punched in a folded square sheet of paper and then the paper was unfolded. Identify the line along which the paper was folded.
Figure (d) was created by punching a single hole. How was the paper folded?
Solution:
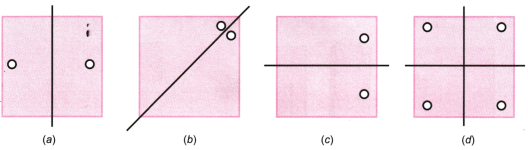
2. Given the line(s) of symmetry, find the other hole(s).
Solution:
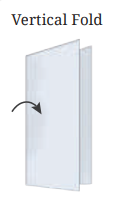
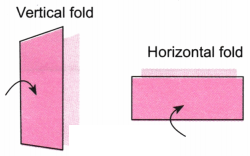
3. Here are some questions on paper cutting.
Consider a vertical fold. We represent it this way:
Similarly, a horizontal fold is represented as follows.
Solution
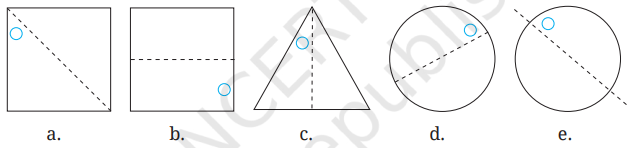
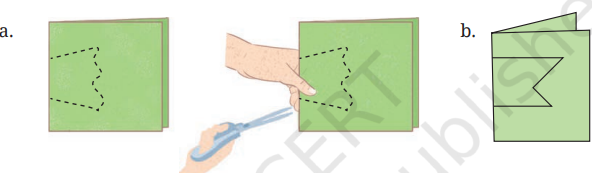
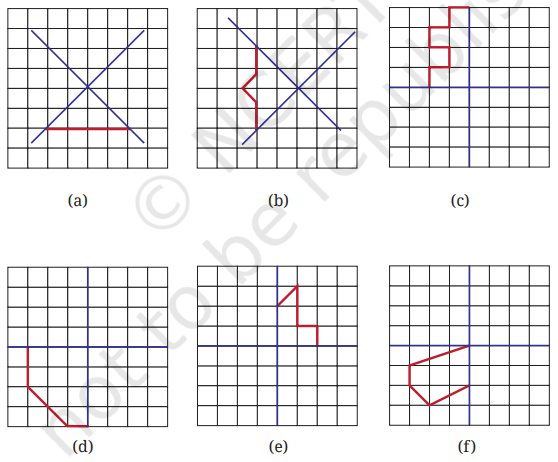
4. After each of the following cuts, predict the shape of the hole when the paper is opened. After you have made your prediction, make the cutouts and verify your answer.
Solution:
(a)
(b)
Solution:
Solution:
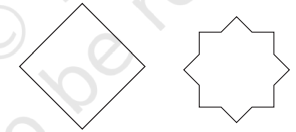
5. Suppose you have to get each of these shapes with some folds and a single straight cut. How will you do it?
(a) The hole in the centre is a square.
Solution:
(b) The hole in the centre is a square.
Solution:
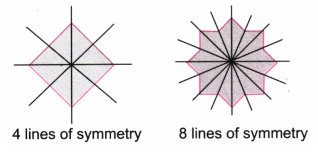
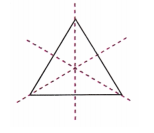
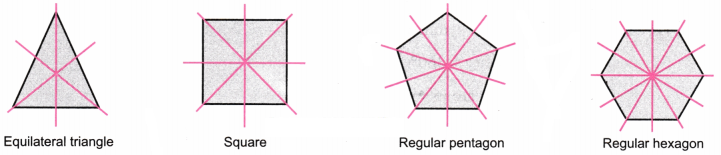
6. How many lines of symmetry do these shapes have?
(i)
Solution:
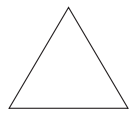
(ii) A triangle with equal sides and equal angles.
Solution:
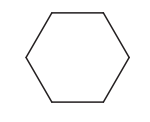
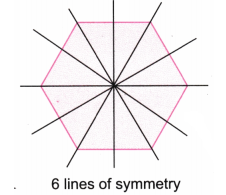
(iii) A hexagon with equal sides and equal angles.
Solution:
7. Trace each figure and draw the lines of symmetry, if any:
Solution:
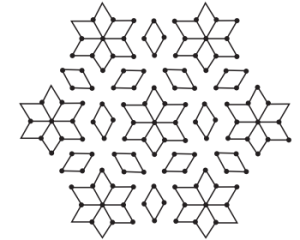
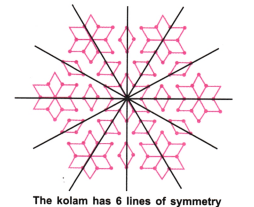
8. Find the lines of symmetry for the kolam below.
Solution:
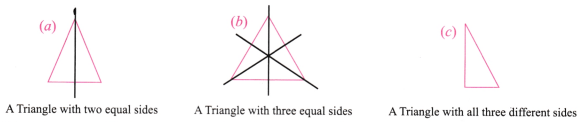
9. Draw the following:
(a) A triangle with exactly one line of symmetry
(b) A triangle with exactly three lines of symmetry
(c) A triangle with no line of symmetry
Is it possible to draw a triangle with exactly two lines of symmetry?
Solution:
No, it is not possible to draw a triangle with exactly two lines of symmetry.
10. Draw the following. In each case, the figure should contain at least one curved boundary.
(a) A figure with exactly one line of symmetry
(b) A figure with exactly two lines of symmetry
(c) A figure with exactly four lines of symmetry
Solution:
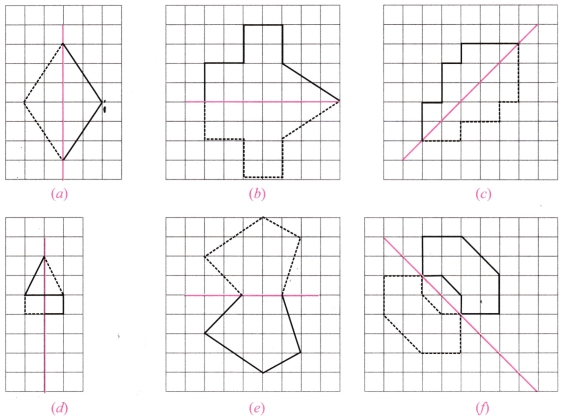
11. Copy the following on squared paper. Complete them so that the pink line is a line of symmetry. Problem (a) has been done for you.
Hint: For (c) and (f), see if rotating the book helps!
Solution:
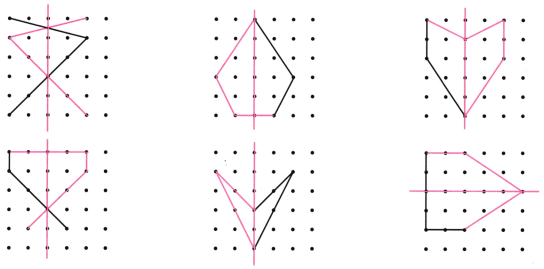
12. Copy the following drawing on squared paper. Complete each one of them so that the resulting figure has the two pink lines as lines of symmetry.
Solution:
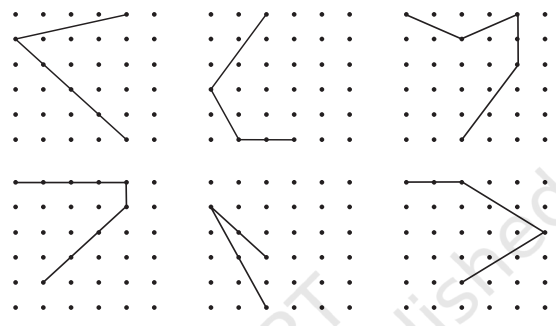
13. Copy the following on a dot grid. For each figure draw two more lines to make a shape that has a line of symmetry.
Solution:
Figure it Out (Page 235)
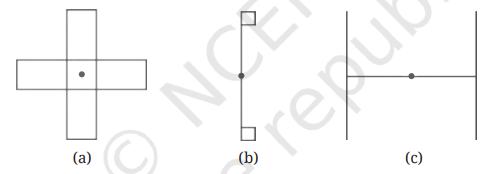
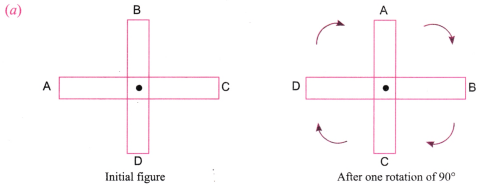
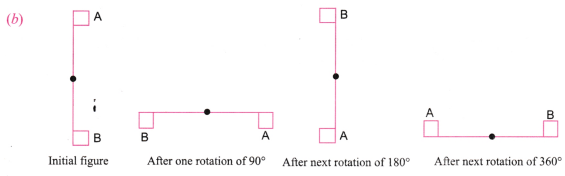
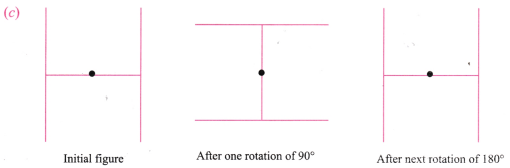
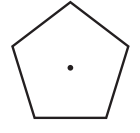
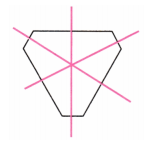
1. Find the angles of symmetry for the given figures about the point marked.
Solution:
To find the angle of symmetry, let’s rotate the figure by 90°.
The figure after rotation of 90° is exactly the same. Hence, 90° is the angle of symmetry.
A rotation of 90° results in the figure above. Does not overlap with the original figure. This figure comes back to its original shape only after one complete rotation through 360°. Hence, 360° is the angle of symmetry.
The figure after rotation of 180° is exactly the same. Hence, 180° is the angle of symmetry.
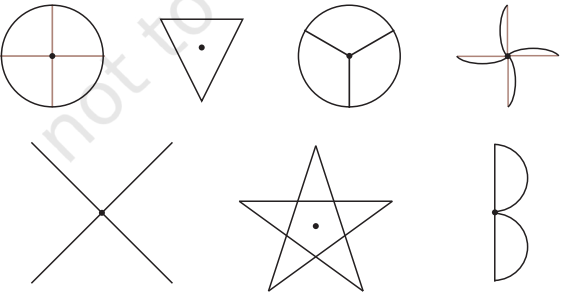
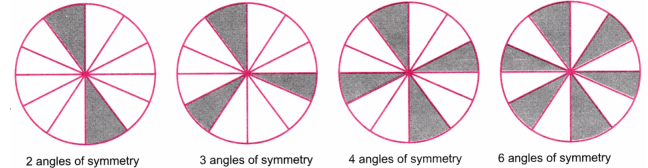
2. Which of the following figures have more than one angle of symmetry?
Solution:
All except (g) have more than one angle of symmetry.
3. Give the order of rotational symmetry for each figure:
(a)
Solution: 2
(b)
Solution: 1
(c)
Solution: 6
(d)
Solution: 3
(e)
Solution: 4
(f)
Solution: 5
Figure it Out (Page 238)
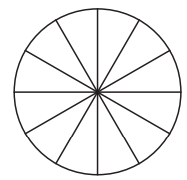
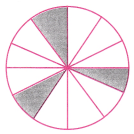
1. Color the sectors of the circle below so that the figure has
(a) 3 angles of symmetry
(b) 4 angles of symmetry
(c) what are the possible numbers of angles of symmetry you can obtain by coloring the sectors in different ways?
Solution:
(a) Will look same after every rotation of 120°.
(b) Will look same after every rotation of 90°.
(c) Four ways are possible.
2. Draw two figures other than a circle and a square that have both reflection symmetry and rotational symmetry.
Solution:
3. Draw, wherever possible, a rough sketch of
(a) A triangle with at least two lines of symmetry and at least two angles of symmetry.
Solution:
(b) A triangle with only one line of symmetry but not having rotational symmetry.
Solution:
(c) A quadrilateral with rotational symmetry but no reflction symmetry.
Solution:
(d) A quadrilateral with reflection symmetry but not having rotational symmetry.
Solution:
4. In a figure, 60° is the smallest angle of symmetry. What are the other angles of symmetry of this figure?
Solution:
As 60° is the smallest angle, other angles which has multiple of 60° till 360° are angle of symmetry. Here angles are 120°, 180°, 240°, 300°, 360°.
5. In a figure, 60° is an angle of symmetry. The figure has two angles of symmetry less than 60°. What is its smallest angle of symmetry?
Solution:
Smallest angle of symmetry = 60° ÷ 3 = 20°.
6.Can we have a figure with rotational symmetry whose smallest angle of symmetry is
(a) 45°
Solution:
Yes, as 360 is divisible by 45.
(b) 17°
Solution:
No, as 360 is not divisible by 17.
7. This is a picture of the new Parliament Building in Delhi.
(a) Does the outer boundary of the picture have reflction symmetry? If so, draw the lines of symmetries. How many are they?
Solution:
The outer boundary shows rotation symmetry about its center.
Smallest angle of rotation= 360° ÷ 3 = 120°.
Other angles of rotation are 240° and 360°.
(b) Does it have rotational symmetry around its centre? If so, find the angles of rotational symmetry.
Solution:
The outer boundary shows reflection symmetry.
It has 3 lines of symmetry
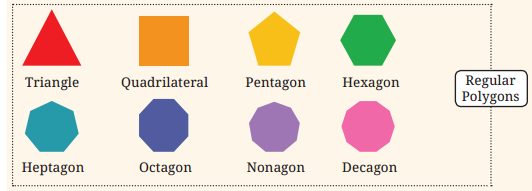
8. How many lines of symmetry do the shapes in the fist shape sequence in Chapter 1, Table 3, the Regular Polygons, have? What number sequence do you get?
Solution:
3 sided regular polygon ( equilateral triangle) has 3 lines of symmetry
4 sided regular polygon ( square) has 4 lines of symmetry
5 sided regular polygon ( regular pentagon) has 5 lines of symmetry
6 sided regular polygon ( regular hexagon) has 6 lines of symmetry We observe the following pattern:
Number of sides in a regular polygon*= number of lines of symmetry. Number sequence : 3, 4, 5, 6, 7, ……………………….
9. How many angles of symmetry do the shapes in the fist shape sequence in Chapter 1, Table 3, the Regular Polygons, have? What number sequence do you get?
Solution:
Number of angles of symmetry = number of lines of symmetry.
Hence we get the number sequence: 3, 4, 5, 6, 7, ………..
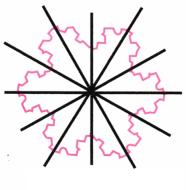
10. How many lines of symmetry do the shapes in the last shape sequence in Chapter 1, Table 3, the Koch Snowflke sequence, have? How many angles of symmetry?
Solution:
11. How many lines of symmetry and angles of symmetry does Ashoka Chakra have?
Solution:
The Ashoka Chakra has 24 spokes spread equally.
24 spokes make 12 pairs.
Line through an opposite pair is a line of symmetry.
Hence, there are 12 lines of symmetry.
Smallest angle of symmetry = 360° ÷ 2 = 30°.
Other angles of symmetry are its multiple up to 360.
Other angles are 60°, 120°, 150°, ………… , 360°. (12 angles in all).
The awnsers are all correct and are easy to be read and written. I am very happy with the awnsers