Figure it Out (Page 132)
1. Find the missing terms:
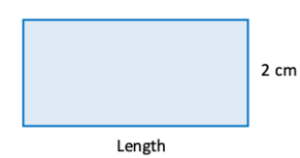
(a) Perimeter of a rectangle = 14 cm; breadth = 2 cm; length = ?
Solution:
perimeter of a rectangle = 2 (l + b)
perimeter of the rectangle = 14 cm
breadth b = 2 cm, l =?
Thus 14 = 2(l + 2)
⇒ 14 = 2l + 4
⇒ 2l = 14 – 4 = 10
⇒ l = 10/2 = 5 cm
(b) Perimeter of a square = 20 cm; side of a length = ?
Solution:
perimeter of the square = 4 × side of the square
4 x side of the square = 20 cm
side of the square = 20/4
side of the square = 5 cm
(c) Perimeter of a rectangle = 12 m; length = 3 m; breadth = ?
Solution:
Perimeter of rectangle = 2 (l + b)
⇒ 12 = 2 (3 + b)
⇒ 12 = 6 + 2b
⇒ 12 – 6 = 2b
⇒ 2b = 6 m
⇒ b = 3 m
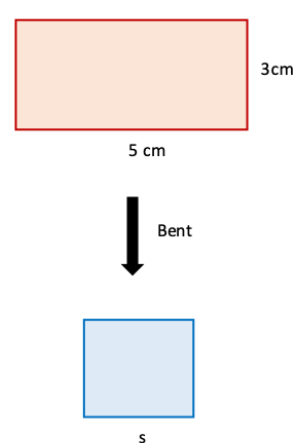
2. A rectangle with side lengths 5 cm and 3 cm is made using a wire. If the wire is straightened and then bent to form a square, what will be the length of the side of the square?
Solution:
Here perimeter of rectangle = 2 (5 + 3)
= 2 × 8
= 16 cm
Now the wire is straightened and then bent to form a square.
∴ Perimeter of square = 16 cm
⇒ 4 x s = 16 cm
⇒ s = 16/4 cm
⇒ s = 4 cm, the required length of the side of the square.
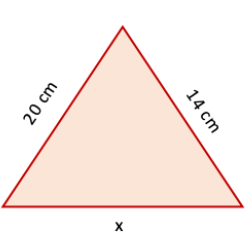
3. Find the length of the third side of a triangle having a perimeter of 55 cm and having two sides of length 20 cm and 14 cm, respectively.
Solution:
Perimeter of triangle = AB + BC + CA
55 = 20 + 14 + x
⇒ 55 = 34 + x
⇒ x = 55 – 34
⇒ x = 21 cm
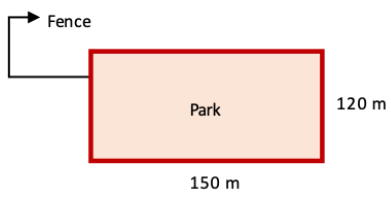
4. What would be the cost of fencing a rectangular park whose length is 150 m and breadth is 120 m if the fence costs ₹ 40 per meter?
Solution:
length of the rectangular park = 150 m and breadth = 120 m
∴ Perimeter = 2 (l + b)
= 2 (150 + 120)
= 2 (270)
= 540 m
Now cost of fencing per meter = ₹ 40
Cost of fencing the rectangular park = ₹ 40 × 540 = ₹ 21600
5. A piece of string is 36 cm long. What will be the length of each side, if it is used to form:
(a) A square,
Solution
Given, a piece of string is 36 cm long = 36 cm
a. Number of sides of square = 4
Perimeter of the square = 36cm
Length of each side = 36/4 =9cm.
(b) A triangle with all sides of equal length, and
Solution
Given, a piece of string is 36 cm long = 36 cm
Number of sides of a triangle with equal length = 3
Perimeter of the triangle = 36 cm
Length of each side = 36 /3 = 12 cm.
Solution
(c) A hexagon (a six-sided closed figure) with sides oil equal length?
Given, a piece of string is 36 cm long = 36 cm
Number of sides of a hexagon with equal length = 6
Perimeter of the hexagon = 36 cm
Length of each side = 36 / 6 = 6cm.
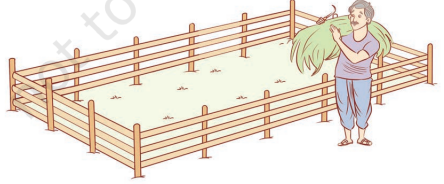
6. A farmer has a rectangular field with having length of 230 m and a breadth of 160 m. He wants to fence it with 3 rounds of rope as shown. What is the total length of rope needed?
Solution:
Perimeter of the rectangular field = 2(l + b)
Here l = 230 m, b = 160 m
∴ Perimeter = 2 (230 + 160)
= 2 (390)
= 780 m
Distance covered by a farmer in one round = 780 m
∴ Total length of rope needed = 3 × 780 = 2340 m
Figure it Out (Page 133, 134)
1. Find out the total distance Akshi has covered in 5 rounds.
Solution:
Length of Akshi’s track= 70 m
Breadth of Akshi’s track= 40 m
Distance covered by Akshi in one round = 2(|ength + breadth)
= 2 (70 + 40)
= 2 (110)
= 220 m.
Total distance covered by Akshi in 5 rounds = 5 x 220 m
= 1100 m.
2. Find out the total distance Toshi has covered in 7 rounds. Who ran a longer distance?
Solution:
Length of Toshi’s track = 60 m
Breadth of Toshi’s track = 30 m
Distance covered by Toshi in one round = 2(|ength + breadth)
= 2(60 + 30)
= 2(90)
= 180 m.
Total distance covered by Toshi in 7 rounds = 7 x 180 m
= 1260 m.
Therefore, Toshi ran a longer distance than Akshi.
Figure it Out (Page 138)
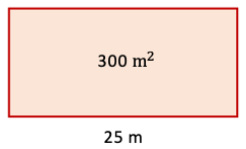
1. The area of a rectangular garden 25 m long is 300 sq m. What is the width of the garden?
Solution:
Given, area of rectangular garden = 300 sq.m
and length = 25 m
area of rectangular field = l × b
⇒ 300 = 25 × b
⇒ b = 12 m
2. What is the cost of tiling a rectangular plot of land 500 m long and 200 m wide at the rate of ₹ 8 per hundred sq m?
Solution:
length = 500 m and breadth = 200 m
Hence the area of the rectangular plot = length × breadth
= 500 × 200
= 1,00,000 m2
Now cost of tilling a rectangular plot = 8/100
Hence the cost of tilling 1,00,000 sq. m of rectangular plot = 8/100 × 100000 = ₹ 8,000
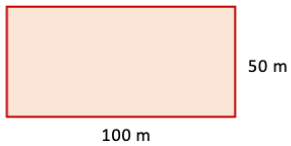
3. A rectangular coconut grove is 100 m long and 50 m wide. If each coconut tree requires 25 sq m, what is the maximum number of trees that can be planted in this grove?
Solution:
Area of rectangular coconut grove = 100 × 50 = 5000 sq. m
Given each coconut tree requires 25 sq. m
then the maximum no. of trees that can be planted in this grove = 5000 / 25 = 200 trees.
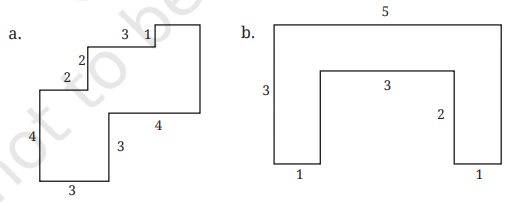
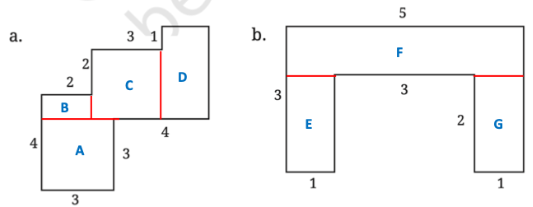
4. By splitting the following figures into rectangles, find their areas (all measures are given in meters):
Solution:
a. Area of the figure = Area of sq A + Area of rect. B + Area of sq C + Area of rect. D
= (3 x 3)+(1 x 2)+{3 x 3)+{4 x 2)
= 9+2+9+8
= 28 m3.
b. Area of the figure = Area of rect. E + Area of rect. F + Area of rect. G
= {1 x 2)+{1 x 5)+{1 x 2)
= 2+5+2
= 9 m3.
Figure it Out (Page 139)
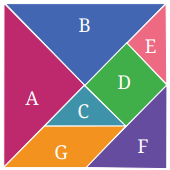
Cut out the tangram pieces given at the end of your textbook.
1. Explore and figure out how many pieces have the same area.
Solution:
There are two pieces (A and B) that have the same area.
2. How many times bigger is Shape D as compared to Shape C? What is the relationship between Shapes C, D, and E?
Solution:
Shape D is two times bigger than shape C. Clearly from the figure, the area of shapes C and E is equal to the area of shape D.
3. Which shape has more area: Shape D or F? Give reasons for your answer.
Solution:
Since the medium triangle and the square are each made up of two small tangram triangles, they each have an area 2x that of the small triangle. Hence both have the same area.
4. Which shape has more area: Shape F or G? Give reasons for your answer.
Solution:
Since the medium triangle and the rhomboid are each made up of two small tangram triangles, they each have an area 2x that of the small triangle. Hence both have the same area.
5. What is the area of Shape A as compared to Shape G? Is it twice as big? Four times as big?
[Hint: In the tangram pieces, by placing the shapes over each other, we can find out that Shapes A and B have the same area, and Shapes C and E have the same area. You would have also figured out that Shape D can be exactly covered using Shapes C and E, which means Shape D has twice the area of Shape C or Shape E, etc.]
Solution:
Shape A has twice the area of shape G.
6. Can you now figure out the area of the big square formed with all seven pieces in terms of the area of Shape C?
Answer:
Let’s say the area of C = x
Area of D = Area of 2C = 2x
Area of E = Area of C = x
Area of F = Area of 2C = 2x
Area of G = Area of 2C = 2x
Area of A = Area of 2F = 2 × 2x = 4x
Area of B = Area of A = 4x
Hence total area of big shape = Area of A + B + C + D + E + F + G
= 4x + 4x + x + 2x + x + 2x + 2x
= 16x
= 16C
That means the area of a big square is 16 times the area of shape C.
7. Arrange these 7 pieces to form a rectangle. What will be the area of this rectangle in terms of the area of Shape C now? Give reasons for your answer.
Solution:
The tangram rectangle with all 7 pieces is a tangram square with 5 pieces extended with two big triangles. All seven tans fit together to form a rectangle. Hence area of this rectangle in terms of Shape C is 16 small triangles.
8. Are the perimeters of the square and the rectangle formed from these 7 pieces different or the same? Give an explanation for your answer.
Solution:
The perimeter of the square is equal to the square formed from these 7 pieces because these are the arrangements of pieces.
Figure it Out (Page 144)
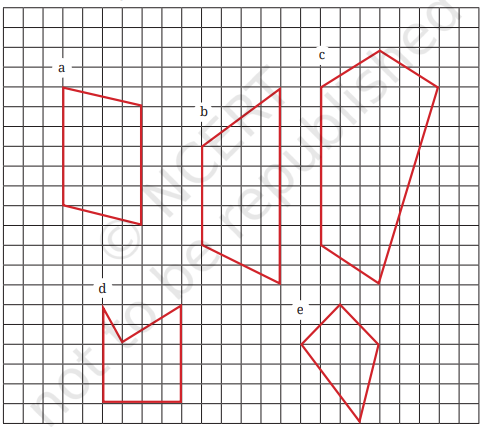
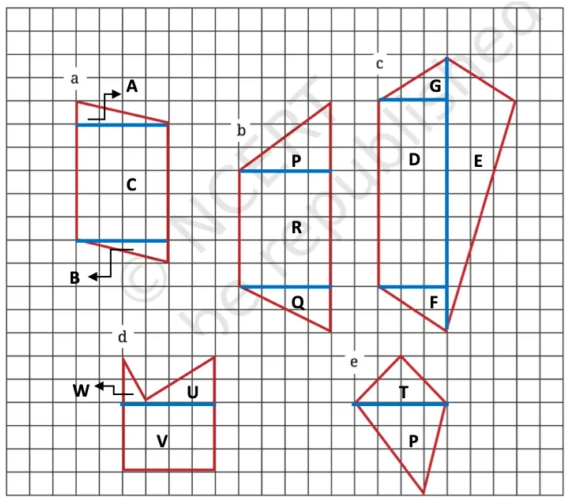
1. Find the areas of the figures below by dividing them into rectangles and triangles.
Solution:
a. Area of the figure = Area of triangle A + Area of triangle B + Area of rect. C
= 3 sq. units + 3 sq. units + 20 sq. units
= 26 sq. units.
b. Area of the figure = Area of triangle P + Area of triangle 0. + Area of rect. R
= 6 sq. units + 4sq. units + 20 sq. units
= 30 sq. units.
c. Area = Area of triangle G + Area of triangle E + Area of triangle F + Area of rect. D
= 3 sq. units + 18 sq. units + 3 sq. units + 24 sq. units
= 48 sq. units.
d. Area of the figure = Area of triangle W + Area of triangle U + Area of rect. V
= 1 sq. units + 3 sq. units + 12 sq. units
= 16 sq. units.
e. Area of the figure = Area of triangle T + Area of triangle P
= 4 sq. units + 7 sq. units
= 11 sq. units.
Figure it Out (Page 149)
1. Give the dimensions of a rectangle whose area is the sum, of the areas of these two rectangles having measurements: 5 m × 10 m and 2 m × 7 m.
Solution:
Area of the new rectangle formed = 5 m x 10 m + 2m x 7m
= 50m2 + 14 m2
= 64 m2
To determine the dimensions of the new rectangle, we need two values that multiply to form 64.
1 m x 54 m
2 m x 32 m
4 m X 16 m
8m x 8m
Any of these pairs could represent dimensions of the new rectangle.
2. The area of a rectangular garden that is 50 m long is 1000 sq m. Find the width of the garden.
Solution:
Length of the garden = 50 m
Area of the garden = 1000 m2
Length x Width = 1000
50 x Width = 1000
Width = 1000 / 50 = 20m
Therefore, the width of the garden = 20 m.
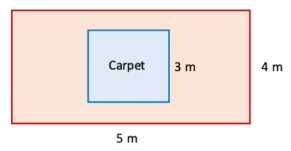
3. The floor of a room is 5 m long and 4 m wide. A square carpet whose sides are 3 m in length is laid on the floor. Find the area that is not carpeted.
Solution:
Length of the room = 5 m
Width of the room = 4 m
Side of square carpet = 3m
Area that is not carpeted = Area of the room — Area of square carpet
= length x breadth – side x side
= 5 x 4 – 3 x 3
= 20 — 9
= 11 m2
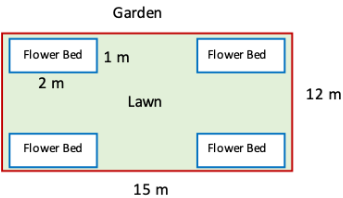
4. Four flower beds having sides 2 m long and 1 m wide are dug at the four corners of a garden that is 15 m long and 12 m wide. How much area is now available for laying down a lawn?
Solution:
Length of garden = 15 m
Width of garden = 12 m
So, the area of the garden = 15 × 12 sq m = 180 sq m
Now, the length of the flower bed = 2 m
Width of flower bed = 1 m
Area of the flower bed = 2 × 1 sq m = 2 sq m
Since, the area of four flower beds = 2 × 4 sq m = 8 sq m
Now the area is available for laying down a lawn = (180 – 8) sq m = 172 sq m
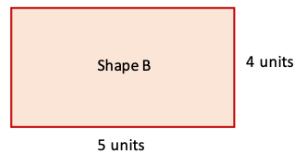
5. Shape A has an area of 18 square units and Shape B has an area of 20 square units. Shape A has a longer perimeter than Shape B. Draw two such shapes satisfying the given conditions.
Solution:

Area of Shape A = 18 m2.
Perimeter of Shape A = 2(9 + 2)
=2(11) = 22 units.
Perimeter of Shape B = 2{5 + 4)
Perimeter of Shape B = 2{5 + 4)
= 2(9) = 13 units
Therefore, Shape A has a longer than Shape B.
6. On a page in your book, draw a rectangular border that is 1 cm from the top and bottom and 1.5 cm from the left and right sides. What is the perimeter of the border?
Solution:
Perimeter of the rectangular border = 2 × [length + width]
= 2 × [1 + 1.5]
= 2 × 2.5
= 5 cm
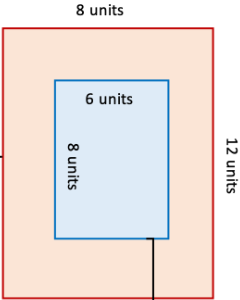
7. Draw a rectangle of size 12 units × 8 units. Draw another rectangle inside it, without touching the outer rectangle that occupies exactly half the area.
Solution:
Area of given rectangle = 12 × 8 = 96 units2
and area of new rectangle = 1 / 2 × 96 = 48 sq. units
∴ Possible sides of new rectangle are 12 × 4, 16 × 3, 8 × 6, 1 × 48
∴ Hence dimensions of the new rectangle fill in the rectangle of 12 × 8 units2 = 8 units × 6 units.




The 6th question have no figure
It is very helpful.
My math H.W