Figure it Out (Page 108)
Question 1. At what number is ‘idli-vada’ said for the 10th time?
Solution:
To determine the 10th occurrence of “idli- vada”; we need to identify the numbers that are multiples of both 3 and 5.
The numbers for which “idli-vada” is said are the multiples of 15.
This sequence is: 15,30,45,60, 75,90, 105, 120,135,150,…
Thus, the 10th number for which players should say “idli-vada” is 150.
Question 2. If the game is played for the numbers from 1 till 90, find out:
(a) How many times would the children say ‘idli ’ (including the times they say ‘idli- vada’)?
(b) How many times would the children say ‘vada ’ (including the times they say ‘idli-vada’)?
(c) How many times would the children say ‘idli-vada ’?
Solution:
(a) Idli is said for multiples of 3. Between 1 and 90 the multiples of 3 are 3, 6, 9, 12, 15, 18, …….. 90. There are 30 such numbers.
Hence the children would say idli 30 times.
(b) Vada is said for multiples of 5. Between 1 and 90 the multiples of 5 are 5, 10,15, 20, 25,…
There are 18 such numbers.
(c) Idli-Vada is said for multiples of both 3 and 5, which is multiple of 15. Between 1 and 90, there are 15, 30, 45, 60, 75, 90. There are 6 such numbers.
Question 3. What if the game was played till 900? How would your answers change?
Solution:
There are 300 multiples of 3 between 1 and 900 and there are 180 multiples of 5 between 1 and 900. There are 60 multiples of 15 between 1 and 900.
(a) “idli” is said: 300 times (including the times “idli-vada” is said).
(b) “vada” is said: 180 times (including the times “idli-vada” is said).
(c) “idli-vada” is said: 60 times.
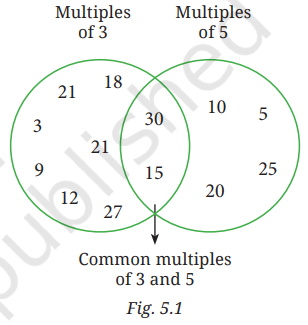
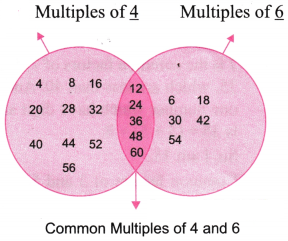
Question 4. Is this figure somehow related to the ‘idli- vada’ game? (Hint: Imagine playing the game till 30. Draw the figure if the game is played till 60.)
Solution:
Yes, this figure is related to the ‘idli-vada’ game. Figure below for game played till 60.
(Page 109)
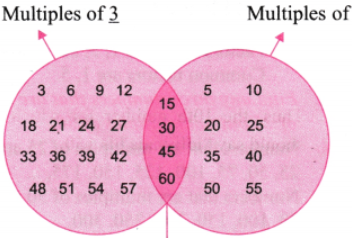
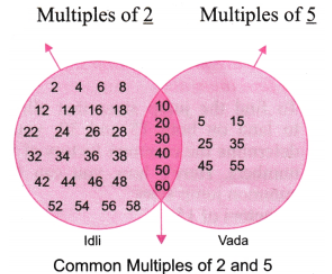
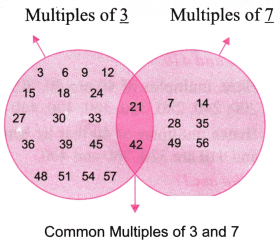
Let us now play the ‘idli-vada ’ game with different pairs of numbers:
(a) 2 and 5
Solution:
(b) 3 and 7
Solution:
(c) 4 and 6
Solution:
Which of the following could be the other number: 2, 3, 5, 8,10?
Answer: 2
(Page 110)
What jump size can reach both 15 and 30? There are multiple jump sizes possible. Try to find them all.
Solution:
Factors of 15:
- 15 can be factored into: 15 = 3 × 5
- The factors of 15 are: 1, 3, 5, 15
Factors of 30:
- 30 can be factored into: 30 = 2 × 3 × 5
- The factors of 30 are: 1, 2, 3, 5, 6, 10, 15, 30
The common factors between these two lists are: 1, 3, 5, 15. So, the jump sizes that will allow Jumpy to land on both 15 and 30 are the common factors of 15 and 30.
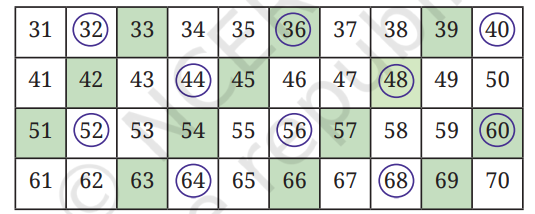
Look at the table below. What do you notice?
1. Is there anything common among the shaded numbers?
Solution:
The shaded numbers in the table are: 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69.
These are all multiples of 3. So, the numbers in shaded boxes are multiples of 3.
2. Is there anything common among the circled numbers?
Solution:
The circled numbers in the table are: 32, 36,40, 44, 48, 52, 56,60, 64, 68.
These are all multiples of 4. So, the numbers in circles are multiples of 4.
3. Which numbers are both shaded and circled? What are these numbers called? (Page 110)
Solution:
The numbers that are both shaded and circled are: 36, 48, 60, 64.
These numbers are called common multiples of 12 (3 and 4 both].
Figure it Out (Page 110)
1. Find all multiples of 40 that lie between 310 and 410.
Answer:
Here, multiples df 40 are 40, 80, 120, 160, 200, 240, 280, 320, 360, 400, 440
Hence multiples of 40 that lie between 310 and 410 are 320, 360 and 400.
2. Who am I?
a. I am a number less than 40. One of my factors is 7.
The sum of my digits is 8.
Answer: The number is 35 [since 3 + 5 = 8 and 35 is divisible by 7].
b. I am a number less than 100. Two of my factors are 3 and 5.
One of my digits is 1 more than the other.
Answer: Common factors of 3 and 5 are 15, 30, 45, 60, 75,90, (which are less than 100). And there is one number which one of digit is 1 more than the other that is 45. So, I am 45.
3. A number for which the sum of all its factors is equal to twice the number is called a perfect number. The number 28 is a perfect number. Its factors are 1, 2, 4, 7, 14 and 28. Their sum is 56 which is twice 28. Find a perfect number between 1 and 10.
Solution:
The only perfect number between 1 and 10 is 6.
- Proper divisors are 1, 2, 3, 6
- Sum of proper divisors: 1 + 2 + 3 + 6 = 12
- 12 is twice of 6, hence 6 is a perfect number.
4. Find the common factors of:
(a) 20 and 28
(b) 35 and 50
(0 4, 8 and 12
(d) 5, 15 and 25
Solution:
(a) Factors of 20 are 1, 2, 4, 5, 10, 20 Factors of 28 are 1, 2, 4, 7, 14, 28 Common factors are 1, 2, 4
(b) Factors of 35 are 1, 5, 7, 35 Factors of 50 are 1, 2,’5, 10, 25, 50 Common factors are 1,5
(c) Factors of 4 are 1, 2, 4 Factors of 8 are 1, 2, 4, 8 Factors of 12 are 1, 2, 3, 4, 6, 12 Common factors are 1, 2, 4
(d) Factors of 5 are 1, 5 Factors of 15 are 1, 3, 5, 15 Factors of 25 are 1, 5, 25 Common factors are 1,5.
5. Find any three numbers that are multiples of 25 but not multiples of 50.
Solution:
Numbers that are multiples of 25 are 25, 50, 75, 100, 125, 150, 175, …
Numbers that are multiples of 50 are 50, 100, 150, 200, 250,300,…
Hence, the numbers that are multiples of 25 but not multiples of 50 are 25, 75, 125, 175,…
6. Anshu and his friends play the ‘idli-vada ’ game with two numbers, which are both smaller than 10. The first time anybody says ‘idli-vada’ is after the number 50. What could the two numbers be which are assigned ‘idli’and ‘vada’?
Solution:
If ‘idli-vada’ is said after number 50 it means that the least common multiple (LCM) of the two numbers must be slightly greater than 50. The LCM of 6 and 9 is 54,’.which is the first common multiple after 50, making 6 and 9 the possible numbers. Hence the two numbers could be 6 and 9.
7. In the treasure hunting game, Grumpy has kept treasures on 28 and 70. What jump sizes will land on both the numbers?
Solution:
Factors of 28 = 1, 2, 4, 7, 14, 28
Factors of 70 = 1,2, 5, 7, 10, 14, 35, 70
Common factors are 1, 2, 7 and 14
Hence jump sizes which will land at both 28 and 70 are 1, 2, 7 and 14.
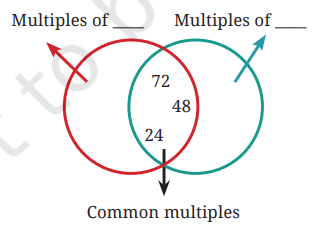
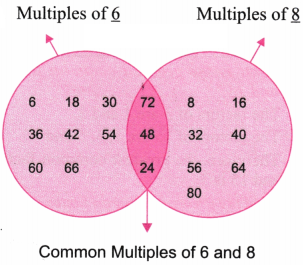
8. In the diagram below, Guna has erased all the numbers except the common multiples. Find out what those numbers could be and fill in the missing numbers in the empty regions.
Solution:
Multiples of 6 Multiples of 8
Here 6 could also be replaced by 3.
As 24, 48, 72, are also common multiples of 3 and 8.
9. Find the smallest number that is a multiple of all the numbers from 1 to 10 except for 7.
Solution:
To find the smallest number that is a multiple of all numbers from 1 to 10 except 7, we calculate the least common multiple of the numbers 1, 2, 3, 4, 5, 6, 8, 9 and 10. The least common multiple of these numbers is 360.
10. Find the smallest number that is a multiple of all the numbers from 1 to 10.
Solution:
To find the smallest number that is a multiple of all the numbers from 1 to 10, we calculate the smallest multiple of 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10. The smallest multiple number of these numbers is 2520.
(Page 113)
How many prime numbers are there from 21 to 30? How many composite numbers are there from 21 to 30?
Answer:
Prime numbers are numbers that have only two divisors: 1 and the number itself. The prime numbers between 21 and 30 are: 23 and 29. So, there are 2 prime numbers.
Composite numbers are numbers that have more than two divisors. The composite numbers between 21 and 30 are: 22, 24, 25, 26, 27, 28, and 30. So, there are 7 composite numbers.
Figure it Out (Page 114)
1. We see that 2 is a prime and also an even number. Is there any other even prime?
Solution:
No, 2 is the only even prime number. Since 2 is the only even number that meets the criteria of a prime number (its only divisors are 1 and 2), it is the only even prime number. All other even numbers are divisible by 2 and at least one other number, so they are not prime.
2. Look at the list of primes till 106. What is the smallest difference between two successive primes? What is the largest difference?
Solution:
To find the smallest difference between two successive prime numbers up to 100, let’s list the prime numbers in that range and calculate the differences between each pair: Prime numbers up to 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Differences between successive primes:
- 3 – 2 = 1
- 5 – 3 = 2
- 7 – 5 = 2
- 11 – 7 = 4
- 13 – 11 = 2
- 17 – 13 = 4
- 19 – 17 = 2
- 23 – 19 = 4
- 29 – 23 = 6
- 31 – 29 = 2
- 37 – 31 = 6
- 41 – 37 = 4
- 43 – 41 = 2
- 47 – 43 = 4
- 53 – 47 = 6
- 59 – 53 = 6
- 61 – 59 = 2
- 67 – 61 = 6
- 71 – 67 = 4
- 73 – 71 = 2
- 79 – 73 = 6
- 83 – 79 = 4
- 89 – 83 = 6
- 97 – 89 = 8
The smallest difference between two successive primes up to 100 is 1 (between the primes 2 and 3).
The largest difference between two successive primes up to 100 is 8, which occurs between the primes 89 and 97.
3. Are there an equal number of primes occurring in every row in the table on the previous page? Which decades have the least number of primes? Which have the most number of primes?
Solution:
There is not an equal number of primes in every row. The number of primes varies between rows. The decade 90-99 has the least number of primes with only 1 prime (97).
The decades 0-9 and 10-19 have the greatest number of primes, each with 4 primes.
4. Which of the following numbers are prime? 23, 51, 37, 26
Solution:
The prime numbers from the list (23, 51, 37, 26) are 23 and 37.
23: Prime (it has no divisors other than 1 and 23).
51: Not prime (it is divisible by 1, 3 and 17).
37: Prime (it has no divisors other than 1 and 37).
26: Not prime (it is divisible by 1, 2 and 13).
5. Write three pairs of prime numbers less than 20 whose sum is a multiple of 5.
Solution:
Three pairs of prime numbers less than 20 whose sum is a multiple of 5 are: (2, 3), (2, 13) and (7, 13).
6. The numbers 13 and 31 are prime numbers. Both these numbers have the same digits 1 and 3. Find such pairs of prime numbers up to 100.
Solution:
The valid pairs of prime numbers up to 100 that consist of the same digits are: (13, 31), (17, 71), (37, 73) and (79, 97).
7. Find seven consecutive composite numbers between 1 and 100.
Solution:
The seven consecutive composite numbers are: 90, 91, 92, 93, 94, 95, 96.
8. Twin primes are pairs of primes having a difference of 2. For example, 3 and 5 are twin primes. So are 17 and 19. Find the other twin primes between 1 and 100.
Solution:
Twin primes between 1 and 100:
(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61) and (71, 73).
9. Identify whether each statement is true or false. Explain.
a) There is no prime number whose units digit is 4.
Solution: True.
A prime number must end in 1, 3, 7, or 9 (except for the number 2) because any number ending in 0, 2, 4, 6 or 8 is divisible by 2.
Thus, there is no prime number whose units digit is 4.
b) A product of primes can also be prime.
Solution: False.
A product of prime numbers is only prime if it involves exactly one prime number. When you multiply two or more prime numbers together, the result is always a composite number, not a prime. As this number has 2 factors now.
c) Prime numbers do not have any factors.
Solution:
False.
Prime numbers have exactly two factors 1 and itself.
d) All even numbers are composite numbers.
Solution:
False.
The number 2 is an even number, but it is not composite. As it is a prime number.
e) 2 is a prime and so is the next number, 3. For every other prime, the next number is composite.
Solution: True.
For every prime number greater than 2, the next number is composite.
10. Which of the following numbers is the product of exactly three distinct prime numbers: 45, 60, 91, 105, 330?
Solution:
Here, 45 = 3 × 3 × 5 (2 distinct primes)
60 = 2 × 2 × 3 × 5(3 distinct primes)
91 = 7 × 13 (2 distinct primes)
105 = 3 × 5 × 7 (3 distinct primes)
330 = 2 × 3 × 5 × 11 (4 distinct primes)
Number 105 is the product of exactly three distinct prime numbers i.e. 3 × 5 × 7.
11. How many three-digit prime numbers can you make using each of 2, 4, and 5 once?
Solution:
2, 4 and 5 cannot form a single prime number.
Because, when its units digit is 2 or 4 it is divided by 2, and when units digits is 5 it is divided by 5 so that’s why 2, 4 and 5 cannot form a prime number.
12. Observe that 3 is a prime number, and 2 x 3 + 1 = 7 is also a prime. Are there other primes for which doubling and adding 1 gives another prime? Find at least five such examples.
Solution:
The five prime numbers for which doubling and adding 1 gives another prime are:
- 2 (since 2 × 2 + 1 = 5)
- 3 (since 2 × 3 + 1 = 7)
- 5 (since 2 × 5 + 1 = 11)
- 11 (since 2 × 11 + 1 = 23)
- 23 (since 2 × 23 + 1 = 47)
(Page 116)
1. Which of the following pairs of numbers are co-prime?
(a) 18 and 35
(b) 15 and 37
(c) 30 and 415
Answer:
(a) Here factors of 18 = 1 × 2 × 3 × 3 and factors of 35 = 1 × 5 × 7
No common factor other than 1.
Hence 18 and 35 are co-prime numbers.
(b) We have factors of 15 = 1 × 3 × 5 and factors of 37 = 1 × 37
No common factor other than 1.
Hence 15 and 37 are co-prime numbers.
(c) Given numbers are 30 and 415 Here factors of 30 = 1 × 2 × 3 × 5 and factors of 415 = 5 × 83
Clearly 5 is a common factor of 30 and 415.
Hence 30 and 415 are not co-prime numbers.
Figure it Out (Page 120)
1. Find the prime factorizations of the following numbers: 64, 104, 105, 243, 320, 141, 1728, 729, 1024, 1331, 1000.
Solution:
(a) The prime factorization of 64 is 2 × 2 × 2 × 2 × 2 × 2.
(b) The prime factorization of 104 is 2 × 2 × 2 × 13.
(c ) The prime factorization of 105 is 3 × 5 × 7.
(d) The prime factorization of 243 is 3 × 3 × 3 × 3 × 3.
(e) The prime factorization of 320 is 2 × 2 × 2 × 2 × 2 × 2 × 5.
(j) The prime factorization of 141 is 3 × 47.
(g) The prime factorization of 1728 is 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3.
(h) The prime factorization of 729 is 3 × 3 × 3 × 3 × 3 × 3.
(f) The prime factorization of 1024 is 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2.
(j) The prime factorization of 1331 is 11 × 11 × 11.
(k) The prime factorization of 1000 is 2 × 2 × 2 × 5 × 5 × 5.
2. The prime factorization of a number has one 2, two 3s, and one 11. What is the number?
Solution:
To find the number, we multiply these prime factors together:
2 × 3 × 3 × 11 = 198
Thus, the number is 198.
3. Find three prime numbers, all less than 30, whose product is 1955.
Solution:
The prime factorization of 1955:
1955 = 5 × 17 × 23
All the factors are prime numbers and are less than 30.
Hence, the three prime numbers whose product is 1955 are 5, 17, and 23.
4. Find the prime factorization of these numbers without multiplying first.
(a) 56 × 25
(b) 108 × 75
(c) 1000 × 81
Solution:
(a) Prime factors of 56 = 2 × 2 × 2 × 7
Prime factors of 25 = 5 × 5
Combined prime factorization of 56 × 25 = 2 × 2 × 2 × 7 × 5 × 5
(b) Prime factors of 108 = 2 × 2× 2 × 3 × 3
Prime factors of 75 = 3 × 5 × 5
Combined prime factorization of
108 × 75 = 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5
(c) Prime factors of 1000 = 2 × 2 × 2 × 5 × 5 × 5
Prime factors of 81 = 3 × 3 × 3 × 3
Combined prime factorization of 1000 × 81 = 2 × 2 × 2 × 5 × 5 × 5 × 3 ×3 × 3 × 3
5. What is the smallest number whose prime factorization has:
(a) three different prime numbers?
(b) four different prime numbers?
Solution:
(a) The smallest prime numbers are 2, 3, and 5. To find the smallest number with these primes as factors, multiply them together:
2 × 3 × 5 = 30
So, the smallest number whose prime factorization has three different prime numbers is 30.
(b) The smallest four prime numbers are 2, 3, 5, and 7. To find the smallest number with these primes as factors, multiply them together:
2 × 3 × 5 × 7 = 210
Thus, the smallest number whose prime factorization has four different prime numbers is 210.
Figure it Out (Page 122)
1. Are the following pairs of numbers co-prime? Guess first and then use prime factorization to verify your answer.
(a) 30 and 45
(b) 57 and 85
(c) 121 and 1331
(d) 343 and 216
Solution:
Solution:
(a) Factors of 30 and 45:
30 = 2 × 3 × 5,
45 = 3 × 3 × 5
Common factors: 3 × 5 = 15, hence 30 and 45 are not a pair of co-prime numbers.
(b) Factors of 57 and 85:
57 = 3 × 19,
85 = 5 × 17
No common factors other than 1, hence 57 and 85 are a pair of co-prime numbers.
(c) Factors of 121 and 1331:
121 = 11 × 11,
1331 = 11×11×11
Common factors: 11 × 11 = 121, hence 121 and 1331 are not a pair of co-prime numbers.
(d) Factors of 343 and 216:
343 = 7 × 7 × 7,
216 = 2 × 2 × 2 × 3 × 3 × 3
No common factors other than 1, hence 343 and 216 are a pair of co-prime numbers.
2. Is the first number divisible by the second? Use prime factorization.
(a) 225 and 27
(b) 96 and 24
(c) 343 and 17
(d) 999 and 99
Solution:
(a) Prime Factors of 225 and 27:
225 = 3 × 3 × 5 × 5 and 27 = 3 × 3 × 3
Since 225 contains 3×3 and does not have enough factors of 3 to match 3×3 × 3, 225 does not have sufficient factors to be divisible by 27.
Therefore, 225 is not divisible by 27.
(b) Prime Factors of 96 and 24:
96 = 2 × 2 × 2 × 2 × 2 × 3 and 24 = 2 × 2 × 2 × 3.
Since 96 includes the required factors to match those in 24, it is divisible by 24.
(c) Prime Factors of 343 and 17:
343 = 7 × 7 × 7 and 17 = 1 × 17
Since the prime factorization of 343 contains the prime factor 7 and not 17, 343 is not divisible by 17.
Thus, 343 is not divisible by 17.
(d) Prime Factors of 999 and 99: t
999 = 3 × 3 × 3 × 37 and 99 = 3 × 3 × 11
Since 999 does not include the factor 11 required for 99, 999 is not divisible by 99.
3. The first number has prime factorization 2 × 3 × 7 and the second number has prime factorization 3 × 7 × 11. Are they co-prime? Does one of them divide the other?
Solution:
The numbers share the common factors 3 and 7. So they are not co-prime since neither number contains all the factors of the other, neither can divide the other.
4. Guna says, “Any two prime numbers are co-prime”. Is he right?
Solution:
Yes, Guna is right. Any two prime numbers are co-prime as they do not have common factor other than 1 which means they are always co-prime. For example, 2 and 3, 5 and 7, 11 and 13.
(Page 124)
Find numbers between 330 and 340 that are divisible by 4. Also, find numbers between 1730 and 1740, and 2030 and 2040, that are divisible by 4. What do you observe?
Solution:
Numbers divisible by 4-:
Between 330 and 340 : 332, 336 and 340.
Between 1730 and 1740 : 1732, 1736 and 1740.
Between 2030 and 2040 :2032, Z036 and 2040.
Is 8536 divisible by 4?
Solution:
Yes, 8536 is divisible by 4.
We can check this by dividing the last two digits (36) by 4. Since 36 is divisible by 4, the
entire number 8536 is divisible by 4.
Consider these statements:
a. Only the last two digits matter when deciding if a given number is divisible by 4.
b. If the number formed by the last two digits is divisible by 4, then the original number is divisible by 4.
c. If the original number is divisible by 4, then the number formed by the last two digits is divisible by 4.
Do you agree? Why or why not?
Solution:
a. Only the last two digits matter when deciding if a given number is divisible by 4. True Because if the number formed by the last two digits is divisible by 4, the entire number is divisible by 4.
b. If the number formed by the last two digits is divisible by 4, then the original number is divisible by 4. True Because this is the rule of divisibility by 4.
c. If the original number is divisible by 4, then the number formed by the last two digits is divisible by 4. True Because if a number is divisible by 4, its last two digits will always form a number that is divisible by 4.
Figure it Out (Page 125, 126)
1. 2024 is a leap year (as February has 29 days). Leap years occur in the years that are multiples of 4, e×cept for those years that are evenly divisible by 100 but not 400.
(a) From the year you were born till now, which years were leap years?
(b) From the year 2024 till 2099, how many leap years are there?
Solution:
(a) From the year 2010 till 2024, there are 4 leap years. 2012, 2016, 2020 and 2024.
(b) The leap years from 2024 and 2099 are:
2024, 2028, 2032, 2036, 2040, 2044, 2048, 2052, 2056, 2060, 2064, 2068, 2072, 2076,, 2080, 2084, 2088, 2092, 2096.
Hence, there are 19 leap years from 2024 till 2099.
2. Find the largest and smallest 4-digit numbers that are divisible by 4 and are also palindromes.
Solution:
Largest 4-digit number divisible by 4 and is also palindrome- 8888
Smallest 4-digit number divisible by 4 and is also palindrome- 2112.
3. Explore and find out if each statement is always true, sometimes true or never true. You can give examples to support your reasoning.
(a) Sum of two even numbers gives a multiple of 4.
Solution:
Sometimes true. Sum of any two even numbers is not always divisible by 4. For example, 6 + 4 = 10 which is not divisible by 4 whereas 2+2 = 4 which is divisible of 4.
(b) Sum of two odd numbers gives a multiple of 4.
Solution:
Sometimes true. Sum of two odd numbers can indeed be even but not necessarily a multiple of 4. For example, 1 + 5 = 6 which is not a multiple of 4 whereas 1+3 = 4, which is a multiple of 4. Similarly 7 + 5 = 12, which is a multiple of 4.
4. Find the remainders obtained when each of the following numbers are divided by
(i) 10
(ii) 5
(iii) 2.
78, 99, 173, 572, 980, 1111, 2345
Solution:
Here we have to divide 78 by 10, 5 and
2 then
5. The teacher asked if 14560 is divisible by all of 2, 4, 5, 8 and 10. Guna checked for divisibility of 14560 by only two of these numbers and then declared that it was also divisible by all of them. What could those two numbers be?
Solution:
If a number is divisible by 8, it will automatically be divisible by 4.
If a number is divisible by 10, it is also divisible by 2 and 5. Therefore, checking divisibility by 8 and 10 confirms divisibility by all other numbers (2, 4, 5).
Thus, the pair of numbers that Guna could check to determine that 14560 is divisible by all of 2, 4, 5, 8, and 10 is: 8 and 5.
6. Which of the following numbers are divisible by all of 2, 4, 5, 8 and 10: 572, 2352, 5600, 6000, 77622160?
Solution:
5600, 6000, 77622160
7. Write two numbers whose product is 10000. The two numbers should not have 0 as the units digit.
Solution:
We need to write factors of 10000.
10000= 10 × 10 × 10 × 10
= 2 × 5 × 2 × 5 × 2 × 5 × 2 × 5
So, 2 × 2 × 2 × 2 = 16 and 5 × 5 × 5 × 5 = 625.
Hence, 16 and 625 are the two numbers whose product is 10000.

nice website
Hi, I just wanted the activities of this chapter, but as there are so many questions, I can’t find the activities…
I recommend that, you can make another section for all the activities of the chapter…