Solutions For All Chapters – Maths Class 6 Ganita Prakash
Figure it out (Page 57, 58)
1. Colour or mark the supercells in the table below.
Solution:
2. Fill the table below with only 4-digit numbers such that the supercells are exactly the coloured cells.
Solution:
3. Fill the table below such that we get as many supercells as possible. Use numbers between 100 and 1000 without repetitions.
Solution:
4. Out of the 9 numbers, how many supercells are there in the table above?
Solution: Out of 9 numbers, there are 5 supercells in the above table.
5. Find out how many supercells are possible for different numbers of cells.
Do you notice any pattern? What is the method to fill a given table to get the maximum number of supercells? Explore and share your strategy.
Solution:
If there are n odd cells then number of supercells = n+1/2
If there are n even cells then number of supercells = n/2
Yes, there is a pattern. Alternate cells can be supercells.
Method to fill a given table to get the maximum number of supercells.
- Make first cell as supercell. After that each alternate cell is to be made supercell.
- No consecutive cells can be supercell except in case of 4 cells because then first and fourth cell can be supercell.
6. Can you fill a supercell table without repeating numbers such that there are no supercells? Why or why not?
Solution:
No, it is not possible to fill a supercell table without repeating numbers such that there are no supercells.
As there are two cases:
Case I: If we fill the cells in descending order then the first cell be supercell.
Case II: If we fill the cells in ascending order then the last cell will be supercell.
If we don’t follow any order, then there will definitely at least one supercell.
7. Will the cell having the largest number in a table always be a supercell? Can the cell having the smallest number in a table be a supercell Why or why not?
Solution:
No, the cell with the largest number in a table is not always a supercell. A supercell means it should be larger than all its neighboring cells. If any of its neighbors have the same or a bigger number, it won’t be a supercell, even if it is the largest number in the table.
Similarly, the smallest number cannot be a supercell. A supercell has to be bigger than all its neighbors. Since it’s the smallest, it can’t be bigger than any neighboring numbers, so it can’t be a supercell.
8. Table in which the cell having the second largest number 750 is not a supercell:
Solution:
| 800 | 750 | 500 | 300 | 450 | 200 | 700 | 470 |
9. Table in which the cell having the second largest number 751 is not a supercell but the second smallest number 250 is a supercell:
| 800 | 751 | 500 | 550 | 450 | 300 | 200 | 250 |
Intext Question (Page 58)
Complete Table 2 with 5-digit numbers whose digits are ‘1’, ‘0’, ‘6’. ‘3’, and ‘9’ in some order. Only a coloured cell should have a number greater than all its neighbours.
Solution:
| 96,310 | 96,301 | 36,109 | 63,109 |
| 10,369 | 13,609 | 60,319 | 19,306 |
| 10,936 | 36,910 | 60,193 | 39,106 |
| 10,369 | 10,963 | 10,639 | 39,610 |
The biggest number in the table is 96, 310.
The smallest even number in the table is 10,936.
The smallest number greater than 50,000 in the table is 60,193.
Figure it out (Page 59)
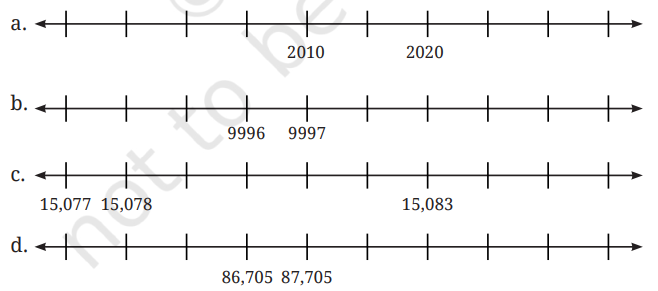
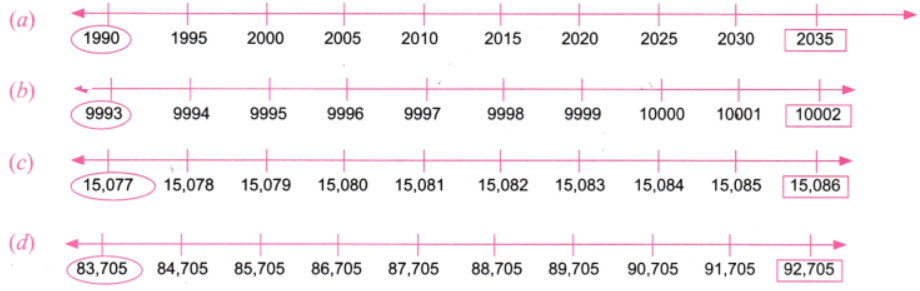
Identify the numbers marked on the number lines below, and label the remaining positions.
Put a circle around the smallest number and a box around the largest number in each of the sequences above.
Answer:
Figure it out (Page 60)
1. Digit sum 14
- a. Write other numbers whose digits add up to 14.
- b. What is the smallest number whose digit sum is 14?
- c. What is the largest 5-digit whose digit sum is 14?
- d. How big a number can you form having the digit sum 14? Can you make an even bigger number?
Solution:
(a) Some numbers whose digits add up to 14 are:
59, 68, 77, 86, 95, 149, 158, 167, 176, 185, 194, 239, 248, 257, 266, 275, 281, 293
(b) The smallest number whose digit sum is 14 = 59.
(c) The largest 5 digit number containing 0 whose digit sum is 14 = 95,000.
The largest 5 digit number not containing 0 whose digit sum is 14 = 92,111.
(d) A very big number having the digit sum 14 can be made. e.g. 95000000000000.
Yes, we can make even bigger number e.g. 9500000000000000000000.
2. Find out the digit sums of all the numbers from 40 to 70. Share your observations with the class.
Solution:
Digit Sums from 40 to 70:
| Number | Digit Sum | Number | Digit Sum |
|---|---|---|---|
| 40 | 4 | 55 | 10 |
| 41 | 5 | 56 | 11 |
| 42 | 6 | 57 | 12 |
| 43 | 7 | 58 | 13 |
| 44 | 8 | 59 | 14 |
| 45 | 9 | 60 | 6 |
| 46 | 10 | 61 | 7 |
| 47 | 11 | 62 | 8 |
| 48 | 12 | 63 | 9 |
| 49 | 13 | 64 | 10 |
| 50 | 5 | 65 | 11 |
| 51 | 6 | 66 | 12 |
| 52 | 7 | 67 | 13 |
| 53 | 8 | 68 | 14 |
| 54 | 9 | 69 | 15 |
| 70 | 7 |
3. Calculate the digit sums of 3-digit numbers whose digits are consecutive (for example, 345). Do you see a pattern? Will this pattern continue?
Answer:
If we take numbers in reverse order, sum of digits will remain same.
Yes, we observe a pattern.
i. e. (first number + 1) × 3 = digit sum.
Intext Question (Page 60)
Question 1. Among the numbers 1-100, how many times will the digit ‘7’occur?
Solution: The total count of 7 that we get is 20.
Question 2. Among the numbers 1-1000, how many times will the digit ‘7’occur?
Solution: The number of times 7 will be written when listing the numbers from 1 to 1000 is 300.
Intext Question (Page 61)
All palindromes using 1, 2, 3
1. The numbers 121, 313, 222 are some examples of palindromes using the digits ‘1’, ‘2’, 3’.
Write all possible 3-digit palindromes using these digits.
Solution:
All possible 3-digit palindromes using only the digits ‘1’, ‘2’, and ‘3’ are:
- 111, 121, 131
- 212, 222, 232
- 313, 323, 333
In total, there are 9 possible 3-digit palindromes using these digits.
Explore
Will reversing and adding numbers repeatedly, starting with a 2-digit number, always give a palindrome? Explore and find out.*
Solution :
You can create a palindrome by following these steps:
- Start with any 2-digit number.
- Reverse the digits of that number.
- Add the original number and the reversed number.
- If the result is a palindrome, you’re done. If not, repeat the process with the result.
Examples:
- Example 1:
- Take 56. Its reverse is 65.
- Add: 56 + 65 = 121 (palindrome).
- Example 2:
- Take 29. Its reverse is 92.
- Add: 29 + 92 = 121 (palindrome).
- Example 3:
- Take 84. Its reverse is 48.
- Add: 84 + 48 = 132 (not a palindrome).
- Reverse 132 (becomes 231).
- Add: 132 + 231 = 363 (palindrome).
Most times, this process will eventually give you a palindrome.
Puzzle time (Page 62)
I am a 5-digit palindrome.
I am an odd number.
My ‘t’ digit is double of my ‘u’ digit.
My ‘h’ digit is double of my ‘t’ digit.
Who am I? _________________
Solution: 12421
Explore (Page 63)
Take different 4-digit numbers and try carrying out these steps. Find out what happens. Check with your friends what they got.
Solution:
For example, take the 4-digit number 3524:
- Arrange in descending order: 5432 (A)
- Arrange in ascending order: 2345 (B)
- Subtract: 5432 – 2345 = 3087 (C)
Repeat the process with 3087:
- Descending order: 8730
- Ascending order: 0378
- Subtract: 8730 – 0378 = 8352
Repeat again:
- Descending order: 8532
- Ascending order: 2358
- Subtract: 8532 – 2358 = 6174
(Page 64)
Try and find out all possible times on a 12-hour clock of each of these types.
Manish has his birthday on 20/12/2012 where the digits ‘2’, ‘0’, ‘1’, and ‘2’ repeat in that order.
Solution:
Possible times: 12:00:21, 10:22:01, 11:22:11
Find some other dates of this form from the past.
His sister Meghana has her birthday on 11/02/2011 where the digits read the same from left to right and from right to left.
Other dates where the same digits repeat: 21/02/2012, 12/02/2012, 02/12/2010, 10/02/2012
Find all possible dates of this form from the past.
Palindromic dates in the past: 11/02/2011, 02/02/2020, 10/02/2001, 12/02/2021
But, will any year’s calendar repeat again after some years? Will all dates and days in a year match exactly with that of another year?
Yes, calendars repeat because of the way our calendar system works with leap years and the cycle of days in a week. A year’s calendar usually repeats after 6, 11, or 28 years, depending on whether it’s a leap year or not.
For example:
- The 2023 calendar will be the same again in 2034 (after 11 years).
- The 2024 calendar (a leap year) will repeat in 2052 (after 28 years).
However, not all dates and days will line up perfectly every time, especially in leap years.
Figure it out (Page 64, 65)
Question 1. Pratibha uses the digits ‘4‘7’, ‘3’and ‘2’ and makes the smallest and largest 4-digit numbers with them: 2347 and 7432. The difference between these two numbers is 7432 – 2347 = 5085. The sum of these two numbers is 9779. Choose 4-digits to make:
(a) the difference between the largest and smallest numbers greater than 5085.
(b) the difference between the largest and smallest numbers less than 5085.
(e) the sum of the largest and smallest numbers greater than 9779.
(d) the sum of the largest and smallest numbers less than 9779.
Solution: Working with 4-digit numbers:
a. Let’s use the digits 9, 8, 1, 0:
Largest number: 9810
Smallest number: 0189 (or simply 189)
Difference: 9810 – 189 = 9621
Since 9621 is greater than 5085, this works.
b. Let’s use the digits 5, 4, 2, 1:
Largest number: 5421
Smallest number: 1245
Difference: 5421 – 1245 = 4176
Since 4176 is less than 5085, this works.
c. Let’s use the digits 9, 8, 7, 3:
Largest number: 9873
Smallest number: 3789
Sum: 9873 + 3789 = 13662
Since 13662 is greater than 9779, this works.
d. Let’s use the digits 4, 3, 2, 0:
Largest number: 4320
Smallest number: 0234 (or simply 234)
Sum: 4320 + 234 = 4554
Since 4554 is less than 9779, this works.
Question 2. What is the sum of the smallest and largest 5-digit palindrome? What is their difference?
Solution:
- Smallest 5-digit palindrome: 10001.
- Largest 5-digit palindrome: 99999.
- Sum: 10001 + 99999 = 110000.
- Difference: 99999 – 10001 = 89998.
3. The time now is 10:01. How many minutes until the clock shows the next palindromic time? What about the one after that?
Solution:
The next palindromic time after 10:01 is 11:11.
The difference between 10:01 and 11:11 is 1 hour and 10 minutes, which equals 70 minutes.
The next palindromic time after 11:11 is 12:21.
The difference between 11:11 and 12:21 is also 1 hour and 10 minutes, or 70 minutes.
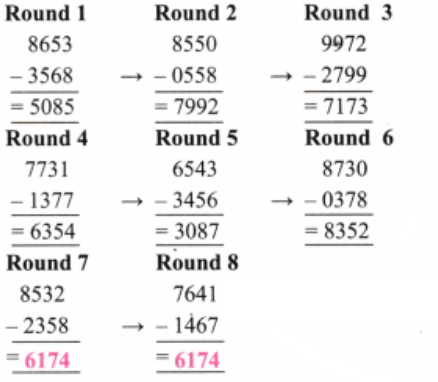
4. How many rounds does the number 5683 take to reach the Kaprekar constant?
Solution:
Figure it out (Page 66)
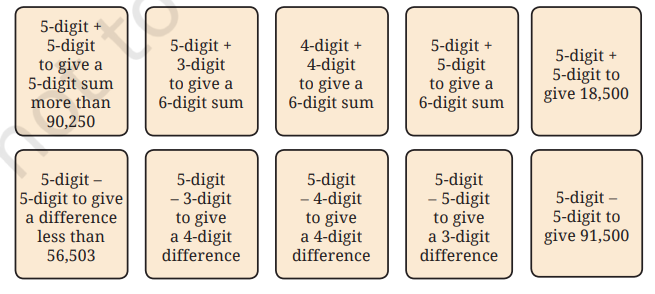
1. Write an example for each of the below scenarios whenever possible.
Could you find examples for all the cases? If not, think and discuss what could be the reason. Make other such questions and challenge your classmates.
Answer:
1. Let’s go through the scenarios presented and provide examples for each:
- 5-digit + 5-digit to give a 5-digit sum more than 90,250:
Example: 50,000 + 45,000 = 95,000 - 5-digit + 3-digit to give a 6-digit sum:
Example: 99,000 + 123 = 99,123 - 4-digit + 4-digit to give a 6-digit sum:
This seems tricky because two 4-digit numbers added together can’t give a 6-digit number. The highest possible sum of two 4-digit numbers is 99,999 + 9,999 = 109,998 (a 5-digit sum). - 5-digit + 5-digit to give a 6-digit sum:
Example: 75,000 + 30,000 = 105,000 - 5-digit + 5-digit to give 18,500:
Example: 9,500 + 9,000 = 18,500 - 5-digit — 5-digit to give a difference less than 56,503:
Example: 90,000 — 50,000 = 40,000 - 5-digit — 3-digit to give a 4-digit difference:
Example: 10,000 — 500 = 9,500 - 5-digit — 4-digit to give a 4-digit difference:
Example: 20,000 – 9,000 = 11,000 - 5-digit — 5-digit to give a 3-digit difference:
Example: 10,500 — 10,200 = 300 - 5-digit — 5-digit to give 91,500:
Example: 99,500 – 8,000 = 91,500
Discussion:
We found examples for all the cases, except for adding two 4-digit numbers to get a 6-digit sum, which is impossible. The largest sum is still a 5-digit number.
Additional challenges for classmates:
- Find a 5-digit number and subtract a 3-digit number to get a 5-digit difference.
- Find a 4-digit number that, when added to a 3-digit number, gives a sum less than 2,000.
- Find two 4-digit numbers that sum to exactly 15,000.
2. Always, Sometimes, Never?
Below are some statements. Think, explore and find out if each of the statements is ‘Always true’, ‘Only sometimes true’, or ‘Never true’. Why do you think so? Write your reasoning and discuss this with the class.
- 5-digit number + 5-digit number gives a 5-digit number
- 4-digit number + 2-digit number gives a 4-digit number
- 4-digit number + 2-digit number gives a 6-digit number
- 5-digit number — 5-digit number gives a 5-digit number
- 5-digit number — 2-digit number gives a 3-digit number
Answer:
Checking whether always, sometimes, or never:
- 5-digit number + 5-digit number gives a 5-digit number
- Sometimes true
If both numbers are small, like 10,000 + 10,000 = 20,000, the result is a 5-digit number. But with large numbers, like 90,000 + 90,000 = 180,000, it becomes a 6-digit number.
- Sometimes true
- 4-digit number + 2-digit number gives a 4-digit number
- Sometimes true
A small 4-digit number, like 1,000 + 50 = 1,050, gives a 4-digit result. But if the 4-digit number is large, like 9,999 + 99 = 10,098, the result is a 5-digit number.
- Sometimes true
- 4-digit number + 2-digit number gives a 6-digit number
- Never true
Even the largest 4-digit number (9,999) and the largest 2-digit number (99) only give a 5-digit result (10,098), not 6 digits.
- Never true
- 5-digit number – 5-digit number gives a 5-digit number
- Sometimes true
If the numbers are close in value, like 90,000 – 50,000 = 40,000, the result is a 5-digit number. But if they’re far apart, like 10,000 – 9,999 = 1, the result is smaller.
- Sometimes true
- 5-digit number – 2-digit number gives a 3-digit number
- Sometimes true
A large 5-digit number, like 10,000 – 9 = 9,991, still gives a 5-digit result. But if the 5-digit number is small, like 1,001 – 9 = 992, it becomes a 3-digit number.
- Sometimes true
Page 67
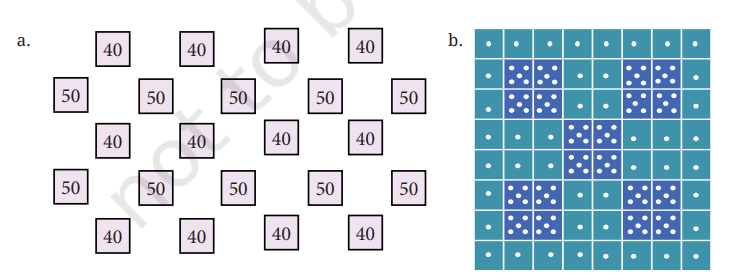
Share and discuss in class the different methods each of you used to solve these questions.
Answer:
Pattern A
- The numbers alternate between 40 and 50.
- Count the number of 40s and 50s to quickly find the sum.
- 40s: 12 numbers
- 50s: 9 numbers
- Sum: (12 × 40) + (9 × 50) = 480 + 450 = 930
Pattern B
- This pattern uses dice with dots.
- Count the dots and multiply to find the sum.
- Total dots: 44
- Dice with 5 dots: 20
- Sum: (44 × 1) + (20 × 5) = 44 + 100 = 144
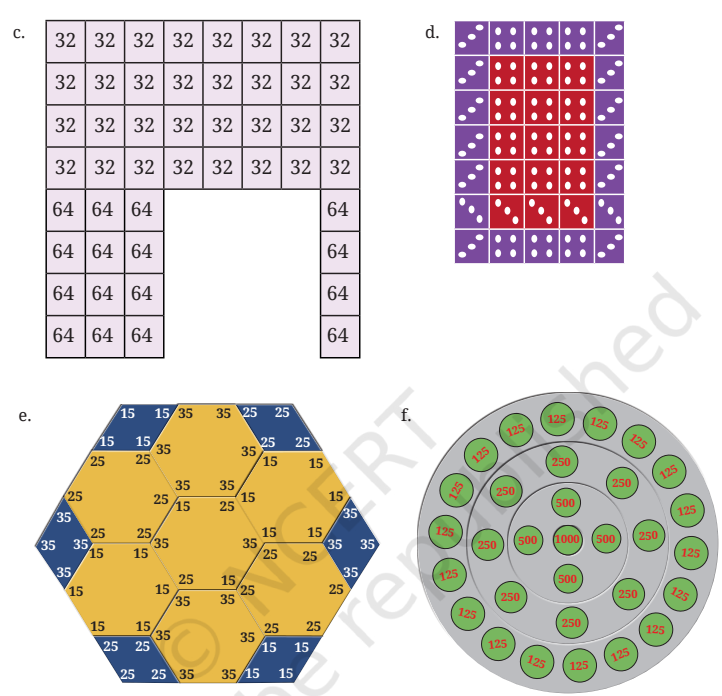
Pattern C
- Rows contain 32s and 64s. Count each and multiply.
- 32s: 32 numbers
- 64s: 16 numbers
- Sum: (32 × 32) + (16 × 64) = 1024 + 1024 = 2048
Pattern D
- Similar to a dice grid. Count the dice with 3 and 4 dots.
- Dice with 3 dots: 17
- Dice with 4 dots: 18
- Sum: (17 × 3) + (18 × 4) = 51 + 72 = 123
Pattern E
- Hexagon shape with numbers 15, 25, and 35. Count and multiply.
- 15s: 12 numbers
- 25s: 6 numbers
- 35s: 6 numbers
- Sum: (12 × 15) + (6 × 25) + (6 × 35) = 180 + 150 + 210 = 540
Pattern F
- Circular pattern with numbers like 125, 250, 500, and 1000. Count each and multiply.
- 125s: 12 numbers
- 250s: 8 numbers
- 500s: 5 numbers
- 1000s: 1 number
- Sum: (12 × 125) + (8 × 250) + (5 × 500) + (1 × 1000) = 1500 + 2000 + 2500 + 1000 = 7000
Methods Discussion
- Adding one by one: Works but is slow when there are many numbers.
- Using multiplication: Faster when numbers repeat.
Estimate the answer (Page 70)
Try to guess within 30 seconds. Check your guess with your friends.
1. Number of words in your maths textbook:
a. More than 5000
b. Less than 5000
Solution :
- Number of words in my maths textbook: More than 5000 because Most textbooks in Class 6 contain many explanations, exercises, and examples, likely exceeding 5000 words.
2. Number of students in your school who travel to school by bus:
a. More than 200
b. Less than 200
Solution :
Number of students in my school who travel by bus: More than 200. In a large school, many students rely on buses, especially if the school serves a wide area.
3. Roshan wants to buy milk and 3 types of fruit to make fruit custard for 5 people. He estimates the cost to be ₹ 100. Do you agree with him? Why or why not?
Solution : No, because the cost can exceed ₹100 depending on the quantity and type of fruits like apples, grapes, or bananas.
4. Estimate the distance between Gandhinagar (in Gujarat) to Kohima (in Nagaland).
[Hint: Look at the map of India to locate these cities.]
Solution : Distance is Approx. 2500-3000 km. These cities are on opposite sides of India, making it a long-distance journey.
5. Sheetal is in Grade 6 and says she has spent around 13,000 hours in school till date. Do you agree with her? Why or why not?
Solution : No, likely closer to 7,200 hours. On average, a school day is 6 hours, with about 200 days in a year. Over 6 years, that totals around 7,200 hours.
6. Earlier, people used to walk long distances as they had no other means of transport. Suppose you walk at your normal pace. Approximately how long would it take you to go from:
a. Your current location to one of your favourite places nearby.
b. Your current location to any neighbouring state’s capital city.
c. The southernmost point in India to the northernmost point in India
Solution :
Walking estimations:
- To a nearby favorite place: 10-30 minutes.
- To a neighbouring state’s capital: Several days to weeks.
- From the southernmost to the northernmost point of India (Kanyakumari to Kashmir): It would take months.
Figure it out (Page 72, 73)
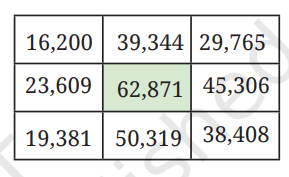
1. There is only one supercell (number greater than all its neighbours) in this grid. If you exchange two digits of one of the numbers, there will be 4 supercells. Figure out which digits to swap.
Solution:
If we swap first and last digit of central number 62,871, we get desired result.
| 16,200 | 39,344 | 29,765 |
| 23,609 | 21,876 | 45,306 |
| 19,381 | 50,319 | 38,408 |
2. How many rounds does your year of birth take to reacall the Kaprekar constant?
Solution:
My year of birth is 2013.
Round 1
Descending order: 3210
Ascending order: 0123
Subtract: 3210 – 0123 = 3087
Round 2
Descending order: 8730
Ascending order: 0378
Subtract: 8730 – 0378 = 8352
Round 3
Descending order: 8532
Ascending order: 2358
Subtract: 8532 – 2358 = 6174
After 3 rounds, I reach the Kaprekar constant 6174.
3. We are the group of 5-digit numbers between 35,000 and 75,000 such that all of our digits are odd. Who is the largest number in our group? Who is the smallest number in our group? Who among us is the closest to 50,000?
Solution:
Possible Odd Digits
- Digits: 1, 3, 5, 7, 9
- Largest number: 73,999
- Smallest number: 35,111
- Closest to 50,000: 51,111
4. Estimate the number of holidays you get in a year including weekends, festivals and vacation. Then try to get an exact number and see how close your estimate is.
Solution:
Holidays in a Year
- Weekends: 104 days
- Summer vacation: 50 days
- Winter vacation: 12 days
- Festival holidays: 12 days
- Public holidays: 4 days
Total estimated holidays = 104 + 50 + 12 + 12 + 4 = 182 days.
5. Estimate the number of litres a mug, a bucket and an overhead tank can hold.
Solution:
As per My House
- Mug: 0.25 – 0.3 litres
- Bucket: 20 litres
- Overhead tank: 1,000 litres
6. Write one 5-digit number and two 3-digit numbers such that their sum is 18,670.
Solution:
- 5-digit number: 12,345
- 3-digit number 1: 789
- 3-digit number 2: 536
Sum: 12,345 + 789 + 536 = 18,670
7. Choose a number between 210 and 390. Create a number pattern similar to those shown in Section 3.9 that will sum up to this number.
Solution:
Simple Addition Pattern
We can create a simple addition pattern using a series of repeated numbers:
- 40 + 40 + 40 + 50 + 50 + 50 + 30 = 300
- Pattern: 40 repeated 3 times, 50 repeated 3 times, and then a 30.
- 40 + 40 + 40 = 120
- 50 + 50 + 50 = 150
- 120 + 150 + 30 = 300
Another method:
- 50 + 50 + 50 + 50 + 50 + 50 = 300
- This pattern repeats the number 50 six times to reach the sum of 300.
We can also modify the pattern:
- 40 + 60 + 50 + 70 + 30 + 50 = 300
8. Recall the sequence of Powers of 2 from Chapter 1, Table 1. Why is the Collatz conjecture correct for all the starting numbers in this sequence?
Solution:
The square of power of 2 is :
1,2,4, 8, 16, 32, 64
Let’s take the number’ 64 as per Collatz Conjecture
- 64 is even, divide by 2 = 32
- 32 is even, divide by 2 = 16
- 16 is even, divide by 2 = 8
- 8 is even, divide by 2 = 4
- 4 is even, divide by 2 = 2
- 2 is even, divide by 2 = 1
Hence Collatz conjecture is correct in all numbers in the power of 2 sequence.
As it is power of 2, and in Collatz Conjecture even number is divided by 2 in each step.
9. Check if the Collatz Conjecture holds for the starting number 100.
Solution:
- 100 is even, divide by 2 =50
- 50 is even, divide by 2 = 25
- 25 is odd, so multiply by 3 and add 1 → 76
- 76 is even, divide by 2 = 38
- 38 is even, divide by 2 = 19
- 19 is odd, so multiply by 3 and add 1 → 58
- 58 is even, divide by 2 = 29
- 29 is odd, so multiply by 3 and add 1 → 88
- 88 is even, divide by 2 = 44
- 44 is even, divide by 2 = 22
- 22 is even, divide by 2 = 11
- 11 is odd, so multiply by 3 and add 1 → 34
- 34 is even, divide by 2 = 17
- 17 is odd, so multiply by 3 and add 1 → 52
- 52 is even, divide by 2 = 26
- 26 is even, divide by 2 = 13
- 13 is odd, so multiply by 3 and add 1 → 40
- 40 is even, divide by 2 = 20
- 20 is even, divide by 2 = 10
- 10 is even, divide by 2 = 5
- 5 is odd, so multiply by 3 and add 1 → 16
- 16 is even, divide by 2 = 8
- 8 is even, divide by 2 = 4
- 4 is even, divide by 2 = 2
- 2 is even, divide by 2 = 1
Yes, the Collatz conjecture holds for the starting number 100.
10. Starting with 0, players alternate adding numbers between 1 and 3. The first person to reach 22 wins. What is the winning strategy now?
Solution:
Game Rules
- Start at 0.
- You and a friend take turns adding 1, 2, or 3.
- The first to make exactly 22 wins.
Who Wins and How?
To win, you want to say 22. Let’s figure out how to get there by thinking backward.
- At 22: You win if you say 22!
- At 19, 20, or 21: If you say these, your friend can add 3, 2, or 1 to hit 22 and win.
- At 18: If you say 18, your friend can only say:
- 19 (18 + 1) → you add 3 to say 22 and win.
- 20 (18 + 2) → you add 2 to say 22 and win.
- 21 (18 + 3) → you add 1 to say 22 and win. So, 18 is a bad spot for your friend because you can always win from there.
- At 14: If you say 14, your friend says:
- 15 (14 + 1) → you add 3 to say 18.
- 16 (14 + 2) → you add 2 to say 18.
- 17 (14 + 3) → you add 1 to say 18. So, 14 is a good spot for you because you can reach 18.
- At 10: If you say 10, your friend says:
- 11 (10 + 1) → you add 3 to say 14.
- 12 (10 + 2) → you add 2 to say 14.
- 13 (10 + 3) → you add 1 to say 14. So, 10 is a bad spot for your friend.
- At 6: If you say 6, your friend says:
- 7 (6 + 1) → you add 3 to say 10.
- 8 (6 + 2) → you add 2 to say 10.
- 9 (6 + 3) → you add 1 to say 10. So, 6 is a bad spot for your friend.
- At 2: If you say 2, your friend says:
- 3 (2 + 1) → you add 3 to say 6.
- 4 (2 + 2) → you add 2 to say 6.
- 5 (2 + 3) → you add 1 to say 6. So, 2 is a bad spot for your friend.
- At 0 (the start): You can say:
- 1 (0 + 1) → your friend can say 2, and you’re in trouble.
- 2 (0 + 2) → your friend is at 2, a bad spot for them!
- 3 (0 + 3) → your friend can say 6, and you’re in trouble.
If you start by saying 2, your friend is stuck in a bad spot. Then, you keep making sure they land on 6, 10, 14, or 18.
The Winning Plan
- Who wins? The first player can always win.
- What to say? Say these numbers: 2, 6, 10, 14, 18, 22.
- How?
- Start by adding 2 to say 2.
- After your friend’s turn, add 1, 2, or 3 to say 6, then 10, then 14, then 18, and finally 22.
For example:
- You say 2.
- If your friend says 4, you add 2 to say 6.
- If they say 7, you add 3 to say 10.
- If they say 12, you add 2 to say 14.
- Keep going until you say 22 and win!








Easy way and correct answer 👌
Thanks for your reply 👍
This is very easy for children to learn
this platform is really helpfull to children ,
especially like these difficult books . keep it
up and help each and every child. thank you
Get easy and clear solutions for Class 6 Perfect for quick learning! ✅