Solutions For All Chapters – Maths Class 6 Ganita Prakash
Figure it out (Page 15, 16, 17)
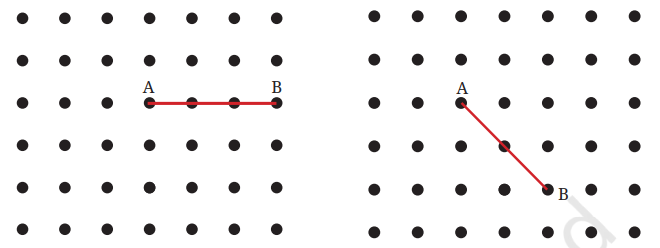
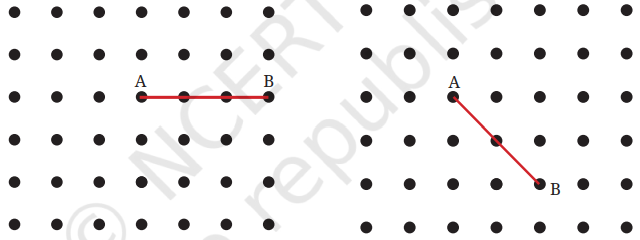
Question 1. Rihan marked a point on a piece of paper. How many lines can he draw that pass through the point?
Sheetal marked two points on a piece of paper. How many different lines can she draw that pass through both of the points?
Can you help Rihan and Sheetal find their answers?
Answer:
Infinite number of lines can be drawn to pass through a point in a plane.
One and only one line can be drawn to pass through two points.
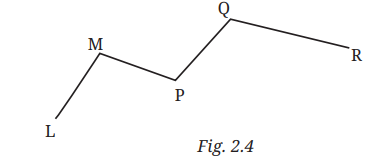
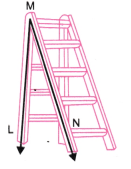
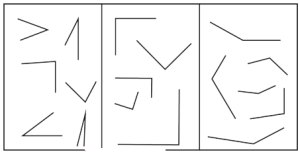
Question 2. Name the line segments in Fig.2.4 below. Which of the five marked points are on exactly one of the line segments? Which are on two of the line segments?
Answer:
Line segments in the given figure are LM, MP, PQ, and QR.
Points on exactly one line segment
- L: It is an endpoint of line segment LM.
- R: It is an endpoint of line segment QR.
Points on two line segments
- M: It is a point where two line segments, LM and MP, meet.
- P: It is a point where two line segments, MP a
- Q: It is a point where two line segments, PQ and QR, meet.
Result:
- Points on one line segment: L, R
- Points on two line segments: M, P, Q
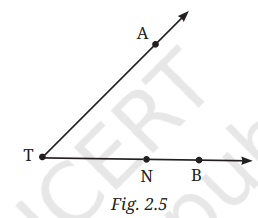
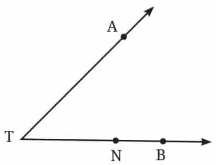
Question 3. Name the rays shown in Fig.2.5 below. Is T the starting point of each of these rays?
Answer:
In the given figure, there are two rays:
- Ray TA: This ray starts at point T and passes through point A, extending infinitely beyond A.
- Ray TB: This ray also starts at point T and passes through point B, extending infinitely beyond B.
So yes, T is the starting point of both rays.
Question 4. Draw a rough figure and write labels appropriately to illustrate each of the following:
a. OP and OQ meet at O.
b. XY and PQ intersect at point M.
c. Line l contains points E and F but not point D.
d. Point P lies on AB.
Answer:
a.
b.
c.
d.
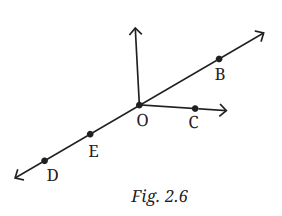
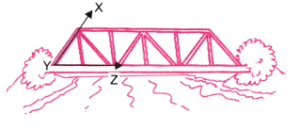
Question 5. In the figure 2.6, name:
a. Five points
b. A line
c. Four rays
d. Five line segments
Answer:
a. Five points: D, E, O, C, and B.
b. A line: BD.
c. Four rays: OD, OB, OC, and ED.
d. Five line segments: DE, EO, OC, BO, and DO.
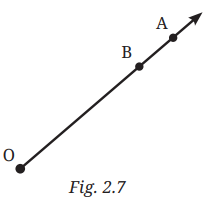
Question 6. Here is a ray OA (Fig. 2.7). It starts at O and passes through the point A. It also passes through the point B.
a. Can you also name it as OB ? Why?
b. Can we write OA as AO? Why or why not?
Answer:
a. Yes, the ray can also be named OB because the ray OA passes through point B as well. Rays are named starting from the initial point and passing through any other point on the ray. Since the ray starts at O and passes through both B and A, it can be named OB.
b. No, we cannot write OA as AO because rays are directional. The ray starts at point O and extends through A, so OA indicates the direction from O to A. Writing it as AO would imply the ray starts at A and goes towards O, which is incorrect in this context because O is the starting point.
Figure it out (Page 19, 20, 21)
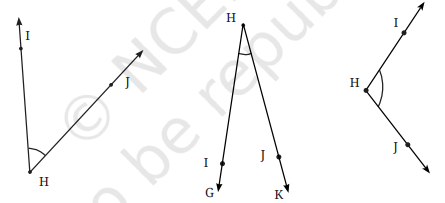
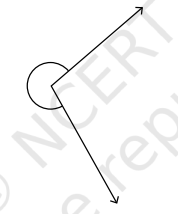
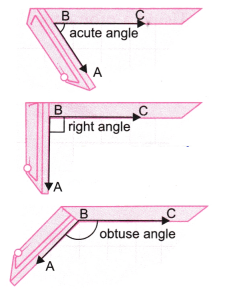
1. Can you find the angles in the given pictures? Draw the rays forming any one of the angles and name the vertex of the angle.
Answer:
The name of the vertex of ∠BDC is D.
The name of the vertex of ∠PQR is Q.
The name of the vertex of ∠LMN is M.
The name of the vertex of ∠XYZ is Y.
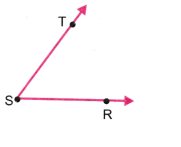
2. Draw and label an angle with arms ST and SR.
Answer:
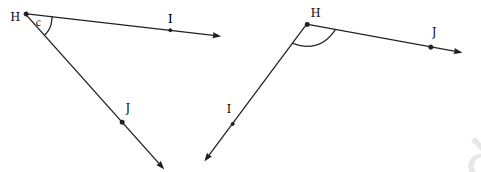
3. Explain why ∠APC cannot be labelled as ∠P
Answer:
There are more than one angle at P, that is, ∠APB, ∠APC and ∠BPC. That is why it can’t be written as ∠APC as ∠P.
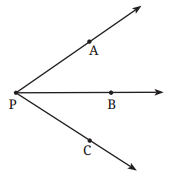
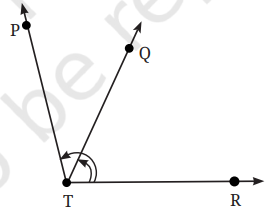
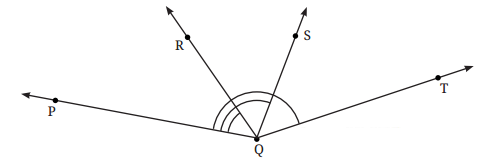
4. Name the angles marked in the given figure.
Answer:
The angles marked in the given figure are ∠RTQ and ∠RTP.
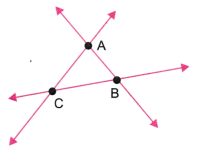
5. Mark any three points on your paper that are not on one line. Label them A, B, C. Draw all possible lines going through pairs of these points. How many lines do you get? Name them. How many angles can you name using A, B, C? Write them down, and mark each of them with a curve as in Fig. 2.9.
Answer:
We get three lines.
These are line AB, line BC and line CA.
Also, we get three angles.
These are ∠ABC, ∠BCA and ∠CAB.
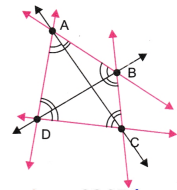
These are line AB, line BC, line CD, line DA, line AC and line BD.
Also, we get twelve angles.
These are ∠BAC; ∠CAD, ∠BAD, ∠ABD, ∠DBC, ∠ABC, ∠BCA, ∠ACD, ∠BCD, ∠CDB, ∠CDA, ∠BDA.
Figure it out (Page 23)
1. Fold a rectangular sheet of paper, then draw a line along the fold created. Name and compare the angles formed between the fold and the sides of the paper. Make different angles by folding a rectangular sheet of paper and compare the angles. Which is the largest and smallest angle you made?
Answer:
The angles formed with the line along the fold created are (∠ AEF), (∠BEF), (∠DFE), and (∠CFE), which are marked as 1, 2, 3, and 4. Out of these angles, (∠AEF) and (∠CFE) are the larger ones, whereas (∠BEF) and (∠DFE) are the smaller ones.
2. In each case, determine which angle is greater and why.
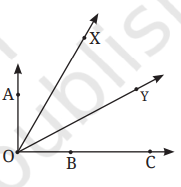
a. ∠AOB or ∠XOY
b. ∠AOB or ∠XOB
c. ∠XOB or ∠XOC
Discuss with your friends on how you decided which one is greater.
Answer:
a. (∠AOB > ∠XOY ), because (∠XOY ) is contained within ( ∠AOB ). It means (∠XOY ) is a part of (∠AOB ).
b. (∠AOB > ∠XOB ), because (∠XOB ) is contained within ( ∠AOB ). It means (∠XOB) is a part of (∠AOB ).
c. ( ∠XOB = ∠XOC ), because both angles are formed with the same rays.
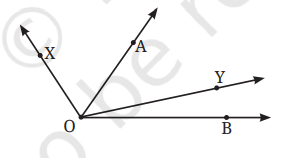
3. Which angle is greater: ∠XOY or ∠AOB? Give reasons.
Answer:
(∠XOB > ∠AOB ), because (∠AOB ) is contained within ( ∠XOB ). It means (∠AOB) is a part of (∠XOB ).
Figure it out (Page 29)
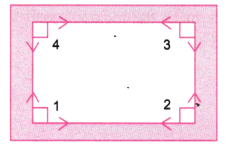
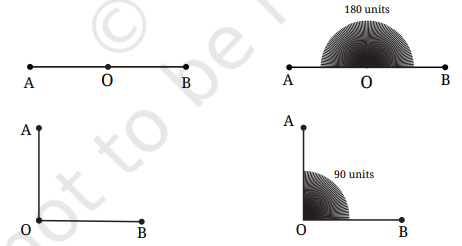
Question 1. How many right angles do the windows of your classroom contain? Do you see other right angles in your classroom?
Answer:
A window has 4 right angles.
∠1, ∠2, ∠3 and ∠4.
Yes. At comers of door. At comers of blackboard etc.
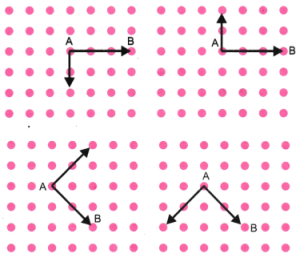
Question 2. Join A to other grid points in the figure by a straight line to get a straight angle. What are all the different ways of doing it?
Answer:
Question 3. Now join A to other grid points in the figure by a straight line to get a right angle. What are all the different ways of doing it?
Answer:
Figure it out (Page 31)
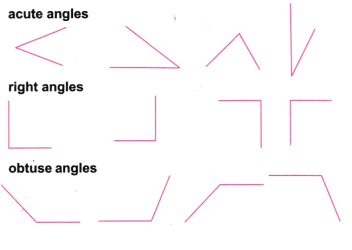
Question 1. Identify acute, right, obtuse and straight angles in the previous figures.
Answer:
Question 2. Make a few acute angles and a few obtuse angles. Draw them in different orientations.
Answer:
Question 3. Do you know what the words acute and obtuse mean? Acute means sharp and obtuse means blunt. Why do you think these words have been chosen?
Answer:
Word ‘acute’ means ‘sharp’. The vertex of the angle appears as a sharp tip.
Word ‘obtuse’ means ‘blunt’. The vertex of the angle appears as a blunt tip.
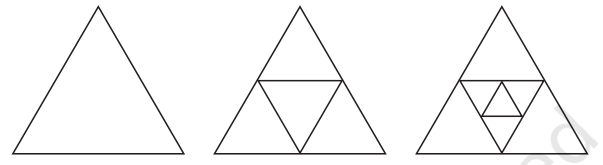
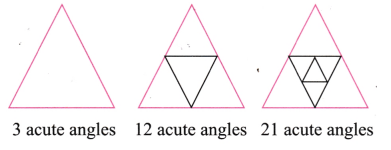
Question 4. Find out the number of acute angles in each of the figures below.
What will be the next figure and how many acute angles will it have? Do you notice any pattern in the numbers?
Answer:
Page 33
What is the measure of a straight angle in degrees? A straight angle is half of a full turn. As a full-turn is 360°, a half turn is 180°. What is the measure of a right angle in degrees? Two right angles together form a straight angle. As a straight angle measures 180°, a right angle measures 90°.
Answer: The measure of a straight angle in degree 180° and the measure of a right angle in degree is 90°.
Figure it out (Page 35)
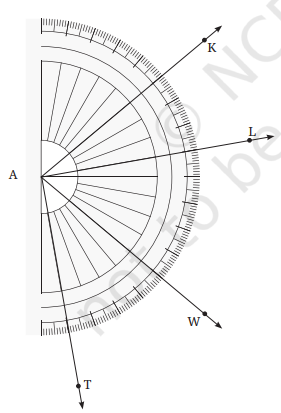
1. Write the measures of the following angles:
a. ∠ KAL
b. ∠WAL
c. ∠TAK
Answer:
(a) ∠KAL = 30°
(b) ∠WAL = 50°
(c) ∠TAK = 120°
Figure it out (Page 40 to 43)
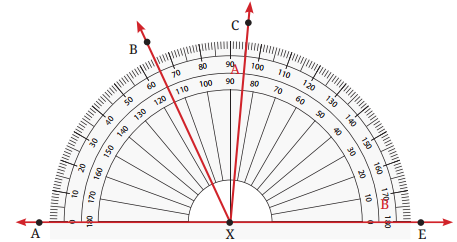
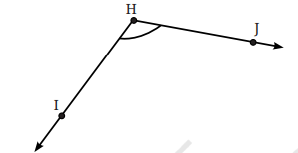
1. Find the degree measures of the following angles using your protractor.
Answer:
(a) ∠IHJ = 47°
(b) ∠IHJ = 24°
(c) ∠IHJ =110°
2. Find the degree measures of different angles in your classroom using your protractor.
Answer:
Angle at comer of blackboard = 90°
Angle at comer of desk = 90°
3. Find the degree measures for the angles given below. Check if your paper protractor can be used here!
Answer:
(a) ∠IHJ = 42°
(b) ∠IHJ =116°
Paper protractor cannot be used here.
4. How can you find the degree measure of the angle given below using a protractor?
Answer:
∠IHJ = 102°
5. Measure and write the degree measures for each of the following angles:
Answer:
(a) Measure of given angle is 78°
(b) Measure of given angle is 120°
(c) Measure of given angle is 58°
(d) Measure of given angle is 130°
(e) Measure of given angle is 127°
(f) Measure of given angle is 60°
6. Find the degree measures of ∠BXE, ∠CXE, ∠AXB and ∠BXC.
Answer:
(a) ∠BXE =115°
(b) ∠CXE = 85°
(c) ∠AXB = 65°
(d) ∠BXC = 30°
7. Find the degree measures of ∠PQR, ∠PQS and ∠PQT.
Answer:
(a) ∠PQR = 45°
(b) ∠PQS = 105°
(c) ∠PQT = 152°
Figure it out (Page 45 to 46)
What are the angles
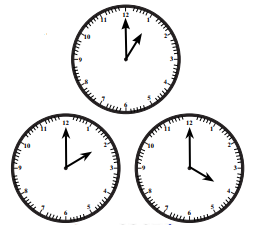
1. Angles in a clock:
(a) The hands of a clock make different angles at different times. At 1 o’clock, the angle between the hands is 30°. Why?
(b) What will be the angle at 2 o’clock? And at 4 o’clock? 6 o’clock?
(c) Explore other angles made by the hands of a clock.
Answer:
1. a. There are 12 numbers on a clock representing 12 hours. The total angle covered in 12 hours is 360°. So, the angle between two successive numbers = 360° ÷ 12 = 30°. That is why at 1 o’clock, the angle between the hands is 30°.
b. The angle at 2 o’clock = 60°
The angle at 4 o’clock = 120°
The angle at 6 o’clock = 180°
(c) The other angle make by hands
2. The angle of a door: Is it possible to express the amount by which a door is opened using an angle? What will be the vertex of the angle and what will be the arms of the angle?
Answer:
Yes, it is possible.
3. Vidya is enjoying her time on the swing. She notices that the greater the angle with which she starts the swinging, the greater is the speed she achieves on her swing. But where is the angle? Are you able to see any angle?
Answer:
Yes, an angle can be seen.
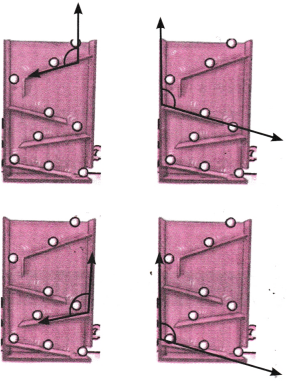
4. Here is a toy with slanting slabs attached to its sides; the greater the angles or slopes of the slabs, the faster the balls roll. Can angles be used to describe the slopes of the slabs?
Answer:
Greater the angle, greater the slope.
For each angle one arm is a side and one arm is the slope.
Figure it out (Page 49)
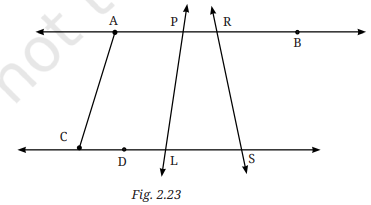
1. In Fig.2.23 below, list all the angles possible. Did you find them all? Now, guess the measures of all the angles. Then, measure the angles with a protractor. Record all your numbers in a table. See how close your guesses are to the actual measures.
Answer:
1. List of angles:
- ∠PAC
- ∠APD
- ∠DPS
- ∠LPR
- ∠PLS
- ∠ARP
- ∠PRS
- ∠RSL
- ∠ALC
Estimated measurements in degrees:
- ∠PAC: 120°
- ∠APD: 90°
- ∠DPS: 120°
- ∠LPR: 60°
- ∠PLS: 90°
- ∠ARP: 30°
- ∠PRS: 150°
- ∠RSL: 90°
- ∠ALC: 120°
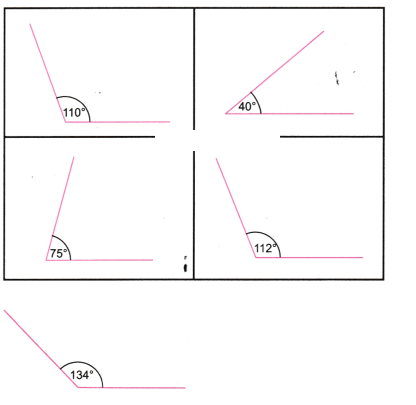
2. Use a protractor to draw angles having the following degree measures:
(a)110°
(b) 40°
(c) 75°
(d)1120
(e) 134°
Answer:
3. Draw an angle whose degree measure is the same as the angle given below:
Also, write down the steps you followed to draw the angle.
Answer:
Step 1. Measure the given angle (∠IHJ = 120°)
Step 2. Using a protractor draw ∠ABC = 120°
Figure it out (Page 53, 54)
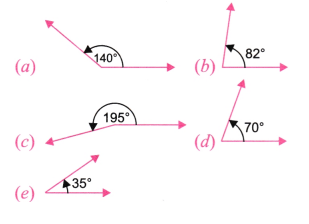
Question 1. Draw angles with the following degree measures:
(a) 140°
(b) 82°
(c) 195°
(d) 70°
(e) 35°
Answer:
Question 2. Estimate the size of each angle and then measure it with a protractor:
Classify these angles as acute, right, obtuse or reflex angles.
Answer:
(a) 45° acute
(b) 165° obtuse
(c) 120° obtuse
(d) 30° acute
(e) 95° obtuse
(f) 350° reflex
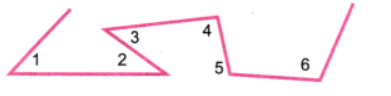
Question 3. Make any figure with three acute angles, one right angle and two obtuse angles.
Answer:
Angles 1, 2 and 3 are acute angles, angle 4 is right angle, angles 5 and 6 are obtuse angles.
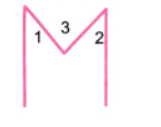
Question 4. Draw the letter ‘M’ such that the angles on the sides are 40° each and the angle in the middle is 60°.
Answer:
∠1 = 30°, ∠2 = 30°, ∠3 = 60°
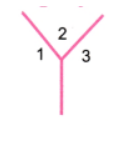
Question 5. Draw the letter ‘Y’ such that the three angles formed are 150°, 60° and 150°.
Answer:
∠1 = 150°, ∠2 = 60°, ∠3 = 150°
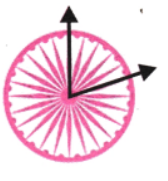
Question 6. The Ashoka Chakra has 24 spokes. What is the degree measure of the angle between two spokes next to each other? What is the largest acute angle formed between two spokes?
Answer:
Angle between two consecutive spokes = 360 ÷ 24 = 15°
Largest acute angle = 5 × 15° = 75°










Thankyou bhai mera kaam karva ne ke liye