1.1 Figure it out (Page 2)
1) Can you think of other examples where mathematics helps us in our everyday lives?
Ans: Examples where mathematics helps in everyday life:
- Budgeting for groceries and household expenses.
- Calculating travel time and distances.
- Measuring ingredients in cooking.
2) How has mathematics helped propel humanity forward? (You might think of examples involving: carrying out scientific experiments; running our economy and democracy; building bridges, houses or other complex structures; making TVs, mobile phones, computers, bicycles, trains, cars, planes, calendars, clocks, etc.)
Ans: How mathematics has helped propel humanity forward:
- Scientific experiments: Through calculations in physics and chemistry.
- Economy and democracy: Used in statistics and predictions for elections and economic planning.
- Building bridges, houses, or complex structures: Engineers use mathematics to ensure structural stability.
1.2 Figure it out (Page 3)
Table 1 Examples of number sequences
| 1, 1, 1, 1, 1, 1, 1, … (All 1’s) |
| 1, 2, 3, 4, 5, 6, 7, … (Counting numbers) |
| 1, 3, 5, 7, 9, 11, 13, … (Odd numbers) |
| 2, 4, 6, 8, 10, 12, 14, … (Even numbers) |
| 1, 3, 6, 10, 15, 21, 28, … (Triangular numbers) |
| 1, 4, 9, 16, 25, 36, 49, … (Squares) |
| 1, 8, 27, 64, 125, 216, … (Cubes) |
| 1, 2, 3, 5, 8, 13, 21, … (Virahanka numbers) |
| 1, 2, 4, 8, 16, 32, 64, … (Powers of 2) |
| 1, 3, 9, 27, 81, 243, 729, … (Powers of 3) |
2) Rewrite each sequence of Table 1 in your notebook, along with the next three numbers in each sequence! After each sequence, write in your own words what is the rule for forming the numbers in the sequence.
Ans: Next three numbers in each sequence:
- All 1’s: 1, 1, 1
- Counting numbers: 8, 9, 10
- Odd numbers: 15, 17, 19
- Even numbers: 16, 18, 20
- Triangular numbers: 36, 45, 55
- Squares: 64, 81, 100
- Cubes: 343, 512, 729
- Powers of 2: 128, 256, 512
- Powers of 3: 2187, 6561, 19683
1.3 Figure it out (Page 5,6)
1) Copy the pictorial representations of the number sequences in Table 2 in your notebook, and draw the next picture for each sequence.
Ans:
2) Why are 1, 3, 6, 10, 15, … called triangular numbers? Why are 1, 4, 9, 16, 25, … called square numbers or squares? Why are 1, 8, 27, 64, 125, … called cubes?
Ans:
Triangular numbers are formed by adding consecutive numbers (1, 3, 6, 10, 15…). These numbers can form equilateral triangles when arranged in dots.
- Square numbers (1, 4, 9, 16…) are called so because they can form perfect squares when arranged in dots.
- Cubes (1, 8, 27, 64…) are called cubes because they represent the volume of cubes with integer side lengths.
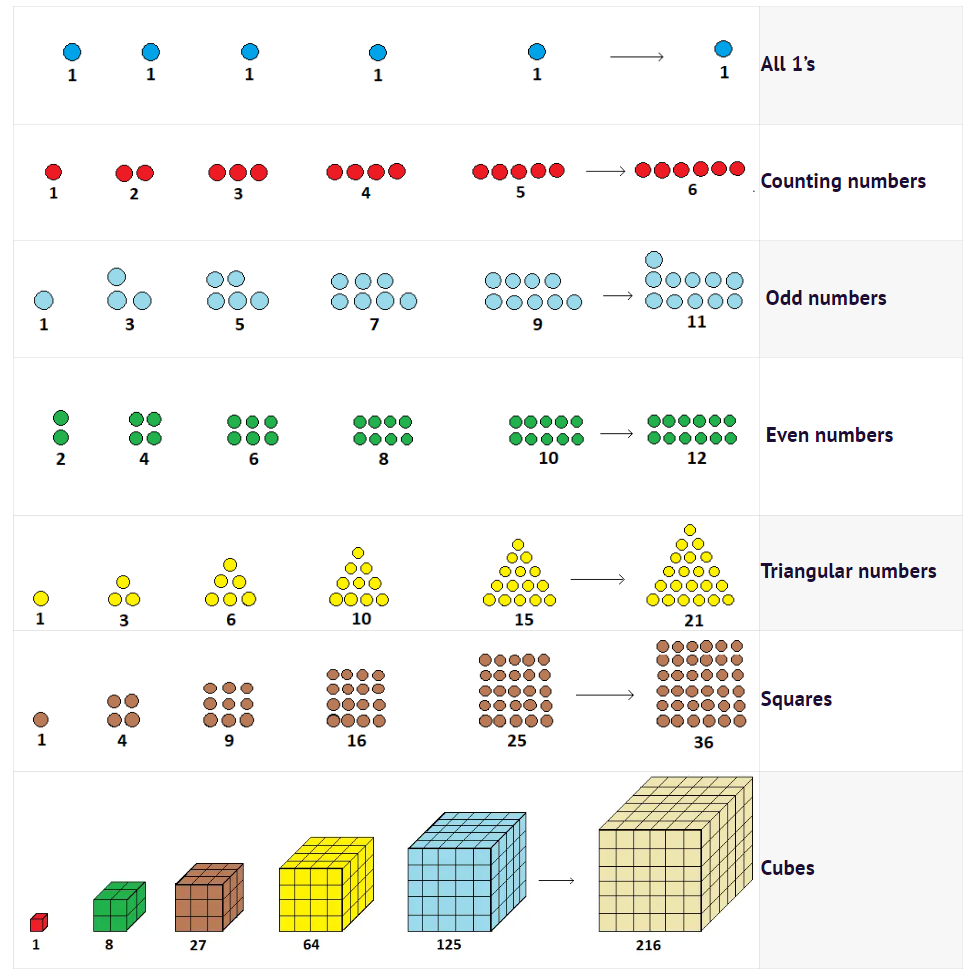
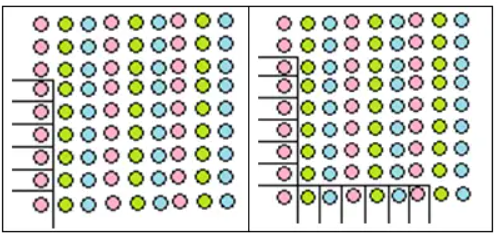
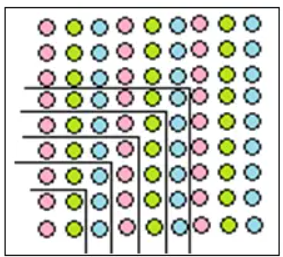
3) You will have noticed that 36 is both a triangular number and a square number! That is, 36 dots can be arranged perfectly both in a triangle and in a square. Make pictures in your notebook illustrating this!
This shows that the same number can be represented differently, and play different roles, depending on the context. Try representing some other numbers pictorially in different ways!
Ans:
Some other same numbers that can be represented differently, and play different roles that is 1225. (35 × 35)
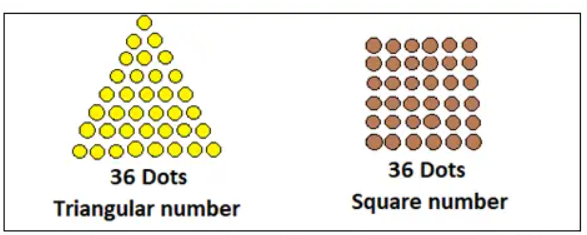
4) What would you call the following sequence of numbers?
That’s right, they are called hexagonal numbers! Draw these in your notebook. What is the next number in the sequence?
Ans:
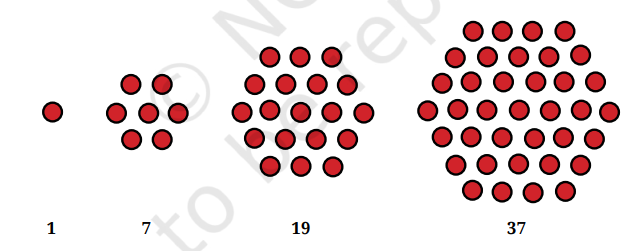
5) Can you think of pictorial ways to visualise the sequence of Powers of 3?
Here is possible way of thinking about Powers of 3:
Ans:
1.4 Figure it out (Page 8,9)
1) Can you find a similar pictorial explanation for why adding counting numbers up and down, i.e., 1, 1 + 2 + 1, 1 + 2 + 3 + 2 + 1, …, gives square numbers?
Ans:
When you add counting numbers up and down, like 1, 1 + 2 + 1, 1 + 2 + 3 + 2 + 1, etc., you are essentially forming symmetrical shapes that resemble squares. For example:
- 1 = 1 (1 square dot)
- 1 + 2 + 1 = 4 (forms a 2×2 square)
- 1 + 2 + 3 + 2 + 1 = 9 (forms a 3×3 square)
Each time, the numbers symmetrically increase and then decrease, giving a perfect square pattern.
2) By imagining a large version of your picture, or drawing it partially, as needed, can you see what will be the value of 1 + 2 + 3 + … + 99 + 100 + 99 + … + 3 + 2 + 1?
Ans:
1 = 1
1 + 2 + 1 = 4
1 + 2 + 3 + 2 + 1 = 9
1 + 2 + 3 + 4 + 3 + 2 + 1 = 16
1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25
1 + 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 + 1 = 36
.
.
1 + 2 + 3 + … + 99 + 100 + 99 + … + 3 + 2 + 1 = 10000
3) Which sequence do you get when you start to add the All 1’ssequence up? What sequence do you get when you add the All 1’s sequence up and down?
Ans:
When we add the All 1’ssequence up we get Counting numbers sequence. (1st picture)
When we add the All 1’ssequence up and down we get Odd numbers sequence. (2nd picture)
4) Which sequence do you get when you start to add the Counting numbers up? Can you give a smaller pictorial explanation?
Ans:
If you add the counting numbers (1, 2, 3, 4, …), you get triangular numbers:
- 1 = 1
- 1 + 2 = 3
- 1 + 2 + 3 = 6
- 1 + 2 + 3 + 4 = 10 This forms the triangular number sequence.
5) What happens when you add up pairs of consecutive triangular numbers? That is, take 1 + 3, 3 + 6, 6 + 10, 10 + 15, … ? Which sequence do you get? Why? Can you explain it with a picture?
Ans:
When we add up pairs of consecutive triangular numbers i.e, 1 + 3, 3 + 6, 6 + 10, 10 + 15, … we get square number sequence.
6) What happens when you start to add up powers of 2 starting with 1, i.e., take 1, 1 + 2, 1 + 2 + 4, 1 + 2 + 4 + 8, … ? Now add 1 to each of these numbers—what numbers do you get? Why does this happen?
Ans:
When you start to add powers of 2:
1
1 + 2 = 3
1 + 2 + 4 = 7
1 + 2 + 4 + 8 = 15
When you add 1 to each of these numbers:
1 + 1 = 2
3 + 1 = 4
7 + 1 = 8
15 + 1 = 16
You get powers of 2 again: 2, 4, 8, 16, …
7) What happens when you multiply the triangular numbers by 6and add 1? Which sequence do you get? Can you explain it with a picture?
Ans:
Multiplying the triangular numbers by 6 and adding 1 gives:
1 x 6 + 1 = 7
3 x 6 + 1 = 19
6 x 6 + 1 = 37
This forms the hexagonal number sequence: 7, 19, 37, …
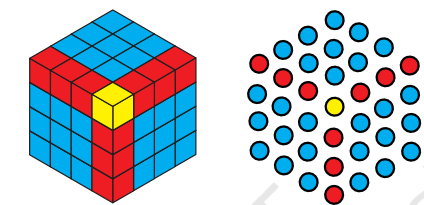
8) What happens when you start to add up hexagonal numbers, i.e., take 1, 1 + 7, 1 + 7 + 19, 1 + 7 + 19 + 37, … ? Which sequence do you get? Can you explain it using a picture of a cube?
Ans:
1
1 + 7 = 8
1 + 7 + 19 = 27
1 + 7 + 19 + 37 = 64
.
.
When we start to add up hexagonal numbers, i.e., 1, 1 + 7, 1 + 7 + 19, 1 + 7 + 19 + 37, we get the cube of consecutive numbers.
9) Find your patterns or relations in and among the sequences in Table 1. Can you explain why they happen with a picture or otherwise?
Ans: 3, 6, 9, 12, 15, 18,……… (consecutive multiples of 3).
10, 15, 20, 25,…….. (first number is 10. Then increase of 5 in each term)
1.5 Figure it out (Page 11)
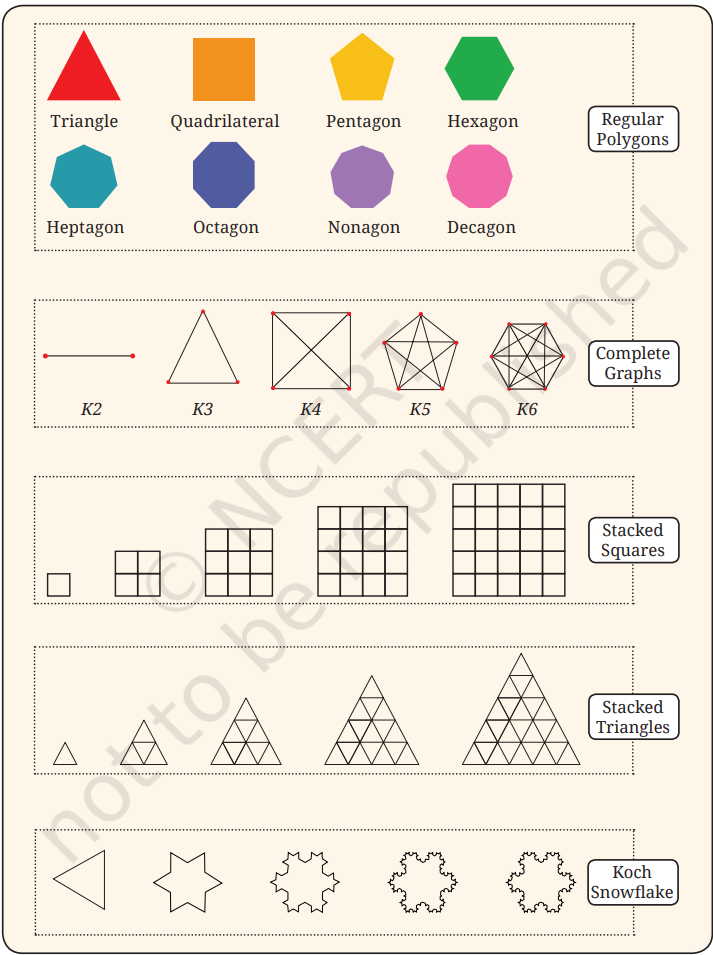
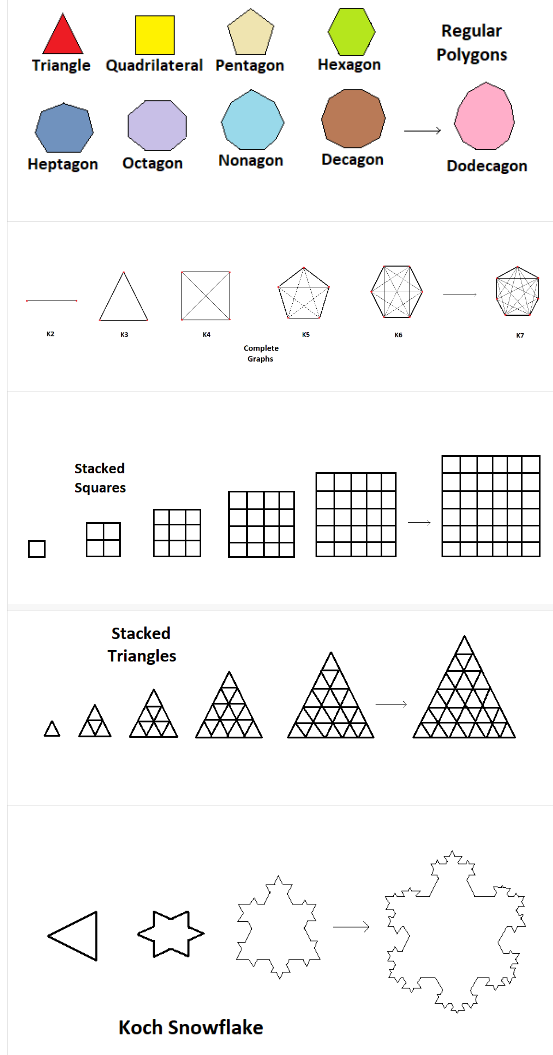
1) Can you recognize the pattern in each of the sequences in Table 3?
Ans:
Regular Polygons: Triangle, quadrilateral, pentagon, hexagon, heptagon, etc.
- Pattern: The number of sides increases by 1 each time, forming a polygon with an additional side.
Complete Graphs: K2, K3, K4, K5, etc.
- Pattern: The number of vertices increases by 1, and the lines connecting every vertex form a complete graph. The number of edges increases accordingly.
Stacked Squares: Squares are stacked upon each other, with additional layers of smaller squares.
- Pattern: More squares are added as layers, increasing the total number of smaller squares.
Stacked Triangles: Triangles stacked upon each other, increasing the number of small triangles in the structure.
- Pattern: As new layers are added, the number of smaller triangles increases.
Koch Snowflake: A fractal pattern where each line segment is replaced by smaller “bumps” in the shape of an equilateral triangle.
- Pattern: Each iteration adds more bumps along the edges, increasing the complexity and the number of line segments.
2) Try and redraw each sequence in Table 3 in your notebook. Can you draw the next shape in each sequence? Why or why not? After each sequence, describe in your own words what is the rule or pattern for forming the shapes in the sequence.
Ans:
Ans:
- Regular Polygons: The next shape after the heptagon (7 sides) is the octagon (8 sides).
- Rule: Increase the number of sides by 1.
- Complete Graphs: After K5 (5 vertices), the next complete graph is K6.
- Rule: Add one more vertex and connect every vertex to all others.
- Stacked Squares: The next shape will have an additional layer of squares stacked below or around the existing structure.
- Rule: Add another layer with additional small squares, expanding the structure.
- Stacked Triangles: The next shape will have one more layer of triangles at the base, increasing the total number of triangles.
- Rule: Add another row of triangles to form a larger stacked structure.
- Koch Snowflake: The next shape will have more intricate and smaller triangular “bumps” added to each side of the snowflake.
- Rule: Each line segment is replaced with 4 smaller segments (one segment for the bump), increasing the total number of segments exponentially.
1.6 Figure it out (Page 11,12)
1) Count the number of sides in each shape in the sequence of Regular Polygons. Which number sequence do you get? What about the number of corners in each shape in the sequence of Regular Polygons? Do you get the same number sequence? Can you explain why this happens?
Ans:
Sides and Corners Sequence: The number of sides and corners in each shape of the regular polygon sequence increases by 1.
- Triangle: 3 sides, 3 corners
- Quadrilateral: 4 sides, 4 corners
- Pentagon: 5 sides, 5 corners
- Hexagon: 6 sides, 6 corners
- Heptagon: 7 sides, 7 corners
Number Sequence: 3, 4, 5, 6, 7… Explanation: The number of sides and corners is the same because each corner corresponds to a side in regular polygons.
2) Count the number of lines in each shape in the sequence of Complete Graphs. Which number sequence do you get?
Ans:
Number of Lines in Complete Graphs Sequence: The number of lines in a complete graph (Kn) increases based on how many vertices are connected.
- K2: 1 line
- K3: 3 lines
- K4: 6 lines
- K5: 10 lines
3) How many little squares are there in each shape of the sequence of Stacked Squares? Which number sequence does this give? Can you explain why?
Ans:
Number of Squares Sequence: As squares are stacked, the number of little squares increases:
- 1st shape: 1 square
- 2nd shape: 4 squares
- 3rd shape: 9 squares
- 4th shape: 16 squares
Number Sequence: 1, 4, 9, 16… Explanation: The number of squares follows the sequence of square numbers, as each shape forms a perfect square grid.
4) How many little triangles are there in each shape of the sequence of Stacked Triangles? Which number sequence does this give? Can you explain why? (Hint: In each shape in the sequence, how many triangles are there in each row?)
Ans:
Number of little triangles sequence of Stacked Triangles = 1, 4, 9, 16, 25
5) To get from one shape to the next shape in the Koch Snowflake sequence, one replaces each line segment ‘—’by a ‘speed bump’. As one does this more and more times, the changes become tinier and tinier with very very small line segments. How many total line segments are there in each shape of the Koch Snowflake? What is the corresponding number sequence? (The answer is 3, 12, 48, …, i.e. 3 times Powers of 4; this sequence is not shown in Table 1)
Ans:
Koch Snowflake Line Segments Sequence:
- 1st shape: 3 line segments
- 2nd shape: 12 line segments
- 3rd shape: 48 line segments
Number Sequence: 3, 12, 48, … Explanation: The number of line segments increases by multiplying the previous number by 4, forming a sequence of 3 times powers of 4.

very nice 👍