Questions Ans For All Chapters – Science Curiosity Class 6
Measurement of Length and Motion
Question 1. Some lengths are given in Column I of Table 5.5. Some units are given in Column II. Match the lengths with the units suitable for measuring those lengths.
Answer:
| Column I | Column II |
| Distance between Delhi and Lucknow | kilometre |
| Thickness of a coin | millimetre |
| Length of an eraser | centimetre |
| Length of school ground | metre |
Question 2. Read the following statements and mark True (T) or False (F) against each.
(i) The motion of a car moving on a straight road is an example of linear motion. [ ]
(ii) Any object which is changing its position with respect to a reference point with time is said to be in motion. [ ]
(iii) 1 km = 100 cm [ ]
Answer:
(i) True
(ii) True
(iii) False
Question 3. Which of the following is not a standard unit of measuring length?
(i) millimetre (ii) centimetre (iii) kilometre (iv) handspan
Answer: (iv) handspan (not a standard unit)
Question 4. Search for the different scales or measuring tapes at your home and school. Find out the smallest value that can be measured using each of these scales. Record your observations in a tabular form.
Answer: You can fill this table by checking the scales and measuring tapes around your home and school.
| Type of Scale, Tape, Device | Smallest Value of Measurement |
|---|---|
| 15 cm Scale | 1 mm |
| Flexible Tape | 1 mm, 1 inch |
| Long Tape Roll | 1 cm, 1 inch |
| Vernier Calliper (from School Lab) | 0.1 mm |
| Screw Gauge (from School Lab) | 0.01 mm |
Question 5. Suppose the distance between your school and home is 1.5 km. Express it in metres.
Answer:
Distance between your school and home = 1.5 km
1 km = 1000 m
So, 1.5 km = 1.5 × 1000 = 1500 meters.
Question 6. Take a tumbler or a bottle. Measure the length of the curved part of the base of glass or bottle and record it.
Answer: Use a flexible tape or string to measure the curved base. Once measured, straighten the string and use a ruler to measure its length. Record the result in centimeters or millimeters, depending on the size.
Question 7. Measure the height of your friend and express it in
(i) metres (ii) centimetres and (iii) millimetres.
Answer: Let’s assume your friend’s height is 1.6 meters.
(i) In meters: 1.6 m
(ii) In centimeters: 1.6 m = 160 cm
(iii) In millimeters: 1.6 m = 1600 mm
Question 8. You are given a coin. Estimate how many coins are required to be placed one after the other lengthwise, without leaving any gap between them, to cover the whole length of the chosen side of a notebook. Verify your estimate by measuring the same side of the notebook and the size of the coin using a 15-cm scale.
Answer:
- Step 1: Estimate the diameter of the coin. Assume it is 2.5 cm.
- Step 2: Measure the length of the notebook side. Suppose the side is 30 cm.
- Step 3: Divide the notebook length by the coin diameter: 30 cm ÷ 2.5 cm = 12 coins.
- Step 4: Verify by placing the coins lengthwise along the notebook edge to see if 12 coins fit.
Question 9. Give two examples each for linear, circular and oscillatory motion.
Answer:
i) Linear motion:
- A car moving on a straight road.
- A train moving along straight tracks.
ii) Circular motion:
- A merry-go-round.
- The hands of a clock.
iii) Oscillatory motion:
- A pendulum in a clock.
- A child swinging on a swing.
Question 10. Observe different objects around you. It is easier to express the lengths of some objects in mm, some in cm and some in m. Make a list of three objects in each category and enter them in the Table 5.6.
Answer:
| Size | Objects |
| mm | Thickness of a coin, a paperclip, a pen cap |
| cm | Length of a pencil, width of a book, a spoon |
| m | Height of a door, length of a table, width of a room |
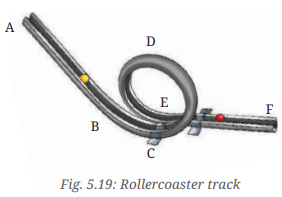
Question 11. A rollercoaster track is made in the shape shown in Fig. 5.19. A ball starts from point A and escapes through point F. Identify the types of motion of the ball on the rollercoaster and corresponding portions of the track.
Answer:
- From A to B: Linear motion
- From B to D: Circular motion (loop part)
- From D to F: Linear motion
Question 12. Tasneem wants to make a metre scale by herself. She considers the following materials for it—plywood, paper, cloth, stretchable rubber and steel. Which of these should she not use and why?
Answer: Tasneem should not use stretchable rubber because it can change shape, making it unreliable for accurate measurements. Other materials like plywood, paper, and steel do not deform easily and are better for making a meter scale.
Question 13. Think, design and develop a card game on conversion of units of length to play with your friends.
Answer:
- Create a deck of cards, each with a measurement (e.g., 1000 mm, 1 m, 150 cm, 1.5 km).
- The goal of the game is to match cards with equivalent measurements. For example, if a player has a card with “1 m,” they could match it with another card showing “100 cm.”
- Add a challenge rule where players must quickly convert a given unit to win a point.
(Page 83)
Question. Would it be convenient to use the unit metre to measure larger lengths, such as the length of a railway track between two cities, or to measure smaller lengths, such as the thickness of a page of a book?
Answer: No, it would not be convenient to use the unit metre for either of these cases. For measuring larger lengths, such as the distance between two cities, it is more appropriate to use kilometres (km). On the other hand, for smaller lengths, like the thickness of a page of a book, a more suitable unit would be millimetres (mm) or centimetres (cm). Different units are chosen based on the scale of the object being measured.
(Page 89)
Question. What do such kilometre stones indicate? How could Padma conclude that she was getting closer to her destination?
Answer: Kilometre stones indicate the distance from a specific point, such as a city or destination. In Padma’s case, the kilometre stones told her how far she was from Delhi. As she noticed the distance decreasing with each kilometre stone (from 70 km to 60 km, etc.), she could conclude that she was getting closer to her destination.
Question. Does this mean that the position of Padma, with respect to the reference point, is changing with time? When does the position of an object change with respect to a reference point? Does it change when an object is moving?
Answer: Yes, Padma’s position is changing with respect to the reference point (Delhi) as time passes. The position of an object changes with respect to a reference point when the object is moving. If an object is stationary, its position remains the same relative to the reference point. Hence, when an object moves, its position changes with respect to that point. Padma’s position changed as she traveled towards Delhi, meaning she was in motion relative to Delhi.


It is very useful for teachers and students.
Good
This solution is very helpful, thanks
This chapter solutions help me much better to learn
Good