14.1
A string of mass 2.50 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, how long does the disturbance take to reach the other end?
Solution :
Mass of the string, M = 2.50 kg
Tension in the string, T = 200 N
Length of the string, l = 20.0 m
Mass per unit length, µ = M/l = 2.50/20 = 0.125 kg m-1
The velocity (v) of the transverse wave in the string is given by the relation:
v = √t/µ
= √200/0.125 = √1600 = 40 m/s
∴ Time taken by the disturbance to reach the other end, t = l/v = 20/40 = 0.5 s.
14.2
A stone dropped from the top of a tower of height 300 m high splashes into the water of a pond near the base of the tower. When is the splash heard at the top given that the speed of sound in air is 340 m s–1? (g= 9.8 m s–2)
Solution :
Height of the tower, s = 300 m
Initial velocity of the stone, u = 0
Acceleration, a = g = 9.8 m/s2
Speed of sound in air = 340 m/s
The time (t1) taken by the stone to strike the water in the pond can be calculated using the second equation of motion, as:
s = ut1 + 1/2 gt12
300 = 0 + 1/2 × 9.8 × t12
∴ t1 = √300 × 2/9.8 = 7.82 s
Time taken by the sound to reach the top of the tower, t2 = 300/340 = 0.88 s
Therefore, the time after which splash is heard, t = t1 + t2
= 7.82 + 0.88 = 8.7 s.
14.3
A steel wire has a length of 12.0 m and a mass of 2.10 kg. What should be the tension in the wire so that speed of a transverse wave on the wire equals the speed of sound in dry air at 20 °C = 343 m s–1.
Solution :
Length of the steel wire, l = 12 m
Mass of the steel wire, m = 2.10 kg
Velocity of the transverse wave, v = 343 m/s
Mass per unit length, µ = m/l = 2.10/12 = 0.175 kg m-1
For Tension T, velocity of the transverse wave can be obtained using the relation:
v = √T/µ
∴ T = vu
= (343)2 × 0.175 = 20588.575 ≈ 2.06 × 104 N.
14.4
Use the formula v = √γP/ρ to explain why the speed of sound in air
a. is independent of pressure,
b. increases with temperature,
c. increases with humidity.
Solution :
a. Take the relation:
v = √γP/ρ ….(i)
where,
Density, ρ = Mass/Volume = M/V
M = Molecular weight of the gas
V = Volume of the gas
Hence, equation (i) reduces to:
v = √γPV/M ….(ii)
Now from the ideal gas equation for n = 1:
PV = RT
For constant T, PV = Constant
Since both M and γ are constants, v = Constant
Hence, at a constant temperature, the speed of sound in a gaseous medium is independent of the change in the pressure of the gas.
b. Take the relation:
v = √γP/ρ ….(i)
For one mole of any ideal gas, the equation can be written as:
PV = RT
P = RT/V ….(ii)
Substituting equation (ii) in equation (i), we get:
v = √γRT/Vρ = √γRT/M …..(iii)
where,
mass, M = ρV is a constant
γ and R are also constants
We conclude from equation (iii) that v ∝ √T
Hence, the speed of sound in a gas is directly proportional to the square root of the temperature of the gaseous medium, i.e., the speed of the sound increases with an increase in the temperature of the gaseous medium and vice versa.
c. Let vm and vd be the speed of sound in moist air and dry air respectively.
Let ρm and ρd be the densities of the moist air and dry air respectively.
However, the presence of water vapour reduces the density of air,
i.e., ρd < ρm
∴ vm > vd
Hence, the speed of sound in mois air is greater than it is in dry air. Thus, in gaseous medium, the speed of sound increases with humidity.
14.5
You have learnt that a travelling wave in one dimension is represented by a function y = f (x, t)where x and t must appear in the combination x – v t or x + v t, i.e. y = f (x ± v t). Is the converse true? Examine if the following functions for y can possibly represent a travelling wave:
a. (x – vt)2
b. log [(x + vt) / x0]
c. 1 / (x + vt)
Solution :
No, the converse is not true. The basic requirements for a wave function to represent a travelling wave is that for all values of x and t, wave function must have finite value.
Out of the given functions for y, no one satisfies this condition. Therefore, none can represent a travelling wave.
14.6
A bat emits ultrasonic sound of frequency 1000 kHz in air. If the sound meets a water surface, what is the wavelength of
a. the reflected sound,
b. the transmitted sound? Speed of sound in air is 340 m s–1 and in water 1486 m s–1.
Solution :
a. Frequency of the ultrasonic sound, ν = 1000 kHz = 106 Hz
Speed of sound in air, va = 340 m/s
The wavelength (λr) of the reflected sound is given by the relation:
λr = v/v
= 340/106 = 3.4 × 10-4 m.
b. Frequency of the ultrasonic sound, ν = 1000 kHz = 106 Hz
Speed of sound in water, vw = 1486 m/s
The wavelength of the transmitted sound is given as:
λr = 1486 × 106 = 1.49 × 10-3 m.
14.7
A hospital uses an ultrasonic scanner to locate tumours in a tissue. What is the wavelength of sound in the tissue in which the speed of sound is 1.7 km s–1? The operating frequency of the scanner is 4.2 MHz.
Solution :
Speed of sound in the tissue, v = 1.7 km/s = 1.7 × 103 m/s
Operating frequency of the scanner, ν = 4.2 MHz = 4.2 × 106 Hz
The wavelength of sound in the tissue is given as:
λ = v/v
= 1.7 × 103 / 4.2 × 106 = 4.1 × 10-4 m.
14.8
A transverse harmonic wave on a string is described by
Where x and y are in cm and t in s. The positive direction of x is from left to right.
a. Is this a travelling wave or a stationary wave?
If it is travelling, what are the speed and direction of its propagation?
b. What are its amplitude and frequency?
c. What is the initial phase at the origin?
d. What is the least distance between two successive crests in the wave?
Solution :
a. The equation of progressive wave travelling from right to left is given by the displacement function:
y (x, t) = a sin (ωt + kx + Φ) ….(i)
The given equation is:
……(ii)
On compaaring both the equations, we find that equation (ii) represents a travelling wave, propgating from right to left. Now using equations (i) and (ii), we can write: ω = 36 rad/s and k = 0.018 m-1 We know that: v = ω/2π and λ = 2π/k Also,
v = vλ
∴ v = (ω/2π) / (2π/k) = ω/k
= 36/0.018 = 2000 cm/s = 20 m/s
Hence, the speed of the given travelling wave is 20 m/s.
b. Amplitude of the given wave, a = 3 cm
Frequency of the given wave:
v = ω/2π = 36 / 2 × 3.14 = 573 Hz
c. On comparing equations (i) and (ii), we find that the intial phase angle, Φ = π/4
d. The distance between two successive crests or troughs is equal to the wavelength of the wave.
Wavelength is given by the relation:
k = 2π/λ
∴ λ = 2π/k = 2 × 3.14 / 0.018 = 348.89 cm =3.49 m.
14.9
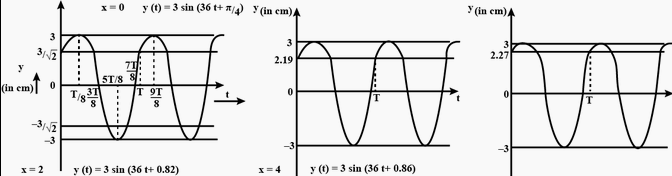
For the wave described in Exercise 14.8, plot the displacement (y) versus (t) graphs for x = 0, 2 and 4 cm. What are the shapes of these graphs? In which aspects does the oscillatory motion in travelling wave differ from one point to another: amplitude, frequency or phase?
Solution :
All the waves have different phases.
The given transverse harmonic wave is:
y(x, t) =3 sin (36t +0.018x + π/4) . . . . . . . . . . . ( 1 )
For x = 0, the equation reduces to:
y( 0, t ) =3 sin ( 36t +0 + π/4 ) . . . . . . . . . . . ( 2 )
Also,
ω = 2 π/t = 36 rad/s
=> t = π/18 secs.
Now, plotting y vs. t graphs using the different values of t, as listed in the given table
| t (s) | 0 | T/8 | 2T/7 | 3T/8 | 4T/8 | 5T/8 | 6T/8 | 7T/8 |
| y (cm) | 3/√2 | 3 | 3/√2 | 0 | -3/√2 | –3 | -3/√2 | 0 |
For x = 0, x = 2, and x = 4, the phases of the three waves will get changed. This is because amplitude and frequency are invariant for any change in x. The y-t plots of the three waves are shown in the given figure.
14.10
For the travelling harmonic wave y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35) Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of
a. 4 m,
b. 0.5 m,
c. λ/2
d. 3λ/4
Solution :
Equation for a travelling harmonic wave is given as:
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
= 2.0 cos (20πt – 0.016πx + 0.70 π)
Where,
Propagation constant, k = 0.0160 π
Amplitude, a = 2 cm
Angular frequency, ω= 20 π rad/s
Phase difference is given by the relation:
Φ = kx = 2π/λ
a. For x = 4 m = 400 cm
Φ = 0.016 π × 400 = 6.4 π rad
b. For 0.5 m = 50 cm
Φ = 0.016 π × 50 = 0.8 π rad
c. For x = λ/2
Φ = 2π/λ × λ/2 = π rad
d. For x = 3λ/4
Φ = 2π/λ × 3λ/4 = 1.5π rad.
14.11
The transverse displacement of a string (clamped at its both ends) is given by
Where x and y are in m and t in s. The length of the string is 1.5 m and its mass is 3.0 ×10–2 kg.
Answer the following:
a. Does the function represent a travelling wave or a stationary wave?
b. Interpret the wave as a superposition of two waves travelling in opposite directions. What is the wavelength, frequency, and speed of each wave?
c. Determine the tension in the string.
Solution :
a. The general equation representing a stationary wave is given by the displacement function:
y (x, t) = 2a sin kx cos ωt
This equation is similar to the given equation:
Hence, the given equation represents a stationary wave.
b. A wave travelling along the positive x-direction is given as:
y1 = a sin (ωt – kx)
The wave travelling along the positive x-direction is given as:
y2 = a sin (ωt + kx)
The supposition of these two waves yields:
y = y1 + y2 = a sin (ωt – kx) – a sin (ωt + kx)
= a sin (ωt) cos (kx) – a sin (kx) cos (ωt) – a sin (ωt) cos (kx) – a sin (kx) cos (ωt)
= 2 a sin (kx) cos (ωt)
∴Wavelength, λ = 3 m
It is given that:
120π = 2πν
Frequency, ν = 60 Hz
Wave speed, v = νλ
= 60 × 3 = 180 m/s
c. The velocity of a transverse wave travelling in a string is given by the relation:
v = √T/µ ….(i)
where,
Velocity of the transverse wave, v = 180 m/s
Mass of the string, m = 3.0 × 10–2 kg
Length of the string, l = 1.5 m
Mass per unit length of the string, µ = m/l
= 3.0 × 1.5 = 10-2
= 2 × 10-2 kg m-1 Tension in the string = T
From equation (i), tension can be obtained as:
T = v2μ
= (180)2 × 2 × 10–2
= 648 N
14.12
(i) For the wave on a string described in Exercise 15.11, do all the points on the string oscillate with the same (a) frequency, (b) phase, (c) amplitude? Explain your answers. (ii) What is the amplitude of a point 0.375 m away from one end?
Solution :
All the points on the string
(i) have the same frequency except at the nodes (where frequency is zero)
(ii) have thse same phase everywhere in one loop except at the nodes.
However, the amplitude of vibration at different points is different.
Form:
Given that,
Frequency =60Hz
∴ From the above equation of wave, we see that all points on the string oscillate with same phase and frequency except the nodes (endpoints).
We can also see that amplitude of the wave changes for different ‘x’.
ii) Amplitude of a point at 0.375m i.e., x=0.375m
14.13
Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent (i) a traveling wave, (ii) a stationary wave or (iii) none at all:
a. y = 2 cos (3x) sin (10t)
b. y = 2 √x – vt
c. y = 3 sin (5x – 0.5t) + 4 cos (5x – 0.5t)
d. y = cos x sin t + cos 2x sin 2t
Solution :
a. The given equation represents a stationary wave because the harmonic terms kx and ωt appear separately in the equation.
b. The given equation does not contain any harmonic term. Therefore, it does not represent either a travelling wave or a stationary wave.
c. The given equation represents a travelling wave as the harmonic terms kx and ωt are in the combination of kx – ωt.
d. The given equation represents a stationary wave because the harmonic terms kx and ωt appear separately in the equation. This equation actually represents the superposition of two stationary waves.
14.14
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5 × 10–2 kg and its linear mass density is 4.0 × 10–2 kg m–1. What is
a. the speed of a transverse wave on the string, and
b. the tension in the string?
Solution :
a. Mass of the wire, m = 3.5 × 10–2 kg
Linear mass density, μ = m/l = 4.0 × 10-2 kg m-1
Frequency of vibration, v = 45 Hz
∴ length of the wire, l = m/μ
= 3.5 × 10–2 / 4.0 × 10-2
= 0.875 m
The wavelength of the stationary wave (λ) is related to the length of the wire by the relation:
λ = 2l/m
where,
n = Number of nodes in the wire
For fundamental node, n = 1:
λ = 2l
λ = 2 × 0.875 = 1.75 m
The speed of the transverse wave in the string is given as:
v = νλ= 45 × 1.75 = 78.75 m/s
b. The tension produced in the string is given by the relation:
T = v2µ
= (78.75)2 × 4.0 × 10–2 = 248.06 N
14.15
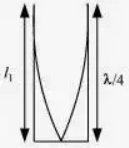
A metre – long tube open at one end, with a movable piston at the other end, shows resonance with a fixed frequency source (a tuning fork of frequency 340 Hz) when the tube length is 25.5 cm or 79.3 cm. Estimate the speed of sound in air at the temperature of the experiment. The edge effects may be neglected.
Solution :
Frequency of the turning fork, ν = 340 Hz
Since the given pipe is attached with a piston at one end, it will behave as a pipe with one end closed and the other end open, as shown in the given figure.
Such a system produces odd harmonics. The fundamental note in a closed pipe is given by the relation:
l1 = π/4 where, length of pipe, l1 = 25.5 cm = 0.255 m
∴ λ = 4l1 = 4 × 0.255 = 1.02 m
The speed of the sound is given by the relation:
v = vλ = 340 × 1.02 = 346.8 m/s.
14.16
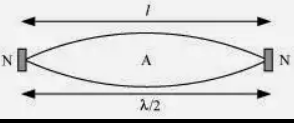
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53 kHz. What is the speed of sound in steel?
Solution :
Length of the steel rod, l = 100 cm = 1 m
Fundamental frequency of vibration, ν = 2.53 kHz = 2.53 × 103 Hz
When the rod is plucked at its middle, an antinode (A) is formed at its centre, and nodes (N) are formed at its two ends, as shown in the given figure.
The distance between two successive node is λ/2 ∴ l = λ/2 λ = 2l = 2 × l = 2 m The speed of sound in steel is given by the relation:
v = νλ
= 2.53 × 103 × 2
= 5.06 × 103 m/s
= 5.06 km/s
14.17
A pipe 20 cm long is closed at one end. Which harmonic mode of the pipe is resonantly excited by a 430 Hz source? Will the same source be in resonance with the pipe if both ends are open? (Speed of sound in air is 340 m s–1).
Solution :
First (Fundamental); No
Length of the pipe, l = 20 cm = 0.2 m
Source frequency = nth normal mode of frequency, νn = 430 Hz
Speed of sound, v = 340 m/s
In a closed pipe, the nth normal mode of frequency is given by the relation:
Hence, the first mode of vibration frequency is resonantly excited by the given source. In a pipe open at both ends, the nth mode of vibration frequency is given by the relation:
vn = nv/2l
n = 2lvn/v
14.18
Two sitar strings A and B playing the note ‘Ga’ are slightly out of tune and produce beats of frequency 6 Hz. The tension in the string A is slightly reduced and the beat frequency is found to reduce to 3 Hz. If the original frequency of A is 324 Hz, what is the frequency of B?
Solution :
Frequency of string A, fA = 324 Hz
Frequency of string B = fB
Beat’s frequency, n = 6 Hz
Beat’s Frequency is given as:
n=|fA−fB|
6=|324−fB|
fB=330Hz or 318Hz
Frequency decreases with a decrease in the tension in a string.
This is because frequency is directly proportional to the square root of tension. It is given as:
v ∝ √T
Hence, the beat frequency cannot be 330 Hz
∴ fB = 318 Hz.
14.19
Explain why (or how):
a. In a sound wave, a displacement node is a pressure antinode and vice versa,
b. Bats can ascertain distances, directions, nature, and sizes of the obstacles without any “eyes”,
c. A violin note and sitar note may have the same frequency, yet we can distinguish between the two notes,
d. Solids can support both longitudinal and transverse waves, but only longitudinal waves can propagate in gases, and
e. The shape of a pulse gets distorted during propagation in a dispersive medium.
Solution :
a. A node (N) is a point where the amplitude of vibration is the minimum and pressure is the maximum.
An antinode (A) is a point where the amplitude of vibration is the maximum and pressure is the minimum.
Therefore, a displacement node is nothing but a pressure antinode, and vice versa.
b. Bats emit ultrasonic waves of large frequencies. When these waves are reflected from the obstacles in their path, they give them the idea about the distance, direction, size and nature of the obstacle.
c. The overtones produced by a sitar and a violin, and the strengths of these overtones, are different. Hence, one can distinguish between the notes produced by a sitar and a violin even if they have the same frequency of vibration.
d. This is because solids have both, the elasticity of volume and elasticity of shape, whereas gases have only the volume elasticity.
e. A sound pulse is a combination of waves of different wavelength. As waves of different λ travel in a dispersive medium with different velocities, therefore, the shape of the pulse gets distorted.
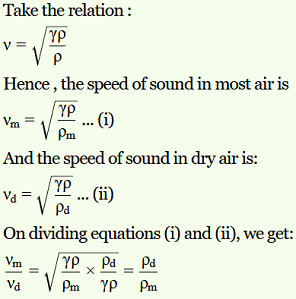

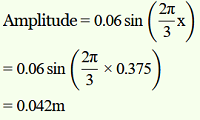
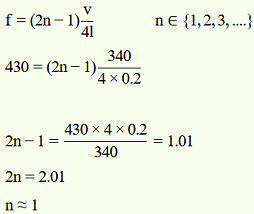
Leave a Reply