13.1
Which of the following examples represent periodic motion?
a. A swimmer completing one (return) trip from one bank of a river to the other and back.
b. A freely suspended bar magnet displaced from its N-S direction and released.
c. A hydrogen molecule rotating about its center of mass.
d. An arrow released from a bow.
Solution :
a. The swimmer’s motion is not periodic. Though the motion of a swimmer is to and fro but will not have a definite period.
b. The motion of a freely-suspended magnet, if displaced from its N-S direction and released, is periodic because the magnet oscillates about its position with a definite period of time.
c. When a hydrogen molecule rotates about its centre of mass, it comes to the same position again and again after an equal interval of time. Such a motion is periodic.
d. An arrow released from a bow moves only in the forward direction. It does not come backward. Hence, this motion is not a periodic.
13.2
Which of the following examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
a. the rotation of earth about its axis.
b. motion of an oscillating mercury column in a U-tube.
c. motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower most point.
d. general vibrations of a polyatomic molecule about its equilibrium position.
Solution :
a. It is periodic but not simple harmonic motion because it is not to and fro about a fixed point.
b. It is a simple harmonic motion because the mercury moves to and fro on the same path, about the fixed position, with a certain period of time.
c. It is simple harmonic motion because the ball moves to and fro about the lowermost point of the bowl when released. Also, the ball comes back to its initial position in the same period of time, again and again.
d. A polyatomic molecule has many natural frequencies of oscillation. Its vibration is the superposition of individual simple harmonic motions of a number of different molecules. Hence, it is not simple harmonic, but periodic.
13.3
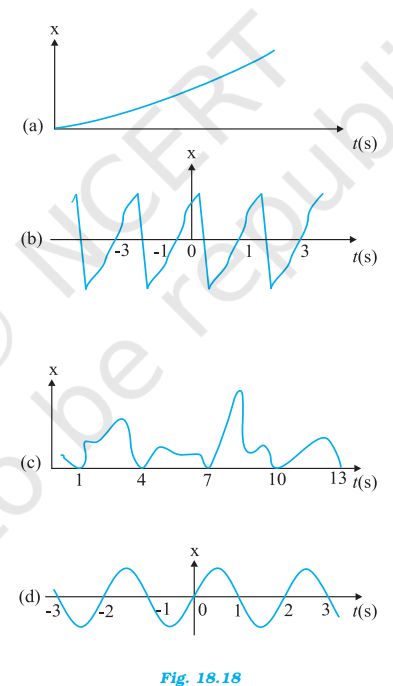
Fig. 13.18 depicts four x-t plots for linear motion of a particle. Which of the plots represent periodic motion? What is the period of motion (in case of periodic motion) ?
Solution :
a. It is not a periodic motion. This represents a unidirectional, linear uniform motion. There is no repetition of motion in this case.
b. In this case, the motion of the particle repeats itself after 2 s. Hence, it is a periodic motion, having a period of 2 s.
c. It is not a periodic motion. This is because the particle repeats the motion in one position only. For a periodic motion, the entire motion of the particle must be repeated in equal intervals of time.
d. In this case, the motion of the particle repeats itself after 2 s. Hence, it is a periodic motion, having a period of 2 s.
13.4
Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (ω is any positive constant):
a. sin ωt – cos ωt
b. sin3 ωt
c. 3 cos (π/4 – 2ωt)
d. cos ωt + cos 3ωt + cos 5ωt
e. exp (–ω2t2)
Solution :
a. SHM
The given function is:
sin ωt – cos ωt
b. Periodic but not SHM
The given function is:
sin3 ωt
sin3 ωt = 1/4 [3 sin ωt – sin3ωt]
The terms sin ωt and sin ωt individually represent simple harmonic motion (SHM). However, the superposition of two SHM is periodic and not simple harmonic.
Ites period is: 2π/ω
c. SHM
The given function is:
This function represents simple harmonic motion because it can be written in the form: a cos (ωt + Φ)Its period is: 2π/2ω = π/ω
d. Periodic, but not SHM
The given function is cosωt + cos3ωt + cos5ωt. Each individual cosine function represents SHM. However, the superposition of three simple harmonic motions is periodic, but not simple harmonic.
e. Non-periodic motion
The given function exp(-ω2t2) is an exponential function. Exponential functions do not repeat themselves. Therefore, it is a non-periodic motion.
f. The given function 1 + ωt + ω2t2 is non-periodic.
13.5
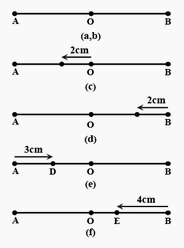
A particle is in linear simple harmonic motion between two points, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
a. at the end A,
b. at the end B,
c. at the mid-point of AB going towards A,
d. at 2 cm away from B going towards A,
e. at 3 cm away from A going towards B, and
f. at 4 cm away from B going towards A.
Solution :
From above figure, where A and B represent the two extreme positions of a SHM. FOr velocity, the direction from A to B is taken to b positive. The acceleration and the force, along AP are taken as positive and alsong Bp are taken as negative.
a. At the end A, the particle executing SHM is momentarily at rest being its extreme position of motion. Therefore, its velocity is zero. Acceleration is positive because it is directed along AP, Force is also Positive since the force is directed along AP.
b. At the end B, velocity is zero. Here, acceleration and force are negative as they are directed along BP.
c. At the mid point of AB going towards A, the particle is at its mean position P, with a tendency to move along PA. Hence, velocity is positive. Both acceleration and force are zero.
d. At 2 cm away from B going towards A, the particle is at Q, with a tendency to move along QP, which is negative direction. Therefore, velocity, acceleration and force all are positive.
e. At 3 cm away from A going towards B, the particle is at R, with a tendency to move along RP, which is positive direction. Here, velocity, acceleration all are positive.
f. At 4 cm away from A going towards A, the particles is at S, with a tendency to move along SA, which is negative direction. Therefore, velocity is negative but acceleration is directed towards mean position, along SP. Hence it is positive and also force is positive similarly.
13.6
Which of the following relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion?
a. a = 0.7x
b. a = –200x2
c. a = –10x
d. a = 100x3
Solution :
In SHM, acceleration a is related to displacement by the relation of the form a = -kx, which is for relation (c).
13.7
The motion of a particle executing simple harmonic motion is described by the displacement function,
x (t) = A cos (ωt + φ).
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is ω cm/s, what are its amplitude and initial phase angle? The angular frequency of the particle is π s–1. If instead of the cosine function, we choose the sine function to describe the SHM: x = B sin (ωt + α), what are the amplitude and initial phase of the particle with the above initial conditions.
Solution :
Initially, at t = 0;
Displacement, x = 1 cm
Initial velocity, v = ω cm/ sec.
Angular frequency, ω = π rad/s–1
It is given that, x(t) = A cos(ωt + Φ) 1 = A cos(ω × 0 + Φ) = A cos Φ A cosΦ = 1 …(i)
Velocity, v= dx/dt
ω = -A ωsin(ωt + Φ)
1 = -A sin(ω × 0 + Φ) = -A sin Φ
A sin Φ = -1 …(ii)
Squaring and adding equations (i) and (ii), we get:
A2 (sin2 Φ + cos2 Φ) = 1 + 1
A2 = 2
∴ A = √2 cm
Dividing equation (ii) by equation (i), we get:
tanΦ = -1
∴ Φ = 3π/4 , 7π/4,……
SHM is given as:
x = Bsin (ωt + α)
Putting the given values in this equation, we get:
1 = B sin [ω × 0 + α] = 1 + 1
B sin α = 1 …(iii)
Velocity, v = ωBcos (ωt + α)
Substituting the given values, we get:
π = π B sin α
B sin α = 1 …(iv)
Squaring and adding equations (iii) and (iv), we get:
B2 [sin2 α + cos2 α] = 1 + 1
B2 = 2
∴ B = √2 cm
Dividing equation (iii) by equation (iv), we get:
B sin α / B cos α = 1/1
tan α = 1 = tan π/4
∴ α = π/4, 5π/4,……
13.8
A spring balance has a scale that reads from 0 to 50 kg. The length of the scale is 20 cm. A body suspended from this balance, when displaced and released, oscillates with a period of 0.6 s. What is the weight of the body?
Solution :
Maximum mass that the scale can read, M = 50 kg
Maximum displacement of the spring = Length of the scale, l = 20 cm = 0.2 m
Time period, T = 0.6 s
Maximum force exerted on the spring, F = Mg
where,
g = acceleration due to gravity = 9.8 m/s2
F = 50 × 9.8 = 490
∴ Spring constant, k = F/l = 490/0.2 = 2450 N m-1.
Mass m, is suspended from the balance.
13.9
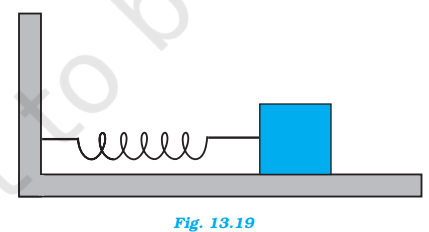
A spring having with a spring constant 1200 N m–1 is mounted on a horizontal table as shown in Fig. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
Solution :
Spring constant, k = 1200 N m–1
Mass, m = 3 kg
Displacement, A = 2.0 cm = 0.02 cm
(i) Frequency of oscillation v, is given by the relation:
Hence, the maximum velocity of the mass is 0.4 m/s.
13.10
In Exercise 13.9, let us take the position of mass when the spring is upstretched as x = 0, and the direction from left to right as the positive direction of x-axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwatch (t = 0), the mass is
(a) at the mean position,
(b) at the maximum stretched position, and
(c) at the maximum compressed position.
In what way do these functions for SHM differ from each other, in frequency, in amplitude or the initial phase?
Solution :
Distance travelled by the mass sideways, a = 2.0 cm
Angular frequency of oscillation:
The functions neither differ in amplitude nor in frequency. They differ in initial phase.
13.11
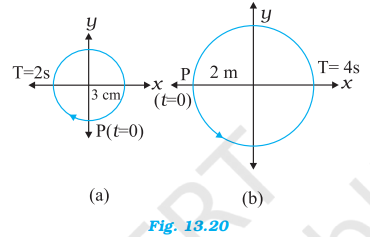
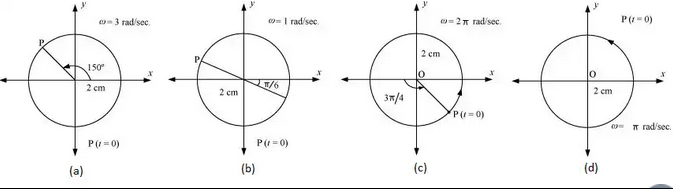
Figures 13.20 correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure.
Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.
Solution :
(a) Time period, t = 2 s
Amplitude, A = 3 cm
At time, t = 0, the radius vector OP makes an angle π/2 with the positive x-axis,.e., phase angle Φ = +π/2
Therefore, the equation of simple harmonic motion for the x-projection of OP, at the time t, is given by the displacement equation:
(b) Time Period, t = 4 s
Amplitude, a = 2 m
At time t = 0, OP makes an angle π with the x-axis, in the anticlockwise direction, Hence, phase angle Φ = +π
Therefore, the equation of simple harmonic motion for the x-projection of OP, at the time t, is given as:
13.12
Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t = 0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s).
a. x = –2 sin (3t + π/3)
b. x = cos (π/6 – t)
c. x = 3 sin (2πt + π/4)
d. x = 2 cos πt
Solution :
a.
If this equation is compared with the standard SHM equation
then we got,
Amplitude, A = 2 cm
Phase angle, Φ = 5π/6 = 150°.
Angular velocity = ω = 2π/T = 3rad/sec.
b.
If this equation is compared with the standard SHM equation
than we got,
Amplitude, A = 1
Phase angle, Φ = -π/6 = -30°.
Angular velocity, ω = 2π/T = 1 rad/s.
The motion of the particle can be plotted as shown in fig. 10(b).
c.
If this equation is compared with the standard SHM equation
Amplitude, A = 3 cm
Phase angle, Φ = 3π/4 = 135°
Angular velocity, ω = 2π/T = 2 rad/s.
The motion of the particle can be plotted as shown in fig. 10(c).
d.
x = 2 cos πt
If this equation is compared with the standard SHM equation
Amplitude, A = 2 cm
Phase angle, Φ = 0
Angular velocity, ω = π rad/s.
The motion of the particle can be plotted as shown in fig. 10(d).
13.13
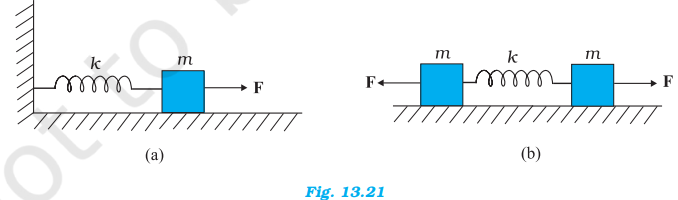
Figure 13.21(a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure 13.21 (b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in Fig. 13.21(b) is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in Fig. (a) and the two masses in Fig. (b) are released, what is the
period of oscillation in each case ?
Solution :
a. The maximum extension of the spring in both cases will = Flk, where k is the spring constant of the springs used.
b. In Fig. 13.21(a) if x is the extension in the spring, when mass m is returning to its mean position after being released free, then restoring force on the mass iss F = -kx, i.e., F ∝ x As, this F is directed towards mean position of the mass, hence the mass attached to the spring will execute SHM.
Spring factor = spring constant = k
inertia factor = mass of the given mass = m
As time period,
In Fig.13.21(b), we have a two body system of spring constant k and reduced mass,
µ = m × m / m + m = m/2.
Inertia factor = m/2
Spring factor = k
13.14
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rad/min, what is its maximum speed?
Solution :
Angular frequency of the piston, ω = 200 rad/ min.
Stroke = 1.0 m
Amplitude, A = 1.0/2 = 0.5 m
The maximum speed (vmax) of piston is given by the relation:
vmax = Aω = 200 × 0.5 = 100m/min.
13.15
The acceleration due to gravity on the surface of moon is 1.7 ms–2. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s? (g on the surface of earth is 9.8 ms–2)
Solution :
Acceleration due to gravity on the surface of moon, g’ = 1.7 m s–2 Acceleration due to gravity on the surface of earth, g = 9.8 m s–2
Time period of a simple pendulum on earth, T = 3.5 s
Hence, the time period of the simple pendulum on the surface of moon is 8.4 s.
13.16
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
Solution :
The bob of the simple pendulum will experience the acceleration due to gravity and the centripetal acceleration provided by the circular motion of the car.
Acceleration due to gravity = g
Centripetal acceleration = v2/R
where,
v is the uniform speed of the car
R is the radius of the track
Effective acceleration (g’) is given as:
13.17
Cylindrical piece of cork of density of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
where ρ is the density of cork. (Ignore damping due to viscosity of the liquid).
Solution :
Base area of the cork = A Height of the cork = h Density of the liquid = ρ1 Density of the cork = ρ
In equilibrium:
Weight of the cork = Weight of the liquid displaced by the floating cork
Let the cork be depressed slightly by x. As a result, some extra water of a certain volume is displaced. Hence, an extra up-thrust acts upward and provides the restoring force to the cork.
Up-thrust = Restoring force, F = Weight of the extra water displaced
F = –(Volume × Density × g)
Volume = Area × Distance through which the cork is depressed
Volume = Ax
∴ F = – A x ρ1 g …..(i)
According to the force law:
F = k x
k = F/x
where, k is constant
k = F/x = -Aρ1 g ….(ii)
The time period of the oscillations of the cork:
T = 2π √m/k ….(iii)
where,
m = Mass of the cork
= Volume of the cork × Density
= Base area of the cork × Height of the cork × Density of the cork
= Ahρ
Hence, the expression for the time period becomes:
13.18
One end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
Solution :
Area of cross-section of the U-tube = A
Density of the mercury column = ρ
Acceleration due to gravity = g
Restoring force, F = Weight of the mercury column of a certain height
F = –(Volume × Density × g)
F = –(A × 2h × ρ × g) = –2Aρgh = –k × Displacement in one of the arms (h)
Where,
2h is the height of the mercury column in the two arms
k is a constant, given by k = -F/h = 2Aρg
where,
m is the mass of the mercury column
Let l be the length of the total mercury in the U-tube.
Mass of mercury, m = Volume of mercury × Density of mercury = Alρ
Hence, the mercury column executes simple harmonic motion with time period 2π √l/2g .
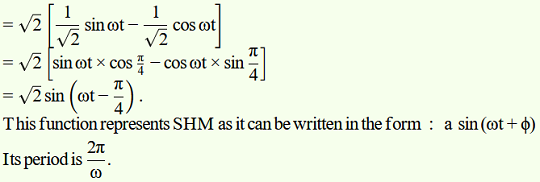
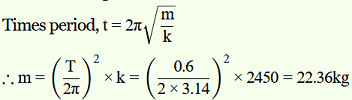


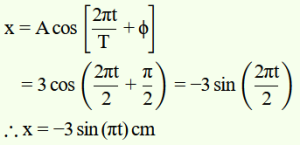
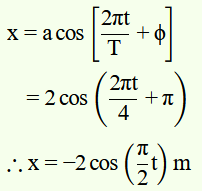
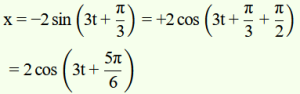
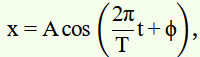
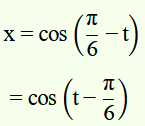
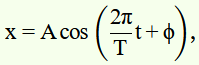
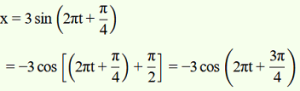
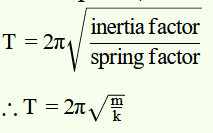
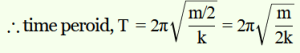


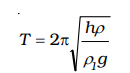
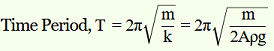
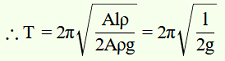
Leave a Reply