10.1
The triple points of neon and carbon dioxide are 24.57 K and 216.55 K respectively. Express these temperatures on the Celsius and Fahrenheit scales.
Solution :
Kelvin and Celsius
scales are related as:
TC = TK – 273.15 … (i)
Celsius and Fahrenheit scales are related as:
TF = (9/5)TC + 32 ….(ii)
For neon:
TK = 24.57 K
∴ TC = 24.57 – 273.15 = –248.58°C
TF = (9/5)TC + 32
= (9/5) × (-248.58) +32
= 415.440 F
For carbon dioxide:
TK = 216.55 K
∴ TC= 216.55 – 273.15 = –56.60°C
TF = (9/5)TC + 32
= (9/5) × (-56.60) +32
= -69.880 C
10.2
Two absolute scales A and B have triple points of water defined to be 200 A and 350 B. What is the relation betweenTA andTB?
Solution :
Triple point of water on absolute scaleA,T1 = 200 A
Triple point of water on absolute scale B,T2 = 350 B
Triple point of water on Kelvin scale, TK = 273.15 K
The temperature 273.15 K on Kelvin scale is equivalent to 200 A on absolute scale A.
T1 = TK
200 A = 273.15 K
∴ A = 273.15/200
The temperature 273.15 K on Kelvin scale is equivalent to 350 B on absolute scale B.
T2 = TK
350 B = 273.15
∴ B = 273.15/350
TA is triple point of water on scale A.
TB is triple point of water on scale B.
∴ 273.15/200 × TA = 273.15/350 × TB
Therefore, the ratioTA :TB is given as 4 : 7.
10.3
The electrical resistance in ohms of a certain thermometer varies with temperature according to the approximate law:
R =Ro [1 + α (T – To)]
The resistance is 101.6 Ω at the triple-point of water 273.16 K, and 165.5 Ω at the normal melting point of lead (600.5 K). What is the temperature when the resistance is 123.4 Ω?
Solution :
It is given that:
R =R0 [1 + α (T – T0)] … (i)
where,
R0 andT0 are the initial resistance and temperature respectively
R andT are the final resistance and temperature respectively
α is a constant
At the triple point of water,T0 = 273.15 K
Resistance of lead,R0 = 101.6 Ω
At normal melting point of lead,T = 600.5 K
Resistance of lead,R = 165.5 Ω
Substituting these values in equation (i), we get:
R =Ro [1 + α (T – To)]
165.5 = 101.6 [ 1 + α(600.5 – 273.15) ]
1.629 = 1 + α (327.35)
∴ α = 0.629 / 327.35 = 1.92 × 10-3 K-1
For resistance,R1 = 123.4 Ω
R1 =R0 [1 + α (T – T0)]
where,
T is the temperature when the resistance of lead is 123.4 Ω
123.4 = 101.6 [ 1 + 1.92 × 10-3( T – 273.15) ]
Solving forT, we get
T = 384.61 K.
10.4
Answer the following:
a. The triple-point of water is a standard fixed point in modern thermometry. Why? What is wrong in taking the melting point of ice and the boiling point of water as standard fixed points (as was originally done in the Celsius scale)?
b. There were two fixed points in the original Celsius scale as mentioned above which were assigned the number 0 °C and 100 °C respectively. On the absolute scale, one of the fixed points is the triple-point of water, which on the Kelvin absolute scale is assigned the number 273.16 K. What is the other fixed point on this (Kelvin) scale?
c. The absolute temperature (Kelvin scale)T is related to the temperaturetc on the Celsius scale by
tc =T – 273.15
Why do we have 273.15 in this relation, and not 273.16?
d. What is the temperature of the triple-point of water on an absolute scale whose unit interval size is equal to that of the Fahrenheit scale?
Solution :
a. The triple point of water has a unique value of 273.16 K. At particular values of volume and pressure, the triple point of water is always 273.16 K. The melting point of ice and boiling point of water do not have particular values because these points depend on pressure and temperature.
b. The absolute zero or 0 K is the other fixed point on the Kelvin absolute scale.
c. The temperature 273.16 K is the triple point of water. It is not the melting point of ice. The temperature 0°C on Celsius scale is the melting point of ice. Its corresponding value on Kelvin scale is 273.15 K.
Hence, absolute temperature (Kelvin scale)T, is related to temperaturetc, on Celsius scale as:
tc =T – 273.15
d. LetTF be the temperature on Fahrenheit scale andTK be the temperature on absolute scale. Both the temperatures can be related as:
(TF – 32) / 180 = (TK – 273.15) / 100 ….(i)
LetTF1 be the temperature on Fahrenheit scale andTK1 be the temperature on absolute scale. Both the temperatures can be related as:
(TF1 – 32) / 180 = (TK1 – 273.15) / 100 ….(ii)
It is given that:
TK1 –TK = 1 K
Subtracting equation (i) from equation (ii), we get:
(TF1 -TF) / 180 = (TK1 -TK) / 100 = 1 / 100
TF1 -TF = (1 ×180) / 100 = 9/5
Triple point of water = 273.16 K
∴ Triple point of water on absolute scale = 273.16 × (9/5) = 491.69
10.5
Two ideal gas thermometers Aand Buse oxygen and hydrogen respectively. The following observations are made:
| Temperature | Pressure thermometer A | Pressure thermometer B |
| Triple-point of water | 1.250 × 105 Pa | 0.200 × 105 Pa |
| Normal melting point of sulphur | 1.797 × 105 Pa | 0.287 × 105 Pa |
a. What is the absolute temperature of normal melting point of sulphur as read by thermometers A and B?
b. What do you think is the reason behind the slight difference in answers of thermometers A and B? (The thermometers are not faulty). What further procedure is needed in the experiment to reduce the discrepancy between the two readings?
Solution :
a. Triple point of water,T = 273.16 K.
At this temperature, pressure in thermometer A,PA = 1.250 × 105 Pa
LetT1 be the normal melting point of sulphur.
At this temperature, pressure in thermometer A,P1 = 1.797 × 105 Pa
According to Charles’ law, we have the relation:
PA /T = P1 /T1
∴T1 = (P1T) /PA = (1.797 × 10 × 273.16) / (1.250 × 105)
= 392.69 K
Therefore, the absolute temperature of the normal melting point of Sulphur as read by thermometer A is 392.69 K.
At triple point 273.16 K, the pressure in thermometer B,PB = 0.200 × 105 Pa
At temperatureT1, the pressure in thermometer B, P2 = 0.287 × 105 Pa
According to Charles’ law, we can write the relation:
PB /T = P1 /T1
(0.200 × 105) / 273.16 = (0.287 × 105) /T1
∴T1 = [ (0.287 × 105) / (0.200 × 105) ] × 273.16 = 391.98 K
Therefore, the absolute temperature of the normal melting point of sulphur as read by thermometer B is 391.98 K.
b. The oxygen and hydrogen gas present in thermometers A and B respectively are not perfect ideal gases. Hence, there is a slight difference between the readings of thermometers A and B.
To reduce the discrepancy between the two readings, the experiment should be carried under low pressure conditions. At low pressure, these gases behave as perfect ideal gases.
10.6
A steel tape 1m long is correctly calibrated for a temperature of 27.0 °C. The length of a steel rod measured by this tape is found to be 63.0 cm on a hot day when the temperature is 45.0 °C. What is the actual length of the steel rod on that day? What is the length of the same steel rod on a day when the temperature is 27.0 °C? Coefficient of linear expansion of steel = 1.20 × 10–5 K–1.
Solution :
Length of the steel tape at temperatureT = 27°C,l = 1 m = 100 cm
At temperatureT1 = 45°C, the length of the steel rod,l1 = 63 cm
Coefficient of linear expansion of steel,α = 1.20 × 10–5 K–1
Letl2 be the actual length of the steel rod andl’ be the length of the steel tape at 45°C.
l’ = l + αl(T1 – T)
∴ l’ = 100 + 1.20 × 10-5 × 100(45 – 27)
= 100.0216 cm
Hence, the actual length of the steel rod measured by the steel tape at 45°C can be calculated as:
l2 = (100.0216 / 100) × 63 = 63.0136 cm
Therefore, the actual length of the rod at 45.0°C is 63.0136 cm. Its length at 27.0°C is 63.0 cm.
10.7
A large steel wheel is to be fitted on to a shaft of the same material. At 27 °C, the outer diameter of the shaft is 8.70 cm and the diameter of the central hole in the wheel is 8.69 cm. The shaft is cooled using ‘dry ice’. At what temperature of the shaft does the wheel slip on the shaft? Assume coefficient of linear expansion of the steel to be constant over the required temperature range: αsteel = 1.20 × 10–5 K–1.
Solution :
The given temperature,T = 27°C can be written in Kelvin as:
27 + 273 = 300 K
Outer diameter of the steel shaft atT,d1 = 8.70 cm
Diameter of the central hole in the wheel atT,d2 = 8.69 cm
Coefficient of linear expansion of steel,αsteel = 1.20 × 10–5 K–1
After the shaft is cooled using ‘dry ice’, its temperature becomesT1.
The wheel will slip on the shaft, if the change in diameter, Δd = 8.69 – 8.70
= – 0.01 cm
TemperatureT1, can be calculated from the relation:
Δd =d1αsteel (T1 –T)
0.01 = 8.70 × 1.20 × 10–5 (T1 – 300)
(T1 – 300) = 95.78
∴ T1= 204.21 K
= 204.21 – 273.16
= –68.95°C
Therefore, the wheel will slip on the shaft when the temperature of the shaft is –69°C.
10.8
A hole is drilled in a copper sheet. The diameter of the hole is 4.24 cm at 27.0 °C. What is the change in the diameter of the hole when the sheet is heated to 227 °C? Coefficient of linear expansion of copper = 1.70 × 10–5 K–1.
Solution :
Initial temperature,T1 = 27.0°C
Diameter of the hole atT1,d1 = 4.24 cm
Final temperature,T2 = 227°C
Diameter of the hole atT2 =d2
Co-efficient of linear expansion of copper,αCu= 1.70 × 10–5 K–1
For co-efficient of superficial expansionβ,and change in temperature ΔT, we have the relation:
Change in area (∆) / Original area (A) = β∆T
[ (πd22/ 4) – (πd12 / 4) ] / (πd11 / 4) = ∆A /A
∴ ∆A /A = (d22 -d12) / d12
But β = 2α
∴ (d22 -d12) /d12 = 2α∆T
(d22 /d12) – 1 = 2α(T2 -T1)
d22 / 4.242 = 2 × 1.7 × 10-5 (227 – 27) +1
d22 = 17.98 × 1.0068 = 18.1
∴d2 = 4.2544 cm
Change in diameter =d2 –d1 = 4.2544 – 4.24 = 0.0144 cm
Hence, the diameter increases by 1.44 × 10–2 cm.
10.9
A brass wire 1.8 m long at 27 °C is held taut with little tension between two rigid supports. If the wire is cooled to a temperature of –39 °C, what is the tension developed in the wire, if its diameter is 2.0 mm? Co-efficient of linear expansion of brass = 2.0 × 10–5 K–1; Young’s modulus of brass = 0.91 × 1011 Pa.
Solution :
Initial temperature,T1 = 27°C
Length of the brass wire atT1,l = 1.8 m
Final temperature,T2 = –39°C
Diameter of the wire,d = 2.0 mm = 2 × 10–3 m
Tension developed in the wire =F
Coefficient of linear expansion of brass,α = 2.0 × 10–5 K–1
Young’s modulus of brass,Y = 0.91 × 1011 Pa
Young’s modulus is given by the relation:
γ = Stress / Strain = (F/A) / (∆L/L)
∆L =F XL / (A XY) ……(i)
Where,
F = Tension developed in the wire
A = Area of cross-section of the wire.
ΔL = Change in the length, given by the relation:
ΔL =αL(T2 –T1) … (ii)
Equating equations (i) and (ii), we get:
αL(T2 -T1) =FL / [ π(d/2)2X Y ]
F = α(T2 – T1)πY(d/2)2
F = 2 × 10-5 × (-39-27) × 3.14 × 0.91 × 1011 × (2 × 10-3 / 2 )2
= -3.8 × 102 N
(The negative sign indicates that the tension is directed inward.)
Hence, the tension developed in the wire is 3.8 ×102 N.
10.10
A brass rod of length 50 cm and diameter 3.0 mm is joined to a steel rod of the same length and diameter. What is the change in length of the combined rod at 250 °C, if the original lengths are at 40.0 °C? Is there a ‘thermal stress’ developed at the junction? The ends of the rod are free to expand (Co-efficient of linear expansion of brass = 2.0 × 10–5 K–1, steel = 1.2 × 10–5 K–1).
Solution :
Initial temperature,T1 = 40°C
Final temperature,T2 = 250°C
Change in temperature, ΔT =T2 –T1 = 210°C
Length of the brass rod atT1,l1 = 50 cm
Diameter of the brass rod atT1,d1 = 3.0 mm
Length of the steel rod at T2,l2 = 50 cm
Diameter of the steel rod atT2,d2 = 3.0 mm
Coefficient of linear expansion of brass, α1 = 2.0 × 10–5K–1
Coefficient of linear expansion of steel, α2 = 1.2 × 10–5K–1
For the expansion in the brass rod, we have:
Change in length (∆l1) / Original length (l1) = α1ΔT
∴ ∆l1 = 50 × (2.1 × 10-5) × 210
= 0.2205 cm
For the expansion in the steel rod, we have:
Change in length (∆l2) / Original length (l2) = α2ΔT
∴ ∆l1 = 50 × (1.2 × 10-5) × 210
= 0.126 cm
Total change in the lengths of brass and steel,
Δl = Δl1 + Δl2
= 0.2205 + 0.126
= 0.346 cm
Total change in the length of the combined rod = 0.346 cm
Since the rod expands freely from both ends, no thermal stress is developed at the junction.
10.11
The coefficient of volume expansion of glycerin is 49 × 10–5 K–1. What is the fractional change in its density for a 30 °C rise in temperature?
Solution :
Coefficient of volume expansion of glycerin,αV = 49 × 10–5 K–1
Rise in temperature, ΔT = 30°C
Fractional change in its volume = ΔV/V
This change is related with the change in temperature as:
ΔV/V =αV ΔT
VT2 -VT1 = VT1 αV ΔT
(m /ρT2)- (m /ρT1) = (m /ρT1)αV ΔT
Where,
m = Mass of glycerin
ρT1 = Initial density atT1
ρT2 = Initial density atT2
(ρT1 – ρT2 ) / ρT2 = Fractional change in density
∴ Fractional change in the density of glycerin = 49 ×10–5 × 30 = 1.47 × 10–2.
10.12
A 10 kW drilling machine is used to drill a bore in a small aluminium block of mass 8.0 kg. How much is the rise in temperature of the block in 2.5 minutes, assuming 50% of power is used up in heating the machine itself or lost to the surroundings. Specific heat of aluminium = 0.91 J g–1 K–1.
Solution :
Power of the drilling machine,P = 10 kW = 10 × 103 W
Mass of the aluminum block,m = 8.0 kg = 8 × 103 g
Time for which the machine is used, t = 2.5 min = 2.5 × 60 = 150 s
Specific heat of aluminium,c = 0.91 J g–1 K–1
Rise in the temperature of the block after drilling = δT
Total energy of the drilling machine =Pt
= 10 × 103 × 150
= 1.5 × 106 J
It is given that only 50% of the power is useful.
Useful energy, ∆Q = (50/100) × 1.5 × 106 = 7.5 × 105 J
But ∆Q =mc∆T
∴ ∆T = ∆Q /mc
= (7.5 × 105) / (8 × 103 × 0.91)
= 103o C
Therefore, in 2.5 minutes of drilling, the rise in the temperature of the block is 103°C.
10.13
A copper block of mass 2.5 kg is heated in a furnace to a temperature of 500 °C and then placed on a large ice block. What is the maximum amount of ice that can melt? (Specific heat of copper = 0.39 J g–1 K–1; heat of fusion of water = 335 J g–1).
Solution :
Mass of the copper block,m = 2.5 kg = 2500 g
Rise in the temperature of the copper block, Δθ = 500°C
Specific heat of copper, C = 0.39 J g–1 °C–1
Heat of fusion of water, L = 335 J g–1
The maximum heat the copper block can lose, Q =mCΔθ
= 2500 × 0.39 × 500
= 487500 J
Letm1 g be the amount of ice that melts when the copper block is placed on the ice block.
The heat gained by the melted ice,Q =m1L
∴m1 =Q /L = 487500 / 335 = 1455.22 g
Hence, the maximum amount of ice that can melt is 1.45 kg.
10.14
In an experiment on the specific heat of a metal, a 0.20 kg block of the metal at 150 °C is dropped in a copper calorimeter (of water equivalent 0.025 kg) containing 150 cm3 of water at 27 °C. The final temperature is 40 °C. Compute the specific heat of the metal. If heat losses to the surroundings are not negligible, is your answer greater or smaller than the actual value for specific heat of the metal?
Solution :
Mass of the metal,m = 0.20 kg = 200 g
Initial temperature of the metal,T1 = 150°C
Final temperature of the metal,T2 = 40°C
Calorimeter has water equivalent of mass,m’ = 0.025 kg = 25 g
Volume of water, V = 150 cm3
Mass (M) of water at temperatureT = 27°C:
150 × 1 = 150 g
Fall in the temperature of the metal:
ΔT =T1 –T2 = 150 – 40 = 110°C
Specific heat of water,Cw = 4.186 J/g/°K
Specific heat of the metal =C
Heat lost by the metal,θ =mCΔT … (i)
Rise in the temperature of the water and calorimeter system:
ΔT′’ = 40 – 27 = 13°C
Heat gained by the water and calorimeter system:
Δθ′′ =m1CwΔT’
= (M +m′)Cw ΔT’ … (ii)
Heat lost by the metal = Heat gained by the water and colorimeter system
mCΔT = (M +m’)Cw ΔT’
200 × C × 110 = (150 + 25) × 4.186 × 13
∴C = (175 × 4.186 × 13) / (110 × 200) = 0.43 Jg-1K-1
If some heat is lost to the surroundings, then the value ofC will be smaller than the actual value.
10.15
Given below are observations on molar specific heats at room temperature of some common gases.
| Gas | Molar Specific Heat CV ( cal mol-1 K-1) |
| Hydrogen | 4.87 |
| Nitrogen | 4.97 |
| Oxygen | 5.02 |
| Nitric oxide | 4.99 |
| Carbon monoxide | 5.01 |
| Chlorine | 6.17 |
The measured molar specific heats of these gases are markedly different from those for monatomic gases. Typically, molar specific heat of a monatomic gas is 2.92 cal/mol K. Explain this difference. What can you infer from the somewhat larger (than the rest) value for chlorine?
Solution :
The gases listed in the given table are diatomic. Besides the translational degree of freedom, they have other degrees of freedom (modes of motion).
Heat must be supplied to increase the temperature of these gases. This increases the average energy of all the modes of motion. Hence, the molar specific heat of diatomic gases is more than that of monatomic gases.
If only rotational mode of motion is considered, then the molar specific heat of a diatomic gas = (5/2)R
= (5/2) × 1.98 = 4.95 cal mol-1 K-1
With the exception of chlorine, all the observations in the given table agree with (5/2)R.
This is because at room temperature, chlorine also has vibrational modes of motion besides rotational and translational modes of motion.
10.16
A child running a temperature of 101°F is given an antipyrin (i.e. a medicine that lowers fever) which causes an increase in the rate of evaporation of sweat from his body. If the fever is brought down to 98 °F in 20 min, what is the average rate of extra evaporation caused, by the drug? Assume the evaporation mechanism to be the only way by which heat is lost. The mass of the child is 30 kg. The specific heat of human body is approximately the same as that of water, and latent heat of evaporation of water at that temperature is about 580 cal g–1.
Solution :
Initial temperature of the body of the child,T1 = 101°F
Final temperature of the body of the child,T2 = 98°F
Change in temperature, ΔT = [ (101 – 98) × (5/9) ] o C
Time taken to reduce the temperature, t = 20 min
Mass of the child, m = 30 kg = 30 × 103 g
Specific heat of the human body = Specific heat of water =c
= 1000 Cal/kg/ °C
Latent heat of evaporation of water,L = 580 cal g–1
The heat lost by the child is given as:
∆θ =mc∆T
= 30 × 1000 × (101 – 98) × (5/9)
= 50000 cal
Letm1 be the mass of the water evaporated from the child’s body in 20 min.
Loss of heat through water is given by:
∆θ =m1L
∴m1 = ∆θ /L
= (50000 / 580) = 86.2 g
∴ Average rate of extra evaporation caused by the drug =m1 /t
= 86.2 / 200
= 4.3 g/min.
10.17
A ‘thermacole’ icebox is a cheap and efficient method for storing small quantities of cooked food in summer in particular. A cubical icebox of side 30 cm has a thickness of 5.0 cm. If 4.0 kg of ice is put in the box, estimate the amount of ice remaining after 6 h. The outside temperature is 45 °C, and co-efficient of thermal conductivity of thermacole is 0.01 J s–1 m–1 K–1. [Heat of fusion of water = 335 × 103 J kg–1]
Solution :
Side of the given cubical ice box,s = 30 cm = 0.3 m
Thickness of the ice box,l = 5.0 cm = 0.05 m
Mass of ice kept in the ice box,m = 4 kg
Time gap,t = 6 h = 6 × 60 × 60 s
Outside temperature,T = 45°C
Coefficient of thermal conductivity of thermacole,K = 0.01 J s–1 m–1 K–1
Heat of fusion of water,L = 335 × 103 J kg–1
Let m’ be the total amount of ice that melts in 6 h.
The amount of heat lost by the food:
θ =KA(T – 0)t / l
Where,
A = Surface area of the box = 6s2 = 6 × (0.3)2 = 0.54 m3
θ = 0.01 × 0.54 × 45 × 6 × 60 × 60 / 0.05 = 104976 J
But θ = m’L
∴m’ = θ/L
= 104976/(335 × 103) = 0.313 kg
Mass of ice left = 4 – 0.313 = 3.687 kg
Hence, the amount of ice remaining after 6 h is 3.687 kg.
10.18
A brass boiler has a base area of 0.15 m2 and thickness 1.0 cm. It boils water at the rate of 6.0 kg/min when placed on a gas stove. Estimate the temperature of the part of the flame in contact with the boiler. Thermal conductivity of brass = 109 J s –1 m–1 K–1; Heat of vaporisation of water = 2256 × 103 J kg–1.
Solution :
Base area of the boiler, A = 0.15 m2
Thickness of the boiler, l = 1.0 cm = 0.01 m
Boiling rate of water, R = 6.0 kg/min
Mass, m = 6 kg
Time, t = 1 min = 60 s
Thermal conductivity of brass, K = 109 J s –1 m–1 K–1
Heat of vaporisation, L = 2256 × 103 J kg–1
The amount of heat flowing into water through the brass base of the boiler is given by:
θ =KA(T1 -T2)t / l ….(i)
where,
T1 = Temperature of the flame in contact with the boiler
T2 = Boiling point of water = 100°C
Heat required for boiling the water:
θ = mL … (ii)
Equating equations (i) and (ii), we get:
∴mL = KA(T1 -T2)t /l
T1 -T2 =mLl /KAt
= 6 × 2256 × 103 × 0.01 / (109 × 0.15 × 60)
= 137.98 o C
Therefore, the temperature of the part of the flame in contact with the boiler is 237.98°C.
10.19
Explain why:
a. a body with large reflectivity is a poor emitter
b. a brass tumbler feels much colder than a wooden tray on a chilly day
c. an optical pyrometer (for measuring high temperatures) calibrated for an ideal black body radiation gives too low a value for the temperature of a red hot iron piece in the open, but gives a correct value for the temperature when the same piece is in the furnace
d. the earth without its atmosphere would be inhospitably cold
e. heating systems based on circulation of steam are more efficient in warming a building than those based on circulation of hot water
Solution :
a. A body with a large reflectivity is a poor absorber of light radiations. A poor absorber will in turn be a poor emitter of radiations. Hence, a body with a large reflectivity is a poor emitter.
b. Brass is a good conductor of heat. When one touches a brass tumbler, heat is conducted from the body to the brass tumbler easily. Hence, the temperature of the body reduces to a lower value and one feels cooler.
Wood is a poor conductor of heat. When one touches a wooden tray, very little heat is conducted from the body to the wooden tray. Hence, there is only a negligible drop in the temperature of the body and one does not feel cool
Thus, a brass tumbler feels colder than a wooden tray on a chilly day.
c. An optical pyrometer calibrated for an ideal black body radiation gives too low a value for temperature of a red hot iron piece kept in the open.
Black body radiation equation is given by:
E = σ (T4 – T04)
Where,
E = Energy radiation
T = Temperature of optical pyrometer
To = Temperature of open space
σ = Constant
Hence, an increase in the temperature of open space reduces the radiation energy.
When the same piece of iron is placed in a furnace, the radiation energy, E = σ T4
d. Without its atmosphere, earth would be inhospitably cold. In the absence of atmospheric gases, no extra heat will be trapped. All the heat would be radiated back from earth’s surface.
e. A heating system based on the circulation of steam is more efficient in warming a building than that based on the circulation of hot water. This is because steam contains surplus heat in the form of latent heat (540 cal/g).
10.20
A body cools from 80 °C to 50 °C in 5 minutes. Calculate the time it takes to cool from 60 °C to 30 °C. The temperature of the surroundings is 20 °C.
Solution :
According to Newton’s law of cooling, we have:
(-dT/T) =K(T -T0)
dT /K(T -T0) = -Kdt ….(i)
Where,
Temperature of the body =T
Temperature of the surroundings =T0 = 20°C
K is a constant
Temperature of the body falls from 80°C to 50°C in time, t = 5 min = 300 s
Integrating equation (i), we get:
The temperature of the body falls from 60°C to 30°C in time = t
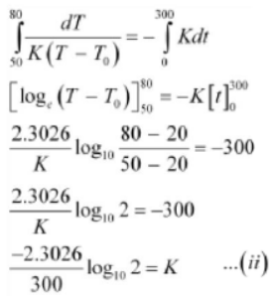
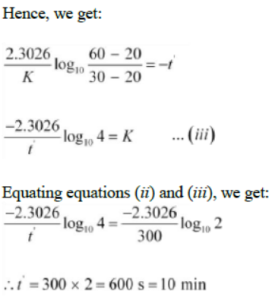
Leave a Reply