नोट्स भौतिक विज्ञान Notes Chapter 9 Bhautik Vigyan Class 11 Physics Hindi Medium

बरनौली की प्रमेय लिखिए तथा सिद्ध कीजिए, नियम स्पष्ट करें, समीकरण, उपयोग, परिभाषा

बरनौली की प्रमेय

जब कोई असंपीड्य तथा अश्यान द्रव अथवा गैस धारा रेखीय प्रवाह में बहता है तो इसके मार्ग के प्रत्येक बिंदु पर इसके एकांक आयतन की कुल ऊर्जा अर्थात् दाब ऊर्जा, गतिज ऊर्जा तथा स्थितिज ऊर्जा का योग एक नियतांक होता है इसे बरनौली की प्रमेय (Bernoulli theorem in Hindi) कहते हैं। अतः

\({ P + \frac{1}{2}ρv^2 + ρgh }\) = नियतांक

ρg से भाग करने पर

\(\frac{P}{ρg} \) + \( \frac{v^2}{2g} \) + h = नियतांक

दाब शीर्ष + वेग शीर्ष + गुरुत्वीय शीर्ष = नियतांक

यही बरनौली प्रमेय का समीकरण है बरनौली की प्रमेय उर्जा संरक्षण के सिद्धांत पर आधारित होती हैं।

बरनौली प्रमेय की उत्पत्ति (सिद्ध)

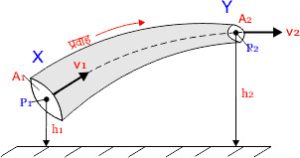
मानो कोई असंपीड्य तथा अश्यान द्रव किसी असमान अनुप्रस्थ काट वाली नली में धारा रेखीय प्रवाह में प्रवाहित हो रहा है जैसे चित्र में दिखाया गया है।

माना अनुप्रस्थ काट X का क्षेत्रफल A1 तथा दाब P1 है एवं इसकी पृथ्वी से ऊंचाई h1 है। तथा दाब P2 है एवं इसकी पृथ्वी से ऊंचाई h2 है। चूंकि A2 का क्षेत्रफल A1 से कम है। अतः अविरतता के सिद्धांत से Y का वेग v2 तथा X का वेग v1 से अधिक होगा।

माना द्रव का प्रवाह X सिरे से 1 सेकेंड के लिए होता है जिसमें वह v1 दूरी तय कर लेता है इस द्रव पर (P1 × A1) का बल आरोपित होता है तो एक सेकंड में X सिरे में प्रवेश करने वाले द्रव पर किया गया कार्य
W1 = P1 × A1 × v1
इसी प्रकार Y सिरे पर कार्य
W2 = P2 × A2 × v2
अतः द्रव पर किया गया कुल कार्य
W = W1 – W2
W = (P1 × A1 × v1) – (P2 × A2 × v2)
चूंकि सततता के समीकरण से प्रत्येक काट पर एक सेकंड में प्रवाहित आयतन समान होता है तो
A1v1 = A2v2 = V आयतन

तो कार्य W = (P₁ – P₂)V

या W = (P₁ – P₂)\(\large \frac{m}{ρ} \)समी.①

यदि 1 सेकंड में X सिरे पर प्रवेश करने वाले द्रव की गतिज ऊर्जा \(\large \frac{1}{2} \) mv₁² तथा Y सिरे पर गतिज ऊर्जा \( \large \frac{1}{2} \) mv₂² है तो

गतिज ऊर्जा में परिवर्तन

∆K = \( \large \frac{1}{2} \) mv₂² – \( \large \frac{1}{2} \) mv₁²

∆K = \( \large \frac{1}{2} \) m(v₂² – v₁²)  समी.②

अब X सिरे की स्थितिज ऊर्जा mgh₁ तथा Y सिरे पर स्थितिज ऊर्जा mgh₂ है तो

स्थितिज ऊर्जा में परिवर्तन

∆U = mgh₂ – mgh₁

∆U = mg(h₂ – h₁)   समी.③

चूंकि द्रव की ऊर्जा में परिवर्तन उसमें किए गए कार्य के कारण ही होती है तो

W = ∆K + ∆U

समी.① , ② व ③ के मान रखने पर

(P₁ – P₂)\( \large \frac{m}{ρ} \) = \( \large \frac{1}{2} \) m(v₂² – v₁²) + mg(h₂ – h₁)

P₁ – P₂ = \( \large \frac{1}{2} \) ρ(v₂² – v₁²) + ρg(h₂ – h₁)

P₁ + \( \large \frac{1}{2} \) ρv₁² + ρgh₁ = P₂ + \( \large \frac{1}{2} \) ρv₂² + ρgh₂
अतः \( { P + \frac{1}{2}ρv^2 + ρgh } \) = नियतांक

यही बरनौली की प्रमेय का समीकरण हैं।