उपग्रह का कक्षीय वेग क्या है, सूत्र, मान, परिक्रमण काल का सूत्र, कक्षीय चाल
उपग्रह का कक्षा वेग/चाल
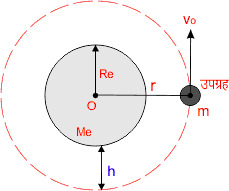
माना पृथ्वी का द्रव्यमान Me तथा त्रिज्या Re है पृथ्वी सतह से h ऊंचाई पर एक उपग्रह है जिसका द्रव्यमान m है। यह उपग्रह पृथ्वी के चारों ओर वृत्तीय कक्षा में परिक्रमण कर रहा है तो पृथ्वी द्वारा उपग्रह पर लगने वाला गुरुत्वाकर्षण बल
F = G\( \large \frac{M_e m}{r^2} \) समी.①
चूंकि उपग्रह पृथ्वी के चारों ओर एक वृत्तीय पथ पर गति कर रहा है तो उस पर लगने वाला अभिकेंद्र बल
F = \( \large \frac{m v_o}{r} \) समी.②
समी.① व समी.② से
\( \large \frac{m v_o}{r} \) = G\( \large \frac{M_e m}{r^2} \)
vo2 = G\( \large \frac{M_e}{r} \)
vo = \( \sqrt{\frac{GM_e}{r}} \)
लेकिन r = Re + h है तो
vo = \(\sqrt{\frac{GM_e}{R_e + h}} \)
यदि पृथ्वी सतह पर गुरुत्वीय त्वरण g है तब
g = \( \large \frac{GM_e}{R_e^2} \)
GMe = gRe2
अब GMe का मान उपरोक्त समीकरण में रखने पर
vo = \( \sqrt{\frac{gR_e^2}{R_e + h}} \)
\({ v_o = \sqrt{R_e^2 \frac{g}{R_e + h}} } \)यदि कोई उपग्रह पृथ्वी तल से इतने समीप है कि Re की तुलना में h को शून्य (नगण्य) मान सकते हैं तो
vo = \( \sqrt{\frac{gR_e^2}{R_e}} \)
\( { v_o = \sqrt{gR_e}} \)यही कक्षीय वेग/चाल का सूत्र है कक्षीय वेग का मान उपग्रह के द्रव्यमान पर निर्भर नहीं करता है यह उपग्रह की ऊंचाई पर निर्भर करता है। उपग्रह की ऊंचाई बढ़ाने पर कक्षीय वेग का मान घटता है। कक्षीय वेग (orbital speed of satellite in Hindi) को vo से प्रदर्शित करते हैं।
कक्षीय वेग का मान
सूत्र vo = \( \sqrt{gR_e} \) से
पृथ्वी का गुरुत्वीय त्वरण g = 9.8 मीटर/सेकंड2 तथा पृथ्वी की त्रिज्या Re = 6.4 × 106 मीटर होती है तो कक्षीय वेग का मान
vo = \( \small \sqrt{9.8 × 6.4 × 10^6} \)
vo = 7919.6 मीटर/सेकंड
vo = 7.92 किमी/सेकंड
या \( {v_o = \sqrt{8 किमी/सेकंड} \)
अतः कक्षीय वेग का मान 8 किमी/सेकंड होता है।
परिक्रमण काल (period of revolution of satellite)
यदि उपग्रह का परिक्रमण काल T है एवं इसकी पृथ्वी के केंद्र से दूरी r है तो उपग्रह के परिक्रमण काल का सूत्र
T = उपग्रह की परिधि / कक्षीय चाल
T = \( \large \frac{2πr}{v_o} \)
चूंकि r = Re + h तथा vo का मान रखने पर
T = \( \large \frac{2π(R_e + h)}{\sqrt{GM_e/r}} \)
T = \( \large \frac{2π}{\sqrt{GM_e}} × r^{3/2} \)
\( { T = 2π \sqrt{\frac{(R_e + h)^3}{GM_e} } } \)परंतु GMe = gRe2 रखने पर
T = 2π \( \sqrt{\frac{(R_e + h)^3}{gR_e^2} } \)
अथवा \( { T = \frac{2π}{R_e} \sqrt{\frac{(R_e + h)^3}{g} }} \)
यदि उपग्रह, पृथ्वी के अति समीप है तो h<<R
अतः h को नगण्य मानने पर
T = 2π \( \sqrt{\frac{R_e^3}{gR_e^2} } \)
\( { T = 2π \sqrt{\frac{(R_e}{g} } } \)यह उपग्रह के परिक्रमण काल का सूत्र है। उपग्रह का परिक्रमण काल, उपग्रह की ऊंचाई h पर निर्भर करता है h बढ़ाने पर T का मान बढ़ जाता है।
सूत्र T = 2π \( \sqrt{\frac{R_e}{g} } \) से
g = 9.8 मीटर/सेकंड2 तथा पृथ्वी की त्रिज्या Re = 6.4 × 106 मीटर रखने पर परिक्रमण काल
T = 2π \( \sqrt{\frac{6.4 × 10^6}{9.8} } \)
T = 5079 सेकंड
या \( { T = 84.6\, मिनट } \)
अतः परिक्रमण काल का मान 84.6 मिनट होता है।
Leave a Reply