गुरुत्वीय त्वरण g का मान न्यूनतम और अधिकतम, सूत्र, मात्रक, परिभाषा
गुरुत्व (gravity)
पृथ्वी द्वारा किसी वस्तु को अपने केंद्र की ओर आकर्षित करने को उसका गुरुत्व भी कहते हैं।
वास्तव में गुरुत्व, गुरुत्वाकर्षण का ही एक विशिष्ट उदाहरण है।
गुरुत्वीय त्वरण
पृथ्वी की ओर मुक्त रूप से गिरती किसी वस्तु के वेग में प्रति सेकंड से होने वाली वृद्धि को पृथ्वी का गुरुत्वीय त्वरण (acceleration due to gravity in Hindi) कहते हैं। इसे g से प्रदर्शित करते हैं।
गुरुत्वीय त्वरण का मान वस्तु के आकार, द्रव्यमान पर निर्भर नहीं करता है यह केवल वस्तु के स्थान पर निर्भर करता है।
यदि किसी वस्तु का द्रव्यमान m हो तो उस पर आरोपित गुरुत्वीय बल
F = mg
जहां g गुरुत्वीय त्वरण है तो
g = F/m
अतः गुरुत्वीय त्वरण का मात्रक मीटर/सेकंड2 अथवा न्यूटन/किग्रा होता है। एवं विमीय सूत्र [LT-2] है गुरुत्वीय त्वरण एक सदिश राशि है।
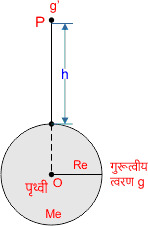
पृथ्वी तल से ऊपर जाने पर गुरुत्वीय त्वरण g का मान
g = G \(\frac{M_e}{R_e^2} \) समी.①
यदि पृथ्वी तल से h ऊंचाई पर गुरुत्वीय त्वरण g’ है जैसा चित्र में दिखाया गया है तो
g’ = G\( \frac{M_e}{(R_e + h)^2} \) समी.②
समी.② को समी.① से भाग देने पर
\( \large \frac{g’}{g} \) = \( \frac{GM_e}{(R_e + h)^2} \) × \( \frac{R_e^2}{GM_e} \)
\( \large \frac{g’}{g} \) = \( \frac{R_e^2}{(R_e + h)^2} \)
\( \large \frac{g’}{g} \) = \( \frac{R_e^2}{R_e^2(1 + h/R_e)^2} \)
\( \large \frac{g’}{g} \) = \( \frac{1}{(1 + h/R_e)^2} \)
g’ = \( \frac{g}{(1 + h/R_e)^2} \)
अर्थात \( { g’ < g } \)
अतः समीकरण द्वारा स्पष्ट होता है कि पृथ्वी तल से ऊपर जाने पर गुरुत्वीय त्वरण g का मान घटता है।
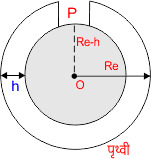
पृथ्वी तल से ऊपर जाने पर गुरुत्वीय त्वरण g का मान
माना पृथ्वी का द्रव्यमान Me तथा त्रिज्या Re है तो पृथ्वी सतह पर गुरुत्वीय त्वरण
g = G\( \frac{M_e}{R_e^2} \) समी.①
यदि हम पृथ्वी में सुरंग बनाकर h गहराई नीचे चले जाते हैं तो यह पृथ्वी (Re – h) त्रिज्या की रह जाएगी। एवं पृथ्वी का द्रव्यमान M’e हो जाता है। यदि h गहराई पर गुरुत्वीय त्वरण g’ है तो
यदि हम पृथ्वी में सुरंग बनाकर h गहराई नीचे चले जाते हैं तो यह पृथ्वी (Re – h) त्रिज्या की रह जाएगी।
एवं पृथ्वी का द्रव्यमान M’e हो जाता है। यदि h गहराई पर गुरुत्वीय त्वरण g’ है तो
g’ = G\( \frac{M_e}{(R_e + h)^2} \) समी.②
समी.② को समी. ① से भाग देने पर
\( \large \frac{g’}{g} \) = \( \frac{GM’_e}{(R_e – h)^2} \) × \( \frac{R_e^2}{GM_e} \)
\( \large \frac{g’}{g} \) = \( \frac{M’_e R_e^2}{M’_e(R_e – h)^2} \)
यदि पृथ्वी का घनत्व ρ है तो
Me = \( \frac{4}{3} \) πRe3ρ
(चूंकि पृथ्वी गोल है इसलिए यह गोले का घनत्व है जहां Re त्रिज्या है।)
तथा M’e = \( \frac{4}{3} \)π(Re – h)3ρ
अतः Me तथा M’e का मान रखने पर
\( \large \frac{g’}{g} \) = \( \frac{4/3π(R_e – h)^3ρ R_e^2}{4/3πR_e^3 ρ (R_e – h)^2} \)
\(\large\frac{g’}{g} \) = \( \frac{R_e – h}{R_e} \)
\( \large\frac{g’}{g} \) = \( (1-\frac{h}{R_e}) \)
g’ = g\( (1-\frac{h}{R_e}) \)
अर्थात \({ g’ < g } \)
अतः इस समीकरण द्वारा स्पष्ट होता है कि पृथ्वी तल से नीचे जाने पर गुरुत्वीय त्वरण g का मान घटता है।
गुरुत्वीय त्वरण के मान में परिवर्तन
1. गुरुत्वीय त्वरण g का मान पृथ्वी के ध्रुवो़ पर अधिकतम होता है।
2. गुरुत्वीय त्वरण g का मान भूमध्य रेखा पर न्यूनतम होता है।
3. पृथ्वी के केंद्र पर गुरुत्वीय त्वरण का मान शून्य होता है।
4. पृथ्वी सतह से नीचे तथा ऊपर जाने पर गुरुत्वीय त्वरण का मान घटता है।

Good notes