नोट्स भौतिक विज्ञान Notes Chapter 7 Bhautik Vigyan Class 11 Physics Hindi Medium

केप्लर के ग्रहों की गति संबंधी नियम, प्रथम, द्वितीय, तृतीय, तीनों नियम की उत्पत्ति

ग्रहों की गति संबंधी केप्लर के नियम

केप्लर ने सौर परिवार में सूर्य के चारों ओर परिक्रमा करने वाले ग्रहों की गति संबंधी निम्नलिखित तीन नियम दिए, जो निम्न प्रकार से हैं।

(1) कक्षाओं का नियम
(2) क्षेत्रीय चाल का नियम
(3) परिक्रमण काल का नियम

1. प्रथम नियम (कक्षाओं का नियम)

प्रत्येक ग्रह सूर्य के परितः दीर्घ वृत्ताकार पथ पर गति करते हैं तथा सूर्य उस दीर्घ वृत्त के किसी एक फोकस पर होता है। विभिन्न ग्रहों की कक्षाएं भिन्न-भिन्न होती हैं। यह केप्लर का प्रथम नियम है इसे कक्षाओं का नियम (law of orbits) भी कहते हैं।

2. द्वितीय नियम (क्षेत्रीय चाल का नियम)

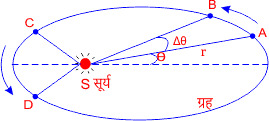
किसी ग्रह को सूर्य से मिलाने वाली रेखा बराबर समय अंतरालों में बराबर क्षेत्रफल पार करती है। अर्थात प्रत्येक ग्रह की क्षेत्रीय चाल नियत रहती है इसे केप्लर का द्वितीय नियम कहते हैं। एवं इसे क्षेत्रीय चाल का नियम (law of areal velocity) भी कहते हैं।

अतः चित्र द्वारा स्पष्ट होता है। कि जब ग्रह, सूर्य के नजदीक होता है तो उसकी चाल अधिकतम होती है। और जब ग्रह, सूर्य से दूर चला जाता है तो ग्रह की चाल न्यूनतम होती है। प्रस्तुत चित्र में ग्रह की कक्षा को ही दर्शाया गया है।

यदि कोई ग्रह सूर्य की परिक्रमा करते हुए एक निश्चित समयांतराल में कक्षा के बिंदु A से B बिंदु तक जाता है एवं उतनी ही समयांतराल में बिंदु C से D बिंदु तक जाता है तब इस नियम के अनुसार
∆ASB का क्षेत्रफल = ∆CSD का क्षेत्रफल

3. तृतीय नियम (परिक्रमण काल का नियम)

सूर्य के परितः किसी भी ग्रह का परिक्रमण काल का वर्ग उस ग्रह की दीर्घवृत्ताकार कक्षा के अर्द्ध दीर्घ अक्ष की तृतीय घात के अनुक्रमानुपाती होता है। इसे केप्लर का तृतीय नियम कहते हैं। तथा इसे परिक्रमण काल का नियम (law of periods) भी कहते हैं।

माना किसी ग्रह का सूर्य के चारों ओर परिक्रमण काल T है तथा इसकी दीर्घ वृत्ताकार कक्षा का अर्द्ध दीर्घ अक्ष a है तो इस नियम के अनुसार

T ∝ a³

केप्लर के नियम से न्यूटन के निष्कर्ष

केप्लर के दूसरे नियम के अनुसार, किसी ग्रह का क्षेत्रफलीय वेग नियत रहता है तब दीर्घ वृत्ताकार कक्षा में ग्रह का वेग नियत होगा। अतः ग्रह पर केंद्र (सूर्य) की ओर

एक अभिकेंद्र बल F लगता है तो

अभिकेंद्र बल F = \( \large \frac{mv^2}{r} \)

यहां m द्रव्यमान, v ग्रह का रेखीय वेग है तथा r वृत्ताकार कक्षा की त्रिज्या है।

यदि T ग्रह का आवर्तकाल हो तब

v = \( \large \frac{2πr}{T} \)

(चूंकि v = rω ⇒ 2πrn ⇒ \( \large \frac{2πr}{T} \)

v का मान रखने पर अभिकेंद्र बल

F = \( \large \frac{m}{r} (\frac{2πr}{T})^2 \)

F = \( \large \frac{4π^2mr}{T^2} \)

F = \( \large \frac{m × 4π^2r}{kr^3} \) (चूंकि ‌T ∝ a³ ⇒ ka³ से)

F = \( \large (\frac{4π^2}{k}) (\frac{m}{r^2}) \)

अतः F ∝\( \large \frac{m}{r^2} \)

इस प्रकार केप्लर के नियम से न्यूटन ने तीन निष्कर्ष निकाले

1. ग्रह पर एक बल कार्य करता है जिसकी दिशा सूर्य की ओर होती है।

2. यह बल ग्रह तथा सूर्य के बीच की औसत दूरी के वर्ग के व्युत्क्रमानुपाती होता है। F ∝ \(\large \frac{1}{r^2} \) यह बल ग्रह के द्रव्यमान के अनुक्रमानुपाती होता है। (F ∝ m)
3. यह बल ग्रह के द्रव्यमान के अनुक्रमानुपाती होता है। (F ∝ m)

इस प्रकार हम देखते हैं कि केप्लर के नियम से न्यूटन ने तीन निष्कर्ष निकाले।
ध्यान दें –

यह तीनों निष्कर्ष F ∝ \( \large \frac{m}{r^2} \) सूत्र से ही बनाए गए हैं कोई अपने मन से नहीं है यहां प्रयोग किया गया बल अभिकेंद्र बल है।