जड़त्व आघूर्ण क्या है, परिभाषा, मात्रक, भौतिक महत्व
जड़त्व आघूर्ण
सरल रेखीय गति में न्यूटन के प्रथम नियमानुसार, यदि कोई वस्तु विराम की अवस्था में है तो वह विरामावस्था में ही रहेगी अथवा यदि कोई वस्तु एकसमान चाल से सीधी रेखा में चल रही है तो वह चलती ही रहेगी। जब तक उस पर कोई बाह्य बल न लगाया जाए, इस बाह्य बल के कारण वस्तु अपनी अवस्था परिवर्तन का विरोध करती है वस्तु के इस गुण को जड़त्व कहते हैं।
इसी प्रकार घूर्णन गति में कोई पिंड किसी अक्ष के परितः किसी कोणीय वेग से घूर्णन करता है तो उसमें अपनी अवस्था परिवर्तन का विरोध करने का एक गुण होता है। जिसके कारण पिंड अपनी प्रारंभिक अवस्था में बने रहने का प्रयास करता है पिंड के इस गुण को जड़त्व आघूर्ण (moment of inertia) कहते हैं। इसे I से प्रदर्शित करते हैं।
इस प्रकार हम देखते हैं कि रेखीय गति में जो महत्व जड़त्व का है वही महत्व कोणीय (घूर्णन) गति में जड़त्व आघूर्ण का है। दोनों में अंतर सिर्फ यह है कि जड़त्व वस्तु के केवल द्रव्यमान पर निर्भर करता है। जबकि जड़त्व आघूर्ण
द्रव्यमान के साथ उसकी घूर्णन अक्ष से दूरी पर भी निर्भर करता है।
जड़त्व आघूर्ण का सूत्र
पिंड के किसी कण का जड़त्व आघूर्ण उस कण के द्रव्यमान तथा उसकी घूर्णन अक्ष से दूरी के वर्ग के गुणनफल के बराबर होता है। अर्थात
I = mr2
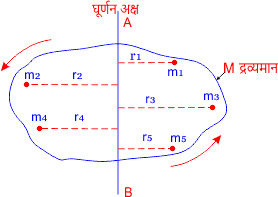
माना M द्रव्यमान का एक पिंड अक्ष के परितः घूर्णन कर रहा है। माना पिंड छोटे-छोटे कणों से मिलकर बना है जिनके द्रव्यमान क्रमशः m1, m2, m3, …….. हैं एवं इनकी घूर्णन अक्ष से दूरी क्रमशः r1, r2, r3, …….. हैं तो
पहले कण का जड़त्व आघूर्ण I1 = m1r12
दूसरे कण का जड़त्व आघूर्ण I2 = m2r22
तीसरे कण का जड़त्व आघूर्ण I3 = m3r32
इसी प्रकार आगे भी ……..
यदि पूरे पिंड का घूर्णन अक्ष के परितः जड़त्व आघूर्ण I है तो
I = I1 + I2 + I3 + ……….
I = m1r12 + m2r22 + m3r32 + ……….
\( { I = Σmr^2 } \)अतः इस समीकरण द्वारा स्पष्ट होता है कि किसी पिंड का किसी अक्ष के परितः जड़त्व आघूर्ण, पिंड के प्रत्येक कण के द्रव्यमान तथा उसकी घूर्णन अक्ष से दूरी के वर्ग के गुणनफल के बराबर होता है।
जड़त्व आघूर्ण का SI मात्रक किग्रा-मीटर2 होता है। एवं विमीय सूत्र [ML2T0] तथा इसका C.G.S. पद्धति में मात्रक ग्राम-सेमी2 होता है। जड़त्व आघूर्ण न तो सदिश राशि है और न ही अदिश। यह एक प्रदिश (टेंसर) राशि है टेंसर राशि का मान अलग-अलग दिशाओं के लिए अलग-अलग होता है।
जड़त्व आघूर्ण का भौतिक महत्व
किसी पिंड का जड़त्व आघूर्ण उसकी घूर्णन गति में वही कार्य करता है जो उसका द्रव्यमान रेखीय गति में करता है। क्योंकि किसी पिंड का द्रव्यमान ही उसके जड़त्व की माप है।
अन्य अंतर किसी पिंड का जड़त्व केवल उसके द्रव्यमान पर निर्भर करता है जबकि पिंड का जड़त्व आघूर्ण पिंड के द्रव्यमान एवं घूर्णन अक्ष के चारों ओर द्रव्यमान के वितरण पर भी निर्भर करता है। यही जड़त्व आघूर्ण भौतिक महत्व है।
कुछ महत्वपूर्ण आकृतियों के जड़त्व आघूर्ण के सूत्र
1. वृत्ताकार छल्ला या वलय I = mr2
2. वृत्ताकार डिस्क I = \( \large \frac{1}{2} \)mr2
3. ठोस बेलन I = \( \large \frac{1}{2} \) mr2
4. ठोस गोला I = \( \large \frac{2}{5} \)mr2
5. खोखला गोला (गोलीय कोश) I = \( \large \frac{2}{3} \) mr2
घूर्णन त्रिज्या (radius of gyration)
यदि पिंड के संपूर्ण द्रव्यमान को किसी एक बिंदु पर केंद्रित माना जाए, एवं जिसकी घूर्णन अक्ष से लंबवत दूरी इतनी हो कि अगर दूरी के वर्ग को पिंड के द्रव्यमान से गुणा करें तो घूर्णन अक्ष के परितः पिंड का जड़त्व आघूर्ण प्राप्त हो जाए। तो इस दूरी को घूर्णन त्रिज्या कहते हैं। इसे K से प्रदर्शित करते हैं।
माना M द्रव्यमान के किसी पिंड का जड़त्व आघूर्ण I है तब
I = MK2
I = MK2
\({ K = \sqrt{\frac{I}{M}} } \)अतः किसी पिंड का घूर्णन अक्ष के परितः जड़त्व आघूर्ण तथा उसके द्रव्यमान के अनुपात का वर्गमूल उस पिंड की घूर्णन त्रिज्या कहलाती है।
अतः किसी पिंड का घूर्णन अक्ष के परितः जड़त्व आघूर्ण तथा उसके द्रव्यमान के अनुपात का वर्गमूल उस पिंड की घूर्णन त्रिज्या कहलाती है।
Leave a Reply