नोट्स भौतिक विज्ञान Notes Chapter 6 Bhautik Vigyan Class 11 Physics Hindi Medium

कोणीय वेग तथा रेखीय वेग में संबंध बताइए, सूत्र और परिभाषा, विमा

जब कोई कण किसी वृत्त की परिधि पर घूमता है तो उसका कोणीय विस्थापन समय के साथ परिवर्तित होता जाता है।अर्थात
वृत्तीय गति करते हुए किसी कण के कोणीय विस्थापन की समय के साथ परिवर्तन की दर को कोणीय वेग (angular velocity in Hindi) कहते हैं। इसे ω (ओमेगा) से प्रदर्शित किया जाता है‌‌।
माना कोई कण जिसका ∆t सूक्ष्म समयांतराल में, कोणीय विस्थापन ∆θ है तब कण का कोणीय वेग

माना कोई कण जिसका ∆t सूक्ष्म समयांतराल में, कोणीय विस्थापन ∆θ है तब कण का कोणीय वेग

\( ω = कोणीय विस्थापन/समयांतराल} = ∆θ/∆t

यह कोणीय वेग का सूत्र है इसका मात्रक रेडियन/सेकंड होता है। तथा कोणीय वेग की विमा

[M⁰L⁰T^-1] होती है।

चूंकि हम जानते हैं कि कोई कण एक वृत्तीय चक्कर पूरा करने में 360° यानी 2π घूम जाता है। एवं इस पूर्ण चक्र में लगा समय कण का परिक्रमण काल (T) कहलाता है। तो कण का औसत कोणीय वेग

कहलाता है। तो कण का औसत कोणीय वेग
ω = 2π/T
या ω = 2πn
जहां n कण की आवृत्ति है।

रेखीय वेग

जब कोई कण रेखीय गति करता है तो उसका रेखीय विस्थापन समय के साथ परिवर्तित होता जाता है। अर्थात
रेखीय गति करते हुए किसी कण के रेखीय विस्थापन की समय के साथ परिवर्तन की दर को रेखीय वेग (linear velocity in Hindi) कहते हैं।
माना कोई कण जिसका ∆t सूक्ष्म समयांतराल में, रेखीय विस्थापन ∆s है तब कण का रेखीय वेग
v = रेखीय विस्थापन/समयांतराल

v = ∆s/∆t

यह रेखीय वेग का सूत्र है इसका मात्रक मीटर/सेकंड होता है। यह एक सदिश राशि है।

कोणीय वेग तथा रेखीय वेग में संबंध

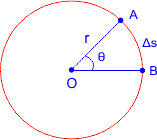
यदि कोई कण एक निश्चित त्रिज्या के वृत्त की परिधि पर एकसमान चाल से चलता है माना कण ∆t समयांतराल में वृत्त की परिधि पर ∆s दूरी घूम जाता है। यदि कण का कोणीय विस्थापन ∆θ हो तो

कण का कोणीय वेग

ω = [latex]\small lim \) \( \large \frac{∆θ}{∆t} \)

जहां lim ∆t→0 है

ω = \( \small lim \) \( \large \frac{1}{∆t} \) × ∆θ

ω = \( \small lim \) \( \large \frac{1}{∆t} × \frac{∆s}{r} \)(चूंकि ∆θ = \( \large \frac{∆s}{r} \)

ω = \( \small lim \) \( \large \frac{∆s}{∆t} × \frac{1}{r} \)

ω = \( \large v × \frac{1}{r} \) (चूंकि \( \large \frac{∆s}{∆t} \) = v)

ω = \( \large \frac{v}{r} \)

\( { v = rω } \)

रेखीय वेग = त्रिज्या × कोणीय वेग

यह कोणीय वेग और रेखीय वेग में संबंध का सूत्र है। (relation between angular velocity and linear velocity in Hindi)

सूत्र से स्पष्ट है कि कण केंद्र से जितनी अधिक दूरी पर होगा, उसका रेखीय वेग उतना ही अधिक होगा।