नोट्स भौतिक विज्ञान Notes Chapter 5 Bhautik Vigyan Class 11 Physics Hindi Medium

यांत्रिक ऊर्जा संरक्षण का नियम लिखिए, सूत्र

यांत्रिक ऊर्जा संरक्षण का नियम

जब बल संरक्षी होता है तो कण की यांत्रिक ऊर्जा नियत रहती है। अतः
कुल ऊर्जा = गतिज ऊर्जा + स्थितिज ऊर्जा = नियत
E = K + U = नियत

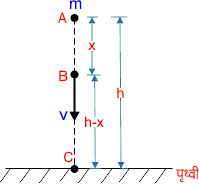
माना m द्रव्यमान का कोई पिंड है जो पृथ्वी से h ऊंचाई पर बिंदु A पर स्थित है। जब पिंड गुरुत्व के आधीन मुक्त रूप से गिरना प्रारंभ करता है तो बिंदु A पर पिंड का वेग शून्य होता है तो पिंड की –

बिंदु A पर

गतिज ऊर्जा K = 0
स्थितिज ऊर्जा U = mgh
तब पिंड की कुल ऊर्जा = गतिज ऊर्जा + स्थितिज ऊर्जा
पिंड की कुल ऊर्जा = 0 + mgh
पिंड की कुल ऊर्जा = mgh समी.①

बिंदु B पर

चित्र में बिंदु B बिंदु A से x मीटर नीचे की ओर है यदि पिंड का वेग v है तब गति के तृतीय समीकरण से

v² = u² + 2gx

चूंकि प्रारंभिक वेग u शून्य है तो

v² = 0 + 2gx
v² = 2gx

पिंड की गतिज ऊर्जा K = \( \large \frac{1}{2} \) mv²

v² का मान रखने पर पिंड की गतिज ऊर्जा

K = \( \large \frac{1}{2} \) m × 2gx

K = mgx

पिंड की स्थितिज ऊर्जा U = mg(h – x)

U = mgh – mgx

अतः बिंदु B पर संपूर्ण ऊर्जा E = K + U

E = mgx + mgh – mgx
E = mgh समी.②

बिंदु C पर

पृथ्वी के निकट बिंदु C पर यदि वेग v’ है तो

v’² = u² + 2gh

v’² = 0 + 2gh

v’² = 2gh

पिंड की गतिज ऊर्जा K = \( \large \frac{1}{2} \) mv’²
K = \( \large \frac{1}{2} \) m × 2gh

K = mgh

पिंड की स्थितिज ऊर्जा U = mgh

U = mg × 0
U = 0

अतः बिंदु C पर संपूर्ण ऊर्जा E = K + U

E = mgh + 0

E = mgh समी.③

अर्थात् समीकरण ①, ② तथा ③ से स्पष्ट है कि वस्तु के प्रत्येक बिंदु पर गतिज ऊर्जा एवं स्थितिज ऊर्जा का योग सदैव नियत रहता है। अतः गुरुत्वीय बल के अंतर्गत वस्तु की कुल यांत्रिक ऊर्जा नियत रहती है।