अभिकेंद्र त्वरण क्या है, सूत्र, व्यंजक
एकसमान वृत्तीय गति के लिए अभिकेंद्र त्वरण का व्यंजक ज्ञात कीजिए? यह सवाल महत्वपूर्ण है और एग्जाम में जरूर आता है। तो चलिए अभिकेंद्र त्वरण के बारे में जानते हैं।
अभिकेंद्र त्वरण
जब कोई पिंड एकसमान चाल से वृत्तीय पथ पर गति करता है तो पिंड की चाल अचर होते हुए भी उसकी दिशा लगातार बदलती रहती है। अतः पिंड का वेग भी लगातार बदलता रहता है इस प्रकार पिंड पर उसके केंद्र की ओर एक दिष्ट त्वरण लगता है इस त्वरण को अभिकेंद्र त्वरण (centripetal acceleration in Hindi) कहते हैं। अभिकेंद्र त्वरण की दिशा सदैव वृत्त के केंद्र की ओर होती है। इसे a से प्रदर्शित करते हैं।
एकसमान वृत्तीय गति में अभिकेंद्र त्वरण का व्यंजक
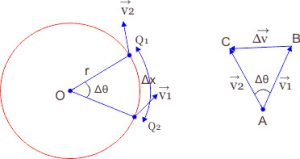
माना कोई पिंड एकसमान चाल v से वृत्तीय पथ पर गति करता है चित्र में वृत्त का O केंद्र तथा r त्रिज्या है।
माना एक सूक्ष्म समय अंतराल ∆t में पिंड वृत्तीय पथ पर बिंदु Q1 से Q2 विस्थापित होता है। तथा इस दौरान वह ∆x दूरी तय करता है एवं पिंड को केंद्र से मिलाने वाली रेखा भी ∆θ कोण घूम जाती है।
यदि बिंदु Q1 व Q2 पर वेग v1 व v2 हैं। तो ∆OQ1Q2 तथा वेक्टर त्रिभुज ABC समरूप हैं। अतः \(\frac{Q_1Q_2}{Q_1O}\) = \( \frac{BC}{AB} \)
\( \frac{∆x}{r} \) = \( \frac{∆v}{v} \)
चूंकि ∆t समय बहुत छोटा है तब ∆θ भी छोटा होगा। इस स्थिति में चाप Q1 Q2 को भी लगभग ∆x के बराबर मान लेते हैं अतः
\( \frac{∆x}{r} \) = \( \frac{∆v}{v} \)
दोनों ओर ∆t द्वारा भाग करने पर
\( \frac{∆x}{r} × \frac{1}{∆t} \) = \( \frac{∆v}{v} × \frac{1}{∆t} \)
\( \frac{∆v}{∆t} \) = \((\frac{v}{r}) × \frac{∆x}{∆t} \)
यदि ∆t समयांतराल बहुत छोटा हो तो (∆t→0) तब
lim \( \frac{∆v}{∆t} \) = \( (\frac{v}{r}) \) × lim \( \frac{∆x}{∆t} \)
परिभाषा से lim \(\frac{∆v}{∆t} \) तात्कालिक त्वरण a एवं \( \frac{∆x}{∆t} \) तात्कालिक रेखीय वेग v है। तब उपरोक्त समीकरण
a = \( \frac{v}{r} × v \)
\( { a = \frac{v^2}{r} } \)
अभिकेंद्र त्वरण का मान कोणीय वेग के पदों में
चूंकि v = rω से
a = \( \frac{r^2 ω^2}{r} \) × v
\( { a = rω^2 } \)यही एकसमान वृत्तीय गति में अभिकेंद्र त्वरण का व्यंजक है।
Leave a Reply