समतल में गति
सभी भौतिक राशियों को अदिश एवं सदिश राशियों में वर्गीकृत किया जाता है। दोनों में अंतर सिर्फ यह है कि सदिश राशियों में दिशा का संबंध होता है जबकि अदिश राशियां में ऐसा नहीं होता है।
जैसे- दूरी और विस्थापन दोनों राशियां एक समान ही प्रतीत होती हैं दोनों के मात्रक भी एक जैसे ही होते हैं। लेकिन दूरी एक अदिश राशि है जबकि विस्थापन एक सदिश राशि है।
अदिश राशियों को जोड़ना, घटाना, गुणा व भाग करना साधारण गणित के नियमों द्वारा ही किया जाता है। लेकिन सदिश राशि में ऐसा नहीं होता है। सदिश राशियों को जोड़ने, घटाने, गुणा व भाग करने के नियम हैं जिन्हें सदिश बीजगणित कहते हैं।
एकांक सदिश
वह सदिश जिसका परिमाण एक होता है एकांक सदिश कहलाता है। इसे A द्वारा दर्शाया जाता है।
एकांक सदिश = सदिश/सदिश का परिमाण
\( \widehat{A} = \frac{\overrightarrow {A}} {\overrightarrow{|A|}} \)लंबकोणीय एकांक सदिश
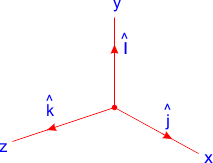
लंबकोणीय अक्षों x, y तथा z के अनुदिश एकांक सदिश को लंबकोणीय एकांक सदिश(वेक्टर) कहते हैं। इन्हें क्रमशः \( \widehat{i} \), \( \widehat{j} \) तथा \( \widehat{k} \) से प्रदर्शित करते हैं।
\( \widehat{i} = \widehat{j} = \widehat{k} \)
किसी भौतिक राशि के सदिश होने के लिए उसमें परिमाण के साथ दिशा भी होनी चाहिए। एवं वह राशि सदिश नियमों का पालन भी करती हो। इसके कुछ बिंदु-
• किसी सदिश के समकोणिक घटक का परिमाण सदिश के परिमाण से अधिक नहीं हो सकता है।
• यदि \( \small \overrightarrow{A} + \overrightarrow{B} + \overrightarrow{C} \) = 0 तब \( \small \overrightarrow{A} , \overrightarrow{B} तथा \overrightarrow{C} \) समतलीय वेक्टर हैं।
• यदि \( \small \overrightarrow{A} + \overrightarrow{B} = \overrightarrow{C} \) तब भी \( \small \overrightarrow{A} , \overrightarrow{B} तथा \overrightarrow{C} \) समतलीय वेक्टर होते हैं।
भिन्न परिमाण वाले दो वेक्टरो का योग शून्य वेक्टर नहीं हो सकता है।
• जब कोई खिलाड़ी गेंद को क्षैतिज से अगर 45° के झुकाव पर फेंकता है तो गेंद अधिकतम दूरी पर जाती है।
• जब दो सदिश परस्पर लंबवत होते हैं तो उस दशा में दो अशून्य सदिशों का अदिश गुणनफल शून्य होता है।
• जब दो सदिश परस्पर समांतर होते हैं अर्थात् उनके बीच कोण 0 या 180° होता है तो उस दशा में दो सदिशों का अदिश गुणन अधिकतम होता है।

Bahut achhe Notes he