सदिश और अदिश राशि किसे कहते हैं अंतर लिखिए, वेक्टर एवं स्केलर राशियां
आपने भौतिकी में यह तो जरूर सुना होगा कि वेग सदिश राशि है तथा चाल अदिश राशि है कोई सदिश राशि होती है तो कोई अदिश राशि, आखिर इसका मतलब क्या है।
तो प्रस्तुत अध्याय के अंतर्गत हम सदिश और अदिश राशियां क्या है इन के बीच अंतर और उदाहरण सहित अध्ययन करेंगे।
अदिश राशि
वह भौतिक राशियां जिनमें केवल परिमाण होता है इनकी कोई दिशा नहीं होती है इस प्रकार की राशियों को अदिश राशि (scalar quantity in Hindi) कहते हैं।
अदिश राशि के उदाहरण
अदिश राशि के अनेकों उदाहरण हैं जैसे – द्रव्यमान, दूरी, समय, ताप, आयतन, घनत्व, कार्य, शक्ति, ऊर्जा, आवेश, चाल, विभव, आवृत्ति, विशिष्ट ऊष्मा आदि।
अदिश राशि को जोड़ना, घटाना, गुणा व भाग करना साधारणतः गणित के नियमों की सहायता से ही होता है।
सदिश राशि
वह भौतिक राशियां जिनमें परिमाण के साथ-साथ दिशा भी ज्ञात होती है इस प्रकार की राशियों को सदिश राशि (vector quantity in Hindi) कहते हैं।
सदिश राशि के उदाहरण
सदिश राशि के अनेकों उदाहरण हैं जैसे – वेग, संवेग, आवेग, विस्थापन, बल , त्वरण, भार, विद्युत क्षेत्र, धारा घनत्व आदि।
ध्यान दें –
विद्युत धारा और विद्युत क्षेत्र दोनों अलग राशियां हैं। विद्युत धारा एक अदिश राशि है जबकि विद्युत क्षेत्र एक सदिश राशि है।
सदिश राशियों को जोड़ने, घटाने, गुणा व भाग करने के लिए कोई बीजगणितीय नियम लागू नहीं होता है। इसके अपने नियम हैं वही लागू होते हैं। जिन्हें सदिश बीजगणित कहते हैं।
सदिश राशियों को → तीर द्वारा व्यक्त किया जाता है यह तीर सदिश राशियों के ऊपर लगाया जाता है इस तीर की लंबाई उस राशि के परिमाण को तथा तीर की नोक उस राशि की दिशा को प्रदर्शित करती है जिसके ऊपर यह लगा है।
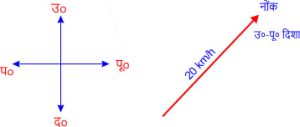
चित्र में दिखाया गया है कि कोई A व्यक्ति 20 किलोमीटर/घंटे की चाल से उत्तर-पूर्व दिशा में जा रहा है यह दिशा का ज्ञान तीर द्वारा हुआ है। यहां वेग पर तीर लगाया लगेगा \( \overrightarrow{v} \) । चूंकि वेग सदिश राशि है।
सदिश राशियों को लिखना
1. v = u + at
सदिश रूप में \( \overrightarrow{v} = \overrightarrow{u} + \overrightarrow{a} t \)
जो सदिश राशि होती है उनके ऊपर → लगा देते हैं यह वेग, त्वरण a सदिश राशि हैं। जबकि समय t अदिश राशि है इसलिए इस पर तीर नहीं लगाया गया है।
2. s = ut + \( \frac{1}{2}\) at 2 सदिश रूप में → \( \overrightarrow{s} = \overrightarrow{u}t + \frac{1}{2} \overrightarrow{a} t^2 \)
एकांक सदिश
वह सदिश जिसका परिमाण 1 होता है एकांक सदिश कहलाता है।
माना \( \overrightarrow{A} \) एक सदिश है जिसका परिमाण A है तो \( \overrightarrow{A} \) /A को एकांक सदिश कहते हैं इसे \( \widehat{A} \) द्वारा प्रदर्शित किया जाता है।
एकांक सदिश का सूत्र
\({\widehat{A} = \frac{\overrightarrow{A}}{A} = \frac{\overrightarrow{A}}{|\overrightarrow{A}|} } \)एकांक सदिश के सदिश गुणनफल के दो नियम होते हैं।
(1) \( \widehat{i} \) × \( \widehat{i} \) = \( \widehat{j} \) × \( \widehat{j} \) = \( \widehat{k} \) × \( \widehat{k} \) = 0
(1) \( \widehat{i} \) × \( \widehat{j} \) = \( \widehat{k} \), \( \widehat{j} \) × \( \widehat{k} \) = \( \widehat{i} \) , \( \widehat{k} \) × \( \widehat{i} \) = \( \widehat{j} \)
शून्य सदिश
वह सदिश जिसका परिमाण शून्य होता है शून्य सदिश कहलाता है।
\( {\overrightarrow{A} = 0 } \)
विपरीत सदिश
वह सदिश जिसका परिमाप बराबर होता है परंतु दिशाएं विपरीत होते हैं विपरीत सदीश कहलाते हैं।
\( {\overrightarrow{A} = – \overrightarrow{B} } \) \( {\overrightarrow{B} = – \overrightarrow{C} } \)

Leave a Reply