गति के समीकरण का निगमन ग्राफीय तथा कलन विधि से, प्रथम, द्वितीय, तृतीय
गति के समीकरण
गति के समीकरण (equation of motion in Hindi) को ज्ञात करने की दो विधियों है-
(1) ग्राफीय विधि
(2) कलन विधि
कलन विधि में समाकलन किया जाता है समाकलन के नियमों का प्रयोग करके निगमन करते हैं।
जबकि ग्राफीय विधि में ग्राफ बनाकर ज्यामिति के नियमों का प्रयोग करके गति के तीनो समीकरण का निगमन करते हैं।
1. ग्राफीय विधि द्वारा गति के समीकरण का निगमन
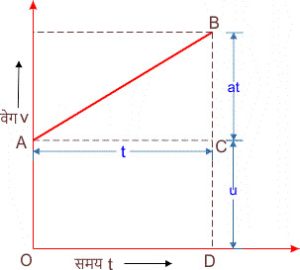
माना कोई वस्तु प्रारंभिक वेग u तथा त्वरण a से चलना शुरु करती है t समय पश्चात वस्तु का वेग v हो जाता है।
? गति का प्रथम समीकरण
माना वस्तु का समय t = 0 पर प्रारंभिक वेग u है जो चित्र में CD = AO से दर्शाया गया है। t समय पश्चात वस्तु का वेग v हो जाता है। तो
हम जानते हैं कि वेग समय ग्राफ की ढाल से वस्तु का त्वरण ज्ञात होता है तो वस्तु का त्वरण
a = सरल रेखा AB की ढाल
a = CB/AC
a = \(\frac{BD-CD}{AC} \)
a = \(\frac{V-U}{T} \)
at = v – u
V = u + at
? गति का द्वितीय समीकरण
गतिशील वस्तु द्वारा चली गई दूरी
s = समलंब चतुर्भुज BDOA का क्षेत्रफल
s = (त्रिभुज ABC + चतुर्भुज BDOA) का क्षेत्रफल
s = \(\frac{1}{2} \) (AC × CB) + CD × AC
s = \(\frac{1}{2} \) (t × at) + u × t
s = \(\frac{1}{2} \) at2 + ut
? गति का तृतीय समीकरण
प्रथम समीकरण v = u + at से
t = \(\frac{v-u}{a} \)
गतिशील वस्तु द्वारा t समय में चली गई दूरी
s = \(\frac{1}{2} \) × (समांतर भुजाओं का योग × लंबवत दूरी)
s = \(\frac{1}{2} \) × (OA × BD) × AC
s = \(\frac{1}{2} \) × (u × v) × t
t का मान रखने पर
s = \(\frac{1}{2} \) × (u × v) × (\(\frac{v-u}{a} \))
2as = (v + u)(v – u)
सूत्र (a + b)(a – b) =
सूत्र (a + b)(a – b) = a2 – b2 से
2as = v2 – u2
2. कलन विधि से गति के समीकरण
माना एक गतिशील वस्तु एकसमान त्वरण a से एक सरल रेखा में गति कर रही है t = 0 समय पर वस्तु का प्रारंभिक वेग u है एवं t समय पश्चात इसका वेग v हो जाता है। यदि t समय के में वस्तु का विस्थापन s है। तब गति के समीकरण –
? गति का प्रथम समीकरण
गतिशील वस्तु का त्वरण a = \(\frac{dv}{dt} \)
या dv = adt
समाकलन करने पर
\( \int^v_u dv = a \int^t_0 dt \) \( [v]^v_u = a [t]^t_0 \)v – u = a(t – 0)
v – u = at

Very much