सरल लोलक का आवर्तकाल के लिए व्यंजक, सूत्र, नियम
सरल लोलक
जब किसी छोटे और भारी पिंड को किसी भारहीन पिंड एवं लम्बाई में न बढ़ने वाले धागे के एक सिरे से पिंड को बांधकर धागे को किसी घर्षण रहित दीवार (छत) से लटका दें। तो इस प्रकार बने समायोजन को सरल लोलक (simple pendulum) कहते हैं।
सरल लोलक की गति सरल आवर्त गति का एक उदाहरण है। व्यवहार में यह समायोजन संभव नहीं है।
सरल लोलक के आवर्तकाल का व्यंजक
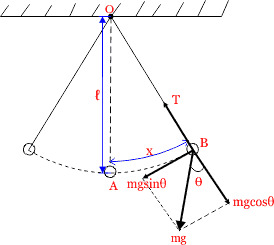
माना m द्रव्यमान के किसी गोलक को ℓ लंबाई के धागे के किसी बिंदु से लटकाया गया है।
जब इस गोलक को साम्य स्थिति में A से x दूरी विस्थापिन करके छोड़ दिया जाता है तो यह सरल लोलक दोलन करने लगता है।
यदि किसी क्षण बिंदु B पर सरल लोलक की स्थिति में भार mg को दो घटकों में वियोजित करने पर
क्षैतिज घटक = mgcosθ
ऊर्ध्वाधर घटक = mgsinθ
ऊर्ध्वाधर घटक सदैव साम्य स्थिति की ओर होता है अतः इसे प्रत्यानयन बल F कहते हैं।
तो F = – mgsinθ
या ma = – mg\( \large (\frac{x}{ℓ}) \)
a = – g\( \large (\frac{x}{ℓ}) \) समी.①
अतः a ∝ – x
या त्वरण = – विस्थापन
यहां त्वरण सदैव विस्थापन के अनुक्रमानुपाती होता है।
अतः सरल लोलक की गति सरल आवर्त गति है।
तो समी.① से
a = g\( \large (\frac{x}{ℓ}) \)
\( \large \frac{x}{a} \) = \( \large \frac{ℓ}{g} \)
चूंकि सरल लोलक का आवर्तकाल T = 2π विस्थापन/त्वरण होता है तो
विस्थापन/त्वरण या \( \large \frac{x}{a} \) का मान रखने पर
\( T = 2π \sqrt{\frac{ℓ}{g}} \)यह सरल लोलक का आवर्तकाल का सूत्र है। सरल लोलक का आवर्तकाल (time period of simple pendulum) पिंड के द्रव्यमान पर निर्भर नहीं करता है।
सेकंड लोलक
जब किसी लोलक का आवर्तकाल 2 सेकंड होता है तो इस प्रकार की लोलक को सेकंड लोलक (second’s pendulum) कहते हैं।
अतः सरल लोलक का आवर्तकाल के सूत्र से
अतः सरल लोलक का आवर्तकाल के सूत्र से
T = 2π\(\sqrt{\frac{ℓ}{g}} \)
चूंकि आवर्तकाल 2 सेकंड है तो
T = 2 रखने पर
T = 2π\( \sqrt{\frac{ℓ}{g}} \)
चूंकि आवर्तकाल 2 सेकंड है तो
T = 2 रखने पर
\( { l = \frac{g}{π^2} } \)माना किसी स्थान पर g = 9.8 मीटर/सेकंड2, T = 2 सेकंड हो तो
ℓ = \( \frac{9.8}{(3.14)^2} \)
ℓ = 0.992 मीटर
ℓ = 99.2 सेमी
अतः स्पष्ट होता है कि किसी सरल लोलक की लंबाई 99.2 सेमी कर दें। तो उसका आवर्तकाल 2 सेकंड होगा। तब उसे सेकंड लोलक कहते हैं।
Leave a Reply