स्प्रिंग का संयोजन, श्रेणीक्रम तथा समांतर क्रम, स्प्रिंग की गति, दोलन, उदाहरण नियतांक
जब किसी पिंड के किसी लटके हुए स्प्रिंग के निचले सिरे से बांध दिया जाता है तो पिंड के भार के कारण वह स्प्रिंग नीचे की ओर झुकने लगता है। अर्थात स्प्रिंग की लंबाई में वृद्धि हो जाती है। तो स्प्रिंग का आवर्तकाल
\( { T = 2π \sqrt {\frac{m}{k}} } \)जहां m – वस्तु का द्रव्यमान
k – बल नियतांक
T – आवर्तकाल
चूंकि आवृत्ति n = \( \frac{1}{T} \) हो तो
\( { n = \frac{1}{2π} \sqrt {\frac{k}{m}} } \)या 2πn = \( \sqrt{\frac{k}{m}} \)
चूंकि ω = 2πn होता है तब
कोणीय वेग \( { ω = \sqrt {\frac{k}{m}} } \)
स्प्रिंग का समांतर क्रम संयोजन
माना दो स्प्रिंग हैं जिनको समांतर क्रम में जोड़कर उनमें एक पिंड को लटकाया गया है। माना दोनों स्प्रिंग के बल नियतांक k1 व k2 हैं जो एक दूसरे से भिन्न होंगे जैसे चित्र में दिखाया गया है।
माना पिंड पर लगने वाला बल F तथा दोनों स्प्रिंग पर लगने वाला बल क्रमशः F1 व F2 हैं। तब यह बल एक दूसरे के समान होंगे। तो
F = F1 = F2
यदि पहले स्प्रिंग की लंबाई में वृद्धि y1 व दूसरी स्प्रिंग की लंबाई में वृद्धि y2 हो तो
y = y1 + y2
या \( \frac{F}{y} \) = \( \frac{F}{y_1} \) + \( \frac{F}{y_2} \)
\( \frac{1}{y} \) = \( \frac{1}{y_1} \) + \( \frac{1}{y_2} \)
जहां k तुल्य बल नियतांक है तो
सूत्र T = 2π \( \small \sqrt{\frac{m}{k}} \) से
\( { T = 2π \sqrt {\frac{m}{k_1 + k_2}} } \)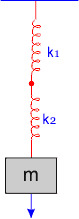
Leave a Reply