सरल आवर्त गति का विस्थापन समीकरण, त्वरण का मान, वेग, आवर्तकाल
इस लेख में सरल आवर्त गति का विस्थापन समीकरण प्राप्त करेंगे करते हैं। एवं इसके वेग और त्वरण का मान क्या होता है इसे भी प्राप्त करते हैं। एवं इससे संबंधित परिभाषाएं जैसे आयाम, आवृत्ति, आवर्तकाल तथा कला की परिभाषा का अध्ययन करते हैं।
सरल आवर्त गति का विस्थापन समीकरण
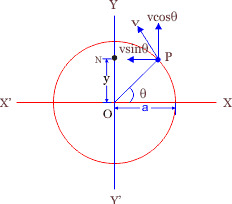
माना एक कण P, a त्रिज्या के एक वृत्तीय पथ पर चक्कर लगा रहा है। माना कण बिंदु B से चलना प्रारंभ करता है तथा t सेकंड में कण, θ कोण घूम जाता है।
यदि कण का कोणीय वेग ω है तो
ω = \( \large \frac{θ}{t} \)
या θ = ωt
यदि t सेकंड में प्रक्षेप N का मूलबिंदु O से विस्थापन y है तो
sinθ = \( \large \frac{y}{a} \)
या y = asinθ
θ का मान प्रस्तुत समीकरण में रखने पर
y = asinωt
यह सरल आवर्त गति का विस्थापन समीकरण है।
सरल आवर्त गति संबंधी परिभाषाएं
1. आयाम
सरल आवर्त गति में विस्थापन के अधिकतम मान को उसका आयाम कहते हैं। इसे a से प्रदर्शित करते हैं।
2. आवृत्ति
एक सेकंड में कण द्वारा किए गए कंपनों की संख्या को उसकी आवृत्ति कहते हैं। इसे n से दर्शाया जाता है।
\( { n = \frac{1}{T} = \frac{ω}{2π} } \)आवर्तकाल
सरल आवर्त गति में सर द्वारा एक कंपन को पूरा करने में लगे समय को उसका आवर्तकाल कहते हैं। इसे T से प्रदर्शित करते हैं।
\( { T = \frac{2π}{ω} }\)सरल आवर्त गति का विस्थापन समीकरण
y = asin(ωt + Φ)
जहां Φ कण की प्रारंभिक कला है।
सरल आवर्त गति में कण का वेग
मानव को एण वृत्त की परिधि पर गति कर रहा है तो उसके वेग v को दो घटकों में वियोजित कर सकते हैं।
क्षैतिज घटक = vsinθ
ऊर्ध्वाधर घटक = vcosθ
यह ऊर्ध्वाधर घटक = vcosθ कण की गति N के समांतर है। अतः सरल आवर्त गति में कण का वेग u हो तो
u = vcosθ
θ = ωt तथा v = rω रखने पर
u = aωcosωt
u = aω\( \small \sqrt{cos^2ωt} \)
u = aω\( \small \sqrt{1 – sin^2ωt} \)
चूंकि y = asinωt तब sinωt = \( \large \frac{y}{a} \) से
u = aω\( \small \sqrt{1 – \frac{y^2}{a^2}} \)
u = aω × \( \small \frac{ \sqrt{ a^2 – y^2}}{a} \)
\( { u = ω \sqrt{ a^2 – y^2} } \)यह सरल आवर्त गति करते हुए पिंड के वेग का सूत्र है।
सरल आवर्त गति में कण का त्वरण
जब कोई कण किसी वृत्त की परिधि पर गति करता है तो उस पर एक अभिकेंद्र बल कार्य करता है इस बल को दो घटकों में वियोजित करने पर
क्षैतिज घटक = \( \large \frac{v^2}{a} \)cosθ
ऊर्ध्वाधर घटक = \( \large \frac{v^2}{a} \)sinθ
यहां क्षैतिज घटक कण की गति के समांतर है लेकिन विपरीत दिशा में है अतः सरल आवर्त गति में कण का वेग u हो
तो u = – \( \large \frac{v^2}{a} \)sinθ
y = asinθ से sinθ = \( \large \frac{y}{a} \) रखने पर
u = – \(\large \frac{v^2}{a} × \frac{y}{a} \)sinθ
u = – \( \large \frac{v^2}{a} \)× ysinθ
u = – ω2y
या त्वरण ∝ विस्थापन
Leave a Reply