प्रश्न 1: दो समान्तर श्रेणी के n पदों का योग 5n+4: 9n+6 के अनुपात में है। उनके 18 वें पदों का अनुपात ज्ञात कीजिए।
समाधान:
मान लेते हैं कि पहली और दूसरी श्रेणी के प्रथम पद और सामान्य अन्तर क्रमशः \(a_1 , a_2\)और \(d_1 , d_2\)हैं।
तब,
(पहले AP के n पदों का योग) / (दूसरे AP के n पदों का योग) = \(\frac{(5n+4)}{(9n+6)}\)
LHS से अंश और हर दोनों को (n/2) काट दें
अब समीकरण (1) में n= 35 प्रतिस्थापित करें, {चूँकि (n-1)/2 = 17}
तब समीकरण (1) बन जाता है
अब, हम यह कह सकते हैं।
प्रथम AP का 18वाँ पद/ द्वितीय AP का 18वाँ पद =
अब, (2) और (3) से हम कह सकते हैं कि,
प्रथम AP का 18वाँ पद/ द्वितीय AP का 18वाँ पद = 179/321
अतः दोनों A.P. के 18वें पदों का अनुपात 179:321 है।
प्रश्न 2: 8 और 26 के बीच पाँच संख्याएँ इस प्रकार डालें कि परिणामी अनुक्रम एक AP हो
समाधान:
मान लीजिए कि \(A_1,A_2,A_3,A_4 और A_5,8\) और 26 के बीच की पाँच संख्याएँ हैं, जिससे AP का अनुक्रम 8,\(A_1,A_2,A_3,A_4,A_5,26\) हो जाता है।
यहाँ, a= 8, l =26, n= 5
इसलिए, 26= 8+(7-1)d
इसलिए यह बन जाता है,
26 = 8+6 दिन
6d = 26-8 = 18
अतः संख्या 8 और 26 के बीच आवश्यक पाँच संख्याएँ 11, 14, 17, 20, 23 हैं।
प्रश्न 3:किसी गुणोत्तर श्रेणी के 5वें, 8वें और 11वें पद क्रमशः p, q और s हैं। सिद्ध कीजिए कि \(q^2 = ps\)
समाधान:
मान लें कि:
5वाँ पद = P
8वाँ पद = q
11वाँ पद = s
सिद्ध करना है कि:\(q^2 = ps\)
हम समीकरण इस प्रकार लिख सकते हैं:
समीकरण (2) को (1) से भाग देने पर, हमें प्राप्त होता है
\(r^3 = q/p …(4)\)समीकरण (3) को (2) से भाग देने पर, हमें प्राप्त होता है
\(r^3 = s/q …(5)\)अब समीकरण (4) और (5) को समान करने पर हमें प्राप्त होता है
q/p = s/q
यह बन जाता है, \(q^2 = ps\)
प्रश्न 4: 1 से 100 तक के उन पूर्णांकों का योग ज्ञात करें जो 2 या 5 से विभाज्य हों।
समाधान:
1 से 100 तक के पूर्णांक, जो 2 से विभाज्य हैं, 2, 4, 6 ….. 100 हैं।
इससे एक समान्तर श्रेणी बनती है, जिसका प्रथम पद तथा सामान्य अंतर दोनों 2 के बराबर होते हैं।
⇒ 100 = 2+(n-1)2
⇒ n= 50
इसलिए, 1 से 100 तक के पूर्णांकों का योग जो 2 से विभाज्य हैं, इस प्रकार दिया गया है:
2 + 4 + 6 + …+ 100 = (50/2)[2(2)+(50-1)(2)]
= (50/2)(4+98)
= 25(102)
= 2550
1 से 100 तक के पूर्णांक, जो 5, 10…. 100 से विभाज्य हैं
इससे एक समान्तर श्रेणी बनती है, जिसका प्रथम पद तथा सामान्य अंतर दोनों 5 के बराबर होते हैं।
इसलिए, 100= 5+(n-1)5
⇒5n = 100
⇒ n= 100/5
⇒ n= 20
इसलिए, 1 से 100 तक के पूर्णांकों का योग जो 2 से विभाज्य हैं, इस प्रकार दिया गया है:
5+10+15+…+100= (20/2)[2(5)+(20-1)(5)]
= (20/2)(10+95)
= 10(105)
= 1050
अतः 1 से 100 तक के पूर्णांक, जो 2 और 5 दोनों से विभाज्य हैं, 10, 20, ….. 100 हैं।
इससे एक समान्तर श्रेणी बनती है, जिसमें प्रथम पद तथा सामान्य अंतर दोनों 10 के बराबर होते हैं।
इसलिए, 100= 10+(n-1)10
⇒10n = 100
⇒ n= 100/10
⇒ n= 10
10+20+…+100= (10/2)[2(10)+(10-1)(10)]
= (10/2)(20+90)
= 5(110)
= 550
इसलिए, आवश्यक राशि है:
= 2550+ 1050 – 550
= 3050
अतः 1 से 100 तक के पूर्णांकों का योग, जो 2 या 5 से विभाज्य हैं, 3050 है।
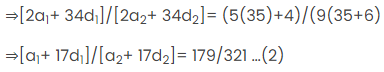
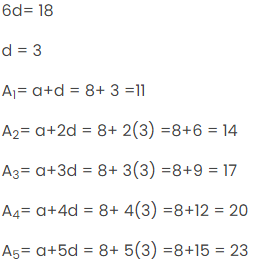
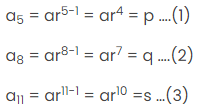
Leave a Reply