प्रश्न 1: उस वृत्त की त्रिज्या ज्ञात कीजिए जिसमें 60° का केन्द्रीय कोण 37.4 सेमी लंबाई के चाप को काटता है (π = 22/7 लीजिए)।
समाधान:
दिया गया,
चाप की लंबाई = l = 37.4 सेमी
केंद्रीय कोण = θ = 60° = 60π/180 रेडियन = π/3 रेडियन
हम वह जानते हैं,
आर = एल/θ
= (37.4) * (π / 3)
= (37.4) / [22 / 7 * 3]
= 35.7 सेमी
अतः वृत्त की त्रिज्या 35.7 सेमी है।
प्रश्न 2: एक पहिया एक मिनट में 360 घूर्णन करता है। यह एक सेकंड में कितने रेडियन घूमता है?
समाधान:
दिया गया है,
1 मिनट में पहिया द्वारा किए गए घूर्णनों की संख्या = 360
1 मिनट = 60 सेकंड
1 सेकंड में किए गए घूर्णनों की संख्या = 360/60 = 6
1 घूर्णन में बना कोण = 360°
6 घूर्णनों में बना कोण = 6 × 360°
6 चक्करों में कोण का रेडियन माप = 6 × 360 × π/180
= 6 × 2 × π
= 12π
अतः पहिया एक सेकंड में 12π रेडियन घूमता है।
प्रश्न . 3: √3 cosec 20° – sec 20° का मान ज्ञात कीजिए।
समाधान:
√3 कोसेक 20° – सेकंड 20°
प्रश्न 4: यह सिद्ध करें कि tan 3x tan 2x tan x = tan 3x – tan 2x – tan x.
समाधान:
मान लें 3x = 2x + x
दोनों तरफ “tan” लें,
tan3x = tan (2x + x)
हम जानते हैं,
tan (x + y) = \(\frac{tan x + tan y}{1 – tan x tan y} \)
tan 3x = (tan 2x + tan x)/ (1- tan 2x tan x)
tan 3x(1 – tan 2x tan x) = tan 2x + tan x
tan 3x – tan 3x tan 2x tan x = tan 2x + tan x
tan 3x – (tan 2x + tan x) = tan 3x tan 2x tan x
इसलिए, tan 3x – tan 2x – tan x = tan 3x tan 2x tan x
प्रश्न. 5: सिद्ध कीजिए कि:
समाधान:
LHS
= RHS
अतः सिद्ध हुआ।
प्रश्न. 6: cos 570° sin 510° + sin (-330°) cos (-390°) का मान ज्ञात कीजिए।
समाधान:
LHS = cos(570°) sin(510°) + sin(−330°) cos(−390°)
= cos(570°) sin(510°) + [−sin(330°)] cos(390°) (क्योंकि sin(−x)=−sinx और cos(−x)=cosx )
= cos(570°) sin(510°) − sin(330°) cos(390°)
= cos(90×6+30) sin(90×5+60) −sin(90×3+60)cos(90×4+30)
= − cos(30°) cos(60°) − [−cos(60°)]cos(30°)
= − cos(30°) cos(60°) + cos(30°) sin(60°)
= 0
प्रश्न 7: यह सिद्ध करें कि 2sin β + 4cos(α+β) sin α sinβ + cos2(α+ β) = cos 2α.
समाधान:
LHS
= 2sin β + 4cos(α + β)sinαsinβ + cos2(α + β)
= 2sin β + 4(cosαcosβ–sinαsinβ) sinαsinβ+ (cos2αcos2β–sin2αsin2β)
= 2sinβ + 4sinαcosαsinβcosβ–4sinαsinβ + cos2αcos2β–sin2αsin2β
= (1–cos2β)–(2sinα)(2sinβ) + cos2αcos2β
= (1–cos2β)–(1–cos2α)(1–cos2β) + cos2αcos2β
= cos 2α
अतः, सिद्ध हुआ कि 2sin β + 4cos(α + β)sinαsinβ + cos2(α + β) = cos2α.

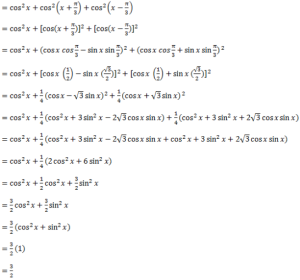
Leave a Reply