प्रश्न 1: सिग्नम फ़ंक्शन की सीमा लिखें।
समाधान:
वास्तविक फलन f: R → R द्वारा परिभाषित
इसे सिग्नम फ़ंक्शन कहते हैं। f का डोमेन = R, f का परिसर = {1, 0, – 1}
प्रश्न 2: कार्तीय गुणनफल A × A में 9 तत्व हैं जिनमें से (–1, 0) और (0,1) पाए जाते हैं। समुच्चय A और A × A के शेष तत्व ज्ञात कीजिए।
समाधान:
हम जानते हैं कि
यदि n(A) = p और n(B) = q, तो n(A × B) = pq
दिया गया है,
n(A × A) = 9
n(A) ×n(A) = 9,
n(A) = 3 ……(i)
क्रमित युग्म (-1, 0) और (0, 1) A × A के नौ तत्वों में से दो हैं।
इसलिए, A × A = {(a, a) : a ∈ A}
अतः, -1, 0, 1 A के तत्व हैं। …..(ii)
(i) और (ii) से,
A = {−1,0,1}
समुच्चय A × A के शेष तत्त्व (-1, -1), (-1, 1), (0, -1), (0, 0), (1, -1), (1, 0) एवं (1, 1) हैं।
प्रश्न 3: फ़ंक्शन f: A—R. f(x) =\(x^2\)– 1. को व्यक्त करें, जहाँ A = {-4, 0, 1, 4) को क्रमित युग्मों के समूह के रूप में व्यक्त करें।
समाधान:
दिया गया है,
A = {−4,0,1,4}
f(x)=\(x^2\)−1
f(−4) = \((−4)^2\)– 1 = 16 – 1=15
f(0)=\((0)^2\) − 1=−1
f(1)=\((1)^2\)−1=0
f(4)=\((4)^2\) – 1 = 16 – 1 =15
इसलिए, क्रमित युग्मों का समूह = {(-4, 15), (0, -1), (1, 0), (4, 15)}
प्रश्न 4: मान लीजिए कि A = {1, 2, 3,…,14}। A से A तक R = {(x, y) : 3x – y = 0, इस प्रकार कि x, y ∈ A} से संबंध R परिभाषित करें। इसका परिसर, प्रांत और सह प्रांत निर्धारित करें और लिखें।
समाधान:
यह दिया गया है कि A से A तक संबंध R, R = {(x, y): 3x – y = 0, जहाँ x, y ∈ A} द्वारा दिया गया है।
इसका अर्थ है कि R = {(x, y) : 3x = y, जहाँ x, y ∈ A}
अतः, R = {(1, 3), (2, 6), (3, 9), (4, 12)}
हम जानते हैं कि R का डोमेन दिए गए संबंध में क्रमित युग्मों के सभी प्रथम तत्वों के समुच्चय के रूप में परिभाषित किया गया है।
अतः R का डोमेन = {1, 2, 3, 4}
सहप्रांत निर्धारित करने के लिए, हम जानते हैं कि संपूर्ण समुच्चय A, संबंध R का सहप्रांत है।
इसलिए, R का सहप्रान्त = A = {1, 2, 3,…,14}
जैसा कि ज्ञात है कि, R की सीमा को क्रमित युग्म संबंध में सभी द्वितीय तत्वों के समुच्चय के रूप में परिभाषित किया गया है।
इसलिए, R का परिसर = {3, 6, 9, 12} द्वारा दिया गया है
प्रश्न 5: मान लीजिए f(x) = \(x^2\)और g(x) = 2x + 1 दो वास्तविक फलन हैं।
(f + g) (x), (f –g) (x), (fg) (x), (f/g) (x)
समाधान:
दिया गया,
f(x) = \(x^2\)और g(x) = 2x + 1
(f + g)(x) = \(x^2\)+ 2x + 1
(f – g)(x) = \(x^2\) -(2x + 1) = \(x^2\) – 2x – 1
(fg)(x) = \(x^2\)(2x + 1) = \(2x^3\) + \(x^2\)
(f/g)(x) = \(x^2\)/(2x + 1), x ≠ -1/2
प्रश्न 6: फ़ंक्शन को पुनः परिभाषित करें: f(x) = |x – 1| – |x + 6| इसका डोमेन भी लिखें।
समाधान:
दिया गया फ़ंक्शन f(x) = |x – 1| – |x + 6|
फ़ंक्शन का पुनर्परिभाषित रूप है:
इस फ़ंक्शन का डोमेन R है।
प्रश्न 7: फ़ंक्शन f को निम्न द्वारा परिभाषित किया गया है
f(x) का ग्राफ बनाएं।
समाधान:
f(x) = 1 – x, x < 0, इससे प्राप्त होता है
f(– 4) = 1 – (– 4)= 5;
f(– 3) =1 – (– 3) = 4,
f(– 2) = 1 – (– 2)= 3
f(–1) = 1 – (–1) = 2; आदि,
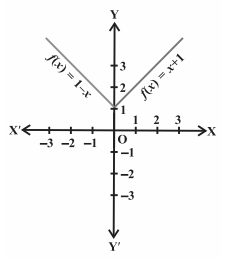
इसके अलावा, f(1) = 2, f (2) = 3, f (3) = 4, f(4) = 5 और इसी प्रकार f(x) = x + 1, x > 0 के लिए।
इस प्रकार, f का ग्राफ नीचे चित्र में दिखाया गया है।
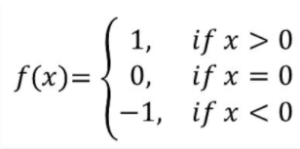
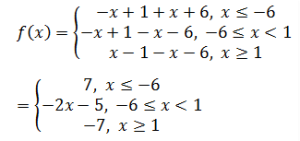
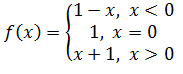
Leave a Reply