त्रिविमीय ज्यामिति का परिचय
प्रश्न 1: उन बिन्दुओं के समुच्चय का समीकरण ज्ञात कीजिए जो बिन्दुओं (1, 2, 3) और (3, 2, –1) से समान दूरी पर हैं।
समाधान:
मान लीजिए कि P (x, y, z) वह बिंदु है जो दो बिंदुओं A(1, 2, 3) और B(3, 2, –1) से समान दूरी पर है।
इस प्रकार, हम कह सकते हैं कि, PA = PB
दोनों पक्षों पर वर्ग लेने पर हमें प्राप्त होता है
\(PA^2 = PB^2\)
यह मतलब है कि,
अब उपरोक्त समीकरण को सरल करें, हमें यह मिलता है:
⇒ –2x –4y – 6z + 14 = –6x – 4y + 2z + 14
⇒ – 2x – 6z + 6x – 2z = 0
⇒ 4x – 8z = 0
⇒ x – 2z = 0
अतः बिन्दुओं के समुच्चय के लिए आवश्यक समीकरण x – 2z = 0 है।
प्रश्न 2: सिद्ध कीजिए कि बिंदु: (0, 7, 10), (–1, 6, 6) और (–4, 9, 6) एक समकोण त्रिभुज के शीर्ष हैं
समाधान:
मान लीजिए दिए गए बिंदु A = (0, 7, 10), B = (–1, 6, 6), और C = (–4, 9, 6) हैं।
अब, बिंदुओं के बीच की दूरी ज्ञात कीजिए:
दिए गए बिंदु पाइथागोरस प्रमेय की शर्त को पूरा करते हैं।
अतः, दिए गए बिंदु समकोण त्रिभुज के शीर्ष हैं।
प्रश्न 3: बिंदु P(6, 7, 8) से XY – तल (XY-plane) की लंबवत दूरी ज्ञात कीजिए।
(a) 8
(b) 7
(c) 6
(d) उपरोक्त में से कोई नहीं
समाधान:
सही उत्तर विकल्प (a) है।
प्रश्न 4: यदि निर्देशांक समतलों के समांतर बिंदुओं (2, 3, 5) और (5, 9, 7) से होकर खींचे गए समतलों द्वारा एक समांतर चतुर्भुज का निर्माण किया जाता है, तो समांतर चतुर्भुज के किनारों की लंबाई और विकर्ण की लंबाई ज्ञात कीजिए।
समाधान:
मान लीजिए A = (2, 3, 5), B = (5, 9, 7)
समांतर चतुर्भुज के किनारों की लंबाई ज्ञात करने के लिए = 5 – 2, 9 – 3, 7 – 5
इसका मतलब है कि 3, 6, 2.
अब, विकर्ण की लंबाई ज्ञात करें = √(3 2 + 6 2 + 2 2 )
= √(9+36+4)
= √49
= 7
इसलिए, एक समांतर चतुर्भुज के विकर्ण की लंबाई 7 इकाई है।
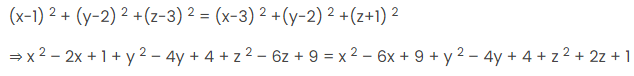



Leave a Reply