प्रश्न 1: निम्नलिखित समुच्चयों को रोस्टर रूप में लिखें।
(i) A = {x | x 10 से कम एक धनात्मक पूर्णांक है तथा \( 2^x \)– 1 एक विषम संख्या है}
(ii) C = {x : \( x^2 \) + 7x – 8 = 0, x ∈ R}
समाधान:
(i) 2x – 1 सदैव x के सभी धनात्मक पूर्णांक मानों के लिए एक विषम संख्या होती है क्योंकि 2x एक सम संख्या है।
विशेष रूप से,\( 2^x \) – 1 x = 1, 2, … , 9 के लिए एक विषम संख्या है।
इसलिए, A = {1, 2, 3, 4, 5, 6, 7, 8, 9}
(ii) \( x^2 \) + 7x – 8 = 0
(x + 8) (एक्स – 1) = 0
x = – 8 या x = 1
इसलिए, C = {– 8, 1}
प्रश्न 2: निम्नलिखित समुच्चयों को रोस्टर रूप में लिखें:
(i) A = {x : x एक पूर्णांक है और –3 ≤ x < 7}
(ii) B = {x : x, 6 से छोटी एक प्राकृतिक संख्या है}
समाधान:
(i) A = {x : x एक पूर्णांक है और –3 ≤ x < 7}
पूर्णांक हैं…-5, -4, -3, -2, -2, 0, 1, 2, 3, 4, 5, 6, 7, 8,…..
A = {-3, -2, -1, 0, 1, 2, 3, 4, 5, 6}
(ii) B = {x : x, 6 से छोटी एक प्राकृतिक संख्या है}
प्राकृतिक संख्याएँ हैं 1, 2, 3, 4, 5, 6, 7, ……
B = {1, 2, 3, 4, 5}
प्रश्न 3: दिया गया है कि N = {1, 2, 3, …, 100}, तो
(i) N का उपसमुच्चय A लिखिए जिसके अवयव विषम संख्याएँ हैं।
(ii) N का उपसमुच्चय B लिखिए जिसके अवयव x + 2 द्वारा निरूपित होते हैं, जहाँ x ∈ N है।
समाधान:
(i) A = {x | x ∈ N और x विषम है}
A = {1, 3, 5, 7, …, 99}
(ii) B = {y | y = x + 2, x ∈ N}
1 ∈ N, y = 1 + 2 = 3
2 ∈ N, y = 2 + 2 = 4, इत्यादि।
इसलिए, B = {3, 4, 5, 6, … , 100}
प्रश्न 4: मान लीजिए X = {1, 2, 3, 4, 5, 6}। यदि n, X के किसी भी सदस्य को दर्शाता है, तो निम्न को समुच्चयों के रूप में व्यक्त करें:
(i) n ∈ X परंतु 2n ∉ X
(ii) n + 5 = 8
(iii) n, 4 से बड़ा है
समाधान:
(i) X = {1, 2, 3, 4, 5, 6} के लिए यह दिया गया है कि n ∈ X, परंतु 2n ∉ X.
मान लीजिए, A = {x | x ∈ X तथा 2x ∉ X}
अब, 1 ∉ A क्योंकि 2.1 = 2 ∈ X
2 ∉ A क्योंकि 2.2 = 4 ∈ X
3 ∉ A क्योंकि 2.3 = 6 ∈ X
लेकिन 4 ∈ A क्योंकि 2.4 = 8 ∉ X
5 ∈ A क्योंकि 2.5 = 10 ∉ X
6 ∈ A क्योंकि 2.6 = 12 ∉ X
इसलिए, A = {4, 5, 6}
(ii) मान लीजिए B = {x | x ∈ X तथा x + 5 = 8}
यहाँ, B = {3} क्योंकि x = 3 ∈ X और 3 + 5 = 8 है तथा X से संबंधित कोई अन्य तत्व नहीं है जिससे x + 5 = 8 हो।
(iii) मान लीजिए C = {x | x ∈ X, x > 4}
इसलिए, C = {5, 6}
प्रश्न 5: मान लीजिए U = {1, 2, 3, 4, 5, 6}, A = {2, 3} तथा B = {3, 4, 5}.
A′, B′, A′ ∩ B′, A ∪ B ज्ञात कीजिए और इससे दर्शाइए कि (A ∪ B)′ = A′∩ B′.
समाधान:
दिया गया,
U = {1, 2, 3, 4, 5, 6}, A = {2, 3} और B = {3, 4, 5}
A′ = {1, 4, 5, 6}
B′ = { 1, 2, 6 }
अतः, A′ ∩ B′ = { 1, 6 }
साथ ही, A ∪ B = { 2, 3, 4, 5 }
(A ∪ B)′ = { 1, 6 }
इसलिए, ( A ∪ B )′ = { 1, 6 } = A′ ∩ B′
प्रश्न 6: समुच्चयों के गुणों का उपयोग करके यह सिद्ध करें कि सभी समुच्चयों A और B के लिए A – (A ∩ B) = A – B
समाधान:
A – (A ∩ B) = A ∩ (A ∩ B)′ (चूँकि A – B = A ∩ B′)
= A ∩ (A′ ∪ B′) [डी मॉर्गन के नियम से)
= (A∩A′) ∪ (A∩ B′) [वितरण नियम से]
= φ∪(A ∩ B′)
= A ∩ B′ = A – B
अतः, सिद्ध हुआ कि A – (A ∩ B) = A – B।
प्रश्न 7: मान लीजिए U = {1, 2, 3, 4, 5, 6, 7}, A = {2, 4, 6}, B = {3, 5} और C = {1, 2, 4, 7}, तो ज्ञात कीजिए
(i) A′ ∪ (B ∩ C′)
(ii) (B – A)∪(A – C)
समाधान:
दिया गया,
U = {1, 2, 3, 4, 5, 6, 7}, A = {2, 4, 6}, B = {3, 5} और C = {1, 2, 4, 7}
(i) A′ = {1, 3, 5, 7}
C′ = {3, 5, 6}
B ∩ C′ = {3, 5}
A′ ∪ (B ∩ C′) = {1, 3, 5, 7}
(ii) B – A = {3, 5}
A – C = {6}
(B– A) ∪ (A – C) = {3, 5, 6}
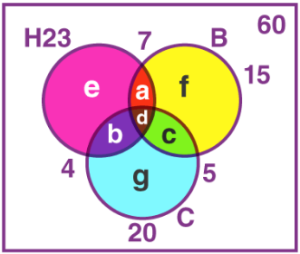
प्रश्न 8: 60 छात्रों की एक कक्षा में, 23 छात्र हॉकी खेलते हैं, 15 बास्केटबॉल खेलते हैं, 20 क्रिकेट खेलते हैं और 7 हॉकी और बास्केटबॉल दोनों खेलते हैं, 5 क्रिकेट और बास्केटबॉल दोनों खेलते हैं, 4 हॉकी और क्रिकेट दोनों खेलते हैं, 15 कोई भी तीन खेल नहीं खेलते। पता लगाएँ:
(i) कितने छात्र हॉकी, बास्केटबॉल और क्रिकेट खेलते हैं।/>
(ii) कितने छात्र केवल हॉकी खेलते हैं और क्रिकेट नहीं खेलते।
(iii) कितने छात्र हॉकी और क्रिकेट खेलते हैं लेकिन बास्केटबॉल नहीं खेलते।
समाधान:
दिए गए डेटा का वेन आरेख है:
15 छात्र तीनों खेलों में से कोई भी नहीं खेलते।
n(H ∪ B ∪ C) = 60 – 15 = 45
n(H ∪ B∪ C) = n(H) + n(B) + n(C) – n(H ∩ B) – n(B ∩ C) – n(C ∩ H) + n(H ∩ B ∩ C)
45 = 23 + 15 + 20 – 7 – 5 – 4 + d
45 = 42 + d
d = 45 − 42 = 3
वे छात्र जो तीनों खेल खेलते हैं = 3
इसलिए, हॉकी, बास्केटबॉल और क्रिकेट खेलने वाले छात्रों की संख्या = 3
a + d = 7
a = 7 – 3 = 4
b + d = 4
b = 4 – 3 = 1
a + b + d + e = 23
4 + 1 + 3 + e = 23
e = 15
इसी प्रकार, c = 2, g = 14, f = 6
वे छात्र जो केवल हॉकी खेलते हैं और क्रिकेट नहीं खेलते = a + e = 4 + 15 = 19
वे छात्र जो हॉकी और क्रिकेट खेलते हैं लेकिन बास्केटबॉल नहीं खेलते = b = 1
प्रश्न 9: मान लीजिए U = {x : x ∈ N, x ≤ 9}; A = {x : x एक सम संख्या है, 0 < x < 10}; B = {2, 3, 5, 7}. समुच्चय (AUB) लिखिए।
समाधान:
मान लीजिए U = {x : x ∈ N, x ≤ 9}; A = {x : x एक सम संख्या है, 0 < x < 10}; B = {2, 3, 5, 7}
U = {1,2,3,4,5,6,7,8,9}
A = {2,4,6,8}
A∪ B = {2,3,4,5,6,7,8}
(A ∪ B)′= {1,9}
प्रश्न 10: एक स्कूल में 600 छात्रों के एक सर्वेक्षण में, 150 छात्रों को चाय पीते हुए पाया गया, 225 कॉफी पीते हुए, 100 दोनों चाय और कॉफी पीते हुए पाए गए। पता लगाएँ कि कितने छात्र न तो चाय और न ही कॉफी पीते हैं।
समाधान:
दिया गया,
कुल छात्रों की संख्या = 600
चाय पीने वाले छात्रों की संख्या = n(T) = 150
कॉफ़ी पीने वाले छात्रों की संख्या = n(C) = 225
चाय और कॉफ़ी दोनों पीने वाले छात्रों की संख्या = n(T ∩ C) = 100
n(T∪C) = n(T) + n(C) – n(T∩C)
= 150 + 225 − 100
= 375 – 100
= 275
अतः, न तो चाय और न ही कॉफी पीने वाले छात्रों की संख्या = 600 – 275 = 325

Thank you