Page 1.2 Ex – 1.1
Q1.
Answer :
Well-defined collections are sets.
Example:
The collection of good teachers in a school is not a set, It is a collection.
Thus, we can say that every set is a collection, but every collection is not necessarily a set.
The collection of vowels in English alphabets is a set.
Q2.
(i) The collection of all natural numbers less than 50 is a set because it is well defined.
(ii) The collection of good hockey players is not a set because the goodness of a hockey player is not defined here. So, it is not a set.
(iii) The collection of all girls in a class is a set, as it is well defined that all girls of the class are being talked about.
(iv) The collection of the most talented writers of India is a set because it is well defined.
(v) The collection of difficult topics in mathematics is not a set because a topic can be easy for one student while difficult for the other student.
(vi) The collection of all months of a year beginning with the letter J is a set given by {January, June, July}
(vii) A collection of novels written by Munshi Prem Chand is a set because one can determine whether the novel is written by Munshi Prem Chand or not.
(Viii) The collection of all question in this chapter is a set because one can easily check whether it is a question of the chapter or not.
(ix) A collection of most dangerous animals of the world is not a set because we cannot decide whether the animal is dangerous or not.
(x) The collection of prime integers is set given by {2, 3, 5……..}
Q3.
(i) 4 ∈ Α
(ii) −4 ∉ Α
(iii) 12
∉ Α
(iv) 9 ∈ Α
(v) 0 ∈ Α
(vi) −2 ∉ Α
Page 1.7 Ex – 1.2
Q1.
In this form, a set is defined by listing elements, separated by commas, within braces {}.
(i) {a, b, c, d}
(ii) {1, 2, 3, 4}
(iii) {11, 13, 17, 19}
(iv) {2, 4, 6, 8, 10,…}
(v) ϕ(vi) {2, 3, 5}
(vii) {17, 26, 35, 44, 53, 62, 71, 80}
(viii) {T, R, I, G, O, N, M, E, Y}
(ix) {B, E, T, R}
Q2.
Answer : Set-builder form:
To describe a set, a variable x (each element of the set) is written inside braces. Then, after putting a colon, the common property P(x) possessed by each element of the set is written within braces.
(i) {x:x∈N, x<7}(ii) {x: x=1n, x∈N}(iii) {x:x=3n, n∈Z+}(iv) {x:x∈N, 9<x<16}(v) {x:x=0}(vi) {x2:x∈N, 1≤n≤10}(vii) {x:x=2n, n∈N}(viii) {5n:n∈N, 1≤n≤4}
Q3. Answer :
(i) A={0,±1,±2,±3}(ii) B=1,13,15,17,19(iii) C={0,1,2,3,4}(iv) D={A,E,I,O,U}(v) E={February,April,June,September,November}(vi) F={M,I,S,P}
Q4.
Answer :
(i) A={0,±1,±2,±3}(ii) B=1,13,15,17,19(iii) C={0,1,2,3,4}(iv) D={A,E,I,O,U}(v) E={February,April,June,September,November}(vi) F={M,I,S,P}
Q5.
Answer :
The set of vowels in the English alphabet that precede q is {a, e, i, o}.
Q6.
Answer :
The set of all positive integers whose cube is odd is {2n + 1 : n∈ Z, n≥0}.
Q7.
Answer :
The set-builder form of the set
12, 25, 310, 417, 526, 637, 750
is
nn2+1:n∈N,n≤7
Page 1.10 Ex – 1.3
Q1.
Answer :
(i) All natural numbers that end with 0 are even & divisible by 5. Therefore, the given set is not an example of empty set.
(ii) 2 is an even prime number. Therefore, the given set is not an example of empty set.
(iii) There is no rational number whose square is 2 such that x2-2 = 0. Therefore, it is example of empty set.
(iv) It is not possible that x<8 and, at the same time, x>12. Therefore, it is an example of empty set.
(v) There is no common point in two parallel lines. Therefore, it is an example of empty set.
Q2.
Answer :
(i) There can be infinite concentric circles in a plane. Therefore, it is an infinite set.
(ii) There are 26 letters in the set of English alphabet. Therefore, it is a finite set.
(iii) {x ∈ N : x > 5} = {6,7,8,9,…}. There will be infinite numbers. So, it an infinite set.
(iv) There are finite elements in the set {x = ∈ N : x < 200}. Therefore, it is a finite set.
(v) In this set, x ∈ Z , so there would be infinite elements in the set {x ∈ Z : x < 5}. Therefore, it is an infinite set.
(vi) In this set, x ∈ R. We know real numbers include all numbers, i.e., decimal numbers, rational numbers and irrational numbers.
So, there would be infinite elements in the set {x ∈ R : 0 < x < 1}. Therefore, it is an infinite set.
Page 1.11 Ex – 1.3
Q3.
Answer :
Two sets A & B are equal if every element of A is a member of B & every element of B is a member of A.
(i) A=1, 2, 3
(ii) B=x∈R : x2-2x+1=0
Set B would be {1}.
(iii) C=1, 2, 2, 3
It can be written as {1, 2, 3} because we do not repeat the elements while writing the elements of a set.
∴ C = {1, 2, 3}
(iv) D=x∈R : x3-6×2+11x-6=0 includes elements {1, 2, 3}.
∴ D = {1, 2, 3}
Hence, we can say that A = C = D.
Q4.
Answer :
A = {r, e, a, p}
B = {p, a, e, r}
C = {r, o, p, e}
Here, A = B because every element of A is a member of B & every element of B is a member of A.
But every element of C is not a member of A & B.
Also, every element of A and B is not a member of C.
Therefore, we can say that these sets are not equal.
Q5.
Answer :
Two sets A & B are equivalent if their cardinal numbers are equal, i.e., n(A) = n(B).
n(A) = 3
n(B) = 5
n(C) = 3
n(D) =5
Therefore, equivalent sets are (A and C) and (B and D).
Q6.
Answer :
(i) A = {2, 3}
B = {-2, -3}
A is not equal to B because every element of A is not a member of B & every element of B is not a member of A.
(ii) A = {W, O, L, F}
B = {F, O, L, W}
Here, A = B because every element of A is a member of B & every element of B is a member of A.
Q7.
Answer :
Equal sets:
(a) B and D, because every element of B is a member of D & every element of D is a member of B.
(b) C and F, because every element of C is a member of F & every element of F is a member of C
Equivalent sets:
(a) A, E and H {∵ n(A) = n(E) =n(H) = 2}
(b) B, D and G {∵ n(B) = n(D) =n(G) = 4}
(c) C and F {∵ n(C) = n(F) = 3}
Q8.
Answer :
A = {1, 2}
B = {1, 2}
C = {3, 1}
D = {1, 3}
E = {1, 2, 1, 1} = {1, 2}
F = {1, 1, 3} = {1, 3}
∴ A = B = E and C = D = F
Q9.
Answer :
Letters required to spell CATARACT are {C, A, T, R}. Let this set be denoted as E.
E = {C, A, T, R}
Letters required to spell TRACT are {T, R, A, C}. Let this set be denoted as F.
F = {T, R, A, C}
The two sets E & F are equal because every element of E is a member of F & every element of F is a member of E.
Page 1.18 Ex – 1.4
Q1.
Answer :
(i) False It is not necessary that for any two sets A & B, either A⊆B or B⊆A.It is not satisfactory always. Let: A={1,2} & B={α,β,γ}Here, neither A⊆B nor B⊆A.
(ii) False A={-1,0,1,2,3} is a finite set that is a subset of infinite set Z.
(iii) True Every subset of a finite set is a finite set.
(iv) Falseϕ does not have a proper subset.
(v) False{a,b,a,b,a,b,…} will be equal to {a,b}, which is a finite set.
(vi) True{a,b,c} and {1,2,3} are equivalent sets because the number of elements in both the sets are same.
(vii) FalseIn the set A={1,2}, subsets can be {ϕ}, {1} and {2}, which are finite.
Q2.
Answer :
(i) True
(ii) False
It should be written as {a} ⊂{b,c,a} or a∈{b,c,a}.
(iii) False
It should be written as {a} ⊂{b,c,a} or a∈{b,c,a}.
(iv) True
(v) False
The element of the set {x ; x + 8 = 8} is {0}. Therefore, it is not an empty or null set.
Q3.
Answer :
We have:
A={x : x satisfies x2-8x+12=0.}={2,6}
B = {2, 4, 6}
C = {2, 4, 6, 8,…}
D = {6}
Therefore, we can say that D⊂A⊂B⊂C.
Q4.
Answer :
(i) True
A rational number is any mn, where m and n are any integers (n≠0). Any integer can be put into that form by setting n = 1. Therefore, the set of all integers is contained in the set of all rational numbers.
(ii) True
All crows are birds. Therefore, the set of all crows is contained in the set of all birds.
(iii) False
Every square can be a rectangle, but every rectangle cannot be a square.
(iv) True
Every real number can be written in the (a + bi) form. Thus, we can say that the set of all real numbers is contained in the set of all complex numbers.
(v) False
P = {a}
B = {{a}} = {P}
P≠{P}
(vi) True
We have:
A = {x:x is a letter of the word LITTLE} = {L, I, T, E}
B = {x:x is a letter of the word TITLE} = {T, I, L, E}
Sets A & B are equal because every element of A is a member of B & every element of B is a member of A.
Q5.
Answer :
Here, (viii) is correct.
The correct forms of each of the incorrect statements are:
(i) a∈a, b, c
(ii) a⊂a, b, c
(iii) {a}∈{a, b}
(iv) {a}⊂a, b
(v) b, c∈a,b, c
(vi) {a,b}⊄{a,{b,c}}
(vii) ϕ⊂a, b
(ix) x:x+3=3≠ϕ
Q6.
Answer :
A = {a, b, {c, d}, e}
(i) False
The correct statement would be {c, d}⊂A.
(ii) True
(iii) True
(iv) True
(v) False
The correct statement would be {a}⊂ A or a ∈ A.
(vi) True
(vii) False
The correct statement would be a, b, e⊂A.
(viii) False
The correct statement would be {a, b, c} ⊄ A.
(ix) False
A null set is a subset of every set. Therefore, the correct statement would be ϕ⊂A.
(x) False
ϕ is an empty set; in other words, this set has no element. It is denoted by ϕ. Therefore, the correct statement would be ϕ⊂A.
Page 1.19 Ex – 1.4
Q7.
Answer :
(i) False
If it could be 1∉A , then it would be true .
(ii) False
The correct form would be 1, 2, 3∈A or {1, 2, 3}⊂A.
(iii) True
(iv) True
(v) False
A null set is a subset of every set. Therefore, the correct form would be ϕ ⊂ A.
(vi) True
Q8.
Answer :
(i) True
(ii) True
(iii) False
The correct form would be 1⊂A.
(iv) True
(v) False
The correct form would be 1∈A.
(vi) True
(vii) True
(viii) True
(ix) True
Q9.
Answer :
(i) ϕ ,{a}(ii) ϕ,{0},{1},{0,1}(iii) ϕ,{a},{b},{c},{a,b},{b,c},{a,c},{a,b,c}(iv) ϕ,{1},{{1}},{1,{1}}(v) ϕ,{ϕ}
Q10.
Answer :
(i) {1}, {2}
(ii) {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}
(iii) No proper subsets are there in this set.
Q11.
Answer :
We know that the total number of subsets of a finite set consisting of n elements is 2n.
Therefore, the total number of proper subsets of a set consisting of n elements is 2n-1.
Q12.
Answer :
To prove: A⊆ϕ⇔A=ϕ
Proof:
Let:
A⊆ϕ
If A is a subset of an empty set, then A is the empty set.
∴ A=ϕ
Now, let A=ϕ.
This means that A is an empty set.
We know that every set is a subset of itself.
∴ A⊆ϕ
Thus, we have:
A⊆ϕ⇔A=ϕ
Q13.
Answer :
Let x∈A⇒x∈B ∵A⊆B⇒x∈C ∵B⊆C∴x∈A⇒ x∈C⇒A⊆C …1It is given tha,C⊆A …(2)From 1 and 2, we have A=C
Q14.
Answer :
Given : A=ϕ This means P(A) ={ϕ}.Hence, P(A) would have one element.
Q15.
Answer :
(i) The set of all triangles in a plane
(ii) The set of all triangles in a plane
Q16.
Answer :
Given:
X=8n-7n-1:n∈N and Y=49n-1:n∈N
To prove:
X⊆Y
Let: xn=8n-7n-1, n∈N⇒ x1=8-7-1=0For any n⩾2, we have: xn=8n-7n-1=(1+7)n -7n-1⇒xn=C0n+C1n.7+C2n.72+C3n.73+…+Cnn.7n-7n-1⇒xn=1+7n+C2n.72+C3n.73+…+7n-7n-1 [∵ C0n=1 and C1n=n]⇒xn=72{C2n+C3n.7+C4n72+…+Cnn.7n-2}⇒xn=49{C2n+C3n.7+C4n72+…+Cnn.7n-2}Thus, xn is some positive integral multiple of 49 for all n⩾2. X consists of all those positive integral multiples of 49 that are of the form 49{C2n+C3n.7+C4n72+…+Cnn.7n-2} along with zero.Y={49(n-1):n∈N} implies that it consists of all integral multiples of 49 along with zero.∴ X⊆Y
Page 1.23 Ex – 1.5
Q1.
Answer :
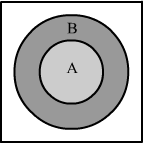
From the Venn diagrams given below, we can clearly say that if A and B are two sets such that A⊂B, then
(i) Form the given Venn diagram, we can see that A∩B = A
(ii) Form the given Venn diagram, we can see that A∪B = B
Q2.
Answer :
Given:
A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7, 8}, C = {7, 8, 9, 10, 11} and D = {10, 11, 12, 13, 14}
(i) A∪B = {1, 2, 3, 4, 5, 6, 7, 8}
(ii) A∪C = {1, 2, 3, 4, 5, 7, 8, 9, 10, 11}
(iii) B∪C = {4, 5, 6, 7, 8, 9, 10, 11}
(iv) B∪D = {4, 5, 6, 7, 8, 10, 11, 12, 13, 14}
(v) A∪B∪C = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
(vi) A∪B∪D = {1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 14}
(vii) B∪C∪D = {4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}
(viii) A∩B∪C = {4, 5}
(ix) A∩B∩B∩C = ϕ
(x) A∪D∩B∪C = {4, 5, 10, 11}
Q3.
Answer :
A=x:x∈N={1,2,3,…}B=x:x-2n, n∈N={2,4,6,8,…} C=x:x=2n-1, n∈N={1,3,5,7,…}
D = {x:x is a prime natural number.} = {2, 3, 5, 7,…}
(i) A∩B = B
(ii) A∩C = C
(iii) A∩D = D
(iv) B∩C = ϕ
(v) B∩D = {2}
(vi) C∩D = D-{2}
Q4.
Answer :
Given:
A = {3, 6, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}
(i) A-B = {3, 6, 15, 18, 21}
(ii) A-C = {3, 15, 18, 21}
(iii) A-D = {3, 6, 12, 18, 21}
(iv) B-A = {4, 8, 16, 20}
(v) C-A = {2, 4, 8, 10, 14, 16}
(vi) D-A = {5, 10, 20}
(vii) B-C = {20}
(viii) B-D = {4, 8, 12, 16}
Q5.
Answer :
Given:
U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 2, 3, 4}, B= {2, 4, 6, 8} and C = {3, 4, 5, 6}
(i) A’ = {5, 6, 7, 8, 9}
(ii) B’ = {1, 3, 5, 7, 9}
(iii) A∩C’ = {1, 2, 5, 6, 7, 8, 9}
(iv) A∪B’ = {5, 7, 9}
(v) A” = {1, 2, 3, 4} = A
(vi) B-C’ = {1, 3, 4, 5, 6, 7, 9}
Q6.
Answer :
Given:
U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {2, 4, 6, 8} and B = {2, 3, 5, 7}
We have to verify:
(i) A∪B’=A’∩B’
LHS
A∪B ={2,3,4,5,6,7,8}A∪B ‘={1,9}
RHS
A’={1,3,5,7,9}B’={1,4,6,8,9}A’∩B’={1,9}
LHS = RHS
Hence proved.
(ii) A∩B’=A’∪B’
LHS
A∩B={2}A∩B’={1,3,4,5,6,7,8,9}
RHS
A’={1,3,5,7,9}B’={1,4,6,8,9}A’∪B’={1,3,4,5,6,7,8,9}
LHS = RHS
Hence proved.
Page 1.29 Ex – 1.6
Q1.
Answer :
We have to find the smallest set A such that A∪1, 2=1, 2, 3, 5, 9.
The union of the two sets A & B is the set of all those elements that belong to A or to B or to both A & B.
Thus, A must be {3, 5, 9}.
Q2.
Answer :
Given:
A = {1, 2, 4, 5}, B = {2, 3, 5, 6} and C = {4, 5, 6, 7}
We have to verify the following identities:
(i) A∪B∩C=A∪B∩A∪C
LHS
(B∩C)={5,6}A∪(B∩C)={1,2,4,5,6}
RHS
A∪B={1,2,3,4,5,6}A∪C={1,2,4,5,6,7}A∪B∩A∪C={1,2,4,5,6}
LHS = RHS
∴ A∪B∩C=A∪B∩A∪C
(ii) A∩B∪C=A∩B∪A∩C
LHS
(B∪C)={2,3,4,5,6,7}A∩(B∪C)={2,4,5}
RHS
A∩B={2,5}A∩C={4,5}A∩B∪A∩C={2,4,5}
LHS = RHS
∴ A∩B∪C=A∩B∪A∩C
(iii) A∩B-C=A∩B-A∩C
LHS
(B-C) ={2,3}A∩(B-C)={2}
RHS
(A∩B)={2,5}(A∩C)={4,5}(A∩B)-(A∩C)={2}
LHS = RHS
∴ A∩B-C=A∩B-A∩C
(iv) A-B∪C=A-B∩A-C
LHS
(B∪C)={2,3,4,5,6,7}A-(B∪C)={1}
RHS
(A-B)={1,4}(A-C)={1,2}(A-B)∩(A-C)={1}
LHS = RHS
∴ A-B∪C=A-B∩A-C
(v) A-B∩C=A-B∪A-C
LHS
(B∩C)={5,6}A-(B∩C)={1,2,4}
RHS
(A-B)={1,4}(A-C)={1,2}(A-B)∪(A-C)={1,2,4}
LHS = RHS
∴ A-B∩C=A-B∪A-C
(vi) A∩B∆C=A∩B∆A∩C
LHS
(B∆C)=(B-C)∪(C-B)(B-C)={2,3}(C-B)={4,7}(B-C)∪(C-B)={2,3,4,7}⇒(B∆C)={2,3,4,7}A∩(B∆C)={2,4}
RHS
(A∩B)={2,5}(A∩C)={4,5}(A∩B)∆(A∩C)={(A∩B)-(A∩C)}∪{(A∩C)-(A∩B)}(A∩B)-(A∩C)={2}(A∩C)-(A∩B)={4}{(A∩B)-(A∩C)}∪{(A∩C)-(A∩B)}={2,4}⇒(A∩B)∆(A∩C)={2,4}
LHS = RHS
∴ A∩B∆C=A∩B∆A∩C
Q3.
Answer :
Given:
U = {2, 3, 5, 7, 9}
A = {3, 7}
B = {2, 5, 7, 9}
To prove :
(i) A∪B’=A’∩B’
(ii) A∩B’=A’∪B’
Proof :
(i) LHS:
(A∪B)={2,3,5,7,9}(A∪B)’=ϕ
RHS:
A’={2,5,9}B’={3}A’∩B’=ϕLHS=RHS
∴ A∪B’=A’∩B’
(ii) LHS:
(A∩B)={7}(A∩B)’={2,3,5,9}
RHS:
A’={2,5,9}B’={3}A’∪B’={2,3,5,9}
LHS = RHS
∴ A∩B’=A’∪B’
Q4.
Answer :
We have that the following statements are equivalent:
(i) A⊂B
(ii) A-B=ϕ
(iii) A∪B=B
(iv) A∩B=A
Proof:
Let A⊂BLet x be an arbitary element of (A-B). Now,x∈(A-B)⇒x∈A & x∉B (Which is contradictory) Also,∵A⊂B⇒A-B⊆ϕ …(1) We know that null sets are the subsets of every set.∴ϕ ⊆ A-B …(2)From (1) & (2), we get,(A-B)=ϕ∴(i)=(ii)Now, we have,(A-B)=ϕThat means that there is no element in A that does not belong to B.Now, A∪B=B∴(ii)=(iii) We have,A∪B=B⇒A⊂B⇒A∩B=A∴(iii)=(iv)We have, A∩B=AIt should be possible if A⊂B.Now,A⊂B∴ (iv)=(i)We have,(i)=(ii)=(iii)=(iv) Therefore, we can say that all statements are equivalent.
Q5.
Answer :
(i) Let A = {2, 4, 5, 6}, B = {6, 7, 8, 9} and C = {6, 10, 11, 12,13}
So, A∩B=6 and A∩C=6Hence, A∩B=A∩C but B≠C
(ii) Let z∈C-B …(1)⇒z∈C and z∉B⇒z∈C and z∉A ∵A⊂B⇒z∈C-A …(2)From (1) and (2), we getC-B⊂C-A
Q6.
Answer :
(i) LHS = A∪A∩B⇒LHS=A∪A∩A∪B ⇒LHS=A∩A∪B ∵A⊂A∪B⇒LHS=A = RHS
(ii) LHS=A∩A∪B⇒LHS=A∩A∪A∩B ⇒LHS=A∪A∩B ⇒LHS=A = RHS
Q7.
Answer :
Let us consider the following sets,
A = {5, 6, 10 }
B = {6,8,9}
C = {9,10,11}
Clearly, A∩B=6B∩C=9, A∩C=10 and A∩B∩C = ϕIt means that, A∩B,B∩C and A∩C are non empty setsand A∩B∩C = ϕ
Q8.
Answer :
Let a∈A⇒a∉B ∵A∩B=ϕ.
⇒a∈B’
Thus, a∈A and a∈B’ ⇒ A⊆B’.
Q9.
Answer :
i A-B and A∩BLet a∈A-B⇒a∈A and a∉B⇒a∉A∩BHence, A-B and A∩B are disjoint sets.ii B-A and A∩BLet a∈B-A⇒a∈B and a∉A⇒a∉A∩BHence, B-A and A∩B are disjoint sets.iii A-B and B-A A-B=x:x∈A and x∉B B-A=x:x∈B and x∉AHence, A-B and B-A are disjoint sets.
Q10.
Answer :
LHS=A∪B∪A∩B’⇒LHS=A∪B∩A∪A∪B∩B’⇒LHS=A∪B∩A∪A∪B∩B’⇒LHS=A∪A∪B∩B’⇒LHS=A∪A∩B’∪B∩B’ ∵ B∩B=ϕ⇒LHS=A∪A∩B’⇒LHS=A=RHS
Page 1.30 Ex – 1.6
Q11.
Answer :
i Let a∈A.⇒a∈U⇒a∈A’∪B ∵ U=A’∪B⇒a∈B ∵a∉A’Hence, A⊂B.
ii Let a∈A.⇒a∉A’⇒a∉B’ ∵B’⊂A’⇒a∈BHence, A⊂B.
Q12.
Answer :
False.Let X∈PA∪PB⇒ X∈PA or X∈PB⇒X⊂A or X⊂B⇒X⊂A∪B⇒X∈PA∩B ∴PA∪PB ⊂PA∪B …1Again, let X∈PA∪BBut X∉PA or x∉PB For example let A=2,5 and B=1,3,4 and take X=1,2,3,4So, X∉PA∪PBThus, PA∪B is not necessarily a subset of PA∪PB.
Q13.
Answer :
(i) RHS=A∩B∪A-B⇒RHS=A∩B∪A∩B’⇒RHS=A∩B∪A∩A∩B∪B’⇒RHS=A∩A∪B’∩B∪B’⇒RHS=A∩A∪B’∩U⇒RHS=A∩A∪B’⇒RHS=A=LHS
(ii) LHS=A∪B-A⇒LHS=A∪B∩A’⇒LHS=A∪B∩A∪A’⇒LHS=A∪B∩U⇒LHS=A∪B=RHS
Page 1.37 Ex – 1.7
Q1.
LHS=A’-B’=A’∩B” ∵C-D=C∩D’=A’∩B=B∩A’=B-A ∵C∩D’=C-DRHS=B-A
So, LHS = RHS
Q2.
Answer :
(i)
LHS=A∩A’∪B =A∩A’∪A∩B =ϕ∪A∩B =A∩B=RHS
Hence proved.
(ii)
LHS=A-A-B =A-A∩B’ =A∩A∩B” =A∩A’∪B” =A∩A’∪B =A∩A’∪A∪B =∅∪A∪B =A∪B=RHS
Hence proved.
(iii)
LHS=A∩A∪B’ =A∩A’∩B’ =A∩A’∩A∩B’ =ϕ∩A∩B’ =ϕ=RHS ϕ∩A=ϕ
Hence proved.
(iv)
LHS=A ΔA∩B =A-A∩B∪A∩B-A =A∩A∩B’∪A∩B∩A’ =A∩A’∪B’∪A∩B∩A’ =A∩A’∪A∩B’∪A∩A’∩B∩A’ =ϕ∪A∩B’∪ϕ∩B∩A’ =A∩B’∪ϕ =A∩B’ =A-B=RHS .
Hence proved.
Q3.
Answer :
Let a∈C-B⇒a∈C and a∉B⇒a∈C and a∉A ∵A⊂B ⇒a∈C-A Hence, C-B⊂C-A
Page 1.45 Ex – 1.8
Q1.
Answer :
We know:
n(A∪B)=n(A)+n(B)-n(A∩B)⇒50=28+32-n(A∩B)⇒n(A∩B)=60-50=10
Q2.
Answer :
Given:nP=40nP∪Q=60nP∩Q=10To find:nQWe know:nP∪Q=nP+nQ-nP∩Q⇒60=40+nQ-10⇒nQ=30
Page 1.46 Ex – 1.8
Q3.
Answer :
Let A be the number of teachers who teach mathematics & B be the number of teachers who teach physics.
Given:nA=12nA∪B=20nA∩B=4 To find: nBWe know: nA∪B=nA+nB-nA∩B⇒20=12+nB-4⇒nB=20-8=12 Therefore, 12 teachers teach physics.
Q4.
Answer :
Let A denote the set of the people who like tea & B denote the set of the people who like coffee.
Given:n(A∪B)=70n(A)=52n(B)=37To find:n(A∩B)We know: n(A∪B)=n(A)+n(B)-n(A∩B)⇒70=52+37-n(A∩B)⇒n(A∩B)=19Therefore, 19 people like both tea & coffee.
Q5.
Answer :
Given:
n A=20, n A∪B=42 and n A∩B=4
(i) We know:n(A∪B)=n(A)+n(B)-n(A∩B)⇒42=20+n(B)-4⇒n(B)=26(ii) n(A-B)=n(A)-n(A∩B)⇒n(A-B)=20-4=16(iii) We know that sets follow the commutative property. ∴n(A∩B)=n(B∩A)n(B-A)=n(B)-n(B∩A)⇒n(B-A)=26-4=22
Q6.
Answer :
Let A & B denote the sets of the Indians who like oranges & bananas, respectively.
Given:nA =76%nB=62%nA∪B=100%nA∩B=? We know:nA∪B=nA+nB-nA∩B⇒100=76+62-nA∩B⇒nA∩B=38Therefore, 38% of the Indians like both oranges & bananas.
Q7.
Answer :
Let A & B denote the sets of the persons who like Hindi & English, respectively.
Given:nA =750nB =460nA∪B=950(i) We know:nA∪B=nA+nB-nA∩B⇒950=750+460-nA∩B⇒nA∩B=260Thus, 260 persons can speak both Hindi and English.(ii) nA-B=nA-nA∩BnA-B=750-260=490Thus, 490 persons can speak only Hindi.(iii) nB-A=nB-nA∩B⇒ nB-A=460-260 =200Thus, 200 persons can speak only English.
Q8.
Answer :
Let A & B denote the sets of the persons who drink tea & coffee, respectively .
Given:nA∪B=50nA=30nA-B=14(i) nA-B=nA-nA∩B⇒14=30-nA∩B⇒nA∩B=16Thus, 16 persons drink tea and coffee both.(ii) nA∪B=nA+nB-nA∩B⇒50=30+nB-16⇒nB=36We have to find nB-A⇒nB-A=nB-nA∩B⇒nB-A=36-16=20Thus, 20 persons drink coffee but not tea.
Q9.
Answer :
Given:nH=25nT=26nI=26nH∩I=9nH∩T=11nT∩I=8nH∩T∩I=3(i) We know: nH∪T∪I=nH+nT+nI-nH∩T-nT∩I-nH∩I+nH∩T∩I⇒ nH∪T∪I=25+26+26-11-8-9+3=52Thus, 52 people can read at least one of the newspapers.(ii) Now, we have to calculate the number of people who read exactly one newspaper.We have:nH+nT+nI-2nH∩T-2nT∩I-2nH∩I+3nH∩T∩I=25+26+26-22-16-18+9=30Thus, 30 people can read exactly one newspaper.
Q10.
Answer :
Let A, B & C be the sets of members in basketball team, hockey team & football team, respectively.
Given:nA=21nB=26nC=29nA∩B=14nB∩C=15nA∩C=12n(A∩B∩C)=8We know:nA∪B∪C=nA+nB+nC-nA∩B-nB∩C-nA∩C+nA∩B∩C⇒nA∪B∪C=21+26+29-14-15-12+8=43
Therefore, there are 43 members in all teams.
Q11.
Answer :
Let A & B denote the sets of the persons who can speak Hindi & Bengali, respectively.
Given:nA∪B=1000nA=750nB=400nA∪B=nA+nB-nA∩B⇒1000=750+400-nA∩B⇒nA∩B=150Number of persons who can speak both Hindi and Bengali=nA∩B=150 Number of persons who can speak only Hindi =nA-B=nA-nA∩B =750-150 =600Number of persons who can speak only Bengali=nB-A=nB-nA∩B =400-150 =250
Q12.
Answer :
Let F, H B denote the sets of students who watch football, hockey and basketball, respectively.
Also, let U be the universal set.
We have:
n(F) = 285, n(H) = 195, n(B) = 115, n(F∩B) = 45, n(F∩H) = 70 and n(H∩B) = 50
Also, we know:
n(F’∩H’∩B’) = 50
⇒n(F∪H∪B)’= 50
⇒n(U) – n(F∪H∪B) = 50
⇒500 – n(F∪H∪B) = 50
⇒n(F∪H∪B) = 450
Number of students who watch all three games = n(F∩H∩B)
⇒n(F∪H∪B) – n(F) – n(H) – n(B) + n(F∩B) + n(F∩H) + n(H∩B)
⇒450 – 285 – 195 – 115 + 45 + 70 + 50
⇒20
Number of students who watch exactly one of the three games
= n(F) + n(H) + n(B) – 2{n(F∩B) + n(F∩H) + n(H∩B)} + 3{n(F∩H∩B)}
= 285 + 195 + 115 – 2(45 + 70 + 50) + 3(20)
= 325
Q13.
Answer :
Let A, B C be the sets of the persons who read magazines A, B and C, respectively. Also, let U denote the universal set.
We have: n(U) = 100
n(A) = 28, n(B) = 30, n(C) = 42, n(A∩B) = 8, n(A∩C) = 10, n(B∩C) = 5 and n(A∩B∩C) = 3
Now,
Number of persons who read none of the three magazines = n(A’∩B’∩C’)
= n(A∪B∪C)’
= n(U) – n(A∪B∪C)
= n(U) – {n(A) + n(B) + n(C) – n(A∩B) – n(A∩C) – n(B∩C) + n(A∩B∩C)}
= 100 – (28 + 30 + 42 – 8 – 10 – 5 + 3)
= 20
Number of students who read magazine C only = n(C∩A’∩B’)
= n{C∩(A∪B)’}
= n(C) – n{C∩(A∪B)}
= n(C) – n{(C∩A) ∪ (C∩B)}
= n(C) – n{(C∩A) + (C∩B)-(A∩B∩C)}
= 42 – (10 + 5 – 3)
= 30
Q14.
Answer :
Let E, H and S be the sets of students who study English, Hindi and Sanskrit, respectively.
Also, let U be the universal set.
Now, we have:
n(E) = 26, n(S) = 48, n(E∩S) = 8 and n(S∩H) = 8
Also,
n(E∩H’) = 23
⇒n(E) – n(E∩H) = 23
⇒26 – n(E∩H) = 23
⇒n(E∩H) = 3
Therefore, the number of students studying English and Hindi is 3
n(E∩H’∩S’) = 18
⇒n(E) – n{E∩(H∪S)’} = 18
⇒26 – n{(E∩H)∪(E∩S)}= 18
⇒26 – {3 + 8 – n(E∩H∩S)} = 18
⇒n(E∩H∩S) = 3
Also,
n(E’∩H’∩S’) = 24
⇒n(U) – n(E∪H∪S) = 24
⇒n(E∪H∪S) = 76
∴ Number of students studying Hindi = n(E∪H∪S) – n(E) – n(S) + n(E∩H) + n(E∩S) + n(S∩H) – n(E∩H∩S)
= 76 – 24 – 48 + 3 + 8 + 8 – 3
= 18
Q15.
Answer :
Let P1, P2 and P3 denote the sets of persons liking products P1, P2 and P3, respectively.
Also, let U be the universal set.
Thus, we have:
n(P1) = 21, n(P2) = 26 and n(P3) = 29
And,
n(P1∩P2) = 14, n(P1∩P3) = 12, n(P2∩P3) = 14 and n(P1∩P2∩P3) = 8
Now,
Number of people who like only product P3:
nP3∩P1’∩P2’= nP3∩P1∪P2’=n P3 – nP3∩P1∪P2=nP3 – nP3∩P1∪P3∩P2=nP3 – nP3∩P1+nP3∩P2-nP1∩P2∩P3=29 – 12+14-8=11
Therefore, the number of people who like only product P3 is 11
Page 1.48 (Very Short Answers)
Q1.
Answer :
A set having n elements has 2n subsets or elements.
Q2.
Answer :
We know that a set of n elements has 2n subsets or elements.
A null set has no element(s) in it.
∴ Number of elements in the power set of null set = 20 = 1
Q3.
Answer :
A = {x:x ∈ N and x is a multiple of 3.}
= {3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45,…}
B = {x:x ∈ N and x is a multiple of 5.}
={5, 10, 15, 20, 25, 30, 35, 40, 45,…}
Thus, we have:
A∩B = {15, 30, 45,…}
= {x:x ∈ N, where x is a multiple of 15.}
Q4.
Answer :
We know that nA∪B=nA+nB-nA∩B nA∪B is minimum when nA∩B is maximumso, nA∩B=3Hence, nA∪B=nA+nB-nA∩B =3+6-3 = 6
Q5.
Answer :
We have:
A = {x ∈ C : x2 = 1}
⇒A = {-1, 1}
And,
B = {x ∈ C : x4 = 1}
⇒B = {x4-1 = 0}
⇒B = {x2-1×2+1 =0}
Q6.
Answer :
B’-A’ = Not B – Not A = Nothing common in them =∅
Q7.
Answer :
We know that nA∪B=nA+nB-nA∩B nA∪B is maximum when nA∩B is minimumso, nA∩B=0Hence, nA∪B=nA+nB-nA∩B =4+7-0 = 11
Q8.
Answer :
We have:
A=x, y : y=1x, 0 ≠x ∈ R
= {1,1, 2,12, 3,13, 4,14, …}
And,
B=x, y : y=-x, x ∈ R
= 1, -1, 2, -2, 3, -3, 4, -4, …
Thus, we get:
A∩B = ∅
Q9.
Answer :
We have:
A = 0, 1, 1, e, 2, e2, 3, e3, …
B = 0, 1, 1, e-1, 2, e-2, 3, e-3, …
Thus, we get:
A∩B = 0, 1
Q10.
Answer :
We have:
nA = 20, nB = 25 and nA∪B = 40
We know:
nA∪B = nA + nB – nA∩B⇒nA∩B = nA + nB -nA∪B
= 20 + 25 – 40
= 5
Q11.
Answer :
nA = 115, nB = 326 and nA-B = 47Now,nA – nA∩B = nA-B⇒115 – nA∩B = 47⇒nA∩B = 68
Thus, we get:
nA∪B = nA + nB – nA∩B
= 115 + 326 – 68
= 373
Page 1.48 (Multiple Choice Questions)
Q1.
Answer :
(b) A
The complement of the complement of a set is the set itself.
Q2.
Answer :
(c) A∩B’
A-B belongs to those elements of A that do not belong to B.
∴ A-B = A∩B’
Page 1.49 (Multiple Choice Questions)
Q3.
Answer :
(d) 2n
The total number of subsets of a finite set consisting of n elements is 2n.
Q4.
Answer :
(a) A
A∩(A∪B)= (A∩A)∪(A∩B)=A∪(A∩B)=A
Q5.
Answer :
(d) none of these
4∉A
{4} ⊄ A
B⊄ A
Thus, we can say that none of these options satisfy the given relation.
Q6.
Answer :
(b) A-B∪B-A
The symmetric difference of A and B is given by :-
(A-B)∪(B-A)
Q7.
Answer :
(b) {1, 2, 4, 5}
Here,
A = {1, 2, 3} and B = {3, 4, 5}
The symmetric difference of A and B is given by :-
(A-B)∪(B-A)
Now, we have:
(A-B)={1,2}(B-A)={4,5}(A-B)∪(B-A)={1,2,4,5}
Q8.
Answer :
(c) A∪B-A∩B
A-B∪B-A = A∩B’∪B∩A’=A∪B∩A’∩B’∪B∩A’ Using distribution law=A∪B∩A∪A’∩B’∪B∩B’∪A’ Using distribution law=A∪B∩U∩U∩B’∪A’ A∪A’=U=B’∪B =A∪B∩B’∪A’ A∪B∩U=A∪B and U∩B’∪A’=B’∪A’ =A∪B ∩A∩B’ A∩B’=B’∪A’=A∪B ∩A∪B-A∩B=A∪B-A∩B
Q9.
Answer :
(c) A-B=A-B’
It includes all those elements of A which do not belongs to complement of B which is equal to A∩B but not equal to
A-B .
Therefore, (c) is false .
Q10.
Answer :
(a) A∩B-C=A∩B-A∩C
Let x be any arbitrary element of A∩B-C.
Thus, we have,
x∈A∩B-C⇒ x ∈A and x ∈B-C
⇒x∈A and x∈B and x∉C⇒x∈A and x∈B and x∈A and x∉C⇒xA∩B and x∉A∩C⇒x∈A∩B – A∩C⇒A∩B-C⊆A∩B – A∩CSimilarly, A∩B – A∩C⊆A∩B-CHence, A∩B-C=A∩B – A∩C
Q11.
Answer :
(c) [4, 5)
A=x : x ∈ R, x ≥ 4 and B = x ∈ R : x < 5
A∩B=[4,5)
Q12.
Answer :
(c) 300
n(A’∩B’) = nA∪B’
=nU – n(A∪B)= 700 – 200+300-100= 300
Q13.
Answer :
We know:
nA∪B = nA + nB – nA∩B
Now,
nA∩B = nA + nB – n(A∪B)
= 16 + 14 – 25
= 5
Q14.
Answer :
(c) 31
The number of proper subsets of any set is given by the formula 2n-1, where n is the number of elements in the set.
Here,
n = 5
∴ Number of proper subsets of A = 25-1 = 31
Q15.
Answer :
(c) x:x≠x
Q16.
Answer :
(a) n A+nB
Two sets are disjoint if they do not have a common element in them, i.e., A∩B = ∅.
∴ nA∪B = nA + nB
Q17.
Answer :
(a) B⊆A
The union of two sets is a set of all those elements that belong to A or to B or to both A and B.
If A∪B = A, then B⊆A.
Q18.
Answer :
(d) 20
We have:
n(A∩B) = nA + nB – n(A∪B) =70 + 60 – 110 =20
Page 1.50 (Multiple Choice Questions)
Q19.
Answer :
(d) A∩Bc
A and B are two sets.
A∩B is the common region in both the sets.
A∩Bc is all the region in the universal set except A∩B.
Now,
A∩A∩Bc = A∩Bc
Q20.
Answer :
(b) A∩B
A = {x:x is a multiple of 3}
A = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, …
B = {x:x is a multiple of 5.}
B = 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, …
Now, we have:
A-B = 3, 6, 9, 12, 18, 21, 24, 27, 33, 36, 39, 42, 48, …
= A∩B
Q21.
Answer :
(c) 60%
Suppose C and B represents the population travel by car and Bus respectively.
nC∪B = nC + nB – nB∩C =0.20 + 0.50 – 0.10 =0.6 or 60%
Q22.
Answer :
(b) B⊂A
Only this case is possible.
Q23.
Answer :
Disclaimer: The question in the book has some error, so, none of the options are matching with the solution.
The required information is not available in the question.
Q24.
Answer :
(c) 6, 4
ATQ :
2m-1=48+2n-1⇒2m-2n = 48⇒2m-2n = 26-24By comparing we get:m=6 and n=4
Q25.
Answer :
(c) 60
Let M, P and C denote the sets of students who have opted for mathematics, physics, and chemistry, respectively.
Here,
nM = 100, nP = 70 and n(C) = 40
Now,
nM∩P = 30, nM∩C = 28, nP∩C = 23 and nM∩P∩C = 18
Number of students who opted for only mathematics:
nM∩P’∩C’ = nM∩P∪C’ =nM – nM∩P∪C =nM – nM∩P∪M∩C =nM – nM∩P+nM∩C-nM∩P∩C =100 – 30+28-18 =60
Therefore, the number of students who opted for mathematics alone is 60


But only 25 question’s answers of mcq of chapter1 is provided here whereas 30 questions are there in mcq