Page 2.8 Ex – 2.1
Q1.
Answer :
(i) a3+1, b-23=53, 13
By the definition of equality of ordered pairs, we have:
a3+1, b-23=53, 13
⇒a3+1 = 53 and b-23=13⇒a3= 53-1 and b = 13+23⇒a3=23 and b = 1⇒a = 2 and b = 1
(ii) (x + 1, 1) = (3, y − 2)
By the definition of equality of ordered pairs, we have:
(x+1) = 3 and 1 = (y-2)⇒x = 2 and y = 3
Q2.
Answer :
The ordered pairs (x, −1) and (5, y) belong to the set {(a, b) : b = 2a − 3}.
Thus, we have:
x = a and −1 = b such that b = 2a − 3.
∴ −1 = 2x − 3
or, 2x = 3 − 1 = 2
or, x = 1
Also,
5 = a and y = b such that b = 2a − 3.
∴ y = 2(5) − 3
or, y = 10 − 3 = 7
Thus, we get:
x = 1 and y = 7
Q3.
Answer :
Given:
a ∈ [−1, 2, 3, 4, 5] and b ∈ [0, 3, 6]
We know:
−1 + 6 = 5, 2 + 3 = 5 and 5 + 0 = 5
Thus, possible ordered pairs (a, b) are {(−1, 6), (2, 3), (5, 0)} such that a + b = 5.
Q4.
Answer :
Given:
a ∈ [2, 4, 6, 9] and b ∈ [4, 6, 18, 27]
Here,
2 divides 4, 6 and 18 and 2 is less than all of them.
6 divides 18 and 6 and 6 is less than 18.
9 divides 18 and 27 and 9 is less than 18 and 27.
Now,
Set of all ordered pairs (a, b) such that a divides b and a < b = {(2, 4), (2, 6), (2, 18), (6, 18), (9, 18), (9, 27)}
Q5.
Answer :
Given:
A = {1, 2} and B = {1, 3}
Now,
A × B = {(1, 1), (1, 3), (2, 1), (2, 3)}
B × A = {(1, 1), (1, 2), (3, 1), (3, 2)}
Q6.
Answer :
Given:
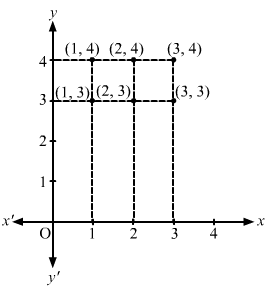
A = {1, 2, 3} and B = {3, 4}
Now,
A × B = {(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)}
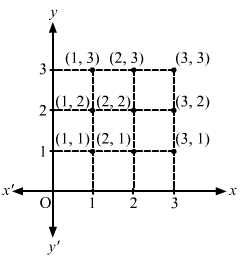
To represent A × B graphically, follow the given steps:
(a) Draw two mutually perpendicular lines—one horizontal and one vertical.
(b) On the horizontal line, represent the elements of set A; and on the vertical line, represent the elements of set B.
(c) Draw vertical dotted lines through points representing elements of set A on the horizontal line and horizontal lines through points representing elements of set B on the vertical line.
The points of intersection of these lines will represent A × B graphically.
Q7.
Answer :
Given :
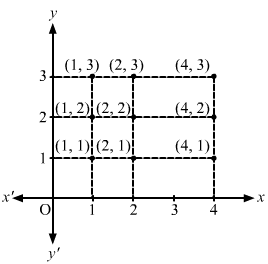
A = {1, 2, 3} and B = {2, 4}
Now,
A × B = {(1, 2), (1, 4), (2, 2), (2, 4), (3, 2), (3, 4)}
B × A = {(2, 1), (2, 2), (2, 3), (4, 1), (4, 2), (4, 3)}
A × A = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}
B × B = {(2, 2), (2, 4), (4, 2), (4, 4)}
We observe:
(A × B) ∩ (B × A) = {(2, 2)}
Q8.
Answer :
Given:
n(A) = 5 and n(B) = 4
Thus, we have:
n(A × B) = 5(4) = 20
A and B are two sets having 3 elements in common.
Now,
Let:
A = (a, a, a, b, c) and B = (a, a, a, d)
Thus, we have:
(A × B) = {(a, a), (a, a), (a, a), (a, d), (a, a), (a, a), (a, a), (a, d), (a, a), (a, a), (a, a), (a, d), (b, a), (b, a), (b, a), (b, d), (c, a), (c, a), (c, a), (c, d)}
(B × A) = {(a, a), (a, a), (a, a), (a, b), (a, c), (a, a), (a, a), (a, a), (a, b), (a, c), (a, a), (a, a), (a, a), (a, b), (a, c), (d, a), (d, a), (d, a), (d, b), (d, c)}
[(A × B) ∩ (B × A)] = {(a, a), (a, a), (a, a), (a, a), (a, a), (a, a), (a, a), (a, a), (a, a)}
∴ n[(A × B) ∩ (B × A)] = 9
Q9.
Answer :
Case (i): Let:
A = (a, b, c)
B = (e, f)
Now, we have:
A × B = {(a, e}), (a, f), (b,e), (b, f), (c, e), (c, f)}
B × A = {(e, a), (e, b), (e, c), (f, a), (f, b), (f, c)}
Thus, they have no elements in common.
Case (ii): Let:
A = (a, b, c)
B = (a, f)
Thus, we have:
A × B = {(a, a}), (a,f), (b, a), (b, f), (c,a), (c, f)}
B × A = {(a, a), (a, b), (a, c), (f, a), (f, b), (f, c)}
Here, A × B and B × A have two elements in common.
Thus, A × B and B × A will have elements in common iff sets A and B have elements in common.
Q10.
Answer :
A is the set of all first entries in ordered pairs in A × B and B is the set of all second entries in ordered pairs in A × B.
Also,
n(A) = 3 and n(B) = 2
∴ A = {x, y, z} and B = {1, 2}
Q11.
Answer :
Given:
A = {1, 2, 3, 4}
R = {(a, b) : a ∈ A, b ∈ A, a divides b}
We know:
1 divides 1, 2, 3 and 4.
2 divides 2 and 4.
3 divides 3.
4 divides 4.
∴ R = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 4), (3, 3), (4, 4)}
Q12.
Answer :
Given:
A = {−1, 1}
Thus, we have:
A × A = {(−1, −1), (−1, 1), (1, −1), (1, 1)}
And,
A × A × A = {(−1, −1, −1), (−1, −1, 1), (−1, 1, −1), (−1, 1, 1), (1, −1, −1), (1, −1, 1), (1, 1, −1), (1, 1, 1)}
Q13.
Answer :
(i) False
Correct statement:
If P = {m, n} and Q = {n, m}, then P × Q = {(m, n), (m, m), (n, n), (n, m)}.
(ii) False
Correct statement:
If A and B are non-empty sets, then A × B is a non-empty set of an ordered pair (x, y) such that x ∈ A and y ∈ B.
(iii) True
A = {1, 2} and B = {3, 4}
Now,
(B ∩ ϕ) = ϕ
The Cartesian product of any set and an empty set is an empty set.
∴ A × (B ∩ ϕ) = ϕ
Page 2.9 Ex – 2.1
Q14.
Answer :
Given:
A = {1, 2}
Now,
A × A = {(1, 1), (1, 2), (2, 1), (2, 2)}
∴ A × A × A = {(1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 1), (2, 1, 2), (2, 2, 1), (2, 2, 2)}
Q15.
Answer :
Given:
A = {1, 2, 4} and B = {1, 2, 3}
(i) A × B = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (4, 1), (4, 2), (4, 3)}
(ii) B × A = {(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (2, 4), (3, 1), (3, 2), (3, 4)}
(iii) A × A = {(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (2, 4), (4, 1), (4, 2), (4, 4)}
(iv) B × B = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}
Page 2.12 Ex – 2.2
Q1.
Answer :
Given:
A = {1, 2, 3}, B = {3, 4} and C = {4, 5, 6}
Now,
(A × B) = {(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)}
(B × C) = {(3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6)}
∴ (A × B) ∩ (B × C) = {(3, 4)}
Q2.
Answer :
Given:
A = {2, 3}, B = {4, 5} and C ={5, 6}
Also,
(B ∪ C) = {4, 5, 6}
Thus, we have:
A × (B ∪ C) = {(2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3,6)}
And,
(B ∩ C) = {5}
Thus, we have:
A × (B ∩ C) = {(2, 5), (3, 5)}
Now,
(A × B) = {(2, 4), (2, 5), (3, 4), (3, 5)}
(A × C) = {(2, 5), (2, 6), (3, 5), (3, 6)}
∴ (A × B) ∪ (A × C) = {(2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
Q3.
Answer :
Given:
A = {1, 2, 3}, B = {4} and C = {5}
(i) A × (B ∪ C) = (A × B) ∪ (A × C)
We have:
(B ∪ C) = {4, 5}
LHS: A × (B ∪ C) = {(1, 4), (1, 5), (2, 4), (2, 5), (3, 4), (3, 5)}
Now,
(A × B) = {(1, 4), (2, 4), (3, 4)}
And,
(A × C) = {(1, 5), (2, 5), (3, 5)}
RHS: (A × B) ∪ (A × C) = {(1, 4), (2, 4), (3, 4), (1, 5), (2, 5), (3, 5)}
∴ LHS = RHS
(ii) A × (B ∩ C) = (A × B) ∩ (A × C)
We have:
(B ∩ C) = ϕ
LHS: A × (B ∩ C) = ϕ
And,
(A × B) = {(1, 4), (2, 4), (3, 4)}
(A × C) = {(1, 5), (2, 5), (3, 5)}
RHS: (A × B) ∩ (A × C) = ϕ
∴ LHS = RHS
(iii) A × (B − C) = (A × B) − (A × C)
We have:
(B − C) = ϕ
LHS: A × (B − C) = ϕ
Now,
(A × B) = {(1, 4), (2, 4), (3, 4)}
And,
(A × C) = {(1, 5), (2, 5), (3, 5)}
RHS: (A × B) − (A × C) = ϕ
∴ LHS = RHS
Q4.
Answer :
Given:
A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}
(i) A × C ⊂ B × D
LHS: A × C = {(1, 5), (1, 6), (2, 5), (2, 6)}
RHS: B × D = {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)}
∴ A × C ⊂ B × D
(ii) A × (B ∩ C) = (A × B) ∩ (A × C)
We have:
(B ∩ C) = ϕ
LHS: A × (B ∩ C) = ϕ
Now,
(A × B) = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)}
(A × C) = {(1, 5), (1, 6), (2, 5), (2, 6)}
RHS: (A × B) ∩ (A × C) = ϕ
∴ LHS = RHS
Q5.
Answer :
Given:
A = {1, 2, 3}, B = {3, 4} and C = {4, 5, 6}
(i) A × (B ∩ C)
Now,
(B ∩ C) = {4}
∴ A × (B ∩ C) = {(1, 4), (2, 4), (3, 4)}
(ii) (A × B) ∩ (A × C)
Now,
(A × B) = {(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)}
And,
(A × C) = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
∴ (A × B) ∩ (A × C) = {(1, 4), (2, 4), (3, 4)}
(iii) A × (B ∪ C)
Now,
(B ∪ C) = {3, 4, 5, 6}
∴ A × (B ∪ C) = {(1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 5), (3, 6)}
(iv) (A × B) ∪ (A × C)
Now,
(A × B) = {(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)}
And,
(A × C) = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
∴ (A × B) ∪ (A × C) = {(1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 5), (3, 6)}
Q6.
Answer :
(i) (A ∪ B) × C = (A × C) ∪ (B × C)
Let (a, b) be an arbitrary element of (A ∪ B) × C.
Thus, we have:
Again, let (x, y) be an arbitrary element of (A × C) ∪ (B × C).
Thus, we have:
From (i) and (ii), we get:
(A ∪ B) × C = (A × C) ∪ (B × C)
(ii) (A ∩ B) × C = (A × C) ∩ (B×C)
Let (a, b) be an arbitrary element of (A ∩ B) × C.
Thus, we have:
Again, let (x, y) be an arbitrary element of (A × C) ∩ (B × C).
Thus, we have:
From (iii) and (iv), we get:
(A ∩ B) × C = (A × C) ∩ (B × C)
Q7.
Answer :
Let: (x, y) ∈(A×B)∴ x∈A, y∈BNow,∵(A×B)⊆(C×D) ∴(x,y) ∈(C×D) Or, x∈C and y ∈DThus, we have: A⊆C & B⊆D
Page 2.21 Ex – 2.3
Q1.
Answer :
Given:
A = {1, 2, 3} and B = {4, 5, 6}
Thus, we have:
A × B = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
(i) {(1, 6), (3, 4), (5, 2)}
Since it is not a subset of A × B, it is not a relation from A to B.
(ii) {(1, 5), (2, 6), (3, 4), (3, 6)}
Since it is a subset of A × B, it is a relation from A to B.
(iii) {(4, 2), (4, 3), (5, 1)}
Since it is not a subset of A × B, it is not a relation from A to B.
(iv) A × B
Since it is a subset (equal to) of A × B, it is a relation from A to B.
Q2.
Answer :
Given:
(x, y) ∈ R ⇔ x is relatively prime to y.
Here,
2 is co-prime to 3 and 7.
3 is co-prime to 7 and 10.
4 is co-prime to 3 and 7.
5 is co-prime to 3, 6 and 7.
Thus, we get:
R = {(2, 3), (2, 7), (3, 7), (3, 10), (4, 3), (4, 7), (5, 3), (5, 6), (5, 7)}
Domain of R = {2, 3, 4, 5}
Range of R = {3, 7, 6, 10}
Q3.
Answer :
Given:
A is the set of the first five natural numbers.
∴ A = {1, 2, 3, 4, 5}
The relation is defined as:
(x, y) ∈ R ⇔ x ≤ y
Now,
R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 2), (2, 3), (2, 4), (2, 5), (3, 3), (3, 4), (3, 5), (4, 4), (4, 5), (5, 5)}
R-1 = {(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (2, 2), (3, 2), (4, 2), (5, 2), (3, 3), (4, 3), (5, 3), (4, 4), (5, 4), (5, 5)}
(i) Domain of R-1 = {1, 2, 3, 4, 5}
(ii) Range of R = {1, 2, 3, 4, 5}
Q4.
Answer :
(i) R = {(1, 2), (1, 3), (2, 3), (3, 2), (5, 6)}
R−1 = {(2, 1), (3, 1), (3, 2), (2, 3), (6, 5)}
(ii) R = {(x, y) : x, y ∈ N, x + 2y = 8}
On solving x + 2y = 8, we get:
x = 8 – 2y
On putting y = 1, we get x = 6.
On putting y = 2, we get x = 4.
On putting y = 3, we get x = 2.
∴ R = {(6, 1), (4, 2), (2, 3)}
Or,
R−1 = {(1, 6), (2, 4), (3, 2)}
(iii) R is a relation from {11, 12, 13} to {8, 10, 12} defined by y = x − 3.
x belongs to {11, 12, 13} and y belongs to {8, 10, 12}.
Also, 11 − 3 = 8 and 13 − 3 = 10
∴ R = {(11, 8), (13,10)}
Or,
R−1 = {(8, 11), (10,13)}
Q5.
Answer :
(i) A relation R from the set [2, 3, 4, 5, 6] to the set [1, 2, 3] is defined by x = 2y.
Putting y = 1, 2, 3 in x = 2y, we get:
x = 2, 4, 6
∴ R = {(2, 1), (4, 2), (6, 3)}
(ii) A relation R on the set [1, 2, 3, 4, 5, 6, 7] defined by (x, y) ∈ R ⇔ x is relatively prime to y.
Here,
2 is relatively prime to 3, 5 and 7.
3 is relatively prime to 2, 4, 5 and 7.
4 is relatively prime to 3, 5 and 7.
5 is relatively prime to 2, 3, 4, 6 and 7.
6 is relatively prime to 5 and 7.
7 is relatively prime to 2, 3, 4, 5 and 6.
∴ R = {(2, 3), (2, 5), (2, 7), (3, 2), (3, 4), (3, 5), (3, 7), (4, 3), (4, 5), (4, 7), (5, 2), (5, 3), (5, 4), (5, 6), (5, 7), (6, 5), (6, 7), (7, 2), (7, 3), (7,4), (7, 5), (7, 6)}
(iii) A relation R on the set [0, 1, 2,…, 10] is defined by 2x + 3y = 12.
x = 12-3y2
Putting y = 0, 2, 4, we get:
x = 6, 3, 0
∴ R = {(0, 4), (3, 2), (6, 0)}
(iv) A relation R from the set A = [5, 6, 7, 8] to the set B = [10, 12, 15, 16, 18] defined by (x, y) ∈ R ⇔ x divides y.
Here,
5 divides 10 and 15.
6 divides 12 and 18.
8 divides 16.
∴ R = {(5, 10), (5, 15), (6, 12), (6, 18), (8,16)}
Page 2.22 Ex – 2.3
Q6.
Answer :
Let R be a relation in N defined by (x, y) ∈ R ⇔ x + 2y = 8.
We have:
x = 8-2y
For y = 3, 2, 1, we have:
x = 2, 4, 6
∴ R = {(2, 3), (4, 2), (6, 1)}
And,
R−1 = {(3, 2), (2, 4), (1, 6)}
Q7.
Answer :
Given:
A = (3, 5) and B = (7, 11)
Also,
R = {(a, b) : a ∈ A, b ∈ B, a − b is odd}
a are the elements of A and b are the elements of B.
So, R is an empty relation from A to B.
Hence proved.
Q8.
Answer :
We have:
A = {1, 2} and B = {3, 4}
Now,
n (A×B) =n(A) ×n(B) = 2×2 = 4
There are 2n relations from A to B, where n is the number of elements in their Cartesian product.
∴ Number of relations from A to B is 24 = 16.
Q9.
Answer :
(i) R = {(x, x + 5): x ∈ (0, 1, 2, 3, 4, 5)}
We have:
R = {(0, 0 + 5), (1, 1 + 5), (2, 2 + 5), (3, 3 + 5), (4, 4 + 5), (5, 5 + 5)}
Or, R = {(0, 5), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)}
∴ Domain (R) = {0, 1, 2, 3, 4, 5}
Range (R) = {5, 6, 7, 8, 9, 10}
(ii) R = {(x, x3) : x is a prime number less than 10}
We have:
x = 2, 3, 5, 7
x3 = 8, 27, 125, 343
Thus, we get:
R = {(2, 8), (3, 27), (5, 125), (7, 343)}
Domain (R) = {2, 3, 5, 7}
Range (R) = {8, 27, 125, 343}
Q10.
Answer :
(i) R = {(a, b) : a ∈ N, a < 5, b = 4}
We have:
a = 1, 2, 3, 4
b = 4
R = {(1, 4), (2, 4), (3, 4), (4, 4)}
Domain (R) = {1, 2, 3, 4}
Range (R) = {4}
(ii) S=a, b : b=a-1, a ∈ Z and a ≤3
Now,
a = -3, -2, -1, 0, 1, 2, 3
b = -3-1 = 4b = -2-1 =3b = -1-1 =2b = 0-1 =1b = 1-1 =0b = 2-1 =1b = 3-1 =2
Thus, we have:
b = 4, 3, 2, 1, 0, 1, 2
Or,
S = {(-3, 4), (-2, 3), (-1, 2), (0, 1), (1, 0), (2, 1), (3, 2)}
Domain (S) = {-3, -2, -1, 0, 1, 2, 3}
Range (S) = {0, 1, 2, 3, 4}
Q11.
Answer :
Any relation in A can be written as a set of ordered pairs.
The only ordered pairs that can be included are (a, a), (a, b), (b, a) and (b, b).
There are four ordered pairs in the set, and each subset is a unique combination of them.
Each unique combination makes different relations in A.
{ } [the empty set]
{(a, a)}
{(a, b)}
{(a, a), (a, b)}
{(b, a)}
{(a, a), (b, a)}
{(a, b), (b, a)}
{(a, a), (a, b), (b, a)}
{(b, b)}
{(a, a), (b, b)}
{(a, b), (b, b)}
{(a, a), (a, b), (b, b)}
{(b, a), (b, b)}
{(a, a), (b, a), (b, b)}
{(a, b), (b, a), (b, b)}
{(a ,a), (a, b), (b, a), (b, b)}
Number of elements in the Cartesian product of A and A = 2×2=4
∴ Number of relations = 24=16
Q12.
Answer :
Given:
A = (x, y, z) and B = (a, b)
Now,
Number of elements in the Cartesian product of A and B=3×2=6
Number of relations from A to B = 26=64
Q13.
Answer :
Given: R = [(a, b) : a, b ∈ N and a = b2]
(i) (a, a) ∈ R for all a ∈ N.
Here, 2 ∈N, but 2≠22.
∴ (2,2)∉R
False
(ii) (a, b) ∈ R ⇒ (b, a) ∈ R
∵ 4 = 22
(4, 2) ∈ R, but (2,4)∉R.
False
(iii) (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R
∵ 16 = 42 and 4 = 22
∴ (16, 4) ∈ R and (4, 2) ∈ R
Here,
(16,2)∉R
False
Q14.
Answer :
A = [1, 2, 3,…, 14]
R = {(x, y) : 3x − y = 0, where x, y ∈ A}
Or,
R = {(x, y) : 3x = y, where x, y ∈ A}
As
3×1 = 33×2 = 63×3 = 93×4 = 12
Or,
R = {(1, 3), (2, 6), (3, 9), (4, 12)}
Domain (R) = {1, 2, 3, 4}
Range (R) = {3, 6, 9, 12}
Co-domain (R) = A
Q15.
Answer :
R = {(x, y) : y = x + 5, x is a natural number less than 4, x, y ∈ N}
(i) ∵ x = 1, 2, 3
∴ y = 1 + 5, 2 + 5, 3 + 5
y = 6, 7, 8
Thus, we have:
R = {(1, 6), (2, 7), (3, 8)}
(ii)
Now,
Domain (R) = {1, 2, 3}
Range (R) = {6, 7, 8}
Q16.
Answer :
A = [1, 2, 3, 5] and B = [4, 6, 9]
R = {(x, y) : the difference between x and y is odd, x ∈ A, y ∈ B}
For x = 1,
4-1 = 3 and 6-1 = 5
y = 4, 6
For x = 2,
9-2 = 7
y = 9
For x = 3,
4-3 = 1 and 6-3 = 3
y = 4, 6
For x = 5,
5-4 =1 and 6-5 =1
y = 4, 6
Thus, we have:
R = {(1, 4), (1, 6), (2, 9), (3, 4), (3, 6), (5, 4), (5, 6)}
Q17.
Answer :
R = {(x, x3) : x is a prime number less than 10}
x = 2, 3, 5, 7
x3 = 8, 27, 125, 343
R = {(2, 8), (3, 27), (5, 125), (7, 343)}
Q18.
Answer :
A = [1, 2, 3, 4, 5, 6]
R = {(a, b) : a, b ∈ A, b is exactly divisible by a}
(i) Here,
2 is divisible by 1 and 2.
3 is divisible by 1 and 3.
4 is divisible by 1 and 4.
5 is divisible by 1 and 5.
6 is divisible by 1, 2, 3 and 6.
∴ R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (5, 5), (6, 6)}
(ii) Domain (R) = {1, 2, 3, 4, 5, 6}
(iii) Range (R) = {1, 2, 3, 4, 5, 6}
Q19.
Answer :
(i) We have:
5-2 = 3
6-2 = 4
7-2 = 5
∴ R = {(x,y) : y = x-2, x∈P, y∈Q}
(ii) R = {(5, 3), (6, 4), (7, 5)}
(iii) Domain (R) = {5, 6, 7}
Range (R) = {3, 4, 5}
Page 2.23 Ex – 2.3
Q20.
Answer :
R = {(a, b) : a, b ∈ Z, a − b is an integer}
We know:
Difference of any two integers is always an integer.
Thus, for all a, b ∈ Z, we get a − b as an integer.
∴ Domain (R) = Z
And,
Range (R) = Z
Q21.
Answer :
We have:
(a, b) ∈ R1 ⇔ 1 + ab > 0
Let:
a = 1, b = -12 and c = -4
Now,
1,-12∈R1 and -12,-4∈R1, as 1+-12 >0 and 1+-12-4>0.
But 1+1×-4 <0.
∴ (1,-4) ∉R1
And,
(a, b) ∈ R1 and (b , c) ∈ R1
Thus, (a, c) ∈ R1 is not true for all a, b, c ∈ R.
Q22.
Answer :
We are given ,
(a, b) R (c, d) ⇔ a + d = b + c for all (a, b), (c, d) ∈ N × N
(i) (a, b) R (a, b) for all (a, b) ∈ N × N
∵ a+b = b+a for all a,b ∈N∴(a,b) R (a,b) for all a,b ∈N
(ii) (a, b) R (c, d) ⇒ (c, d) R (a, b) for all (a, b), (c, d) ∈ N × N
(a,b) R (c,d) ⇒a+ d = b+c ⇒c+b = d+a ⇒(c,d) R (a,b)
(iii) (a, b) R (c, d) and (c, d) R (e, f) ⇒ (a, b) R (e, f) for all (a, b), (c, d), (e, f) ∈ N × N
(a,b) R (c,d) and (c,d) R (e,f)⇒a+d = b+c and c+f = d+e⇒a+d+c+f = b+c+d+e ⇒a+f = b+e ⇒(a,b) R (e,f)
Page 2.26 (Very Short Answers)
Q1.
Answer :
Given:
A = {1, 2, 4}, B = {2, 4, 5} and C = {2, 5}
Now,
(A − C) = {1, 4}
(B − C) = {4}
Thus, we have:
(A − C) × (B − C) = {(1, 4), (4, 4)}
Q2.
Answer :
Given:
n(A) = 3 and n(B) = 4
Now, we have:
n(A × A × B) = nA×A×nB = 3×3×4 = 36
Q3.
Answer :
We need to find (x, y) ∈ R such that x2 + y2 = 9.
Now,32+02 = 9⇒-32+02= 9
x can take values -3, 0 and 3.
∴ Domain (R) = {-3, 0, 3}
Q4.
Answer :
Given:
R = {(x, y) : x, y ∈ Z, x2 + y2 ≤ 4}
We know:
-22+02 ≤422+02 ≤4-12+02 ≤412+02 ≤4-12+12 ≤402+02 ≤412+12 ≤4-12+-12 ≤4
∴ Domain (R) = {-2, -1, 0, 1, 2}
Q5.
Answer :
Given:
A = (11, 12, 13) and B = (8, 10, 12)
R is defined by (y = x − 3) from A to B.
We know:
8 = 11-3
10 = 13-3
∴ R = {(11, 8), (13, 10)}
Or,
R-1 = {(8, 11), (10, 13)}
Q6.
Answer :
Given:
A = {1, 2, 3}
R=a, b : a2-b2≤5, a, b ∈A
We know that
12-12 ≤5,22-22 ≤5,32-32 ≤5,12-22 ≤5,22-12 ≤5,22-32 ≤5,32-22 ≤5
Thus, R ={(1,1),(2,2),(3,3),(1,2),(2,1),(2,3),(3,2)}
Q7.
Answer :
R = [(x, y) : x, y ∈ Z, y = 2x − 4]
(a, -2) and (4, b2) ∈ R
So, -2 = 2(a) -4⇒2= 2a ⇒a =1
Also, b2 = 24-4⇒b2 =4⇒b = ±2
Thus, a =1 and b = ±2
Q8.
Answer :
Given:
R = {(2, 1), (4, 7), (1, −2), …}
We can observe that
1 = 3×2 – 57 = 3×4 – 5-2 = 3×1 – 5
Thus, the linear relation between the components of the ordered pairs of the relation R is y = 3x – 5.
Q9.
Answer :
Given:
A = {1, 3, 5} and B = {2, 4}
R = {(x, y) : x, y ∈ A × B and x > y}
A × B = {(1,2),(1,4),(3,2),(3,4),(5,2),(5,4)}
As 3 > 2, 5 > 2 and 5 > 4,
we have R = {(3,2),(5,2),(5,4)}
Q10.
Answer :
R = {(x, y) : x, y ∈ W, 2x + y = 8}
As y = 8-2xFor x = 0, y = 8For x =1, y = 6For x = 2, y = 4For x = 3, y = 2For x = 4, y = 0For x = 5, y <0So, y <0 for all x>5
∴ Domain (R) = {0,1,2,3,4} and Range (R) = {0,2,4,6,8}
Q11.
Answer :
Given:
(x, 1), (y, 2), (z, 1) are in A × B
n(A) = 3 and n(B) = 2
(x,1) ∈A×B ⇒ x∈A , 1∈BSimilarly, y∈A, 2∈Band z∈A, 1∈B
So, A = {x,y,z} and B = {1,2}
Q12.
Answer :
Given:
A = {1, 2, 3, 5} and B = {4, 6, 9}
R = {(x, y) : x − y is odd}
Since 1-4 = -3 is odd, we have:
1-6 = -5 is odd
2-9 = -7 is odd
3-4 =-1 is odd
3-6 = -3 is odd
5-4 = 1 is odd
5-6 = -1 is odd
∴ R = {(1,4),(1,6),(2,9),(3,4),(3,6),(5,4),(5,6)}
Page 2.26 (Multiple Choice Questions)
Q1.
Answer :
(b) {(1, 4)}
A = {1, 2, 4}, B = {2, 4, 5} and C = {2, 5}
(A − B) = {1}
(B − C) = {4}
So, (A − B) × (B − C) = {(1,4)}
Q2.
Answer :
(d) none of these
A = {1, 2, 3, 4, 5, 6, 7, 8, 9}
x R y ⇔ y = 3x
For x = 1, y = 3
For x = 2, y = 6
For x = 3, y = 9
Thus, R = {(1,3),(2,6),(3,9)}
Page 2.27 (Multiple Choice Questions)
Q3.
Answer :
(a) {(3, 3), (3, 1), (5, 2)}
A = {1, 2, 3}, B ={1, 3, 5}
R = {(1, 3), (2, 5), (3, 3)}
∴ R−1 = {(3,1),(5,2),(3,3)}
Q4.
Answer :
(c) {1}
A = {1, 2, 3} and B = {1, 4, 6, 9}
R is a relation from A to B defined by: x is greater than y.
Then R = {(2,1),(3,1)}
∴ Range (R) = {1}
Q5.
Answer :
(c) {−2, −1, 0, 1, 2}
R = {(x, y) : x, y ∈ Z, x2 + y2 ≤ 4}
We know that,
-22+02 ≤4⇒22+02 ≤4⇒-12+02 ≤4⇒12+02 ≤4⇒-12+12 ≤4⇒02+02 ≤4⇒12+12 ≤4⇒-12+-12 ≤4)2+02 ≤4(2)2+02 ≤4(−1)2+02 2)2+02 ≤4(2)2+02 ≤4(−1)2+02 (−2)2+02 ≤4(2)2+02 ≤4(−1)2+02 ≤4(1)2+02 ≤4(−1)2+(1)2 ≤4
Hence, domain (R) = {-2,-1,0,1,2,}
Q6.
Answer :
(d) {2, 3, 4, 5}
Given:
From {2, 3, 4, 5} to {3, 6, 7, 10}, x R y ⇔ x is relatively prime to y
2 is relatively prime to 3,7
3 is relatively prime to 7,10
4 is relatively prime to 3,7
5 is relatively prime to 3,6,7
So, domain of R is {2,3,4,5}
Q7.
Answer :
(d) i ϕ 1
We have i =12+02 = 1
Thus, i ϕ 1 satisfies x ϕ y ⇔ x = y.
Q8.
Answer :
(c) {2, 4, 6}
x + 2y = 8
⇒ x = 8 – 2y
For y = 1, x = 6
y = 2, x = 4
y = 3, x = 2
Then R = {(2,3),(4,2),(6,1)}
∴ Domain of R = {2,4,6}
Q9.
Answer :
(a) [(8, 11), (10, 13)]
R is a relation from [11, 12, 13] to [8, 10, 12], defined by y = x − 3
Now, we have:
11- 3 = 8
13 – 3 = 10
So, R = {(13,10),(11,8)}
∴ R−1 = {(10,13),(8,11)}
Q10.
Answer :
(c) pq
n(A × B) = n(A) × n(B)
= p × q = pq
Q11.
Answer :
(c) R ⊆ A × B
If R is a relation from set A to set B, then R is always a subset of A × B.
Q12.
Answer :
(a) 2mn
Given: n(A) = m
n(B) = n
∴ nA×B = mn
Then, the number of relations from A to B is 2mn .
Q13.
Answer :
(b) 2n2
Given : A finite set with n elements
Its Cartesian product with itself will have n2 elements.
∴ Number of relations on A = 2n2
Page 3.7 Ex – 3.1
Q1.
Answer :
A function is a set of ordered pairs with the property that no two ordered pairs have the same first component and different second components.
Sometimes we say that a function is a rule (correspondence) that assigns to each element of one set, X, only one element of another set, Y.
The elements of set X are often called inputs and the elements of set Y are called outputs.
The domain of a function is the set of all first components, x, in the ordered pairs.
The range of a function is the set of all second components, y, in the ordered pairs.
A function can be defined by a set of ordered pairs.
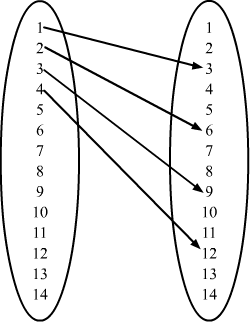
Example: {(1,a), (2, b), (3, c), (4,a)} is a function, since there are no two pairs with the same first component.
The domain is then the set {1,2,3,4} and the range is the set {a, b, c}.
Q2.
Answer :
A function is a correspondence between two sets of elements, such that for each element in the first set there is only one corresponding element in the second set.
The first set is called the domain and the set of all corresponding elements in the second set is called the range.
Let A = {1, 2, 3} and B = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Let f : A → B be the correspondence which assigns to each element in A its square.
Hence,
f (1) = 12 = 1
f (2) = 22 = 4
f (3) = 32 = 9
Since for each element (1 or 2 or 3) of A, there is exactly one element of B, so f is a function.
In this case, every element of B is not an image of some element of A.
Q3.
Answer :
Differences between relation and function
If R is a relation from A to B, then domain of R may be a subset of A. But if f is a function from A to B, then domain f is equal to A.
In a relation from A to B, an element of A may be related to more than one element in B. But in a function from A to B, each element of A must be associated to one and only one element of B.
Thus, every function is a relation, but every relation is not necessarily a function.
Q4.
Answer :
(a) Given:
f (x) = x2 − 2x − 3
f (−2) = (− 2)2 − 2(− 2) − 3
= 4 + 4 – 3
= 8 − 3 = 5
f (−1) = (−1)2 − 2(−1) − 3
= 1+ 2 − 3
= 3 − 3 = 0
f (0) = (0)2 − 2(0) − 3
= 0 − 0 − 3
= − 3
f (1) = (1)2 − 2(1) − 3
= 1 − 2 − 3
=1 − 5 = − 4
f (2) = (2)2 – 2(2) − 3
= 4 − 4 – 3
= 4 – 7 = − 3
Thus, range of f(A) = (− 4, − 3, 0, 5).
(b) Let x be the pre-image of 6.
Then,
f(6) = x2 − 2x − 3 = 6
⇒ x2 − 2x − 9 = 0
⇒ x=1±10
Since x=1±10∉A, there is no pre-image of 6.
Let x be the pre-image of -3. Then,
f(− 3) ⇒ x2 − 2x − 3 = − 3
⇒ x2 − 2x = 0
⇒ x = 0, 2
Clearly 0,2∈A. So, 0 and 2 are pre-images of −3.
Let x be the pre-image of 5. Then,
f(5) ⇒ x2 − 2x − 3 = 5
⇒ x2 − 2x − 8 = 0
⇒ (x − 4) (x + 2) = 0 ⇒ x = 4, − 2
Since -2∈A, − 2 is the pre-image of 5.
Hence,
pre-images of 6, − 3 and 5 are ϕ,0,2,,-2 respectively.
Page 3.8 Ex – 3.1
Q5.
Answer :
f (1) = 4 × 1 + 1 = 5 [By using f (x) = 4x + 1, x > 0]
f (- 1) = 3 × (-1) – 2 [By using f (x) = 3x – 2, x < 0]
= – 3 – 2 = – 5
f (0) = 1 [By using f (x) = 1, x = 0]
f (2) = 4 × 2 + 1 [By using f (x) = 4x + 1, x > 0]
= 9
Hence,
f (1) = 5, f (-1) = – 5, f (0) = 1 and f (2) = 9.
Q6.
Answer :
(a) Given:
f (x) = x2
Range of f = R+ (Set of all real numbers greater than or equal to zero)
(b) Given:
f (x) = x2
⇒ x2 = 4
⇒ x = ± 2
∴ {x : f (x) = 4 } = { – 2, 2}.
(c) { y : f (y) = -1}
⇒ f (y) = -1
It is clear that x2 = -1 but x2 ≥ 0 .
⇒ f (y) ≠ -1
∴ {y : f (y) = -1} = Φ
Q7.
Answer :
Given:
f : R+ → R
and f (x) = logex ………….(i)
(a) f : R+ → R
Thus, the image set of the domain f = R .
(b) {x : f (x) = -2
⇒ f (x ) = -2 …..(ii)
From equations (i) and (ii), we get :
logex = -2
⇒ x = e-2
Hence, { x : f (x) = – 2} = { e – 2} . [Since logab = c ⇒ b = ac]
(c) f (xy) = loge(xy) {From(i)}
= logex + logey [Since logemn = loge m + logen]
= f (x) + f (y)
Thus, f (xy) = f (x) + f (y)
Hence, it is clear that f (xy) = f (x) + f (y) holds.
Q8.
Answer :
(a) Given:
{(x, y) : y = 3x, x ∈ {1, 2, 3}, y ∈ [3,6, 9, 12]}
On substituting x = 1, 2, 3 in x, we get :
y = 3, 6, 9, respectively.
∴ R = {(1, 3) , (2, 6), (3, 9)}
Hence, we observe that each element of the given set has appeared as the first component in one and only one ordered pair in R . So, R is a function in the given set.
(b) Given:
{(x, y) : y > x + 1, x = 1, 2 and y = 2, 4, 6}
On substituting x = 1, 2 in y > x + 1, we get :
y > 2 and y > 3, respectively.
R = {(1, 4), (1, 6), (2, 4), (2, 6)}
We observe that 1 and 2 have appeared more than once as the first component of the ordered pairs. So, it is not a function.
(c) Given:
{(x, y) : x + y = 3, x, y, ∈ [0, 1, 2, 3]}
x + y = 3
∴ y = 3 – x
On substituting x = 0,1, 2, 3 in y, we get:
y = 3, 2, 1, 0, respectively.
∴ R = {(0, 3), (1, 2), (2, 1), (3, 0)}
Hence, we observe that each element of the given set has appeared as the first component in one and only one ordered pair in R . So, R is a function in the given set.
Q9.
Answer :
It is given that
f : R → R and g : C → C are two function defined as f (x) = x2 and g (x) = x2 .
Thus,
domain ( f ) = R and domain ( g ) = C .
Since, domain ( f ) ≠ domain ( g ),
f (x) and g (x) are not equal functions.
Q10.
Answer :
(i) Given:
f (x) = x2
Range of f(x) = R+ (set of all positive integers)
= {y ∈ R| y ≥ 0}
(ii) Given:
g(x) = sin x
Range of g(x) = {y ∈ R : -1 ≤ y ≤ 1}
(iii) Given:
h (x) = x2 + 1
Range of h (x) = {y ∈ R : y ≥ 1}
Q11.
Answer :
(a) Given:
f1 = {(1, 1), (2, 11), (3, 1), (4, 15)}
f1 is a function from X to Y.
(b) Given:
f2 = {(1, 1), (2, 7), (3, 5)}
f2 is not a function from X to Y because 2 ∈ X has no image in Y.
(c) Given:
f3 = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}
f3 is not a function from X to Y because 2 ∈ X has two images, 9 and 11, in Y.
Q12.
Answer :
Given:
A ={12, 13, 14, 15, 16, 17}
f : A → Z be defined by f (x) = the highest prime factor of x.
f (12) = the highest prime factor of 12 = 3
f (13) = the highest prime factor of 13 = 13
f (14) = the highest prime factor of 14 = 7
f (15) = the highest prime factor of 15 = 5
f (16) = the highest prime factor of 16 = 2
f (17) = the highest prime factor of 17 = 17
The range of f is the set of all f (x), where x∈A.n∈A
Therefore,
range of f = {2, 3, 5, 7, 13, 17}.
Q13.
Answer :
If f : A → B is such that y ∈ B, then f-1{ y }={x ∈ A: f (x) = y}.
In other words, f -1{ y} is the set of pre – images of y.
Let f-1{17} = x .
Then, f (x) =17 .
⇒ x2 +1 = 17
⇒ x2 = 17 – 1 = 16
⇒ x = ± 4
∴ f-1{17} = {- 4,4}
Again,
let f-1{-3} = x .
Then, f (x) = – 3
⇒ x2 + 1 = – 3
⇒ x2 = – 3 – 1 = – 4
⇒ x=-4
Clearly, no solution is available in R.
So f-1{- 3} = Φ .
Q14.
Answer :
(c) R3 = [(p, 1), (q, 2), (p, 2), (s, 3)
All the relations in (a), (b) and (d) have a unique image in B for all the elements in A.
R3 is not a function from A to B because p ∈ A has two images, 1 and 2, in B.
Hence, option (c) is not a function.
Q15.
Answer :
Given:
A ={9, 10, 11, 12, 13}
f : A → N be defined by f (n) = the highest prime factor of n.
f (9) = the highest prime factor of 9 = 3
f (10) = the highest prime factor of 10 = 5
f (11) = the highest prime factor of 11 = 11
f (12) = the highest prime factor of 12 = 3
f (13) = the highest prime factor of 13 = 13
The range of f is the set of all f (n), where n∈A.
Therefore,
range of f = {3, 5, 11, 13}
Q16.
Answer :
The function f is defined by fx=x20⩽x⩽33×3⩽x⩽10
It is observed that for 0 ≤ x < 3, f (x) = x2 .
3 < x ≤ 10, f (x) = 3x
Also, at x = 3, f(x) = 32 = 9. And
f (x) = 3 × 3 = 9.
That is, at x = 3, f (x) = 9.
Therefore, for 0 ≤ x ≤ 10, the images of f (x) are unique.
Thus, the given relation is a function.
Again,
the relation g is defined as gx=x2,0⩽x⩽23x,2⩽x⩽10
It can be observed that for x = 2, g(x) = 22 = 4 and also,
g(x) = 3 × 2 = 6.
Hence, 2 in the domain of the relation g corresponds to two different images, i.e. 4 and 6.
Hence, this relation is not a function.
Hence proved.
Q17.
Answer :
Given:
f(x) = x2
Therefore,
f1.1-f11.1-1=1.12-121.1-1=1.21-10.1=0.210.1=2.1
Page 3.11 Ex – 3.2
Q1.
Answer :
Given:
f (x) = x2 – 3x + 4
Therefore,
f (2x + 1) = (2x + 1)2 – 3(2x + 1) + 4
= 4x2 + 1 + 4x – 6x – 3 + 4
= 4x2 – 2x + 2
Now,
f (x) = f (2x + 1)
⇒ x2 – 3x + 4 = 4x2 – 2x + 2
⇒ 4x2 – x2 – 2x + 3x + 2 – 4 = 0
⇒ 3x2 + x – 2 = 0
⇒ 3x2 + 3x – 2x – 2 = 0
⇒ 3x(x + 1) – 2(x +1) = 0
⇒ (3x – 2)(x +1) = 0
⇒ (x + 1) = 0 or ( 3x – 2) = 0
⇒x=-1 or x=23
Hence, x=-1,23.
Q2.
Answer :
Given:
f (x) = (x – a)2(x – b)2
Thus,
f (a + b) = (a + b – a)2(a + b – b)2
= b2a2
Hence, f (a + b) = a2b2 .
Page 3.12 Ex – 3.2
Q3.
Answer :
Given:
fx=ax-bbx-a
Let y = f (x) .
⇒ y( bx – a) = ax – b
⇒ xyb – ay = ax – b
⇒ xyb – ax = ay – b
⇒ x(by – a) = ay – b
⇒x=ay-bby-a
⇒ x = f (y)
Q4.
Answer :
Given:
fx=11-x
Thus,
ffx=f11-x
=11-11-x
=11-x-11-x=1-x-x=x-1x
Again,
fffx=fx-1x
=11-x-1x=1x-x+1x=x1=x
Therefore, f[f{f(x)}] = x.
Hence proved.
Q5.
Answer :
Given:
f(x) = (a − xn)1/n, a > 0
Now,
f{ f (x)} = f (a − xn)1/n
= [a – {(a – xn)1/n}n]1/n
= [ a – (a – xn)]1/n
= [ a – a + xn)]1/n = (xn)1/n = x(nx1/n) = x
Thus, f(f(x)) = x.
Hence proved.
Q6.
Answer :
Given:
fx=x2,when x<0x,when 0≤x<11x,when x≥1
Now,
(a) f12=12 [ Using f (x) = x, 0 ≤ x < 1]
(b) f (-2) = ( – 2)2 = 4
(c) f1=11=1
(d) f3=13
(e) f-3
Since x is not defined in R, f-3 does not exist.
Q7.
Answer :
Given:
fx=x3-1×3 …(i)
Thus,
f1x=1×3-11×3
=1×3-11×3
∴f1x=1×3-x3 …(ii)
fx+f1x=x3-1×3+1×3-x3
=x3-1×3+1×3-x3=0
Hence, fx+f1x=0 .
Q8.
Answer :
Given:
fx=2×1+x2
Thus,
ftanθ=2tanθ1+tan2θ
=2×sin θcos θ1+sin2θcos2θ= 2 sin θ cos θ×cos2θcos2θ+sin2θ= 2 sin θ cos θ1 ∵cos2θ+sin2θ =1=sin 2θ ∵ 2 sin θ cos θ = sin 2θ
Hence, f (tan θ) = sin 2θ.
Q9.
Answer :
Given:
afx+bf1x=1x-5 …(i)
⇒af1x+bfx=11x-5
⇒af1x+bfx=x-5 …(ii)
On adding equations (i) and (ii), we get:
afx+bfx+bf1x+af1x=1x-5+x-5
⇒a+bfx+a+bf1x=1x+x-10
⇒fx+f1x=1a+b1x+x-10 …(iii)
On subtracting (ii) from (i), we get:
afx-bfx+bf1x-af1x=1x-5-x+5
⇒a-bfx-f1xa-b=1x-x
⇒fx-f1x=1a-b1x-x …(iv)
On adding equations (iii) and (iv), we get:
2fx=1a+b1x+x-10+1a-b1x-x
⇒2fx=a-b1x+x-10+a+b1x-xa+ba-b
⇒2fx=ax+ax-10a-bx-bx+10b+ax-ax+bx-bxa2-b2
⇒2fx=2ax-10a+10b-2bxa2-b2
⇒fx=1a2-b2×122ax-10a+10b-2bx
=1a2-b2ax-5a+5b-bx
Therefore,
fx=1a2-b2ax-bx-5a+5b
=1a2-b2ax-bx-5a-ba2-b2
=1a2-b2ax-bx-5a-ba-ba+b
=1a2-b2ax-bx-5a+b
Hence,
fx=1a2-b2ax-bx-5a+b
Q10.
Answer :
Given:
fx=x+1x-1
Therefore,
ffx=fx+1x-1
=x+1x-1+1x+1x-1-1
=x+1+x-1x-1x+1-x+1x-1=2xx-12x-1=2×2=x
Thus,
f [ f {(x)}] = x
Hence proved.
Page 3.20 Ex – 3.3
Q1.
Answer :
(i) Given: fx=1x
Domain of f :
We observe that f (x) is defined for all x except at x = 0.
At x = 0, f (x) takes the intermediate form 10.
Hence, domain ( f ) = R -{ 0 }
(ii) Given: fx=1x-7
Domain of f :
Clearly, f (x) is not defined for all (x – 7) = 0 i.e. x = 7.
At x = 7, f (x) takes the intermediate form 10.
Hence, domain ( f ) = R – { 7 }.
(iii) Given: fx=3x-2x+1
Domain of f :
Clearly, f (x) is not defined for all (x + 1) = 0, i.e. x = – 1.
At x = -1, f (x) takes the intermediate form 10.
Hence, domain ( f ) = R – { -1 }.
(iv) Given: fx=2x+1×2-9
Domain of f :
Clearly, f (x) is defined for all x ∈ R except for x2 – 9 ≠ 0, i.e. x = ± 3.
At x = -3, 3, f (x) takes the intermediate form 10.
Hence, domain ( f ) = R – { – 3, 3 }.
(v) Given: fx=x2 +2x+1×2-8x+12
=x2+2x+1×2-6x-2x+12
=x2+2x+1xx-6-2x-6
=x2+2x+1x-6x-2
Domain of f : Clearly, f (x) is a rational function of x as x2+2x+1×2-8x+12 is a rational expression.
Clearly, f (x) assumes real values for all x except for all those values of x for which x2 – 8x + 12 = 0, i.e. x = 2, 6.
Hence, domain ( f ) = R – {2,6}.
Q2.
Answer :
(i) Given: fx=x-2
Clearly, f (x) assumes real values if x – 2 ≥ 0.
⇒ x ≥ 2
⇒ x ∈ [2, ∞)
Hence, domain (f) = [2, ∞) .
(ii) Given: fx=1×2-1
Clearly, f (x) is defined for x2 – 1 > 0 .
(x + 1)(x – 1) > 0 [ Since a2 – b2 = ( a + b)(a – b)]
x < -1 and x > 1
x ∈ (-∞ , – 1) ∪ (1, ∞)
Hence, domain (f) = (- ∞ , – 1) ∪ (1, ∞)
(iii) Given: fx=9-x2
We observe that f (x) is defined for all satisfying
9 – x2 ≥ 0 .
⇒ x2 – 9 ≤ 0
⇒ (x + 3)(x – 3) ≤ 0
⇒ -3 ≤ x ≤ 3
x ∈ [ – 3, 3]
Hence, domain ( f ) = [ -3, 3]
(iv) Given: fx=x-23-x
Clearly, f (x) assumes real values if
x – 2 ≥ 0 and 3 – x > 0
⇒ x ≥ 2 and 3 > x
⇒ x ∈ [2, 3)
Hence, domain ( f ) = [2, 3) .
Q3.
Answer :
(i)
Given:
fx=ax+bbx-a
Domain of f : Clearly, f (x) is a rational function of x as ax+bbx-ais a rational expression.
Clearly, f (x) assumes real values for all x except for all those values of x for which ( bx – a) = 0, i.e. bx = a.
⇒x=ab
Hence, domain ( f ) = R-ab
Range of f :
Let f (x) = y
⇒ax+bbx-a=y
⇒ (ax + b) = y (bx – a)
⇒ (ax + b) = (bxy – ay)
⇒ b + ay = bxy – ax
⇒ b + ay = x(by – a)
⇒x=b+ayby-a
Clearly, f (x) assumes real values for all x except for all those values of x for which ( by – a) = 0, i.e. by = a.
⇒y=ab.
Hence, range ( f ) = R-ab
(ii)
Given:
fx=ax-bcx-d
Domain of f : Clearly, f (x) is a rational function of x as ax-bcx-dis a rational expression.
Clearly, f (x) assumes real values for all x except for all those values of x for which ( cx – d) = 0, i.e. cx = d.
⇒x=dc.
Hence, domain ( f ) = R-dc
Range of f :
Let f (x) = y
⇒ax-bcx-d=y
⇒ (ax – b) = y( cx – d)
⇒ (ax – b) = (cxy – dy)
⇒ dy – b = cxy – ax
⇒ dy – b = x(cy – a)
⇒x=dy-bcy-a
Clearly, f (x) assumes real values for all x except for all those values of x for which ( cy – a) = 0, i.e. cy = a.
⇒y=ac.
Hence, range ( f ) = R-ac .
(iii)
Given: fx=x-1
Domain ( f ) : Clearly, f (x) assumes real values if x – 1 ≥ 0 ⇒ x ≥ 1 ⇒ x ∈ [1, ∞) .
Hence, domain (f) = [1, ∞)
Range of f : For x ≥ 1, we have:
x – 1 ≥ 0
⇒x-1≥0
⇒ f (x) ≥ 0
Thus, f (x) takes all real values greater than zero.
Hence, range (f) = [0, ∞) .
(iv)
Given: fx=x-3
Domain ( f ) : Clearly, f (x) assumes real values if x – 3 ≥ 0 ⇒ x ≥ 3 ⇒ x ∈ [3, ∞) .
Hence, domain ( f ) = [3, ∞)
Range of f : For x ≥ 3, we have:
x – 3 ≥ 0
⇒x-3≥0
⇒ f (x) ≥ 0
Thus, f (x) takes all real values greater than zero.
Hence, range (f) = [0, ∞) .
(v)
Given:
fx=x-22-x
Domain ( f ) :
Clearly, f (x) is defined for all x satisfying: if 2 – x ≠ 0 ⇒ x ≠ 2.
Hence, domain ( f ) = R – {2}.
Range of f :
Let f (x) = y
⇒ x-22-x=y
⇒ x – 2 = y (2 – x)
⇒ x – 2 = – y (x – 2)
⇒ y = – 1
Hence, range ( f ) = {- 1}.
(vi)
The given real function is f (x) = |x – 1|.
It is clear that |x – 1| is defined for all real numbers.
Hence, domain of f = R.
Also, for x ∈ R, (x – 1) assumes all real numbers.
Thus, the range of f is the set of all non-negative real numbers.
Hence, range of f = [0, ∞) .
(vii)
f (x) = – | x |, x ∈ R
We know that
x=x,x≥0-xx<0
∴fx=-x=-x,x≥0x,x<0
Since f(x) is defined for x ∈ R, domain of f = R.
It can be observed that the range of f (x) = – | x | is all real numbers except positive real numbers.
∴ The range of f is (– ∞, 0).
(viii) Given:
fx=9-x2
(9-x2) ≥0⇒9 ≥x2 ⇒x ∈-3,3
9-x2 is defined for all real numbers that are greater than or equal to – 3 and less than or equal to 3.
Thus, domain of f (x) is {x : – 3 ≤ x ≤ 3} or [– 3, 3].
For any value of x such that – 3 ≤ x ≤ 3, the value of f (x) will lie between 0 and 3.
Hence, the range of f (x) is {x: 0 ≤ x ≤ 3} or [0, 3] .
Page 3.41 Ex – 3.4
Q1.
Answer :
(a) Given:
f (x) = x3 + 1 and g (x) = x + 1
Thus,
(f + g) (x) : R → R is given by (f + g) (x) = f (x) + g (x) = x3 + 1 + x + 1 = x3 + x + 2.
(f – g) (x) : R → R is given by (f – g) (x) = f (x) – g (x) = (x3 + 1) – (x + 1 ) = x3 + 1 – x – 1 = x3 – x.
cf : R → R is given by (cf) (x) = c(x3 + 1).
(fg) (x) : R → R is given by (fg) (x) = f(x).g(x) = (x3 + 1) (x + 1) = (x + 1) (x2 – x + 1) (x + 1) = (x + 1)2 (x2 – x + 1).
1f:R–1→R is given by1fx=1fx=1×3+1.
fg:R–1→R is given byfgx=fxgx=x3+1x+1=x+1×2-x+1x+1=x2-x+1 .
Note that : (x3 + 1) = (x + 1) (x2 – x + 1)]
(b) Given:
fx=x-1 and gx=x+1
Thus,
(f + g) ) : [1, ∞) → R is defined by (f + g) (x) = f (x) + g (x) = x-1+x+1.
(f – g) ) : [1, ∞) → R is defined by (f – g) (x) = f (x) – g (x) = x-1-x+1 .
cf : [1, ∞) → R is defined by (cf) (x) = cx-1 .
(fg) : [1, ∞) → R is defined by (fg) (x) = f(x).g(x) = x-1×x+1=x2-1 .
1f:1,∞→R is defined by 1fx=1fx=1x-1.
fg:[1,∞)→R is defined by fgx=fxgx=x-1x+1=x-1x+1.
Q2.
Answer :
Given:
f(x) = 2x + 5 and g(x) = x2 + x
Clearly, f (x) and g (x) assume real values for all x.
Hence,
domain (f) = R and domain (g) = R.
∴ Df∩Dg=R .
Now,
(i) (f + g) : R → R is given by (f + g) (x) = f (x) + g (x) = 2x + 5 + x2 + x = x2 + 3x + 5.
Hence, domain ( f + g) = R .
(ii) (f – g) : R → R is given by (f – g) (x) = f (x) – g (x) = (2x + 5) – (x2 + x) = 5 + x – x2
Hence, domain ( f – g) = R.
(iii) (fg) : R → R is given by (fg) (x) = f(x).g(x) = (2x + 5)(x2 + x)
= 2x3 + 2x2 + 5x2 + 5x
= 2x3 + 7x2 + 5x
Hence, domain ( f.g) = R .
(iv) Given:
g(x) = x2 + x
g(x) = 0 ⇒ x2 + x = 0 = x(x+ 1) = 0
⇒ x = 0 or (x + 1) = 0
⇒ x = 0 or x = – 1
Now,
fg:R–1,0→R is given by fgx=fxgx=2x+5×2+x .
Hence, domainfg=R–1,0.
Q3.
Answer :
Given:
fx=-1,-2⩽x⩽0x-1,0<x⩽2
Thus,
gx=fx+fx
=x-1+1 ,-2⩽x⩽0x-1+(-x+1),0<x<1x-1+x-1,1≤x≤2=x,-2⩽x⩽00,0<x<12x-2,1≤x≤2
Q4.
Answer :
Given:
fx=x+1and gx=9-x2
Clearly, fx=x+1 is defined for all x ≥ -1.
Thus, domain (f) = [ -1, ∞]
Again,
gx=9-x2 is defined for
9 -x2 ≥ 0 ⇒ x2 – 9 ≤ 0
⇒ x2 – 32 ≤ 0
⇒ (x + 3)(x – 3) ≤ 0
⇒ x∈-3,3
Thus, domain (g) = [- 3, 3]
Now,
domain ( f ) ∩ domain( g ) = [ -1, ∞] ∩ [- 3, 3]
= [ -1, 3]
(i) ( f + g ) : [ – 1 , 3] → R is given by ( f + g ) (x) = f (x) + g (x) = x+1+9-x2 .
(ii) ( g – f ) : [ -1 , 3] → R is given by ( g – f ) (x) = g (x)- f (x) = 9-x2-x+1 .
(iii) (fg) : [ -1 , 3] → R is given by (fg) (x) = f(x).g(x) = x+1.9-x2=x+19-x2=9 +9x-x2-x3 .
(iv) fg:-1,3→R is given by fgx=fxgx=x+19-x2=x+19-x2 .
(v) gf:-1,3→R is given by gfx=gxfx=9-x2x+1=9-x2x+1 .
(vi) 2f-5g:-1,3→R is given by 2f-5gx=2x+1-59-x2
=2x+1-45-5×2 .
(vii) f2+7f:-1,∞→R is given by f2+7fx=f2x+7fx {Since domain(f) = [- 1, ∞]}
=x+12+7x+1=x+1+7x+1
(viii) 5g:-3,3→R is defined by 5gx=59-x2. {Since domain(g) = [- 3, 3]}
Q5.
Answer :
Given:
f(x) = loge (1 − x) and g(x) = [x]
Clearly, f(x) = loge (1 − x) is defined for all ( 1 – x) > 0.
⇒ 1 > x
⇒ x < 1
⇒ x ∈ ( -∞, 1)
Thus, domain (f ) = ( – ∞, 1)
Again,
g(x) = [x] is defined for all x ∈ R.
Thus, domain (g) = R
∴ Domain (f) ∩ Domain (g) = ( – ∞, 1) ∩ R
= ( – ∞, 1)
Hence,
(i ) ( f + g ) : ( -∞, 1) → R is given by ( f + g ) (x) = f (x) + g (x) = loge (1 − x) + [ x ].
(ii) (fg) : ( – ∞, 1) → R is given by (fg) (x) = f(x).g(x) = loge (1 − x)[ x ] = [ x ]loge (1 − x).
(iii) Given:
g(x) = [ x ]
If [ x ] = 0,
x ∈ (0, 1)
Thus,
domainfg=domainf∩domaing-x:gx=0
fg:-∞,0→R is defined by fgx=fxgx=loge1-xx.
(iv) Given:
f(x) = loge (1 − x)
⇒1fx=1loge1-x
1fx is defined if loge( 1-x) is defined and loge(1 – x) ≠ 0.
⇒ (1- x) > 0 and (1 – x) ≠ 0
⇒ x < 1 and x ≠ 0
⇒ x ∈ ( – ∞, 0)∪ (0, 1)
Thus, domaingf=-∞,0∪0,1 = ( – ∞, 1) .
gf:-∞,0∪0,1→R defined by gfx=gxfx=xloge1-x
(f + g)( -1) = f( -1) + g( -1)
= loge{1 – (- 1)}+ [ -1]
= loge 2 – 1
Hence, (f + g)( – 1) = loge 2 – 1
(fg)(0) = loge ( 1 – 0) × [0] = 0
fg12=does not exist.
gf12=12loge1-12=0
Q6.
Answer :
Given:
fx=x+1,gx=1xand hx=2×3-3
Clearly, f (x) is defined for x + 1 ≥ 0 .
⇒ x ≥ – 1
⇒ x ∈ [ -1, ∞]
Thus, domain ( f ) = [ -1, ∞] .
Clearly, g (x) is defined for x ≠ 0 .
⇒ x ∈ R – { 0} and h(x) is defined for all x such that x ∈ R .
Thus,
domain ( f ) ∩ domain (g) ∩ domain (h) = [ – 1, ∞] – { 0}.
Hence,
(2f + g – h) : [ – 1, ∞] – { 0} → R is given by:
(2f + g – h)(x) = 2f (x) + g (x) – h (x)
=2x+1+1x-2×2+3
(2f+g-h)(1) =22+1-2+3 = 22+4-2=22+2
(2f + g – h) (0) does not exist because 0 does not lie in the domain x ∈[ – 1, ∞] – {0}.
Page 3.42 Ex – 3.4
Q7.
Answer :
Here,
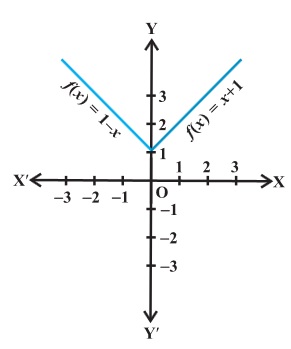
f (x) = 1 – x for x < 0. So,
f (- 4) = 1 – ( – 4) = 5
f (- 3) = 1 – ( – 3) = 4
f (-2) = 1 – ( – 2) = 3
f (-1) = 1 – (- 1) = 2 etc.
Also, f(x) = 1 for x = 0.
Lastly, f (x) = x + 1 for, x > 0.
and f (1) = 2, f (2) = 3, f (3) = 4, f (4) = 5 and so on.
Thus, the graph of f is as shown below:
Q8.
Answer :
f, g : R → R is defined, respectively, by f(x) = x + 1 and g(x) = 2x − 3.
(f + g) (x) = f(x) + g(x)
= (x + 1) + (2x – 3)
= 3x – 2
∴ (f + g) (x) = 3x – 2
(f – g)(x) = f(x) – g(x)
= (x + 1) – (2x – 3)
= x + 1 – 2x + 3
= -x + 4
∴ (f – g) (x) = – x + 4
fgx=fxgx,gx≠0,x∈R
⇒fgx=x+12x-3,2x-3≠0 or 2x≠3
⇒fgx=x+12x-3,x≠32
Q9.
Answer :
It is given that f : [0, ∞) → R and g : R → R such that fx=x and g(x) = x .
Df+g=[0,∞)∩R=[0,∞)
So, f + g : [0, ∞) → R is given by
f+gx=fx+gx=x+x
Df-g=Df∩Dg=[0,∞)∩R=[0,∞)
So, f – g : [0, ∞) → R is given by
f-gx=fx-gx=x-x
Dfg=Df∩Dg=[0,∞)∩R=[0,∞)
So, fg : [0, ∞) → R is given by
fgx=fxgx=x.x=x32
Dfg=Df∩Dg-x:gx=0=0,∞
So,fg:0,∞→R is given by
fgx=fxgx=xx=1x
Q10.
Answer :
Given:
f (x) = x2 and g (x) = 2x + 1
Clearly, D (f) = R and D (g) = R
∴ Df±g=Df∩Dg=R∩R=R
Dfg=Df∩Dg=R∩R=R
Dfg=Df∩Dg-x:gx=0=R∩R–12=R–12
Thus,
(f + g) (x) : R → R is given by (f + g) (x) = f (x) + g (x) = x2 + 2x + 1= (x + 1)2 .
(f – g) (x) : R → R is given by (f – g) (x) = f (x) – g (x) = x2 – 2x -1.
(fg) (x) : R → R is given by (fg) (x) = f(x).g(x) = x2(2x + 1) = 2x3 + x2 .
fg:R–12→R is given byfgx=fxgx=x22x+1.
Page 3.43 Ex – 3.4
Q1.
Answer :
Given:
f (x) = | x |, x ∈ R
We know that
x=x,x≥0-xx<0
It can be observed that the range of f (x) = | x | is all real numbers except negative real numbers.
∴ The range of f is [0, ∞) .
Page 3.43 (Very Short Answers)
Q2.
Answer :
Given:
fx+1x=x2+1×2
=x2+1×2+2-2
=x+1×2-2
Thus,
fx+1x=x+1×2-2
Hence,
f (x) = x2 – 2 , where | x | ≥ 2.
Q3.
Answer :
Given : f(x) = sin [x], where -π4≤x≤π4.
-π4≤x≤π4⇒-7.85 ≤ x ≤ 0.785∴ x∈-7.85, 7.85Or x = {0,1}Thus, range of f(x) = sin [x] is{sin 0, sin1} = {0, sin 1}
Q4.
Answer :
f(x) = cos [π2]x + cos [−π2] x
Thus, f(π) = cosπ2 π+cos -π2 π⇒f(π) =cos 9.8π+ cos-9.8π⇒f(π) =cos 10π+ cos 9π⇒f(π) =1+(-1) = 0
Q5.
Answer :
Since f(x) = cos [x], where -π2<x<π2,
-π2<x<π2⇒-1.57< x < 1.57⇒[x] ∈ {-1,0,1,2}Thus, cos [x] = {cos (-1), cos 0, cos1, cos 2 } .Range of f(x) = {cos 1, 1, cos 2} .
Q6.
Answer :
f(x) = ex-[x], x ∈ R
We know that x-[x] ={x}, which is the fractional part of any number x.Thus, f(x) = e{x}Also, 0 ≤ {x} <1⇒e0 ≤e{x} <e1⇒1≤f(x) < eThus range of f(x) is [1, e) .
Page 3.44 (Very Short Answers)
Q7.
Answer :
Given:
fx=αxx+1, x≠-1
Since f(f(x)) = x,ααxx+1αxx+1+1 =x⇒α2xαx+x+1 =x⇒α2x -αx2 -(x2+x) = 0Solving the quadratic equation in α:α = x2±x4+4x(x2+x)2x ⇒ α = x+1 or -1Since, α≠ x+1, α = -1.
Q8.
Answer :
Given:
fx=1-1x
Now,
f1x=1-11x=1-x
⇒ff1x=f1-x
Again,
If fx=1-1x
Thus,
f1-x=1-11-x
=1-x-11-x=-x1-x=-x-x-1=xx-1
Q9.
Answer :
Given:
fx=x-22-x
Domain ( f ) :
Clearly, f (x) is defined for all x satisfying: if 2 -x ≠ 0 ⇒ x ≠ 2.
Hence, domain ( f ) = R – {2}
Range of f :
Let f (x) = y
⇒ x-22-x=y
⇒ x – 2 = y (2 – x)
⇒ x – 2 = – y (x – 2)
⇒ y = – 1
Hence, range ( f ) = {- 1}.
Q10.
Answer :
Given:
f(x) = 4x − x2, x ∈ R
Now,
f(a + 1) = 4(a + 1) – (a + 1)2
= 4a + 4 – (a2 + 1 + 2a)
= 4a + 4 – a2 – 1 – 2a
= 2a – a2 + 3
f(a – 1) = 4(a – 1) – (a – 1)2
= 4a – 4 – (a2 + 1 – 2a)
= 4a – 4 – a2 – 1 + 2a
= 6a – a2 – 5
Thus,
f(a + 1) − f(a − 1) = ( 2a – a2 + 3) – (6a – a2 – 5)
= 2a – a2 + 3 – 6a + a2 + 5
= 8 – 4a
= 4(2 – a)
Q11.
Answer :
Given : f(x) = x2, g(x) = tan x and h(x) = loge x.
(hogof) π4 = hgfπ4
= hgπ4 2= hgπ4= htan π4= h1= loge 1 =0
Q12.
Answer :
Given:
fx=1x-x
We know that
x=x,if x≥0-x,if x<0
⇒x-x=x-x=0,if x≥0x+x=2x,if x<0
⇒ x – | x| ≤ 0 for all x.
⇒1x-x does not take any real values for any x ∈ R.
⇒ f (x) is not defined for any x ∈ R.
Hence,
domain ( f ) = Φ and range ( f ) = Φ .
Q13.
Answer :
fx=x-x
Since f(x) is defined for all values of x, x∈R.Or dom (f(x)) = RSince, x-[x] = {x}, which is the fractional part of any real number x, f(x) = {x} …..(1)We know that 0 ≤ {x}<1⇒0 ≤{x} <1⇒0 ≤ f(x) <1 {from(1)}Thus, range of f(x) is [0,1).
Q14.
Answer :
fx=x-x
We know that[x] – x =-{x}, which is the fractional part of any real number x.Thus, f(x) =-{x} .Since {x} is always a positive number, f(x) is not defined for any x.Or dom (f) = φThus, range (f) = φ.
Page 3.44 (Multiple Choice Questions)
Q1.
Answer :
(c) {(1, 3), (2, 2), (3, 3)}
We have
R = {(1, 3), (2, 2), (3, 3)}
We observe that each element of the given set has appeared as first component in one and only one ordered pair of R.
So, R = {(1, 3), (2, 2), (3, 3)} is a function.
Q2.
Answer :
(c) {−3, 3}
If f : A → B, such that y ∈ B, then f-1{ y }={x ∈ A: f (x) = y}.
In other words, f-1{ y} is the set of pre-images of y.
Let f-1{9} = x
Then, f (x) = 9
⇒ x2 = 9
⇒ x = ± 3
∴f-1{9} = {- 3, 3}.
Q3.
Answer :
(b) {(x, y) : x, y ∈, R, y2 = x}
y2 =x gives two values of y for a value of x.i.e. there are two images for a value of x.For example: (2)2 =4 and (-2)2 =4Thus, it is not a function.
Q4.
Answer :
(d) None of these
Given:
fx=coslogx
⇒fx2=coslogx2⇒fx2=cos2logx
Similarly,
fy2=cos2logy
Now,
fx2y2=coslogx2y2=coslogx2-logy2
and
fx2y2=coslogx2y2=coslogx2+logy2
⇒fx2y2+fx2y2=cos2logx-2logy+cos2logx+2logy⇒fx2y2+fx2y2=2cos2logxcos2logy⇒12fx2y2+fx2y2=cos2logxcos2logy
⇒fx2fy2-12fx2y2+fx2y2=cos2logxcos2logy-cos2logxcos2logy=0
Q6.
Answer :
(d) None of these
f(x) =x-1Since, x2-1 ≠x-1 2 ,f(x2) ≠(f(x)) 2Thus, (i) is wrong.Since, x+y-1 ≠x-1y-1,f(x+y) ≠f(x) f(y)Thus, (ii) is wrong.Since x-1 ≠x-1 = x-1,fx ≠ f(x)Thus, (iii) is wrong.Hence, none of the given options is the answer.
Q7.
Answer :
(b) {cos 1, cos 2, 1}
Since, f(x) = cos [x], where -π2<x<π2,
-π2<x<π2⇒-1.57< x < 1.57⇒[x] ∈ {-1,0,1,2}Thus, cos [x] = {cos (-1), cos 0, cos1, cos 2 }Range of f(x) = {cos 1, 1, cos 2}
Page 3.45 (Multiple Choice Questions)
Q8.
Answer :
(b) {(x, y) : y = |x|, x, y ∈ R}
For every value of x ∈ R, there is a unique value y∈ R.
i.e. there is a unique image for all values of x ∈ R.
Also, values of x occur only once in the ordered pairs.
Thus, it is a function.
Q9.
Answer :
(c) 3f(x)
fx=log 1+x1-x and gx=3x+x31+3×2
Now,1+g(x)1-g(x) = 1+3x+x31+3×21-3x+x31+3×2=1+3×2+3x+x31+3×2-3x-x3=(1+x)3(1-x)3Then, f(g(x)) = log 1+g(x)1-g(x)=log 1+x1-x3=3 log 1+x1-x=3f(x))
Q10.
Answer :
(b) 8
Given:
Number of elements in set A = 3
Number of elements in set B = 2
Therefore, the number of functions that can be defined from A into B is = 23 = 8.
Q11.
Answer :
(c) 2f(x)
fx=log 1+x1-x
Then, f2x1+x2 = log 1+2×1+x21-2×1+x2= log 1+x2+2×1+x21+x2-2×1+x2= log (1+x)2(1-x)2= 2 log 1+x1-x= 2 (f(x))
Q12.
Answer :
(c) 0
Given : f(x) = cos (log x)
Then, fx f4-12 fx4+f4x
= cos (log x)cos(log 4)-12cos logx4+coslog4x= 12coslogx+log4+cos logx-log4-12cos logx4+coslog4x= 12cos (log 4x)+cos log x4-cos log x4-cos log 4x= 12×0 = 0
Q13.
Answer :
(a) 12f2x+f2y
Given:
fx=2x+2-x2
Now,
f(x + y) f(x − y) = 2x+y+2-x-y22x-y+2-x+y2
⇒ f(x + y) f(x − y) = 1422x+2-2y+22y+2-2x
⇒ f(x + y) f(x − y) = 1222x+2-2×2+22y+2-2y2
⇒ f(x + y) f(x − y) = 12f2x+f2y
Q14.
Answer :
(a) -74
2f (x) − 3f1x=x2 (x ≠ 0) ….(1)
Replacing x by 1x:2f1x-3f(x) = 1×2 …(2) Solving equations (1) & (2) -5f(x) = 3×2+2×2⇒f(x) = -15 3×2+2x2Thus, f(2) = -15 34+2×4= -15 3+324 = -74
Q15.
Answer :
(b) 2|x|
f(x) = 2x + |x|
Then, f(2x) + f(−x) − f(x)
=22x+2x+-2x+-x -2x+x=4x-2x-2x+2x+-x-x=0+2x+x-x=2x
Q16.
Answer :
(c) 2f(x)
fx=log 1+x1-x
Then, f2x1+x2 =log 1+2×1+x21-2×1+x2=log 1+x2+2×1+x21+x2-2×1+x2=log (1+x)2(1-x)2=2 log 1+x1-x=2 fx
Q17.
Answer :
(c) 3
fx=x+1x-1
f(f(f(2))) = ff2+12-1=ff(3)=f3+13-1=f(2) = 3
Q18.
Answer :
Given:
fx=coslogex
⇒f1x=cosloge1x⇒f1x=cos-logex⇒f1x=coslogex
Similarly,
f1y=coslogey
Now,
fxy=coslogexy=coslogex+logey
and
fxy=coslogexy=coslogex-logey
⇒fxy+fxy=coslogex-logey+coslogex+logey⇒fxy+fxy=2coslogexcoslogey⇒12fxy+fxy=coslogexcoslogey
⇒f1xf1y-12fxy+fxy=coslogexcoslogey-coslogexcoslogey=0
Q19.
Answer :
(d) x ∈ R, x ≠ 0
Given:
f(x) = x, gx=1x and h(x) = f(x) g(x)
Now,
h(x)=x×1x=1
We observe that the domain of f is ℝ and the domain of g is ℝ-0.
∴ Domain of h = Domain of f ⋂ Domain of g = ℝ∩ℝ-0=ℝ-0
⇒x ∈ R, x ≠ 0
Q20.
Answer :
(a) 1
Given:
fx=sin4 x+cos2 xsin2 x+cos4 x
On dividing the numerator and denominator by cos4 x, we get
fx=tan4 x+sec2 x1+tan2 xsec2 x=1+tan4 x+tan2 x1+tan2 x1+tan2 x=1+tan4 x+tan2 x1+tan4 x+tan2 x=1 (For every x ∈ R)
For x = 2002, we have
f (2002) = 1
Page 3.46 (Multiple Choice Questions)
Q21.
Answer :
(c) (3/4, 1)
Given:
f(x) = cos2x + sin4x
⇒fx=1-sin2x+sin4x
⇒fx=sin2x-122+34
The minimum value of fx is 34.
Also,
sin2x≤1⇒sin2x-12≤12⇒sin2x-122≤14⇒sin2x-122+34≤14+34⇒fx≤1
The maximum value of fx is 1.
∴ f(R) = (3/4, 1)
Q22.
Answer :
As, x=x, x≥0-x<0So, f(x)=xxWhen x<0 i.e. x∈[-4,0)f(x)=x-x=-1and when x>0 i.e. x∈(0,4]f(x)=xx=1 So, range(f)=-1,1
Disclaimer: The question in the book has some error. The solution is created according to the question given in the book.
Q23.
Answer :
(c) −1, −2
f(x) = 2x + 3 and g(x) = x<sup>2</sup> + 7
g(f(x)) = 8⇒f(x)2+7 = 8⇒(2x+3)2+7 = 8⇒x2+3x+2 = 0⇒(x+2)(x+1) = 0⇒x = -1,-2
Q24.
Answer :
(c) -12
Given:
fx= -1,for -2≤x≤0x-1,for 0≤x≤2
We know,
x≥0
⇒ fx=x-1 …(1)
Also,
If x≤0, then x=-x …(2)
∴ {x ∈ [−2, 2]: x ≤ 0 and f (|x|) = x}
= x: x-1=x [Using (1)]
= x: -x-1=x [Using (2)]
= x: 2x=-12
= x: x=-12
= -12
Q25.
Answer :
(a) 0.5
efx=10+x10-x
⇒f(x) = log e10+x10-x …(1)
fx=kf200 x100+x2
⇒log e10+x10-x = k loge10+200×100+x210-200×100+x2 {from (1)}⇒log e10+x10-x = k loge1000+10×2+200×1000+10×2-200x⇒log e10+x10-x = k logex+102x-102⇒log e10+x10-x = 2k logex+10x-10⇒1 = 2k⇒k = 1/2=0.5
Q26.
Answer :
(d) None of these
Given:
fx=27×3+1×3
⇒fx=3x+1x9x2+1×2-3
⇒fx=3x+1x3x+1×2-9
⇒fα=3α+1α3α+1α2-9
Since α and β are the roots of 3x+1x=12,
3α+1α=12 and 3β+1β=12
⇒fα=12122-9 and fβ=12122-9
⇒fα=fβ=12122-9
Disclaimer: The question in the book has some error, so none of the options are matching with the solution. The solution is created according to the question given in the book.
Q27.
Answer :
(a) fα=fβ=-9
Given:
fx=64×3+1×3
⇒fx=4x+1x16x2+1×2-4
⇒fx=4x+1x4x+1×2-12
⇒fα=4α+1α4α+1α2-12 and fβ=4β+1β4β+1β2-12
Since α and β are the roots of 4x+1x=3,
4α+1α=3 and 4β+1β=3
⇒fα=332-12=-9 and fβ=332-12=-9
⇒fα=fβ=-9
Q28.
Answer :
(d) None of these
3fx+5f1x=1x-3 …(1)
Multiplying (1) by 3:15 f1x +9 f(x) = 3x-9 …..(2)Replacing x by 1xin (1):3 f1x +5 f(x) = x-3 Multiplying by 5:15 f1x +25 f(x) = 5x-15 ….(3)Solving (2) and (3):-16 f(x) = 3x-5x+6⇒f(x) = 116-3x+5x-6
Disclaimer: The question in the book has some error, so, none of the options are matching with the solution. The solution is created according to the question given in the book.
Q29.
Answer :
(c) f(x) + f(1 − x) = 1
fx=4x4x+2 ; x ∈ R
f (1-x) = 41-x41-x+2= 42×4x+4=24x+2f(x) +f(1-x) = 4x4x+2+24x+2 = 4x+24x+2 =1
Q30.
Answer :
(a) f(π/2) = 1
f(x) = sin [π2] x + sin [−π2]x
⇒f(x) = sin 9.8x+ sin -9.8x⇒f(x) = sin 9x – sin 10xfπ2 = sin 9×π2 – sin 10×π2⇒fπ2 = 1- 0 =1
Q31.
Answer :
(b) -1-3, -1+3
fx=2-2x-x2
Since, 2-2x-x2≥0, x2+2x-2 ≤0⇒x2-2x-2+1-1≤0⇒x-12-32≤0⇒x–1-3x–1+3 ≤0⇒-1-3 ≤x ≤-1+3Thus, dom(f) = -1-3,-1+3 .
Page 3.47 (Multiple Choice Questions)
Q32.
Answer :
(a) (−∞, −3] ∪ (2, 5)
fx=x+32-x x-5
For f(x) to be defined ,2-xx-5≠0⇒x≠2, 5 ….(1)Also, x+32-xx-5≥0⇒x+32-xx-52-x2x-52≥0⇒x+3x-2x-5≤0⇒x∈(-∞,-3]∪(2,5) ….(2)From (1) and (2),x∈(-∞,-3] ∪(2,5)
Q33.
Answer :
(a) [−1, 2) ∪ [3, ∞)
fx=x+1 x-3x-2
For f(x) to be defined,(x-2) ≠0⇒x ≠ 2 …(1)Also,(x+1)(x-3)(x-2)≥0⇒(x+1)(x-3)(x-2)(x-2)2≥0⇒(x+1)(x-3)(x-2)≥0⇒x ∈ [-1,2)∪[3,∞) …..(2)From (1) and (2),x ∈ [-1,2) ∪ [3,∞)
Q34.
Answer :
(d) [1, 3]
fx=x-1+3-x
For f(x) to be defined, x-1≥0⇒x≥1 …(1)and 3-x ≥0⇒3≤ x …(2)From (1) and (2),x∈[1,3]
Q35.
Answer :
(c) ϕ
fx=x-2x+2+1-x1+x
For f(x) to be defined,x+2 ≠0⇒x ≠-2 …(1)And 1+x ≠0⇒ x ≠ -1 ….(2)Also, x-2x+2 ≥0⇒(x-2)(x+2)(x+2)2 ≥0⇒(x-2)(x+2)≥0⇒x ∈ (-∞,-2) ∪ [2,∞) …(3)And 1-x1+x ≥0⇒(1-x)(1+x)(1+x)2 ≥0⇒(1-x)(1+x) ≥0⇒ x∈ (-∞,-1) ∪ [1,∞) …(4)From (1), (2), (3) and (4), we get,x ∈ϕ .Thus, dom (f(x)) = ϕ.
Q36.
Answer :
(d) R − {0}
f(x) = log |x|
For f(x) to be defined,x >0, which is always true.But x ≠ 0⇒ x ≠ 0Thus, dom (f) = R- {0}.
Q37.
Answer :
(d) [0, 4]
Given:
fx=4x-x2
Clearly, f (x) assumes real values if
4x – x2 ≥ 0
⇒ x(4 – x) ≥ 0
⇒ – x(x – 4) ≥ 0
⇒ x(x – 4) ≤ 0
⇒ x ∈ [0, 4]
Hence, domain (f )= [0, 4].
Q38.
Answer :
(a) [4, ∞)
fx=x-3-2x-4-x-3+2x-4
For f(x) to be defined, x-4 ≥0⇒x-4 ≥ 0⇒ x ≥ 4 ….(1)Also, x-3-2x-4 ≥0⇒x-3-2x-4 ≥0⇒x-3 ≥ 2x-4⇒(x-3)2 ≥ 2x-42⇒x2+9-6x ≥ 4x-4⇒ x2-10x+25 ≥ 0⇒ (x-5) 2 ≥0, which is always true.Similarly, x-3+2x-4≥0 is always true.Thus, dom(f(x))=[4,∞)
Q39.
Answer :
(c) [−3, − 2] ∪ [2, 3]
fx=5 x-x2-6
For f(x) to be defined, 5x-x2-6 ≥0⇒5x-x2-6 ≥0⇒x 2-5x +6 ≤ 0For x>0, x=x⇒x 2-5x +6 ≤ 0⇒(x-2)(x-3) ≤ 0⇒x∈[2,3] ……..(1)For x<0, x=-x⇒x 2+5x +6 ≤ 0⇒ (x+2)(x+3) ≤ 0⇒x∈ [-3,-2] …….(2)From (1) and (2),x∈[-3,-2]∪[2,3] or, dom(f) =[-3,-2]∪[2,3]
Q40.
Answer:
(c) {−1, 1}
fx=xx
Let y = xxFor x>0, x=x⇒y = xx = 1For x <0, =-x⇒y = x-x =-1Thus, range of f(x) is {-1,1}.
Q41.
Answer :
(a) {−1, 1}
fx=x+2x+2 , x ≠ −2
Let y= x+2x+2For x+2 >0,or x>-2 ,y = x+2x+2 = 1For x+2 < 0,or x<-2,y = x+2-(x+2) = -1Thus, y = {-1,1}or range f(x)= {-1,1}.
Q42.
Answer :
(b) [0, ∞)
f(x)=x-1≥0 ∀x∈RThus, range=[0,∞0
Q43.
Answer :
(c) R − {-1/2,1}
fx=x2-xx2+2x
Let y = x2-xx2+2x Also, x≠0⇒y = x(x-1)x(x+2)⇒y = (x-1)(x+2)⇒xy+2y = x-1⇒x = 2y+11-yHere, 1-y ≠ 0.or, y ≠ 1 .Also, x≠0⇒2y+11-y≠0⇒y≠-12Thus, range (f) = R-{-12,1} .
Leave a Reply