Page 15.10 Ex 15.1
Q1.
Answer :
We have, 12x<50⇒x<5012 Dividing both the sides by 12⇒x<256(i) x∈RThen, the solution of the given inequation is -∞,256.(ii) x∈ZThen, the solution of the given inequation is ……….-3, -2, -1, 0, 1, 2, 3, 4.(iii) x∈NThen, the solution of the given inequation is 1, 2, 3, 4.
Q2.
Answer :
-4x>30⇒x<-304 (Dividing both the sides by -4)⇒x<-152(i) x∈RThen, the solution of the given inequation is -∞, -152.(ii) x∈ZThen, the solution of the given inequation is ……….-9, -8.(iii) x∈NThen, the solution of the given inequation is ϕ.
Page 15.11 Ex 15.1
Q3.
Answer :
We have, 4x-2<8⇒4x<8+2 (Transposing -2 to the RHS)⇒4x<10⇒x<104 (Dividing both the sides by 4)⇒x<52(i) x∈RThen, the solution of the given inequation is -∞, 52.(ii) x∈ZThen, the solution of the given inequation is …….-3, -2, -1, 0, 1, 2.(iii) x∈NThen, the solution of the given inequation is 1, 2.
Q4.
Answer :
3x-7>x+1⇒3x-x>1+7 Transposing x to LHS and -7 to RHS⇒2x>8⇒x>4 Dividing both sides by 2Hence, the solution set of the given inequation is 4, ∞
Q5.
Answer :
We have, x+5>4x-10⇒5+10 > 4x-x (Transposing x to the RHS and -10 to the LHS)⇒15>3x⇒3x<15⇒x<5 Dividing both sides by 3⇒x∈-∞, 5Hence, the solution set of the given inequation is -∞, 5.
Q6.
Answer :
3x+9⩾-x+19⇒3x+x⩾19-9 (Transposing -x to the LHS and 9 to the RHS)⇒4x≥10⇒x≥52 (Dividing both the sides by 4)Hence, the solution set of the given inequation is [52, ∞).
Q7.
Answer :
23- x≥x5+4⇒6-2x≥x5+4⇒6-4≥x5+2x Transposing -2x to the RHS and 4 to the LHS⇒2 ≥ 11×5⇒11×5≤2⇒x≤1011 Mltiplying both the sides by 511Thus, the solution set of the given inequation is (-∞, 1011].
Q8.
Answer :
3x-25≤4x-32⇒23x-2≤54x-3⇒6x-4≤20x-15⇒-4+15≤20x-6x (Transposing 6x to the RHS and -15 to the LHS)⇒11 ≤ 14x ⇒14x≥11⇒x≥1114 (Dividing both the sides by 14)Hence, the solution set of the given inequation is [1114, ∞).
Q9.
Answer :
-x-3+4<5-2x⇒-x+3+4<5-2x⇒-x+7<5-2x⇒-x+2x<5-7 Transposing -2x to LHS and 7 to RHS⇒x<-2Hence, the solution set of the given inequation is -∞, -2.
Q10.
Answer :
x5<3x-24-5x-35⇒20×x5<20×3x-24-5x-35 Multiplying both the sides by 20⇒4x<53x-2-45x-3⇒4x<15x-10-20x+12⇒4x<-5x+2⇒4x+5x<2 (Transposing -5x to the LHS) ⇒9x<2⇒x<29 (Dividing both the sides by 9) Hence, the solution set of the given inequation is -∞, 29.
Q11.
Answer :
2x-15≤32+x7⇒14x-1≤152+x ⇒14x-14≤30+15x⇒30+15x≥14x-14⇒15x-14x≥-14-30 (Transposing 14x to the LHS and 30 to the RHS)⇒x≥-44Hence, the solution to the given inequation is [-44, ∞).
Q12.
Answer :
5×2+3×4≥394⇒10x+3×4≥394⇒10x+3x≥39⇒13x≥39⇒x≥3913 (Dividing both the sides by 13)⇒x≥3Hence, the solution set of the given inequation is [3, ∞).
Q13.
Answer :
x-13+4<x-55-2⇒x-13-x-55<-2-4 Transposing 4 to the RHS and x-55 to the LHS⇒5x-1-3x-515<-6⇒5x-5-3x+1515<-6⇒2x+1015<-6⇒2x+10<-90⇒2x<-90-10 Transposing 10 to the RHS⇒2x<-100 ⇒x<-1002 Dividing both the sides by 2⇒x<-50Hence, the solution of the given inequation is -∞, -50.
Q14.
Answer :
2x+34-3<x-43-2⇒2x+34-x-43<-2+3 (Transposing x-43 to the LHS and -3 to the RHS)⇒32x+3-4x-412<1⇒32x+3-4x-4<12 (Multiplying both the sides by 12)⇒6x+9-4x+16<12⇒2x+25<12⇒2x<12-25⇒2x<-13⇒x<-132 (Dividing both the sides by 2)Hence, the solution of the given inequation is -∞, -132.
Q15.
Answer :
5-2×3<x6-5⇒5-2×3-x6<-5 Transposing x6to the LHS⇒25-2x-x6<-5 ⇒10-4x-x6<-5 ⇒10-5×6<-5 ⇒10-5x<-30⇒10+30<5x⇒40<5x⇒5x>40⇒x>405⇒x>8Hence, the solution set of the given inequality is 8, ∞.
Q16.
Answer :
4+2×3≥x2-3⇒4+2×3-x2≥-3⇒8+4x-3×6≥-3⇒8+x≥-18 Multiplying both the sides by 6⇒x≥-26 Transposing 8 to the RHSThus, the solution set of the given inequation is [-26, ∞).
Q17.
Answer :
2x+35-2<3x-25⇒2x+35-3x-65<2 Transposing 3x-25to the LHS and -2 to the RHS⇒2x+3-3x+65<2⇒2x+3-3x+6<10 Multiplying both the sides by 5⇒-x+9<10⇒-x<1⇒x>-1 Multiplying both the sides by -1Hence, the solution set of the given inequation is -1, ∞.
Q18.
Answer :
x-2≤5x+83⇒3x-2≤5x+8 Multiplying both the sides by 3⇒3x-6≤5x+8⇒5x+8≥3x-6⇒5x-3x≥-6-8 Transposing 3x to the LHS and 8 to the RHS⇒2x≥-14⇒x≥-7 Dividing both the sides by 2Hence, the solution of the given inequation is [-7,∞).
Q19.
Answer :
6x-54x+1<0Equating 6x-5 and 4x+1 to zero, we obtain x=56 and -14 as the critical points.
∴ x∈-14,56
Q20.
Answer :
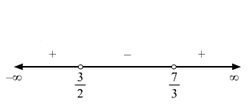
2x-33x-7>0Equating 2x-3 and 3x-7 to zero, we obtain x=32, 73 as the critical points.
∴ x∈-∞,32∪73,∞
Q21.
Answer :
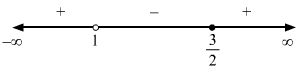
3x-2<1⇒3x-2-1<0⇒3-x+2x-2<0⇒-x+5x-2<0⇒x-5x-2>0
∴ x∈-∞,2∪5,∞
Q22.
Answer :
1x-1≤2⇒1x-1-2≤0⇒1-2x+2x-1≤0⇒-2x+3x-1≤0⇒2x-3x-1≥0
∴ x∈-∞,1∪[32,∞)
Q23.
Answer :
4x+32x-5<6⇒4x+32x-5-6<0⇒4x+3-62x-52x-5<0⇒4x+3-12x+302x-5<0⇒-8x+332x-5<0⇒8x-332x-5>0
x∈-∞,52∪338,∞
Q24.
Answer :
5x-6x+6<1⇒5x-6x+6-1<0⇒5x-6-x-6x+6<0⇒4x-12x+6<0⇒x-3x+6<0
∴ x∈-6, 3
Q25.
Answer :
We have, 5x+84-x<2⇒5x+84-x-2<0⇒5x+8-24-x4-x<0⇒5x+8-8+2×4-x<0⇒7×4-x<0⇒7xx-4>0
∴ x∈-∞,0∪4,∞
Q26.
Answer :
We have, x-1x+3>2⇒x-1x+3-2>0⇒x-1-2x+3x+3>0⇒x-1-2x-6x+3>0⇒-x-7x+3>0 ⇒x+7x+3<0
∴ x∈-7,-3
Q27.
Answer :
We have,
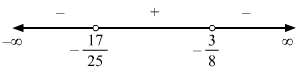
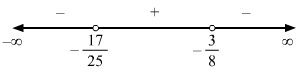
7x-58x+3>4⇒7x-58x+3-4>0⇒7x-5-48x+38x+3>0⇒7x-5-32x-128x+3>0⇒-25x-178x+3>0⇒25x+178x+3<0 (Multiplying by -1 to make the coefficient of x in the LHS positive)
x∈-1725,-38
Q28.
Answer :
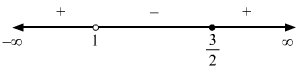
xx-5>12⇒xx-5-12>0⇒2x-x+52(x-5)>0⇒x+52(x-5)>0⇒x+5x-5>0
∴ x∈-∞,-5∪5,∞
Page 15.23 Ex 15.2
Q1.
Answer :
x+3>0⇒x>-3⇒x∈-3,∞ …iAlso, 2x<14⇒x<7 Dividing both the sides by 2⇒x∈-∞,7 …iiThus, the solution of the given set of inequalities is the intersection of i and ii.-3,∞∩-∞,7=-3,7∴ x∈-3,7Thus, the solution of the given set of inequalities is -3,7.
Q2.
Answer :
We have, 2x-7>5-x⇒2x+x>5+7⇒3x>12⇒x>4 ⇒x∈4,∞ …iAlso, 11-5x≤1⇒5x⩾11-1⇒x⩾2⇒x∈[2,∞) …iiSolution set of the given set of inequations is intersection of i and ii4,∞∩[2,∞)=4,∞Thus, the solution set of the given set of inequations is 4,∞.
Q3.
Answer :
We have, x-2>0⇒x>2⇒x∈2,∞ …iAlso, 3x<18⇒x<6⇒x∈-∞,6 …iiSolution of the given set of the inequations is intersection of i and ii2,∞∩-∞,6=(2,6)Thus, (2,6) is the solution of the given set of inequalities.
Q4.
Answer :
We have, 2x+6≥0⇒2x⩾-6⇒x⩾-3⇒x∈[-3,∞) …iAlso, 4x-7<0⇒4x<7⇒x<74⇒x∈-∞,74 …iiThus, the solution of the given inequations is the intersection of i and ii.[-3,∞)∩-∞74=[-3,74)Thus, the solution of the given inequations is [-3,74).
Q5.
Answer :
3x-6>0⇒3x>6⇒x>2⇒x∈2,∞ …iAlso, 2x-5>0⇒2x>5⇒x>52⇒x∈52,∞ …iiSolution of the given set of inequalities is the intersection of i and ii.2,∞∩52,∞=52,∞Thus, the solution of the given set of inequalities is 52,∞.
Q6.
Answer :
2x-3<7⇒2x<7+3⇒x<5⇒x∈-∞, 5 …(i)Also, 2x>-4⇒x>-2 ⇒x∈-2,∞ …(ii)Thus, the solution of the given set of inequalities is the intersection of (i) and (ii).-∞, 5 ∩-2,∞=-2,5Thus, the solution of the given set of inequalities is -2,5.
Q7.
Answer :
We have, 2x+5≤0⇒2x≤-5⇒x≤-52⇒x∈(-∞, -52] … (i)Also, x-3≤0⇒x≤3⇒x∈(-∞, 3] … (ii)Thus, the solution of the given set of inequalities is the intersection of (i) and (ii).(-∞,-52] ∩(-∞,3] = (-∞,-52]Thus, the solution of the given set of inequalities is (-∞,-52].
Q8.
Answer :
5x-1<24⇒5x<24+1⇒x<5 ⇒x∈-∞,5 … (i)Also, 5x+1>-24⇒5x>-24-1⇒x>-5⇒x∈(-5,∞) … (ii)Hence, the solution of the given set of inequalities is the intersection of (i) and (ii).-∞,5 ∩-5,∞=-5, 5Thus, the solution of the given set of inequalities is -5, 5.
Q9.
Answer :
3x-1⩾5⇒3x⩾5+1⇒x≥2⇒x∈[2,∞) … (i)Also, x+2>-1⇒x>-1-2⇒x>-3⇒x∈(-3,∞) … (ii)Hence, the solution of the given set of inequalities is the intersection of (I) and (ii).[2,∞)∩(-3,∞)= [2,∞)Thus, the solution of the given set of inequalities is [2,∞).
Q10.
Answer :
We have,
11-5x>-4⇒-5x>-4-11⇒-5x>-15⇒5x<15 Multiplying both sides by -1⇒x<155 ⇒x<3⇒x∈(-∞,3) … (i)Also, 4x+13≤-11⇒4x≤-11-13⇒4x≤-24⇒x≤-6⇒x∈(-∞,-6] … (ii)Hence, the solution of the given set of inequalities is the intersection of (i) and (ii).(-∞3)∩(-∞,-6]=(-∞,-6]Hence, the solution of the given set of inequalities is (-∞,-6].
Q11.
Answer :
We have, 4x-1≤0⇒4x≤1⇒x≤14 (Dividing both the sides by 4)⇒x∈(-∞,14] …(i)Also, 3-4x<0⇒0> 3-4x⇒4x>3⇒x>34 Dividing both sides by 4⇒x∈34,∞ …(ii)Hence, the solution of the given set of inequalities is the intersection of (i) and (ii).But, -∞14∩34,∞ =ϕThus, the given set of inequations has no solution.
Q12.
Answer :
x+5>2x+1⇒x+5>2x+2⇒2x+2 < x+5⇒2x-x<5-2⇒x<3⇒x∈(-∞, 3) … (i)Also, 2-x<3x+2⇒2-x<3x+6⇒3x+6>2-x⇒3x+x>2-6⇒4x>-4⇒x>-1⇒x∈(-1, ∞) … (ii)Hence, the solution of the given set of inequations is the intersection of (i) and (ii).(-∞, 3) ∩(-1, ∞)=(-1, 3)Thus, the solution of the given set of inequations is (-1, 3).
Q13.
Answer :
2x-6<3x-7⇒2x-12<3x-7⇒3x-7 > 2x-12⇒3x-2x>-12+7⇒x>-5⇒x∈-5,∞ … (i)Also, 11-2x<6-x⇒6-x>11-2x⇒2x-x>11-6⇒x>5⇒x∈5,∞ … (ii)Hence, the solution of the given inequation is the intersection of (i) and (ii).-5,∞∩5,∞=5,∞Hence, the solution of the given inequation is 5,∞.
Q14.
Answer :
5x-7<3x+3⇒5x-7<3x+9⇒5x-3x<9+7⇒2x<16⇒x<8⇒x∈-∞,8 … (i)Also, 1-3×2≥x-4⇒x-4≤1-3×2⇒x+3×2≤1+4⇒2x+3×2≤5⇒5x≤10 ⇒x≤2 ⇒x∈(-∞,2] … (ii)Hence, the solution of the given set of inequalities is the intersection of (i) and (ii).-∞,8∩(-∞,2]=(-∞,2]Hence, the solution of the given set of inequalities is (-∞,2].
Q15.
Answer :
5-2×3<x6-5⇒5-2×3-x6<-5 Transposing x6to the LHS⇒25-2x-x6<-5 ⇒10-4x-x6<-5 ⇒10-5×6<-5 ⇒10-5x<-30⇒10+30<5x⇒40<5x⇒5x>40⇒x>405⇒x>8Hence, the solution set of the given inequality is 8, ∞.
Q16.
Answer :
4+2×3≥x2-3⇒4+2×3-x2≥-3⇒8+4x-3×6≥-3⇒8+x≥-18 Multiplying both the sides by 6⇒x≥-26 Transposing 8 to the RHSThus, the solution set of the given inequation is [-26, ∞).
Q17.
Answer :
2x+35-2<3x-25⇒2x+35-3x-65<2 Transposing 3x-25to the LHS and -2 to the RHS⇒2x+3-3x+65<2⇒2x+3-3x+6<10 Multiplying both the sides by 5⇒-x+9<10⇒-x<1⇒x>-1 Multiplying both the sides by -1Hence, the solution set of the given inequation is -1, ∞.
Q18.
Answer :
x-2≤5x+83⇒3x-2≤5x+8 Multiplying both the sides by 3⇒3x-6≤5x+8⇒5x+8≥3x-6⇒5x-3x≥-6-8 Transposing 3x to the LHS and 8 to the RHS⇒2x≥-14⇒x≥-7 Dividing both the sides by 2Hence, the solution of the given inequation is [-7,∞).
Q19.
Answer :
10≤-5x-2<20⇒10≤-5x+10<20⇒10-10≤-5x<20-10 (Substracting 10 from all three terms)⇒0≤-5x<10⇒0≥x>-2 (Dividing all three terms by -5 )⇒x∈(-2,0]
Hence, the interval (-2,0] is the solution of the given set of inequations.
Q20.
Answer :
-5<2x-3<5⇒-5+3<2x<5+3 Adding 3 throughout⇒-2<2x<8⇒-1<x<4 Dividing throughout by 2⇒x∈-1,4
Hence, the interval (-1,4) is the solution of the given set of inequaltions.
Q21.
Answer :
3x-2<1⇒3x-2-1<0⇒3-x+2x-2<0⇒-x+5x-2<0⇒x-5x-2>0
∴ x∈-∞,2∪5,∞
Q22.
Answer :
1x-1≤2⇒1x-1-2≤0⇒1-2x+2x-1≤0⇒-2x+3x-1≤0⇒2x-3x-1≥0
∴ x∈-∞,1∪[32,∞)
Q23.
Answer :
4x+32x-5<6⇒4x+32x-5-6<0⇒4x+3-62x-52x-5<0⇒4x+3-12x+302x-5<0⇒-8x+332x-5<0⇒8x-332x-5>0
x∈-∞,52∪338,∞
Q24.
Answer :
5x-6x+6<1⇒5x-6x+6-1<0⇒5x-6-x-6x+6<0⇒4x-12x+6<0⇒x-3x+6<0
∴ x∈-6, 3
Q25.
Answer :
We have, 5x+84-x<2⇒5x+84-x-2<0⇒5x+8-24-x4-x<0⇒5x+8-8+2×4-x<0⇒7×4-x<0⇒7xx-4>0
∴ x∈-∞,0∪4,∞
Q26.
Answer :
We have, x-1x+3>2⇒x-1x+3-2>0⇒x-1-2x+3x+3>0⇒x-1-2x-6x+3>0⇒-x-7x+3>0 ⇒x+7x+3<0
∴ x∈-7,-3
Q27.
Answer :
We have,
7x-58x+3>4⇒7x-58x+3-4>0⇒7x-5-48x+38x+3>0⇒7x-5-32x-128x+3>0⇒-25x-178x+3>0⇒25x+178x+3<0 (Multiplying by -1 to make the coefficient of x in the LHS positive)
x∈-1725,-38
Q28.
Answer :
xx-5>12⇒xx-5-12>0⇒2x-x+52(x-5)>0⇒x+52(x-5)>0⇒x+5x-5>0
∴ x∈-∞,-5∪5,∞
Page 15.26 Ex 15.3
Q1.
Answer :
Let the smaller odd positive integer be x. Then, the other odd positive integer shall be x + 2.
Therefore, as per the given conditions:
x+2<10 and x+x+2>11⇒x<8 and 2x>9⇒x<8 and x>92Since x is an odd integer,Therefore, x=5,7Hence, pairs are (5,7),(7,9).
Q2.
Answer :
Let x be the smaller of the two odd natural numbers. Then, the other odd natural number will be x + 2.
Therefore, as per the given conditions:
x>10 and x+x+2<40⇒x>10 and 2x+2<40⇒x>10 and x<19⇒10<x<19∴ x∈11, 13, 15, 17Hence, the pairs are (11,13), (13,15), (15,17), (17,19).
Q3.
Answer :
Let x be the smaller even integer. Then, the other even integer shall be x + 2.
Therefore, as per the given condition:
x>5 and x+x+2<23⇒x>5 and 2x+2<23⇒x>5 and 2x<21⇒x>5 and x<212∴ x∈6, 8, 10Hence, the pairs are (6,8), (8,10),(10,12).
Q4.
Answer :
Let x be the minimum marks he scores in the third test.
Then, 65+70+x3≥65⇒135+x3≥65⇒135+x≥195 (Multiplying both the sides by 3)⇒x≥195-135⇒x≥60Hence, the minimum marks Rohit should score in the third test should be 60.
Q5.
Answer :
Suppose the temperature of the solution is x degree Celsius.
∴ x in Fahrenheit = 95x+32
Then, as per the given condition:
86<95x+32<95⇒86-32<95x<95-32 (Subtratcting 32 throughout)⇒54<95x<63⇒59×54<59×95x<59×63 (Multiplying by 59 throughout)⇒30<x<35Hence, the range of the temperature in degree Celsius is between 30°C and 35°C.
Page 15.27 Ex 15.3
Q6.
Answer :
Let x degree Fahrenheit be the temperature of the solution.
Then, 30°C<x°F<35°CNow, F = 95C+32⇒95×30+32<x°F<95×35+32⇒54+32<x<63+32⇒86°<x°<95°Hence, the range of the temperature in Fahrenheit is between 86° and 95°.
Q7.
Answer :
Let x be the minimum marks scored in the last paper.
Then, 90≤87+95+92+94+x5≤100⇒90≤368+x5≤100⇒450≤368+x≤500⇒450-368≤368+x-368≤500-368⇒82≤x≤132But x can not be more than 100⇒ 82≤x≤100Hence, the minimum marks that Shikha must score in the fifth paper is 82.
Q8.
Answer :
To realise profit, revenue must be greater than the cost.
∴ 2x>300+32x⇒2x-32x>300⇒12x>300⇒x>600Thus, the company must sell more than 600 cassettes in a week to realise profit.
Q9.
Answer :
Let the shortest side of the triangle be x cm.
Then, the longest side will be 3x and the third side will be 3x − 2.
∴ Perimeter of the triangle≥61⇒x+3x+3x-2≥61⇒7x≥61+2⇒x≥9 (Dividing throughout by 7)Hence, the minumum length of the shortest side is 9 cm.
Q10.
Answer :
Let x litres of water be added to the 1125 litres of 45% solution of the acid.
Total quantity of mixture is (1125+x) litres.
Total acid content in 1125 litres of mixture = 45% of 1125
It is given that the acid content in the resulting mixture must be more than 25% and less than 30%.∴ 25% of1125+x<45%×1125<30% of (1125+x)⇒25100×1125+x<45100×1125<30100×1125+xMultiplying throughout by 100:28125+25x<50625<33750+30x⇒x<50625-2812525 and x>50625-3375030⇒x<900 and x>562.5Thus, the water to be added should be more than 562.5 litres but less than 900 litres.
Q11.
Answer :
Suppose x litres of 2% solution is added in the existing solution of 8% of boric acid.
Resulting mixture = (640 + x) L
Therefore, as per given conditions:
4% of (640+x)<8% of 640+2% of x<6% of (640+x)⇒4100(640+x)<8100×640+2100×x<6100(640+x)Multiplying throughout by 100:⇒2560+4x<5120+2x<3840+6x⇒2560+4x<5120+2x and 5120+2x<3840+6x⇒2x<2560 and 4x>1280⇒x<1280 and x>320⇒320<x<1280Thus, the amount of solution must be less than 1280 litres but more than 320 litres.
Q12.
Answer :
Let x be the third pH value.
Then, 7.2<7.48+7.85+x3<7.8⇒7.2<15.33+x3<7.8⇒21.6<15.33+x<23.4 Multiplying throughout by 3⇒21.6-15.33<15.33+x-x<23.4-15.33⇒6.27<x<8.07Hence, the range for the pH value for the third reading must be between 6.27 and 8.07
Page 15.30 Ex 15.4
Q1.
Answer :
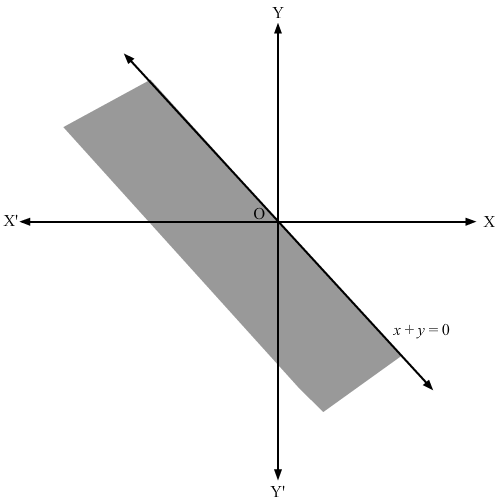
We have,x+2y-y≤0
Converting the given inequation to equation, we obtain x + 2y – y = 0, i.e x + y = 0
Putting y = 0 and x = 0 in this equation, we obtain x = 0 and y = 0.
So, this line intersects the x-axis and the y-axis at (0,0).
We draw the line of the equation x + y = 0
Now we take a point (1, 1) ( any point which does not lie on the line x + y = 0 )
(1, 1) does not satisfy the inequality. So, the region not containing (1, 1)
is represented by the following figure.
Hence, the shaded region represents the in equation.
Q2.
Answer :
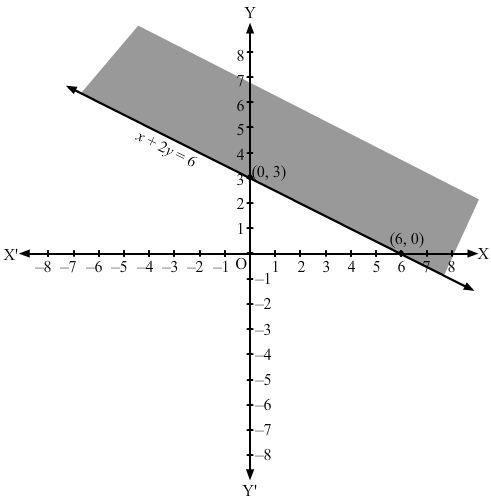
Converting the in equation to equation, we obtain x + 2y = 6, i.e x + 2y – 6 = 0.
Putting y = 0 and x = 0 in this equation, we obtain x = 6 and y = 3.
So, this line meets x-axis at (6,0) and y-axis at (0,3).
We plot these points and join them by a thick line. This divides the xy plane into two parts.
To determine the region represented by the given inequality, consider point O(0,0). Clearly,
(0,0) does not satisfy inequality x+2y≥6.
So, the region that does not contain the origin is represented by the given inequality.
Hence, the shaded region is the solution to the in equation.
Q3.
Answer :
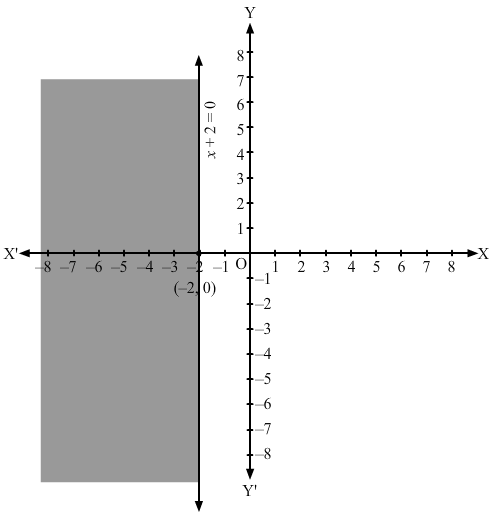
Converting the inequation to equation, we obtain x + 2 = 0, i.e x = -2.
Clearly, it is a parallel line to y-axis at a distance of -2 units from it. This line divides the xy plane into two parts, viz LHS of x = -2 and RHS of x = -2. To determine the region represented by the given inequality, consider point O(0,0). Clearly, (0,0) does not satisfy the inequality. So, the region that does not contain the origin is represented by the given inequality.
Hence, the shaded region is the solution to the inequation.
Q4.
Answer :
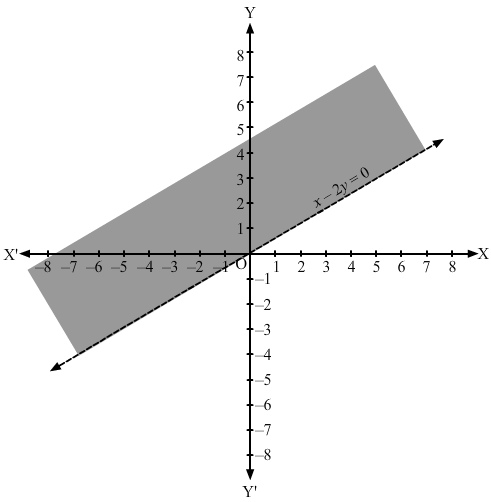
Converting the inequation to equation, we obtain x – 2y = 0
Putting y = 0 and x = 0 in this equation, we obtain x = 0 and y = 0 respectively. So, this line meets the x-axis at (0,0) and the y- axis at (0,0).
If x = 1, then y = 1/2.
So, we have another point (1,1/2).
We plot these points and join them by a thin line. This divides the xy plane into two parts.
We take a point (0, 2) and it does not satisfy the inequation.
Therefore, we shade the region which is opposite to the point (0, 2)
The shaded region is the solution to the inequation.
Q5.
Answer :
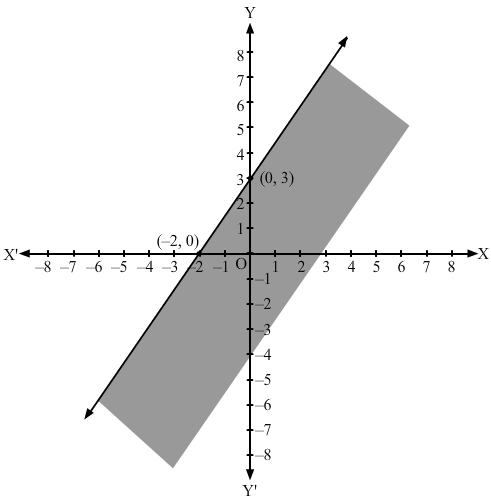
Converting the inequation to equation, we obtain -3x + 2y = 6, i.e -3x + 2y – 6 = 0
Putting y = 0 and x = 0 in this equation, we obtain x = -2 and y = 3 respectively. So, this line meets the x-axis at (-2,0) and the y-axis at (0,3). We plot these points and join them by a thick line.This divides the xy plane in two parts. To determine the region represented by the given inequality, consider point O(0,0). Clearly, (0,0) satisfy the inequality -3x+2y≤6. So, the region containing the origin is represented by the given inequality.
Hence, the shaded region is the solution to the inequation.
Q6.
Answer :
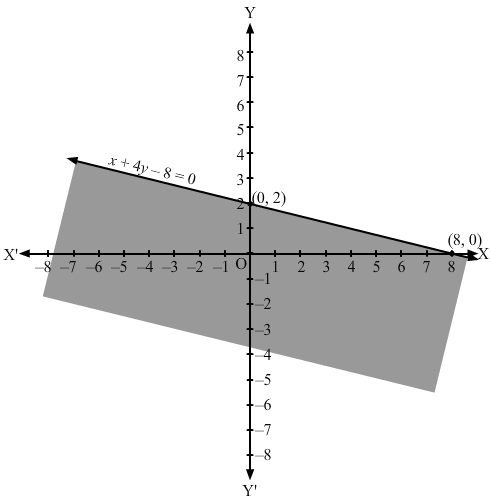
Converting the inequation to equation, we obtain x + 4y – 8 = 0
Putting y = 0 and x = 0 in this equation, we obtain x = 8 and y = 2 respectively. So, this line meets the x-axis at (8,0) and y-axis at (0,2). We plot these points and join them by a thick line. This divides the xy plane into two parts. To determine the region represented by the given inequality, consider point O(0,0). Clearly, (0,0) satisfies the inequality. So, the region containing the origin is represented by the given inequality.
Hence, the shaded region is the solution to the inequation.
Q7.
Answer :
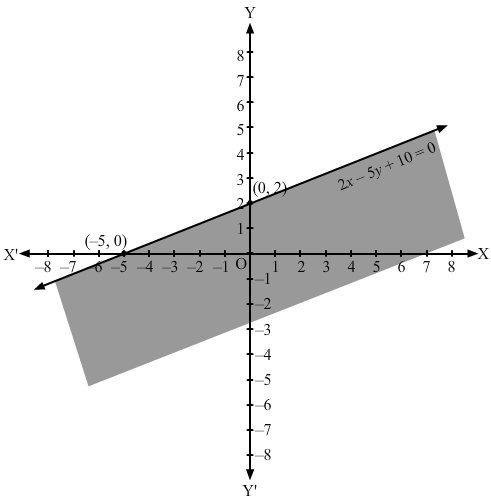
Converting the inequation to equation, we obtain 2x – 5y+10 = 0
Putting y = 0 and x = 0 in this equation, we obtain x = – 5 and y = 2 respectively.
So, this line meets the x-axis at (-5,0) and the y-axis at (0,2).
We plot these points and join them by a thick line.
This divides the xy plane into two parts. To determine the region represented by the given inequality, consider point O(0,0).
Clearly, (0,0) satisfies the inequality.
So, the region containing the origin is represented by the given inequality.
Hence, the shaded region is the solution to the inequation.
Q8.
Answer :
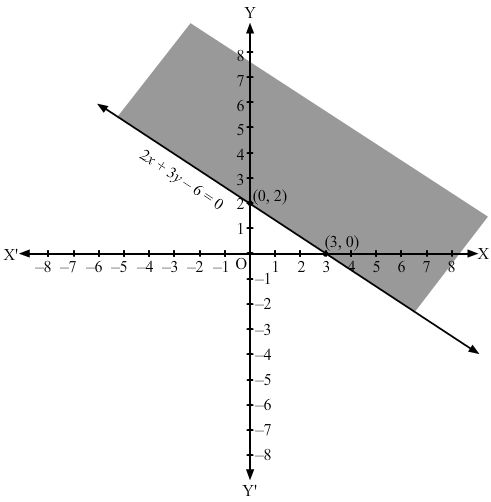
Converting the inequation to equation, we obtain 3y+2x – 6 = 0
Putting y = 0 and x = 0 in this equation, we obtain x = 3 and y = 2 respectively.
So. this line meets the x-axis at (3,0) and y-axis at (0,2).
We plot these points and join them by a thick line.
This divides the xy plane into two parts. To determine the region represented by the given inequality, consider point O(0,0).
Clearly, (0,0) does not satisfy the inequality.
So, the region not containing the origin is represented by the given inequality.
Hence, the shaded region is the solution to the inequation.
Q9.
Answer :
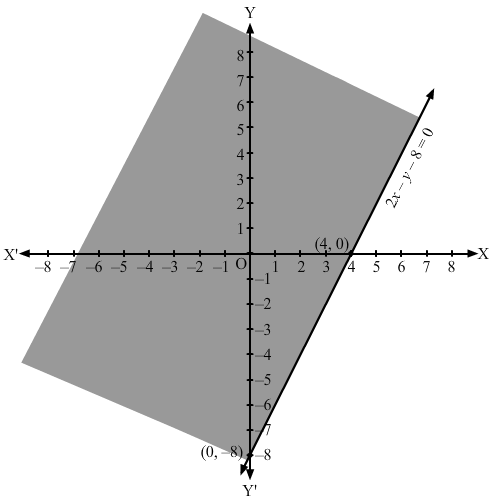
Converting the inequation to equation, we obtain 2x – y – 8 =0
Putting y = 0 and x = 0 in this equation, we obtain x = 4 and y = – 8 respectively.
So, this line meets the x-axis at (4,0) and y-axis at (0, -8).
We plot these points and join them by a thick line.This divides the xy plane into two parts.
To determine the region represented by the given inequality, consider point O(0,0).
Clearly, (0,0) does satisfy the inequality.
So, the region containing the origin is represented by the given inequality.
Hence, the shaded region is the solution to the inequation.
Q10.
Answer :
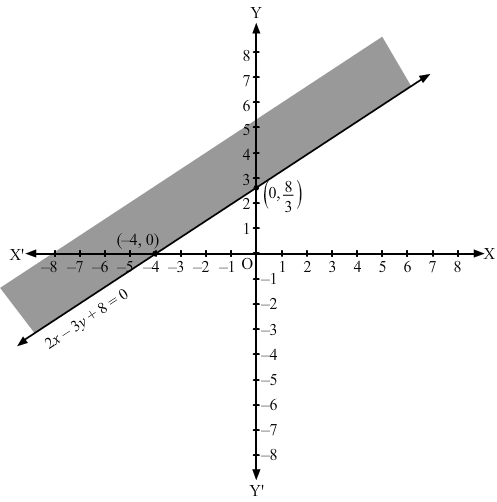
Converting the inequation to equation, we obtain 3x – 2y – x – y + 8 = 0, i.e 2x – 3y + 8= 0
Putting y =0 and x = 0 in this equation, we obtain x = – 4 and y = 8/3 respectively.
So, this line meets the x-axis at (-4, 0) and y-axis at (0,8/3).
We plot these points and join them by a thick line.
This divides the xy plane into two parts.
To determine the region represented by the given inequality, consider point O(0,0).
Clearly, (0,0) does not satisfy the inequality.
So, the region that does not contain the origin is represented by the given inequality.
Hence, the shaded region is the solution to the inequation.
Page 15.34 Ex 15.5
Q1.
Answer :
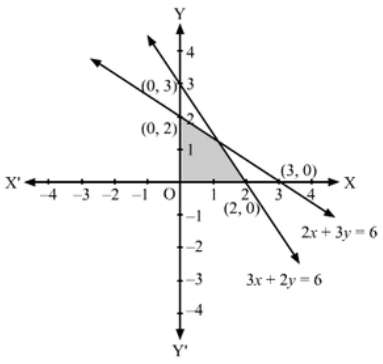
(i) Converting the inequations to equations, we obtain:
2x + 3y = 6, 3x + 2y = 6, x = 0, y = 0
2x + 3y =6: This line meets the x-axis at (3,0) and the y-axis at (0, 2). Draw a thick line joining these points.
We see that the origin (0, 0) satisfies the inequation 2x + 3y ≤ 6
So, the portion containing the origin represents the solution set of the inequation 2x + 3y ≤ 6
3x+2y =6: This line meets the x-axis at (2, 0) and the y-axis at (0, 3). Draw a thick line joining these points.
We see that the origin (0,0) satisfies the inequation 3x + 2y ≤ 6.
So, the portion containing the origin represents the solution set of the inequation 3x + 2y ≤ 6
Clearly, x ≥ 0, y ≥ 0 represents the first quadrant.
Hence. the shaded region in the figure represents the solution set of the given set of inequations.
(ii) Converting the inequations to equations, we obtain:
2x + 3y = 6, x + 4y = 4, x = 0, y = 0
2x + 3y =6: This line meets the x-axis at (3, 0) and the y-axis at (0, 2). Draw a thick line joining these points.
We see that the origin (0,0) satisfies the inequation 2x + 3y ≤ 6.
So, the portion containing the origin represents the solution set of the inequation 2x + 3y ≤ 6
x + 4y = 4: This line meets the x-axis at (4, 0) and the y-axis at (0, 1). Draw a thick line joining these points.
We see that the origin (0,0) satisfies the inequation x + 4y ≤ 4.
So, the portion containing the origin represents the solution set of the inequation x + 4y ≤ 4
Clearly, x ≥ 0, y ≥ 0 represents the first quadrant.
Hence, the shaded region in the figure represents the solution set of the given set of inequations.
(iii) Converting the inequations to equations, we obtain:
x – y=1, x +2y =8, 2x + y = 2, x = 0, y = 0
x – y = 1: This line meets the x-axis at (1, 0) and the y-axis at (0, – 1). Draw a thick line joining these points.
We see that the origin (0, 0) satisfies the inequation x – y ≤ 1 So, the portion containing the origin represents the solution set of the inequation x – y ≤ 1
x + 2y =8: This line meets the x-axis at (8, 0) and the y-axis at (0, 4). Draw a thick line joining these points.
We see that the origin (0, 0) satisfies the inequation x + 2y ≤ 8 So, the portion containing the origin represents the solution set of the inequation x + 2y ≤ 8
2x + y =2: This line meets the x-axis at (1, 0) and the y-axis at (0, 2). Draw a thick line joining these points.
We see that the origin (0, 0) does not satisfy the inequation 2x + y ≥2 So, the portion that does not contain the origin represents the solution set of the inequation 2x + y ≥2
Clearly, x ≥ 0, y ≥ 0 represents the first quadrant.
Hence, the shaded region in the figure represents the solution set of the given set of inequations.
(iv) Converting the inequations to equations, we obtain:
x + y =1, 7x + 9y = 63, x = 6, y = 5
x + y=1: This line meets the x-axis at (1, 0) and the y-axis at (0, 1). Draw a thick line joining these points.
We see that the origin (0, 0) does not satisfy the inequation x + y ≥1 So, the portion not containing the origin represents the solution set of the inequation x + y ≥1
7x + 9y =63: This line meets the x-axis at (9, 0) and the y-axis at (0, 7). Draw a thick line joining these points.
We see that the origin (0, 0) satisfies the inequation 7x + 9y ≤ 63 So, the portion containing the origin represents the solution set of the inequation 7x + 9y ≤ 63
x = 6: This line is parallel to the x-axis at a distance 6 units from it.
We see that the origin (0, 0) satisfies the inequation x ≤ 6 So, the portion containing the origin represents the solution set of the inequation x ≤ 6
y = 5: This line is parallel to the y-axis at a distance 5 units from it.
We see that the origin (0,0) satisfies the inequation y ≤ 5 So, the portion containing the origin represents the solution set of the inequation
y ≤ 5
Clearly, x ≥ 0, y ≥ 0 represents the first quadrant.
Hence, the shaded region in the figure represents the solution set of the given set of inequations.
(v) Converting the inequations to equations, we obtain:
2x + 3y = 35, x = 0, y = 0
2x + 3y = 35: This line meets the x-axis at (17.5, 0) and the y-axis at (0, 35/3). Draw a thick line joining these points.
We see that the origin (0, 0) satisfies the inequation 2x + 3y ≤ 35 So, the portion containing the origin represents the solution set of the inequation 2x + 3y ≤ 35
x = 2: This line is parallel to the x-axis at a distance 2 units from it.
We see that the origin (0, 0) does not satisfy the inequation x ≥2 So, the portion that does not contain the origin represents the solution set of the inequation x ≥2
y = 3: This line is parallel to the y-axis at a distance 3 units from it.
We see that the origin (0, 0) does not satisfies the inequation y ≥ 3 So, the portion opposite to the origin represents the solution set of the inequation y ≥ 3
Clearly, x ≥ 0, y ≥ 0 represents the first quadrant.
Hence, the shaded region in the figure represents the solution set of the given set of inequations.
Q2.
Answer :
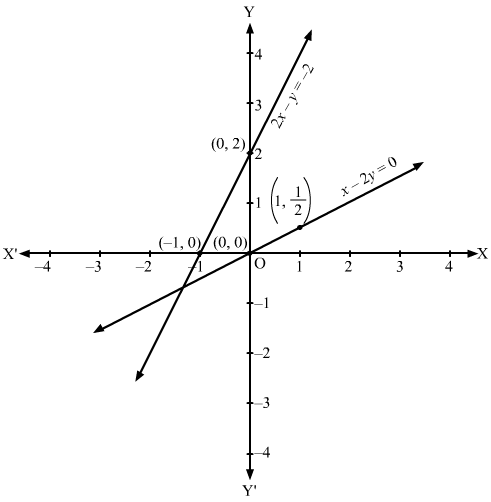
(i) Converting the inequations to equations, we obtain:
x – 2y = 0, 2x – y = -2, x = 0, y = 0
x – 2y = 0: This line meets the x-axis at (0, 0) and y-axis at (0, 0). If x = 1, then y = 1/2,
so we have another point (1, 1/2). Draw a thick line through (0, 0) and (1, 1/2).
We see that the origin (1, 0) satisfies the inequation x + 2y ≤ 3 So, the portion containing the (1, 0) represents the solution set of the inequation x – 2y ≤ 0
2x – y = -2: This line meets the x-axis at (-1, 0) and y-axis at (0, 2). Draw a thick line joining these points.
We see that the origin (0, 0) does not satisfy the inequation 2x – y ≤-2 So, the portion not containing the origin represents the solution set of the inequation 2x – y ≤ -2
Clearly, x ≥ 0, y ≥ 0 represents the first quadrant.
We see in the figure that there is no common region in all the lines. Hence, the solution set to the given set of inequations is empty.
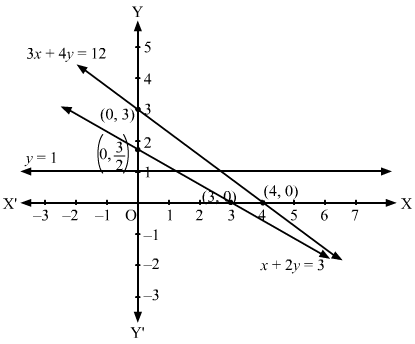
(ii) Converting the inequations to equations, we obtain:
x + 2y = 3, 3x + 4y =12, y = 1
x + 2y = 3: This line meets the x-axis at (3, 0) and y-axis at (0, 3/2). Draw a thick line joining these points.
We see that the origin (0, 0) satisfies the inequation x + 2y ≤ 3. So, the portion containing the origin represents the solution set of the inequation x + 2y ≤ 3
3x + 4y =12: This line meets the x-axis at (4, 0) and y-axis at (0, 3). Draw a thick line joining these points.
We see that the origin (0, 0) does not satisfy the inequation 3x + 4y ≥12 So, the portion not containing the origin represents the solution set of the inequation 3x + 4y ≥ 12
y = 1: This line is parallel to x-axis at a distance of 1 unit from it.
We see that the origin (0, 0) does not satisfy the inequation y ≥ 1 So, the portion not containing the origin represents the solution set of the inequation y ≥ 1
Clearly, x ≥ 0, y ≥ 0 represents the first quadrant.
We see in the figure that there is no common region in all the lines. Hence, the solution set to the given set of inequations is empty.
Q3.
Answer :
Considering the line 2x + 3y = 6, we find that the shaded region and the origin (0, 0) are on the opposite side of this line and (0, 0) does not satisfy the inequation 2x + 3y ≥ 6 So, the first inequation is 2x + 3y ≥ 6
Considering the line 4x + 6y = 24, we find that the shaded region and the origin (0, 0) are on the same side of this line and (0, 0) satisfies the inequation 4x + 6y ≤ 24 So, the corresponding inequation is 4x + 6y ≤ 24
Considering the line x – 2y = 2, we find that the shaded region and the origin (0, 0) are on the same side of this line and (0, 0) satisfies the inequation x – 2y ≤ 2 So, the corresponding inequation is x – 2y ≤ 2
Considering the line -3x + 2y = 3, we find that the shaded region and the origin (0, 0) are on the same side of this line and (0, 0) satisfies the inequation -3x + 2y ≤ 3 So, the corresponding inequation is -3x + 2y ≤ 3
Also, the shaded region is in the first quadrant. Therefore, we must have x ≥0 and y≥0
Thus, the linear inequations comprising the given solution set are given below:
2x + 3y ≥ 6, 4x + 6y ≤ 24, x – 2y ≤ 2, -3x + 2y ≤ 3, x≥0 and y≥0
Page 15.35 Ex 15.5
Q4.
Answer :
Considering the line x + y = 4, we find that the shaded region and the origin (0, 0) are on the same side of this line and (0, 0) does not satisfy the inequation x + y ≤ 4 So, the first inequation is x + y ≤ 4
Considering the line y = 3, we find that the shaded region and the origin (0, 0) are on the same side of this line and (0, 0) satisfies the inequation y ≤ 3 So, the corresponding inequation is y ≤ 3
Considering the line x = 3, we find that the shaded region and the origin (0, 0) are on the same side of this line and (0, 0) satisfies the inequation x ≤ 3 So, the corresponding inequation is x ≤ 3
Considering the line x + 5y = 4, we find that the shaded region and the origin (0, 0) are on the opposite side of this line and (0, 0) does not satisfy the inequation x + 5y ≥4 So, the corresponding inequation is x + 5y ≥4
Considering the line 6x + 2y = 8, we find that the shaded region and the origin (0, 0) are on the opposite side of this line and (0, 0) does not satisfy the inequation 6x + 2y ≥8 So, the corresponding inequation is 6x + 2y ≥8
Also the shaded region is in the first quadrant. Therefore, we must have x ≥ 0 and y ≥ 0
Thus, the linear inequations comprising the given solution set are given below:
x + y ≤ 4, y ≤ 3, x ≤ 3, x + 5y ≥4, 6x + 2y ≥8, x ≥ 0 and y ≥ 0
Q5.
Answer :
Converting the inequations to equations, we obtain:
x + y = 9, 3x + y = 12 , x = 0, y = 0
x + y = 9: This line meets the x-axis at (9, 0) and y-axis at (0, 9). Draw a thick line through these points.
Now, we see that the origin (0, 0) does not satisfy the inequation x + y ≥ 9 Therefore, the potion that does not contain the origin is the solution set to the inequaltion x + y ≥ 9
3x + y = 12: This line meets the x-axis at (4, 0) and y-axis at (0, 12). Draw a thick line through these points.
Now, we see that the origin (0, 0) does not satisfy the inequation 3x + y ≥12. Therefore, the potion that does not contain the origin is the solution set to the inequaltion 3x + y ≥12.
Also, x ≥ 0, y ≥ 0 represents the first quadrant. Hence, the solution set lies in the first quadrant.
We see that in this solution set, the shaded region is unbounded (infinite). Hence, the solution set to the given set of inequalities is an unbounded set.
Q6.
Answer :
(i) Converting the inequations to equations, we obtain:
2x + y = 8, x + 2y = 8, x + y = 6
2x + y = 8: This line meets the x-axis at (4, 0) and y-axis at (0, 8). Draw a thick line through these points.
Now, we see that the origin (0, 0) does not satisfy the inequation 2x + y ≥ 8.
Therefore, the region that does not contain the origin is the solution of the inequality 2x + y ≥8
x + 2y = 8: This line meets the x-axis at (8, 0) and y-axis at (0, 4). Draw a thick line through these points.
Now, we see that the origin (0, 0) does not satisfy the inequation x + 2y ≥ 8
Therefore, the region that does not contain the origin is the solution of the inequality x + 2y ≥ 8
x + y = 6: This line meets the x-axis at (6, 0) and y-axis at (0, 6). Draw a thick line through these points.
Now, we see that the origin (0, 0) satisfies the inequation x + y ≤6 Therefore, the region containing the origin is the solution of the inequality x + y ≤6
Hence, the solution to the inequalities is the intersection of the above three solutions. Thus, the shaded region represents the solution set of the given set of inequalities.
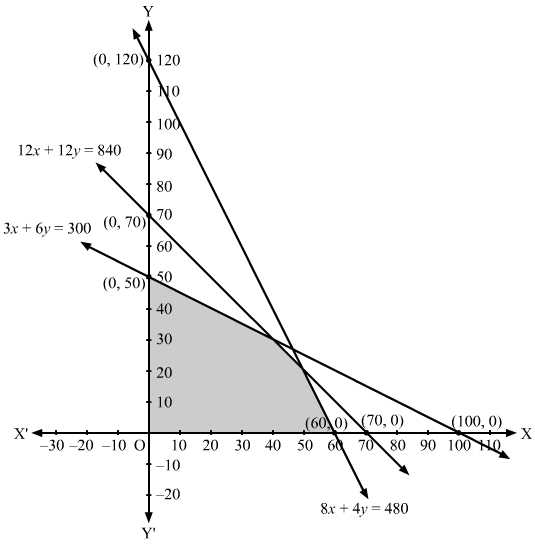
(ii) Converting the inequations to equations, we obtain:
12x + 12y = 840, 3x + 6y = 300, 8x + 4y = 480, x = 0, y = 0
12x + 12y = 840: This line meets the x-axis at (70, 0) and y-axis at (0, 70). Draw a thick line through these points.
Now, we see that the origin (0, 0) satisfies the inequation 12x + 12y ≤ 840
Therefore the region containing the origin is the solution of the inequality 12x + 12y ≤ 840
3x + 6y =300: This line meets the x-axis at (100, 0) and y-axis at (0, 50). Draw a thick line through these points.
Now, we see that the origin (0, 0) satisfies the inequation 3x + 6y ≤300
Therefore, the region containing the origin is the solution of the inequality 3x + 6y ≤300
8x + 4y = 480: This line meets the x-axis at (60, 0) and y-axis at (0, 120). Draw a thick line through these points.
Now, we see that the origin (0, 0) satisfies the inequation 8x + 4y ≤ 480 Therefore, the region containing the origin is the solution of the inequality 8x + 4y ≤ 480
Also, x ≥ 0, y ≥ 0 represens the first quadrant. So, the solution set must lie in the first quadrant.
Hence, the solution to the inequalities is the intersection of the above three solutions. Thus, the shaded region represents the solution set of the given set of inequalities.
(iii) Converting the inequations to equations, we obtain:
x + 2y = 40, 3x + y = 30, 4x + 3y = 60
x + 2y = 40: This line meets the x-axis at (40, 0) and y-axis at (0, 20). Draw a thick line through these points.
We see that the origin (0,0) satisfies the inequation x + 2y ≤ 40
Therefore, the region containing the origin is the solution of the inequality x + 2y ≤ 40
3x + y = 30: This line meets the x-axis at (10, 0) and y-axis at (0, 30). Draw a thick line through these points.
We see that the origin (0, 0) does not satisfy the inequation 3x + y ≥ 30
Therefore, the region that does not contain the origin is the solution of the inequality 3x + y ≥ 30
4x + 3y = 60: This line meets the x-axis at (15, 0) and y-axis at (0, 20). Draw a thick line through these points.
We see that the origin (0, 0) does not satisfy the inequation 4x + 3y ≥ 60 Therefore, the region that does not contain the origin is the solution of the inequality 4x + 3y ≥ 60
Also, x ≥ 0, y ≥ 0 represents the first quadrant. So, the solution set must be in the first quadrant.
Hence, the solution to the inequalities is the intersection of the above three solutions. Thus, the shaded region represents the solution set of the given set of inequalities.
(iv) Converting the inequations to equations, we obtain:
5x + y = 10, 2x + 2y = 12, x + 4y = 12
5x + y =10: This line meets the x-axis at (2, 0) and y-axis at (0, 10). Draw a thick line through these points.
We see that the origin (0, 0) does not satisfy the inequation 5x + y ≥ 10
Therefore, the region that does not contain the origin is the solution of the inequality 5x + y ≥10
2x + 2y = 12: This line meets the x-axis at (6, 0) and y-axis at (0, 6). Draw a thick line through these points.
We see that the origin (0, 0) does not satisfy the inequation 2x + 2y ≥ 12
Therefore, the region that does not contain the origin is the solution of the inequality 2x + 2y ≥ 12
x + 4y = 12: This line meets the x-axis at (12, 0) and y-axis at (0, 3). Draw a thick line through these points.
We see that the origin (0, 0) does not satisfy the inequation x + 4y ≥ 12
Therefore, the region that does not contain the origin is the solution of the inequality
x + 4y ≥ 12
Also, x ≥ 0, y ≥ 0 represents the first quadrant. So, the solution set must be in the first quadrant.
Hence, the solution to the inequalities is the intersection of the above three solutions. Thus, the shaded region represents the solution set of the given set of inequalities.
Here, the solution set is unbounded region.
Page 15.35 (Very Short Answers)
Q1.
Answer :
We have,x2x-2>0Equating both the numerator and the denominator with zero, we obtain x=0 and x=2 as critical points.Plotting these points on the real line, we see that the real line is divided into three regions.
Therefore, the solution set of the given inequality is x∈(2,∞).
Q2.
Answer :
We have,x+1x≥2⇒x2+1x≥2⇒x2+1x-2≥0⇒x2-2x+1x≥0⇒(x-1)2x≥0⇒Either (x-1)2≥0 and x > 0 or (x-1)2<0 and x<0.But, (x-1)2 is always greater than zero. ∴(x-1)2≥0 and x > 0⇒x > 0⇒x∈0, ∞
Q3.
Answer :
We have:Therefore, the solution of the given inequality is x∈(2,∞)
x2-2x+1x-4<0⇒(x-1)2(x-4)<0Equating each one to zero, we obtain x=1 and x= 4.Therefore, 1 and 4 are critical points.Drawing the number lines, we get:
Therefore, the solution set of the given inequality is x∈-∞, 1∪1, 4herefore, the solution of the given inequality is x∈(2,∞)
Q4.
Answer :
We have,2-x=x-2Now 2 cases arise.CASE 1: When 2-x≥0, then 2-x=2-x⇒2-x=x-2⇒2-x=x-2⇒2x=4⇒x=2So, this condition is satisfied when x =2.CASE 2: When 2-x<0 i.e. when x>2, then 2-x=-(2-x)⇒2-x=x-2⇒-(2-x)=x-2⇒-2+x=x-2⇒ -2=-2So, this condition is satisfied when x>2Hence, from the given two cases, the solution set of the given equation is [2,∞)
Q5.
Answer :
We have,x-1≤3 and x-1≥1We know:x-a≤r⇒a-r≤x≤a+rAnd, x-a≥r⇒x≤a-r or x≥a+r∴ 1-3≤x≤1+3 and x≤1-1 or x≥1+1⇒-2≤x≤4 and x≤0 or x≥2⇒x∈[-2,4] and x∈(-∞,0] ∪[2,∞)⇒x∈-2, 0 U 2, 4
Q6.
Answer :
We have:1x-2>4Here, two cases arise.CASE 1: When 1x-2>0, then 1x-2=1x-2∴ 1x-2>4⇒ 1x-2-4>0⇒1x>6⇒x∈0, 16 …(i)CASE 2: When 1x-2<0, then 1x-2=-1x-2∴ -1x+2>4⇒-1x>2⇒1x<-2⇒x∈-∞,-12 …(ii)Hence, the solution set of the given in equation is the union of (i) and (ii).∴ x∈-∞,-12∪0, 16
Q7.
Answer :
We have, x+2×2+1>12⇒x+2×2+1-12>0⇒2x+2-x2+12×2+1>0⇒2x+4-x2-12×2+1>0⇒-x2+2x+32×2+1>0To make the fraction of the left side positive, either the numerator or the denominator should be positive or both should be negative.Since, it is clear that the denominator is positive, the numerator must be positive.-x2+2x+3>0⇒x2-2x-3<0⇒x-3x+1<0Now, to make the left side negative, one of these i.e. (x-3) or (x+1) should be positive and the other should be negative.Also, x+1>x-3∴ x+1>0 and x-3<0⇒x>-1 and x<3⇒x∈-1, 3 The integral solution of x is 0, 1, 2.Hence, there are 3 integral solutions of the given inequation.
Page 15.36 (Very Short Answers)
Q8.
Answer :
We have,5x+2<3x+8 and x+2x-1<4⇒2x<6 and x+2x-1-4<0⇒x<3 and x+2-4x+4x-1<0⇒x∈(-∞,3) and -3x+6x-1<0⇒x∈(-∞,3) and -x+2x-1<0For -x+2x-1<0, critical points are 1 and 2.⇒x∈(2,∞)∪ (-∞,1)∴ x∈(-∞,1)∪(2,3)
Q9.
Answer :
We have:x+1x>2⇒x+1x-2>0CASE 1: When x+1x>0, then x+1x=x+1xNow, x+1x-2>0⇒x+1x-2>0⇒x2+1-2xx>0⇒(x-1)2x>0⇒x>0 and x≠ 1⇒x∈(0,1)U(1,∞) …iCASE 2: When x+1x<0, then x+1x=-(x+1x)Now, x+1x-2>0⇒-x-1x-2>0⇒-x2-1-2xx>0⇒x2+1+2xx<0 Multiplying both sides by -1⇒(x+1)2x<0⇒x<0 and x≠-1⇒x∈(-∞,-1)U(-1, 0) …iiThus, the solution set of the given inequation is the union of i and ii (0,1)U(1,∞ )∪(-∞,-1)U(-1, 0)=R–1, 0, 1∴ x∈R–1, 0,
Q10.
Answer :
We have:x-1≥x-3⇒x-1-x-3≥0The LHS of the inequation has two seperate modulus. Equating these to zero, we obtain x=1,3 as critical points.These points divide the real line in three regions, i.e (-∞,1], [1,3], [3,∞).CASE 1: When -∞<x≤1, then x-1=-(x-1) and x-3=-(x-3)∴ x-1-x-3≥0⇒-(x-1)–(x-3)≥0⇒-x+1+x-3≥0⇒-2≥0But this is not possible.CASE 2: When 1≤x≤3, then x-1=x-1and x-3 =-(x-3)∴ x-1-x-3≥0⇒x-1+x-3≥0⇒⇒2x≥4⇒x≥2⇒x∈[2,∞)CASE 3: When 3≤x<∞, then x-1=x-1 and x-3 =x-3∴ x-1-x-3≥0⇒x-1-x+3≥0 ⇒2≥0This is true.Hence, the solution to the given inequality comes from cases 2 and 3.[2,∞)U [3,∞)= [2,∞)∴ x∈[2,∞)
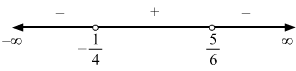






















Leave a Reply