Page 24.16 Ex 24.1
Q1.
Answer :
Let (h, k) be the centre of a circle with radius a.
Thus, its equation will be x-h2+y-k2=a2.
(i) Here, h = −2, k = 3 and a = 4
∴ Required equation of the circle:
x+22+y-32=42
⇒x+22+y-32=16
(ii) Here, h = a, k = b and radius = a2+b2
∴ Required equation of the circle:
x-a2+y-b2=a2+b2
⇒x2+y2-2ax-2by=0
(iii) Here, h = 0, k = −1 and radius = 1
∴ Required equation of the circle:
x-02+y+12=12
⇒x2+y2+2y=0
(iv) Here, h = acosα, k = asinα and radius = a
∴ Required equation of the circle:
x-acosα2+y-asinα2=a2
⇒x2+a2cos2α-2axcosα+y2+a2sin2α-2aysinα=a2⇒x2+a2sin2α+cos2α-2axcosα+y2-2aysinα=a2⇒x2+a2-2axcosα+y2-2aysinα=a2⇒x2+y2-2axcosα-2aysinα=0
(v) Here, h = a, k = a and radius = 2a
∴ Required equation of the circle:
x-a2+y-a2=2a2
⇒x2+a2-2ax+y2+a2-2ay=2a2⇒x2+y2-2ay-2ax=0
Q2.
Answer :
Let (h, k) be the centre of a circle with radius a.
Thus, its equation will be x-h2+y-k2=a2.
(i) Given:
(x − 1)2 + y2 = 4
Here, h = 1, k = 0 and a = 2
Thus, the centre is (1, 0) and the radius is 2.
(ii) Given:
(x + 5)2 + (y + 1)2 = 9
Here, h = −5, k = −1 and radius = 3
Thus, the centre is (−5, −1) and the radius is 3.
(iii) Given:
x2+y2-4x+6y=5
The given equation can be rewritten as follows:
x-22+y+32-4-9=5
⇒x-22+y+32=18
Thus, the centre is (2, −3).
And, radius = 18=32
(iv) Given:
x2+y2-x+2y-3=0
The given equation can be rewritten as follows:
x-122+y+12-14-1-3=0
⇒x-122+y+12=174
Thus, the centre is 12,-1 and and the radius is 172.
Q3.
Answer :
Let (h, k) be the centre of a circle with radius a.
Thus, its equation will be x-h2+y-k2=a2.
Given:
h = 1, k = 2
∴ Equation of the circle = x-12+y-22=a2 …(1)
Also, equation (1) passes through (4, 6).
∴ 4-12+6-22=a2
⇒9+16=a2⇒a=5 ∵a>0
Substituting the value of a in equation (1):
x-12+y-22=25
⇒x2+1-2x+y2+4-4y=25⇒x2-2x+y2-4y=20⇒x2+y2-2x-4y-20=0
Thus, the required equation of the circle is x2+y2-2x-4y-20=0.
Q4.
Answer :
The point of intersection of the lines x + 3y = 0 and 2x − 7y = 0 is (0, 0).
Let (h, k) be the centre of a circle with radius a.
Thus, its equation will be x-h2+y-k2=a2.
The point of intersection of the lines x + y + 1 = 0 and x − 2y + 4 = 0 is (−2, 1).
∴ h = −2, k = 1
∴ Equation of the required circle = x+22+y-12=a2 …(1)
Also, equation (1) passes through (0, 0).
∴ 0+22+0-12=a2
⇒4+1=a2⇒a=5 ∵a>0
Substituting the value of a in equation (1):
x+22+y-12=5
⇒x2+4+4x+y2+1-2y=5⇒x2+4x+y2-2y=0
Hence, the required equation of the circle is x2+y2+4x-2y=0.
Q5.
Answer :
Let (h, k) be the centre of a circle with radius a.
Thus, its equation will be x-h2+y-k2=a2.
The centre of the required circle lies on the positive direction of the y-axis at a distance 6 from the origin.
Thus, the coordinates of the centre are (0, 6).
∴ h = 0, k = 6
∴ Equation of the circle = x-02+y-62=a2 …(1)
Also, a = 4
Substituting the value of a in equation (1):
x-02+y-62=16
⇒x2+y2+36-12y=16⇒x2+y2-12y+20=0
Hence, the required equation of the circle is x2+y2-12y+20=0.
Q6.
Answer :
Let (h, k) be the centre of a circle with radius a.
Thus, its equation will be x-h2+y-k2=a2.
The intersection point of 2x + y = 6 and 3x + 2y = 4 is (8, −10).
The diameters of a circle intersect at the centre.
Thus, the coordinates of the centre are (8, −10).
∴ h = 8, k = −10
Thus, the equation of the required circle is x-82+y+102=a2 …(1)
Also, a = 10
Substituting the value of a in equation (1):
x-82+y+102=100
⇒x2+y2-16x+64+100+20y=100⇒x2+y2-16x+20y+64=0
Hence, the required equation of the circle is x2+y2-16x+20y+64=0.
Q7.
Answer :
Let (h, k) be the centre of a circle with radius a.
Thus, its equation will be x-h2+y-k2=a2.
(i) Let the required equation of the circle be x-h2+y-k2=a2.
It is given that the circle passes through the points (6, 0) and (0, 6).
∴ 6-h2+0-k2=62
And, 0-h2+6-k2=62
⇒6-h2+-k2=36⇒36+h2-12h+k2=36⇒h2+k2=12h …(1)
Also, h2+36+k2-12k=36
⇒h2+k2=12k …(2)
From (1) and (2), we get:
12k=12h⇒h=k
∴ From equation (2), we have:
k2+k2=12k⇒k2-6k=0⇒kk-6=0⇒k=6 ∵k>0
Consequently, we get:
h = 6
Hence, the required equation of the circle is x-62+y-62=36 or x2+y2-12x-12y+36=0.
(ii) Let the required equation of the circle be x-h2+y-k2=a2 .
It is given that the circle with radius 6 units touches the x-axis at a distance of 5 units from the origin.
∴ a = 6, h = 5
Hence, the required equation is x-52+y-02=62 or x2+y2-10x-11=0.
(iii) Let the required equation of the circle be x-h2+y-k2=a2.
It is given that the circle touches both the axes.
Thus, the required equation will be x2+y2-2ax-2ay+a2=0.
Also, the circle passes through the point (2, 1).
∴4+1-4a-2a+a2=0
⇒a2-6a+5=0⇒a2-5a-a+5=0⇒a=1,5
Hence, the required equation is x2+y2-2x-2y+1=0 or x2+y2-10x-10y+25=0.
(iv) Let the required equation of the circle be x-h2+y-k2=a2.
Given:
k = −15, a = 17
The circle passes through the point (0, 0).
∴ Equation of the circle:
0-h2+0-152=172
⇒ h=±8
Hence, the required equation of the circle is x-82+y+152=172 or x+82+y+152=172, i.e. x2+y2±16x+30y=0.
Q8.
Answer :
It is given that the centre is at the point (3, 4).
Let the equation of the circle be x-h2+y-k2=a2.
∴ Equation of the required circle = x-32+y-42=a2 …(1)
Also, the circle touches the straight line 5x + 12y − 1 = 0.
∴ a=53+124-152+122=6213⇒a2=53+124-113=3844169
So, from equation (1), we have:
x-32+y-42=3844169
⇒x2+y2-6x-8y=3844169-25
⇒169×2+y2-6x-8y+381=0
Hence, the required equation of the circle is 169×2+y2-6x-8y+381=0.
Q9.
Answer :
If the circle lies in the third quadrant, then its centre will be (−a, −a).
The centre lies on x − 2y = 3.
∴ -a+2a=3⇒a=3
∴ Required equation of the circle = x+32+y+32=9
=x2+y2+6x+6y+9=0
If the circle lies in the fourth quadrant, then its centre will be (a, −a),
∴ a+2a=3⇒a=1
∴ Required equation of the circle = x-12+y+12=1
= x2+y2-2x+2y+1=0
Q10.
Answer :
Let the required equation of the circle be x-h2+y-k2=a2.
The point of intersection of the lines 2x − 3y + 4 = 0 and 3x + 4y − 5 = 0 is -117, 2217.
∴ Centre = -117,2217
Also, the circle passes through the origin.
∴ a2=1172+22172=485289
Hence, the required equation of the circle is x+1172+y-22172=485289.
Q11.
Answer :
It is given that a circle of radius 4 units touches the coordinate axes in the first quadrant.
Centre of the given circle = (4, 4)
The equation of the given circle is x-42+y-42=16.
The images of this circle with respect to the line mirrors x = 0 and y = 0. They have their centres at -4, 4 and 4, -4, respectively.
∴ Required equations of the images = x+42+y-42=16 and x-42+y+42=16
= x2+y2+8x-8y+16=0 and x2+y2-8x+8y+16=0
Q12.
Answer :
Centre of the given circle = 1, 1
Radius of the given circle = 1
This circle is rolled along the positive direction of the x-axis. When it makes one complete roll, its centre moves horizontally through a distance equal to its circumference, i.e 2π.
Thus, the coordinates of the centre of the new circle will be 1+2π, 1.
Hence, the required equation of the circle is x-1-2π2+y-12=1.
Q13.
Answer :
Clearly, the centre of the circle lies on the line 4y = x + 7.
The circle passes through A (−3, 4) and B (5, 4).
The slope of the segment joining A and B is zero.
Therefore, the slope of the perpendicular bisector of AB is not defined.
Hence, the perpendicular bisector of AB will be parallel to the y-axis and will pass through -3+52, 4+42 = 1, 4.
The equation of the perpendicular bisector is x=1.
The intersection point of the perpendicular bisector and 4y = x + 7 is 1, 2.
∴ Centre = 1, 2
Radius = 5-12+4-22=20
Hence, the required equation of the circle is x2+y2-2x-4y-15=0.
Q14.
Answer :
OC is the perpendicular distance from (3, −1) to 2x − 5y + 18 = 0.
∴ OC=23-5-1+184+25=6+5+184+25=29
⇒ Radius = OC2+OB2=29+9=38
∴ Required equation = x-32+y+12=38
= x2+y2-6x+2y=28
Q15.
Answer :
Case I: The centre lies in first quadrant.
Let the required equation be x-h2+y-k2=a2.
Here, AB = 8 units and L (0, 3)
In △CAM:
⇒CA2=CM2+AM2
⇒CA2=32+42⇒CA=5⇒CL=CA=5
∴ Coordinates of the centre = 5, 3
And, radius of the circle = 5
x-52+y-32=25, i.e. x2+y2-10x-6y=-9
Case II: The centre lies in the second quadrant.
Coordinates of the centre = -5, 3
And, radius of the circle= 5
x+52+y-32=25, i.e. x2+y2+10x-6y=-9
Hence, the equation of the required circle is x±52+y-32=25, i.e. x2+y2±10x-6y=-9.
Q16.
Answer :
Let the required equation of the circle be x-h2+y-k2=a2.
The circle passes through the points (0, 3) and (0, −3).
∴ 0-h2+3-k2=a2 …(1)
And, 0-h2+-3-k2=a2 …(2)
Solving (1) and (2), we get:
k=0
Given:
Radius = 5
∴ a2 = 25
So, from equation (2), we have:
h2+9=25⇒h=±4
Hence, the required equation is x±42+y2=25, which can be rewritten as x2±8x+y2-9=0.
Q17.
Answer :
According to question, the centre of the required circle lies on the line x + y − 9 = 0.
Let the coordinates of the centre be t, 9-t.
Let the radius of the circle be a.
Here, a is the distance of the centre from the line 2x − y + 1 = 0.
∴ a=2t-9+t+122+-12=3t-85⇒a2=3t-852 …1
Therefore, the equation of the circle is x-t2+y-9-t2=a2. …(2)
The circle passes through (2, 5).
∴ 2-t2+5-9-t2=a2
⇒2-t2+5-9-t2=3t-852 Using 1⇒52t2-12t+20=9t2+64-48t⇒t-62=0⇒t=6
Substituting t = 6 in (1):
a2=1052
Substituting the values of a2 and t in equation (2), we find the required equation of circle to be x-62+y-32=20.
Page 24.24 Ex 24.2
Q1.
Answer :
(i) The given equation can be rewritten as x2+y2+23x-24y-24=0.
∴ Centre = -3,-4
And, radius = 32+42+24=49=7
(ii) The given equation can be rewritten as x2+y2-3×2+5y2-72=0.
∴ Centre = 34,-54
And, radius = 342+-542+72=34+5616=9016=3104
(iii) The given equation can be rewritten as x2+y2+2xcosθ+2ysinθ-8=0.
∴ Centre = -cosθ,-sinθ
And, radius = -cosθ2+-sinθ2+8=1+8=3
(iv) The given equation can be rewritten as x2+y2-2ax2-2by2=0.
∴ Centre = a2,b2
And, radius = a22+b22=12a2+b2
Q2.
Answer :
(i) Let the required circle be x2+y2+2gx+2fy+c=0. …(1)
It passes through (5, 7), (8, 1) and (1, 3).
Substituting the coordinates of these points in equation (1):
74+10g+14f+c=0 …(2)
65+16g+2f+c=0 …(3)
10+2g+6f+c=0 …(4)
Simplifying (2), (3) and (4):
g=-296, f=-196, c=563
Equation of the required circle:
x2+y2-29×3-19y3+563=0
⇒3×2+y2-29x-19y+56=0
(ii) Let the required circle be x2+y2+2gx+2fy+c=0. …(1)
It passes through (1, 2), (3, −4) and (5, −6).
Substituting the coordinates of these points in equation (1):
5+2g+4f+c=0 …(2)
25+6g-8f+c=0 …(3)
61+10g-12f+c=0 …(4)
Simplifying (2), (3) and (4):
g=-11, f=-2, c=25
The equation of the required circle is x2+y2-22x-4y+25=0.
(iii) Let the required circle be x2+y2+2gx+2fy+c=0. …(1)
It passes through (5, −8), (−2, 9) and (2, 1).
Substituting the coordinates of these points in equation (1):
89+10g-16f+c=0 …(2)
85-4g+18f+c=0 …(3)
5+4g+2f+c=0 …(4)
Simplifying (2), (3) and (4):
g=58, f=24, c=-285
The equation of the required circle is x2+y2+116x+48y-285=0.
(iv) Let the required circle be x2+y2+2gx+2fy+c=0. …(1)
It passes through (0, 0), (−2, 1) and (−3, 2).
Substituting the coordinates of these points in equation (1):
c=0 …(2)
5-4g+2f+c=0 …(3)
13-6g+4f+c=0 …(4)
Simplifying (2), (3) and (4):
g=-32, f=-112, c=0
The equation of the required circle is x2+y2-3x-11y=0.
Q3.
Answer :
Let the required equation of the circle be x2+y2+2gx+2fy+c=0. …(1)
It is given that the circle passes through (3, −2), (−2, 0).
∴ 13+6g-4f+c=0 …(2)
4-4g+c=0 …(3)
The centre lies on the line 2x − y = 3.
∴ -2g+f-3=0 …(4)
Solving (2), (3) and (4):
g=32, f=6, c=2
Hence, the required equation of circle is x2+y2+3x+12y+2=0.
Q4.
Answer :
Let the required equation of the circle be x2+y2+2gx+2fy+c=0. …(1)
It is given that the circle passes through (3, 7), (5, 5).
∴ 58+6g+14f+c=0 …(2)
50+10g+10f+c=0 …(3)
The centre lies on the line x − 4y = 1.
∴ -g+4f-1=0 …(4)
Solving (2), (3) and (4):
g=3, f=1, c=-90
Hence, the required equation of the circle is x2+y2+6x+2y-90=0.
Q5.
Answer :
Let the required equation of the circle be x2+y2+2gx+2fy+c=0. …(1)
It is given that the circle passes through (3, −2), (1, 0), (−1, −2).
∴ 13+6g-4f+c=0 …(2)
1+2g+c=0 …(3)
5-2g-4f+c=0 …(4)
Solving (2), (3) and (4):
g=-1, f=2, c=1
Theerefore, the equation of the circle is x2+y2-2x+4y+1=0. …(5)
We see that the point (1, −4) satisfies the equation (5).
Hence, the points (3, −2), (1, 0), (−1, −2) and (1, −4) are concyclic.
Q6.
Answer :
Let the required equation of the circle be x2+y2+2gx+2fy+c=0. …(1)
It is given that the circle passes through (5, 5), (6, 4), (−2, 4).
∴ 50+10g+10f+c=0 …(2)
52+12g+8f+c=0 …(3)
20-4g+8f+c=0 …(4)
Solving (2), (3) and (4):
g=-2, f=-1, c=20
Thus, the equation of the circle is x2+y2-4x-2y-20=0. …(5)
We see that the point (7, 1) satisfies equation (5).
Hence, the points (5, 5), (6, 4), (−2, 4) and (7, 1) lie on the circle.
Also, centre of the required circle = 2, 1
Radius of the required circle = 4+1+20=5
Q7.
Answer :
In ∆ABC:
(i) Let AB represent the line x + y + 3 = 0. …(1)
Let BC represent the line x − y + 1 = 0. …(2)
Let CA represent the line x = 3. …(3)
Intersection point of (1) and (3) is 3,-6.
Intersection point of (1) and (2) is (−2, −1).
Intersection point of (2) and (3) is (3, 4).
Therefore, the coordinates of A, B and C are 3,-6, (−2, −1) and (3, 4), respectively.
Let the equation of the circumcircle be x2+y2+2gx+2fy+c=0.
It passes through A, B and C.
∴ 45+6g-12f+c=0
5-4g-2f+c=0
25+6g+8f+c=0
∴ g=-3, f=1, c=-15
Hence, the required equation of the circumcircle is x2+y2-6x+2y-15=0.
(ii) In ∆ABC:
Let AB represent the line 2x + y − 3 = 0. …(1)
Let BC represent the line x + y − 1 = 0. …(2)
Let CA represent the line 3x + 2y − 5 = 0. …(3)
Intersection point of (1) and (3) is (1, 1).
Intersection point of (1) and (2) is (2, −1).
Intersection point of (2) and (3) is (3, −2).
The coordinates of A, B and C are (1, 1), (2, −1) and (3, −2), respectively.
Let the equation of the circumcircle be x2+y2+2gx+2fy+c=0.
It passes through A, B and C.
∴ 2+2g+2f+c=0
5+4g-2f+c=0
13+6g-4f+c=0
∴ g=-132, f=-52, c=16
Hence, the required equation of the circumcircle is x2+y2-13x-5y+16=0.
(iii) In ∆ABC:
Let AB represent the line x + y = 2. …(1)
Let BC represent the line 3x − 4y = 6. …(2)
Let CA represent the line x − y = 0. …(3)
Intersection point of (1) and (3) is (1, 1).
Intersection point of (1) and (2) is (2, 0).
Intersection point of (2) and (3) is (−6, −6).
The coordinates of A, B and C are (1, 1), (2, 0) and (−6, −6), respectively.
Let the equation of the circumcircle be x2+y2+2gx+2fy+c=0.
It passes through A, B and C.
∴ 2+2g+2f+c=0
4+4g+c=0
72-12g-12f+c=0
∴ g=2, f=3, c=-12
Hence, the required equation of the circumcircle is x2+y2+4x+6y-12=0.
Q8.
Answer :
The given equations of the circles are as follows:
x2 + y2 − 4x − 6y − 12 = 0, …(1)
x2 + y2 + 2x + 4y − 10 = 0 …(2)
And, x2 + y2 − 10x − 16y − 1 = 0 …(3)
The centre of circle (1) is (2, 3).
The centre of circle (2) is (−1, −2).
The centre of circle (3) is (5, 8).
The area of the triangle formed by the points (2, 3), (−1, −2) and (5, 8) is 122-10-15+55 = 12-25+25 = 0.
Hence, the centres of the circles x2 + y2 − 4x − 6y − 12 = 0, x2 + y2 + 2x + 4y − 10 = 0 and x2 + y2 − 10x − 16y − 1 = 0 are collinear.
Q9.
Answer :
Let the radii of the circles x2 + y2 = 1, x2 + y2 − 2x − 6y − 6 = 0 and x2 + y2 − 4x − 12y − 9 = 0 be r1, r2 and r3, respectively.
∴ r1=1, r2=-12+-32+6=4, r3=-22+-62+9=7
Now, r2-r1=r3-r2=3
∴ r1, r2 and r3 are in A.P.
Q10.
Answer :
According to the question, the circle passes through the origin.
Let the equation of the circle be x2+y2-2hx-2ky=0.
The circle cuts off chords of lengths 4 and 6 on the positive sides of the x-axis and the y-axis, respectively.
∴ Centre = 42, 62=2, 3=h, k
⇒h=2, k=3
∴ Required equation:
x2+y2+2-2x+2-3y=0
⇒x2+y2-4x-6y=0
Q11.
Answer :
Let the equation of the required circle be x2+y2+2gx+2fy+c=0.
The centre of the circle x2 + y2 − 6x + 12y + 15 = 0 is (3, −6).
Area of the required circle = 2πr2
Here, r = radius of the given circle
Now, r = 9+36-15=30
∴ Area of the required circle = 2π30=60π
Let R be the radius of the required circle.
∴ 60π=πR2⇒R2=60
Thus, the equation of the required circle is x-32+y+62=60, i.e. x2+y2-6x+12y=15.
Q12.
Answer :
Let the equation of the required circle be x2+y2+2gx+2fy+c=0.
It passes through (1, 1) and (2, 2).
∴ 2g+2f+c=-2 …(1)
And, 4g+4f+c=-8 …(2)
From (1) and (2), we have:
-2g-2f=6⇒g+f=-3 …(3)
∴ From (2) and (3), we have:
c=4
Also, g2+f2-c=1⇒g2+f2=1+c=5⇒g+f2-2gf=5⇒gf=2
Using (3), we get:
g=-2,-1
Correspondingly, we have:
f=-1,-2
Therefore, the required equations of the circles are x2+y2-4x-2y+4=0 and x2+y2-2x-4y+4=0.
Hence, there are two such circles.
Q13.
Answer :
Since, the circles are concentric.
⇒Centre of required circle = Centre of x2 + y2 − 4x − 6y − 3 = 0
The centre of the required circle is (2, 3).
We know that if a circle with centre (h, k) touches the y-axis, then h is the radius of the circle.
Thus, the radius is 2.
∴ Equation of the circle:
x-22+y-32=22
⇒x2+y2-4x-6y+9=0
Page 24.28 Ex 24.3
Q1.
Answer :
(2, −3) and (−2, 4) are the ends points of the diameter of a circle. The equation of this circle is x-2x+2+y+3y-4=0.
⇒x2-4+y2-4y+3y-12=0⇒x2+y2-y-16=0 …(1)
Equation (1) can be rewritten as
x2+y-122-14-16=0⇒x2+y-122=654
∴ Centre is 0,12 and radius is 652.
Page 24.29 Ex 24.3
Q2.
Answer :
Since the intercept lies on the y-axis, by putting x = 0 in the given equation, we get:
y2-4y-5=0
⇒y=-1, 5
Thus, the length of the intercept on the y-axis is (5 + 1) = 6 units.
Q3.
Answer :
According to the question:
Sides of the square are x = 6, x = 9, y = 3 and y = 6.
The vertices of the square are (6, 6), (9, 6), (9, 3) and (6, 3).
And, the vertices of two diagonals are (6, 6), (9, 3) and (9, 6), (6, 3).
Hence, the equation of the circle is x-6x-9+y-6y-3 or x2+y2-15x-9y+72=0.
Q4.
Answer :
Given:
Sides of the rectangle:
x − 3y = 4 …(1)
3x + y = 22 …(2)
x − 3y = 14 …(3)
And, 3x + y = 62 …(4)
The intersection of (1) and (2) is (7, 1).
The intersection of (2) and (3) is (8, −2).
The intersection of (3) and (4) is (20, 2).
The intersection of (1) and (4) is (19, 5).
Hence, the vertices of the rectangle are (7, −1), (8, −2), (20, 2) and (19, 5).
The vertices of the diagonals are (7, −1), (20, 2) and (19, 5), (8, −2).
Thus, the required equation of the circle is x-7x-20+y-1y-2=0 or x2+y2-27x-3y+142=0.
Q5.
Answer :
Roots of equation x2 + 2ax − b2 = 0 are -a±a2+b2.
Roots of equation x2 + 2px − q2 = 0 are -p±p2+q2.
Therefore, coordinates of A and B are -a+a2+b2, -p+p2+q2 and -a-a2+b2, -p-p2+q2 respectively.
Hence, equation of circle is x+a-a2+b2x+a+a2+b2 + y+p-p2+q2y+p+p2+q2=0.
⇒x+a2-a2-b2+y+p2-p2-q2=0
⇒x2+y2+2ax+2yp-p2-q2=0.
Also, radius of circle is a2+b2+p2+q2.
Q6.
Answer :
Given:
ABCD is a square with side a units.
Let AB and AD represent the x-axis and the y-axis, respectively.
Thus, the coordinates of B and D are (a, 0) and (0, a), respectively.
The end points of the diameter of the circle circumscribing the square are B and D.
Thus, equation of the circle circumscribing the square is x-ax-0+y-0y-a=0 or x2+y2-ax+y=0.
Q7.
Answer :
The equation of the line can be rewritten as x=y-62.
Substituting the value of x in the equation of the circle, we get:
y-622+ y2-2y-9=0
⇒y-62+ 4y2-8y-36=0⇒y2+36-12y+ 4y2-8y-36=0⇒5y2-20y=0⇒y2-4y=0⇒yy-4=0⇒y=0,4
At y = 0, x = −3
At y = 4, x = −1
Therefore, the coordinates of A and B are -1,4 and -3,0.
∴ Equation of the circle with AB as its diameter:
x+1x+3+y-4y-0=0
⇒x2+4x+y2-4y+3=0
Q8.
Answer :
Putting x = 0 in 3x + 4y = 12:
y = 3
Putting y = 0 in 3x + 4y = 12:
x = 4
Thus, the line 3x + 4y = 12 meets the axes of coordinates at points A (0, 3) and B (4, 0).
The equation of the circle with AB as the diameter is x-0x-4+y-3y-0=0 or x2-4x+y2-3y=0.
Hence, the required equation is x2-4x+y2-3y=0.
Q9.
Answer :
The coordinates of A and B are 0,1m and 1l,0, respectively.
Here, the end points of the diameter of the circumcircle are A and B.
∴ Required equation of the circle:
x-0x-1l+y-1my-0=0
⇒x2-xl+y2-ym=0
Q10.
Answer :
Case I:
If the required circle passes through the origin and (a, b), then the end points of the diameter of the circle will be (0, 0) and (a, b).
∴ Required equation of circle:
x-0x-a+y-0y-b
or x2+y2-ax-by=0
Case II:
If the required circle passes through the origin and (−a, −b), then the end points of the diameter of the circle will be (0, 0) and (−a, −b).
∴ Required equation of circle:
x-0x+a+y-0y+b
or x2+y2+ax+by=0
Hence, the equation of the required circle is x2+y2±ax±by=0.
Q11.
Answer :
It is given that the end points of the diameter of the circle are (−4, 3) and (12, −1).
∴ Required equation of circle:
x+4x-12+y-3y+1
or x2+y2-8x-2y-51=0 …(1)
Putting x = 0 in (1):
y2 − 2y − 51 = 0
⇒ y2 − 2y − 51 = 0
⇒ y=1 ± 213
Hence, the intercepts made by it on the y-axis is 1+213-1+213=413.
Q12.
Answer :
Suppose a=2
From the figure, we see that there will be four circles that pass through the origin and cut off equal chords of length a from the straight lines y=±x.
AB, BC, CD and DA are the diameters of the four circles.
Also, C1A=a2=OC1
Thus, the coordinates of A are a2,a2.
In the same way, we can find the coordinates of B, C and D as -a2,a2, -a2,-a2 and a2,-a2, respectively.
The equation of the circle with AD as the diameter is x-a2x-a2+y-a2y+a2=0, which can be rewritten as x2+y2-2ax=0, i.e. x2+y2-2x=0.
Similarly, the equations of the circles with BC, CD and AB as the diameters are x2+y2+2x=0, x2+y2+2y=0 and x2+y2-2y=0, respectively.
Page 24.29 (Very Short Answers)
Q1.
Answer :
Since the intercept lies on the y-axis, by putting x = 0 in the given equation, we get:
y2-4y-5=0
⇒y=-1, 5
Thus, the length of the intercept on the y-axis is (5 + 1) = 6 units.
Page 24.30 (Very Short Answers)
Q2.
Answer :
We need to find the coordinates of the centre of the circle passing through (0, 0), (4, 0) and (0, −6).
Let the equation of the circle be x-h2+y-k2=a2.
Putting x = y = 0:
h2+k2=a2 …(1)
Putting x = 4, y = 0 in the equation of the circle:
4-h2+0-k2=a2⇒16+h2-8h+k2=a2⇒16-8h+a2=a2 From (1)⇒h=2
Putting x = 0, y = −6 in the equation of the circle:
0-h2+-6-k2=a2⇒36+h2+12k+k2=a2⇒36+12k+a2=a2 From (1)⇒k=-3
Hence, the centre of the circle is 2,-3.
Q3.
Answer :
The equation of the required circle is x-12+y-22=a2.
The circle passes through (−2, 6).
∴ -2-12+6-22=a2
⇒9+16=a2⇒a=5
∴ Area of the required circle = πa2=π52=25π square units
Q4.
Answer :
The roots of the equations x2 + 2ax − b2 = 0 and x2 + 2px − q2 = 0 are -a±a2+b2 and -p±p2+q2.
Therefore, the coordinates of P and Q are -a+a2+b2, -p+p2+q2 and -a-a2+b2, -p-p2+q2 , respectively.
So, the required equation of the circle is x+a-a2+b2x+a+a2+b2 + y+p-p2+q2y+p+p2+q2=0.
⇒x+a2-a2-b2+y+p2-p2-q2=0
x2+y2+2ax+2yp-p2-q2=0
Q5.
Answer :
The centre of the circle x2 + y2 − 8x + 4y − 8 = 0 is (4, −2).
The radius of the unit circle is 1.
∴ Required equation of circle:
x-42+y+22=1,
⇒ x2+y2-8x+4y+19=0
Q6.
Answer :
According to the question, we have:
-a22+a-122-5 ≤ 5⇒-a22+a-122 ≤ 30
⇒a2+a-12≤120⇒2a2-2a-119≤0Using quadratic formula: a=2±22-42-11922⇒a=2±9564⇒a=1±15.462⇒a=-7.23, 8.23⇒-7.23≤a≤8.23⇒a=-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8 If a∈ℤ
The number of integral values of a is 16.
Q7.
Answer :
It is given that the circle touches the y-axis at the origin.
Thus, the centre of the circle is (h,0) and its radius is h.
Hence, the equation of the circle is x-h2+y2=h2, i.e. x2+y2-2xh=0.
Also, the circle passes through (3, 4).
∴ 25-6h=0⇒h=256
Hence, the required equation of the circle is x-2562+y2=2562, i.e. 3×2+y2-25x=0.
Q8.
Answer :
Let us put y = mx in the equation (x + 10)2 + (y + 10)2 = 180.
Now, we have:
(x + 10)2 + (mx + 10)2 = 180
On simplifying, we get:
x2m2+1+20xm+1+20=0
∴ Discriminant (D) = 400m+12-80(m2+1)=4102m+1m+2
It is given that the line y = mx does not intersect the circle (x + 10)2 + (y + 10)2 = 180.
∴ D < 0
⇒4102m+1m+2<0⇒m∈-2,-12
Q9.
Answer :
From the figure, we can see that the vertices of the square are (2, 5), (6, 5), (2, 9) and (6, 9).
The vertices of the diagonals are (2, 9), (6, 5) and (2, 5),(6, 9).
∴ Coordinates of the centre = 6+22, 5+92=4, 7
Page 24.30 (Multiple Choice Questions)
Q1.
Answer :
(b) 23,-1
To find the centre:
Coefficient of x2 = Coefficient of y2
∴ λ=2λ-3⇒λ=3
Therefore, the given equation can be rewritten as 3×2+3y2-4x+6y-1=0.
∴ x2+y2-43x+2y-13=0
Thus, the coordinates of the centre is 23,-1.
Q2.
Answer :
(d) none of these
The given equation is 2x2 + λxy + 2y2 + (λ − 4) x + 6y − 5 = 0, which can be rewritten as x2+λxy2+y2+λ-42x+3y-52=0.
Comparing the given equation with x2+y2+2gx+2fy+c=0, we get:
λ=0
∴ x2+y2-2x+3y-52=0
∴ Radius = -12+322+52=1+94+52=234=232
Q3.
Answer :
(a) a point
The radius of the given circle = 12+-22-5=0
Hence, the radius of the given circle is zero, which represents a point.
Q4.
Answer :
(c) (−3, 1)
If the equation (4a − 3) x2 + ay2 + 6x − 2y + 2 = 0 represents a circle, then we have:
Coefficient of x2 = Coefficient of y2
⇒ 4a-3=a
⇒ a = 1
∴ Equation of the circle = x2+y2+6x-2y+2=0
Thus, the coordinates of the centre is -3, 1.
Q5.
Answer :
(a) 32
The equation of the circle is 3x2 + 3y2 + λxy + 9x + (λ − 6) y + 3 = 0.
∴ Coefficient of xy = 0
⇒λ=0
Q6.
Answer :
According to the question:
-λ22+λ-122-5 ≤ 5⇒-λ22+λ-122 ≤ 30
λ2+λ-12≤120⇒2λ2-2λ-119≤0Using quadratic formula:⇒λ=2±22-42-11922⇒λ=2±9564⇒λ=1±2392⇒λ=-7.23, 8.23⇒-7.23 ≤ λ ≤ 8.23⇒λ=-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8 If λ∈ℤ
Thus, the number of integral values of λ is 16.
Page 24.31 (Multiple Choice Questions)
Q7.
Answer :
(a) x2 + y2 − 2x − 4y + 4 = 0
Let the required equation of the circle be x-h2+y-k2=a2.
Comparing the given equation x2 − y2 −2x + 4y − 3 = 0 with ax2+by2+2hxy+2gx+2fy+c=0, we get:
a=1, b=-1, h=0, g=-1, f=2, c=-3
Intersection point = hf-bgab-h2, gh-afab-h2 = -1-1, -2-1=1, 2
Thus, the centre of the circle is 1, 2.
The equation of the required circle is x-12+y-22=a2.
Since circle passes through (1, 1), we have:
1=a2
∴ Equation of the required circle:
x-12+y-22=1
⇒ x2+y2-2x-4y+4=0
Q8.
Answer :
(a) x2 + y2 − 2x − 2y − 3 = 0
The centre of the circumcircle is (1, 1).
Radius of the circumcircle = 1+12+1-22=5
∴ Equation of the circle:
x-12+y-12=5
⇒x2+y2-2x-2y-3=0
Q9.
Answer :
(c) (−∞, −3) ∪ (4, ∞)
The given equations of the circles are x2 + y2 + x − 2y − 14 = 0 and x2 + y2 = 13.
Since (2, k) lies outside the given circles, we have:
4+k2+2-2k-14>0 and 4+k2>13
⇒k2-2k-8>0 and k2>9
⇒k-4k+2>0 and k2>9
⇒k>4 or k3 or k4 and k<-3
⇒k∈-∞,-3∪4,∞
Q10.
Answer :
(a) (−1, 3)
The given equation of the curve is x2+y2=25.
Since (λ, λ + 1) lies inside the region bounded by the curve x2+y2=25 and the y-axis, we have:
λ2+λ+12<25, provided λ+1>0
⇒λ2+λ2+1+2λ<25, λ>-1⇒2λ2+2λ-24<0, λ>-1⇒λ2+λ-12<0, λ>-1⇒λ-3λ+4<0, λ>-1⇒-4<λ<3, λ>-1⇒λ∈-1,3
Q11.
Answer :
(b) 4 (x2 + y2 − x − y) + 1 = 0
The line 4x + 3y = 6 cuts the coordinate axes at 32, 0 and 0, 2.
The coordinates of the incentre is ax1+bx2+cx3a+b+c, ay1+by2+cy3a+b+c.
Here, a=52, b=32, c=2, x1=0, y1=0, x2=0, y2=2, x3=32, y3=0
Thus, the coordinates of the incentre:
0+0+36, 0+3+06=12, 12
The equation of the incircle:
x-122+y-122=a2
Also, radius of the incircle = ss-as-bs-cs
Here, s=a+b+c2=52+32+22=3
∴ Radius of the incircle = 33-a3-b3-c3
=33-523-323-23= 312323= 12
The equation of circle:
x-122+y-122=14
⇒ 4×2+y2-x-y+1=0
Q12.
Answer :
(a) 15
The centre of the circle x2 + y2 = 9 is (0, 0).
Let us denote it by C1.
The centre of the circle x2 + y2+ 8y + c = 0 is (0, −4).
Let us denote it by C2.
The radius of x2 + y2 = 9 is 3 units.
x2 + y2+ 8y + c = 0
⇒ x-02+y+42=16-c = 16-c2
Therefore, the radius of the above circle is 16-c.
Let the circles touch each other at P.
∴ C1C2 = PC2 + PC1
⇒ PC2 = 4 − 3 = 1
⇒ PC2 = 1 = 16-c
⇒ c = 15
Q13.
Answer :
(b) ± 4
The equation of the circle is x2 + y2 + 2ax + 8y + 16 = 0.
Its centre is -a,-4 and its radius is a units.
Since the circle touches the x-axis, we have:
-a+a2+4-02=a
⇒ a=±4
Q14.
Answer :
(c) x2 + y2 ± 10x ± 10y + 25 = 0
Case I: If the circle lies in the first quadrant:
The equation of a circle that touches both the coordinate axes and has radius a is x2+y2-2ax-2ay+a2=0.
The given radius of the circle is 5 units, i.e. a=5.
Thus, the equation of the circle is x2+y2-10x-10y+25=0.
Case II: If the circle lies in the second quadrant:
The equation of a circle that touches both the coordinate axes and has radius a is x2+y2+2ax-2ay+a2=0.
The given radius of the circle is 5 units, i.e. a=5.
Thus, the equation of the circle is x2+y2+10x-10y+25=0.
Case III: If the circle lies in the third quadrant:
The equation of a circle that touches both the coordinate axes and has radius a is x2+y2+2ax+2ay+a2=0.
The given radius of the circle is 5 units, i.e. a=5.
Thus, the equation of the circle is x2+y2+10x+10y+25=0.
Case IV: If the circle lies in the fourth quadrant:
The equation of a circle that touches both the coordinate axes and has radius a is x2+y2-2ax+2ay+a2=0.
The given radius of the circle is 5 units, i.e. a=5.
Thus, the equation of the circle is x2+y2-10x+10y+25=0.
Hence, the required equation of the circle is x2 + y2 ± 10x ± 10y + 25 = 0.
Q15.
Answer :
(d) x2 + y2 − 6x − 8y = 0
The centre of the required circle is 62, 82=3, 4.
The radius of the required circle is 32+42=25=5.
Hence, the equation of the circle is as follows:
x-32+y-42=52
⇒ x2+y2-6x-8y=0
Q16.
Answer :
(b) x2 + y2 − 3x + 4y = 0
The centre of the circle x2 + y2 − 3x + 4y − c = 0 is 32,-2.
Therefore, the centre of the required circle is 32,-2.
The equation of the circle is x-322+y+22=a2. …(1)
Also, circle (1) passes through (−1, −2).
∴ -1-322+-2+22=a2
⇒ a=52
Substituting the value of a in equation (1):
x-322+y+22=522⇒2x-324+y+22=254⇒2x-32+4y+22=25⇒x2+y2-3x+4y=0
Hence, the required equation of the circle is x2+y2-3x+4y=0.
Q17.
Answer :
(a) g2<c
Given:
x2 + y2 + 2gx + 2fy + c = 0 …(1)
The given circle intersects the x-axis.
The equation of circle becomes x2 + 2gx + c = 0. …(2)
Solving equation (2):
∴ Discriminant, D = 4g2-4c≥0
⇒4g2-4c≥0⇒g2-c≥0⇒g2≥c
Hence, if g2<c, then the given circle will not intersect the x-axis.
Page 24.32 (Multiple Choice Questions)
Q18.
Answer :
(a) 22536
Let ABC be the required equilateral triangle.
The equation of the circle is x2 + y2 − 6x − 8y − 25 = 0.
Therefore, coordinates of the centre O is 3, 4.
Radius of the circle = OA = OB = OC = 9+16+25=52
In ∆BOD, we have:
sin60°=DBBO⇒DB=3252⇒BC=2BD=352=56
Now, area of △ABC = 34BC2=34562=31504=3752=32256 square units
Q19.
Answer :
(d) 6
The equation of the circle that touches the axes of coordinates is x2+y2-2cx-2cy+c2=0.
Also, x2+y2-2cx-2cy+c2=0 touches the line x3+y4=1 or 4x + 3y -12 = 0.
Since the circle lies in the first quadrant, it centre is is c, c.
From the figure, we have:
4c+3c-1242+32=c⇒7c-125=c⇒c=6
Q20.
Answer :
(a) 1
x2 + y2 = a …(1)
And, x2 + y2 − 6x − 8y + 9 = 0 …(2)
Let circles (1) and (2) touch each other at point P.
The centre of the circle x2 + y2 = a, O, is (0, 0).
The centre of the circle x2 + y2 − 6x − 8y + 9 = 0, C1, is (3, 4).
Also, radius of circle (1) = a = OP
Radius of circle (2) = 9+16-9=4 = C1P
From figure, we have:
C1O=C1P+OP⇒32+42=4+a⇒5=4+a⇒a=1
Q21.
Answer :
(d) none of these
The end points of the diameter of a circle are (x, 3) and (3, 5).
According to the question, we have:
x+32=2, y=5+32⇒x=1, y=4
Q22.
Answer :
(b) −11
The centre of the circle x2 + y2 + 6x + 8y − 5 = 0 is (−3, −4).
The circle x2 + y2 + 2gx + 2fy + c = 0 is concentric with the circle x2 + y2 + 6x + 8y − 5 = 0.
Thus, the centre of x2 + y2 + 2gx + 2fy + c = 0 is (−3, −4).
∴ g=3, f=4
Also, it is given that (−3, 2) lies on the circle x2 + y2 + 2gx + 2fy + c = 0.
∴ -32+22+23-3+242+c=0
⇒9+4-18+16+c=0⇒c=-11
Q23.
Answer :
(c) 2x + y = 0
Let the diameter of the circle be y = mx.
Since the diameter of the circle passes through its centre, (1, −2) satisfies the equation of the diameter.
∴ m=-2
Substituting the value of m in the equation of diameter:
y=-2x
⇒ 2x+y=0
Hence, the required equation of the diameter is 2x+y=0.
Q24.
Answer :
(b) x2 + y2 − ax − by = 0
Centre of the circle is a2,b2 and its radius is a22+b22=12a2+b2.
Equation of circle:
x-a22+y-b22=14a2+b2
⇒2x-a2+2y-b2=a2+b2
⇒4×2+a2-4ax+4y2+b2-4by=a2+b2
⇒x2-ax+y2-by=0
Q25.
Answer :
(a) 1a2+1b2=1c
Given:
x2 + y2 + 2ax + c = 0 …(1)
And, x2 + y2 + 2by + c = 0 …(2)
For circle (1), we have:
Centre = -a,0 = C1
For circle (2), we have:
Centre = 0,-b = C2
Let the circles intersect at point P.
∴ Coordinates of P = Mid point of C1C2
⇒ Coordinates of P = -a+02,0-b2=-a2,-b2
Now, we have:
PC1=radius of 1⇒-a+a22+0-b22=a2-c⇒a42+b42=a2-c …3
Also, radius of circle 1 = radius of circle 2⇒a2-c=b2-c⇒a2=b2 …4
From (3) and (4), we have:
a22=a2-c⇒a22=c⇒2a2=1c⇒1a2+1a2=1c⇒1a2+1b2=1c
Page 25.21 Ex 25.1
Q1.
Answer :
(i) Let P (x, y) be any point on the parabola whose focus is S (3, 0) and the directrix is 3x + 4y = 1.
Draw PM perpendicular to 3x + 4y = 1.
Then, we have:
SP=PM⇒SP2=PM2⇒x-32+y-02=3x+4y-19+162⇒x-32+y2=3x+4y-152⇒25x-32+y2=3x+4y-12⇒25×2-150x+25y2+225=9×2+16y2+1+24xy-8y-6x⇒16×2+9y2-24xy-144x+8y+224=0
(ii) Let P (x, y) be any point on the parabola whose focus is S (1, 1) and the directrix is x + y + 1 = 0.
Draw PM perpendicular to x + y + 1 = 0.
Then, we have:
SP=PM⇒SP2=PM2⇒x-12+y-12=x+y+11+12⇒x-12+y-12=x+y+122⇒2×2+1-2x+y2+1-2y=x2+y2+1+2xy+2y+2x⇒2×2+2-4x+2y2+2-4y=x2+y2+1+2xy+2y+2x⇒x2+y2-2xy-6x-6y+3=0
(iii) Let P (x, y) be any point on the parabola whose focus is S (0, 0) and the directrix is 2x − y − 1 = 0.
Draw PM perpendicular to 2x − y − 1 = 0.
Then, we have:
SP=PM⇒SP2=PM2⇒x-02+y-02=2x-y-14+12⇒x2+y2=2x-y-152⇒5×2+5y2=4×2+y2+1-4xy+2y-4x⇒x2+4y2+4xy-2y+4x-1=0
(iv) Let P (x, y) be any point on the parabola whose focus is S (2, 3) and the directrix is x − 4y + 3 = 0.
Draw PM perpendicular to x − 4y + 3 = 0.
Then, we have:
SP=PM⇒SP2=PM2⇒x-22+y-32=x-4y+31+162⇒x-22+y-32=x-4y+3172⇒17×2+4-4x+y2-6y+9=x2+16y2+9-8xy-24y+6x⇒17×2-68x-102y+17y2+13×17=x2+16y2+9-8xy-24y+6x⇒16×2+y2+8xy-74x-78y+212=0
Q2.
Answer :
Let P (x, y) be any point on the parabola whose focus is S (2, 3) and the directrix is x − 4y + 3 = 0.
Draw PM perpendicular to x − 4y + 3=0.
Then, we have:
SP=PM⇒SP2=PM2⇒x-22+y-32=x-4y+31+162⇒x-22+y-32=x-4y+3172⇒17×2+4-4x+y2-6y+9=x2+16y2+9-8xy-24y+6x⇒17×2-68x+17y2-102y+13×17=x2+16y2+9-8xy-24y+6x⇒16×2+y2+8xy-74x-78y+212=0
Length of the latus rectum = 2(Length of the perpendicular from the focus on the directrix)
= 2(Length of the perpendicular from (2, 3) on the directrix)
= 22-12+316+1=2-717=2717=1417 units
Q3.
Answer :
In a parabola, the vertex is the mid-point of the focus and the point of intersection of the axis and the directrix.
Let (x1, y1) be the coordinates of the point of intersection of the axis and directrix.
(i) It is given that the vertex and the focus of a parabola are (−2, 2) and (−6, −6), respectively.
∴ Slope of the axis of the parabola = -6-2-6+2=-8-4=2
Slope of the directrix = -12
Let the directrix intersect the axis at K (r, s).
∴ r-62=-2, s-62=2⇒r=2, s=10
∴ Required equation of the directrix:
y-10=-12x-2
⇒ 2y+x-22=0.
Now, let P (x, y) be any point on the parabola whose focus is S (−6, −6), and the directrix is 2y+x-22=0.
Draw PM perpendicular to 2x+y+22=0.
Then, we have:
SP=PM⇒SP2=PM2⇒x+62+y+62=2y+x-2252⇒5×2+12x+36+y2+12y+36=4y2+x2+484+4xy-88y-44x⇒4×2+y2-4xy+104x+148y-124=0⇒2x-y2-426x+37y-31=0
(ii) It is given that the vertex and the focus of a parabola are (0, 0) and (0, −3), respectively.
Thus, the slope of the axis of the parabola cannot be defined.
Slope of the directrix = 0
Let the directrix intersect the axis at K (r, s).
∴ r+02=0,s-32=0⇒r=0, s=3
∴ Required equation of directrix:
y=3
Let P (x, y) be any point on the parabola whose focus is S (0, −3) and the directrix is y=3.
Draw PM perpendicular to y=3.
Then, we have:
SP=PM⇒SP2=PM2⇒x-02+y+32=y-312⇒x2+y2+6y+9=y2-6y+9⇒x2=-12y
(iii) It is given that the vertex and the focus of a parabola are (−1, −3) and (0, −3), respectively.
Thus, the slope of the axis of the parabola is zero.
And, the slope of the directrix cannot be defined.
Let the directrix intersect the axis at K (r, s).
∴ r+02=-1,s-32=-3⇒r=-2, s=-3
∴ Required equation of the directrix:
x+2=0
Let P (x, y) be any point on the parabola whose focus is S (0, −3) and the directrix is x+2=0.
Draw PM perpendicular to x+2=0.
Then, we have:
SP=PM⇒SP2=PM2⇒x-02+y+32=x+212⇒x2+y2+6y+9=x2+4x+4⇒y2+6y-4x+5=0
(iv) It is given that the vertex and the focus of a parabola are (a’, 0) and (a, 0), respectively.
Thus, the slope of the axis of the parabola is zero.
And, the slope of the directrix cannot be defined.
Let the directrix intersect the axis at K (r, s).
∴ r+a2=a’, s+02=0⇒r=2a’-a, s=0
∴ Required equation of the directrix is x-2a’+a=0.
Let P (x, y) be any point on the parabola whose focus is S (a, 0), and the directrix is x-2a’+a=0.
Draw PM perpendicular to x-2a’+a=0.
Then, we have:
SP=PM⇒SP2=PM2⇒x-a2+y-02=x-2a’+a12⇒y2=x-2a’+a2-x-a2⇒y2=x2+4a’2+a2-4a’x-4aa’+2ax-x2-a2+2ax⇒y2=4a’2-4a’x-4aa’+4ax⇒y2=-4a’-ax-a’
(v) The point of intersection of x+y=1 and x-y=3 is (2, −1).
Thus, the vertex and the focus of the parabola are (2, −1) and (0, 0), respectively.
∴ Slope of the axis of the parabola = 0+10-2=-12
The slope of the directrix is 2.
Let the directrix intersect the axis at K (r, s).
∴ r+02=2,s+02=-1⇒r=4, s=-2
The required equation of the directrix is y+2=2x-4, which can be rewritten as y-2x+10=0.
Let P (x, y) be any point on the parabola whose focus is S (0, 0) and directrix is y-2x+10=0.
Draw PM perpendicular to y-2x+10=0.
Then, we have:
SP=PM⇒SP2=PM2⇒x-02+y-02=y-2x+1052⇒5×2+5y2=y-2x+102⇒x2+4y2+4xy+40x-20y-100=0⇒x+2y2+40x-20y-100=0
Q4.
Answer :
(i) Given:
y2 = 8x
On comparing the given equation with y2=4ax:
4a=8⇒a=2
∴ Vertex = (0, 0)
Focus = (a, 0) = (2, 0)
Equation of the directrix:
x = −a
i.e. x = −2
Axis = y = 0
Length of the latus rectum = 4a = 8 units
(ii) Given:
4×2 + y = 0
⇒-y4=x2
On comparing the given equation with x2=-4ay:
4a=14⇒a=116
∴ Vertex = (0, 0)
Focus = (0, −a) = 0,-116
Equation of the directrix:
y = a
i.e. y=116
Axis = x = 0
Length of the latus rectum = 4a = 14 units
(iii) Given:
y2 − 4y − 3x + 1 = 0
⇒y-22-4-3x+1=0⇒y-22=3x+1⇒y-22=3x–1
Let Y=y-2, X=x+1
Then, we have:
Y2=3X
Comparing the given equation with Y2=4aX:
4a=3⇒a=34
∴ Vertex = (X = 0, Y = 0) = x=-1, y=2
Focus = (X = a, Y = 0) = x+1=34, y-2=0=x=-14, y=2
Equation of the directrix:
X = −a
i.e. x+1=-34⇒x=-74
Axis = Y = 0
i.e. y-2=0⇒y=2
Length of the latus rectum = 4a = 3 units
(iv) Given:
y2 − 4y + 4x = 0
⇒y-22-4+4x=0⇒y-22=-4x-1
Let Y=y-2, X=x-1
Then, we have:
Y2=-4X
Comparing the given equation with Y2=-4aX:
4a=4⇒a=1
∴ Vertex = (X = 0, Y = 0) = x=1, y=2
Focus = (X = −a, Y = 0) = x-1=-1, y-2=0=x=0, y=2
Equation of the directrix:
X = a
i.e. x-1=1⇒x=2
Axis = Y = 0
i.e. y-2=0⇒y=2
Length of the latus rectum = 4a = 4 units
(v) Given:
y2 + 4y + 4x −3 = 0
⇒y+22-4+4x-3=0⇒y+22=-4x-74
Let Y=y+2, X=x-74
Then, we have:
Y2=-4X
Comparing the given equation with Y2=-4aX:
4a=4⇒a=1
∴ Vertex = (X = 0, Y = 0) = x=74, y=-2
Focus = (X = −a, Y = 0) = x-74=-1, y+2=0=x=34, y=-2
Equation of the directrix:
X = a
i.e. x-74=1⇒x=114
Axis = Y = 0
i.e. y+2=0⇒y=-2
Length of the latus rectum = 4a = 4 units
(vi) Given:
y2 = 8x + 8y
⇒y-42=8x+2
Putting Y=y-4, X=x+2:
Y2=8X
On comparing the given equation with Y2=4aX:
4a=8⇒a=2
∴ Vertex = (X = 0, Y = 0) = x=-2, y=4
Focus = (X = a, Y = 0) = x+2=2, y-4=0=x=0, y=4
Equation of the directrix:
X = −a
i.e. x+2=-2⇒x+4=0
Axis = Y = 0
i.e. y-4=0⇒y=4
Length of the latus rectum = 4a = 8
(vii) Given:
4(y − 1)2 = − 7 (x − 3)
⇒y-12=-74x-3
Let Y=y-1, X=x-3
Then, we have:
Y2=-74X
Comparing the given equation with Y2=-4aX:
4a=74⇒a=716
∴ Vertex = (X = 0, Y = 0) = x=3, y=1
Focus = (X = −a, Y = 0) = x-3=-716, y-1=0=x=4116, y=1
Equation of the directrix:
X = a
i.e. x-3=716⇒x=5516
Axis = Y = 0
i.e. y-1=0 ⇒ y = 1
Length of the latus rectum = 4a = 74 units
(viii) Given:
y 2 = 5x − 4y − 9
⇒y2+4y=5x-9⇒y+22=5x-5=5x-1
Putting Y=y+2, X=x-1:
Y2=5X
Comparing the given equation with Y2=4aX:
4a=5⇒a=54
∴ Vertex = (X = 0, Y = 0) = x=1, y=-2
Focus = (X = a, Y = 0) = x-1=54, y+2=0=x=94, y=-2
Equation of the directrix:
X = −a
i.e. x-1=-54⇒x=-14
Axis = Y = 0
i.e. y+2=0⇒y=-2
Length of the latus rectum = 4a = 5 units
(ix) Given:
x2 = 6x−y−14
⇒x-32=-y-14+9⇒x-32=-y-5=-y+5
Let Y=y+5, X=x-3
Then, we have:
X2=-Y
Comparing the given equation with X2=-4aY:
4a=1⇒a=14
∴ Vertex = (X = 0, Y = 0) = x=3, y=-5
Focus = (X = 0, Y = −a) = x-3=0, y+5=-14=x=3, y=-214
Equation of the directrix:
Y = a
i.e. y+5=14⇒y=-194
Axis = X = 0
i.e. x-3=0⇒x=3
Length of the latus rectum = 4a = 1 units
Q5.
Answer :
The given equation of the parabola is y2 = 4px.
Let PQ be the double ordinate of length 8p of the parabola y2=4px.
Then, we have:
PR = RQ = 4p
Let AR = x1
Then, the coordinates of P and Q are x1,4p and x1,-4p, respectively.
Now, P lies on y2=4px.
∴ 4p2=4px1
⇒x1=4p
So, the coordinates of P and Q are 4p, 4p and 4p,-4p, respectively.
The coordinates of A are (0, 0).
∴ m1=slope of AP=4p-04p-0=1And, m2=slope of AQ=-4p-04p-0=-1
Now, m1m2=-1
Thus, AP is perpendicular to AQ.
Hence, the lines from the vertex to its extremities are at right angles.
Q6.
Answer :
The given equation of the parabola is x2 = 12y.
On comparing the given equation with x2=4ay:
a = 3
Required area = 12LL’×OS=12×12×3=18 square units
Page 25.22 Ex 25.1
Q7.
Answer :
The given equation of the directrix is 3x − 4y = 2. (1)
∴ Slope of the directrix = -3-4=34
Also, the axis is perpendicular to the directrix.
∴ Slope of the axis = -43
The focus lies on the axis of the parabola.
∴ Equation of the axis:
y-3=-43x-3
⇒ 3y-9=-4x+12
⇒ 3y+4x-21=0 (2)
Solving equations (1) and (2):
x=185, y=115
Therefore, the intersection point of the axis and directrix is 185,115.
Also, length of the latus rectum = 2 (Length of the perpendicular from the focus on the directrix)
=233+-43-216+9=2-516+9=2 square units
Q8.
Answer :
Putting x = 3y in the given equation of the parabola:
9y2=9y⇒9yy-1=0⇒y=0,1
At y = 0, x = 0
At y = 1, x = 3
Therefore, at (1, 3), the abscissa is three times that of the ordinate.
Q9.
Answer :
CASE I:
Let the equation of the required parabola be y2=4ax (1)
Since (1) passes through (2, 3), we have:
9=4a2⇒a=98
Thus, the required equation is y2=49×8, i.e. 2y2=9x.
CASE II:
Let the equation of the required parabola be y2=-4ax (2)
Since (2) passes through (2, 3), we have:
9=-4a2⇒a=-98
Thus, the required equation is y2=-4-9×8, i.e. 2y2=9x.
Hence, in either case, the required equation of the parabola is 2y2=9x.
Q10.
Answer :
Let the equation of the directrix be y = a.
Comparing with y = 2:
a = 2
Equation of the parabola with directrix y =a is x2=-4ay.
Hence, the required equation of the parabola is x2=-8y.
Q11.
Answer :
Given:
The vertex and the focus of the parabola are (3, 2) and (5, 2), respectively.
∴ Slope of the axis of the parabola = 0
Slope of the directrix cannot be defined.
Let the directrix intersect the axis at K (r, s).
∴ r+52=3,s+22=2⇒r=1, s=2
Required equation of the directrix is x-1=0, which can be rewritten as x = 1.
Let P (x, y) be any point on the parabola whose focus is S (5, 2) and the directrix is x =1.
Draw PM perpendicular to x = 1.
Then, we have:
SP=PM⇒SP2=PM2⇒x-52+y-22=x-112⇒x2+25-10x+y2+4-4y=x2+1-2x⇒25-10x+y2+4-4y-1+2x=0⇒y2-4y-8x+28=0
Q12.
Answer :
The given equation of the parabola is x2 = 12y.
Comparing the given equation with x2=4ay:
a = 3
Required area = 12LL’×OS=12×12×3=18 square units
Q13.
Answer :
Let X’OX be the bridge and PAQ be the suspension cable.
The suspension cable forms a parabola with the vertex at (0, 6).
Let the equation of the parabola formed by the suspension cable be x-02=4ay-6. (1)
It passes through P (−50, 30) and Q (50, 30).
∴ 2500=4a30-6
Page 25.23 (Very Short Answers)
Q1.
Answer :
Clearly, the axis of symmetry of the given parabola is the x-axis.
Q2.
Answer :
Given:
y2+6y+2x+5=0
⇒y+32+2x-4=0⇒y+32=-2x-2 1
Let Y = y+3, X=x-2
From (1), we have:
Y2=-2X (2)
Putting 4a=2:
a=12
Focus = X=-12, Y=0=x=32, y=-3
Vertex = X=0, Y=0=x=2, y=-3
Thus, we have:
Focus = 32,-3
Vertex = 2,-3
Distance between the vertex and the focus:
32-22+-3+32122=12 units
Q3.
Answer :
Given:
x2 − 4x − 8y + 12 = 0
⇒x-22-4-8y+12=0⇒x-22=8y-1 1
Let Y = y−1, X=x-2
∴ From (1), we have:
X2=8Y (2)
Comparing with x2=4ay:
a=2
Directrix = Y = −a
⇒ y − 1 = −a
⇒y = −a + 1
= −2 + 1
= −1
Therefore, the required equation of the directrix is y=-1.
Q4.
Answer :
Let P (x, y) be any point on the parabola whose focus is S (0, 0) and the directrix is x + y = 4.
Draw PM perpendicular to x + y = 4.
Then, we have:
SP=PM⇒SP2=PM2⇒x-02+y-02=x+y-41+12⇒x2+y2=x+y-422⇒2×2+2y2=x2+y2+16+2xy-8y-8x⇒x2+y2-2xy+8x+8y-16=0
Q5.
Answer :
Let OP be the chord.
Let the coordinates of P be x1, y1.
From the figure, we have:
OP2=x12+y12 (1)
And, tanπ4=y1x1
⇒x1=y1 (2)
Also, x1, y1 lies on the parabola.
∴ y12=4ax1 (3)
Using (2) and (3), we get:
x12=4ax1⇒x1=4a …(4)
∴ From (4), (1) and (2), we have:
OP2=4a2+4a2=32a2⇒OP=42a
Therefore, the length of the chord is 42a units.
Q6.
Answer :
Let S (a, 0) be the focus of the given parabola.
Let the end points of the focal chord be P at2, 2at and Qat2, -2at.
SP and SQ are segments of the focal chord with lengths b and c, respectively.
∴ SP = b, SQ = c
Also, SP =a-at2+4a2t2= a1+t2And, SQ =a-at2+4a2t2= a1+1t2
Now, we have:
1SP+1SQ=1a1+t2+t2a1+t2=1a
⇒1b+1c=1a⇒b+cbc=1a⇒a=bcb+c
∴ Length of the latus rectum = 4a = 4bcb+c
Q7.
Answer :
The coordinates of the focal chord are P at2, 2at and Q at2, -2at.
Comparing y2 = 8x with y2=4ax:
a = 2
Therefore, the coordinates of the focus S is 2, 0.
Given:
SP = 6
∴ 2-2t22+4t2=6⇒t4+2t2-8=0⇒t2=2
Thus, we have:
SQ = 2-2t22+4t2=2-222+42 = 3
Q8.
Answer :
Given:
The focus S is at (−2, 1) and the directrix is the line x + y − 3 = 0.
The slope of the line perpendicular to x + y − 3 = 0 is 1.
The axis of the parabola is perpendicular to the directrix and passes through the focus.
∴ Equation of the axis of the parabola = y-1=1x+2 (1)
Intersection point of the directrix and axis is the intersection point of (1) and x + y − 3 = 0.
Let the intersection point be K.
Therefore, the coordinates of K are (0, 3).
Let (h, k) be the coordinates of the vertex, which is the mid-point of the line segment joining K and the focus.
∴ h=0-22, k=3+12h=-1, k=2
Q9.
Answer :
Given:
The vertex and the focus of a parabola are (−1, 1) and (2, 3), respectively.
∴ Slope of the axis of the parabola = 3-12+1=23
Slope of the directrix = −32
Let the directrix intersect the axis at K (r, s).
∴ r+22=-1,s+32=1⇒r=-4, s=-1
Now, required equation of the directrix:
y+1=-32x+4
⇒3x+2y+14=0
Page 25.24 (Multiple Choice Questions)
Q1.
Answer :
(a) (5/4, 1)
Given:
The equation of the parabola is y2 − x − 2y + 2 = 0.
⇒y-12-1=x-2⇒y-12=x-1
Let X = x-1, Y = y-1
∴ Y2=X
Comparing with Y2=4aX:
a=14
Focus = X=a, Y=0=X=14, Y=0=x=14+1, y=1=x=54, y=1
Hence, the focus is at (5/4, 1).
Q2.
Answer :
(b) (a, −a)
Given:
The equation of the parabola is (y + a)2 = 8a (x − a).
Putting X= x-a, Y=y+a:
Y2=8aX
Vertex = X=0, Y=0=x-a=0, y+a=0=x=a, y=-a
Hence, the vertex is at (a, −a).
Q3.
Answer :
(c) (−1, 2)
Given:
The focus S is at (−2, 1) and the directrix is the line x + y − 3 = 0.
The slope of the line perpendicular to x + y − 3 = 0 is 1.
The axis of the parabola is perpendicular to the directrix and passes through the focus.
∴ Equation of the axis of the parabola = y-1=1x+2 (1)
Intersection point of the directrix and the axis is the intersection point of (1) and x + y − 3 = 0.
Let the intersection point be K.
Therefore, the coordinates of K will be (0, 3).
Let (h, k) be the coordinates of the vertex, which is the mid-point of the segment joining K and the focus.
∴ h=0-22, k=3+12h=-1, k=2
Hence, the coordinates of the vertex are (−1, 2).
Q4.
Answer :
(b) x2 − 2xy + y2 + 6ax + 10ay − 7a2 = 0
Given:
The vertex is at (a, 0) and the directrix is the line x + y = 3a.
The slope of the line perpendicular to x + y = 3a is 1.
The axis of the parabola is perpendicular to the directrix and passes through the vertex.
∴ Equation of the axis of the parabola = y-0=1x-a (1)
Intersection point of the directrix and the axis is the intersection point of (1) and x + y = 3a.
Let the intersection point be K.
Therefore, the coordinates of K are 2a, a.
The vertex is the mid-point of the segment joining K and the focus (h, k).
∴ a=2a+h2, 0=a+k2h=0, k=-a
Let P (x, y) be any point on the parabola whose focus is S (h, k) and the directrix is x + y = 3a.
Draw PM perpendicular to x + y = 3a.
Then, we have:
SP=PM⇒SP2=PM2⇒x-02+y+a2=x+y-3a22⇒x2+y+a2=x+y-3a22⇒2×2+2y2+2a2+4ay=x2+y2+9a2+2xy-6ax-6ay⇒x2+y2-7a2+10ay+6ax-2xy=0
Q5.
Answer :
(a) x = 0
Given:
x = t2 + 1 (1)
y = 2t + 1 (2)
From (1) and (2):
x=y-122+1
On simplifying:
y-12=4x-1
Let Y=y-1 and X=x-1
∴ Y2=4X
Comparing it with y2 = 4ax:
a = 1
Therefore, the equation of the directrix is X = −a , i.e. x-1=-1⇒x=0.
Q6.
Answer :
(a) 3x + 2y + 14 = 0
Given:
The vertex and the focus of a parabola are (−1, 1) and (2, 3), respectively.
∴ Slope of the axis of the parabola = 3-12+1=23
Slope of the directrix = −32
Let the directrix intersect the axis at K (r, s).
∴ r+22=-1,s+32=1⇒r=-4, s=-1
Equation of the directrix:
y+1=-32x+4
⇒3x+2y+14=0
Q7.
Answer :
(c) parabola
Suppose PQ is a double ordinate of the parabola y2=4ax.
Let R and S be the points of trisection of the double ordinates.
Let h,k be the coordinates of R.
Then, we have:
OL = h and RL = k
∴RS=RL+LS=k+k=2k⇒PR=RS=SQ=2k⇒LP=LR+RP=k+2k=3k
Thus, the coordinates of P are h, 3k, which lie on y2=4ax.
∴ 9k2=4ah
Hence, the locus of the point (h, k) is 9y2=4ax, i.e. y2=4a9x, which represents a parabola.
Q8.
Answer :
(a) x + 2y = 4
Given:
The vertex and the focus of a parabola are (1, 4) and (2, 6), respectively.
∴ Slope of the axis of the parabola = 6-42-1=2
Slope of the directrix = −12
Let the directrix intersect the axis at K (r, s).
∴ r+22=1,s+62=4⇒r=0, s=2
Equation of the directrix:
y-2=-12x-0
⇒ x + 2y = 4
Q9.
Answer :
(b) 1/2
Given:
The vertex and the focus of a parabola are V and S, respectively.
The given equation of parabola can be rewritten as follows:
y+32-9+5+2x=0
⇒y+32+2x=4⇒y+32=4-2x⇒y+32=-2x-2
Let Y=y+3, X=x-2
Then, the equation of parabola becomes Y2=-2X.
Vertex = X=0, Y=0=x-2=0, y+3=0=x=2, y=-3
Comparing with y2 = 4ax:
4a=2⇒a=12
Focus = X=-12, Y=0=x-2=-12, y+3=0=x=32, y=-3
⇒ SV = 2-322+-3+32=12
Q10.
Answer :
(c) y = −1
Given:
x2 − 4x − 8y + 12 = 0
⇒x-22-4-8y+12=0⇒x-22=8y-8⇒x-22=8y-1
Putting X = x − 2, Y = y − 1:
X2=8Y
Comparing with X2=4aY:
a = 2
Equation of the directrix:
Y=-a
⇒ Y=-2
⇒y-1=-2⇒y=-2+1⇒y=-1
Q11.
Answer :
(a) x2 + y2 − 2xy + 8x + 8y − 16 = 0
Let P (x, y) be any point on the parabola whose focus is S (0, 0) and the directrix is x + y = 4.
Draw PM perpendicular to x + y = 4.
Then, we have:
SP=PM⇒SP2=PM2⇒x-02+y-02=x+y-422⇒x2+y2=x+y-422⇒2×2+2y2=x2+y2+16+2xy-8x-8y⇒x2+y2-2xy+8x+8y-16=0
Q12.
Answer :
(c) (−1, 2)
Let the coordinates of P and Q be at12, 2at1 and at22, 2at2, respectively.
Slope of PQ = 2at2-2at1at22-at12 ……(1)
But, the slope of PQ is equal to the slope of 2x − y + 4 = 0.
∴ Slope of PQ = -2-1=2
From (1),
2at2-2at1at22-at12=2 …..(2)
Putting 4a = 8,
a = 2
∴ Focus of the given parabola = (a, 0) = 2, 0.
Using equation (2):
4t2-t12t22-t12=2
t2-t1t22-t12=1
⇒t1+t2=1
As, points P and Q lie on 2x-y+4=0
⇒P(at12, 2at1) or P(2t12, 4t1) lie on line 2x-y+4=0⇒22t12-4t1+4=0⇒t12-t1+1=0 …(3)Also, Q(at22, 2at2) or P(2t22, 4t2) lie on line 2x-y+4=0⇒22t22-4t2+4=0⇒t22-t2+1=0 …(4)Adding (3) and (4), we get,⇒t12-t1+1+t22-t2+1=0⇒t12+t22-t1+t2+2=0⇒t12+t22-1+2=0 t1+t2=1, proved above⇒t12+t22=-1
Let x1, y1 be the mid-point of PQ.
Then, we have:
y1=2at2+2at12=2t1+t2=2
And, x1=at12+at222=t12+t22=-1
⇒ x1, y1=-1, 2
Q13.
Answer :
(a) 42a
Let OP be the chord.
Let the coordinates of P be x1, y1.
From the figure, we have:
OP2=x12+y12 (1)
And, tanπ4=y1x1
⇒x1=y1 (2)
Also, x1, y1 lies on the parabola.
∴ y12=4ax1 (3)
Using (2) and (3):
x12=4ax1⇒x1=4a (4)
∴ From (4), (1) and (2), we have:
OP2=4a2+4a2=32a2⇒OP=42a
Therefore, the length of the chord is 42a units.
Q14.
Answer :
(b) a parabola
Comparing the given equation with ax2 + by2 + 2hxy + 2gx+2fy + c =0, we get:
a=16, b=1, h=4
We have: h2=16=ab
Thus, the given equation represents a parabola.
Page 25.24 (Multiple Choice Questions)
Q15.
Answer :
(c) 8
Given:
y2 + 8x − 2y + 17 = 0
⇒y-12-1+8x+17=0⇒y-12+8x+16=0⇒y-12=-8x+2
Let X=x+2, Y=y-1
∴ Y2=-8X
Comparing with y2=4ax:
a = 2
Length of the latus rectum = 4a = 8 units
Q16.
Answer :
(a) (−4, 1)
Given:
x2 + 8x + 12y + 4 = 0
⇒x+42-16+12y+4=0⇒x+42+12y-12=0⇒x+42=-12y-1
Let X=x+4, Y=y-1
∴ X2=-12Y
Vertex = X=0,Y=0=x+4=0,y-1=0=x=-4,y=1
Hence, the vertex is at (−4, 1).
Q17.
Answer :
(a) (1, 2)
Given:
(y − 2)2 = 16 (x − 1)
Let X=x-1, Y=y-2
∴ Y2=16X
Vertex = X=0, Y=0=x-1=0, y-2=0=x=1, y=2
Hence, the vertex is at (1, 2).
Q18.
Answer :
(c) 1/2
Given:
4y2 + 2x − 20y + 17 = 0
⇒y2+x2-5y+174=0⇒y-522+x2-2=0⇒y-522=-1×2-2⇒y-522=-12x-4
Let X=x-4, Y=y-52
∴ Y2=-X2
∴ Length of the latus rectum = 4a = 12 units
Q19.
Answer :
(c) 8
Given:
x2 − 4x − 8y + 12 = 0
⇒x-22-8y+8=0⇒x-22=8y-8=8y-1
Let X=x-2, Y=y-1
∴ X2=8Y
∴ Length of the latus rectum = 4a = 8 units
Q20.
Answer :
(c) (−1/4, 0)
Given:
Equation of the parabola = y = 2x2 + x
⇒x2+x2=y2⇒x+142=y2+116⇒x+142=8y+116⇒x+142=12y+18
Let X=x+14, Y=y+18
∴ X2=12Y
Comparing with X2=4aY:
a=18
Focus = X=0, Y=a=x=-14, y=0
Hence, the focus is at (−1/4, 0).
Q21.
Answer :
(d) x = 2at, y = at2
Substituting x = 2at, y = at2 in the given equation:
2at2=4aat2⇒4a2t2=4a2t2
Hence, (2at, at2) lies on the parabola x2 = 4ay.
Q22.
Answer :
(d) x2 + y2 − 2xy − 18x − 10y − 45 = 0
Let P (x, y) be any point on the parabola whose focus is S (1, −1) and the directrix is x + y + 7 = 0.
Draw PM perpendicular to x + y + 7 = 0.
Then, we have:
SP=PM⇒SP2=PM2⇒x-12+y+12=x+y+71+12⇒x-12+y+12=x+y+722⇒2×2+1-2x+y2+1+2y=x2+y2+49+2xy+14y+14x⇒2×2+2-4x+2y2+2+4y=x2+y2+49+2xy+14y+14x⇒x2+y2-45-10y-2xy-18x=0
Hence, the required equation is x2 + y2 − 2xy − 18x − 10y − 45 = 0.
Page 26.16 Ex 26.1
Q1.
Answer :
Let S(1,-2) be the focus and ZZ’ be the directrix.Let P(x,y) be any point on the ellipse and let PM be the perpendicular from P on the directix.Then by the definition of an ellipse, we have:SP=e.PM, where e=12⇒SP2 = e2.PM2⇒(x-1)2 + (y+2)2 =122.3x-2y+5(3)2+(-2)22⇒x2+1-2x+y2+4+4y= 14.9×2+4y2+25-12xy-20y+30×13⇒52(x2+1-2x+y2+4+4y) = 9×2+4y2+25-12xy-20y+30x⇒52×2+52-104x+52y2+208+208y= 9×2+4y2+25-12xy-20y+30x⇒43×2+48y2-134x+228y+12xy+235=0This is the equation of the required ellipse.
Q2.
Answer :
(i)
Let S(0,1) be the focus and ZZ’ be the directrix.Let P(x,y) be any point on the ellipse and let PM be the perpendicular from P on the directrix.Then by the definition, we have:SP=e×PM⇒SP=12×PM⇒2SP=PM⇒4SP2=PM2⇒4×2+y-12=x+y12+122⇒4×2+y2+1-2y=x2+y2+2xy2⇒8×2+8y2+8-16y=x2+y2+2xy⇒7×2+7y2-2xy-16y+8=0This is the required equation of the ellipse.
(ii)
Let S(-1,1) be the focus and ZZ’ be the directrix.Let P(x,y) be any point on the ellipse and let PM be the perpendicular from P on the directrix.Then by the definition, we have:SP=e×PM⇒SP=12×PM⇒2SP=PM⇒4SP2=PM2⇒4x+12+y-12=x-y+312+-122⇒4×2+1+2x+y2+1-2y=x2+y2+9-2xy-6y+6×2⇒8×2+8+16x+8y2+8-16y=x2+y2+9-2xy-6y+6x⇒7×2+7y2+2xy-10y+10x+7=0This is the required equation of the ellipse.
(iii)
Let S(-2,3) be the focus and ZZ’ be the directrix.Let P(x,y) be any point on the ellipse and let PM be the perpendicular from P on the directrix.Then by the definition, we have: SP=e×PM⇒SP=45×PM⇒54SP=PM⇒2516SP2=PM2⇒2516x+22+y-32=2x+3y+422+322⇒2516×2+4+4x+y2+9-6y=4×2+9y2+16+12xy+24y+16×13⇒325×2+4+4x+y2+9-6y=164×2+9y2+16+12xy+24y+16x⇒325×2+1300+1300x+325y2+2925-1950y=64×2+144y2+256+192xy+384y+256x⇒261×2+181y2+1044x-2309y-192xy+3969=0This is the required equation of the ellipse.
(iv)
Let S(1,2) be the focus and ZZ’ be the directrix.Let P(x,y) be any point on the ellipse and let PM be the perpendicular from P on the directrix.Then by the definition, we have:SP=e×PM⇒SP=12×PM⇒2SP=PM⇒4SP2=PM2⇒4x-12+y-22=3x+4y-532+422⇒4×2+1-2x+y2+4-4y=9×2+16y2+25+24xy-40y+30×25⇒100×2+100-200x+100y2+400-400y=9×2+16y2+25+24xy-40y-30x⇒91×2+84y2-24xy-360y-170x+475=0This is the required equation of the ellipse.
Q3.
Answer :
(i) 4×2+9y2=1⇒x214+y219=1This is of the form x2a2+y2b2=1, where a2=14 and b2=19, i.e. a=12and b=13.Clearly a>bNow, e=1-b2a2⇒e=1-1914⇒e=1-49⇒e=53Coordinates of the foci=±ae, 0=±56,oLength of the latus rectum= 2b2a =2×1912 =49
(ii) 5×2+4y2=1⇒x215+y214=1This is of the form x2a2+y2b2=1, where a2=15 and b2=14, i.e. a=15and b=12. Clearly b>aNow, e=1-a2b2⇒e=1-1514⇒e=1-45⇒e=15Coordinates of the foci=0,±be= 0,±125Length of the latus rectum= 2a2b =2×1512 =45
(iii) 4×2+3y2=1⇒x214+y213=1This is of the form x2a2+y2b2=1, where a2=14 and b2=13, i.e. a=12and b=13. Clearly, b>aNow, e=1-a2b2⇒e=1-1413⇒e=1-34⇒e=12Coordinates of the foci=0,±be= 0,±123Length of the latus rectum= 2a2b =2×1413 =32
(iv) 25×2+16y2=1600⇒x264+y2100=1This is of the form x2a2+y2b2=1, where a2=64 and b2=100, i.e. a=8 and b=10.Clearly, b>aNow, e=1-a2b2⇒e=1-64100⇒e=36100⇒e=610 or 35Coordinates of the foci= 0,±6Length of latus rectum= 2a2b =2×6410 =645
Q4.
Answer :
Let the equation of the ellipse be x2a2+y2b2=1 …(1) It passes through the point -3,1.∴ 9a2+1b2=1 … (2)Also, e=25Now, b2=a21-e2⇒b2=a21-25⇒b2=3a25Substituting the value of b2 in eq. (2), we get:9a2+53a2=1⇒27+53a2=1⇒a2=323⇒b2=3×3235or 325Substituting the values of a and b in eq. (1), we get: 3×232+5y232=1⇒3×2+5y2=32This is the required equation of the ellipse.
Q5.
Answer :
(i) e=12 and foci=(±2,0)Coordinates of the foci=±ae, 0We have ae=2 ⇒a×12=2⇒a=4Now, e=1-b2a2⇒12=1-b216On squaring both sides, we get:14=16-b216⇒64-4b2=16⇒b2=484⇒b2=12Now, x2a2+y2b2=1⇒x216+y212=1⇒3×2+4y248=1⇒3×2+4y2=48This is the required equation of the ellipse.
(ii) e=23 and length of the latus rectum=5We have 2b2a=5⇒2b2=5a⇒b2=5a2Now, e=1-b2a2⇒23=1-5a2a2On squaring both sides, we get:49=2a-52a⇒8a=18a-45⇒a=92∴b2=454Substituting the values of a2 and b2, we get:x2a2+y2b2=1⇒4×281+4y245=1⇒20×2+36y2405=1⇒20×2+36y2=405This is the required equation of the ellipse.
(iii) e=12 and semi major axis=4i.e. a=4We have e=1-b2a2⇒12=1-b216On squaring both sides, we get:14=16-b216⇒16=64-4b2⇒b2=12Substituting the values of a2 and b2, we get:x2a2+y2b2=1⇒x216+y212=1⇒3×2+4y248=1⇒3×2+4y2=48This is the required equation of the ellipse.
(iv) e=12 and major axis=12i.e., 2a=12 or a=6We have e=1-b2a2⇒12=1-b236On squaring both sides, we get:14=36-b236⇒36=144-4b2⇒b2=27Substituting the values of a2 and b2, we get:x2a2+y2b2=1⇒x236+y227=1⇒3×2+4y2108=1⇒3×2+4y2=108This is the required equation of the ellipse.
(v) The ellipse passes through 1,4 and -6,1.x2a2+y2b2=1⇒1a2+16b2=1Let 1a2=α and 1b2=βThen α+16β=1 ..(1)It also passes through -6,1.x2a2+y2b2=1⇒36a2+1b2=1⇒36α+β=1 …(2)Solving eqs. (1) and (2), we get:α=3115 and β=7115Substituting the values, we get: 3×2115+7y2115=1⇒3×2+7y2115=1⇒3×2+7y2=115This is the required equation of ellipse.
(vi) Vertices ±5,0 and focus ±4,0The coordinates of its vertices and foci are±a,0 and ±ae,0, respectively.i.e. a=5 and ae=4∴ e=45Now, b2=a21-e2⇒b2=251-1625⇒b2=9∴x225+y29=1This is the required equation of the ellipse.
(vii) Vertices 0,±13 and focus 0,±5The coordinates of its vertices and foci are0,±b and 0,±be, respectively.i.e. b=13 and be=5∴e=513Now, a2=b21-e2⇒a2=1691-25169⇒a2=144∴x2144+y2169=1This is the required equation of the ellipse.
(viii) Vertices ±6,0 and focus ±4,0The coordinates of its vertices and foci are ±a,0 and ±ae,0, respectively.i.e., a=6 and ae=4∴e=46or23Now, b2=a21-e2⇒b2=361-1636⇒b2=20∴ x236+y220=1This is the required equation of the ellipse.
(ix) Let the equation of the ellipse be x2a2+y2b2=1. End of major axis=±3,0 End of minor axis=0,±2But the coordinates of the end points of the major and the minor axes are (±a,0) and 0,±b, respectively.∴ a=3 and b=2Then x29+y24=1This is the required equation of the ellipse.
(x) Let the equation of the ellipse be x2a2+y2b2=1. End of major axis=0,±5 End of minor axis=±1,0But the coordinates of the end points of the major and the minor axes are (±a,0) and 0,±b, respectively.∴a=1 and b=5Then x21+y25=1This is the required equation of the ellipse.
(xi )Length of major axis=26Foci=±5,0We have 2a=26⇒a=13Also, ae=5⇒e=513Now, e=1-b2a2⇒513=1-b2169On squaring both sides, we get:25169=169-b2169⇒b2=144Now, x2a2+y2b2=1⇒x2169+y2144=1This is the required equation of the ellipse.
(xii) Length of minor axis=16 and foci=0,±6i.e. 2b=16⇒b=8and be=6⇒e=68Now, e=1-a2b2⇒68=1-a264On squaring both sides, we get: 3664=64-a264⇒a2=28×264+y228=1This is the required equation of the ellipse.
(xiii) Foci=±3,0 and a=4i.e. ae=3⇒e=34Now, e=1-b2a2⇒34=1-b216On squaring both sides, we get: 916=16-b216⇒b2=7∴x216+y27=1 This is the required equation of the ellipse
Page 26.17 Ex 26.1
Q6.
Answer :
Let the equation of the ellipse be x2a2+y2b2=1 …(1)Then the coordinates of the foci are (±ae,0). Also, e=13We have ae=4⇒a.13=4⇒a=12Now, b2=a2(1-e2)⇒b2=1221-132⇒b2=14489⇒b2=128 Substituting the values of a2 and b2 in eq. (1), we get:x2144+y2128=1This is the required equation of the ellipse.
Q7.
Answer :
According to the question, the minor axis is equal to the distance between the foci. i.e. 2b=2ae and 2b2a=10 or b2=5a ⇒b=ae⇒b2=a2e2⇒b2=a21-b2a2 ∵e=1-b2a2⇒b2=a2-b2⇒a2=2b2⇒a2=10a ∵ b2=5a ⇒ a=10⇒b2=5a ⇒b2=50 Substituting the values of a and b in the equation of an ellipse, we get:x2100+y250=1∴x2+2y2=100This is the required equation of the ellipse.
Q8.
Answer :
(i) When the major axis is parallel to the x-axis.Let (x-x1)2a2+(y-y1)2b2=1 …(1)Here, x1 and y1 are -2 and 3, respectively, and 3 and 2 are the lengths of the axes. Substituting the value in eq. (1), we get: (x+2)29+(y-3)24=1⇒4(x2+4+4x)+9(y2+9-6y)36=1⇒4×2+16+16x+9y2+81-54y=36⇒4×2+9y2+16x-54y+61=0This is the required equation of the ellipse.
(ii) When the major axis is parallel to the y-axis.Let (x-x1)2b2+(y-y1)2a2=1 …
(1)Here, x1 and y1 are -2 and 3, respectively, and 3 and 2 are the lengths of the axes.Substituting the value in eq. (1), we get:(x+2)24+(y-3)29=1⇒9(x2+4+4x)+4(y2+9-6y)36=1⇒9×2+36+36x+4y2+36-24y=36⇒9×2+4y2+36x-24y+36=0This is the required equation of the ellipse.
Q9.
Answer :
(i) According to the question, the latus rectum is half its minor axis. i.e.2b2a=12×2b⇒2b2=ab⇒2b=aNow, e=1-b24b2⇒e=1-14⇒e=322) According to the question, the latus rectum is half its minor axis. i.e. 2b2a=12×2a⇒2b2=a2⇒a2=2b2Now, e=1-b22b2⇒e=1-12⇒e=12
Q10.
Answer :
(i) x2+2y2-2x+12y+10=0⇒x2-2x+2y2+6y=-10⇒x2-2x+1+2y2+6y+9=-10+18+1⇒x-12+2y+32=9⇒x-129+y+3292=9Here, x1=1 and y1=-3Also, a=3 and b=32Centre= 1,-3Major axis=2a⇒2×3=6Minor axis=2b⇒2×32=32e=1-b2a2⇒e=1-929⇒e=12Foci= x1±ae,y1 =1±32,-3
(ii) x2+4y2-4x+24y+31=0⇒x2-4x+4y2+6y=-31⇒x2-4x+4+4y2+6y+9=-31+36+4⇒x-22+4y+32=9⇒x-229+y+3294=9Here, x1=2 and y1=-3 Also, a=3 and b=32Centre=x1,y1=2,-3Major axis=2a = 2×3 =6Minor axis=2b =2×32 =3e=1-b2a2⇒e=1-949⇒e=32Foci= x1±ae,y1 =2±332,-3
(iii) 4×2+y2-8x+2y+1=0⇒4×2-2x+y2+2y=-1⇒4×2-2x+1+y2+2y+1=-1+4+1⇒4x-12+y+12=4⇒x-121+y+124=1Here, x1=1 and y1=-1 Also, a=1 and b=2Centre=x1,y1=1,-1Major axis=2b =2×2 =4Minor axis=2a =2×1 =2e=1-a2b2⇒e=1-14⇒e=32Foci =x1,y1±be =1,-1±3
(iv) 3×2+4y2-12x-8y+4=0⇒3×2-4x+4y2-2y=-4⇒3×2-4x+4+4y2-2y+1=-4+12+4⇒3x-22+4y-12=12⇒x-224+y-123=1Here, x1=2, y1=1Also, a=2 and b=3Centre=x1, y1=2,1Major axis=2a =2×2 =4Minor axis=2b =2×3 =23e=1-b2a2⇒e=1-34⇒e=12Foci= x1±ae,y1 =2±1,1
(v) 4×2+16y2-24x-32y-12=0⇒4×2-6x+16y2-2y=12⇒4×2-6x+9+16y2-2y+1=12+36+16⇒4x-32+16y-12=64⇒x-3216+y-124=9Centre= 3,1Major axis=2a =2×4 =8Minor axis=2b =2×2 =4e=1-b2a2⇒e=1-416⇒e=32Foci= x±ae,y =3±23,1(vi) x2-2x+4y2=0⇒x2-2x+4y2=0⇒x2-2x+1+4y2=1⇒x-12+4y2=1⇒x-121+y214=9Centre= 1,0Major axis=2a =2×1 =2Minor axis=2b =2×12 =1e=1-b2a2⇒e=1-141⇒e=32Foci =x±ae,y =1±32,0
Q11.
Answer :
Let the equation of the ellipse be x2a2+y2b2=1 … (1)Then ae=3 Also x=4 and y=1 [Ellipse passing through (4,1)]Substituting the values of x and y in eq. (1), we get: 42a2+12b2=1⇒16a2+1b2=1Now, b2=a2(1-e2)⇒b2=a2-a2e2⇒b2=a2-9 or a2=b2+9 …2⇒16a2+1b2=1⇒16b2+a2=a2b2⇒16b2+b2+9=b2b2+9⇒17b2+9=b4+9b2⇒b4-8b2-9=0⇒b2-9b2+1⇒b=±3Substituting the value of b in eq. (2), we get:a=32∴x218+y29=1This is the required equation of the ellipse.
Q12.
Answer :
Let the ellipse be x2a2+y2b2=1. …1e=23 and latus rectum=5 (Given)Now,2b2a=5⇒2b2=5a …(2)⇒2a2(1-e2)=5a [∵b2=a2(1-e2)]⇒2a21-49=5a⇒2a2 ×59=5a⇒10a2=45a⇒a=92 Substituting the value of a in eq. (2), we get:2b2=5×92⇒b2=454Substituting the values of a2and b2in eq. (1), we get:x2814+y2454=1⇒4×281+4y245=1This is the required equation of the ellipse.
Q13.
Answer :
Let the equation of the ellipse bex2a2+y2b2=1 and let e=34. Also, let the foci be on the y-axis.∴a2=b21-e2⇒a2=b21-916⇒a2=716b2⇒x2a2+7y216a2=1 …(1)It passes through 6,4.Then 36a2+11216a2=1⇒576+11216a2=1⇒16a2=688⇒a2=43Now, b2=16a27⇒b2=6887 Substituting the values of a2 and b2 in eq. (1), we get:x243+7y2688=1This is the required equation of the ellipse.
Q14.
Answer :
Let the ellipse be x2a2+y2b2=1 and it passes through the points (4,3) and (-1,4).∴16a2+9b2=1and 1a2+16b2=1Let α=1a2 and β=1b2Then 16α+9β=1 and α+16β=1Solving these two equations, we get:α=7247 and β=15247⇒1a2=7247and 1b2=15247 …(1) Substituting eq. (1) in the equation of an ellipse, we get:7×2247+15y2247=1This is the required equation of the ellipse.
Q15.
Answer :
Let the equation of the ellipse be x2a2+y2b2=1 …(1) It passes through the point -3,1.∴ 9a2+1b2=1 …( 2)and e=25Now, b2=a21-e2⇒b2=a21-25⇒b2=a2×35or3a25Substituting the value of b2 in eq. (2), we get: 9a2+53a2=1⇒27+53a2=1⇒a2=323⇒b2=3×3235 or 325 Substituting the values of a and b in eq. (1), we get: 3×232+5y232=1⇒3×2+5y2=32This is the required equation of the ellipse.
Q16.
Answer :
The distance between the foci is 8 units.i.e. 2ae=8 … (1)The distance between the directrices is 18 units.i.e. 2ae=18 … (2)Comparing eqs. (1) and (2), we get:e=82aSubstituting the value of e in eq. (2), we get: 2a82a=18⇒4a2=18×8⇒a2=36 or a =6Now, 2ae=8⇒12e=8 or e=23Then b2=a2(1-e2)⇒b2=361-49⇒b2=36×59⇒b2=20∴x236+y220=1This is the required equation of ellipse.
Q17.
Answer :
Let the equation of the required ellipse bex2a2+y2b2=1 …(1)Since the vertices of the ellipse are on the y-axis, the coordinates of the vertices are (0,±b).∴ b=10Now, a2=b2(1-e2)⇒a2=1001-452⇒a2=100×925⇒a2=36
Q18.
Answer :
Let AB be the rod making an angle θ with OX and let P (x, y) be the point on it such that AP = 3 cm.
Then, PB = AB – AP = (12 – 3) cm = 9 cm [∵ AB = 12 cm]
From P, draw PQ⊥OY and PR⊥OX.
In △PBQ, we have:cos θ =PQPB=x9In △PRA, we have:sin θ =PRPA=y3Since sin2 θ +cos2 θ=1, we have:y32+x92=1⇒x281+y29=1Thus, the locus of a point P on the rod is x281+y29=1.
Substituting the values of a2 and b2 in equation (1), we get: x236+y2100=1⇒100×2+36y23600=1∴100×2+36y2=3600This is the required equation of the ellipse.
Page 26.19 (Very Short Answers)
Q1.
Answer :
The lengths of the semi major and the semi minor axes of the ellipse are 2 and 3, respectively. Their corresponding equations are y-5=0 and x+3 =0.So, a=2 and b=3The equation of the ellipse is given byx+324+y-523=1⇒3x+32+4y-52=12⇒3×2+9+6x+4y2+25-10y=12⇒3×2+27+18x+4y2+100-40y=12⇒3×2+4y2+18x-40y+115=0
Page 26.20 (Very Short Answers)
Q2.
Answer :
9×2+5y2-18x-2y-16=0⇒9×2-2x+5y2-2y5=16⇒9×2-2x+1+5y2-2y5+125=16+9+15⇒9x-12+5y-152=1265⇒x-1212645+y-15212625=1⇒a2=12645 and b2=12625Clearly, a<bNow, e=1-a2b2⇒e=1-1264512625⇒e=1-59⇒e=23
Q3.
Answer :
3×2-6x+4y2+8y-5=0⇒3(x2-2x)+4(y2+2y)=5⇒3(x2-2x+1)+4(y2+2y+1)=5+3+4⇒3(x-1)2+4(y+1)2=12⇒3(x-1)212+4(y+1)212=1⇒(x-1)24+(y+1)23=1Compairing it withx2a2+y2b2=1, we get:a=2 and b=3Here, a>b, so the major and the minor axes of the ellipse are along the x-axis and y-axis, respectively.Now, e=1-b2a2⇒e=1-34⇒e=14∴ e=12 and centre = 1,-1
Q4.
Answer :
The given equation of the ellipse is 4×2+9y2=36 …
(i)⇒x29+y24=1This is of the form x2a2+y2b2=1, where a2=9 and b2=4 i.e a=3 and b=2Clearly a>b, therefore the major axis and minor axis of the ellipse are along x axis and y axis respectively .Let , e be the ecentricity of the ellipse . Then, ∴ e=1-b2a2⇒e=1-49 =53Therefore, coordinates of focus at S i.e ae, 0=5,0& coordinates of focus at S’ =-ae, 0=-5,0It is given that PSQ is a focal chord As we know that , SP+S’P=2a⇒4+S’P=6 ∵SP=4⇒S’P=2Let coordinates of P be m,nAs S’P=2∴n-02+m+52=2⇒n2+m2+5+25m=4 …(ii)& SP=4∴n-02+m-52=4⇒n2+m2+5-25m=16 …(iii)Subtracting eq (iii) from eq (ii) , we get 45m=-12⇒m=-35& we get n=45∴ Coordinates of P are -35,45 and coordinates of S are 5,0∴ Equation of the line segment PS which is extended to PQ is given by x+2y=5 …(iv)Solving eq (i) & (iv) we get , x=-35 and y=45 which are the coordinates of P& x= 66550 and y=-8550 which would be the coordinates of Q.∴ S’Q=-8550-02+66550+52 =265
Q5.
Answer :
According to the question, the latus rectum is half its minor axis.i.e. 2b2a=12×2b⇒2b=aNow, e=1-b2a2⇒e=1-b24b2⇒e=1-14⇒e=32
Q6.
Answer :
According to the question, the distance between the foci of an ellipse is equal to the length of the latus rectum. i.e. 2b2a=2ae⇒e=b2a2But e=1-b2a2Then e=1-e Squaring both sides, we get:e2+e-1=0⇒e=-1±1+42 ∵Ecentricity cannot be negative ⇒e=5-12
Q7.
Answer :
We know that the focal distance of a point B(0, b) is a±e.0 =ai.e. SB=SB’=a∴SB+SB’=2a Since ∆BSS’ is equilateral, we have:SB=SS’=S’B=2ae⇒2ae+2ae=2a⇒4ae=2a⇒e=24⇒e=12
Q8.
Answer :
According to the question, the minor axis of the ellipse subtends an equilateral triangle with the vertex at one end of the major axis. AB=a2+b2 We know that ABC is an equilateral triangle.∴ AB=BB’ ⇒a2+b2=2bOn squaring both sides, we have:a2+b2=4b2⇒a2=3b2Now, e=1-b2a2⇒e=1-b23b2⇒e=1-13⇒e=23
Q9.
Answer :
According to the Pythogoras theorem, we have:OA2+OB2=AB2From the figure, we can see that OA=b2a-02+ae-02=b4a2+a2e2=OB and AB=2b2aNow, 2a2e2+b4a2=4b4a2⇒a2e2+b4a2=2b4a2⇒a2e2=-b4a2+2b4a2⇒a2e2=b4a2⇒e2=b4a4⇒e=b2a2We know that e=1-b2a2e=1-eOn squaring both sides, we get: e2+e-1=0⇒e=-1±1+42 ∵ Ecentricity cannot be negative⇒e=5-12
Page 26.20 (Multiple Choice Questions)
Q1.
Answer :
Disclaimer: The equation should be 12×2+4y2+24x-16y+24=0 instead of 12×2+4y2+24x-16y+25=0.(d) all of these12x2+4y2+24x-16y+24=0⇒12×2+2x+4y2-4y=-24⇒12×2+2x+1+4y2-4y+4=-24+12+16⇒12x+12+4y-22=4⇒x+123+y-221=1So, the centre is -1,2.Here, a=3 and b=1The lengths of the axes are 3 and 1.Now, e=1-b2a2e=1-13⇒e=23
Q2.
Answer :
(b) 7×2+7y2+2xy-10y+10x+7=0
Let P(x,y) be any point on the ellipse whose focus and eccentricity are S-1,1 and e=12, respectively.Let PM be the perpendicular from P on the directrix. Then SP=e×PM⇒SP=12×PM⇒2SP=PM⇒4SP2=PM2⇒4x+12+y-12=x-y+312+-122⇒4×2+1+2x+y2+1-2y=x2+y2+9-2xy-6y+6×2⇒8×2+8+16x+8y2+8-16y=x2+y2+9-2xy-6y+6x∴7×2+7y2+2xy-10y+10x+7=0This is the required equation of the ellipse.
Q3.
Answer :
(d) x2+y2=a2-b2We have r=aeLet the equation of the circle be x2+y2=r2.Now, x2+y2=a2e2 ∵r=ae⇒ x2+y2=a21-b2a2 ∵e=1-b2a2⇒x2+y2=a2-b2∴ The required equation of the circle is x2+y2=a2-b2.
Q4.
Answer :
(b) e=32According to the question, the latus rectum is half its minor axis.i.e. 2b2a=12×2b⇒2b2=ab⇒a=2bNow, e=1-b2a2⇒e=1-b24b2⇒e=1-14⇒e=32
Q5.
Answer :
(a) e=5-12 According to the question, the distance between the foci is equal to the length of the latus rectum.2b2a=2ae⇒b2=a2eNow, e=1-b2a2⇒e=1-a2ea2⇒e=1-eOn squaring both sides, we get:e2+e-1=0⇒e=-1±1+42⇒e=5-12 ∵e cannot be negative
Page 26.21 (Multiple Choice Questions)
Q6.
Answer :
(c) 12According to the question, the minor axis is equal to the distance between the foci.i.e. 2b=2ae⇒e=ba …(1) Now, e=1-b2a2⇒e=1-e2 [From (1)] On squaring both sides, we get:e2=1-e2⇒2e2=1⇒e2=12⇒e=12
Q7.
Answer :
(d) 2ae2Length of the latus rectum=2b2aand e=1-b2a2a2e2=a2-b2⇒b2=a2-a2e2⇒b2=a21-e2∴ Length of the latus rectum=2a21-e2a=2a(1-e2)Length of the major axis=2aDifference between length of latus rectum and length of major axis = 2a-2a(1-e2) =2a-2a+2ae2 =2ae2
Q8.
Answer :
(b) 459×2+25y2=225⇒x225+y29=1Comparing it with x2a2+y2b2=1, we get: a=5 and b=3Here, a>b, so the major and the minor axes of the ellipse are along the x-axis and y-axis, respectively.Now, e=1-b2a2⇒e=1-925⇒e=1625⇒e=45
Q9.
Answer :
(a) 33×2+4y2-6x+8y-5=0⇒3(x2-2x)+4(y2+2y)=5⇒3(x2-2x+1)+4(y2+2y+1)=5+3+4⇒3(x-1)2+4(y+1)2=12⇒(x-1)24+(y+1)23=1So, a=2 and b=3∴Latus rectum=2b2a =2322 =3
Q10.
Answer :
(d) x+y=5 , y=39×2+16y2=144⇒x216+y29=1Equation of the tangent in case of an ellipse is given by y=mx+a2m2+b2⇒y=mx+16m2+9 … (1) Substituting x=2 and y=3, we get:3=2m±16m2+9⇒3-2m=16m2+9On squaring both sides, we get: 3-2m2=16m2+9⇒9+4m2-12m=16m2+9⇒12m2+12m=0⇒12mm+1=0⇒m=0,-1Substituting values of m in eq. (1), we get: For m=0, y=3For m=-1, y=-x+5 or x+y=5
Q11.
Answer :
(d) 534×2+9y2+8x+36y+4=0⇒4(x2+2x)+9(y2+4y)=-4⇒4(x2+2x+1)+9(y2+4y+4)=-4+4+36⇒4(x+1)2+9(y+2)2=36⇒4(x+1)236+9(y+2)236=1⇒(x+1)29+(y+2)24=1Comparing it with x2a2+y2b2=1, we get:a=3 and b=2So, the major and the minor axes of the ellipse are along the x-axis and y-axis, respectively.Now, e=1-b2a2⇒e=1-49⇒e=59⇒e=53
Q12.
Answer :
(c) 534×2+9y2=36⇒x29+y24=1Comparing it with x2a2+y2b2=1, we get:a=3 and b=2Here, a>b, so the major and the minor axes of the ellipse are along the x-axis and y-axis, respectively.Now, e=1-b2a2⇒e=1-49⇒e=59⇒e=53
Q13.
Answer :
(a) 235×2+9y2=1⇒x25+y29=1∴ a=5 and b=3Here, b>a, so the major and the minor axes of the ellipse are along the x-axis and the y-axis, respectively.Now, e=1-a2b2⇒e=1-59⇒e=49⇒e=23
Q14.
Answer :
(b) the latus rectum is 32×2+4y2=9⇒x29+y294=1Here,a>b∴ e=1-b2a2⇒e=1-994⇒e=1-14⇒e=32Latus rectum=2b2a =2×943 =32Focus =±ae,0 =332,0Directrix x=±ae =±332 =23
Q15.
Answer :
(c) 32According to the question, the latus rectum of an ellipse is half its minor axis.i.e. 2b2a=12×2b⇒2b2=ab⇒a=2bNow, e=1-b2a2⇒e=1-b24b2⇒e=1-14⇒e=34⇒e=32
Q16.
Answer :
(b) x-1264+y+1216=1According to the question, the centre is at 1,-1.a=8 Given⇒x-12a2+y+12b2=1 …(1)It passes through point 1,3.i.e. x=1 and y=3Putting these values in eq. (1), we get:1-12a2+3+12b2=1⇒16b2=1⇒b2=16 or b=4Substituting the values of a and b in eq. (1), we get: x-1264+y+1216=1
Q17.
Answer :
(d) 89×2+ 16y2= 144⇒x216+y29=1Here, a=4 and b=3The sum of the focal distances of any point on an ellipse is constant and equal to the length of the major axis of the ellipse.i.e. sum of the focal distances of any point on an ellipse=2a =2×4 =8
Q18.
Answer :
(a) 203e=1 2 GivenNow, e=1-b2a2⇒12=1-b2a2On squaring both sides, we get:14=1-b2a2⇒14=a2-b2a2⇒4a2-4b2=a2⇒3a2=4b2⇒b2a2=34⇒a2=4b23or a=2b3 …(1)Latus rectum=2b2a2If (2,4) and (10,10) are the ends points of a latus rectum. i.e. 10-22+10-42=2b2×32b⇒64+36=3bOn squaring both sides, we get:100=3b2⇒b=103Now, a=2b3⇒a=203×13⇒a=203So, the length of the semi major axis is 203.
Q19.
Answer :
(c) 2 <λ <5×22-λ+y2λ-5+1=0⇒x2λ-2+y25-λ=1To represent the equation of ellipse, we have: λ-2>0⇒λ>2and5-λ>0⇒5<λ∴ 2<λ<5
Q20.
Answer :
(b) 459×2-18x+25y2-100y-116=0⇒9(x2-2x)+25(y2-4y)=116⇒9(x2-2x+1)+25(y2-4y+4)=116+100+9⇒9(x-1)2+25(y-2)2=225⇒9(x-1)2225+25(y-2)2225=1⇒(x-1)225+(y-2)29=1Comparing it with x2a2+y2b2=1, we get:a=5 and b=3Here, a>b, so the major and the minor axes of the ellipse are along the x-axis and y-axis, respectively.Now, e=1-b2a2⇒e=1-925⇒e=1625⇒e=45
Q21.
Answer :
(d) 223Length of the major axis =2bLength of the minor axis=2aAccording to question, the major axis of the ellipse is three times the minor axis.i.e. 2b=3(2a)⇒2b=6a⇒a=2b/6⇒a=b/3, b=3aHere, a<b, so the major and the minor axes of the ellipse are along the x-axis and the y-axis, respectively.Now, e=1-a2b2⇒e=1-b29b2⇒e=1-19⇒e=89⇒e=223
Page 26.22 (Multiple Choice Questions)
Q22.
Answer :
(a) 3525×2+16y2=400⇒x216+y225=1 …(1)Comparing equation (1) with x2a2+y2b2=1, we get: a2=16 and b2=25Here, a<b, so the major and the minor axes of the given ellipse are along the y-axis and the x-axis, respectively.Now, e=1-a2b2⇒e=1-1625⇒e=925⇒e=35
Q23.
Answer :
(a) 235×2+9y2=1⇒x215+y219=1Comparing with the standard equation of the ellipse, we get: a2=15 and b2=19, i.e. a=15 and b=13Here, a>b Now, e=1-b2a2⇒e=1-1915⇒e=1-59⇒e=49⇒e=23
Q24.
Answer :
(c) 53
4×2+9y2=36⇒x29+y24=1 .. (1)Compairing equation (1 ) with x2a2+y2b2=1, we geta2=9 and b2=4Here, a>b, so the major and the minor axes of the given ellipse are along the x-axis and the y-axis, respectively.Now, e=1-b2a2⇒e=1-49⇒e=59⇒e=53
Page 27.13 Ex 27.1
Q1.
Answer :
Let S be the focus and Px,y be any point on the hyperbola.
Draw PM perpendicular to the directrix.
By definition:
SP = ePM
⇒x–12+y-12=3×x-y+32
Squaring both the sides, we get:
x+12+y-12=92x-y+32⇒x2+2x+1+y2-2y+1=92×2+y2+9-2xy-6y+6x⇒2×2+4x+2+2y2-4y+2=9×2+9y2+81-18xy-54y+54x⇒7×2+7y2+50x-50y-18xy+77=0
Equation of the hyperbola:
7×2+7y2+50x-50y-18xy+77=0
Q2.
Answer :
(i) Let S be the focus and Px,y be any point on the hyperbola.
Draw PM perpendicular to the directrix.
By definition:
SP = ePM
⇒ (x-0)2+(y-3)2=2x+y-12
Squaring both the sides:
(x-0)2+(y-3)2=4x+y-122⇒x2+y2+9-6y=2×2+y2+1+2xy-2y-2x⇒x2+y2+4xy+2y-4x-7=0
∴ Equation of the hyperbola = x2+y2+4xy+2y-4x-7=0
(ii) Let S be the focus and Px,y be any point on the hyperbola.
Draw PM perpendicular to the directrix.
By definition:
SP = ePM
⇒(x-1)2+(y-1)2=23x+4y+85
Squaring both the sides:
(x-1)2+(y-1)2=43x+4y+852⇒x2+1-2x+y2+1-2y=4259×2+16y2+64+24xy+64y+48x⇒25×2+25-50x+25y2+25-50y=36×2+64y2+256+96xy+256y+192x⇒11×2+39y2+96xy+306y+242x+206=0
∴ Equation of the hyperbola = 11×2+39y2+96xy+306y+242x+206=0
(iii) Let S be the focus and Px,y be any point on the hyperbola.
Draw PM perpendicular to the directrix.
By definition:
SP = ePM
⇒(x-1)2+(y-1)2=32x+y-15
Squaring both the sides:
(x-1)2+(y-1)2=32x+y-152⇒x2+1-2x+y2+1-2y=354×2+y2+1+4xy-2y-4x⇒5×2+5-10x+5y2+5-10y=12×2+3y2+3+12xy-6y-12x⇒7×2-2y2+12xy+4y-2x-7=0
∴ Equation of the hyperbola = 7×2-2y2+12xy+4y-2x-7=0
(iv) Let S be the focus and Px,y be any point on the hyperbola.
Draw PM perpendicular to the directrix.
By definition:
SP = ePM
= ePM
⇒(x-2)2+(y+1)2=22x+3y-113
Squaring both the sides:
(x-2)2+(y+1)2=42x+3y-1132⇒x2+4-4x+y2+1+2y=4134×2+9y2+1+12xy-6y-4x⇒13×2+52-52x+13y2+13+26y=16×2+36y2+4+48xy-24y-16x⇒3×2+23y2+48xy-50y+36x-61=0
∴ Equation of the hyperbola = 3×2+23y2+48xy-50y+36x-61=0
(v) Let S be the focus and Px,y be any point on the hyperbola.
Draw PM perpendicular to the directrix.
By definition:
SP = ePM
⇒(x-a)2+(y-0)2=432x-y+a5
Squaring both the sides:
(x-a)2+(y)2=1692x-y+a52⇒x2-2ax+a2+y2=16454×2+y2+a2-4xy-2ya+4xa⇒45×2-90ax+45a2+45y2=64×2+16y2+16a2-64xy-32ay+64ax⇒19×2-29y2-64xy-32ay+154ax-29a2=0
∴ Equation of the hyperbola = 19×2-29y2-64xy-32ay+154ax-29a2=0
(vi) Let S be the focus and Px,y be any point on the hyperbola.
Draw PM perpendicular to the directrix.
By definition:
SP = ePM
⇒(x-2)2+(y-2)2=2x+y-92
Squaring both the sides:
(x-2)2+(y-2)2=4x+y-922⇒x2-4x+4+y2-4y+4=2×2+y2+81+2xy-18y-18x⇒x2-4x+4+y2-4y+4=2×2+2y2+162+4xy-36y-36x⇒x2+y2+4xy-32y-32x+154=0
∴ Equation of the hyperbola = x2+y2+4xy-32y-32x+154=0
Q3.
Answer :
(i) Equation of the hyperbola:
9×2-16y2=144
This can be rewritten in the following way:
x216-y29=1
This is the standard equation of a hyperbola, where a2=16 and b2=9.
⇒b2=a2(e2-1)⇒9=16(e2-1)⇒e2-1=916⇒e2=2516⇒e=54
Coordinates of the foci are given by ±ae,0, i.e. ±5,0.
Equation of directrices:
x=±ae
⇒x=±454⇒5x±16=0
Length of the latus rectum of the hyperbola is 2b2a.
Length of the latus rectum = 2×94=92
(ii) Equation of the hyperbola:
16×2-9y2=-144
This can be rewritten in the following way:
x29-y216=-1
This is the standard equation of a hyperbola, where a2=9 and b2=16.
⇒a2=b2(e2-1)⇒9=16(e2-1)⇒e2-1=916⇒e2=2516⇒e=54
Coordinates of foci are given by 0,±ae, i.e. 0,±5.
Equation of the directrices:
y=±ae
⇒y=±454⇒5y±16=0
Length of the latus rectum of the hyperbola = 2a2b
Length of the latus rectum = 2×94=92
(iii) Equation of the hyperbola:
4×2-3y2=36
This can be rewritten in the following way:
4×236-3y236=1×29-y212=1
This is the standard equation of a hyperbola, where a2=9 and b2=12.
⇒b2=a2(e2-1)⇒12=9(e2-1)⇒e2-1=43⇒e2=73⇒e=73
Coordinates of the foci are given by ±ae,0, i.e. ±21,0.
Equation of the directrices:
x=±ae
⇒x=±373⇒7x±33=0
Length of the latus rectum of the hyperbola is 2b2a.
⇒2×123=8
(iv) Equation of the hyperbola:
3×2-y2=4
This can be rewritten in the following way:
3×24-y24=1⇒x243-y24=1
This is the standard equation of a hyperbola, where a2=43 and b2=4.
⇒b2=a2(e2-1)⇒4=43(e2-1)⇒e2-1=3⇒e2=4⇒e=2
Coordinates of the foci are given by ±ae,0, i.e. ±433,0.
Equation of the directrices:
x=±ae
x=±432⇒3x±1=0
Length of the latus rectum of the hyperbola = 2b2a
⇒2×443=43
(v) Equation of the hyperbola:
2×2-3y2=5
This can be rewritten in the following manner:
2×25-3y25=1⇒x252-y253=1
This is the standard equation of a hyperbola, where a2=52 and b2=53.
⇒b2=a2(e2-1)⇒53=52(e2-1)⇒e2-1=23⇒e2=53⇒e=53
Coordinates of the foci are given by ±ae,0, i.e. ±566,0.
Equation of the directrices:
x=±ae
x=±5253⇒x=±32⇒2x±3 = 0
Length of the latus rectum of the hyperbola is 2b2a.
⇒2×5352=10325
Q4.
Answer :
Equation of the hyperbola:
25×2-36y2=225
This equation can be rewritten in the following way:
25×2225-36y2225=1⇒x29-y222536=1
This is the standard equation of the hyperbola, where a2=9 and b2=22536.
Length of the transverse = 2a=2×3=6
Length of the conjugate axis = 2b=2×156=5
Eccentricity of the hyperbola is calculated using b2=a2(e2-1).
⇒22536=9e2-1⇒e2-1=2536⇒e2=6136⇒e=616
Length of the latus rectum =2b2a=2×225363=256
The coordinates of the foci are given by ±ae,0.
⇒±612,0
Q5.
Answer :
(i) The equation 16×2-9y2+32x+36y-164=0 can be simplified in the following way:
16(x2+2x)-9y2-4y=164⇒16(x2+2x+1)-9y2-4y+4=164+16-36⇒16(x+1)2-9y-22=144⇒(x+1)29-(y-2)216=1
Thus, the centre is -1,2.
Eccentricity of the hyperbola = a2+b2a=9+163=53
Foci = -1±5,2=-6,2,4,2
Equation of the directrices:
x+1=±ae⇒x=±3×35-1⇒x=±95-1⇒5x-4=0 or 5x+14=0
(ii) The equation x2-y2+4x=0 can be simplified in the following manner:
(x2+4x+4)-y2=4⇒x+22-y2=4⇒(x+2)24-y21=1
Thus, the centre is -2,0.
Eccentricity of the hyperbola = a2+b2a=4+12=52
Foci = -2±5,0
Equation of the directrices:
x+2=±ae⇒x+2=±5
(iii) The equation x2-3y2-2x=8 can be simplified in the following manner:
(x2-2x+1)-3y2=8+1⇒x-12-3y2=9⇒(x-1)29-y23=1
Thus, the centre is 1,0.
Eccentricity of the hyperbola = a2+b2a=9+33=233
Foci = 1±23,0
Equation of the directrices:
x-1=±ae⇒x=1±233
Q6.
Answer :
(i) The distance between the foci is 2ae.
∴2ae=16⇒ae=8
e=2
∴ a2=8⇒a=42
Also, b2=a2(e2-1)⇒b2=32(2-1)⇒b2=32
Therefore, the standard form of the hyperbola is given below:
x232-y232=1×2-y2=32
(ii) The distance between the foci is 2ae.
∴ 2ae=13⇒ae=132
Length of the conjugate axis, 2b=5
⇒b=52
Also, b2=a2(e2-1)⇒522=1322-a2⇒a2=169-254⇒a2=1444=36⇒a=6
Therefore, the standard form of the hyperbola is x236-4y225=1.
or 25×2-144y2=900
(iii) Length of the conjugate axis, 2b=7
⇒b=72
Let the equation of the hyperbola be x2a2-y2b2=1.
It passes through 3,-2.
∴ 32a2-(-2)2722=1⇒32a2-1649=1⇒9a2=1649+1⇒9a2=6549⇒a2=44165
Therefore, the standard form of the hyperbola is 65×2441-4y249=1.
or 65×2-36y2=441
Q7.
Answer :
(i) The centre of the hyperbola is the midpoint of the line joining the two focii.
So, the coordinates of the centre are 6-42,4+42, i.e. 1, 4.
Let 2a and 2b be the length of the transverse and conjugate axis and let e be the eccentricity.
⇒x-12a2-y-42b2=1
Distance between the two focii = 2ae
2ae=6+42+4-42⇒2ae=10⇒ae=5⇒a=52
Also, b2=ae2-a2⇒b2=25-254⇒b2=754
Equation of the hyperbola is given below:
4x-1225-4y-4275=1⇒4×2-2x+125-y2-8y+1675=1⇒4×2-8x+425-4y2-32y+6475=1⇒34×2-8x+4-4y2-32y+64=75⇒12×2-24x+12-4y2+32y-64=75⇒12×2-24x-4y2+32y-127=0
(ii) The centre of the hyperbola is given below:
-8+162,-1-12=4,-1
If the other focus is S’m,n, then it is calculated in the following way:
4=17+m2⇒m=-9 And -1=-1+n2⇒n=-1
Thus, the other focus is -9,-1.
Distance between the vertices: 2a=16+82+-1+12⇒2a=24⇒a=12
Distance between the foci:
2c=17+92+-1+12⇒2c=26⇒c=13
Also, c2=a2+b2⇒b2=169-144⇒b2=25
Equation of the hyperbola is given below:
x-42144-y+1225=1⇒x2-8x+16144-y2+2y+125=1⇒25×2-200x+400-144y2+288y+144=3600⇒25×2-200x-144y2-288y-3344=0
(iii) The centre of the hyperbola is the midpoint of the line joining the two focii.
So, the coordinates of the centre are 4+82,2+22, i.e. 6, 2.
Let 2a and 2b be the length of the transverse and conjugate axis. Let e be the eccentricity.
⇒x-62a2-y-22b2=1
Distance between the two focii = 2ae
2ae=4-82+2-22⇒2ae=16⇒ae=8⇒a=4
Also, b2=ae2-a2⇒b2=64-16⇒b2=48
Equation of the hyperbola:
x-6216-y-2248=1⇒x2-12x+3616-y2-4y+448=1⇒3×2-12x+36-y2-4y+4=48⇒3×2-36x+108-y2+4y-4=48⇒3×2-36x-y2+4y+56=0
(iv) The Vertices of the hyperbola are 0,±7.
∴ b=7
The foci is 0,±283.
∴ be=283
Also, a2=b2e2-1⇒a2=2832-49⇒a2=3439
Therefore, the equation of the hyperbola is-9×2343+y249=1.
Q8.
Answer :
The lengths of the conjugate axis and the transverse axis are 2b and 2a, respectively.
We have:
⇒2b=34×2a⇒b=34a
Using the relation b2=a2(e2-1), we get:
⇒342a2=a2(e2-1)⇒916=e2-1⇒e2=2516⇒e=54
Therefore, the eccentricity of the hyperbola is 54.
Page 27.14 Ex 27.1
Q9.
Answer :
(i) The equation of the hyperbola with centre (x0,y0) is given by
x-x02a2-y-y02b2=1Focus = ae+x0, y0
Vertex = (a+x0, y0)
∴ ae=2 and a=1b2=22-a2⇒b2=22-12⇒b2=3
⇒x-321-y-223=1⇒3x-32-y-22=3
(ii) The equation of the hyperbola with centre (x0,y0) is given by
x-x02a2-y-y02b2=1Focus = ae+x0, y0
∴ ae=-2⇒a=-1b2=22-a2⇒b2=-22–12⇒b2=3
⇒x-621-y-223=1⇒3x-62-y-22=3
Q10.
Answer :
Equation of the hyperbola:
x2a2-y2b2=1
If the axes of the hyperbola are equal, then a=b.
Then, equation of the hyperbola becomes x2-y2=a2.
∴ b2=a2e2-1⇒a2=a2e2-1⇒1=e2-1⇒e2=2⇒e=2
Thus, the centre C0,0 and the focus are given by S2a,0 and S’-2a,0, respectively.
Let Pα,β be any point on the parabola.
So, it will satisfy the equation.
α2-β2=a2
∴ SP2=2a-α2+β2=2a2+α2-22aα+β2
S’P2=-2a-α2+β2=2a2+α2+22aα+β2
Now, SP2.S’P2=2a2+α2-22aα+β22a2+α2+22aα+β2=4a4+4a2α2+β2+α2+β22-8a2α2=4a2a2-2α2+4a2α2+β2+α2+β22=4a2α2-β2-2α2+4a2α2+β2+α2+β22=-4a2α2+β2+4a2α2+β2+α2+β22=α2+β22=CP4
∴ SP.S’P=CP2
Q11.
Answer :
(i) The vertices of the hyperbola are ±2,0 and the foci are ±3,0.
Thus, the value of a=2 and ae=3.
Now, using the relation b2=a2(e2-1), we get:
⇒b2=9-4⇒b2=5
Thus, the equation of the hyperbola is x24-y25=1.
(ii) The vertices of the hyperbola are 0,±5 and the foci are 0,±8
Thus, the value of a=5 and ae=8.
Now, using the relation b2=a2(e2-1), we get:
⇒b2=64-25⇒b2=39
Thus, the equation of the hyperbola is -x239+y225=1.
(iii) The vertices of the hyperbola are 0,±3 and the foci are 0,±5.
Thus, the value of a=3 and ae=5.
Now, using the relation b2=a2(e2-1), we get:
⇒b2=25-9⇒b2=16
Thus, the equation of the hyperbola is -x216+y29=1.
(iv) The foci of the hyperbola are ±5,0 and the transverse axis is 8.
Thus, the value of ae=5 and 2a = 8.
⇒a=4
Now, using the relation b2=a2(e2-1), we get:
⇒b2=25-16⇒b2=9
Thus, the equation of the hyperbola isx216-y29=1.
(v) The foci of the hyperbola are 0,±13 and the conjugate axis is 24.
Thus, the value of ae=13 and 2b = 24.
⇒ b = 12
Now, using the relation b2=a2(e2-1), we get:
⇒a2=169-144⇒a2=25
Thus, the equation of the hyperbola is-x2144+y225=1.
(vi) The foci of the hyperbola are ±35,0 and the latus rectum is 8.
Thus, the value of ae=35
and 2b2a=8⇒b2=4a
Now, using the relation b2=a2(e2-1), we get:
⇒4a=45-a2⇒a2+4a-45=0⇒a-5a+9=0⇒a=-9, 5
b2=-36 or 20
Since negative value is not possible, it is equal to 20.
Thus, the equation of the hyperbola isx225-y220=1.
(vii) The foci of the hyperbola are ±4,0 and the latus rectum is 12.
Thus, the value of ae=4
and 2b2a=12⇒b2=6a
Now, using the relation b2=a2(e2-1), we get:
⇒6a=16-a2⇒a2+6a-16=0⇒a-2a+8=0⇒a=2, or -8
b2=12 or -48
Since negative value is not possible, its value is 12.
Thus, the equation of the hyperbola isx24-y212=1.
(viii) The vertices of hyperbola are ±7,0 and eccentricity is 43
Thus, the value of a=7.
Now, using the relation b2=a2(e2-1), we get:
⇒b2=49169-1⇒b2=49×79=3439
Thus, the equation of the hyperbola isx249-9y2343=1.
(ix) The foci of hyperbola are 0,±10 that pass through 2,3.
Thus, the value of ae=10.By squaring both the sides, we get:ae2=10⇒a2+b2=10⇒b2=10-a2
Let the equation of the hyperbola be y2a2-x2b2=1.
It passes through 2,3.
⇒32a2-2210-a2=1⇒90-9a2-4a2=10a2-a4⇒a4-23a2+90=0⇒a2-18a2-5=0⇒a2=18,5
Now, b2=-8 or 5
If we neglect the negative value, then b2 = 5.
Thus, the equation of the hyperbola isy25-x25=1.
(x) The foci of the hyperbola are 0,±12 and the latus rectum is 36.
Thus, the value of ae=12.
and 2b2a=36⇒b2=18a
Now, using the relation b2=a2(e2-1), we get:
⇒18a=144-a2⇒a2+18a-144=0⇒a+24a-6=0⇒a=-24, or 6
b2=-432 or 108 (but negative value is not possible)
Thus, the equation of the hyperbola isy236-x2108=1.
Page 27.15 (Very Short Answers)
Q1.
Answer :
Equation of the hyperbola:
9 x2 – 16y 2 = 144 ….. (1)
Equation (1) can be rewritten in the following way:
9×2144 – 16y 2144 = 144144⇒x216 – y 29 = 1
⇒x242-y232=1
This becomes the standard equation of the hyperbola with its major axis a=4 and minor axis b=3.
Eccentricity, e = a2+b2a
Substituting the value of a and b, we get:
e = 42+324 =16+94 =54
Therefore, the eccentricity is 54.
Q2.
Answer :
The lengths of the latus rectum and the transverse axis are 2b2a and 2a, respectively.
According to the given statement, length of the latus rectum is half of its trasverse axis.
∴2b2a = 12×2a⇒2b2a = a ⇒ 2b2=a2
Eccentricity, e = a2+b2a
Substituting the value b2=a22, we get:
e = a2+a22a =a32a =32
Therefore, the eccentricity is 32.
Q3.
Answer :
Equation of the hyperbola:
9×2-16y2=144 ….. (1)
This equation (1) can be rewritten in the following way:
⇒9×2144-16y2144=1⇒x216-y29=1
This becomes a standard form of the hyperbola with transverse axis a=4 and conjugate axis b=3.
Eccentricity of the hyperbola, e=a2+b2a =42+324 =16+94 =54
The foci of the hyperbola are of the form ae,0 and -ae,0.
Therefore, the foci are 5,0 and -5,0.4
Q4.
Answer :
The foci of the hyperbola are of the form ae,0 and -ae,0.
Distance between the foci = ae- (-ae2+02 =2ae2 =2ae
Distance between the foci is 16 and eccentricity of the hyperbola is 2.
∴ 2ae=16⇒22a=16⇒a=42
Now, b2=a2(e2-1) ⇒b2=422((2)2-1) ⇒b2=32
Equation of the hyperbola is given below:
x2422-y232=1⇒x232-y232=1
Q5.
Answer :
Equation of the hyperbola:
x2144-y281=125
Simplifying the above equation, we get:
25×2144-25y281=1⇒x214425-y28125=1⇒x21252-y2952=1
This is the standard form of hyperbola with a=125and b=95.
Eccentricity of the hyperbola, e=1252+952125 =1512
The foci of the hyperbola are of the form ae,0 and -ae,0.
So, foci of the hyperbola are 3,0 and -3,0.
The foci of the hyperbola coincide with the foci of the ellipse.
For ellipse,
a=4
Using the relationa2-b2=ae, we get:
42-b2=3⇒16-b2=9⇒b2=7
Therefore, the value of b2 is 7.
Q6.
Answer :
Equation of the hyperbola:
16×2-9y2=144
This equation can be rewritten in the following way:
16×2144-9y2144=1⇒x29-y216=1⇒x232-y242=1
This is the standard form of a hyperbola with a=3 and b=4.
Length of the latus rectum = 2b2a
Substituting the value of a and b, we get:
Length of the latus rectum =2×423=323
Q7.
Answer :
The standard equation of hyperbola is given below:
x2a2-y2b2=1
Let the latus rectum be QR, which passes through one of the focus. QR subtends a right angle at point P.
It passes through the focus ae,±y.
∴ae2a2-y2b2=1⇒y2b2=ae2a2-1⇒y2b2=e2-1⇒y=±be2-1
Now, the slope of PQ is be2-1ae+a and the slope of PR is-be2-1ae+a.
The lines PQ and PR are perpendicular, so the product of the slope is -1.
⇒be2-1ae+a×-be2-1ae+a=-1⇒b2e2-1=ae+a2⇒b2e2-1=a2e+12⇒e2-12=e+12⇒e4-2e2+1=e2+2e+1⇒e4-3e2-2e=0⇒ee3-3e-2=0⇒ee-2e+1e+1=0
∴ e=0,-1,2
The value of e can neither be negative nor zero.
Therefore, the value of eccentricity is 2.
Q8.
Answer :
We have:
x=8secθ, y=8tanθ
On squaring and subtracting, we get:x2-y2=64sec2θ-64tan2θ⇒x2-y2=64⇒x264-y264=1
∴ a = b = 8
Distance between the directrices of hyperbola is 2a2a2+b2.
⇒2×6464+64=12882=162=82
Q9.
Answer :
The vertices of the hyperbola and the foci are ±a,0 and ±ae,0, respectively.
∴ a=3 and ae=5
Using the relation b2=a2e2-1, we get:
⇒b2=ae2-a2⇒b2=25-9⇒b2=16⇒b=4
Therefore, the equation of hyperbola is x29-y216=1.
Q10.
Answer :
The standard form of the ellipse is x218+y24=1, where a2=18 and b2=4.
So, the eccentricity is calculated in the following way:
⇒b2=a2(1-e12)⇒4=18(1-e12)⇒29=1-e12⇒e12=79
The standard form of the hyperbola is x29-y24=1, where a2=9 and b2=4.
So, the eccentricity is calculated in the following way:
b2=a2(e22-1)⇒4=9(e22-1)⇒49=e22-1⇒e22=139
∴ 2e12+e22=2×79+139 =279 =3
Page 27.16 (Multiple Choice Questions)
Q1.
Answer :
(a) 16x2 − 9y2 = 144
The vertices of the hyperbola are ±3,0 and foci are ±5,0.
Thus, the values of a and ae are 3 and 5, respectively.
Now, using the relation b2=a2(e2-1), we get:
b2=25-9⇒b2=16
Equation of the hyperbola is given below:
x29-y216=1⇒16×2-9y2=144
Q2.
Answer :
(c) 2 e12 + e22 = 3
The standard form of the ellipse is x218+y24=1, where a2=18 and b2=4.
So, the eccentricity is calculated in the following way:
b2=a2(1-e12)⇒4=18(1-e12)⇒29=1-e12⇒e12=79
The standard form of the hyperbola is x29-y24=1, where a2=9 and b2=4.
So, the eccentricity is calculated in the following way:
b2=a2(e22-1)⇒4=9(e22-1)⇒49=e22-1⇒e22=139
∴ 2e12+e22=2×79+139 =279 =3
Q3.
Answer :
(a) 82
We have:
x=8secθ, y=8tanθ
On squaring and subtracting:x2-y2= 8sec2θ – 8tan2θ⇒x2- y2=8⇒x28-y28=1
∴ a = b = 8
Distance between the directrices of the hyperbola = 2a2a2+b2
Distance between the directrices=2×6464+64 =12882 =162 =82
Q4.
Answer :
(d) 2xy − 4x + 4y + 1 = 0
Let P(x,y) be any point on the hyperbola.
Then, the distance of any point from the focus is eccentricity times the distance from the directrix.
∴ x-12+y+12=2x-y+12
Squaring both the sides, we get:
(x-1)2+(y+1)2=x-y+12×2-2x+1+y2+1+2y=x2+y2+1-2xy-2y+2x2xy-4x+4y+1=0
Q5.
Answer :
(a) 54
Standard form of a hyperbola = x216-y29=1
Here, a2=16 and y2=9
The eccentricity is calculated in the following way:
b2=a2e2-1⇒9=16e2-1⇒e2-1=916⇒e2=2516⇒e=54
Q6.
Answer :
(a) a hyperbola
Let P(x,y) be any point on the hyperbola x2a2-y2b2=1.By definition, we have:PA=ex-ae=ex-aand PB=ex+ae=ex+a∴ PB-PA=ex+a-ex-a=2a=k
Q7.
Answer :
(c) 32
The lengths of the latus rectum and the transverse axis are 2b2a and 2a, respectively.
According to the given statement, length of the latus rectum is half of its transverse axis.
∴2b2a = 12×2a⇒2b2a = a ⇒ 2b2=a2
Eccentricity, e = a2+b2a
Substituting the value b2=a22 , we get:
e = a2+a22a =a32a =32
∴ Eccentricity is 32
Q8.
Answer :
(b) 52
The equation of the hyperbola is x2-4y2=1.
This can be rewritten in the following way:
x21-y214=1
This is the standard form of a hyperbola, where a2=1 and b2=14.
The value of eccentricity is calculated in the following way:
b2=a2(e2-1)⇒14=(e2-1)⇒e2=54⇒e=52
Q9.
Answer :
(c) length of the transverse axis
Let Px,ybe any point on the hyperbola, and S, S’ be the focus with coordinates ±ae,0.
⇒ S’P-SP=2a
Thus, the difference of the focal distances of any point on the hyperbola is equal to the length of the transverse axis.
Q10.
Answer :
(c) (± 5, 0)
The equation of the hyperbola is given below:
9×2-16y2=144
This equation can be rewritten in the following way:
9×2144-16y2144=1⇒x216-y29=1
This is the standard equation of a hyperbola, where a2=16 and b2=9.
The eccentricity is calculated in the following way:
b2=a2(e2-1)⇒9=16(e2-1)⇒916=e2-1⇒e=54
Foci = ±ae,0=±5,0
Q11.
Answer :
(d) x2 − y2 = 32
The distance between the foci is 2ae.
∴ 2ae=16⇒ae=8
e=2
∴ a2=8⇒a=42
Also, b2=a2(e2-1)⇒b2=32(2-1)⇒b2=32
Standard form of the hyperbola is given below:
x232-y232=1×2-y2=32
Q12.
Answer :
(b) 2 < e22 − e12 < 3
The conic 9×2+4y2=36 can rewritten in the following way:
9×236+4y236=1⇒x24+y29=1
This is the standard equation of an ellipse.
∴ b2=a21-e12⇒9=41-e12 ⇒e12=-54
The conic 9×2-4y2=36 can rewritten in the following way:
9×236-4y236=1⇒x24-y29=1
This is the standard equation of a hyperbola.
∴ b2=a2e22-1⇒9=4e22-1⇒e22=134
∴ e22-e12=134+54=2.5
Page 27.17 (Multiple Choice Questions)
Q13.
Answer :
(b) π4
The hyperbola x2-y2sec2α=5 can be rewritten in the following way:
x25-y25cos2α=1
This is the standard form of a hyperbola, where a2=5 and b2=5cos2α.
⇒b2=a2e12-1⇒5cos2α=5e12-1⇒e12=cos2α+1 …..1
The ellipse x2sec2α+y2=25 can be rewritten in the following way:
x225cos2α+y225=1
This is the standard form of an ellipse, where a2=25 and b2=25cos2α.
b2=a21-e22⇒e22=1-cos2α⇒e22=sin2α ……(2)
According to the question,
cos2α+1=3sin2α⇒2=4sin2α⇒sinα=12⇒α=π4
Q14.
Answer :
(a) (x-1)225/4-(y-4)275/4=1
The centre of the hyperbola is the midpoint of the line joining the two foci.
So, the coordinates of the centre are open parentheses fraction numerator 6 minus 4 over denominator 2 end fraction comma fraction numerator 4 plus 4 over denominator 2 end fraction close parentheses comma space straight i. straight e. space open parentheses 1 comma space 4 close parentheses.
Let 2a and 2b be the length of the transverse and the conjugate axes, respectively. Also, let e be the eccentricity.
⇒x-12a2-y-42b2=1
Now, distance between the two foci = 2ae
2ae=6+42+4-42⇒2ae=10⇒ae=5⇒a=52
Also, b2=ae2-a2⇒b2=25-254⇒b2=754
Equation of the hyperbola is given below:
x-1225/4-y-4275/4=1
Q15.
Answer :
(c) 625
The point of intersection of x-3y=1and the hyperbola x2-4y2=1 is calculated in the following way:
1+3y2-4y2=1⇒1+6y+9y2-4y2=1⇒5y2+6y=0⇒y=0 or y=- 65
If y=0, then x=1.
If y=-65, then x=1+3×-65=-135.
So, the points are 1,0 and -135,-65.
∴ Length = 1+1352+0+652=625
Q16.
Answer :
(b) 32/3
The standard form of the hyperbola 16×2-9y2=144 is x29-y216=1.
Here, a2=9, b2=16
Latus rectum of the hyperbola = 2b2a=2×163=323
Q17.
Answer :
(a) (±5/6,0)
The given equation of hyperbola is 2×2-3y2=5. It can be rewritten in the following way:
2×25-3y25=1⇒x252-y253=1
This is the standard equation of a parabola, where a2=52 and b2=53.
The eccentricity can be calculated in the following way:
b2=a2e2-1⇒53=52e2-1⇒e2-1=23⇒e2=53⇒e=53
Coordinates of the foci = ±ae,0=±56, 0
Q18.
Answer :
(a) 2
We eliminate t in x=a2t+1t,y=a2t-1t.
On squaring both the sides in the equations x=a2t+1t,y=a2t-1t, we get:
4x2a2=t2+1t2+2⇒4x2a2-2=t2+1t2 …1
Also, 4y2a2=t2+1t2-2⇒4y2a2+2=t2+1t2 …2
From (1) and (2), we get:
4x2a2-4y2a2=4⇒x2a2-y2a2=1
This is the standard equation of a hyperbola, where a2=b2.
Eccentricity of the hyperbola, e=a2+a2a=2
Q19.
Answer :
(a) 3 (x − 6)<sup>2</sup> − (y −2)<sup>2</sup> = 3
The equation of the hyperbola with centre (x0,y0) is given by
x-x02a2-y-y02b2=1Focus = ae+x0, y0
∴ ae=-2⇒a=-1b2=22-a2⇒b2=-22–12⇒b2=3
∴ x-621-y-223=1⇒3x-62-y-22=3
Q20.
Answer :
(b) 2
The equations of lines 3x-y-43λ=0 and 3λx+λy-43=0 can be rewritten as 3x-y=43λ and 3λx+λy=43 , respectively.
Multiplying the equations:
3λx2-λy2=48λ⇒3λx248λ-λy248λ=1⇒x216-y248=1
This is the standard equation of a hyperbola, where a2=16 and b2=48.
Eccentricity, e=a2+b2a2⇒e=16+4816⇒e=84⇒e=2
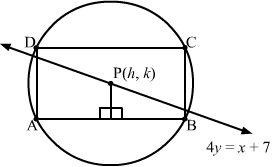
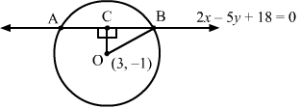
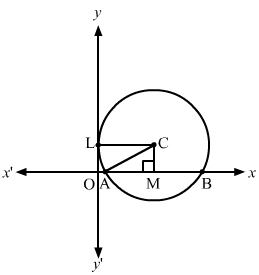
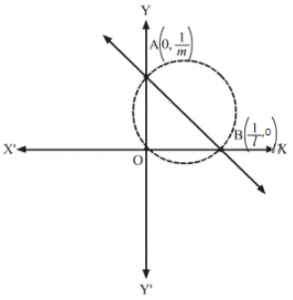
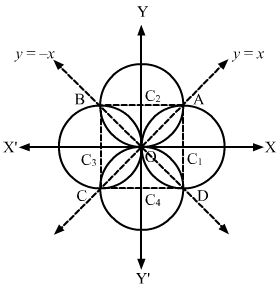
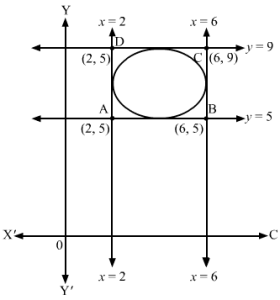
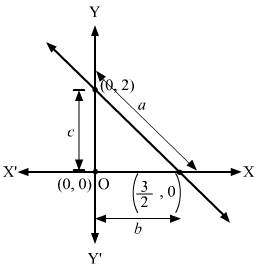
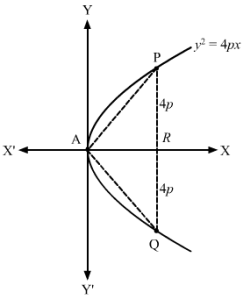
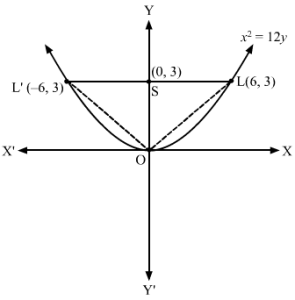
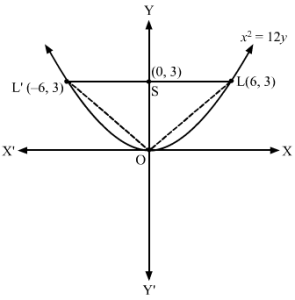
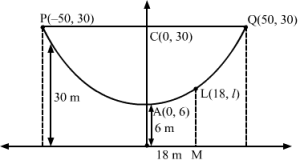
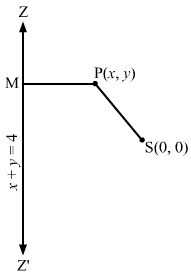
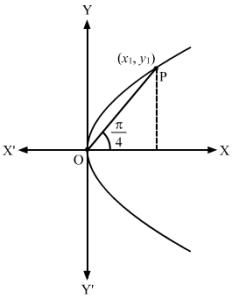
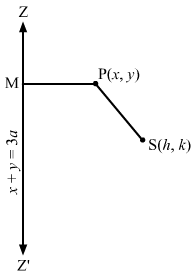
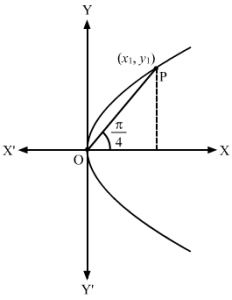
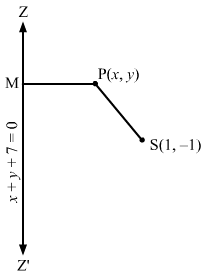
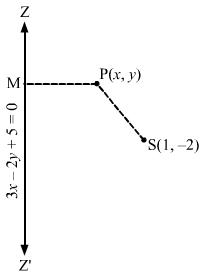
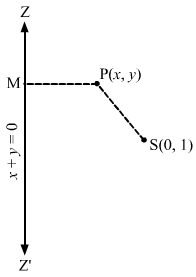
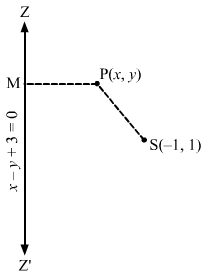
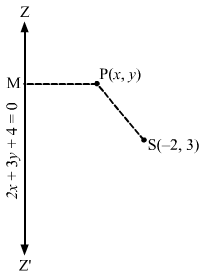
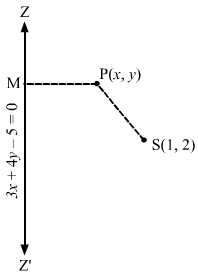

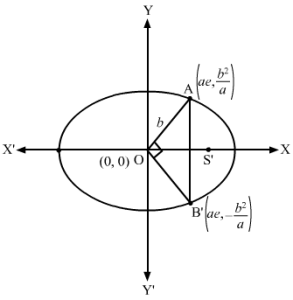
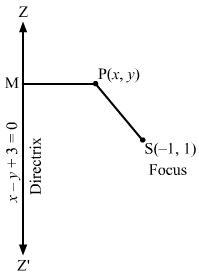
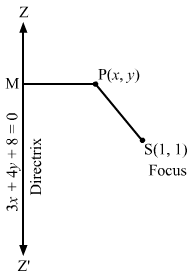
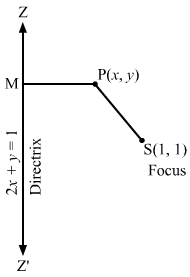
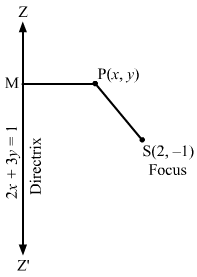
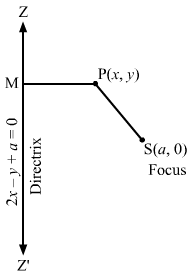
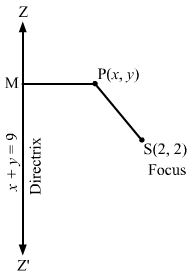
Leave a Reply