Notes For All Chapters Science Class 9
Introduction
What is motion?
State of Rest: An object is said to be in the state of rest if it does not change its position with respect to time and its surroundings.
State of Motion: An object is said to be in the state of motion if it changes its position with respect to time and its surroundings.
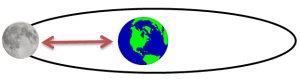
Note: Rest & Motion are relative terms.
Figure 1.
Figure 2.
Take a look at the numbers. Figure 1 shows the car to the right of the tree. Figure 2 shows the car to the left of the tree after 2 seconds. The car must have moved from one location to another because the tree does not move. As a result, the tree serves as the frame of reference in this case.
Motion can be of different types depending upon the type of path by which the object is going through.
(i) Circulatory motion/Circular motion – In a circular path.
(ii) Linear motion – In a straight line path.
Distance and Displacement
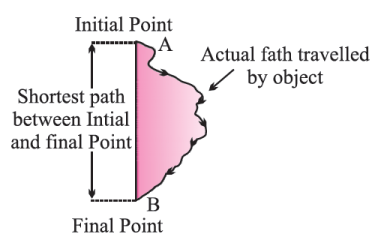
→ The actual path or length travelled by a object during its journey from its initial position to its final position is called the distance.
→ Distance is a scalar quantity which requires only magnitude but no direction to explain it.
Example: Ramesh travelled 65 km. (Distance is measured by odometer in vehicles.)
→ Displacement is a vector quantity requiring both magnitude and direction for its explanation.
Example: Ramesh travelled 65 km south-west from Clock Tower.
→ Displacement can be zero (when initial point and final point of motion are same)
Example: circular motion.
Difference between Distance and Displacement
Distance | Displacement |
| Length of actual path travelled by an object. | Shortest length between initial point and far point of an object. |
| It is scalar quantity. | It is vector quantity. |
| It remains positive, can’t be ‘0’ or negative. | It can be positive (+ve), negative (-ve) or zero. |
| Distance can be equal to displacement (in linear path). | Displacement can be equal to distance or its lesser than distance. |
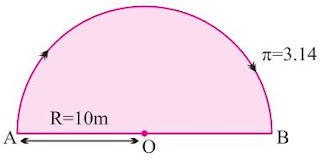
Example 1: A body travels in a semicircular path of radius 10 m starting its motion from point ‘A’ to point ‘B’. Calculate the distance and displacement.
Solution
Total distance travelled by body, S = ?
Given, π = 3.14, R = 10 m
S = πR
= 3.14 × 10 m
= 31.4 m
Total displacement of body, D = ?
Given, R = 10 m
D = 2×R = 2×10 m = 20 m
Example 2: A body travels 4 km towards North then he turn to his right and travels another 4 km before coming to rest. Calculate (i) total distance travelled, (ii) total displacement.
Solution
Total distance travelled = OA + AB
= 4 km + 4 km = 8 km
Total displacement = OB
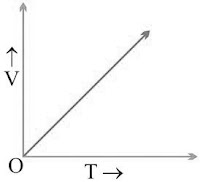
Uniform and Non-uniform Motions
Uniform Motion
→ When a body travels equal distance in equal interval of time, then the motion is said to be uniform motion.
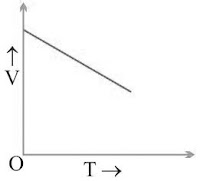
Non-uniform Motion
→ In this type of motion, the body will travel unequal distances in equal intervals of time.
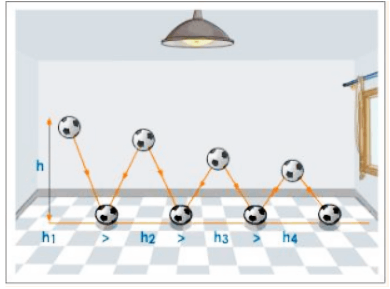
For example, when a rubber ball is dropped from a certain height (h1), it bounces up to a height less than the initial one (h2). It keeps bouncing, but the height to which it rises keeps decreasing (h3, h4). The ball’s distance traveled per unit time decreases. The ball’s speed varies from point to point. This type of speed is known as variable speed.
Non-uniform motion is of two types :
(i) Accelerated Motion : When speed of a body increases with time.
(ii) De-accelerated Motion: When motion of a body decreases with time.
Speed
→ The measurement of distance travelled by a body per unit time is called speed.
• Speed (v) = Distance Travelled/Time Taken = s/t
• SI unit = m/s (meter/second)
→ If a body is executing uniform motion, then there will be a constant speed or uniform motion.
→ If a body is travelling with non-uniform motion, then the speed will not remain uniform but have different values throughout the motion of such body.
→ For non-uniform motion, average speed will describe one single value of speed throughout the motion of the body.
• Average speed = Total distance travelled/Total time taken
Conversion Factor
• Change from km/hr to m/s = 1000m/(60×60)s = 5/18 m/s
Example: What will be the speed of body in m/s and km/hr if it travels 40 kms in 5 hrs ?
Solution
Distance (s) = 40 km
Time (t) = 5 hrs.
Speed (in km/hr) = Total distance/Total time = 40/5 = 8 km/hr
40 km = 40 × 1000 m = 40,000 m
5 hrs = 5 × 60 × 60 sec.
Speed (in m/s) = (40 × 1000)/(5×60 ×60) = 80/36 = 2.22 m/s
Equation of Motion (For Uniformly Accelerated Motion)
First Equation: v = u + at
Final velocity = Initial velocity + Acceleration × Time
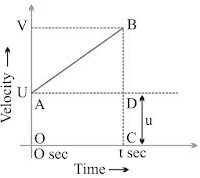
Graphical Derivation
Suppose a body has initial velocity ‘u’ (i.e., velocity at time t = 0 sec.) at point ‘A’ and this velocity changes to ‘v’ at point ‘B’ in ‘t’ secs. i.e., final velocity will be ‘v’.
For such a body there will be an acceleration.
a = Change in velocity/Change in Time
⇒ a = (OB – OA)/(OC-0) = (v-u)/(t-0)
⇒ a = (v-u)/t
⇒ v = u + at
Second Equation: s = ut + ½ at2
Distance travelled by object = Area of OABC (trapezium)
= Area of OADC (rectangle) + Area of ∆ABD
= OA × AD + ½ × AD × BD
= u × t + ½ × t × (v – u)
= ut + ½ × t × at
⇒ s = ut + ½ at2 (∵a = (v-u)/t)
Third Equation: v22 = u2 + 2as
s = Area of trapezium OABC
⇒ v2 = u2 + 2as
Example 1: A car starting from rest moves with uniform acceleration of 0.1 ms-2 for 4 mins. Find the speed and distance travelled.
Solution
u = 0 ms-1 (∵ car is at rest)
a = 0.1 ms-2
t = 4 × 60 = 240 sec.
v = ?
From, v = u + at
v = 0 + (0.1 × 240)
⇒ v = 24 ms-1
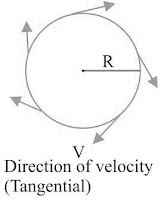
Uniform Circular Motion
→ If a body is moving in a circular path with uniform speed, then it is said to be executing uniform circular motion.
→ In such a motion the speed may be same throughout the motion but its velocity (which is tangential) is different at each and every point of its motion. Thus, uniform circular motion is an accelerated motion.


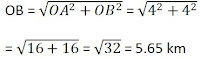
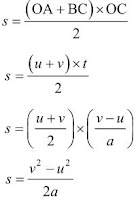
Thanks for free question Bank and notes
this was really helpful