Page 1.12 Ex. 1.2
Q1.
Answer :
(i) Given rational number is
Now we have to express this rational number into decimal form. So we will use long division method as below.
Hence,
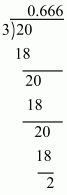
(ii) Given rational number is
Now we have to express this rational number into decimal form. So we will use long division method as below.
Hence,
(iii) Given rational number is
Now we have to express this rational number into decimal form. So we will use long division method as below.
Hence,
Q2.
Answer :
(i) Given rational number is
Now we have to express this rational number into decimal form. So we will use long division method
Hence,
(ii) Given rational number is
Now we have to express this rational number into decimal form. So we will use long division method
Hence,
(iii) Given rational number is
Now we have to express this rational number into decimal form. So we will use long division method
Hence,
(iv) Given rational number is
Now we have to express this rational number into decimal form. So we will use long division method
Hence,
(v) Given rational number is
Now we have to express this rational number into decimal form. So we will use long division method
Hence,
(vi) Given rational number is
Now we have to express this rational number into decimal form. So we will use long division method
Hence,
Page 1.13 Ex. 1.2
Q3.
Answer :
Prime factorization is the process of finding which prime numbers you need to multiply together to get a certain number. So prime factorization of denominators (q) must have only the power of 2 or 5 or both.
Page 1.22 Ex. 1.3
Q1.
Answer :
(i) Given decimal is
Now we have to convert given decimal number into the form
Let
Hence,
(ii) Given decimal is
Now we have to convert given decimal number into form
Let
Hence,
(iii) Given decimal is
Now we have to express the given decimal number into form
Let
Hence,
(iv) Given decimal is 7.010
Now we have to express the given decimal number into form
Let
Hence,
(v) Given decimal is
Now we have to find given decimal number into form
Let
Hence,
(vi) Given decimal is
Now we have to find given decimal number into form
Hence,
Q2.
Answer :
(i) Let
Hence,
(ii) Let
Hence,
(iii) Let
Hence,
(iv) Let
Hence,
(v) Let
Hence,
(vi) Let
Let
Therefore,
Hence,
(vii) Let
Since,
Therefore,
Hence,
Page 1.30 Ex. 1.4
Q1.
An irrational number is a real number that cannot be reduced to any ratio between an integer p and a natural number q.
If the decimal representation of an irrational number is non-terminating and non-repeating, then it is called irrational number. For example
Q2.
Answer :
Every rational number must have either terminating or non-terminating but irrational number must have non- terminating and non-repeating.
A rational number is a number that can be written as simple fraction (ratio) and denominator is not equal to zero while an irrational is a number that cannot be written as a ratio.
Q3.
Answer :
(i) Let
Therefore,
It is non-terminating and non-repeating
Hence is an irrational number
(ii) Let
Therefore,
It is terminating.
Hence is a rational number.
(iii) Let be the rational
Squaring on both sides
Since, x is rational
is rational
is rational
is rational
is rational
But, is irrational
So, we arrive at a contradiction.
Hence is an irrational number
(iv) Let be the rational number
Squaring on both sides, we get
Since, x is a rational number
is rational number
is rational number
is rational number
is rational number
But is an irrational number
So, we arrive at contradiction
Hence is an irrational number
(v) Let be the rational number
Squaring on both sides, we get
Now, x is rational number
is rational number
is rational number
is rational number
is rational number
But is an irrational number
So, we arrive at a contradiction
Hence is an irrational number
(vi) Let
Since, is rational number,
⇒ x – 6 is a rational nu8mber
⇒is a rational number
⇒is a rational number
But we know thatis an irrational number, which is a contradiction
So is an irrational number
(vii) Let
So is a rational number
(viii) Let be rational number
Using the formula
⇒is a rational number
⇒is a rational number
But we know thatis an irrational number
So, we arrive at a contradiction
So is an irrational number.
(ix) Let be the rational number
Squaring on both sides, we get
Now, x is rational
is rational
is rational
is rational
is rational
But, is irrational. So we arrive at contradiction
Hence is an irrational number
(x) Let
It is non-terminating or non-repeating
Hence is an irrational number
(xi) Let
Hence is a rational number
(xii) Given that
It is terminating
Hence it is a rational number
(xiii) Given number
It is repeating
Hence it is a rational number
(xiv) Given number is
It is non-terminating or non-repeating
Hence it is an irrational number.
Q4.
Answer :
(i) Given number is x =
x = 2, which is a rational number
(ii) Given number is
So it is an irrational number
(iii) Given number is
Now we have to check whether it is rational or irrational
So it is a rational
(iv) Given that
Now we have to check whether it is rational or irrational
So it is an irrational number
(v) Given that
Now we have to check whether it is rational or irrational
Since,
So it is a rational number
(vi) Given that
Now we have to check whether it is rational or irrational
Since,
So it is rational number.
Page 1.31 Ex. 1.4
Q5.
Answer :
(i) Given that
Now we have to find the value of x
So it x is an irrational number
(ii) Given that
Now we have to find the value of y
So y is a rational number
(iii) Given that
Now we have to find the value of z
So it is rational number
(iv) Given that
Now we have to find the value of u
So it is an irrational number
(v) Given that
Now we have to find the value of v
So it is an irrational number
(vi) Given that
Now we have to find the value of w
So it is an irrational number
(vii) Given that
Now we have to find the value of t
So it is an irrational number
Q6.
Answer :
(i) Let
And, so
Therefore, and
are two irrational numbers and their difference is a rational number
(ii) Let are two irrational numbers and their difference is an irrational number
Because is an irrational number
(iii) Let are two irrational numbers and their sum is a rational number
That is
(iv) Let are two irrational numbers and their sum is an irrational number
That is
(v) Let are two irrational numbers and their product is a rational number
That is
(vi) Let are two irrational numbers and their product is an irrational number
That is
(vii) Let are two irrational numbers and their quotient is a rational number
That is
(viii) Let are two irrational numbers and their quotient is an irrational number
That is
Q7.
Answer :
Let
Here the decimal representation of a and b are non-terminating and non-repeating. So we observe that in first decimal place a and b have the same digit but digit in the second place of their decimal representation are distinct. And the number a has 3 and b has 1. So a > b.
Hence two rational numbers are lying between
and
Q8.
Answer :
Let and
Here the decimal representation of a and b are non-terminating and non-repeating. So we observe that in first decimal place a and b have the same digit but digit in the second place of their decimal representation are distinct. And the number a has 1 and b has 3. So a < b.
Hence two rational numbers are lying between
and
Q9.
Answer :
Let
Here a and bare rational numbers .Since a has terminating and b has repeating decimal. We observe that in second decimal place a has 1 and b has 2. So a < b.
Hence one irrational number is lying between
and
Q10.
Answer :
Let
Here decimal representation of a and b are non-terminating and non-repeating. So a and b are irrational numbers. We observe that in first two decimal place of a and b have the same digit but digit in the third place of their decimal representation is distinct.
Therefore, a > b.
Hence one rational number is lying between
and
And irrational number is lying between
and
Q11.
Answer :
Let
Here a and b are rational number. So we observe that in first decimal place a and b have same digit .So a < b.
Hence two irrational numbers are and
lying between 0.5 and 0.55.
Q12.
Answer :
Let
Here a and b are rational number. So we observe that in first decimal place a and b have same digit. So a < b.
Hence two irrational numbers are and
lying between 0.1 and 0.12.
Q13.
Answer :
Given that is an irrational number
Now we have to prove is an irrational number
Let is a rational
Squaring on both sides
Now is rational
is rational
is rational
is rational
But, is an irrational
Thus we arrive at contradiction thatis a rational which is wrong.
Hence is an irrational
Q14.
Answer :
Let and
Here we observe that in the first decimal x has digit 7 and y has 8. So x < y. In the second decimal place x has digit 1. So, if we considering irrational numbers
We find that
Hence are required irrational numbers.
Page 1.35 Ex. 1.5
Q1.
Answer :
(i) Every point on the number line corresponds to a real number which may be either rational or an irrational number.
(ii) The decimal form of an irrational number is neither terminating nor repeating.
(iii) The decimal representation of rational number is either terminating, recurring.
(iv) Every real number is either rational number or an irrational number because rational or an irrational number is a family of real number.
Page 1.36 Ex. 1.5
Q2.
Answer :
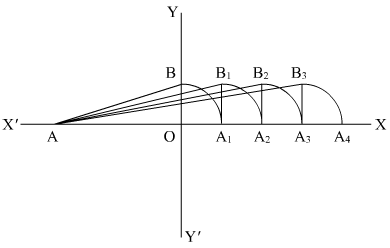
We are asked to represent on the number line
We will follow certain algorithm to represent these numbers on real line
We will consider point A as reference point to measure the distance
(1) First of all draw a line AX and YY’ perpendicular to AX
(2) Consider , so
(3) Take A as center and AB as radius, draw an arc which cuts line AX at A1
(4) Draw a perpendicular line A1B1 to AX such that and
(5) Take A as center and AB1 as radius and draw an arc which cuts the line AX at A2.
Here
So
So A2 is the representation for
(1) Draw line A2B2 perpendicular to AX
(2) Take A center and AB2 as radius and draw an arc which cuts the horizontal line at A3 such that
So point A3 is the representation of
(3) Again draw the perpendicular lineto AX
(4) Take A as center and AB3 as radius and draw an arc which cuts the horizontal line at A4
Here;
A4 is basically the representation of
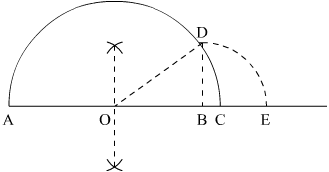
Q3.
Answer :
We are asked to represent the real numbers on the real number line
We will follow a certain algorithm to represent these numbers on real number line
(a)
We will take A as reference point to measure the distance
(1) Draw a sufficiently large line and mark a point A on it
(2) Take a point B on the line such that
(3) Mark a point C on the line such that
(4) Find mid point of AB and let it be O
(5) Take O as center and OC as radius and draw a semi circle. Draw a perpendicular BD which cuts the semi circle at D
(6) Take B as the center and BD as radius, draw an arc which cuts the horizontal line at E
(7) Point E is the representation of
(b)
We will take A as reference point to measure the distance. We will follow the same figure in the part (a)
(1) Draw a sufficiently large line and mark a point A on it
(2) Take a point B on the line such that
(3) Mark a point C on the line such that
(4) Find mid point of AB and let it be O
(5) Take O as center and OC as radius and draw a semi circle. Draw a perpendicular BC which cuts the semi circle at D
(6) Take B as the center and BD as radius, draw an arc which cuts the horizontal line at E
(7) Point E is the representation of
(c)
We will take A as reference point to measure the distance. We will follow the same figure in the part (a)
(1) Draw a sufficiently large line and mark a point A on
(2) Take a point B on the line such that
(3) Mark a point C on the line such that
(4) Find mid point of AB and let it be O
(5) Take O as center and OC as radius and draw a semi circle. Draw a perpendicular BC which cuts the semi circle at D
(6) Take B as the center and BD as radius, draw an arc which cuts the horizontal line at E
(7) Point E is the representation of
Q4.
(i) True, because rational or an irrational number is a family of real number. So every real number is either rational or an irrational number.
(ii) True, because the decimal representation of an irrational is always non-terminating or non-repeating. So is an irrational number.
(iii) False, because we can represent irrational numbers by points on the number line.
Page 1.39 Formative Assessment_MCQ
Q1.
Answer :
The decimal expansion of an irrational number is non-terminating and non- repeating. Thus, we can say that a number, whose decimal expansion is non-terminating and non- repeating, called irrational number. And the decimal expansion of rational number is either terminating or repeating. Thus, we can say that a number, whose decimal expansion is either terminating or repeating, is called a rational number.
Hence the correct option is .
Q2.
Answer :
Since, and
are two irrational number and
Therefore, sum of two irrational numbers may be rational
Now, letand
be two irrational numbers and
Therefore, sum of two irrational number may be irrational
Hence the correct option is .
Q3.
Answer :
The sum of irrational number and rational number is always irrational number.
Let a be a rational number and b be an irrational number.
Then,
As 2ab is irrational therefore is irrational.
Hence is irrational.
Therefore answer is .
Page 1.40 Formative Assessment_MCQ
Q4.
Hence the correct option is.
Q5.
Answer :
Given that
And 7 is not a perfect square.
Hence the correct option is.
Q6.
Answer :
Given that
Here is non-terminating or non-repeating. So it is an irrational number.
Hence the correct option is.
Q7.
Answer :
Given that
Here,, this is the form of
. So this is a rational number
Hence the correct option is.
Q8.
Answer :
Since the given number is repeating, so it is rational number because rational number is always either terminating or repeating
Hence the correct option is.
Q9.
Answer :
The term “natural number” refers either to a member of the set of positive integer.
And natural number starts from one of counting digit .Thus, if n is a natural number then sometimes n is a perfect square and sometimes it is not.
Therefore, sometimesis a natural number and sometimes it is an irrational number
Hence the correct option is.
Q10.
Answer :
Given that
Here is repeating but non-terminating.
Hence the correct option is.
Q11.
Answer :
In basic mathematics, number line is a picture of straight line on which every point is assumed to correspond to real number.
Hence the correct option is.
Q12.
Answer :
Let
Here a and b are rational numbers. So we observe that in first decimal place a and b have distinct. According to question a < b.so an irrational number between 2 and 2.5 is OR
Hence the correct answer is.
Q13.
Answer :
Given decimal numbers are
Here the number is non terminating or non-repeating.
Hence the correct option is.
Q14.
Answer :
We are given the following expression and asked to find out the number of consecutive zeros
We basically, will focus on the powers of 2 and 5 because the multiplication of these two number gives one zero. So
23×34×54×7=23×54×34×7=23×53×5×34×7=2×53×5×34×7=103×5×34×7=5×81×7×1000=2835000
Therefore the consecutive zeros at the last is 3
So the option (a) is correct
Q15.
Answer :
Given that
The correct option is.
Page 1.41 Formative Assessment_MCQ
Q16.
Answer :
Given number is
The correct option is
Q17.
Answer :
Give number is. Now multiplying by
in the given number, we have
Hence the correct option is
Q18.
Answer :
Given that
Now we have to express this number into form
Let X =
The correct option is
Q19.
Answer :
Given that
Now we have to express this number into the form of
The correct option is
Q20.
Answer :
Given that
Now we have to express this number into form
The correct option is
Q21.
Answer :
Given that
Let
Now we have to find the value of
The correct option is
Page 1.5 Ex. 1.1
Q1.
Yes, zero is a rational number because it is either terminating or non-terminating so we can write in the form of , where p and q are natural numbers and q is not equal to zero.
So,
Therefore,
Q2.
Answer :
We need to find 5 rational numbers between 1 and 2.
Consider,
And
Hence 5 rational numbers between 1 and 2 are: OR
.
Q3.
Answer :
We need to find 6 rational numbers between 3 and 4.
Consider,
And
Hence 6 rational numbers between 3 and 4 are
Q4.
Answer :
We need to find 5 rational numbers betweenand
.
Since, LCM of denominators
So, consider
And,
Hence 5 rational numbers between and
are:
OR
Q5.
Answer :
(i) False, because whole numbers start from zero and natural numbers start from one
(ii) True, because it can be written in the form of a fraction with denominator 1
(iii) False
(iv) True, because natural numbers belong to whole numbers
(v) False, because set of whole numbers contains only zero and set of positive integers, whereas set of integers is the collection of zero and all positive and negative integers.
(vi) False, because rational numbers include fractions but set of whole number does not include fractions.
Page 2.12 Ex. 2.1
Q1.
Answer :
We have to simplify the following, assuming thatare positive real numbers
(i) Given
As x is positive real number then we have
Hence the simplified value of is
(ii) Given
As x and y are positive real numbers then we can write
By using law of rational exponents we have
Hence the simplified value of is
(iii) Given
As x and y are positive real numbers then we have
By using law of rational exponents we have
By using law of rational exponents we have
Hence the simplified value of 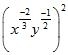
.
iv) x-23 y4 ÷ xy-12=x12-23 y412 ÷ x × y-1212=x12×-23 × y4×12×12 × y-12×12 =x-13 × y2x12 × y-14by using the law of rational exponents, am ÷ an = am-n, we have x-13-12 × y2+14=x-56 × y94 =y94x56v. 243 x10 y5 z105=243 × x10 × y5 × z1015=24315 × x1015 × y5110 × z1015=3515 × x10×15 × y5×15 × z10×15=3 × x2 × y × z2=3x2yz2vi x-4y-1054=x-454y-1054=x-4×54y-10×54=x-5y-252=y252x5
Q2.
Answer :
(1) Given
By using law of rational exponents we have
Hence the value of 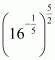
(ii) Given
Hence the value of is
(iii) Given
The value of is
(iv) Given
Hence the value of 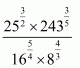
(v) Given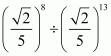
By using the law of rational exponents
Hence the value of 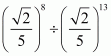
(vi) Given 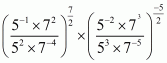
Hence the value of 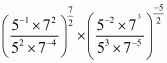
Q3.
Answer :
(i) We have to prove that
By using rational exponent we get,
Hence,
(ii) We have to prove that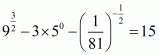
Hence,
(iii) We have to prove that
Now,
Hence,
(iv) We have to prove that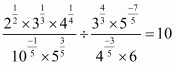
Let
Hence,
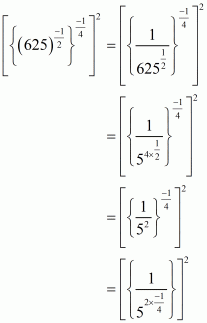
(v) We have to prove that
Let
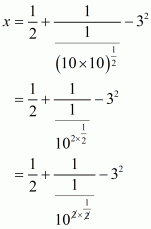
Hence,
(vi) We have to prove that . So,
Let
Hence,
(vii) We have to prove that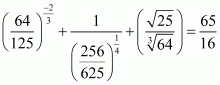
By taking least common factor we get
Hence,
(viii) We have to prove that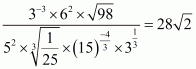
Let
Hence,
(ix) We have to prove that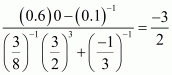
Let
Hence,
Q4.
Answer :
We are given. We have to find the value of
Since
By using the law of exponents we get,
On equating the exponents we get,
Hence,
Q5.
Answer :
From the following we have to find the value of x
(i) Given
By using rational exponents
On equating the exponents we get,
The value of x is
(ii) Given
On equating the exponents
Hence the value of x is
(iii) Given
Comparing exponents we have,
Hence the value of x is
(iv) Given
On equating the exponents of 5 and 3 we get,
And,
The value of x is
(v) Given
On equating the exponent we get
And,
Hence the value of x is
(vi) Given
On equating the exponents we get
And,
Hence the value of x is
Page 2.13 Formative Assessment_VSA
Q1.
Answer :
We have to writein decimal form. So,
Hence the decimal form of is
Q2.
Answer :
State the product law of exponents.
If is any real number and
,
are positive integers, then
By definition, we have
(
factor)
(
factor)
to
factors
Thus the exponent “product rule” tells us that, when multiplying two powers that have the same base, we can add the exponents.
Q3.
Answer :
State the quotient law of exponents.
The quotient rule tells us that we can divide two powers with the same base by subtracting the exponents. If a is a non-zero real number and m, n are positive integers, then
We shall divide the proof into three parts
(i) when
(ii) when
(iii) when
Case 1
When
We have
Case 2
When
We get
Cancelling common factors in numerator and denominator we get,
By definition we can write 1 as
Case 3
When
In this case, we have
Hence, whether
,
or,
Q4.
Answer :
State the power law of exponents.
The “power rule” tell us that to raise a power to a power, just multiply the exponents.
If a is any real number and m, n are positive integers, then
We have,
factors
factors
Hence,
Q5.
Answer :
We have to find the value of L =
By using rational exponents, we get
By using rational exponents we get
By definition we can write as 1
Hence the value of expression is .
Q6.
Answer :
We have to find the value of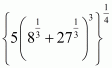
By using rational exponents we get
Hence the simplified value of 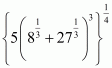
Q7.
Answer :
We have to simplify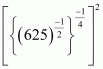
Hence, the value of 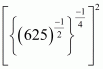
Q8.
Answer :
We have to simplify. So,
By using rational exponents, we get
Hence the value of is
Page 3.13 Ex. 3.2
Q1.
Answer :
(i) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified to.
(ii) We know that rationalization factor foris
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified to.
(iii) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified to.
(iv) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified to.
(v) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified to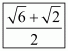
(vi) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified to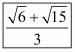
(vii) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified to.
Page 3.14 Ex. 3.2
Q2.
Answer :
(i) We know that rationalization factor of the denominator is. We will multiply numerator and denominator of the given expression
by
, to get
The value of expression can be round off to three decimal places as.
Hence the given expression is simplified to.
(ii) We know that rationalization factor of the denominator is . We will multiply numerator and denominator of the given expression
by
, to get
The value of expression can be round off to three decimal places as
.
Hence the given expression is simplified to.
(iii) We know that rationalization factor of the denominator is. We will multiply numerator and denominator of the given expression
by
, to get
The value of expression can be round off to three decimal places as
.
Hence the given expression is simplified to.
(iv) We know that rationalization factor of the denominator is. We will multiply numerator and denominator of the given expression
by
, to get
The value of expression can be round off to three decimal places as
.
Hence the given expression is simplified to.
(v) Given that
Putting the value of, we get
The value of expression can be round off to three decimal places as
.
Hence the given expression is simplified to.
(vi) We know that rationalization factor of the denominator is. We will multiply numerator and denominator of the given expression
by
, to get
Putting the value of and
, we get
The value of expression can be round off to three decimal places as
.
Hence the given expression is simplified to.
Q3.
Answer :
(i) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified with rational denominator to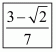
(ii) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified with rational denominator to.
(iii) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified with rational denominator to.
(iv) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified with rational denominator to.
(v) We know that rationalization factor for is
.We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified with rational denominator to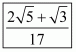
(vi) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified with rational denominator to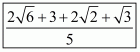
(vii) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified with rational denominator to.
(viii) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified with rational denominator to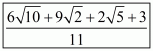
(ix) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified with rational denominator to .
Q4.
Answer :
(i) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified to.
(ii) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified to.
(iii) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified to.
(vi) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified to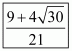
(v) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified to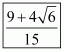
(vi) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Hence the given expression is simplified to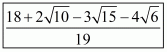
Q5.
Answer :
(i) We know that rationalization factor forand
are
and
respectively. We will multiply numerator and denominator of the given expression
and
by
and
respectively, to get
Hence the given expression is simplified to.
(ii) We know that rationalization factor forand
are
and
respectively. We will multiply numerator and denominator of the given expression
and
by
and
respectively, to get
Hence the given expression is simplified to.
(iii) We know that rationalization factor forand
are
and
respectively. We will multiply numerator and denominator of the given expression
and
by
and
respectively, to get
Hence the given expression is simplified to.
(iv) We know that rationalization factor forand
are
and
respectively. We will multiply numerator and denominator of the given expression
and
by
and
respectively, to get
Hence the given expression is simplified to.
(v) We know that rationalization factor forand
are
and
respectively. We will multiply numerator and denominator of the given expression
and
by
and
respectively, to get
Hence the given expression is simplified to.
Q6.
Answer :
(i) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
On equating rational and irrational terms, we get
Hence, we get.
(ii) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
On equating rational and irrational terms, we get
Hence, we get.
(iii) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
On equating rational and irrational terms, we get
Hence, we get.
(iv) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
On equating rational and irrational terms, we get
Hence, we get.
(v) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
On equating rational and irrational terms, we get
Hence, we get.
(vi) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
On equating rational and irrational terms, we get
Hence, we get.
Q7.
Answer :
We know that. We have to find the value of
.
As therefore,
We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Putting the value of and
, we get
Hence the value of the given expression.
Page 3.15 Ex. 3.2
Q8.
Answer :
We know that. We have to find the value of
. As
therefore,
We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Putting the value of x and , we get
Hence the given expression is simplified to.
Q9.
Answer :
We know that rationalization factor for is
. We will multiply denominator and numerator of the given expression
by
, to get
Putting the values of and
, we get
Hence value of the given expression is.
Q10.
Answer :
(i) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Putting the values of, we get
Hence the given expression is simplified to.
(ii) We know that rationalization factor for is
. We will multiply numerator and denominator of the given expression
by
, to get
Putting the value of, we get
Hence the given expression is simplified to.
Q11.
Answer :
We have,
It can be simplified as
On squaring both sides, we get
The given equation can be rewritten as.
Therefore, we have
Hence, the value of given expression is.
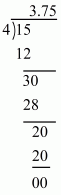
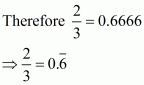
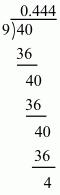
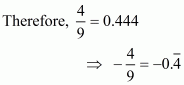
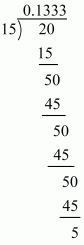
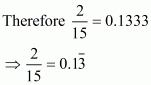
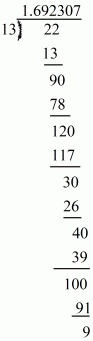
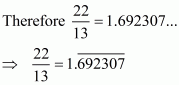
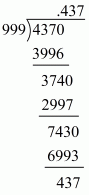
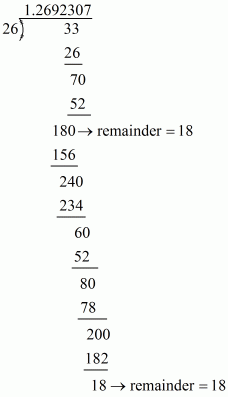
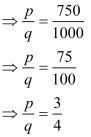
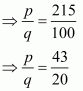
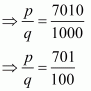
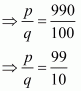
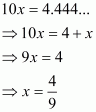
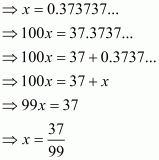
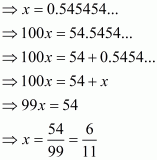
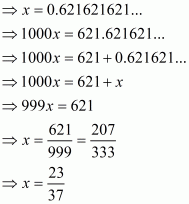
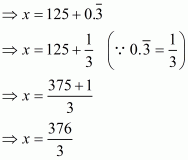
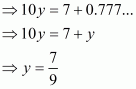
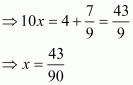
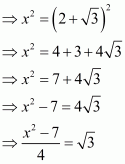
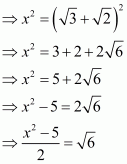
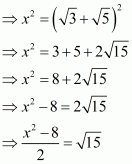
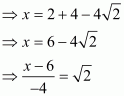
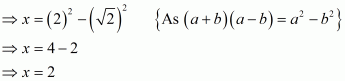
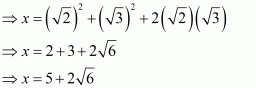
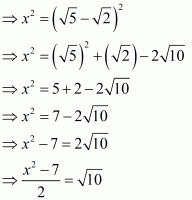
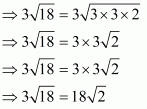
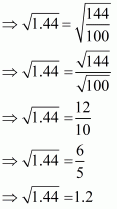
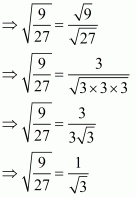
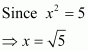
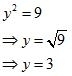
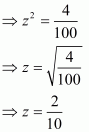
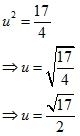
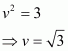
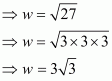
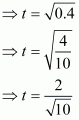
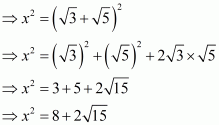
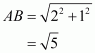
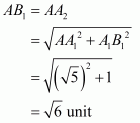
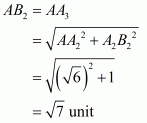
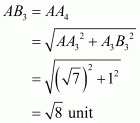
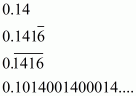
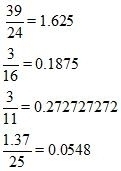
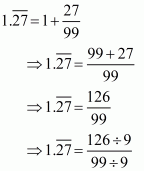
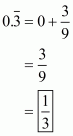
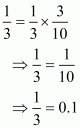
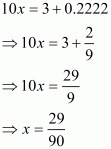
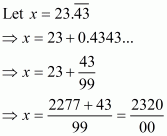
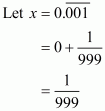
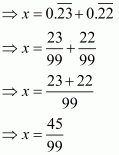
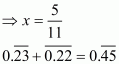
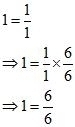
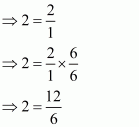
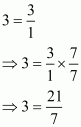
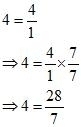
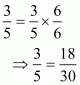
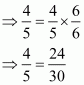
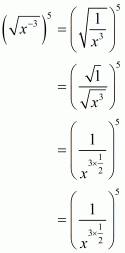
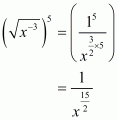
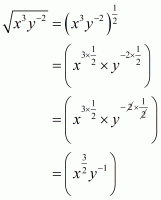
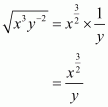
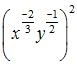
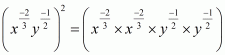
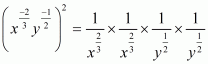
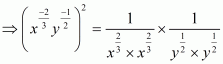
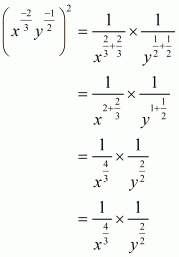
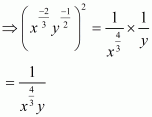
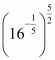
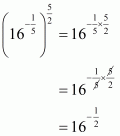
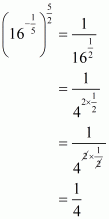
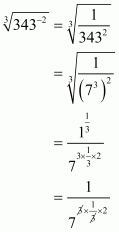
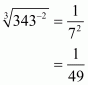
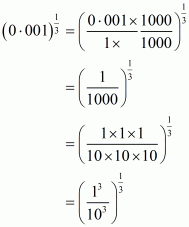
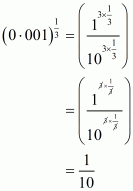
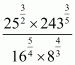
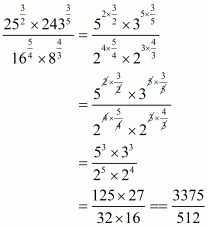
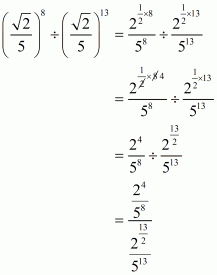
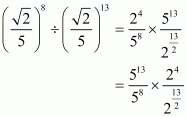
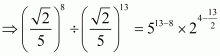
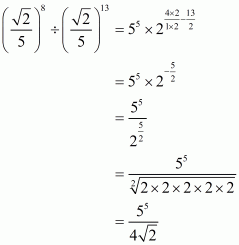
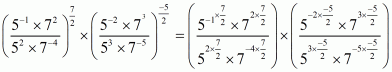
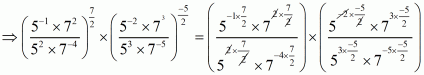
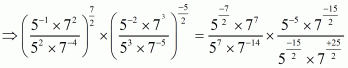
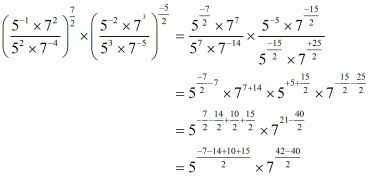
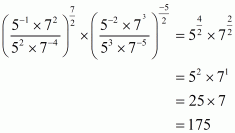
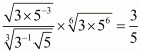
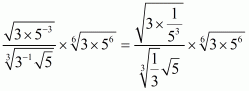
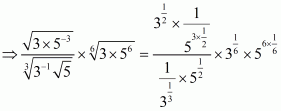
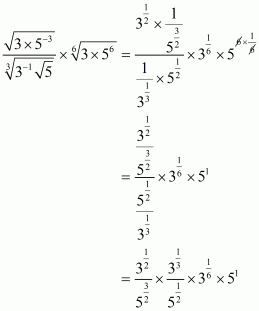
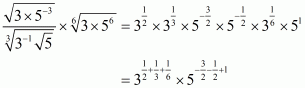
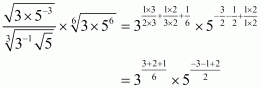
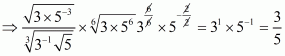
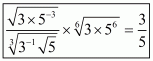
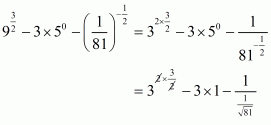
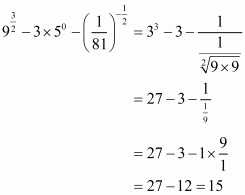
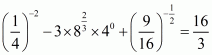
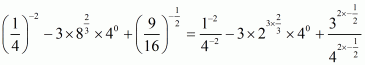
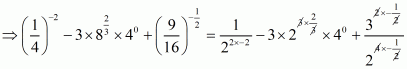
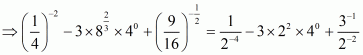
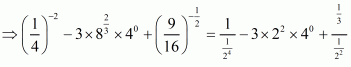
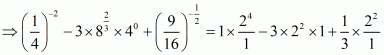
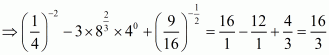
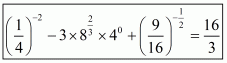
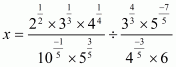
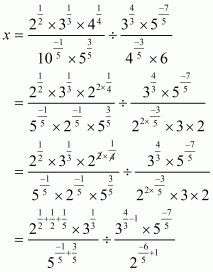
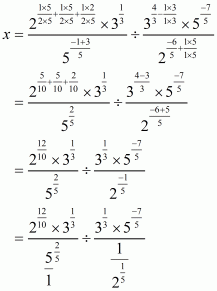
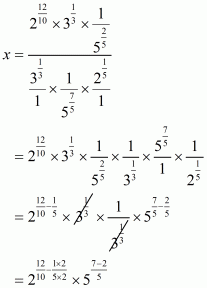
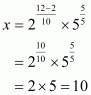
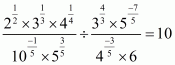
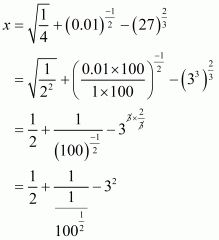
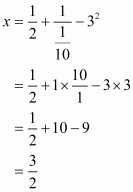
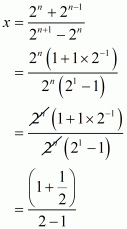
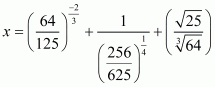
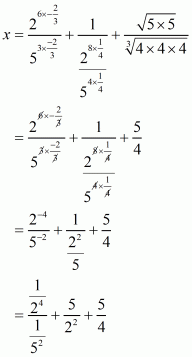
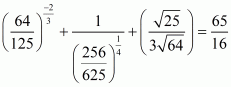
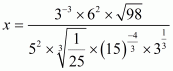
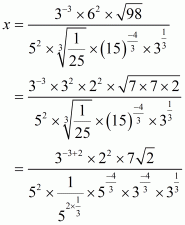
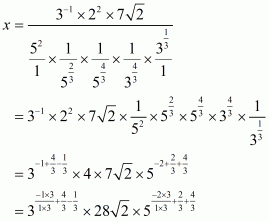
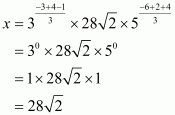
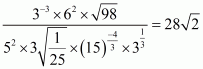
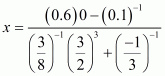
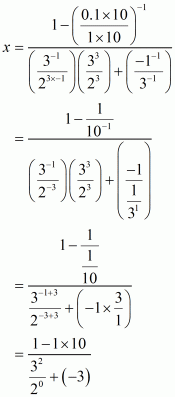
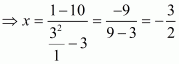
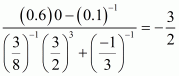
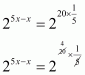
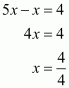
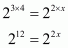
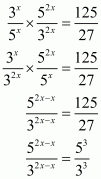
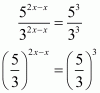
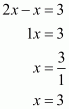
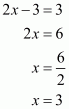
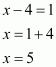
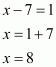
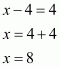
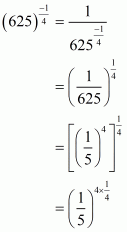
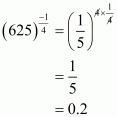
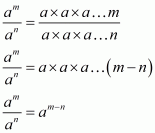
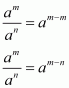
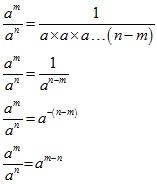
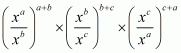
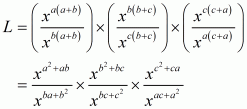
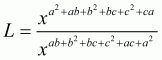
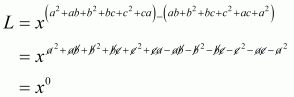
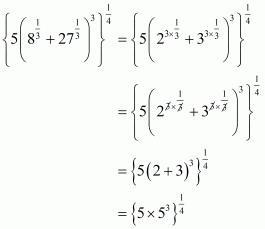
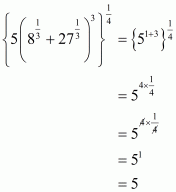
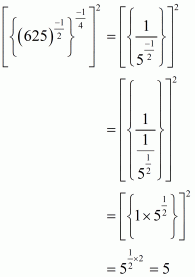
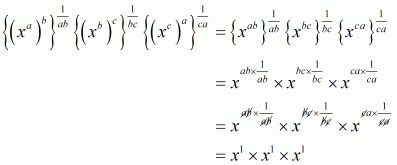
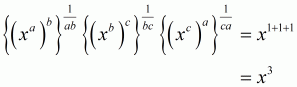
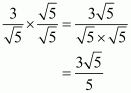
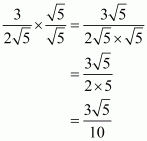
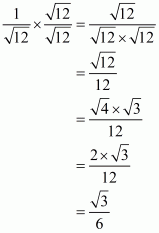
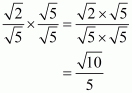
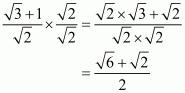
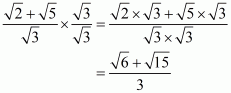
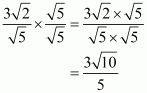
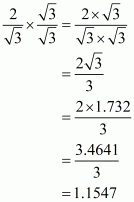
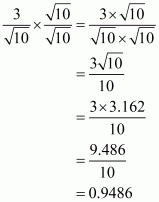
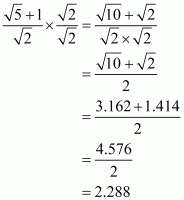
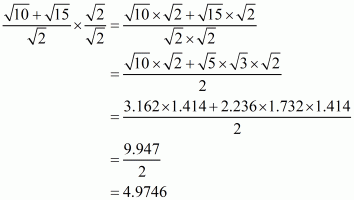
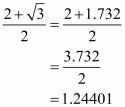
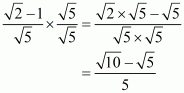
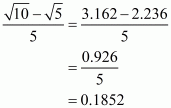
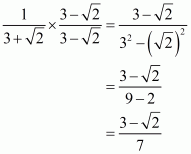
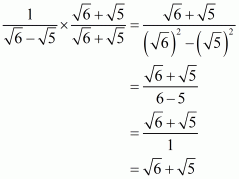
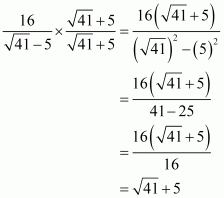
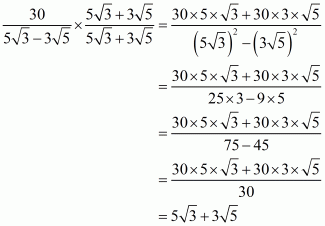
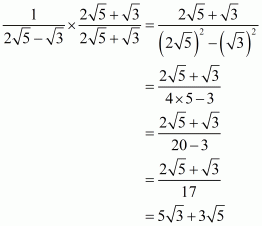
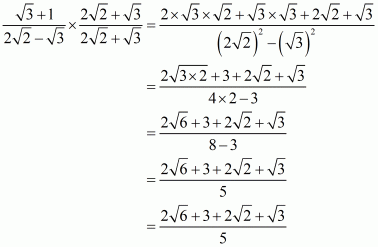
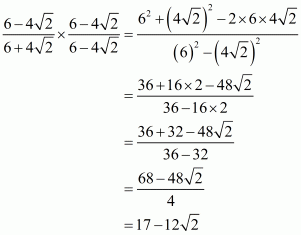
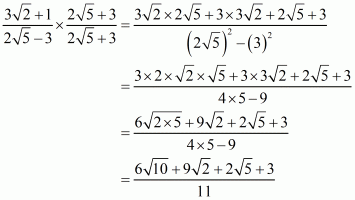
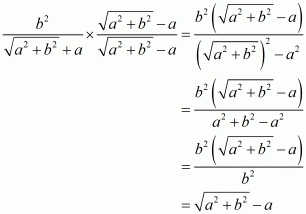
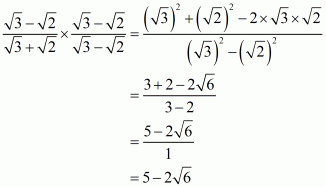
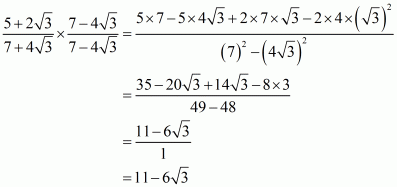
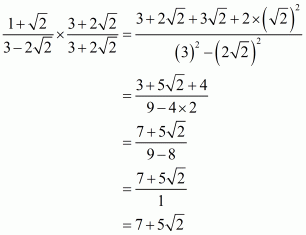
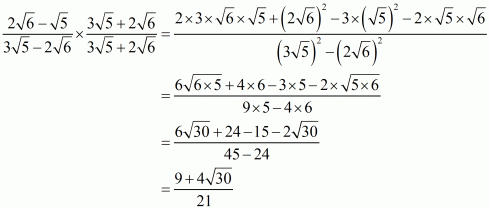
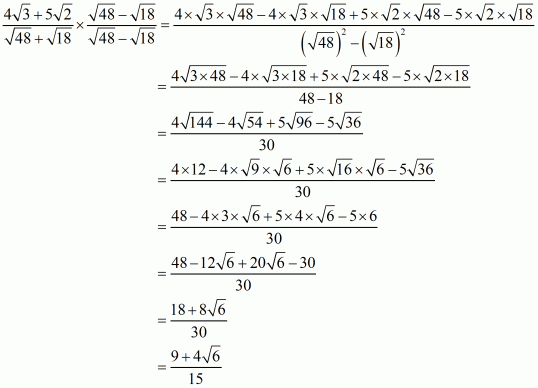
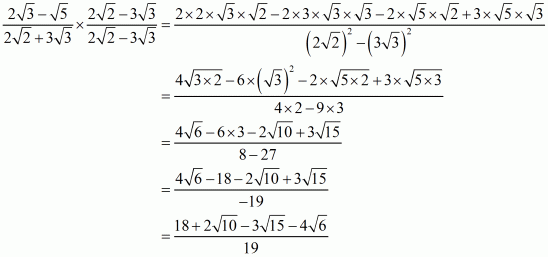
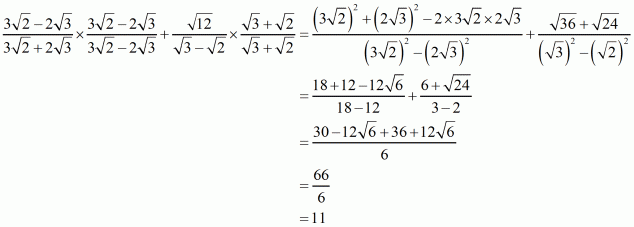
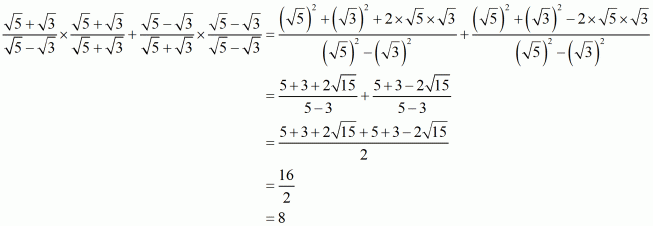
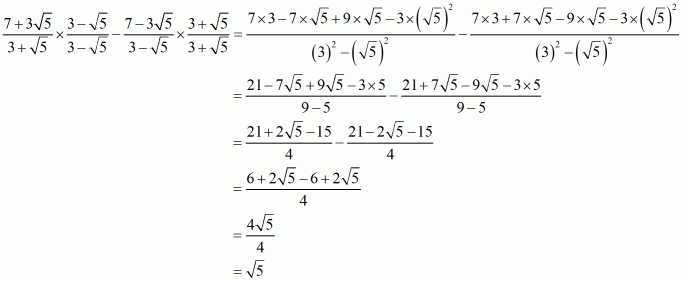
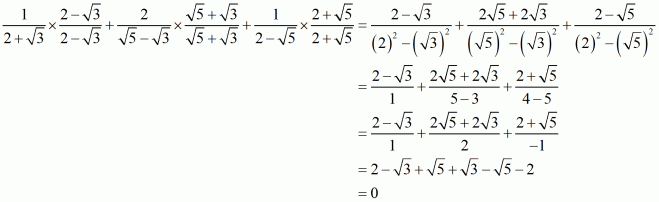
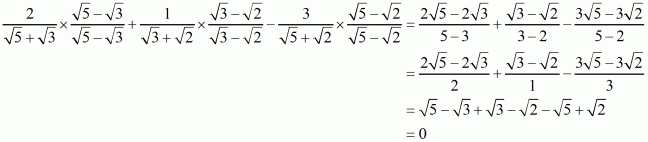
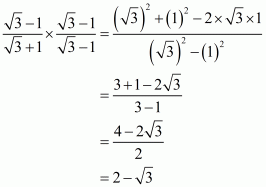
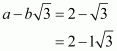
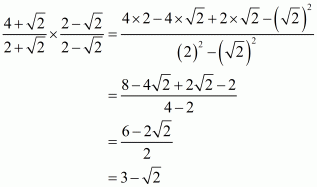
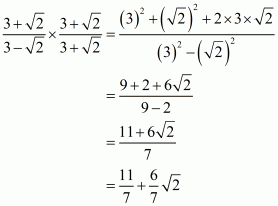
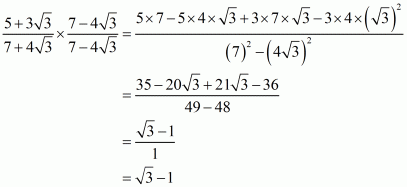
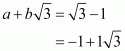
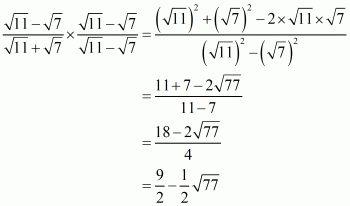
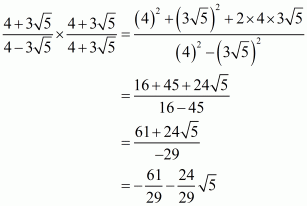
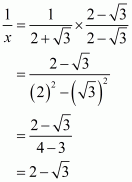
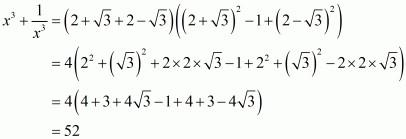
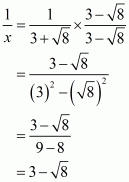
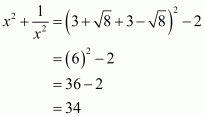
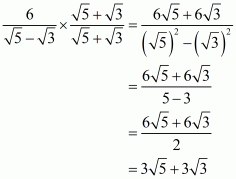
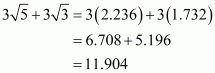
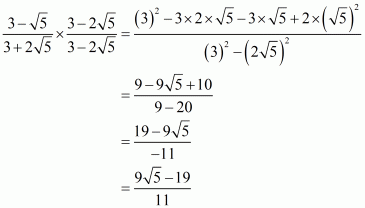
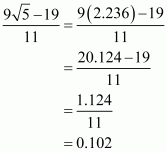
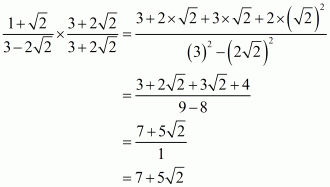
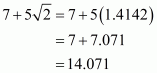
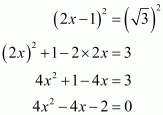
Leave a Reply