Page 13.3 Ex. 13.1
Q1.
Answer :
(i) We are given
Comparing the given equation with ,we get
(ii) We are given
Comparing the given equation with ,we get
(iii) We are given
Comparing the given equation with ,we get
(iv) We are given
Comparing the given equation with ,we get
(v) We are given
Comparing the given equation with ,we get
(vi) We are given
Comparing the given equation with ,we get
(vii) We are given
Comparing the given equation with ,we get
(viii) We are given
Comparing the given equation with ,we get
Q2.
Answer :
(i) We are given,
Now, in two variable forms the given equation will be
(ii) We are given,
Now, in two variable forms the given equation will be
(iii) We are given,
Now, in two variable forms the given equation will be
(iv) We are given,
Now, in two variable forms the given equation will be
Q3.
Answer :
Let the cost of fountain pen be x and cost of ball pen be y.
According to the given equation, we have
Page 13.23 Ex. 13.3
Q1.
Answer :
(i) We are given,
x + y = 4
We get,
y = 4 – x,
Now, substituting x = 0 in y = 4 – x, we get
y = 4
Substituting x = 4 in y = 4 – x, we get
y = 0
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given
| x | 0 | 4 |
| y | 4 | 0 |
(ii) We are given,
We get,
Now, substituting x = 0 in y = x – 2, we get
Substituting x = 2 in y = x – 2, we get
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| x | 0 | 2 |
| y | –2 | 0 |
(iii) We are given,
We get,
Now, substituting in ,we get
Substituting x = –6 in ,we get
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| x | 0 | 6 |
| y | 6 | 0 |
(iv) We are given,
Now, substituting x = 1 in ,we get
Substituting x = 3 in ,we get
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| x | 1 | 3 |
| y | 2 | 6 |
(v) We are given,
We get,
Now, substituting x = 0 in ,we get
Substituting x = 5 in ,we get
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| x | 0 | 5 |
| y | 3 | 0 |
(vi) We are given,
We get,
Now, substituting x = 0 in ,we get
Substituting x = 4 in ,we get
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| x | 0 | 4 |
| y | –6 | 0 |
(vii) We are given,
We get,
Now, substituting x = 5 in ,we get
Substituting x = 8 in ,we get
y = 5
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| x | 5 | 8 |
| y | 4 | 5 |
(viii) We are given,
We get,
Now, substituting x = 1 in ,we get
Substituting x = 5 in ,we get
Thus, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation
| x | 1 | 5 |
| y | –1 | –2 |
Q2.
Answer :
We observe that x = 3 and y = 12 is the solution of the following equations
So, we get the equations of two lines passing through (3, 12) are, 4x – y = 0 and 3x – y + 3 = 0.
We know that passing through the given point infinitely many lines can be drawn. So, there are infinitely many lines passing through (3,12)
Q3.
Answer :
Total fare of Rs y for covering the distance of x km is given by
Where, Rs y is the total fare (x – 1) is taken as the cost of first kilometer is already given Rs 15 and 1 has to subtracted from the total distance travelled to deduct the cost of first kilometer.
Q4.
Answer :
Total charges of Rs 27 of which Rs x for first three days and Rs y per day for 4 more days is given by
Here, is taken as the charges for the first three days are already given at Rs x and we have to find the charges for the remaining four days as the book is kept for the total of 7 days.
Q5.
Answer :
The number given to us is in the form of yx,
where y represents the ten’s place of the number
And x represents the unit’s place of the number
Now, the given number is
number obtained by reversing the digits of the number is
It is given to us that the original number is 27 more than the number obtained by reversing its digits
So,
Q6.
Answer :
The number given to us is in the form of yx.
where y represents the ten’s place of the number
And x represents the units place of the number
Now, the given number is
number obtained by reversing the digits of the number is
It is given to us that the sum of these two numbers is 121
So,
Q7.
Answer :
The required graph is below:-
By plotting the given points (3, 5) and (–1, 3) on a graph paper, we get the line BC.
We have already plotted the point A (1, 4) on the given plane by the intersecting lines.
Therefore, it is proved that the straight line passing through (3, 5) and (–1, 3) also passes through A (1, 4).
Q8.
Answer :
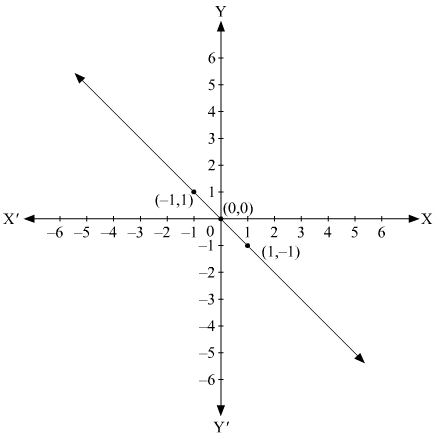
We are given co-ordinates (1, –1) and (–1, 1) as the solution of one of the following equations.
We will substitute the value of both co-ordinates in each of the equation and find the equation which satisfies the given co-ordinates.
(i) We are given,
Substituting ,we get
Substituting ,we get
Therefore, the given equationdoes not represent the graph in the figure.
(ii) We are given,
Substituting ,we get
Substituting ,we get
Therefore, the given solutions satisfy this equation. Thus, it is the equation whose graph is given.
Page 13.24 Ex. 13.3
Q9.
Answer :
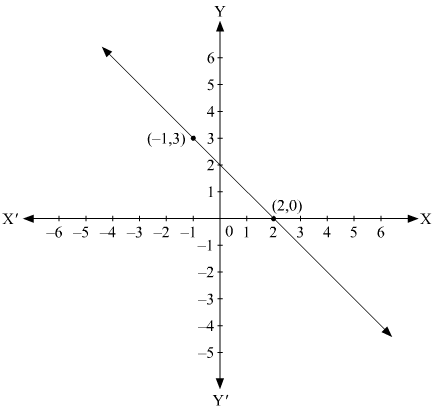
We are given co-ordinates (–1, 3) and (2, 0) as the solution of one of the following equations.
We will substitute the value of both co-ordinates in each of the equation and find the equation which satisfies the given co-ordinates.
(i) We are given,
Substituting ,we get
Substituting ,we get
Therefore, the given solutions does not satisfy this equation.
(ii) We are given,
Substituting ,we get
Substituting ,we get
Therefore, the given solutions does not completely satisfy this equation.
(iii) We are given,
Substituting ,we get
Substituting ,we get
Therefore, the given solutions satisfy this equation. Thus, it is the equation whose graph is given.
Q10.
Answer :
It is given that the point lies on the given equation,
Clearly, the given point is the solution of the given equation.
Now,
Substituting in the given equation, we get
Page 13.32 Ex. 13.4
Q1.
Answer :
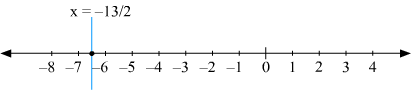
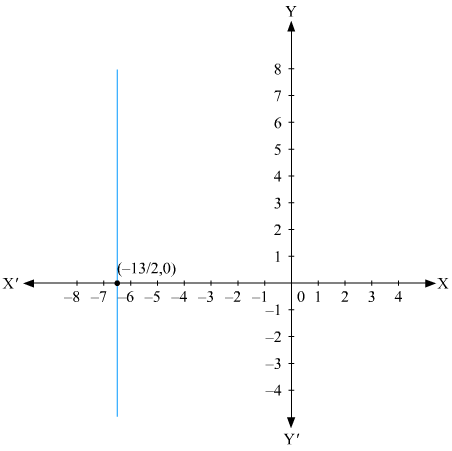
(i) We are given,
x = 2
The representation of the solution on the number line, when given equation is treated as an equation in one variable.
The representation of the solution on the Cartesian plane, it is a line parallel to y axis passing through the point (2, 0) is shown below
(ii) We are given,
We get,
The representation of the solution on the number line, when given equation is treated as an equation in one variable.
The representation of the solution on the Cartesian plane, it is a line parallel to x axis passing through the point A(0, –3) is shown below
(iii) We are given,
The representation of the solution on the number line, when given equation is treated as an equation in one variable.
The representation of the solution on the Cartesian plane, it is a line parallel to x axis passing through the point (0, 3) is shown below
(iv) We are given,
We get,
The representation of the solution on the number line, when given equation is treated as an equation in one variable.
The representation of the solution on the Cartesian plane,it is a line parallel to y axis passing through the point is shown below
(v) We are given,
We get,
The representation of the solution on the number line, when given equation is treated as an equation in one variable.
The representation of the solution on the Cartesian plane, it is a line parallel to y axis passing through the point is shown below
Q2.
Answer :
We are given,
We get,
The representation of the solution on the number line, when given equation is treated as an equation in one variable.
The representation of the solution on the Cartesian plane, it is a line parallel to y axis passing through the point is shown below
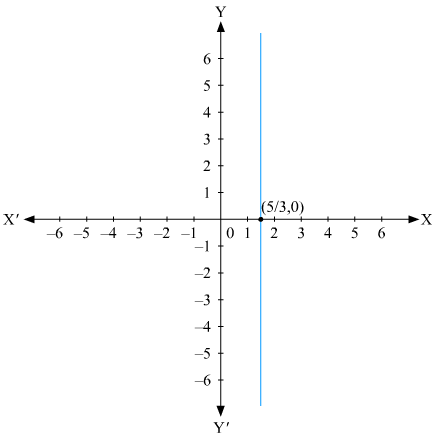
Q3.
Answer :
We are given,
we get,
The representation of the solution on the number line, when given equation is treated as an equation in one variable.
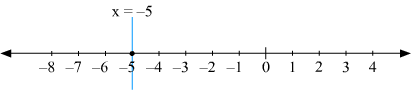
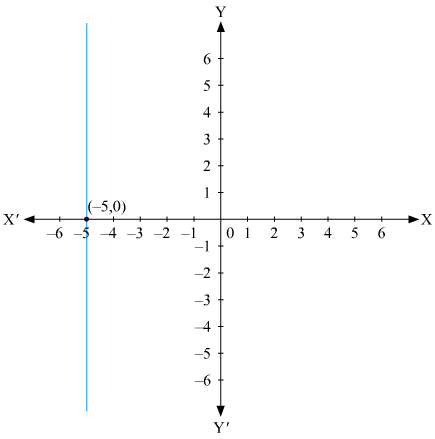
The representation of the solution on the Cartesian plane, it is a line parallel to y axis passing through the point (–5, 0) is shown below
Q4.
Answer :
(i) We are given the co-ordinates of the Cartesian plane at (0,3).
For the equation of the line parallel to x axis ,we assume the equation as a one variable equation independent of x containing y equal to 3.
We get the equation as
(ii) We are given the co-ordinates of the Cartesian plane at (0,-4).
For the equation of the line parallel to x axis ,we assume the equation as a one variable equation independent of x containing y equal to -4.
We get the equation as
(iii) We are given the co-ordinates of the Cartesian plane at (2,-5).
For the equation of the line parallel to x axis ,we assume the equation as a one variable equation independent of x containing y equal to -5.
We get the equation as
(iv) We are given the co-ordinates of the Cartesian plane at (3,4).
For the equation of the line parallel to x axis ,we assume the equation as a one variable equation independent of x containing y equal to 4.
We get the equation as
Q5.
Answer :
(i) We are given the co-ordinates of the Cartesian plane at (4,0).
For the equation of the line parallel to y axis ,we assume the equation as a one variable equation independent of y containing x equal to 4.
We get the equation as
(ii) We are given the co-ordinates of the Cartesian plane at (–2,0).
For the equation of the line parallel to y axis ,we assume the equation as a one variable equation independent of y containing x equal to –2.
We get the equation as
(iii) We are given the co-ordinates of the Cartesian plane at (3,5).
For the equation of the line parallel to y axis, we assume the equation as a one variable equation independent of y containing x equal to 3.
We get the equation as
(iv) We are given the co-ordinates of the Cartesian plane at (−4,−3).
For the equation of the line parallel to y axis, we assume the equation as a one variable equation independent of y containing x equal to −4.
We get the equation as
Page 13.32 Formative Assessment_VSA
Q1.
The equation of line representing x axis is given by
Q2.
The equation of line representing y axis is given by
Q3.
We are given the co-ordinates of the Cartesian plane at (0,4).
For the equation of the line parallel to x axis, we assume the equation as a one variable equation independent of x containing y equal to 4.
We get the equation as
Q4.
We are given the co-ordinates of the Cartesian plane at (3,5).
For the equation of the line parallel to x axis, we assume the equation as a one variable equation independent of x containing y equal to 5.
We get the equation as
Q5.
We are given the co-ordinates of the Cartesian plane at (–3,–7).
For the equation of the line parallel to y axis, we assume the equation as a one variable equation independent of y containing x equal to –3.
We get the equation as
Q6.
We are given the co-ordinates of the Cartesian plane at (–4,6).
For the equation of the line parallel to x axis, we assume the equation as a one variable equation independent of x containing y equal to 6.
We get the equation as
Q7.
We are given,
we get,
The representation of the solution on the number line, when given equation is treated as an equation in one variable.
Q8.
Answer :
We are given,
we get,
The representation of the solution on the Cartesian plane, it is a line parallel to y axis passing through the point is shown below
Q9.
Answer :
We are given lies on the graph of linear equation
.
So, the given co-ordinates are the solution of the equation.
Therefore, we can calculate the value of a by substituting the value of given co-ordinates in equation.
Substituting in equation
, we get
Q10.
Answer :
We are given lies on the graph of linear equation
.
So, the given co-ordinates are the solution of the equation.
Therefore, we can calculate the value of k by substituting the value of given co-ordinates in equation.
Substituting in equation
, we get
Page 13.33 Formative Assessment_MCQ
Q1.
Answer :
We are given (4, 19)as the solution of equation
Substituting x = 4 and y = 19, we get
Therefore, the correct answer is (b).
Q2.
Answer :
We are given (a, 4) lies on the graph of linear equation 3x + y = 10.
So, the given co-ordinates are the solution of the equation 3x + y = 10.
Therefore, we can calculate the value of a by substituting the value of given co-ordinates in equation 3x + y = 10.
Substituting x = a and y = 4 in equation 3x + y = 10, we get
No option is correct.
Q3.
Answer :
We are given,
we get,
We will substitute in
to get the co-ordinates for the graph of
at x axis
Co-ordinates for the graph of are
.
Therefore, the correct answer is (a).
Q4.
There are infinite numbers of linear equations that are satisfied by as
(i) Every solution of the linear equation represent a point on the line.
(ii) Every point on the line is the solution of the linear equation.
Therefore, the correct answer is (d).
Q5.
The equation is represented by a point on the number line.
Therefore, the correct answer is (b).
Q6.
We are given as the solution of linear equation, which we have to find?
The equation is which can be proved by
Substituting in the equation
, we get
Therefore, the correct answer is (a).
Q7.
We are given as the solution of equation
Substituting, we get
Therefore, the correct answer is (b).
Q8.
Distance between the graph of equations, say D
D = Distance of co-ordinate on negative side of x axis + Distance of co-ordinate on positive side of x axis
Distance of co-ordinate on negative side of x axis = x = 3 units
Distance of co-ordinate on positive side of x axis = x = 2 units
Therefore, the correct answer is (d).
Q9.
Distance between the graph of equations, say D
D = Distance of co-ordinate on negative side of y axis + Distance of co-ordinate on positive side of y axis
Distance of co-ordinate on negative side of y axis = y = 1 units
Distance of co-ordinate on positive side of y axis = y = 3 units
Therefore, the correct answer is (b).
Page 13.6 Ex. 13.2
Q1.
Answer :
(i) We are given,
Substituting x = 1 in the given equation, we get
Substituting x = 2 in the given equation, we get
(ii) We are given,
Substituting in the given equation, we get
Substituting in the given equation, we get
(iii) We are given,
Substituting x = 0 in the given equation, we get
Substituting x = 4 in the given equation, we get
(iv) We are given,
Substituting x = 0 in the given equation, we get
Substituting x = 3 in the given equation, we get
Q2.
Answer :
(i) We are given,
Substituting x = 0 in the given equation, we get
Substituting y = 0 in the given equation, we get
(ii) We are given,
Substituting in the given equation, we get
Substituting y = 0 in the given equation, we get
(iii) We are given,
Substituting x = 0 in the given equation, we get
Substituting y = 0 in the given equation, we get
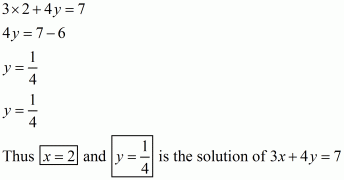
Q3.
Answer :
We are given,
2x – y = 6
(i) In the equation 2x – y = 6,we have
Substituting x = 3 and y = 0 in 2x – y, we get
is the solution of 2x – y = 6.
(ii) In the equation 2x – y = 6, we have
Substituting x = 0 and y = 6 in 2x – y,we get
is not the solution of 2x – y = 6.
(iii) In the equation 2x – y = 6,we have
Substituting x = 2 and y = –2 in 2x – y, we get
is the solution of 2x – y = 6.
(iv) In the equation 2x – y = 6, we have
Substituting and y = 0 in 2x – y, we get
is not the solution of 2x – y = 6.
(v) In the equation 2x – y = 6, we have
Substituting and y = –5 in 2x – y, we get
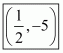
Q4.
Answer :
We are given,
is the solution of equation
.
Substituting and
in
,we get
Q5.
Answer :
We are given,
is the solution of equation
.
Substituting and
in
,we get
Page 13.7 Ex. 13.2
Q6.
We are given,
is the solution of equation
.
Substituting and
in
,we get
Q7.
We are given,
is the solution of equation
.
Substituting and
in
,we get
Using quadratic factorization
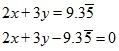
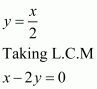


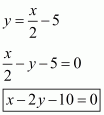
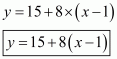
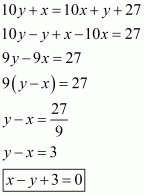
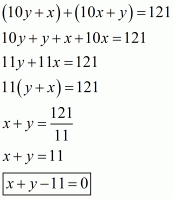
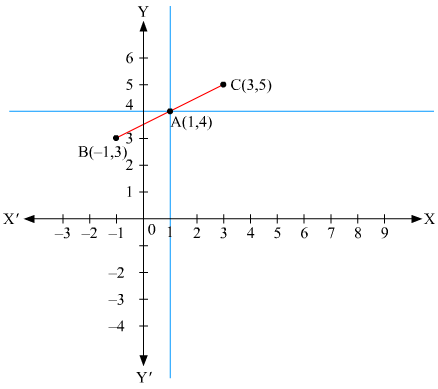
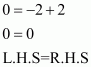
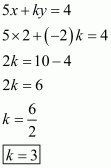
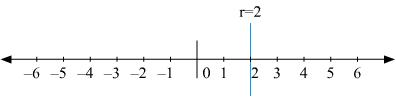
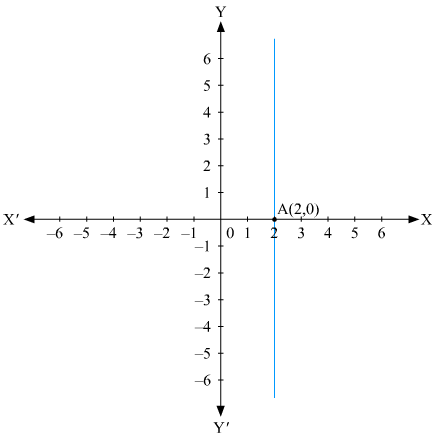
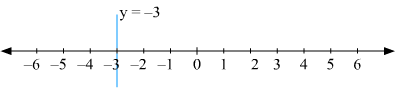
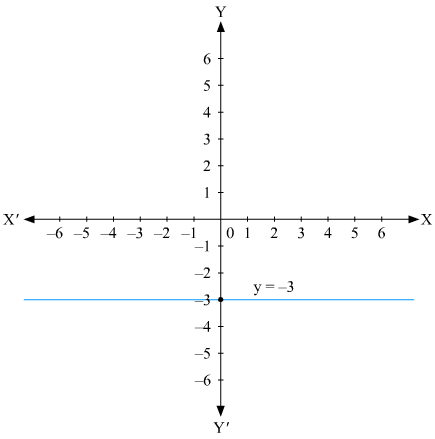
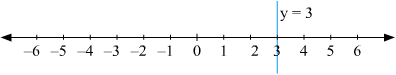
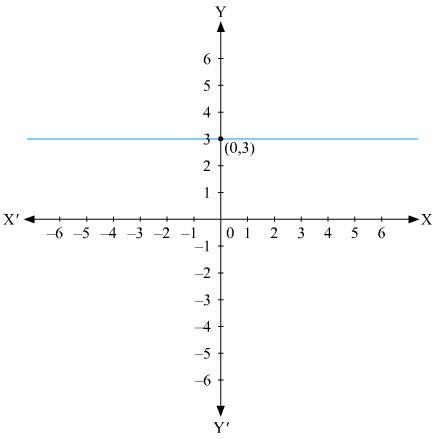
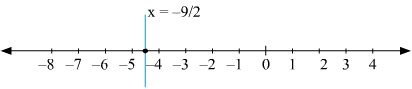
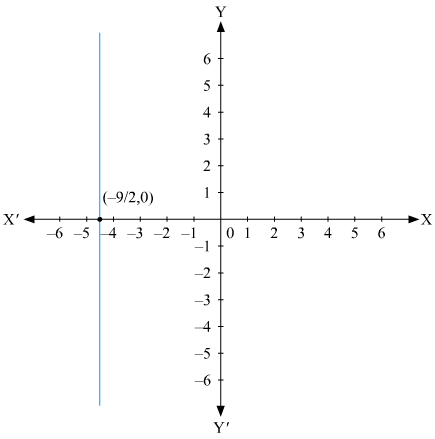
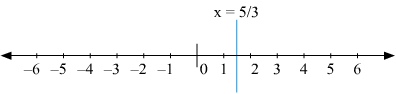
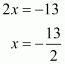
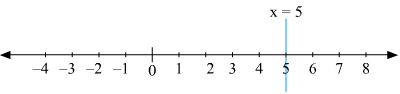
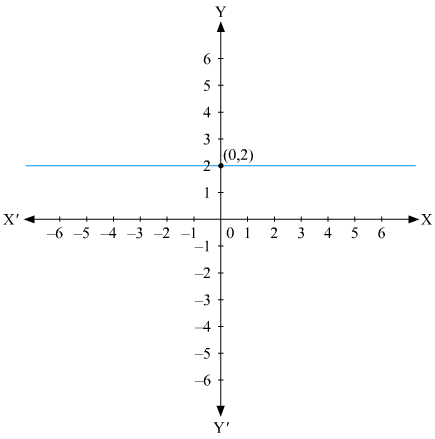
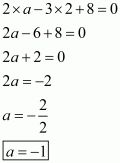
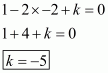
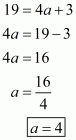
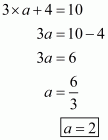
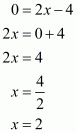
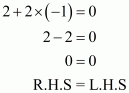

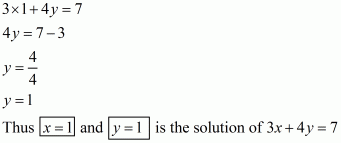
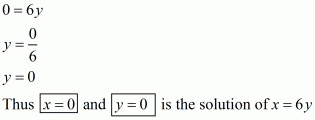
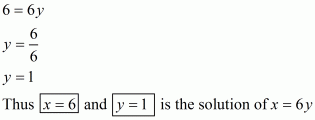
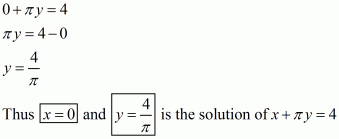
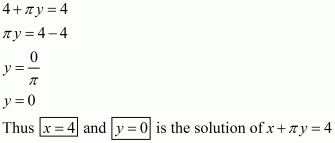
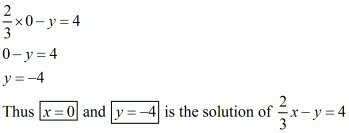
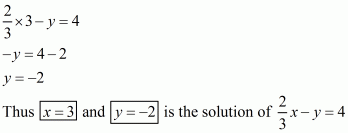
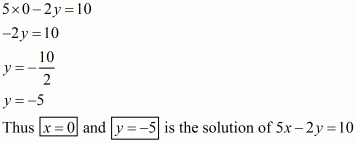
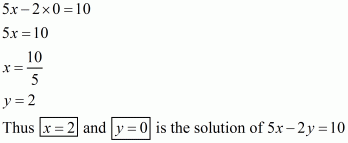
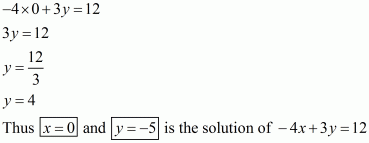
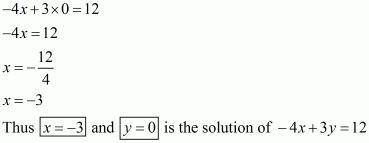
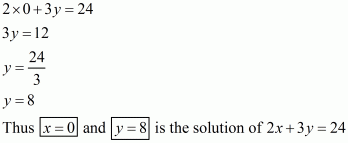
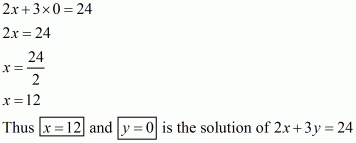
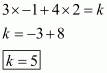
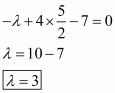
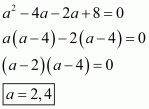

Leave a Reply