Page 12.8 Ex. 12.1
Q1.
Answer :
Whenever we are given the measurement of all sides of a triangle, we basically look for Heron’s formula to find out the area of the triangle.
If we denote area of the triangle by A, then the area of a triangle having sides a, b, c and s as semi-perimeter is given by;
Where,
We are given:
a =150 cm
b=120 cm
c =200 cm
Here we will calculate s,
So the area of the triangle is:
Q2.
Answer :
Whenever we are given the measurement of all sides of a triangle, we basically look for Heron’s formula to find out the area of the triangle.
If we denote area of the triangle by A, then the area of a triangle having sides a, b, c and s as semi-perimeter is given by;
Where,
We are given:
a = 9 cm, b = 12 cm, c = 15 cm
Here we will calculate s,
So the area of the triangle is:
Q3.
Answer :
Whenever we are given the measurement of all sides of a triangle, we basically look for Heron’s formula to find out the area of the triangle.
If we denote area of the triangle by A, then the area of a triangle having sides a, b, c and s as semi-perimeter is given by;
Where,
We are given:
a = 18 cm
b = 10 cm, and perimeter = 42 cm
We know that perimeter = 2s,
So 2s = 42
Therefore s = 21 cm
We know that, so
So the area of the triangle is:
Q4.
Answer :
Whenever we are given the measurement of all sides of a triangle, we basically look for Heron’s formula to find out the area of the triangle.
If we denote area of the triangle by ‘Area’, then the area of a triangle having sides a, b, c and s as semi-perimeter is given by;
Where,
We are given:
AB = 15 cm, BC = 13 cm, AC = 14 cm
Here we will calculate s,
So the area of the triangle is:
Now draw the altitude from point B on AC which intersects it at point D.BD is the required altitude. So if you draw the figure, you will see,
Here . So,
Q5.
Answer :
Whenever we are given the measurement of all sides of a triangle, we basically look for Heron’s formula to find out the area of the triangle. If we denote area of the triangle by A, then the area of a triangle having sides a, b, c and s as semi-perimeter is given by;
Where,
We are given, and
Here,
Using these data we will find the sides of the triangle. Suppose the sides of the triangle are as follows,
Since, so
Now we know each side that is,
Now we know all the sides. So we can use Heron’s formula.
The area of the triangle is;
Q6.
Answer :
Whenever we are given the measurement of all sides of a triangle, we basically look for Heron’s formula to find out the area of the triangle. If we denote area of the triangle by A, then the area of a triangle having sides a, b, c and s as semi-perimeter is given by;
Where,
We are given, and
Here,
Using these data we will find the sides of the triangle. Suppose the sides of the triangle are as follows,
Since, so
Now we know each side that is,
Now we know all the sides. So we can use Heron’s formula.
The area of the triangle is;
Q7.
Answer :
Whenever we are given the measurement of all sides of a triangle, we basically look for Heron’s formula to find out the area of the triangle. If we denote area of the triangle by A, then the area of a triangle having sides a, b, c and s as semi-perimeter is given by;
Where,
We are given two sides of the triangle and.
That is a = 78 dm, b = 50 dm
We will find third side c and then the area of the triangle using Heron’s formula.
Now,
Use Heron’s formula to find out the area of the triangle. That is
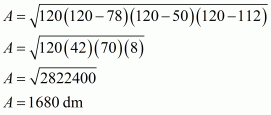
Consider the triangle ΔPQR in which
PQ=50 dm, PR=78 dm, QR=120 dm
Where RD is the desired perpendicular length
Now from the figure we have
Q8.
Answer :
Whenever we are given the measurement of all sides of a triangle, we basically look for Heron’s formula to find out the area of the triangle.
If we denote area of the triangle by A, then the area of a triangle having sides a, b, c and s as semi-perimeter is given by;
Where,
We are given: a = 35 cm; b = 54 cm; c = 61 cm
The area of the triangle is:
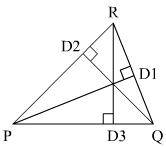
Suppose the triangle is ΔPQR and focus on the triangle given below,
In which PD1, QD2 and RD3 are three altitudes
Where PQ=35 cm, QR=54 cm, PR=61 cm
We will calculate each altitude one by one to find the smallest one.
Case 1
In case of ΔPQR:
Case 2
Case 3
The smallest altitude is QD2.
The smallest altitude is the one which is drawn on the side of length 61 cm from apposite vertex.
Q9.
Answer :
Whenever we are given the measurement of all sides of a triangle, we basically look for Heron’s formula to find out the area of the triangle.
If we denote area of the triangle by A, then the area of a triangle having sides a, b, c and s as semi-perimeter is given by;
Where,
We are given, and
Here,
Using these data we will find the sides of the triangle. Suppose the sides of the triangle are as follows,
Since 2s=144, so
Now we know each side that is,
Now we know all the sides. So we can use Heron’s formula.
The area of the triangle is;
We are asked to fin out the height corresponding to the longest side of the given triangle. The longest side is c and supposes the corresponding height is H then,
Q10.
Answer :
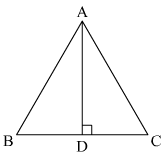
We are given that and its base is (3/2) times each of the equal sides. We are asked to find out the length of each side, area of the triangle and height of the triangle. In this case ‘height’ is the perpendicular distance drawn on the base from the apposite vertex.
In the following triangle ΔABC
BC = a, AC = b, AB = c and AB = AC
Let the length of each of the equal sides be x and a, b and c are the side of the triangle. So,
Since .This implies that,
Therefore all the sides of the triangle are:
All the sides of the triangle are 18 cm, 12 cm, and 12 cm.
Whenever we are given the measurement of all sides of a triangle, we basically look for Heron’s formula to find out the area of the triangle.
If we denote area of the triangle by Area, then the area of a triangle having sides a, b, c and s as semi-perimeter is given by;
Where,
To calculate area of the triangle we need to find s:
The area of the triangle is:
Now we will find out the height, say H. See the figure, in which AD = H
So,
Q11.
Answer :
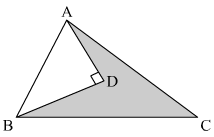
We are given the following figure with dimensions.
Figure:
Let the point at which angle is be D.
AC = 52 cm, BC = 48 cm, AD = 12 cm, BD = 16 cm
We are asked to find out the area of the shaded region.
Area of the shaded region=Area of triangle ΔABC−area of triangle ΔABD
In right angled triangle ABD, we have
Area of the triangle ΔABD is given by
Whenever we are given the measurement of all sides of a triangle, we basically look for Heron’s formula to find out the area of the triangle.
If we denote area of the triangle by Area, then the area of a triangle having sides a, b, c and s as semi-perimeter is given by;
Where,
Here a = 48 cm, b = 52 cm, c = 20 cm and
Therefore the area of a triangle ΔABC is given by,
Now we have all the information to calculate area of shaded region, so
Area of shaded region = Area of ΔABC − Area of ΔABD
The area of the shaded region is 384 cm2.
Page 12.23 Formative Assessment_VSA
Q1.
Answer :
Area of a triangle say having base 5 cm and altitude 4 cm is given by
, where
Base = 5 cm; Height = 4 cm
Q2.
Answer :
The area of a triangle having sides a, b, c and s as semi-perimeter is given by,
, where
Therefore the area of a triangle, say having sides 3 cm, 4 cm and 5 cm is given by
a = 3 cm ; b = 4 cm ; c = 5 cm
Now, area
Q3.
Answer :
Let us assume triangle ABC be the given isosceles triangle having sides AB = AC and base BC. The area of a triangle ABC, say A having given sides AB and AC equals to y cm and given base BC equals to x cm is given by
Where,
Base = BC = x cm; Height =
Q4.
Answer :
Area of an equilateral triangle having each side a cm is given by
Area of the given equilateral triangle having each equal side equal to 4 cm is given by
a = 4 cm
Q5.
Answer :
Area of an equilateral triangle, say A having each side a cm is given by
Area of the given equilateral triangle having each equal side equal to x cm is given by
a = x cm
Q6.
Answer :
The area of a triangle having sides a, b, c and s as semi-perimeter is given by,
, where,
It is given the sides of a triangular field are in the ratio 3:4:5 and perimeter=144 m
Therefore, a: b: c = 3:4:5
We will assume the sides of triangular field as
Substituting the value of x in, we get sides of the triangle as
Area of a triangular field, say A having sides a, b , c and s as semi-perimeter is given by
Q7.
Answer :
Altitude of a equilateral triangle, having side a is given by
Substituting the given value of altitude h cm, we get
Area of a equilateral triangle, say A having each side a cm is given by
Area of the given equilateral triangle having each equal side equal to is given by;
Q8.
Answer :
We are given assumed value is the area of a given triangle ABC
We assume the sides of the given triangle ABC be a, b, c
The area of a triangle having sides a, b, c and s as semi-perimeter is given by,
Where,
We take the sides of a new triangle as 2a, 2b, 2c that is twice the sides of previous one
Now, the area of a triangle having sides 2a, 2b, and 2c and as semi-perimeter is given by,
, where
Now,
Q9.
Answer :
The area of a triangle having sides a, b, c and s as semi-perimeter is given by,
Where,
We take the sides of a new triangle as 2a, 2b, 2c that is twice the sides of previous one
Now, the area of a triangle having sides 2a, 2b, and 2c and as semi-perimeter is given by,
Where,
Now,
Therefore, increase in the area of the triangle
Percentage increase in area
Page 12.24Formative Assessment_VSA
Q10.
Answer :
Area of an equilateral triangle having each side a cm is given by
Now, Area of an equilateral triangle, say if each side is tripled is given by
a = 3a
Therefore, increase in area of triangle
Percentage increase in area
Page 12.24Formative Assessment_MCQ
Q1.
The area of a triangle having sides a, b, c and s as semi-perimeter is given by,
, where
Therefore the area of a triangle say A, having sides 16 cm, 30 cm and 34 cm is given by
a = 16 cm ; b = 30 cm ; c = 34 cm
Therefore the area of the triangle is
Q2.
Answer :
Hence, the correct option is (d).
Q3.
Answer :
The area of a triangle having sides a, b, c and s as semi-perimeter is given by,
, where
Therefore the area of a triangle having sides 7 cm, 9 cm and 14 cm is given by
a = 7 cm ; b = 9 cm ; c = 14 cm
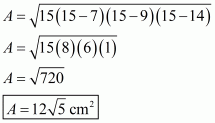
Therefore the answer is (a).
Q4.
Answer :
The area of a triangle having sides a, b, c and s as semi-perimeter is given by,
, where
Therefore the area of a triangular field, say A having sides 325 m, 300 m and 125 m is given by
a = 325 m ; b = 300 m ; c = 125 m
Therefore, the correct answer is (a).
Q5.
Answer :
The area of a triangle having sides a, b, c and s as semi-perimeter is given by,
, where
Therefore the area of a triangle, say A having sides 50 cm, 78 cm and 112 cm is given by
The area of a triangle, having p as the altitude will be,
Where, A = 1680
We have to find the smallest altitude, so will substitute the value of the base AC with the length of each side one by one and find the smallest altitude distance i.e. p
Case 1
Case 2
Case 3
Therefore, the answer is (b).
Q6.
Answer :
The area of a triangle having sides a, b, c and s as semi-perimeter is given by,
, where
We need to find the altitude to the smallest side
Therefore the area of a triangle having sides 11 m, 60 m and 61 m is given by
a = 11 m ; b = 60 m ; c = 61 m
The area of a triangle having base AC and height p is given by
We have to find the height p corresponding to the smallest side of the triangle. Here smallest side is 11 m
AC = 11 m
Therefore, the answer is (d).
Q7.
Answer :
The area of a triangle having sides a, b, c and s as semi-perimeter is given by,
, where
We need to find the altitude corresponding to the longest side
Therefore the area of a triangle having sides 11 cm, 15 cm and 16 cm is given by
a = 11 m ; b = 15 cm ; c = 16 cm
The area of a triangle having base AC and height p is given by
We have to find the height p corresponding to the longest side of the triangle.Here longest side is 16 cm, that is AC=16 cm
Therefore, the answer is (c).
Q8.
Answer :
We are given the area of an isosceles right triangle and we have to find its perimeter.
Two sides of isosceles right triangle are equal and we assume the equal sides to be the base and height of the triangle. We are asked to find the perimeter of the triangle
Let us take the base and height of the triangle be x cm.
Area of a isosceles right triangle, say A having base x cm and height x cm is given by
A = 8 cm2; Base = Height = x cm
Using Pythagorean Theorem we have;
Let ABC be the given triangle
Perimeter of triangle ABC, say P is given by
AB = 4 cm; BC = 4 cm; AC =
Therefore, the answer is (b).
Q9.
Answer :
We are given that triangle ABC has equal perimeter as to the perimeter of an equilateral triangle having side 9 cm. The sides of triangle ABC are consecutive integers. We are asked to find the smallest side of the triangle ABC
Perimeter of an equilateral triangle, say P having side 9 cm is given by
Let us assume the three sides of triangle ABC be x, x+1, x−1
Perimeter of triangle ABC, say P1 is given by
P1 = AB + BC + AC
AB = x; BC = x +1; AC = x−1. Since P1 = P. So
By using the value of x, we get the sides of triangle as 8 cm, 9 cm and 10 cm
Therefore, the answer is (c).
Q10.
Answer :
Area of triangle ABC is given 40 cm2.
Also
We are asked to find the area of the triangle BDC
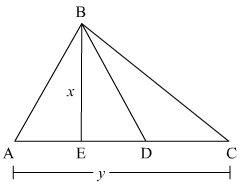
Let us take BE perpendicular to base AC in triangle ABC.
We assume AC equal to y and BE equal to x in triangle ABC
Area of triangle ABC, say A is given by
We are given the ratio between AD to DC equal to 3:2
So,
In triangle BDC, we take BE as the height of the triangle
Area of triangle BDC, say A1 is given by
Therefore, the answer is (a).
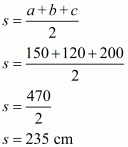

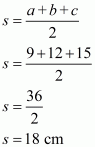

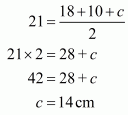
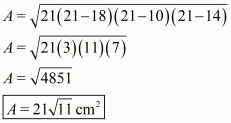
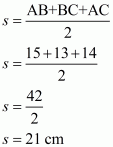
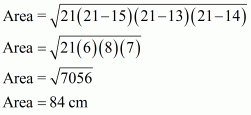
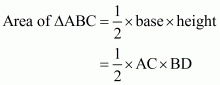
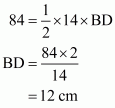
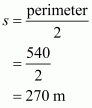
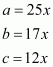
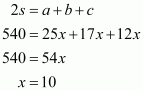
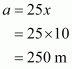
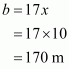
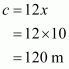
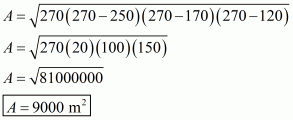
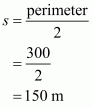
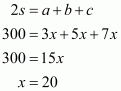
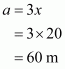
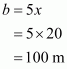
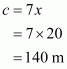
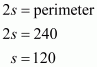
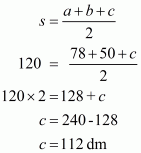
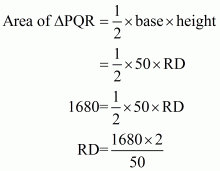
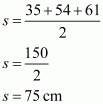
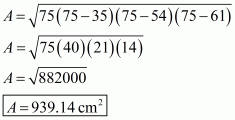
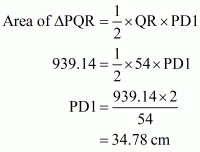
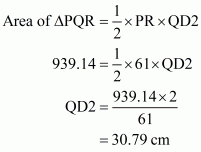
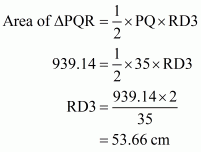

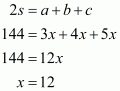
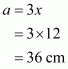
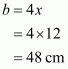
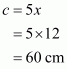
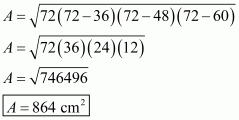
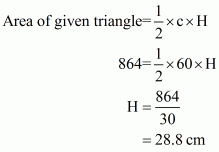
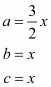
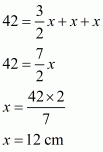
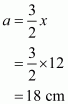
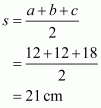
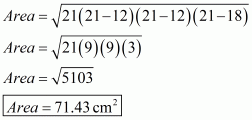
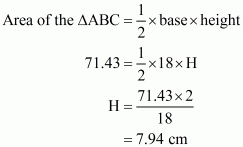
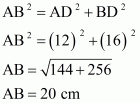
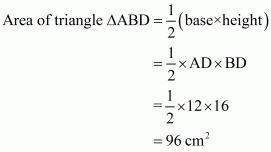
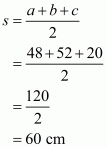
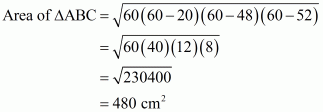
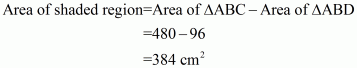
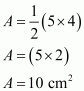
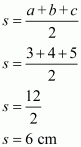
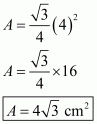
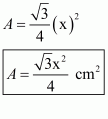
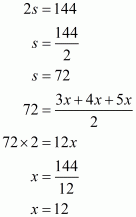
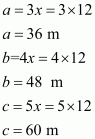
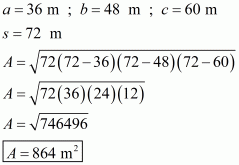
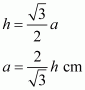
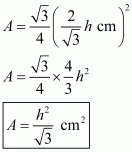



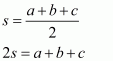
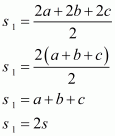
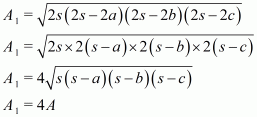
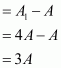
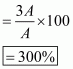
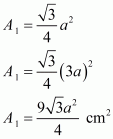
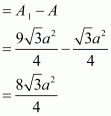
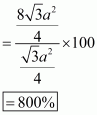
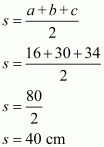
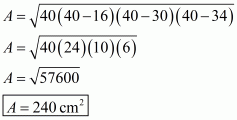
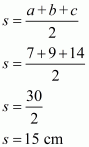
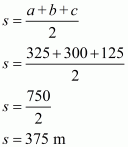
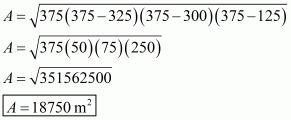
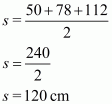
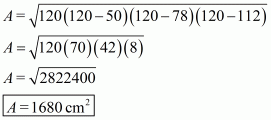
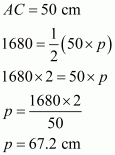
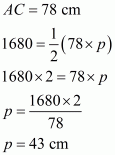
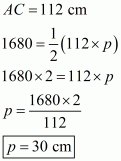
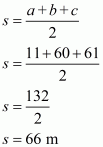
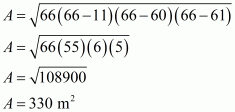
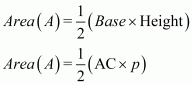
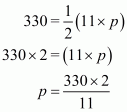
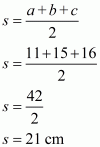
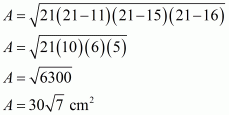
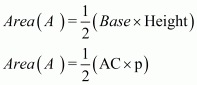
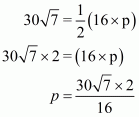
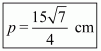
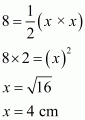
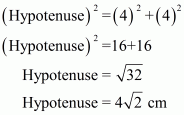
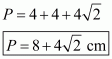
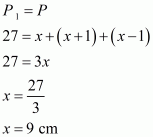
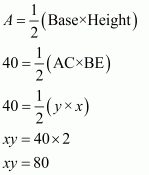
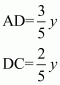
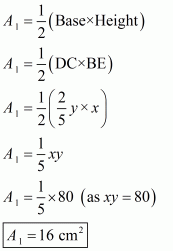

Leave a Reply