Notes Class 9 Maths Chapter 7 Triangles

Notes For All Chapters Maths Class 9

1. Triangle: A closed figure formed by three intersecting lines is called a triangle (‘Tri’ means ‘three’). A triangle has three sides, three angles and three vertices.

e.g., In triangle ABC, denoted as ∆ABC. AB, BC, CA are the three sides, ∠A, ∠B, ∠C are the three angles and A, B, C are three vertices.

2. Congruence of Triangles: Two triangles are congruent if the sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle.
If ∆PQR is congruent to ∆ABC, we write ∆PQR = ∆ABC.
Note: Congruent triangles corresponding parts are equal and we write in short ‘CPCT’ for Corresponding Parts of Congruent Triangles.

3. Criteria for Congruence of Triangles.

• SAS congruence rule: Two triangles are congruent if two sides and the included angle of one triangle are equal to the sides and the included angle of the other triangle.
• ASA congruence rule: Two triangles are congruent if two angles and the included sides of one triangle are equal to two angles and the included side of another triangle.
• AAS congruence rule: Two triangles are congruent if any two pairs of angles and one pair of corresponding sides are equal.
• SSS congruence rule: Two triangles are congruent if three sides of one triangle are equal to the sides of the other triangle.
• RHS congruence rule: If in two right triangles, hypotenuse and one side of a triangle are equal to the hypotenuse and one side of other triangles, then the two triangles are congruent.

4. Properties of a Triangle

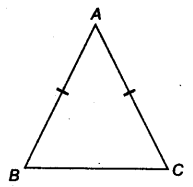
• Isosceles triangle: A triangle in which two sides are equal is called an isosceles triangle. So, ∆ABC is an isosceles triangle with AB = AC.
  
• Theorem 1: Angles opposite to equal sides of an isosceles triangle are equal.
  i.e., ∠B = ∠C
• Theorem 2: The sides opposite to equal angles of a triangle are equal. i.e., AB = AC

5. Inequalities in a Triangle

• If two sides of a triangle are unequal, the angle opposite to the longer side is larger (or greater).
• In any triangle, the side opposite to the larger (or greater) angle is longer (converse of (i)).
• The sum of any two sides of a triangle is greater than the third side, i.e., AB + BC > CA.