Solutions For All Chapters Maths Class 7
Ex 9.2 Class 7 Maths Question 1.
Find the circumference of the circles with the following radius. (Take π = 22/7)
(a) 14 cm
(b) 28 mm
(c) 21 cm
Solution:
(a) Given: Radius (r) = 14 cm
∴ Circumference = 2πr = 2 × 22/7 × 14
= 88 cm
(b) Given: Radius (r) = 28 mm
∴ Circumference = 2πr = 2 × 22/7 × 28
= 176 mm
(c) Given: Radius (r) = 21 cm
∴ Circumference = 2πr = 2 × 22/7 × 21
= 132 cm
Ex 9.2 Class 7 Maths Question 2.
Find the area of the following circles, given that (Take π = 22/7)
(a) radius = 14 mm
(b) diameter = 49 m
(c) radius = 5 cm
Solution:
(a) Here, r = 14 mm
∴ Area of the circle = πr2
= π × 14 × 14 = 22/7 × 14 × 14
(b) Here, diameter = 49 m 49
(c) Here, radius = 5 cm
Ex 9.2 Class 7 Maths Question 3.
If the circumference of a circular sheet is 154 m, find its radius. Also find the area of the sheet. (Take π = 22/7)
Solution:
Given: Circumference = 154 m
∴ 2πr = 154
Ex 9.2 Class 7 Maths Question 4.
A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds offence. Also find the cost of the rope, if it costs ₹ 4 per metre. (Take π = 22/7)
Solution:
Diameter of the circular garden = 21 m
∴ Radius = 21/2 m
∴ Circumference = 2πr = 2 × 22/7 × 21/2
= 66 m
Length of rope needed for 2 rounds
= 2 × 66 m = 132 m
Cost of the rope = ₹4 × 132 = ₹ 528
Ex 9.2 Class 7 Maths Question 5.
From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)
Solution:
Radius of the circular sheet = 4 cm
∴ Area = πr² = π × 4 × 4 = 16π cm²
Radius of the circle to be removed = 3 cm
∴ Area of sheet removed = πr² = 9π cm²
Area of the remaining sheet
= (16π – 9π) cm² = 7π cm²
= 7 × 3.14 cm² = 21.98 cm²
Hence, the required area = 21.98 cm².
Ex 9.2 Class 7 Maths Question 6.
Saima wants to put a lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one metre of the lace costs ₹ 15. (Take π = 3.14)
Solution:
Diameter of the table cover = 1.5 m
∴ Radius = 1.5/2 = 0.75 m
∴ Length of the lace = 2πr = 2 × 3.14 × 0.75
= 4.710 m
Cost of the lace = ₹ 15 × 4.710 = ₹ 70.65
Ex 9.2 Class 7 Maths Question 7.
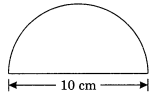
Find the perimeter of the adjoining figure, which is a semicircle including its diameter.
Solution:
Given: Diameter = 10 cm
Hence, the required perimeter
= 25.7 cm. (approx.)
Ex 9.2 Class 7 Maths Question 8.
Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15 m². (Take π = 3.14)
Solution:
Given:
Diameter = 1.6 m
∴ Radius = 1.6/2 = 0.8 m
Area of the table-top = πr²
= 3.14 × 0.8 × 0.8 m²
= 2.0096 m²
∴ Cost of polishing = ₹ 15 × 2.0096
= ₹ 30.14 (approx.)
Ex 9.2 Class 7 Maths Question 9.
Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find the radius of that circle. Also find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or the square? (Take π = 22/7)
Solution:
Length of the wire to be bent into a circle = 44 cm
2πr = 44
Now, the length of the wire is bent into a square.
Here perimeter of square
= Circumference of line k
Length of each side of the square
= Perimeter/4 = 44/4 =11 cm
Area of the square = (Side)² = (11)² = 121 cm²
Since, 154 cm² >121 cm²
Thus, the circle encloses more area.
Ex 9.2 Class 7 Maths Question 10.
From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed, (as shown in the given figure below). Find the area of the remaining sheet. (Take π = 22/7)
Solution:
Radius of the circular sheet = 14 cm
∴ Area = πr² =22/7 × 14 × 14 cm²
= 616 cm²
Area of 2 small circles = 2 × πr²
= 2 × 22/7 × 3.5 × 3.5 cm²
= 77.0 cm²
Area of the rectangle = l × b
= 3 × 1 cm² = 3 cm²
Area of the remaining sheet after removing the 2 circles and 1 rectangle
= 616 cm² – (77 + 3) cm²
= 616 cm² – 80 cm² = 536 cm²
Ex 9.2 Class 7 Maths Question 11.
A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
Solution:
Side os the square sheet = 6 m
∴ Area of the sheet = (Side)² = (6)² = 36 cm²
Radius of the circle = 2 cm
∴ Area of the circle to be cut out = πr2
= 22/7 × 2 × 2 = 88/7 cm²
Area of the left over sheet
Ex 9.2 Class 7 Maths Question 12.
The circumference of a circle is 31.4 cm. Find the radius and the area of the circle. (Take π = 3.14)
Solution:
Circumference of the circle = 31.4 cm
2πr = 31.4
∴ r = 31.4/2 × 3.14 = 5cm
Area of the circle = πr² = 3.14 × 5 × 5 = 78.5 cm²
Hence, the required radius = 5 cm and area = 78.5 cm².
Ex 9.2 Class 7 Maths Question 13.
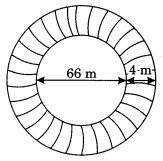
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (Take π = 3.14)
Solution:
Diameter of the flower bed = 66 m .
∴ Radius = 66/2 = 33 m
Let r1 = 33 m
Width of the path = 4 m
Radius of the flower bed included path
= 33 m + 4 m = 37m
Let r2 = 37m
Area of the circular path
=
= 3.14 (37²– 33²)
= 3.14 × (37 + 33) (37 – 33) [Y a² – b² = (a + b)(a-b)]
= 3.14 × 70 × 4 = 879.20 m²
Hence, the required area = 879.20 m²
Ex 9.2 Class 7 Maths Question 14.
A circular flower garden has an area of 314 m². A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler can water the entire garden?
[Take π = 3.14]
Solution:
Area of the flower garden = 314 m²
Radius of the circular portion covered by the sprinkler = 12 m
∴ Area = 7πr² = 3.14 × 12 × 12
= 3.14 × 144 m² = 452.16 m²
Since 452.16 m² > 314 m²
Yes, the sprinkler will water the entire garden.
Ex 9.2 Class 7 Maths Question 15.
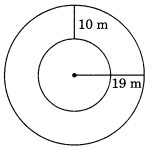
Find the circumference of the inner and the outer circles, shown in the given figure. (Take π = 3.14)
Solution:
Radius of the outer circle = 19 m
∴ Circumference of the outer circle = 2πr
= 2 × 3.14 × 19 = 3.14 × 38 m
= 119.32 m
Radius of the inner circle
= 19m – 10m = 9m
∴ Circumference = 2πr = 2 × 3.14 × 9
= 56.52 m
Here the required circumferences are 56.52 m and 119.32 m.
Ex 9.2Class 7 Maths Question 16.
How many times a wheel of radius 28 cm must rotate to go 352 m? (Take π = 22/7)
Solution:
Radius of the wheel = 28 cm
∴ Circumference = 2πr = 2 × 22/7 × 28 = 176 cm
Number of rotations made by the wheel in going 352 m or 35200 cm
= 35200/176 = 200
Hence, the required number of rotation = 200.
Ex 9.2 Class 7 Maths Question 17.
The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in 1 hour? (Take π = 3.14)
Solution:
Length of minute hand = 15 cm
∴ Radius = 15 cm
Circumference = 2πr
= 2 × 3.14 × 15 cm = 94.2 cm
Since the minute hand covers the distance in 1 hour equal to the circumference of the circle. Here the required distance covered by the minute hand = 94.2 cm.
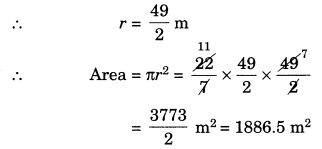
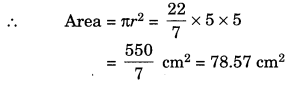
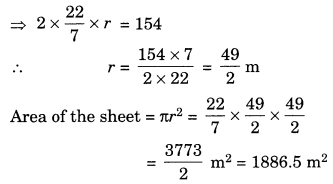

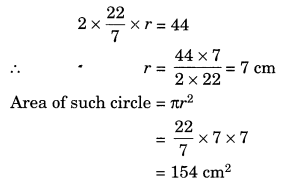
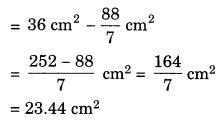

Thank you sooooo much, Madam, for teaching in such an easy method and providing free education to us.
For this reason, I kindly request you to take online classes for me, Mansi Madam.
Thank you helping ☺️😊
Thankyou so much evidyarthi 🙂🙂
Thanks evidyarthi I like your thoughts for helping us.
thank you very much evidyarthi
your app is best and your technology and your brain with grateful things
thank you very much evidyarthi
Nice answer 👌
1hour
Thank you
Thanks a lot for this; it helped me complete my work on time.
Good 😊, hai
thank to this website and this website owner also because this helps me alot for completing my school maths and also helps me class test in which i got 20/20
SPECIAL THANKS TO EVIDYARTI
Sir today is my maths paper so 👍👍👍👍🙂
Bhai, maza aa gaya! Wow, the answers were so good, and the other features were also amazing.
Thank you!
Super
I love this website I was having a math test of this exercise and I was absent but now I am very happy and I got 80/80 thanks a lot
Very helpful 🙂😃😃😃😃
I really loved the site thanks a lot ☺️
Thank you for helping me 🙏
Thank you! I’ve browsed many sites, like Byju’s, searching for answers but couldn’t find what I needed. I’ve bookmarked this site, and I’m truly grateful. Thanks again!
Thank you I did my work successfully with the help of yours
Thank you for helping me!
You helpful e vidyarthi thank you so much
Thanks for helping me
Thanks for help I am feel gratitude for you
Thank you aaj apki vejha se mera Kaam pura ho gya
Thank you for helping me 🙏
Thanks , it helps a lot
Thank u for your great help
Thank you aaj mera maths me help karane ke liye