Solutions For All Chapters Ganit Class 6
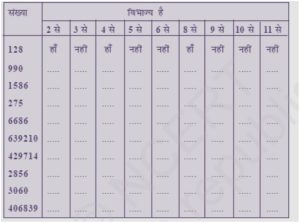
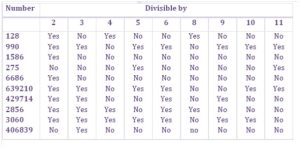
Q1. विभाज्यता की जांच के नियमों का प्रयोग करते हुए, पता कीजिए कि निम्नलिखित संख्याओं में से कौन सी संख्याएँ 2 से विभाज्य है ; 3 से विभाज्य हैं ; 4 से विभाज्य हैं ; 5 से विभाज्य हैं, 6 से विभाज्य हैं, 8 से विभाज्य हैं, 9 से विभाज्य हैं, 10 से विभाज्य हैं या 11 से विभाज्य है (हाँ या नहीं कहिए) :
हल :
Q2. विभाज्यता की जांच के नियमों द्वारा ज्ञात कीजिए कि निम्नलिखित में से कौन – सी संख्याएँ 4 से विभाज्य हैं और कौन – सी 8 से विभाज्य हैं :
(a) 572
हल : 572, 4 से विभाज्य है क्योंकि इसका इकाई और दहाई का अंक 72, 4 विभाज्य है |
572, 8 से अभाज्य है क्योंकि इसकी अंतिम तीन संख्या 572, 8 से अभाज्य है |
(b) 726352
हल : 726352, 4 से विभाज्य है क्योंकि इसका इकाई और दहाई का अंक 52, 4. से विभाज्य है |726352,4 से विभाज्य है क्योंकि इसकी अंतिम तीन संख्या 572, 8 से विभाज्य है |
(c) 5500
हल : (c) 5500 से विभाज्य है क्योंकि इसका इकाई और दहाई का अंक 00, 4 विभाज्य है |
5500, 8 से अभाज्य है क्योंकि इसकी अंतिम तीन संख्या 00, 8 से अभाज्य है |
(d) 6000
हल : (d) 6000, 4 से विभाज्य क्योंकि इसका इकाई और दहाई का अंक 0, 4 से विभाज्य है |
6000, 8 से विभाज्य क्योंकि इसका अंतिम तीन संख्या 0,8 से अभाज्य है |
(e) 12159
हल : (e) 12159, 4 और 8 से अभाज्य है |
(f) 14560
हल : (f) 14560, 4 से विभाज्य क्योंकि इसका इकाई और दहाई का अंक 60, 4 से विभाज्य है |
14560, 8 से विभाज्य क्योंकि इसका अंतिम तीन संख्या 560,8 से अभाज्य है |
(g) 21084
हल : (g) 21084, 4 से विभाज्य क्योंकि इसका इकाई और दहाई का अंक 84, 4 से विभाज्य है |
21084, 8 से विभाज्य क्योंकि इसका इकाई और दहाई का अंक 84, 8 से विभाज्य है
(h) 795072
हल : (h) 31795072 , 4 से विभाज्य क्योंकि इसका इकाई और दहाई का अंक 72, 4 से विभाज्य है|
31795072 , 8 से विभाज्य है क्योंकि इसका इकाई और दहाई का अंक 72, 8 से विभाज्य है |
(i) 1700
हल : (i) 1700,4 से विभाज्य है क्योंकि इसका इकाई और दहाई का अंक 0, 4 से विभाज्य है |
1700,4 से अभाज्य है क्योंकि इसके अंतिम तीन अंक 0, 4 से अभाज्य है |
(j) 2150
हल : (j) 5500,4 से विभाज्य है क्योंकि इसका इकाई और दहाई अंक 0, 4 से विभाज्य है |
5500,8 से अभाज्य है क्योंकि इसका इकाई और दहाई अंक 0, 8 से अभाज्य है |
Q3. विभाज्यता की जांच के नियमों द्वारा ज्ञात कीजिए कि निम्नलिखित में से कौन- सी संख्याएँ 6 से विभाज्य है :
(a) 297144
हल : यह संख्या 2 से विभाज्य है क्योंकि यह सम संख्या है |
यह 3 से विभाज्य है क्योंकि इन संख्याओं का योग 27 है |
यह संख्या 2 और 3 दोनों से विभाज्य नहीं है इसलिए यह 6 से भी विभाज्य है |
(b) 1258
हल : यह संख्या 2 से विभाज्य है क्योंकि यह सम संख्या है |
यह 3 से विभाज्य नहीं है क्योंकि इन संख्याओं कुल योग 16 है जो की सम संख्या है |
यह संख्या 2 और 3 दोनों से विभाज्य नहीं है इसलिए यह 6 से भी विभाज्य है |
(c) 4335
हल : यह संख्या 2 से अभाज्य है क्योंकि यह विषम संख्या है |
यह संख्या 3 से विभाज्य है क्योंकि इन सख्याओं का योग 15 है जो की विषम संख्या है |
(d) 61233
हल : यह संख्या 2 से अभाज्य है क्योंकि यह सम संख्या नहीं है |
यह संख्या 3 से विभाज्य है क्योंकि 15 एक विभाज्य संख्या है |
यह संख्या 2 और 3 दोनों से विभाज्य नहीं है इसलिए यह 6 से भी विभाज्य है |
(e) 901352
हल : यह संख्या 2 से विभाज्य है जो की एक सम संख्या है |
यह संख्या 3 से अभाज्य है क्योंकि इन संख्याओं का योग 20 है जो की 3 से अभाज्य है |
यह संख्या 2 और 3 दोनों से विभाज्य नहीं है इसलिए यह 6 से भी विभाज्य नहीं है |
(f) 438750
हल : यह संख्या 2 से विभाज्य है क्योंकि यह एक सम संख्या है |
यह संख्या 3 से अभाज्य है क्योंकि इन संख्याओं का योग 27 है जो की 3 से अभाज्य है |
यह संख्या 2 और 3 दोनों से विभाज्य है इसलिए यह 6 से भी विभाज्य है |
(g) 1790184
हल : यह संख्या 2 से विभाज्य है क्योंकि यह एक सम संख्या है |
यह संख्या 3 से विभाज्य है क्योंकि इन संख्याओं का कुल योग 30 है जो की 3 से विभाज्य है |
यह संख्या 2 और 3 दोनों से विभाज्य नहीं है इसलिए यह 6 से भी विभाज्य है |
(h) 12583
हल : यह संख्या 2 से अभाज्य है क्योंकि यह एक विषम संख्या है |
यह संख्या 3 से अभाज्य है क्योंकि इन संख्याओं का कुल योग 19 है जो की अभाज्य है |
यह संख्या 2 और 3 दोनों से विभाज्य नहीं है इसलिए यह 6 से भी विभाज्य है |
(i) 639210
हल : यह संख्या 2 से विभाज्य है क्योंकि यह एक सम संख्या है |
यह 3 से अभाज्य है क्योंकि इस संख्या का योग 21 है जो की एक अभाज्य संख्या है |
यह संख्या 2 और 3 दोनों से विभाज्य नहीं है इसलिए यह 6 से भी विभाज्य नहीं है |
(j) 17852
हल : यह एक सम संख्या है जो की 2 से विभाज्य है |
यह एक अभाज्य संख्या है क्योंकि इन संख्याओं का कुल योग 23 है जो की 3 से अभाज्य है |
यह संख्या 2 और 3 दोनों से विभाज्य नहीं है इसलिए यह 6 से भी विभाज्य नहीं है |
Q4. विभाज्यता की जांच के नियमों द्वारा ज्ञात कीजिए कि निम्नलिखित में से कौन सी संख्याएँ 11 से विभाज्य है :
(a) 5445
विषम संख्या का योग = 4 + 5 = 9
सम संख्या का योग = 4 + 5 = 9
दोनों संख्याओं में अंतर = 9 – 9 = 0
(b) 10824
विषम संख्या का योग = 4 + 8 + 1 = 13
सम संख्याओं का योग = 2 + 0 = 2
दोनों संख्याओं में अंतर = 13 – 2 = 11
(c) 7138965
विषम संख्या का योग = 5 + 9 + 3 + 7 = 24
सम संख्याओं का योग = 6 + 8 + 1 = 15
दोनों संख्याओं में अंतर = 24 – 15 = 9
(d) 70169308
विषम संख्याओं का योग = 8 + 3 + 6 + 0 = 17
सम संख्याओं का योग = 0 + 9 + 1 + 7 = 17
दोनों संख्याओं में अंतर = 24 – 15 = 9
(e) 10000001
विषम संख्याओं का योग = 1 + 0 + 0 + 0 = 1
सम संख्याओं का योग = 0 + 0 + 0 + 1 = 1
दोनों संख्याओं में अंतर = 1 – 1 = 0
(f) 901153
विषम संख्याओं का योग = 3 + 1 + 0 = 4
सम संख्याओं का योग = 5 + 1 + 9 = 15
दोनों संख्याओं में अंतर = 15 – 4 = 11
Q5. निम्नलिखित में रिक्त स्थानों में सबसे छोटा अंक तथा सबसे बड़ा अंक लिखिए, जिससे संख्या 3 से विभाज्य हो ;
(a) …….6724
(b) 4765…….2
हल : (a) सबसे छोटी संख्या 2 है = 26724 = 2 + 6 + 7 + 2 + 4 = 21
सबसे बड़ी संख्या 8 है = 86724 = 8 + 6 + 7 + 2 + 4 = 27
(b) हम जानते है की 3 से विभाज्य संख्या 3 है
इसलिए
सबसे छोटी संख्या : 0 = 476502 = 4 + 7 + 6 + 5 + 0 + 2 = 24
सबसे बड़ी संख्या : 9 = 476592 = 4 + 7 + 6 + 5 + 0 + 2 = 33
प्रश्न 6.निम्नलिखित में रिक्त स्थानों में ऐसा अंक लिखिए ताकि संख्या 11 से विभाज्य हो
(a) 92 _______ 389
हल:
92 _______ 389 के लिए विषम स्थानों के अंकों का योग = 9 + 3 + 2 = 14
और सम स्थानों के अंकों का योग = 8 + अभीष्ट अंक + 9 = अभीष्ट अंक + 17
इन अंकों के योग का अन्तर = अभीष्ट अंक + 17 – 14 = अभीष्ट अंक + 3
(अभीष्ट अंक + 3) को 11 बनाने के लिए हमारे पास अभीष्ट संख्या 8 होनी चाहिए। (∵ 3 + 8 = 11)
इसलिए अभीष्ट अंक = 8
(b) 8 _______ 9484
हल:
8 _______ 9484 के लिए, विषम स्थानों के अंकों का योग
= 4 + 4 + अभीष्ट अंक
= 8 + अभीष्ट अंक
और सम स्थानों के अंकों का योग = 8 + 9 + 8 = 25
अंकों के योग में अन्तर = 25 – (8 + अभीष्ट अंक) = 17 – अभीष्ट अंक
(17 – अभीष्ट अंक) को 11 बनाने के लिए हमारे पास अभीष्ट संख्या 6 होनी चाहिए। (∵ 17 -6 = 11)
इसलिए अभीष्ट अंक = 6
Leave a Reply