Solutions For All Chapters – गणित Class 6
Ex 12.2 – बीजगणित
प्रश्न 1. तीन संख्याओं 15, 28 और 14 के योग पर विचार कीजिए। हम यह योग दो प्रकार से प्राप्त कर सकते हैं।
(a) हम पहले 15 और 28 को जोड़कर 43 प्राप्त कर सकते हैं और 43 में 14 जोड़कर कुल योग 57 प्राप्त कर सकते हैं।
(b) हम पहले 28 और 14 को जोड़कर 42 प्राप्त कर सकते हैं और फिर इसे 15 में जोड़कर कुल योग 57 प्राप्त कर सकते हैं।
इस प्रकार (15 + 28) + 14 = 15 + (28 + 14) हआ।
ऐसा किसी भी तीन संख्याओं के लिए किया जा सकता है। यह गुण संख्याओं के योग का साहचर्म (Associative) गुण कहलाता है। इस गुण को चर a, b और c का प्रयोग करते हुए एक व्यापक रूप में व्यक्त कीजिए।
उत्तर: (a + b) + c = a + (b + c)
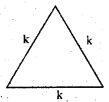
प्रश्न 2. समबाहु त्रिभुज की एक भुजा को k से दर्शाया जाता है। इस समबाहु त्रिभुज के परिमाप को k का प्रयोग करते हुए व्यक्त कीजिए।
उत्तर: हम जानते हैं कि समबाहु त्रिभुज तीन भुजाओं से बनी होती है।
समबाह त्रिभज की एक भजा है।
समबाहु त्रिभुज़ का परिमाप = भुजाओं की लम्बाइयों का योग = k + k + k = 3k
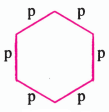
प्रश्न 3. एक समषड्भुज (Regular hexagon) (आकृति-6) की एक भुजा को p से व्यक्त किया गया है। p का प्रयोग करते हुए समषड्भुज के परिभाप को व्यक्त कीजिए। (संकेत- एक समषड्भुज की सभी भजाएँ बराबर होती हैं और सभी कोण बराबर होते हैं।
उत्तर: समषड्भुज का परिमाप = षड्भुज भुजाओं की लम्बाइयों का भाग
= P + P + P + P + P + P
= 6P
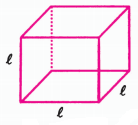
प्रश्न 4. घन (Cube) एक त्रिविमीय (Three dimensional) आकृति है, जैसा कि आकृति 7 में दिखाया गया है। इसके 6 फलक होते हैं और ये सभी सर्वसम। (identical) वर्ग होते हैं। घन के एक किनारे की लम्बाई l से दी जाती है। घन के किनारों की कुल लम्बाई के लिए एक सूत्र ज्ञात कीजिए।
उत्तर:
घन का परिमाप = 16
भुजाओं की लम्बाइयों का योग = l + l + l + l + l + l + l + l + l + l + l + l + l + l + l + l = 16l
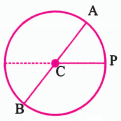
प्रश्न 5. वृत का व्यास वह रेखाखंड है जो वृत्त पर स्थित दो बिन्दुओं को जोड़ता है और उसके केन्द्र से होकर जाता है। वृत्त की त्रिज्या (r) उस पर स्थित किसी बिन्दु p को केन्द्र c से जोड़ने वाली रेखाखंड की लम्बाई है। संलग्न आकृति-8 में AB वृत्त का व्यास है और C उसका केन्द्र है। वृत्त के व्यास (d) को उसकी त्रिज्या (r) के पदों में व्यक्त कीजिए।
उत्तर:
वृत्त का व्यास = PC + AC
d = r + r = 2r

Leave a Reply