कक्षा 6 गणित एनसीईआरटी समाधान प्रश्नावली 11 (Ex 11.2) क्षेत्रमिति

Solutions For All Chapters Ganit Class 6

Q1. एक समबाहु त्रिभुज की भुजा को l से दर्शाया जाता है | इस समबाहु त्रिभुज के परिमाप को l का प्रयोग करते हुए व्यक्त कीजिए |

हल : समबाहु त्रिभुज की भुजा = l

इसलिए, समबाहु त्रिभुज का परिमाप = 3 x भुजा = 3l

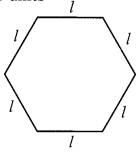
Q2. एक सम षड्भुज (Regular hexagon) की एक भुजा को l से व्यक्त किया गया है (आकृति 11.10) | l का प्रयोग  करते हुए, इस षड्भुज के परिमाप को व्यक्त कीजिए | (संकेत : एक सम षड्भुज की सभी 6 भुजाएँ बराबर होती हैं और सभी कोण बराबर होते हैं ) |

हल : षड्भुज की भुजा = l

इसलिए, षड्भुज का परिमाप = 6 x भुजा = 6l

Q3. घन (cube) एक त्रिविमीय (three dimensional) आकृति होती है, जैसा कि आकृति 11.11 में दिखाया गया है | इसके 6 फलक होते है और ये सभी सर्वसम (identical) वर्ग होते हैं| घन के एक किनारे की लंबाई l से दी जाती है घन के किनारों की कुल लंबाई के लिए एक सूत्र ज्ञात कीजिए |   

हल : घन की लंबाई = l

घनों के किनारों की संख्या = 12

इसलिए, कुल लंबाई = 12 x l = 12l

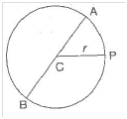
Q4. वृत्त का एक व्यास वह रेखाखण्ड है जो वृत्त पर स्थित दो बिन्दुओं को जोड़ता है और उसके केन्द्र से होकर जाता है | संलग्न आकृति 11.12 में, AB वृत्त का व्यास है और C उसका केन्द्र है | वृत्त के व्यास (d) को उसकी त्रिज्या (r) के पदों में व्यक्त कीजिए |

हल : त्रिज्या की लंबाई दुगुनी है इस रेखाचित्र में

इसलिए, d – 2r

Q5. तीन संख्याओं 14, 27 और 13 के योग पर विचार कीजिए | हम यह योग दो प्रकार से ज्ञात कर सकते है :

(a) हम पहले 14 और 27 को जोड़कर ४१ प्राप्त कर सकते हैं और फिर 41 में 13 जोड़कर कुल योग 54 प्राप्त कर सकते हैं | या 

(b) हम पहले 27 और 13 को जोड़कर 40 प्राप्त कर सकते हैं और फिर इसे 14 में जोड़कर कुल योग 54 प्राप्त कर सकते हैं | इस प्रकार, (14 + 27) + 13 = 14 + (27 + 13 ) हुआ | 

ऐसा किन्हीं भी तीन संख्याओं के लिए किया जा सकता है | यह गुण संख्याओं के योग का साहचर्य (associative) गुण कहलाता है | इस गुण को जिसे हमें पूर्ण संख्याओं के अध्याय में पद चुके है, चर a,b और c का प्रयोग करते हुए, एक व्यापक रूप में व्यक्त कीजिए |

हल : (a + b) + c = a + (b + c)