समाकलनों के अनुप्रयोग
प्रश्न सं. 1: दीर्घवृत्त \(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\) द्वारा परिबद्ध क्षेत्रफल ज्ञात कीजिए।
समाधान:
दिया गया, \(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\)
\(\frac{y^2}{b^2} = 1 – \frac{x^2}{a^2}\) \(\frac{y^2}{b^2} = \frac{a^2 – x^2}{a^2}\)
\(y^2\) = \(\frac{b^2}{a^2} (a^2 – x^2)\)
उपरोक्त व्यंजक में y का धनात्मक मान प्रतिस्थापित करने पर, क्योंकि OAB प्रथम चतुर्थांश में स्थित है।
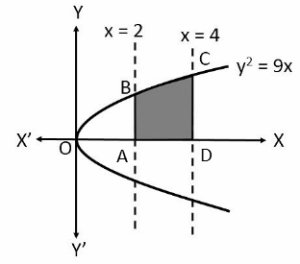
प्रश्न सं. 2: प्रथम चतुर्थांश में \(y^2\) = 9x, x = 2, x = 4 और x-अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
समाधान:
हम नीचे दिए अनुसार पहले वक्र में \(y^2\) = 9x, x = 2, x = 4 और x-अक्ष की आकृति बना सकते हैं ।
\(y^2\) = 9x
y = ±√(9x)
y = ±3√x
हम y का धनात्मक मान ले सकते हैं क्योंकि अभीष्ट क्षेत्रफल प्रथम चतुर्थांश में है।
अभीष्ट क्षेत्रफल ABCD से घिरा छायांकित क्षेत्र है।
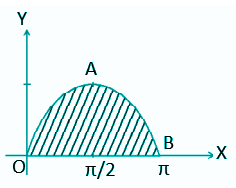
प्रश्न सं. 3: 0 और π के बीच वक्र y = sin x का क्षेत्रफल ज्ञात कीजिए।
समाधान:
दिया गया, y = sin x
OAB का क्षेत्रफल
= – [cos π – cos 0]
= -(-1 -1)
= 2 वर्ग इकाई
प्रश्न सं. 4: दोनों परवलय y = \(x^2\) और \(y^2\) = x द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
समाधान:
दोनों परवलय y = \(x^2\) और \(y^2\) = x द्वारा परिबद्ध क्षेत्रफल को ज्ञात करने के लिए, हमें सबसे पहले इन दोनों परवलयों के बीच के बिंदुओं को खोजने की आवश्यकता होती है।
1. पहले y = \(x^2\) और \(y^2\) = x को एक-दूसरे के बराबर रखते हैं:
\(x^2 = y\) और \(y^2\) = x
2. y = \(x^2\) को \(y^2\) = x में रखते हुए, हमें बिंदु मिलते हैं जहाँ ये दोनों परवलय एक-दूसरे को काटते हैं:
\(x^2\) = \(x^{1/2}\)
सरल बनाने पर, हमें मिलते हैं बिंदु (0,0) और (1,1)।
3. अब हमें इन बिंदुओं के बीच का क्षेत्रफल ज्ञात करना है।

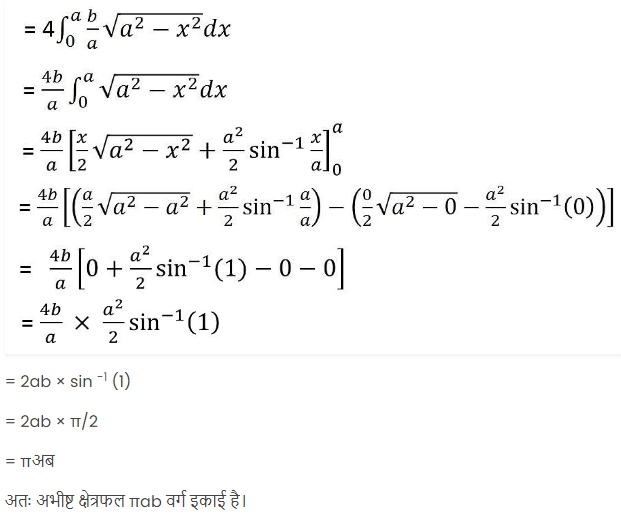
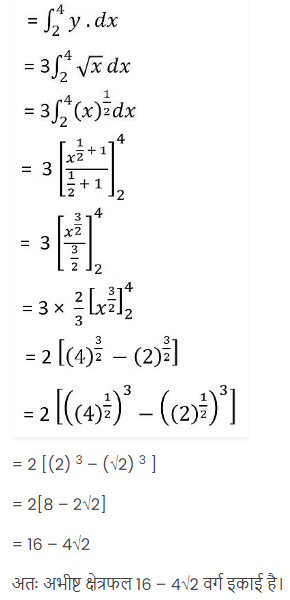
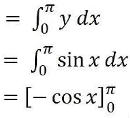


Leave a Reply