प्रश्न 1: मूल्यांकन करें: ∫ 3ax/(\(b^2 +c^2 x^2\))dx
समाधान:
समाकल का मूल्यांकन करने के लिए, I = ∫ 3ax/(\(b^2 +c^2 x^2\))dx
v = \(b^2 +c^2 x^2\) लेते हैं, तो
dv = \(2c^2\)x dx
इस प्रकार, ∫ 3ax/(\(b^2 +c^2 x^2\))dx
= (3ax/\(2c^2\)x)∫dv/v
अब, अंश और हर दोनों पर x को रद्द करें, हमें मिलता है
= (3ax/\(2c^2\))∫dv/v
= (3a/\(2c^2\) )log |b2 +c2x2| + C
जहाँ C एक मनमाना स्थिरांक है
प्रश्न 2:\(∫tan^8 x sec^4\)x dx निर्धारित करें
समाधान:
दिया गया: \(∫tan^8 x sec^4\)x dx
मान लीजिए I = \(∫tan^8 x sec^4\)x dx — (1)
अब, विभाजित करें \(sec^4 x = (sec^2 x) (sec^2 x)\)
अब, (1) में प्रतिस्थापित करें
इसे इस प्रकार लिखा जा सकता है:
अब, पदों को x के सापेक्ष समाकलित करने पर हमें प्राप्त होता है:
प्रश्न 3: निम्नलिखित फलन का प्रतिअवकलज लिखिए:\(3x^2 + 4x^3\)
समाधान:
दिया गया: \(3x^2 + 4x^3\)
दिए गए फ़ंक्शन का प्रतिअवकलज इस प्रकार लिखा जाता है:
∫\(3x^2 + 4x^3 dx = 3(x^3/3) + 4(x^4/4)\)
= \(x^3 + x^4\)
इस प्रकार, \(3x^2 + 4x^3\) का प्रतिअवकलज = \(x^3 + x^4\)
प्रश्न 4: “f” का प्रतिअवकलज F निर्धारित करें, जिसे f(x) = \(4x^3 – 6\) द्वारा परिभाषित किया गया है, जहाँ F(0) = 3
समाधान:
दिया गया फलन: f(x) = \(4x^3 – 6\)
अब, फ़ंक्शन को एकीकृत करें:
∫\(4x^3 – 6 dx = 4(x^4 /4)- 6x + C\)
∫\(4x^3 – 6 dx = x^4 – 6x + C\)
इस प्रकार, फ़ंक्शन F का प्रतिअवकलज \(x^4 – 6x + C\) है, जहाँ C एक स्थिरांक है
साथ ही, यह भी दिया गया है कि, F(0) = 3,
अब, प्राप्त प्रतिअवकलज फलन में x = 0 प्रतिस्थापित करने पर, हमें प्राप्त होता है:
\((0)^4\)– 6(0) + C = 3
इसलिए, C = 3.
अब, प्रतिअवकलज फलन में C = 3 प्रतिस्थापित करें
अतः अभीष्ट प्रतिअवकलज फलन \(x^4\)– 6x + 3 है।
प्रश्न 5: प्रतिस्थापन द्वारा एकीकरण का उपयोग करके दिए गए फ़ंक्शन को एकीकृत करें: x के संबंध में 2x sin(\(x^2 +1\))
समाधान:
दिया गया फ़ंक्शन: 2x sin(\(x^2 +1\))
हम जानते हैं कि \(x^2\)+ 1 का व्युत्पन्न 2x है।
अब प्रतिस्थापन विधि का उपयोग करें, हमें मिलता है
\(x^2\) + 1 = t, अतः 2x dx = dt.
इसलिए, हमें प्राप्त होता है ∫ 2x sin (\(x^2\)+1) dx = ∫ sint dt
= – cos t + C
= – cos (\(x^2\)+ 1) + Cजहाँ C एक मनमाना स्थिरांक है
इसलिए, प्रतिस्थापन विधि द्वारा एकीकरण का उपयोग करते हुए 2x sin(\(x^2 +1\)) का प्रतिअवकलज = – cos (\(x^2\)+ 1) + C है
प्रश्न 6: एकीकृत करें: ∫\(sin^3 x cos^2 x dx\)
समाधान:
दिया गया है ∫\(sin^3 x cos^2 x dx\)
इसे इस प्रकार लिखा जा सकता है:
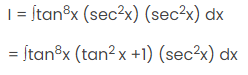

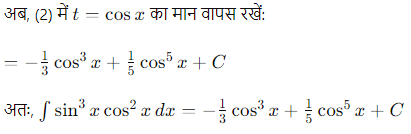

Leave a Reply