सांतत्य तथा अवकलनीयता
प्रश्न 1: फलन f(x) = sin x . cos x की सातत्यता की व्याख्या करें
समाधान:
हम जानते हैं कि sin x और cos x सतत फलन हैं। यह भी ज्ञात है कि दो सतत फलनों का गुणनफल भी एक सतत फलन होता है।
अतः, फलन f(x) = sin x . cos x एक सतत फलन है।
प्रश्न 2:संयुक्त फलन y = f[f(x)] के असंततता बिंदु निर्धारित करें, दिया है कि, f(x) = 1/x-1.
समाधान:
दिया गया है कि, f(x) = 1/x-1
हम जानते हैं कि फ़ंक्शन f(x) = 1/x-1, x = 1 पर असंतत है
अब, x ≠1 के लिए,
f[f(x)]= f(1/x-1)
= 1/[(1/x-1)-1]
= x-1/ 2-x, जो कि बिन्दु x = 2 पर असतत है।
इसलिए, असंततता के बिंदु x = 1 और x = 2 हैं।
प्रश्न 3: यदि f(x) = |cos x|, तो f'(3π/4) ज्ञात कीजिए
समाधान:
दिया गया है कि, f(x) = |cos x|
जब π/2 <x< π, cos x < 0,
इस प्रकार, |cos x| = -cos x
इसका अर्थ है कि, f(x) = -cos x
अतः, f'(x) = sin x
इसलिए, f'(3π/4) = sin (3π/4) = 1/√2
f'(3π/4) = 1/√2
प्रश्न 4: [3, 5] में निम्नलिखित फलन f (x) = (x – 3) (x – 6) (x – 9) के लिए माध्य मान प्रमेय का सत्यापन करें
समाधान:
=36±12.496
c=8.8&c=4.8
c∈(3,5)
f(x)=(x−3)(x−6)(x−9) on [3,5]
प्रश्न 5: x = 0 पर फलन f = |x| की सातत्यता की व्याख्या कीजिए।
समाधान:
दिए गए फ़ंक्शन से, हम परिभाषित करते हैं कि,
f(x) = {-x, यदि x<0 और x, यदि x≥0
यह स्पष्ट रूप से उल्लेख किया गया है कि फ़ंक्शन 0 पर परिभाषित है और f(0) = 0 है। फिर 0 पर f की बायीं ओर की सीमा है
इसी प्रकार दाएँ हाथ की ओर,
\(Lim_{x→0+} f(x)= Lim_{x→0+} (x) = 0\)इसलिए, बाएं हाथ और दाएं हाथ की सीमा दोनों के लिए, फ़ंक्शन का मान बिंदु x = 0 पर संपाती होता है।
इसलिए, फलन f बिंदु x = 0 पर सतत है।
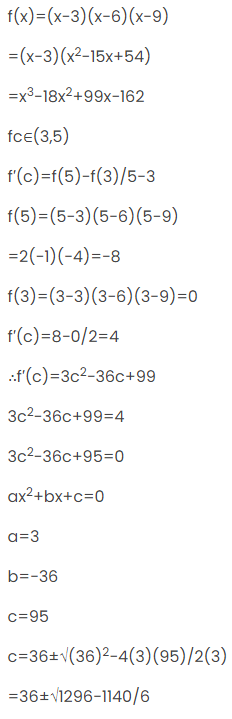
Leave a Reply