प्रश्न 1: निम्नलिखित रेखीय प्रोग्रामिंग समस्या (LPP) को ग्राफ़िक रूप से हल करें:
लक्ष्य: Z = 2x + 3y को अधिकतम करें, दिए गए बंधनों के साथ:
बंधन:
x + y ≤ 4
x ≥ 0
y ≥ 0
समाधान:
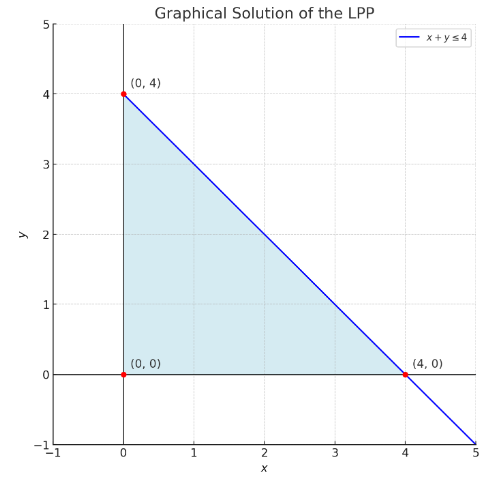
इस समस्या को हल करने के लिए, सबसे पहले हम दिए गए बंधनों का ग्राफ़ बनाते हैं और समाधान क्षेत्र की पहचान करते हैं।
बंधन 1: x + y ≤ 4
इस समीकरण को x + y = 4 के रूप में लिखें और इसके ग्राफ़ के लिए बिंदु निर्धारित करें:
जब x = 0, तब y = 4 (बिंदु: (0,4))
जब y = 0, तब x = 4 (बिंदु: (4,0))
इन बिंदुओं को मिलाकर एक रेखा खींचें।
बंधन 2: x ≥ 0
यह बताता है कि x-अक्ष पर सभी बिंदु गैर-ऋणात्मक होंगे, यानी यह रेखा y-अक्ष के दाईं ओर स्थित होगी।
बंधन 3: y ≥ 0
यह बताता है कि y-अक्ष पर सभी बिंदु गैर-ऋणात्मक होंगे, यानी यह रेखा x-अक्ष के ऊपर स्थित होगी।
ग्राफ़:
ग्राफ़ पर बंधन x + y ≤4 का क्षेत्र x और y अक्ष से बंधा हुआ है।
समाधान क्षेत्र वह भाग होगा जहाँ सभी बंधन मिलते हैं। यह x-अक्ष और y-अक्ष के सकारात्मक हिस्से में होगा, और
x + y = 4 रेखा के नीचे होगा।
अब, हम इस क्षेत्र के कोनों (corner points) को पहचानते हैं, क्योंकि अधिकतम या न्यूनतम मान हमेशा कोनों पर होता है।
कोने (corner points):
1. (0, 0)
2. (4, 0)
3. (0, 4)
ऊपर दिए गए ग्राफ़ में, समाधान क्षेत्र को हल्के नीले रंग से दर्शाया गया है, और कोने के बिंदुओं को लाल बिंदुओं के रूप में दर्शाया गया है। इन बिंदुओं पर Z = 2x + 3y के मान निम्नलिखित हैं:
बिंदु (0, 0 ) पर: Z = 2(0) + 3(0) = 0
बिंदु (4, 0 ) पर: Z = 2(4) + 3(0) = 8
बिंदु (0, 4) पर: Z = 2(0) + 3(4) = 12
Z का अधिकतम मान 12 है, जो बिंदु (0, 4) पर प्राप्त होता है। इसलिए, Z = 12 अधिकतम है।
प्रश्न सं. 2: निम्नलिखित रैखिक प्रोग्रामिंग समस्या को ग्राफ़िक रूप से हल करें:
Z = 200 x + 500 y को निम्न प्रतिबंधों के अधीन न्यूनतम करें:
x + 2y ≥ 10
3x + 4y ≤ 24
x ≥ 0, y ≥ 0
समाधान:
दिया गया,
न्यूनतम करें Z = 200 x + 500 y … (1)
निम्नलिखित बाधाओं के अधीन:
x + 2y ≥ 10 … (2)
3x + 4y ≤ 24 … (3)
x ≥ 0, y ≥ 0 … (4)
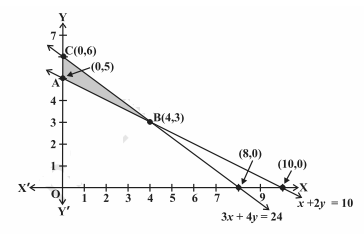
आइए नीचे दिए अनुसार x + 2y = 10 और 3x + 4y = 24 का ग्राफ बनाएं।
उपरोक्त चित्र में छायांकित क्षेत्र समीकरण द्वारा निर्धारित व्यवहार्य क्षेत्र ABC है।
बाधाओं की प्रणाली (2) से (4), जो कि परिबद्ध है। कोने बिंदु A, B और C के निर्देशांक क्रमशः (0,5), (4,3) और (0,6) हैं।
इन बिंदुओं पर Z = 200x + 500y की गणना।
| कोने का बिंदु | Z का मान |
| (0, 5) | 2500 |
| (4, 3) | 2300← न्यूनतम |
| (0, 6) | 3000 |
अतः Z का न्यूनतम मान 2300 बिन्दु (4, 3) पर है।
प्रश्न संख्या 3: एक विनिर्माण कंपनी दो प्रकार के टेलीविजन सेट बनाती है; एक ब्लैक एंड व्हाइट और दूसरा कलर। कंपनी के पास एक सप्ताह में अधिकतम 300 सेट बनाने के संसाधन हैं। एक ब्लैक एंड व्हाइट सेट बनाने में 1800 रुपये और एक रंगीन सेट बनाने में 2700 रुपये लगते हैं। कंपनी टेलीविजन सेट बनाने के लिए एक सप्ताह में 648000 रुपये से अधिक खर्च नहीं कर सकती है। यदि उसे प्रति ब्लैक एंड व्हाइट सेट 510 रुपये और प्रति रंगीन सेट 675 रुपये का लाभ होता है, तो प्रत्येक प्रकार के कितने सेट का उत्पादन किया जाना चाहिए ताकि कंपनी को अधिकतम लाभ हो? इस समस्या को LPP के रूप में सूत्रबद्ध करें, यह देखते हुए कि उद्देश्य लाभ को अधिकतम करना है।
समाधान:
मान लीजिए x और y क्रमशः प्रत्येक सप्ताह बनाए गए काले और सफेद सेटों तथा रंगीन सेटों की संख्या को दर्शाते हैं।
इस प्रकार x ≥ 0, y ≥ 0
कंपनी प्रति सप्ताह अधिकतम 300 सेट बना सकती है, इसलिए, x + y ≤ 300.
सेट के निर्माण की साप्ताहिक लागत (रुपये में) 1800x + 2700y है और कंपनी 648000 रुपये तक खर्च कर सकती है।
इसलिए, 1800x + 2700y ≤ 648000
या
2x + 3y ≤ 720
x काले और सफेद सेट और y रंगीन सेट पर कुल लाभ (510x + 675y) रुपये है।
मान लीजिए उद्देश्य फलन Z = 510x + 675y है।
इसलिए, समस्या का गणितीय सूत्रीकरण इस प्रकार है।
बाधाओं के अधीन Z = 510x + 675y को अधिकतम करें:
x + y ≤ 300
2x + 3y ≤ 720
x ≥ 0, y ≥ 0
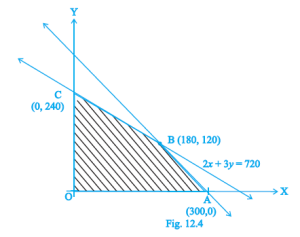
x + y = 30 और 2x + 3y = 720 का ग्राफ नीचे दिया गया है।
| कोने का बिंदु | Z का मान |
| A(300, 0) | 153000 |
| B(180, 120) | 172800 = अधिकतम |
| C(0, 240) | 162000 |
अतः अधिकतम लाभ तब होगा जब 180 काले और सफेद सेट तथा 120 रंगीन सेट उत्पादित किये जायेंगे।
प्रश्न संख्या 4: एक आहार विशेषज्ञ दो प्रकार के खाद्य पदार्थों को इस तरह मिलाना चाहता है कि मिश्रण में विटामिन की मात्रा कम से कम 8 यूनिट विटामिन ए और 10 यूनिट विटामिन सी हो। खाद्य पदार्थ ‘I’ में 2 यूनिट/किग्रा विटामिन ए और 1 यूनिट/किग्रा विटामिन सी होता है। खाद्य पदार्थ ‘II’ में 1 यूनिट/किग्रा विटामिन ए और 2 यूनिट/किग्रा विटामिन सी होता है। खाद्य पदार्थ ‘I’ को खरीदने के लिए 50 रुपये प्रति किलोग्राम और खाद्य पदार्थ ‘II’ को खरीदने के लिए 70 रुपये प्रति किलोग्राम खर्च होता है। इस तरह के मिश्रण की लागत को कम करने के लिए इस समस्या को एक रैखिक प्रोग्रामिंग समस्या के रूप में सूत्रबद्ध करें।
समाधान:
माना मिश्रण में x किग्रा भोजन ‘I’ तथा y किग्रा भोजन ‘II’ है।
स्पष्टतः, x ≥ 0, y ≥ 0.
नीचे दिए गए आंकड़ों को सारणीबद्ध करें।
| संसाधन | खाना | मांग | |
| I (x) | II (y) | ||
| Vitamin A (units/kg) | 2 | 1 | 8 |
| Vitamin C (units/kg) | 1 | 2 | 10 |
| Cost (Rs/kg) | 50 | 70 | |
यह देखते हुए कि, मिश्रण में कम से कम 8 इकाई विटामिन ए और 10 इकाई विटामिन सी होनी चाहिए।
इस प्रकार, बाधाएँ इस प्रकार हैं:
2x + y ≥ 8
x + 2y ≥ 10
भोजन ‘I’ के x Kg और भोजन ‘II’ के y kg खरीदने की कुल लागत Z = 50x + 70y
अतः, समस्या का गणितीय सूत्रीकरण इस प्रकार है:
Z = 50x + 70y को न्यूनतम करें… (1)
निम्नलिखित बाधाओं के अधीन:
2x + y ≥ 8 … (2)
x + 2y ≥ 10 … (3)
x, y ≥ 0 … (4)
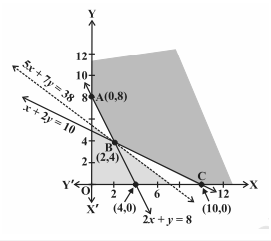
आइए नीचे दिए अनुसार 2x + y = 8 और x + 2y = 10 का ग्राफ बनाएं।
यहाँ, ध्यान दें कि सुसंगत क्षेत्र असीमित है।
आइए कोने बिंदु A(0,8), B(2,4) और C(10,0) पर Z का मान ज्ञात करें।
| कोने का बिंदु | Z का मान |
| A(0, 8) | 560 |
| B(2, 4) | 380 = न्यूनतम |
| C(10, 0) | 500 |
अतः Z का न्यूनतम मान 380 है जो बिन्दु (2, 4) पर प्राप्त होता है।
इसलिए, आहार विशेषज्ञ के लिए इष्टतम मिश्रण रणनीति 2 किलोग्राम भोजन ‘I’ और 4 किलोग्राम भोजन ‘II’ को मिलाना होगी, और इस रणनीति के साथ, मिश्रण की न्यूनतम लागत 380 रुपये होगी।
Leave a Reply