त्रि-विमीय ज्यामिति
प्रश्न 1: उन दो बिंदुओं (– 2, 4, – 5) और (1, 2, 3) से होकर गुजरने वाली रेखा के दिशा कोसाइन (Direction Cosines) ज्ञात करें।
हल:
मान लें कि दो बिंदुओं A(−2,4,−5) और B(1,2,3) से होकर जाने वाली रेखा के दिशा अनुपात l,m,n हैं।
सबसे पहले हम रेखा के दिशा अनुपात (Direction Ratios) ज्ञात करते हैं:
दिशा अनुपात = (\(x_2 − x_1, y_2 − y_1, z_1 – x_1\))
अर्थात,
l = 1 − (−2) = 1 + 2 = 3
m = 2 − 4 = − 2
n = 3 − (−5) = 3 + 5 = 8
अब, दिशा कोसाइन ज्ञात करने के लिए, दिशा अनुपातों को उनकी मापांक से विभाजित करें:
दिशा कोसाइन cosα,cosβ,cosγ ज्ञात करने के लिए:
\(\sqrt{l^2 + m^2 + n^2}\) = \(\sqrt{3^2 + ( – 2)^2 + 8^2}\) = \(\sqrt{9 + 4 + 64}\) = \(\sqrt{77}\)
इस प्रकार:
अतः, उन दो बिंदुओं से होकर गुजरने वाली रेखा के दिशा कोसाइन \(\frac{3}{√77′} \frac{-2}{√77′} \frac{8}{√77}\) होंगे।
प्रश्न 2: यदि एक रेखा x, y और z-अक्षों के साथ क्रमशः 90°, 135°, 45° के कोण बनाती है, तो इसकी दिशा कोसाइन ज्ञात कीजिए।
समाधान:
मान लीजिए रेखा की दिशा कोसाइनें l, m और n हैं।
l = cos 90° = 0
m = cos 135° = -1/√2
n = cos 45° = 1/√2
अतः रेखा की दिशा कोसाइनें 0, -1/√2, तथा 1/√2 हैं।
प्रश्न 3: द्वारा दिए गए रेखाओं के युग्म के बीच का कोण ज्ञात कीजिए।
प्रश्न 4: निम्नलिखित युग्म रेखाओं के बीच का कोण ज्ञात कीजिए।
\(\frac{(x + 3)}{3} = \frac{(y – 1)}{5} = \frac{(z + 3)}{4}\)
\(\frac{(x + 1)}{1} = \frac{(y – 4)}{1} = \frac{(z – 5)}{2}\)
समाधान:
सबसे पहले, हमें इन रेखाओं के निर्देशन अनुपात ज्ञात करने होंगे।
पहली रेखा के लिए निर्देशन अनुपात \(b_1, b_1, c_1\) हैं:
\(a_1 = 3 b_1 = 5, c_1 = 4\)दूसरी रेखा के लिए निर्देशन अनुपात (\(b_2, b_2, c_2\)) हैं:
\(a_2 = 1, b_2 = 1, c_2 = 2\)अब, इन रेखाओं के बीच के कोण 0 का मान ज्ञात करने के लिए हम निम्नलिखित सूत्र का उपयोग करते हैं:
प्रश्न 5: सिद्ध करें कि रेखाएँ \(\frac{x – 5}{7} = \frac{y + 2}{-5} = \frac{z}{1}\) और \(\frac{x}{1} = \frac{y}{2} = \frac{z}{3}\) एक दूसरे के लंबवत हैं।
समाधान:
हमारी दो रेखाएँ हैं:
पहली रेखा \(\frac{x – 5}{7} = \frac{y + 2}{-5} = \frac{z}{1}\)
दूसरी रेखा \(\frac{x}{1} = \frac{y}{2} = \frac{z}{3}\)
पहली रेखा का निदेशक अनुपात (direction ratios) हैं: 7,−5,1.
दूसरी रेखा का निदेशक अनुपात (direction ratios) हैं: 1,2,3.
अब, यह सिद्ध करने के लिए कि ये रेखाएँ एक दूसरे के लंबवत हैं, हमें इनके निदेशक अनुपात का स्केलर गुणनफल (dot product) देखना होगा।
स्केलर गुणनफल:
7 × 1 + (−5) × 2 + 1 × 3 = 7 − 10 + 3 = 0
क्योंकि स्केलर गुणनफल 0 है, इसलिए ये रेखाएँ एक दूसरे के लंबवत हैं।
अतः, यह सिद्ध होता है कि दी गई रेखाएँ एक दूसरे के लंबवत हैं।
प्रश्न 6: उस तल का x-अक्ष, y-अक्ष, और z-अक्ष पर काटे गए अवरोध ज्ञात करें, जो समीकरण 2x + y – z = 5 द्वारा दिया गया है।
समाधान:
किसी तल का x-अक्ष पर अवरोध ज्ञात करने के लिए, हम y और z को 0 मानते हैं।
तल का समीकरण 2x + y – z = 5 है।
y = 0 और z = 0 रखने पर:
2x = 5 ⟹ x = \(\frac{5}{2}\)
अतः, x-अक्ष पर अवरोध \(\frac{5}{2}\) है।
किसी तल का y-अक्ष पर अवरोध ज्ञात करने के लिए, हम x और z को 0 मानते हैं।
तल का समीकरण 2x + y – z = 5 है।
x = 0 और z = 0 रखने पर:
y = 5
अतः, y-अक्ष पर अवरोध 5 है।
किसी तल का z-अक्ष पर अवरोध ज्ञात करने के लिए, हम x और y को 0 मानते हैं।
तल का समीकरण 2x + y – z = 5 है।
x = 0 और y = 0 रखने पर:
− z = 5 ⟹ z = − 5
अतः, z-अक्ष पर अवरोध -5 है।
इस प्रकार, तल द्वारा x-अक्ष, y-अक्ष और z-अक्ष पर क्रमशः काटे गए अवरोध \(\frac{5}{2}\) 5 और -5 हैं।
प्रश्न 7: उन समतलों के समीकरण ज्ञात कीजिए जो तीन बिंदुओं (1, 1, 0), (1, 2, 1), और (–2, 2, –1) से होकर गुजरते हैं।
समाधान:
मान लीजिए, समतल का समीकरण
ax + by + cz + d = 0
इस समीकरण को उन तीन बिंदुओं (1, 1, 0), (1, 2, 1), और (–2, 2, –1) से होकर गुजरना है, इसलिए इन बिंदुओं को इस समीकरण में रखने से:
बिंदु (1, 1, 0) के लिए:
a(1) + b(1) + c(0) + d = 0 या a + b + d = 0…(i)
बिंदु (1, 2, 1) के लिए:
a(1) + b(2) + c(1) + d = 0 या a + 2b + c+ d = 0…(ii)
बिंदु (–2, 2, –1) के लिए:
a(−2) + b(2) + c(−1) + d = 0 या −2a + 2b − c+ d = 0…(iii)
अब समीकरणों (i), (ii), और (iii) को हल करके a, b, c और d के मान निकालते हैं:
पहले, समीकरण (i) और (ii) से c और d के लिए हल करते हैं:
(i) से d = − a − b मान लीजिए।
अब इसे (ii) में रखिए:
a + 2b + c − a − b = 0 या b + c = 0…(iv)
समीकरण (iii) में भी d = − a − b रखिए:
− 2a + 2b − c + (− a − b) = 0 या − 3a + b − c = 0…(v)
(iv) और (v) से b और c के लिए हल करें:
(iv) से c = − b है। इसे (v) में रखिए:
− 3a + b − (−b) = 0 या − 3a + 2b = 0 या b =\(\frac{3a}{2}\)
अब, bका मान (iv) में डालिए:
c = − \(\frac{3a}{2}\)
अब, d = − a − b = − a − \(\frac{3a}{2} = – \frac{5a}{2}।\)
इसलिए, समतल का समीकरण होगा:
\(\frac{2}{3} x + y – z – \frac{5}{2}= 0\)अतः, समतल का समीकरण है:
2x + 3y − 3z − 5 = 0


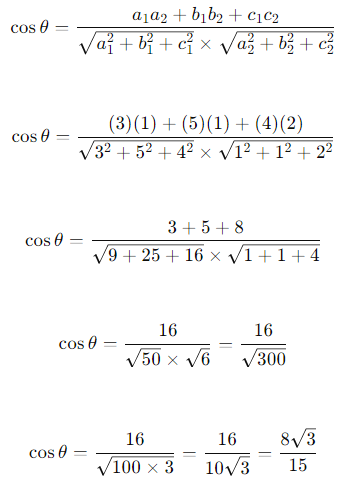


Leave a Reply