Page 23.4 Ex. 23.1
Q1.
Answer :
(i) The vector
OP→
represents the required displacement vector.
(ii) The vector
OQ→
represents the required vector.
(iii) The vector
OR→
represents the required vector.
Q2.
Answer :
The quantities which have only magnitude and which are not related to any
fixed direction in space are called scaler quantities or simply scalars.
The quantities which have both magnitude and direction are called vector quantities or simply vectors.
(i) Mass – Scalar
(ii) Weight(Force) – Vector
(iii) Angle – Scalar
(iv) Directed Disptance- Vector
(v) Magnitude of acceleration – Scalar
Q3.
Answer :
The quantities which have only magnitude and which are not related to any
fixed direction in space are called scaler quantities or simply scalars.
The quantities which have both magnitude and direction are called vector quantities or simply vectors.
(i) Scalar
(ii) Scalar
(iii) Vector
(iv)Vector
(v) Scalar
(vi) Vector
(vii) Vector
Q4.
Answer :
(i) Vectors having the same or parallel supports are called collinear vector.
In the given figure the collinear vectors are
a→, d →; x→, z→, b→ ; c→, y→
(ii) Vectors having the same magnitude and direction are called equal vector.
In the given figure the equal vectors are
b,→ x→ ; c→, y→ ; a→, d→
(iii) Vectors having the same initial point are called co-initial vector.
In the given figure the co-initial vectors are
a→, y→, z→
(iv) The vectors which are collinear but not equal are b→, z→ ; x→, z→
Q5.
Answer :
(i) True, As vectors having the same and parallel support are collinear.
(ii) False, Collinear vectors are parallel vector not equal vectors.
(iii) False.
(iv) False, Collinear vectors may not have a same magnitude.
(v) False, As two collinear vectors are equal only if they have same length and same sense.
Page 23.17 Ex. 23.2
Q1.
Answer :
Given: P, Q and R are collinear such that PQ→ = a→ and QR →= b→. Then,
PQ→+ QR→ = PR→
⇒ PR→ = a→ + b→
Q2.
Answer :
Let ABC be a triangle such that BC→ = a→, AB →= c→ and CA→ = b→. Then,
a→+b→+c→= BC→+CA→+AB→
⇒a→+b→+c→ = BA→+AB→ [∵ BC→+CA→ = BA→]
⇒a→+b→+c→ = BB→ [ Using triangle law]
⇒ a→+b→+c→ = 0→ [ By definition of null vector]
Other possibilities are
i c→+ a→ = b→
ii a→ + b→ = c→
iii b→+ c→ = a→
Q3.
Answer :
Given: a→ , b→ are two non-collinear vectors having same initial points. Complete the parallelogram ABCD such that AB→= a→ and BC→= b→.
In △ABC,
AB→ + BC→ =AC→⇒ a→ + b→ = AC→
In △ABD,
AD→ + DB→ = AB→⇒ b→ + DB→ = a→⇒ DB→ = a→ – b→
Therefore, AC→ and DB→ are the diagonals of a parallelogram whose adjacent sides are a→ and b→ respectively.
Q4.
Answer :
Given: a→ is a vector and m is a scalar such that, ma→ = 0→
Then either m= 0 or, a→ = 0→
Q5.
Answer :
Given: ABCD is a quadrilateral.
We need to find the sum of BA→ + BC→ + CD→ + DA→.
Consider,
BA→ + BC→ + CD→ + DA→= BA→ + DA→ + BC→ + CD→
= BD→ + 2 DA→ + BD→ [∵ BD→ + DA→ = BA→ and BC→ + CD→ = BD→]
= 2 BD→ + DA→= 2 BA→
Q6.
Answer :
Given: ABCDE is a pentagon.
(i) To Prove: AB→ + BC→ + CD→ + DE→ + EA→ = 0→.
Proof: We have,
LHS = AB→ + BC→ + CD→ + DE→ + EA→
= AC→ + CD→ + DA→ [ ∵ AB→ + BC→ = AC→ and DE→ + EA→ = AD→]
= AD→ + DA→ [ ∵ AC→ + CD→ = AD→]
= 0→= RHS
(ii) To Prove: AB→ + AE→ + BC→ + DC→ + ED→ + AC→ = 3 AC→.
Proof: We have,
LHS = AB→ + AE→ + BC→ + DC→ + ED→ + AC→
= AB→ + BC→ + AE→ + ED→ + DC→ + AC→
= AC→ +AD→ + DC→ + AC→ [∵ AB→ + BC→ = AC→ and AE→ + ED→ = AD→]
= AC→ + AD→ + AC→ – AD→ + AC→ [∵ AD→ + DC→= AC→ ⇒ DC→ = AC→ – AD→ ]
= 3 AC→= RHS
Hence proved.
Q7.
Answer :
Given: A regular octagon of eight sides with centre O.
To show: OA→ + OB→ + OC→ + OD→ + OE→ + OF→ + OG→ + OH→ = 0→.
Proof: We know centre of the regular octagon bisects all the diagonals passing through it.
OA→ =-OE→ , OB→ =-OF→ , OD→ =-OH→ and OC→ =-OG→.
⇒ OA→ + OE→ = 0→ , OB→ + OF→ = 0→ , OD→ + OH→ = 0→ and OC→ + OG→ = 0→. …………(i)
Now,
OA→ + OB→ + OC→ + OD→ + OE→ + OF→ +OG→+ OH→=OA→ + OE→ + OB→ + OF→ + OC→ + OG→+ OD→ + OH→= 0→ + 0→ + 0→ + 0→=0→
Hence proved.
Q8.
Answer :
Given: ABCD is a quadrilateral such that AP→ + PB→ + PD→ = PC→.
To show: ABCD is a parallelogram.
Proof: Consider,
AP→ + PB→ + PD→ = PC→⇒ AP→ + PB→ = PC → – PD→
⇒AB→ = DC→ [ ∵ AP→ + PB→ = AB→ and PD→ + DC→ = PC→]
Again,
AP→ + PB→ + PD→ = PC→⇒ AP→ + PD→ = PC→ – PB→
⇒ AD→ = BC→ [ ∵ AP→ + PD→ = AD→ and PB→ + BC→ = PC→]
Since, opposite sides of the quadrilateral are equal and parallel.
Hence, ABCD is a parallelogram.
Q9.
Answer :
AB→+AC→+ AD→+AE→+AF→
Consider ∆ADE,
AD→+DE→+EA→=0AD→+DE→=AE→2AO→+−AB→=AE→ AD→=2AO→ and ED || AB DE→=−AB→∴ AE→+AB→=2AO→ ….. (1)
Now, consider ∆ADC
AC→+CD→+DA→=0AC→+CD→=AD→ ∵CD→=AF→AC→+AF→=2AO→ …..2
Using (1) and (2),
AB→+AE→+AC→+AF→+AD→2AO→+2AO→+2AO→=6AO→
Q10.
Answer :
(i) True.
a→ = -b→
Taking modulus on both sides of the equation, we get,
a→ = -b→
⇒a→ = b→ [ ∵ -b→ = b→ ]
(ii) False.
We cannot say a →= b →⇒a →=±b →
Consider an example,
a→=i+3j and b→=2i+2ja→=12+32 =2 and b→=22+22=2Thus, a→= b→ but a→≠±b→
(iii) False.
We cannot say a →= b →⇒a →=b →
Consider an example,
a→=i+3j and b→=2i+2ja→=12+32 =2 and b→=22+22=2Thus, a→= b→ but a→≠b→
Page 23.35 Ex. 23.3
Q1.
Answer :
Let D, E and F are the midpoints of BC, CA and AB respectively.
Therefore,
OB→+OC→2 = OD→
OB→ + OC→ = 2 OD→ …..1Similarly,OC→+OA→ = 2 OE→ …..2OA→ + OB→ = 2 OF→ …..3
Adding (1), (2) and (3). We get,
2 (OA→ + OB→ + OC→) = 2 (OD→ + OE→ + OF→).⇒ OA→ + OB→ + OC→ = OD→ + OE→ + OF→ .
Hence Proved.
Q2.
Answer :
Let a→, b→ and c→ are the position vectors of the vertices A, B and C respectively.
Then we know that the position vector of the centroid O of the triangle is a→+ b→ + c→3.
Therefore sum of the three vectors OA→, OB→ and OC→ is
OA→ + OB→ + OC→ = a→ – a→+ b→ + c→3 + b→ – a→ + b→ + c→3 + c→ – a→ + b→ + c→3 = a→ + b→ + c→ – 3 a→ + b→ + c→3 = 0→
Hence, Sum of the three vectors determined by the medians of a triangle directed from the vertices is zero.
Q3.
Answer :
Given: a→, b→, c→ and d→ are the position vectors of the four distinct points A, B, C and D.
Also, we have, b→ – a→ =c → – d→.
⇒ AB→ = DC→
Again,
b→ – a→ = c→ – d→⇒ b→ – c→ = a→ – d→⇒ CB→ = DA→
Consequently, AB ∥ DC , CB ∥ DA and AB→ = DC→ , CB→ = DA→. Thus two of its opposite sides are equal and parallel.
Hence, ABCD is a parallelogram.
Q4.
Answer :
Given a parallelogram ABCD and P is the point of intersection of its diagonals. We know the diagonals of a parallelogram, bisect each other. Therefore,
OA→+OC→2= OP→ OA→+OC→=2 OP→ …..1and OB→+OD→2=OP→OB→+OD→=2 OP→ …..2
Adding (1) and (2), We get,
OA→+OB→+OC→+OD→=4OP→
Q5.
Answer :
Let E, F, G and H are the midpoints of the sides AB, BC, CD and DA respectively of say quadrilateral ABCD. By geometry of the figure formed by joining the midpoints E, F, G and H will be a parallelogram. Hence its diagonals will bisect each other, say at Q.
Now, F is the midpoint of BC.
PB⇀ + PC⇀2 = PF⇀∴ PB⇀ + PC⇀ = 2PF⇀ …..1
And, H is the midpoint of AD.
PA⇀ + PD⇀2=PH ⇀∴PA⇀ + PD⇀= 2PH ⇀ …..2
Adding (1) and (2). We get,
PA⇀+ PB⇀+ PC⇀+ PD⇀ =2(PF⇀ + PH⇀) = 2 (2PQ⇀) =4 PQ⇀.
Q6.
Answer :
Let the position vectors of C and D are c→ and d→ respectively. We have,
AC=3 AB. ⇒AC = 3 (AC-BC).⇒2AC =3BC.
⇒ ACBC = 32.
So C divides AB in the ratio of 3:2 externally.
c→ = 2a→- 3b→ 2-3 = 3b→- 2a→.
Position vector of point C is 3b→-2a→
Moreover,
BD = 2 BA.⇒BD = 2(BD-AD).⇒ BD = 2AD.
⇒ BDAD = 21.
∴ d→ = b→- 2a→1-2= 2a→ – b→.
Position vector of point D is 2a→-b→
Q7.
Answer :
Let ABC be a triangle and α→, β→, γ→ be the position vectors of the vertices A, B and C respectively. Let AD, BE and CF be the internal bisectors of ∠A, ∠B and ∠C respectively.
We know that D divides BC in the ratio of AB : AC that is c : b.
Then,
P.V. of D is cγ→ + bβ→c+b.
P.V. of E is cγ→ + aα→c+a.
and P.V. of F is aα→+bβ→a+b.
The point dividing AD in the ratio b+c : a is aα→ + bβ→ + cγ→a+b+c.
The point dividing BE in the ratio of a+c : b is aα→ + bβ→ + cγ→a+b+c.
The point dividing CF in the ratio of a+b : c is aα→ + bβ→ + cγ→a+b+c.
Since the point aα→+ bβ→ + cγ→a+b+c lies on all the three internal bisectors AD, BE and CF.
Hence the internal bisectors are concurrent .
Q8.
Answer :
Let AC and BD intersects at a point P.
We have,
3a→-2b⇀+5c⇀-6d⇀ = 0→.⇒3a→+5c→ =2b→+6d→Since sum of coefficients on both sides of the above equation is 8.so we divide the equation on both sides by 8.⇒3a→+5c→8 = 2b→+6d→8⇒3a→+5c→3+5 = 2b→+6d→2+6
Therefore, P divides AC in the ratio of 3:5 and P divides BD in the ratio of 2:6.
Therefore, position vector of the point of intersection of AC and BD will be
3a→+ 5c→8=2b→+6d→8
Q9.
Answer :
Let the point of intersection of the line segments PR and QS is A. Then
5p→-2q→+6r→-9s→ =0→.⇒5p→+6r→=2q→ + 9s→the sum of the coefficients on both the sides of the above equation is 11.So, we divide the given equation with 11.⇒5p→+6r→11 = 2q→+9s→11
5p→+6r→5+6=2q→+9s→2+9
Q10.
Answer :
Let ABCD is the quadrilateral and P, Q, R, S are mid points of the sides AB, BC, CD, DA respectively.
Join DB to form triangle ABD.
ASSD=APPB⇒SP || DB and SP=12 DB
In triangle BCD
CRRD=CQQB⇒RQ || DB and RQ=12 DB
In quadrilateral PQRS,
SP = RQ and SP || RQ
∴ PQRS is a parallelogram.
Diagonals of a parallelogram bisect each other.
∴ PR and QS bisect each other.
Page 23.36 Ex. 23.3
Q11.
Answer :
Let the position vectors of A, B and C with respect to some origin, O be a→, b→ and c→ respectively.
Let D be the point on BC where bisectors of ∠A meets.
Let d→ be the position vector of D which divides CB internally in the ratio β and γ, where β=AC→ and γ=AB→
Thus, β=c→-a→ and γ=b→-a→
By section formula, the position vector of D is given by
OD→=βb→+γc→β+γLet α=b→-c→
Incentre is the concurrent point of angle bisectors and incentre divides the line AD in the ratio ∝: β + γ.
So, the position vector of incentre is given as,
αa→+βb→+γc→β+γ β+γα+β+γ=αa→+βb→+γc→α+β+γ
Page 23.42 Ex. 23.4
Q1.
Answer :
Given a point -4,-3 such that its position vector a→ is given by
a→ = -4 i ∧- 3 j∧
Then,
a→ = -42 + -32 = 16 + 9 = 25 = 5
Q2.
Answer :
Given a position vector a→ of a point 12, n such that,
a→ = 12 i∧ + n j∧
Then,
a→ = 122 + n2
Also , a→ = 13 (given)
Thus, we get,
122 + n2 = 13⇒ 122 + n2 = 169⇒ n2 = 169 – 144⇒ n2 = 25⇒ n = ±5
Q3.
Answer :
(i) Given a point P3, 2. Let O be the origin. Then, the position vector of a point P3, 2 is OP→ = 3 i∧ + 2 j∧. So component of OP→ along x-axis is a vector of magnitude 3 having its direction along the positive direction of x-axis. Also the component of OP→ along y-axis is a vector of magnitude 2 along the positive direction of y-axis.
(ii) Given a point Q-5, 1. Let O be the origin. Then, the position vector of a point Q-5, 1 is OQ→ =-5 i∧ + j∧. So, component of OQ→ along x-axis is a vector of magnitude 5 having its direction along the negative direction of x-axis. Also, the component of OQ→ along y-axis is a vector of magnitude 1 along the positive direction of y-axis.
(iii) Given a point R-11,-9. Let O be the origin. Then, the position vector of a point R-11,-9 is OR→ =-11 i∧ – 9 j∧. So, component of OR→ along x-axis is a vector of magnitude 11 having its direction along the negative direction of x-axis. Also, the component of OR→ along y-axis is a vector of magnitude 9 along the negative direction of y-axis.
(iv) Given a point S4,-3. Let O be the origin. Then, the position vector of a point S4,-3 is OS→ = 4 i∧ – 3 j∧. So, component of OS→ along x-axis is a vector of magnitude 4 having its direction along the positive direction of x-axis. Also, the component of OS→ along y-axis is a vector of magnitude 3 along the negative direction of y-axis.
Q4.
Answer :
(i) Given: A (4,-1) and B1, 3
Then the position vector AB→ is given by
AB→ = Position vector of B – Position vector of A
= i∧ + 3 j∧ – 4 i∧ – j∧= i∧ + 3 j∧ – 4 i∧ + j∧= -3 i∧ + 4 j∧
So, AB→ = -32 + 42 = 9+16 = 25 = 5
(ii) Given: A-6, 3 and B -2,-5
Then, the position vector AB→ is given by
AB → =Position vector of B – Position vector of A
= -2 i∧-5 j∧ – -6 i∧ + 3 j∧= -2 i∧-5 j∧ + 6 i∧ – 3 j∧= 4 i∧ – 8 j∧
So, AB→ = 42 + -82 = 16 + 64 = 80 = 45
Q5.
Answer :
Let O be the origin. Let Px, y be the required point. Then, P→ is the tip of the position vector OP→ of the point P.
We have,
OP→ = x i⏜ + y j⏜.
and, AB→ = Position vector of B – Position vector of A.
= -2 i⏜ + j⏜ – – i⏜ + 3 j⏜= -2 i⏜ + j⏜ + i⏜-3 j⏜= – i⏜ – 2 j⏜
Given that OP→ = AB→
So, x i⏜ + y j⏜ = – i⏜ -2 j⏜ ⇔ x =-1 , y=-2
Hence, coordinated of the required point is -1.-2
Q6.
Answer :
Let the coordinates of D is x, y.
Since, ABCD is a parallelogram.
∴ AB = DC
We have,
AB→ = DC→⇒ 3i⏜ – -2i⏜ – j⏜ = i⏜ – 2j⏜ – xi⏜ + yj⏜⇒5i⏜ + j⏜= i⏜ 1-x + j⏜ -2-y⇒ 1-x = 5 and 1 =-2-y⇒ x=-4 and y =-3
Hence, the coordinates of D is -4,-3
Q7.
Answer :
Let a→, b→, c→ are the position vectors of the points A3, 4, B5,-6 and C4,-1.
Then,
a→ = 3 i⏜ + 4 j⏜
b→ = 5 i⏜ – 6 j⏜
c→= 4 i⏜ – j⏜
Therefore,
a→ + 2b→ – 3c→ =3 i⏜ + 4 j⏜ + 2 5 i⏜ – 6j⏜ – 3 4 i⏜ – j⏜ = 3 i⏜ + 4 j⏜ + 10 i⏜ – 12 j⏜ – 12 i⏜ + 3j⏜ = i ⏜ – 5 j⏜
Page 23.43 Ex. 23.4
Q8.
Answer :
Given: The points Am,-1, B2, 1 and C 4, 5 are collinear. Let a→, b→ and c→ are the position vectors of the points A, B and C respectively.
We have,
AB→ = b→ – a→⇒AB→ = 2i⏜ + j⏜ – mi⏜ + j⏜⇒ AB→ = 2-mi⏜ + 2j⏜ BC→ = c→ – b→⇒ BC→ = 4i⏜ + 5j⏜ – 2i⏜ – j⏜⇒ BC→ = 2i⏜ + 4j⏜
Since, the given points are collinear. We have,
AB→ = λBC→⇒ 2-mi⏜ + 2j⏜ = λ 2i⏜ + 4j⏜⇒ 2-m = 2λ and 2 = 4λ ⇒ λ = 12⇒ 2-m = 2×12⇒ 2-m = 1⇒ m =1
Q9.
Answer :
Suppose, the given points are A3, 4, B-5, 16, C5, 1.
We have,
AB→ =Position vector of B-Position vector of A = -5i^ + 16j^ – 3i^ – 4j^ = -8i^ + 12j^ =-4 2i^ – 3j^BC→ =Position vector of C-Position vector of B = 5i^ + j^ + 5i^ -16j^ = 10i^ -15j^ =52i^ – 3j^
Therefore, AB→ =-45BC→
Hence, the given points are collinear.
Q10.
Answer :
We have, a→ = 2i⏜ – 3j⏜ and b→ =-6i⏜ + mj⏜
Since, the vectors are collinear. We have,
a→ = λ b→⇒2i⏜ – 3j⏜ = λ -6i⏜ + mj⏜⇒ 2 =-6λ and -3 = λm⇒λ =-13 and m =-3λ =-3-13 = 9
Hence, m = 9
Q11.
Answer :
Let O be the origin and let P5,-3 be the tip of the position vector a→. Then, a→ = OP→ = 5i^ – 3j^. Let the coordinate of B be x, y and A has coordinates 4,-1.
Therefore,
AB→ = Position vector of B – Position vector of A
= xi^ + yj^ – 4i^ – j^= x-4i^ + y+1j¯
Now,
AB→ = a→⇒x-4i^ + y+1j^ = 5i^ – 3j^⇒ x-4 = 5 and y+1 =- 3⇒ x=9 and y=-4
Hence, the coordinates of B are 9,-4.
Q12.
Answer :
Given:- The points A, B, C with position vectors a→, b→, c→ respectively.
Also, a→ = 2i^
b→ =-i^ – 4j^
c→ =-i^ + 4j^
Then,
AB → = b→ – a→⇒ AB→ = -i^- 4j^ – 2i^⇒ AB→ = -3i^ – 4j^Now, AB→ = -32 +- 42=9+16=25=5 BC→ = c→ – b→⇒ BC→ = -i^ + 4j^ – -i^ – 4j^⇒ BC→ =-i^ + 4j^ + i^ + 4j^⇒ BC→ = 8j^
and
AC→ = c→ – a→⇒AC→ = -i^ + 4j^ – 2i^⇒ AC→ = -3i^ + 4j^Now, AC→ = -32 + 42=9+16=25=5
Since, the magnitude of AB and AC is equal.
Hence, the points 2i^, − i^ − 4j^ and −i^ + 4j^ form an isosceles triangle.
Q13.
Answer :
Let a→ = i^ + 3 j^
Then, a→= 12+ (3)2 = 1+3 = 4 = 2
Unit vector parallel to a→ = a^ = a→a→ = 12i^ + 3 j^=12i^ + 32 j^
Q14.
Answer :
Let a→ = 3 i^ + j^
Then, a→ = 32 + 1 = 3+1 = 4 = 2
A unit vector parallel to a→ = a^ = a→a→ = 123 i^ + j^
Hence, Required vector = 4a^ = 4×123 i^ + j^ = 23 i^ + 2j^
Page 23.49 Ex. 23.5
Q1.
Answer :
Given: a→ = 2i^ + 3j^ – 6k^
∴ Magnitude of the vector = a→ = 22+32+-62 = 4+9+36 = 49 = 7
Q2.
Answer :
Let a→ = 3i^ + 4j^ -12k^
Then, a→ = 32+ 42+ -122 = 9+16+144 =169 =13
So, a unit vector in the direction of a→ is given by
a^ = a→a→ = 113 3i^ + 4j^ -12k^=313i^ + 413j^ -1213k^
Q3.
Answer :
Given: a→ = i^ – j^ + 3k^ , b→ = 2i^ + j^- 2k^ and c→=i^ + 2j^ – 2k^ are the position vectors.
Then, Resultant of the vectors = a→ + b→ + c→
= i^ – j^ + 3k^ + 2i^ + j^ – 2k^ + i^ + 2j^ – 2k^= 4i^ + 2j^ – k^
So, a→ + b→ + c→ = 42+ 22 + 12 = 16 + 4 + 1 = 21
∴ Unit vector in the direction of the resultant vector = a→ + b→ + c→a→ + b→ + c→ = 1214i^ + 2j^ – k^
Page 23.50 Ex. 23.5
Q4.
Answer :
a→=i^+j^−k^b→=−2i^+j^+2k^
AC→=a→+b→=−i^+2j^+k^
Let the unit vector along the diagonals AC and BD of the parallelogram be AC^ and BD^.⇒ AC^=−i^+2j^+k^6
Similarly, BD→=b→−a→=-3i^+3k^
⇒ BD^=-3i^+3k^32=-i^+k2
Q5.
Answer :
Given: a→ = 3i^ – j^- 4k^, b→ =-2i^ + 4j^ – 3k^ and c→ = i^ + 2j^ – k^.
Now, 3a→ – 2b→+ 4c→ = 33i^ – j^ – 4k^ – 2-2i^ + 4j^ – 3k^ + 4i^ + 2j^ – k^ = 9i^ – 3j^ – 12k^ + 4i^ – 8j^ + 6k^ + 4i^ + 8j^ – 4k^ = 17i^ – 3j^ – 10k^
Hence, 3a→ – 2b→ + 4c→ = 172 + -32 + -102 = 289+9 + 100 = 398
Q6.
Answer :
Given: PQ→ = 3i^ + 2j^- k^. Let the position vector of P1,-1, 2 is p→ such that p→ = i^-j^+2k^ and the position vector of Qx, y, z is q→ such that q→ = xi^ +yj^+ zk^.
Therefore,
∴ PQ→ = q→ – p→⇒ 3i^ + 2j^ – k^ = xi^ + yj^ + zk^ – i^ – j^ + 2k^⇒ 3i^ + 2j^ – k^ = x-1i^ + y+1j^ + z-2k^⇒ x-1 = 3 , y+1 = 2, z-2 =-1⇒ x= 4 , y=1, z=1
Hence, the coordinates of Q are 4, 1, 1
Q7.
Answer :
Given the points i^-j^, 4i^+3j^+k^ and 2i^-4j^+5k^ Are A, B and C respectively.
Then,
AB→ = 4i^+3j^+k^ – i^+j^ = 3i^+4j^+k^.BC→ = 2i^-4j^+5k^-4i^-3j^-k^ = -2i^-7j^+4k^.CA→ = i^-j^-2i^+4j^-5k^ =-i^+3j^-5k^.
AB→+BC→+CA→ = 3i^+4j^+k^-2i^-7j^+4k^-i^+3j^-5k^ = 0→.
The given points forms a vertices of a triangle.
Now,
AB→ = 9+16+1 = 26.BC→ = 4+49+16 = 69.CA→ = 1+9+25 = 35.
AB→2 + CA→2 =26+35 = 61 ≠ BC→2
The given triangle is not right-angled.
Q8.
Answer :
Given the vertices of a triangle A, B and C with position vectors a1i^ + a2j^ + a3k^, b1i^+b2j^+b3k^ and c1i^+c2j^+c3k^ respectively. Then,
AB→ = (b1-a1)i^ + (b2-a2) j^ + (b3-a3)k^.BC→ = (c1-b1)i^ + (c2-b2) j^ + (b3-a3)k^.CA→ = (a1-c1)i^ + (a2-c2) j^ + (a3-c3) k^.
Therefore, the length of these vectors are:
AB→ = (b1-a1)2+ (b2-a2)2+ (b3-a3)2 .BC→ = (c1-b1)2+(c2-b2)2+(c3-b3)2.CA→ = (a1-c1)2+ (a2-c2)2 + (a3-c3)2.
Q9.
Answer :
Given the vertices of the triangle (1,-1, 2), (2,1, 3) and (-1, 2, -1). Then,
Position vectors are
a→ = i^-j^+2k^.b→= 2i^+j^+3k^.c→ = -i^+2j^-k^.
The centroid of a triangle is given by a→+b→+c→3
So, a→+b→+c→3= i^-j^+2k^ + 2i^+j^+3k^- i^+2j^-k^3 = 2i^+2j^+4k^3=23i^+23j^+43k^.
Q10.
Answer :
(i) Given: R divides the line segment joining the points Pi^ + 2j^ +k^ , Q-i^ +j^+ k^ in the ratio 2 : 1 internally.
Therefore. position vector of R = 2-i^ + j^ + k^ + 1i^ + 2j^ + k^2+1
= 13-i^ + 4j^ + 3k^
(ii) Given: R divides the line segment joining the points Pi^ + 2j^ +k^ , Q-i^ +j^+ k^ in the ratio 2 : 1 externally.
Therefore. position vector of R = 2-i^ + j^ + k^ – 1i^ + 2j^ + k^2-1
= -3i^ + k^
Q11.
Answer :
Given: P2i^ -3j^ + 4k^ and Q4i^ + j^ – 2k
The position vector of the midpoint of the vector
joining these points =Position vector of P+Position vector of Q2
= (2i^ – 3j^ + 4k^ )+ (4i^ + j^ – 2k^)2= 6i^ – 2j^ + 2k^2= 3i^ – j^ + k^
Q12.
Answer :
Let a→ and b→ are the position vectors of the points P1, 2, 3 and Q4, 5, 6
Then,
a→ = i^ + 2j^ + 3k^b→ = 4i^ + 5j^ + 6k^
So,
PQ→ = b→ – a→ = 4i^ + 5j^ + 6k^ – i^ – 2j^ – 3k^ = 3i^ + 3j^ + 3k^
Now, PQ→= 32 + 32 + 32 = 9+9+9 = 33
Therefore, Unit vector parallel to PQ→ = PQ→PQ = 133 3i^ + 3j^ + 3k^ = 13i^+j^+k^
Q13.
Answer :
Given the points A2i^ -j^ + k^, Bi^- 3j^ – 5k^ and C3i^ – 4j^ – 4k^.
Then,
AB→ = Position vector of B – Position vector of A
= i^ – 3j^ – 5k^ – 2i^ -j^ + k^= i^ – 3j^ – 5k^ – 2i^ + j^ – k^= -i^ – 2j^ -6k^
BC→ = Position vector of C – Position vector of B
=3i^ – 4j^ – 4k^ – i^ – 3j^ – 5k^= 3i^ – 4j^ – 4k^ – i^ + 3j^ + 5k^= 2i^ – j^ + k^
CA→ = Position vector of A – Position vector of C
= 2i^ – j^ + k^ – 3i^ – 4j^ – 4k^= 2i^ – j^ + k^ – 3i^ + 4j^ + 4k^= -i^ + 3j^ + 5k^
Clearly, AB→ + BC→ + CA→ = 0→
Now, AB→=-12+-22+-62=1+4+36=41 BC→=22+-12+12=4+1+1=6 CA→=-12+32+52=1+9+25=35Clearly, AB→2= BC→2+ CA→2⇒AB2=BC2+CA2
So, A, B , C forms a right angled triangle.
Q14.
Answer :
Let p→, q→ be the position vectors of the points P2, 3, 4, Q4, 1,-2
Then,
p→ = 2i^+3j^+ 4k^ and q→= 4i^+j^-2k^
Therefore, the position vector of the midpoint of the given points is p→+q→2
∴ p→+q→2 = (2i^+3j^+4k^)+(4i^+j^-2k^)2 = 3i^+2j^+k^
Q15.
Answer :
We have, xi^+j^+k^ is a unit vector.
∴x2+x2+x2=1⇒3x=1⇒x=13⇒x=±13
Q16.
Answer :
We have, a→= i^+j^+k^, b→= 2i^-j^+3k^ and c→= i^-2j^+k^
∴ 2a→-b→+3c→ = 2i^+j^+k^ – 2i^-j^+3k^+ 3i^-2j^+k^ = 3i^-3j^+2k^.
A unit vector parallel to 2a→-b→+3c→ is given by 2a→-b→+3c→2a→-b→+3c→=3i^-3j^+2k^32+-32+22
= 3i^-3j^+2k^22 =322i^-322j^+222k^
Q17.
Answer :
Given points A1,-2,-8, B5, 0,-2, C11, 3, 7.
Therefore, AB→ = 5i^+0j^-2k^ – i^+2j^+8k^ = 4i^+2j^+6k^
BC→ = 11i^+3j^+7k^- 5i^+2k^ = 6i^+3j^+9k^
and, AC→ = 11i^+3j^+7k^ -i^+2j^+8k^ = 10i^+5j^+15k^
Clearly, AB→+BC→= AC→
Hence A, B, C are collinear.
Suppose B divides in the ratio AC in the ratio λ:1. Then the position vector B is
11λ+1λ+1i^ + 3λ-2λ+1j^ + 7λ-8λ+1k^
But the position vector of B is 5i^+0j^-2k^.
11λ+1λ+1 = 5, 3λ-2λ+1 = 0 , 7λ-8λ+1 =-2⇒11λ+1 = 5λ+5, 3λ-2 =0, 7λ-8 =-2λ-2⇒ 6λ = 4, 3λ = 2, 9λ = 6⇒ λ=23, λ=23, λ=23
Q18.
Answer :
We have, a→= i^+j^+k^, b→=4 i^-2j^+3k^ and c→ = i^-2j^+k^.
Then,
2a→-b→+3c→= 2i^+j^+k^ – 4i^-2j^+3k^ + 3i^-2j^+k^ = i^-2j^+2k^.
∴ A unit vector parallel to 2a→-b→+3c→ is 2a→-b→+3c→2a→-b→+3c→=i^-2j^+2k^12+-22+22
= i^-2j^+2k^9 = i^-2j^+2k^3
Hence, Required vector = 63i^-2j^+2k^ = 2i^-4j^+4k^.
Q19.
Answer :
Given the position vectors a→ = 2i^+3j^-k^ and b→ = i^-2j^+k^
∴ Resultant Vector = a→+b→ = 2i^+3j^-k^+i^-2j^+k^ = 3i^+j^
So, a unit vector parallel to the resultant vector is 3i^+j^3i^+j^=3i^+j^32+12 = 3i^+j^10
Hence, required vector = 5×3i^+j^10 = 523i^+j^
Q20.
Answer :
We have,
AP→=position vector of P – position vector of A⇒AP→ = (i^+2j^+3k^) – (-2i^+3j^+5k^) =3i^-j^-2k^ PB→=position vector of B – position vector of P⇒PB→ = (7i^-0j^-k^) – (i^+2j^+3k^) = 6i^-2j^-4k^ Since PB→=2AP→. So, vectors PB→ and AP→ are collinear. But P is a pointcommon to PB→ and AP→.
Hence, P, A, B are collinear points.
Now, CP→= (-3i^ – 2j^ – 5k^) – (i^ + 2j^ + 3k^) =(-4i^ – 4j^ -8k^)PD→ = (i^ + 2j^ + 3k^) – (3i^ + 4j^ + 7k^) =(-2i^ – 2j^ -4k^)Thus, CP→ = 2PD→.So the vectors CP→ and PD→ are collinear.But P is a common point to CP→ and PD→
Hence, C,P,D are collinear points.
Thus A, B, C, D and P are points such that A,P,B and C,P,D are two sets of collinear points.
Hence, AB and CD intersect at point P.
Page 23.59 Ex. 23.6
Q1.
Answer :
We have, A, B ,C with position vectors a→-2b→+3c→, 2a→+3b→-4c→, -7b→+10c→ Then,
AB→ = Position Vector of B – Position Vector of A
= 2a→+3b→-4c→ – a→+2b→-3c→= a→+5b→-7c→
BC→ = Position Vector of C – Position Vector of B
=-7b→+10c→ -2a→-3b→+4c→=-2a→-10b→+14c→=-2 a→+5b→-7c→
∴ BC→ =-2AB→
Hence, AB→ and BC→ are parallel vectors.
But B is a point common to them.
So, AB→ and BC→ are collinear.
Hence, points A, B and C are collinear.
Q2.
Answer :
(i) Given: a→, b→, c→ are non coplanar vectors.
Let the points be A, B, C respectively with position vectors a→, b,→ 3a→-2b→. Then,
AB→= Position vector of B – Position vector of A
= b→-a→
BC→ = Position vector of C – Position vector of B
= 3a→-2b→ – b→= 3a→ – 3b→=-3 b→-a→
∴ BC→=-3AB→
So, AB→ and BC→ are parallel vectors.
But B is a point common to them.
Hence, A, B and C are collinear.
(ii) Given a→, b→, c→ are non coplanar vectors.
Let the points be A, B, C respectively with the position vectors a→+b→+c→, 4a→+3b→, 10a→+7b→-2c→. Then,
AB→ = Position vector of B – Position vector of A
= 4a→+3b→ – a→-b→-c→= 3a→+2b→-c→
BC→= Position vector of C – Position vector of B
=10a→+7b→-2c→-4a→-3b→= 6a→+4b→-2c→= 23a→+2b→-c→
∴ BC→= 2AB→
So, AB→ and BC→ are parallel vectors.
But B is a point common to them.
So, AB→ and BC→ are collinear.
Hence, A, B and C are collinear.
Q3.
Answer :
Let A, B, C be the points with position vectors i^+2j^+3k^, 3i^+4j^+7k^, -3i^-2j^-5k^. Then,
AB→= Position vector of B – Position vector of A
=3i^+ 4j^+ 7k^- i^- 2j^- 3k^= 2i^ + 2j^ + 4k^
BC→ = Position vector of C – Position vector of B
=-3i^- 2j^ – 5k^ – 3i^ – 4j^ – 7k^= -6i^ – 6j^ -12k^= -32i^ + 2j^ + 4k^
∴ BC→ =-3AB→
So, AB→ and BC→ are parallel vectors.
But B is a point common to them.
So, AB→ and BC→ are collinear.
Hence, A, B, C are collinear.
Q4.
Answer :
Let A, B, C be the points with position vectors 10i^+3j^, 12i^-5j^, ai^+11j^. Then,
AB→ = Position vector of B – Position vector of A
= 12i^ – 5j^ – 10i^ – 3j^= 2i^ – 8j^
BC→ = Position vector of C – Position vector of B
=ai^ + 11j^ – 12i^+ 5j^= a-12i^ + 16j^
Since, A, B and C are collinear.
∴ AB→ =λBC→.
⇒ 2i^ – 8j^ = λ a-12i^ + λ16j^⇒ 2 = λ a-12, -8= λ16⇒ 2= λa-12, λ=-12⇒ 2=-12a-12⇒- a+12 = 4⇒ a=8
Q5.
Answer :
Given: a→,b→ are non collinear vectors.
Let the position vectors of points A, B and C be a→+b→, a→-b→, a→+λb^ respectively.
Then,
AB→ = P.V. of B − P.V. of A.
= a→ – b→ – a→ – b→.= -2b→.
BC→ = P.V. of C − P.V. of B.
= a→+λb→ – a→+b→.= b→λ-1.
CA→ = P.V. of A − P.V. of C.
= a→ + b→ – a→ – λb→.= b→ 1-λ.
Now, the position vectors are collinear if and only if AB→ and CA→ is some multiple of BC→.
So,
AB→ =β BC⇀ ⇒-2b=β b⇀λ-1⇒-2 = β λ-1⇒β =-2λ-1
and BC→=-CA→.
Hence, for real values of λ, the given position vectors are parallel.
Q6.
Answer :
We have,
AO→ + OB→ = BO→ + OC→.⇒AO→ – BO→ = OC→ – OB→.⇒OB→ – OA→ = OC→ – OB→.⇒ AB→ = BC→.
Hence A, B and C are collinear points.
Q7.
Answer :
Given the position vectors 2i^-3j^+4k^ and -4i^+6j^-8k^
Let a→= 2i^-3j^+4k^ and b→ = -4i^+6j^-8k^
Then,
b→ =-4i^+6j^-8k^ =-22i^-3j^+4k^ =-2a→
Hence, a→, b→ are collinear.
Page 23.63 Ex. 23.7
Q1.
Answer :
(i) Let the points be A, B and C with position vectors 2i^ + j^ -k^, 3i^ -2j^ + k^ and i^ + 4j^ – 3k^. Then,
AB→ = Position vector of B – Position vector of A
= 3i^ -2j^ + k^ – 2i^ – j^ + k^= i^ – 3j^ + 2k^
BC→ = Position vector of C – Position vector of B
= i^ + 4j^ – 3k^ – 3i^ + 2j^ – k^=-2i^+ 6j^ – 4k^=-2 i^ – 3j^ + 2k^
∴ AB→ =-2BC→.
So, AB→ and BC→ are parallel vectors. But B is a point common to them.
Hence, A, B and C are collinear.
(ii) Let the points be A, B and C with position vectors 3i^-2j^ + 4k^, i^ + j^ + k^ and -i^ + 4j^ -2k^ respectively. Then,
AB→ = Position vector of B – Position vector of A
= i^ + j^ + k^ – 3i^ + 2j^ – 4k^=-2i^ + 3j^ – 3k^
BC→ = Position vector of C – Position vector of B
=-i^ + 4j^ – 2k^ – i^ -j^ – k^=-2i^ + 3j^ – 3k^
∴ AB→ = BC→
So, AB→ and BC→ are parallel vectors.But B is a point common to them.
Hence, A, B and C are collinear.
Q2.
Answer :
(i) Given the points A6,-7,-1, B2,-3, 1 and C4,-5, 0. Then,
AB→ = Position vector of B – Position vector of A
= 2i^ -3j^ + k^ – 6i^ + 7j^+ k^= -4i^ + 4j^ + 2k^=-22i^ -2j^ – k^
BC→ = Position vector of C – Position vector of B
= 4i^ -5j^- 2i^ + 3j^ -k^= 2i^ -2j^-k^
∴ AB→ =-2BC→
So, AB→, BC→ are parallel vectors. But B is a point common to them.
Hence, the given points A, B and C are collinear.
(ii) Given the points A2,-1, 3, B4, 3, 1 and C3, 1, 2. Then,
AB→ = Position vector of B – Position vector of A
= 4i^ + 3j^ + k^ – 2i^+ j^ – 3k^= 2i^ + 4j^ – 2k^= -2-i^ -2j^ + k^
BC→ = Position vector of C – Position vector of B
= 3i^ + j^ + 2k^ – 4i^ – 3j^ – k^= -i^ – 2j^ + k^
∴ AB→ =-2BC→
So, AB→, BC→ are parallel vectors. But B is a point common to them.
Hence, The given points A, B and C are collinear.
(iii) Given the points A1, 2, 7, B2, 6, 3 and C3, 10,-1. Then,
AB→ = Position vector of B – Position vector of A
= 2i^ + 6j^+ 3k^ – i^ – 2j^ – 7k^= i^ + 4j^ – 4k^
BC→ = Position vector of C – Position vector of B.
= 3i^ + 10j^ -k^ – 2i^ – 6j^ – 3k^= i^ + 4j^ – 4k^
∴AB→ = BC→
So, AB→, BC→ are parallel vectors. But B is a point common to them.
Hence, the given points A, B and C are collinear.
(iv) Given the points A-3,-2,-5, B1, 2, 3 and C3, 4, 7. Then,
AB→ = Position vector of B – Position vector of A
= i^ + 2j^ + 3k^ + 3i^ + 2j^ + 5k^= 4i^ + 4j^ + 8k^= 22i^ +2 j^ + 4k^
BC→ = Position vector of C – Position vector of B
= 3i^ + 4j^ + 7k^ – i^ – 2j^ – 3k^=2i^ + 2j^ + 4k^
∴ AB→ = 2BC→
So, AB→, BC→ are parallel vectors. But B is a point common to them.
Hence, the given points A, B and C are collinear.
Q3.
Answer :
(i) The three vectors are coplanar if one of them is expressible as a linear combination of the other two . Let
5a→ + 6b→ + 7c→ = x 7a→ -8b→ + 9c⇀ + y 3a→ + 20b→ + 5c→. = a→ 7x + 3y + b→-8x+20y + c→ 9x + 5y.
⇒ 7x+3y = 5, -8x + 20y = 6 and 9x+5y = 7.
Solving first two of these equations, we get x=12, y=12. Clearly, these values of x and y satisfies the third equation.
Hence, the given vectors are coplanar.
(ii) The three vectors are coplanar if one of them is expressible as a linear combination of the other two. Let
a→-2b→+3c→ = x (-3b→+5c→) + y (-2a→+3b→-4c→). =a→(-2y) + b→ (-3x+3y) + c→ (5x-4y).
⇒-2y=1, -3x+3y=-2 and 5x-4y=3
Solving first two of these equations, we get x=16, y=-12.
These values of x and y does not satisfy the third equation.
Hence, the given vectors are not coplanar.
Page 23.64 Ex. 23.7
Q4.
Answer :
Let the given four points be P, Q, R and S respectively. Three points are coplanar if the vectors PQ→, PR→ and PS→ are coplanar. These vectors are coplanar iff one of them can be expressed as a linear combination of the other two. So, let
PQ→ = xPR→ + yPS→.10i^ -12j^ – 4k^ = x -6i^ + 10j^ – 6k^ + y -4i^ + 2j^ + 10k^.⇒ 10i^ -12j^ – 4k^ = i^ -6x – 4y + j^ 10x + 2y + k^ -6x + 10y.
⇒-6x – 4y = 10, 10x + 2y =-12 and -6x + 10y =-4. [ Equating coefficients of i^, j^, k^ on both sides]
Solving the first of these three equations, we get x=-1 and y=-1. These values also satisfy the third equation.
Hence, the given four points are coplanar.
Q5.
Answer :
(i) Given the vectors P2i^ – j^ + k^, Qi^ – 3j^ – 5k^ and R3i^ – 4j^ – 4k^.
We know the three vectors are coplanar if one of them is expressible as a linear combination of the other two. Let,
2i^ – j^ + k^ = x i^ – 3j^ – 5k^ + y 3i^ – 4j^ – 4k^. = i^ x + 3y + j^ -3x-4y + k^ -5x-4y.
⇒ x+ 3y = 2, -3x-4y =-1, -5x-4y=1 [Equating the coefficients of i^, j^, k^ respectively]
Solving first two of these equation, we get x=-1 , y=1. Clearly these two values satisfy the third equation.
Hence, the given vectors are coplanar.
(ii) Given the vectors Pi^ + j^ + k^, Q2i^ + 3j^ – k^ and R-i^ – 2j^ + 2k^.
We know the three vectors are coplanar if one of them is expressible as a linear combination of the other two. Let,
i^ + j^ + k^ = x 2i^ + 3j^ – k^ + y -i^ – 2j^ + 2k^. = i^ 2x – y + j^ 3x – 2y + k^ -x + 2y.
⇒ 2x- y =1 , 3x- 2y = 1, -x + 2y = 1 [ Equating the coefficients of i^, j^ , k^ respectvely]
Solving first two of these equation , we get x=1, y=1. Clearly these two values satisfy the third equation.
Hence, the given vectors are coplanar.
Q6.
Answer :
(i) Let if possible the given vectors are coplanar. Then one of the given vector is expressible in terms of the other two.
We have,
3i^ + j^-k^ = x(2i^-j^+7k^) + y(7i^-j^+23k^). = i^ (2x+7y) + j^(-x-y) + k^(7x+23y). ⇒2x+7y = 3 , x+y=-1, 7x+23y =-1.By solving the first two equations, we get⇒ x=-2, y=1.
Clearly these values of x and y does not satisfy the third equation.
Hence the given vectors are non-coplanar.
(ii) Let if possible the given vectors are coplanar. Then one of the given vector is expressible in terms of the other two.
We have,
i^+2j^+3k^ = x(2i^+j^+3k^) + y(i^+j^+k^). = i^(2x+y) + j^(x+y)+k^(3x+y).⇒ 2x+y = 1, x+y = 2, 3x+y=3.By solving the first two equation, we get⇒ x=-1, y=3.
Clearly these values of x and y does not satisfy the third equation.
Hence the given vectors are non-coplanar.
Q7.
Answer :
(i) Let if possible the following vectors are coplanar. Then one of the vector is expressible in terms of the other two.
We have,
2a→-b→+3c→ = x(a→+b→-2c→) y(a→+b→-3c→). = a→(x+y) + b→(x+y) + c→(-2x-3y). ⇒ x+y =2 , x+y=-1 , -2x-3y=3.
which is not true, as x+y=2 ≠-1. Hence the given vectors are non-coplanar.
(ii) Let if possible the following vector are coplanar. Then one of the vector is expressible in terms of the other two.
We have,
a→+2b→+3c→ = x(2a→+b→+3c→) + y(a→+b→+c)→ . = a→(2x+y) + b→(x+y) + c→(3x+y).⇒ 2x+y=1, x+y=2, 3x+y=3.
On solving the first two equations we get x=-1, y=3. Clearly the values of x, y does not satisfy the third equation.
Hence the given vectors are non-coplanar.
Q8.
Answer :
Necessary Condition: First let a→,b→,c→ be three coplanar vectors. Then one of them is expressable as a linear combination of the other two. Let c→=xa→+yb→ for some scalars x,y. Then, c→= xa→+ yb→ for some scalars x,y⇒ la→+mb→+nc→= 0, where l=x, m=y, n=-1Thus, if a→,b→,c→ are coplanar vectors, then there exists scalars l, m, n such that la→+mb→+nc→= 0 where l, m, n are all non zero simultaneously.
Sufficient Condition: Let a→, b→, c→ be three vectors such that there exists scalars l, m,n not all zero simulataneously satisfying la→+ mb→+ nc→=0→. We have tp prove that a→, b→, c→ are coplanar vectors.Now, la→+ mb→+ nc→=0→⇒nc→ = -la→- mb→⇒c→ =-1na→+ -mnb→⇒c→ is a linear combination of a→ and b→ .Hence a→, b→, c→ are coplanar vectors.
Q9.
Answer :
Necessary Condition: Firstly , let a→, b→, c→ are coplanar vectors. Then, one of them is expressible as a linear combination of the other two. Let c→= xa→ + yb→ for some scalars x, y. Then,
c→ = xa→ + yb→ for some scalars x, y.
⇒ la→ + mb→ + nc→ = 0→, where l=x, m=y, n=-1.
Thus, if a→, b→, c→ are coplanar vectors, then there exists a scalars l, m, n not all zero simultaneously satisfying la→ + mb→ + nc→ = 0→ where l, m, n are not all zero simultaneously.
Sufficient Condition: Let a→, b→, c→ are three scalars such that there exists scalars l, m, n not all zero simultaneously satisfying la→ + mb→ + nc→= 0→. We have to prove that a→, b→, c→ are coplanar vectors.
Now,
la→ + mb→ + nc→ = 0.→⇒ nc→ =-la→ – mb→.⇒ c→ = -lna→ + -mnb→.
⇒c→ is a linear combination of a→ and b→.
⇒c→ lies in a plane a→ and b→.
Hence, a→, b→, c→ are coplanar vectors.
Q10.
Answer :
Let the given vectors a→ = i^ + 2j^ + 3k^, b→ = 2i^ + j^ + 3k^ and c→ = i^ + j^ + k^˙˙ are coplanar. Then one of the vector is expressible as a linear combination of the other two. Let,
i^ + 2j^ + 3k^ = x 2i^ +j^ + 3k^ + y i^ + j^ + k^. = i^ 2x + y + j^ x + y + k^ 3x + y.
⇒ 2x + y =1, x+ y = 2, 3x + y = 3.
On solving the first two equations we get x=-1, y=3. Clearly the values of x, y does not satisfy the third equation.
Hence the given vectors are non-coplanar.
Now, d→ = 2i^-j^-3k^ which can be expressed as
2i^-j^-3k^ = x(i^+2j^+3k^) + y(2i^+j^+3k^) + z(i^+j^+k^).
= i^(x+2y+z) +j^(2x+y+z) + k^(3x+3y+z) .
⇒x+2y+z=2, 2x+y+z=-1, 3x+3y+z=-3.⇒ x=-83, y=13, z=4
Hence d→ is expressible as the linear combination of a→,b→ and c→.
Page 23.71 Ex. 23.8
Q1.
Answer :
Yes,
Let a vector makes an angle α = 45° , β= 60° , γ = 120° with OX, OY, OZ respectively. Let l, m, n be the direction cosines of the vector. Then,
l = cos 45° = 12 , m = cos 60° = 12 , n = cos 120° = -12
So,
l2 + m2 + n2 = 12 + 14 + 14 = 1
Since, the vector has direction cosines such that l2 + m2 + n2 = 1
Hence, a vector can have direction angles 45°, 60°, 120°
Q2.
Answer :
Let 1, 1, 1 be the direction cosines of a straight line. Then
12+12+12 = 3 ≠ 1
Since direction cosines of a line which makes equal angle with the axes must satisfy l2+m2+n2 = 1.
Hence 1, 1, 1 cannot be the direction cosines of a straight line.
Q3.
Answer :
Let the vector
OP→
makes an angle
α=45° and β = 45°
with
OX, OY
respectively. Suppose
OP→
is inclined at angle
γ
to
OZ
.
Let
l, m, n
be the direction cosines of
OP→
. Then,
l = cos π4 = 12
,
m = cos π4 = 12
and
n = cos γ
Now, we have,
l2 + m2 + n2 = 1⇒ 12 + 12 + n2 = 1⇒ n2 = 0⇒ n = 0⇒ cos γ = cos π2⇒ γ = π2
Hence, the angle made by it with the
z-
axis is
π2
.
Q4.
Answer :
Suppose, vector r→ makes an angle α with each of the axis OX, OY and OZ. Then, its direction cosines are l = cos α , m = cos α and n = cos α i.e. l = m = n.
Now, l2 + m2 + n2 = 1⇒ l2 + l2 + l2 = 1⇒ 3l2 = 1⇒ l2 = 13⇒ l =± 13Since, r→ makes acute angle with the axis.Hence, we take only positive value.
Therefore,
r→ = r→ l i^ + m j^ + n k^ r→ = 6 13 i^ + 13 j^ + 13 k^ = 23 i^ + j^ + k^
Q5.
Answer :
Here, r→ makes an angle 45° with OX and 60° with OY. So,
l = cos 45° = 12 and m = cos 60° = 12
Now, l2+m2+n2=1⇒12+14+n2 = 1⇒ n2 = 14⇒ n=±12
Therefore,
r→ = r→ l i^ + m j^ + n k^ = 8 12i^ + 12 j^ ± 12k^ = 4 2 i^ + j^ ± k^
Q6.
Answer :
(i) We have, 2i^ + 2j^ – k^
The direction cosines are 222+22+-12, 222+22+-12 , -122+22+-12 or, 23 , 23 , -13
(ii) We have, 6i^ – 2j^ – 3k^
The direction cosines are 662+-22+-32 , -262+-22+-32 , -362+-22+-32 or, 67, -27, -37
(iii) We have, 3i^ – 4k^
The direction cosines are 332+0+-42 , 032+0+-42 , -432+0+-42 or, 35, 0, -45
Q7.
Answer :
(i) Let r→ be the given vector, and let it make an angle α, β, γ with OX, OY , OZ respectively. Then, its direction cosines are cos α, cos β, cos γ. So, direction ratios of r→ = i^ – j^ + k^ are proportional to 1,-1, 1. Therefore,
Direction cosine of r→ are 112+ -12 + 12 , -112+ -12 + 12 , 112+ -12 + 12
or, 13, -13, 13.
∴ cos α = 13, cos β =-13, cos γ = 13
α = cos-113 , β = cos-1-13 , γ = cos-113
(ii) Let r→ be the given vector, and let it make an angles α, β, γ with OX, OY, OZ respectively. Then, its direction cosines are cos α, cos β, cos γ. So, direction ratios of r→ = j^ – k^ are proportional to 0, 1,-1. Therefore, direction cosines of r→ are
00+12+-12 , 10+12+-12 , -10+12+-12 or, 0, 12 , -12
∴ cos α=0, cos β = 12 , cos γ = -12
⇒ α = cos-10 , β = cos-112 , γ = cos-1-12⇒ α = π2 , β = π4 , γ = 3π4
(iii) Let r→ be the given vector, and let it make an angle α, β, γ with OX, OY, OZ respectively. Then, its direction cosines are cos α , cos β , cos γ. So, direction ratio of r→ = 4i^ + 8j^ + k^ are proportional to 4, 8, 1
Therefore, direction ratio of r→ are
442+82+12, 842 + 82 + 12 , 142+82+12 or, 49, 89, 19.
∴ α = cos-149 , β = cos-189 , γ = cos-119.
Q8.
Answer :
Let r→ = i^ + j^ + k^ and it make an angle α, β, γ with OX, OY, OZ respectively.Then its direction cosines are cos α, cos β and cos γ. So, Direction ratios of r→ = i^ + j^ + k^ are proportional 1, 1, 1. Therefore, direction cosines of r→ are
112 + 12 + 12 , 112 + 12 + 12 , 112 + 12 + 12 or, 13, 13, 13.
Thus,
cos α = 13 , cos β = 13 and cos γ = 13.
⇒α = β = γ.
Hence, all are equally inclined with the coordinate axis.
Q9.
Answer :
Suppose the vector makes equal angle α with the coordinate axis.
Then, its direction cosines are l = cos α , m = cos α , n = cos α. Therefore, l = m = n.
l2 + m2 + n2 = 1⇒l2 + l2 + l2 = 1⇒ 3l2 = 1⇒ l2 = 13⇒l=13
Hence, direction cosines are 13, 13 , 13.
Q10.
Answer :
The Direction cosines of vector a→ are l = cos π3=12, m = cos π4=12 , n = cos θ
Therefore,
l2 + m2 + n2 = 1⇒14+ 12+ n2 = 1⇒ n2 = 1 – 34⇒ n2 = 14⇒ n = 12 ∵ a→ makes acute angle with k^
⇒ cos θ = 12 ⇒ θ = π3
Since, a→ is the unit vector.
∴ a→ = li^ + mj^ + nk^⇒ a→ = 12i^ + 12j^ + 12k^
Hence, components of a→ are 12i^ + 12j^ + 12k^
Page 23.72 (Very Short Answers)
Q1.
Answer :
A vector whose initial and terminal point are coincident is called a zero vector or null vector. The null vector is denoted by 0→. The magnitude of null vectors is zero.
Q2.
Answer :
A vector whose modulus is unity is called a unit vector.The unit vector in the direction of a vector a→ is denoted by a^.
Thus, a^=1
Q3.
Answer :
A point O is fixed as origin in space (or plane) and P is any point, then OP→ is called a position vector of P with respect to O
Q4.
Answer :
We have, PQ→ + RP→ + QR→ = PQ→ + QR→ + RP→
= PR→ + RP→ [∴ PQ→ + QR→ = PR→]
= 0→
Q5.
Answer :
We have, xa→ + yb→ = 0→
⇒ x= 0 and y=0 [∵ a→ and b→ are non-collinear vectors]
Q6.
Answer :
Let a→ and b→ represents two adjacent sides of a parallelogram ABCD.
∴ AB = DC and AD = BC
⇒DC→ = AB→ = a→ and AD→ = BC→ = b→
In △ABC,
AB→ + BC→ =AC→⇒ a→ + b→ = AC→
In △ABD,
AD→ + DB→ = AB→⇒ b→ + DB→ = a→⇒ DB→ = a→ – b→
Q7.
Answer :
Let ABC be a triangle such that BC→ = a→, CA→ = b→ and AB→ = c→.Then,
a→ + b→ + c→ = BC→ + CA→ + AB→
= BA→ + AB→=0→ [∵ BC→ + CA→ = BA→]
Q8.
Answer :
Given: a→, b→ and c→ are the position vectors of A, B and C respectively. Then,
AB→ = b→ – a→BC→ = c→ – b→CA→ = a→ -c→
Consider,
AB→ + BC→ + CA→ = b→ – a→ + c→ – b→ + a→ – c→ = 0→
Q9.
Answer :
Given: a→, b→, c→ are the position vectors of A, B, C respectively. Then,
AB→ = b→ – a→BC→ = c→ – b→AC→ = c→ – a→
Therefore,
AB→ + BC→ + AC→ = b→ – a→ + c→ – b→ + c→ – a→ = 2 c→ – a→
Q10.
Answer :
Let ABC be a triangle and D, E and F are the midpoints of the sides BC, CA and AB respectively. Also, Let a→, b→, c→ are the position vectors of A, B, C respectively. Then the position vectors of D, E, F are b→ + c→2, c→ + a→2, a→ + b→2 respectively.
The position vector of a point divides AD in the ratio of 2 ; is 1 . a→ + 2b→ + c→22 = a→ + b→ + c→3.
Similarly, Position vectors of the points divides BE, CF in the ratio of 2:1 are equal to a→ + b→ + c→3.
Thus, the point dividing AD in the ratio 2 : 1 also divides BE, CF in the same ratio.
Hence, the medians of a triangle are concurrent and the position vector of the centroid is a→ + b→ + c→3.
Page 23.73 (Very Short Answers)
Q11.
Answer :
Let a→, b→, c→ be the position vectors of the vertices A, B, C respectively. Then, the position vector of the centroid G is a→ + b→ + c→3
Thus,
GA→ + GB→ + GC→ = a→ – a→ + b→ + c→3 + b→ – a→ + b→ + c→3 + c→ – a→ + b→ + c→3 = a→ + b→ + c→ – 3 a→ + b→ + c→3 = a→ + b→ + c→- a→ + b→ + c→ = 0→
Q12.
Answer :
Given: a→ and b→ are the position vectors of points A and B respectively and C is a point on AB such that 3 AC= 2AB.
Let c→ is the position vector of C
Now,
AB→ = b→ – a→
AC→ = c→ – a→
Consider,
3 AC = 2AB⇒ 3 c→ – a→ = 2 b→ – a→⇒ 3c→ – 3a→ = 2b→ – 2a→⇒ 3c→ = 2b→ + a→⇒c→ = 13 2b→+ a→⇒c→ = 13 a→+2b→
Hence, the position vector of C is 13 a→+2b→
Q13.
Answer :
Given: D is the midpoint of the side BC of a triangle ABC such that AB→ + BC→ = λAD→.
Let a→, b→, c→ are the position vectors of AB, BC and CA.
Now, the position vector of D is b→ + c→2. Then,
AB→ = b→ – a→AC→ = c→ – a→AD→ = b→ + c→2 – a→
Now, we have,
AB→ + AC→ = λ AD→⇒ b→ – a→ + c→ – a→ = λ b→ + c→2 -a→⇒b→ + c→ – 2a→ = λ b→ + c→ – 2a→2⇒ λ = 2
Q14.
Answer :
Given: D, E, F are the midpoints of the sides BC, CA, AB respectively. Then, the position vectors of the midpoints D, E, F are given by b→ + c→2, c→ + a→2, a→ + b→2
Now, AD→ + BE→ + CF→= b→ + c→2- a→ + c→ + a→2- b→ + a→ + b→2- c→ =2a→ +b→ + c→2 -a→ +b→ + c→ =a→ +b→ + c→-a→ +b→ + c→ = 0→
Q15.
Answer :
Given a→ a non zero vector with modulus a. Also, ma→ is the unit vector. Therefore,
m a→ = 1⇒m a→ = 1⇒ m a = 1⇒ m= 1a⇒ m =± 1a
Q16.
Answer :
Let, ABC be a given equilateral triangle and its vertices are A(a⇀), B(b⇀) and C(c⇀).
Also, O(0⇀) be the orthocentre of triangle ABC.
We know that centroid and orthocentre of equilateral triangle coincide at one point.
Orthocentre of △ABC=0⇀⇒Centroid △ABC=0⇀⇒a⇀+b⇀+c⇀3=0⇀∴ a⇀+b⇀+c⇀=0⇀
Q17.
Answer :
Suppose r→ makes an angle α with each of the axis ΟΧ,ΟΥ and ΟΖ.
Then, its direction cosines are l=cos α, m=cosα, n=cosα.
Now,
Ι2+m2+n2=1⇒l2 + l2 + l2=1 ∵l=m=n⇒3l2 =1⇒ l2 = 13⇒l = ±13
Since, the angle is acute Hence, we take only positive value
Therefore, unit vector is 13i^ + 13j^ + 13k^.
Q18.
Answer :
Suppose, a vector OP→ makes an angle α, β, γ with OX, OY, OZ respectively. Then, direction cosines of the vector are given by
l = cos α , m = cos β and n = cos γ
Consider,
sin2α + sin2 β + sin2 γ = 1 – cos2α + 1 – cos2β + 1- cos2γ = 3 – cos2α + cos2β + cos2γ = 3 – l2+m2+n2
= 3 – 1 [∵ l2 + m2 + n2 = 1]
= 2
Q19.
Answer :
Suppose a vector r→ makes an angle 45° with ΟΧ, 60° with ΟΥ and having magnitude 12 units.
l = cos 45° = 12 and m = cos 60° = 12
Now, l2+m2+n2=1⇒12+14+n2 = 1⇒ n2 = 14⇒ n=-12 ∵ The angle with the z-axis is obtuse
Therefore,
r→ = r→ l i^ + m j^ + n k^ =12 12i^ + 12 j^ – 12k^ = 6 2 i^ + j^ – k^
Q20.
Answer :
Given: Projection on the coordinate axes are 12, 3, 4 units. Therefore,
Length of vector =122+32+42
= 169
= 13
Q21.
Answer :
The position vectors of A and B are
a→=2i^+3j+4k^b→=-i^+j^+k^
Let C divides AB in the ratio such that AB : CB = 1 : 4
Position vector of C = 1-i^+j^+k^-42i^+3j^+4k^1-4
= -i^+j^+k^-8i^-12j^-16k^-3
= -9i^-11j^-15k^-3
= 3i^+11j^3+5k^
Q22.
Answer :
Given: r→ = 6i^ – 2j^ + 3k^
Then, direction cosines of r⏜ are 662 + -22 + 32 , -262 + -22 + 32 , 362 + -22 + 32 or, 67, -27, 37
Q23.
Answer :
Given: a→=i^+j^ , b→=j^+k^ , c→=k^+i^
Now, a→+b→-2c→=i^+j^+j^+k^-2k^-2i^
=-i^+2j^-k^
Unit vector parallel to a→+b→-2c→=-i^+2j^-k^-12+22+-12
=-i^+2j^-k^6
Q24.
Answer :
Given: a→=i^+2j^ , b→=j^+2k^
Therefore,
3a→-2b→=3i^+6j^-2j^-4k^ =3i^+4j^-4k^
Hence, Unit vector along 3a→-2b→=3i^+4j^-4k^32+42+-42=3i^+4j^-4k^9+16+16=141 3i^+4j^-4k^
Q25.
Answer :
Let A and B be the points with position vectors a→=i^+j^-2k^ , b→=2i^-j^+3k^ respectively.
Let C divide AB externally in the ratio 2 : 3 such that AC : CB = 2 : 3
∴ Position vector of C = 22i^-j^+3k^-3i^+j^-2k^2-3
= 4i^-2j^+6k^-3i^-3j^+6k^-1
= i^-5j^+12k^-1
= -i^+5j^-12k^
Q26.
Answer :
Let a→=i^+j^ , b→=j^+k^ , c→=k^+i^
Then, a→+b→+c →=i^+j^+j^+k^+k^+i^ =2i^+j^+k^
∴ a→+b→+c→=22+22+22=12=23
Therefore, unit vector in the direction of a→+b→+c→=2i^+j^+k^23=13i^+j^+k^
Q27.
Answer :
Given a→=3i^-j^-4k^ , b→=-2i^+4j^-3k^ , c→=i^+2j^-k^
Now, 3a→-2b→+4c→=33i^-j^-4k^-2-2i^+4j^-3k^+4i^+2j^-k^
= 9i^-3j^-12k^+4i^-8j^+6k^+4i^+8j^-4k^
= 17i^-3j^-10k^
∴ 3a→-2b→+4c→=172+-32+-102=289+9+100=398
Q28.
Answer :
A unit vector makes an angle π3 and π2 with j^ and k^
Let Ι, m, n be its direction cosines
∴ l=cosθ , m=cosπ3=12 , n=cosπ2=0
Now
∴ l2+m2+n2=1
⇒ l2+14+0=1
⇒ l2=1-14=34
⇒ l=±32
∴ r→ makes an angle 30° , 150° with i⏜
Since, angle θ is acute.
∴ θ=30°
Q29.
Answer :
We have,
a→=3i^-2j^+6k^ a→=32+-22+62 =9+4+36 =49=7
∴ Unit vector in the direction of a→ = a^=a→a→=17 3i^-2j^+6k^=37i^-27j^+67k^
Q30.
Answer :
Given:
a→=i^+2j^-3k^ , b→=2i^+4j^+9k^ Now, a→+b→=3i^+6j^+6k^ a→+b→=32+62+62=9+36+36 =81=9
Unit vector parallel to a→+b→=a→+b→a→+b→=3i^+6j^+6k^9 =19×3i^+2j^+2k^=13i^+2j^+2k^
Q31.
Answer :
Given:
b→=2i^+j^+2k^b→=22+12+22=4+1+4=9=3
∴ Unit vector = b→b→=132i^+j^+2k^=23i^+13j⏜+23k^
Page 23.74 (Very Short Answers)
Q32.
Answer :
Given: A (3, 4, −2) and B(1, 2, 4)
Let C is the mid point of AB
∴ Position vector of C =3i^+4j^-2k^+i^+2j^+4k^2
=4i^+6j^+2k^2 =2i^+3j^+k^
Q33.
Answer :
Given:
a→=2i^-j^+2k^a→=22+-12+22=4+1+4=9=3
∴ Required Vector =6×a→a→=6×2i^-j^+2k^3=4i^-2j^+4k^
Q34.
Answer :
Given 2 i^+j^+k^ .
Therefore , direction cosines are 222+12+12 ,122+12+12 , 122+12+12 or 12,12,12
So, cosine angle with respect to y-axis is 12
Q35.
Answer :
Let a→= 2i^-j^+3k^ and b→=-2i^+j^-3k^
It can be observed that
a→ = 22+-12+32= 14 b→ = -22+12+-32 = 14
Hence, a→ and b→ are two vectors having same magnitude.
Q36.
Answer :
Let p→ =i^+2j^+3k^ and q→ =2i^+4j^+6k^
Then, direction cosines of p→ are
l = 112+22+32 = 214 , m = 212+22+32= 214 and n = 312+22+32 = 314
Direction cosines of q→ are
l =222+42+62 =2214=114 , m = 422+42+62 =4214= 214 and n = 622+42+62 =6214= 314
The direction cosines of two vectors are same. Hence the two diffrent vectors p→, q→ have same directions.
Q37.
Answer :
Given:
a→=5i^-j^+2k^a→=52+-12+22
=25+1+4=30
∴ Position Vector in the direction of vector =8×a→a→=8305i^-j^+2k^
Q38.
Answer :
Given: i^+2j^+3k^
Then, direction cosines are
112+22+32, 212+22+32 , 312+22+32 or, 114, 214, 314.
Q39.
Answer :
Given:
a→=2i^-3j^+6k^ a→=22+-32+62=4+9+36=49=7
Unit vector = a→a→=2i^-3j^+6k^7 =27i^-37j^+67k^
Q40.
Answer :
Given: Two vectors , let p→= 2i^ -3j^+4k^ and q→= ai^+6j^-8k^
Since the given vectors are collinear, we have,
p→= λq→
⇒2i^-3j^+4k^ = λ ai^+6j^-8k^⇒2i^-3j^+4k^= aλi^+6λj^-8λk^
⇒ λa =2, 6λ=-3 and -8λ=4⇒ λ =-12 and a=-4
Q41.
Answer :
Given: -2i^ + j^ – 5k^
Then, its direction cosines are:
-2-22+12+-52 , 1-22+12+-52 , -5-22+12+-52 or, -230 , 130 , -530
Q42.
Answer :
Given a→=i^-2j^ , b→=2i^-3j^ , c→=2i^+3k^
So, Sum of the three vectors = a→+b→+c→=i^-2j^+2i^-3j^+2i^+3k^
= 5i^-5j^+3k^
Q43.
Answer :
Given: a→=3i^-2j^+6k^
Then,
a→=32+-22+62=9+4+36=49=7
∴ Unit vector = a→a→=3i^-2j^+6k^7 = 37i^ -27j^ + 67k^
Q44.
Answer :
Given: a→ = xi^+2j^-zk^ and b→= 3i^-yj^+k^
Since the two vectors are equal. We have,
xi^+2j^-zk^ = 3i^-yj^+k^⇒ x=3, y=-2, z=-1
∴ x+y+z = 3-2-1=0
Page 23.75 (Multiple Choice Questions)
Q1.
Answer :
(a) 1-3i^+1+3j^
|AO→|=22|AO→|=|BO→|=|CO→|=22=RLet the position vector of O be xi^+yj^.|AO→|=x2+y2∴ x2+y2=8 ….. (1)Also, |BO→|=|CO→|x−32+y−332=x+332+y−32×2−6x+9+y2−63y+27=x2+63x+27+y2−6y+9y6−63=x63+6y=x1+31−3 …..(2)
Substituting y from (2) in (1) we get,
1−32×2+1+32 x2=81−32×2×8=81−32x=1−3y=1+3∴ The position vector of O is 1−3 i^+1+3 j.^AO→=1−3 i^+1+3 j^
Q2.
Answer :
(c) b →- a →
Let ABCDEF be a regular hexagon such that AB→ = a→ and BC→ =b→.We know, AD is parallel to BC such that AD=2BC.
∴ AD→ =2 BC→ = 2b→
In △ABC, we have
AB→ + BC→ = AC→⇒a→+b→ = AC→
In △ACD, we have
AC→ + CD→ = AD→⇒ CD→ = AD→ – AC→⇒ CD→ = 2b→ – a→+b→⇒ CD→ = b→ – a→
Q3.
Answer :
(c) 3 AC = 5 CB
Draw ON, the perpendicular to the line AB
Let i→ be the unit vector along ON
The resultant force R→=3OA→+5OB→ …..1
The angles between i→ and the forces R→, 3OA→, 5OB→ are ∠CON, ∠AON, ∠BON respectively.
R→·i→=3OA→·i→+5OB→·i→
⇒ R⋅1⋅ cos ∠CON = 3 OA→⋅1⋅cos∠AON + 5OB→⋅1⋅cos∠BON
R·ONOC=3OA×ONOA+5OBONOBROC=3+5
R = 8OC→
We know that,
OA→=OC→+CA→⇒3OA→=3OC→+3CA→ …..iOB→=OC→+CB→⇒5OB→=5OC→+5CB→ …..ii
on adding (i) and (ii) we get,
3OA→+5OB→=8OC→+3CA→+5CB→R→=8OC→+3CA→+5CB→8OC→=8OC→+3CA→+5CB→3AC→=5CB→⇒3AC=5CB
Q4.
Answer :
(d) None of these
a→+b→ is collinear with c→
∴ a→+b→=xc→ …..(1)
where x is scalar and x ≠ 0.
b→+c→ is collinear with a→
b→ +c→=ya→ ….. (2)
y is scalar and y ≠ 0
Substracting (2) from (1) we get,
a→ −c→= xc→−ya→a→(1+y)=(1+x)c→
As given a→, c→ are not collinear,
∴ 1 + y = 0 and 1 + x = 0
y = −1 and x = −1
Putting value of x in equation (1)
a→+b→=−c→a→+b→+c→=0
Q5.
Answer :
(b) −40
Given: Three points A60i^ + 3j^, B40i^ – 8j^ and Cai^ – 52j^ are collinear. Then, AB→ = λ BC→.
We have,
AB→ = 40i^ – 8j^ – 60i^ + 3j^ = -20i^ – 11j^
BC→ = ai^ – 52j^ – 40i^ – 8j^ = a-40i^ – 44j^
Therefore,
AB→ =λ BC→⇒-20i^ – 11j^ = λ a-40i^ – λ44j^⇒ λ a-40 =-20 , -44λ =-11 ⇒ λ = 14⇒ a-40 = -80⇒a=-40
Q6.
Answer :
(b) 4 OG→
Let us consider the point O as origin.
G is the mid point of AC.
∴OG→=OA→+OC→22OG→=OA→+OC→ …..1
Also, G is the mid point BD
∴OG→=OB→+OD→22OG→=OB→+OD→ …..2
On adding (1) and (2) we get,
2OG→+2OG→=OA→+OB→+OC→+OD→4OG→=OA→+OB→+OC→+OD→∴OA→+OB→+OC→+OD→=4OG→
Q7.
Answer :
(b) unit vector
Given: The vector cosα cosβ i^ + cosα sin β j^ + sin α k^.
Then,
cosα cos β i^+ cosα sinβ j^ + sinα k^ = cos2α cos2β + cos2α sin2β + sin2α = cos2α + sin2α = 1
Hence, the given vector is a unit vector.
Q8.
Answer :
Option(c)
Given a regular hexagon ABCDEF such that AB→=a→ , BC→= b→ and CD→= c→. Then,
In △ABC, we have
AC→= a→+b→.
In △ACD, we have
AC→+CD→ = AD→.⇒AD→ = AC→+c→.⇒AD→ = a→+b→+c→.
Again, in △ADE, we have
AE→= AD→+DE→.⇒AE→ = a→+b→+c→-a→.⇒ AE→ = b→+c→.
Hence option (c).
Q9.
Answer :
(b) α + β + γ =1
Given: A plane passing through a→ ,b→, c→.
⇒ Lines a→-b→ and c→-a→ lie on the plane.
The parmetric equation of the plane can be written as:
r→=a→+λ1(a→−b→)+λ2(c→−a→)r→=a→(1+λ1−λ2)−λ1b→+λ2 c→Given that r→=αa→+βb→+γc→∴ α+β+γ=1+λ1−λ2−λ1+λ2α+β+γ=1
Q10.
Answer :
Option (b).
Given: O be the circumcentre and O’ be the orthocentre of △ABC. Let G be the centroid of the triangle.
We know that O, G and H are collinear and by geometry O’G→= 2 OG→. This yields,
O’O→ = O’G→+GO→ = 2GO→ + GO→ = 3 GO→.
In other words OO’→ =3OG→.
Since, OG→ = a→+b→+c→3.
∴ OO’→ = 3 × a→+b→+c→3 = a→+b→+c→ = OA→+OB→+OC→.
Page 23.76 (Multiple Choice Questions)
Q11.
Answer :
Given:
a→+c→ = b→+d→⇒c→-d→ = b→-a→⇒AB→=DC→And a→+c→ = b→+d→⇒ c→ -b→= d→-a→⇒AD→=BC→Also, since a→+c→ = b→+d→⇒12(a→+c)→ =12(b→+d→)so, position vector of mid point of BD = position vector of mid point of AC.hence diagonals bisect each other.the given ABCD is a parallelogram.
Option (d).
Q12.
Answer :
(c) 13a→+b→
Taking A as origin. Then, position vector of A, B and C are 0→, a→ and b→ respectively. Then,
Centroid G has position vector 0→+a→+b→3 = a→+b→3
Therefore, AG = a→+b→3 – 0→ = a→+b→3
Q13.
Answer :
(d) 4AB→
AD→=2BC→EB→=2FA→FC→=2AB→
AD→+EB→=2BC→+FA→ =2AO→+FA→ ∵ BC→=AO→
In triangle AOF,
FA→+AO→+FO→=0∴ FA→+AO→=−FO→∴ AD→+EB→=−2FO→
And AB→=−FO→
∴ AD→+EB→=2AB→∴ AD→+EB→+FC→=2AB→+2AB→=4AB→
Q14.
Answer :
(a) form an isosceles triangle
Given: Position vectors of A, B, C are 2i^+j^-k^, 3i^-2j^+k^ and i^+4j^-3k^. Then,
AB→ = 3i^-2j^+k^ – 2i^+j^-k^ = i^-3j^+2k^BC→ = i^+4j^-3k^ – 3i^-2j^+k^ = -2i^+6j^-4k^CA→ = 2i^+j^-k^ – i^+4j^-3k^ =i^-3j^+2k^
Now, AB→=12+-32+22=1+9+4=14 CA→=12+-32+22=1+9+4=14BC→=-22+62+-42=4+36+16=56∴AB=CA→
Hence, the triangle is isosceles as two of its sides are equal.
Q15.
Answer :
(a) (2, −3)
Given position vectors of A, B and C are i^+xj^+3k^, 3i^+4j^+7k^ and yi^-2j^-5k^. Then,
AB→= 3i^+4j^+7k^-i^-xj^-3k^ = 2i^+4-xj^+4k^BC→ = yi^-2j^-5k^-3i^-4j^-7k^ = y-3i^-6j^-12k^
Since, the given vectors are collinear.
∴ AB→=λBC→⇒2i^ +4-xj^+ 4k^ = λ y-3i^ -6λ j^-12λ k^⇒2=λ y-3 , 4-x = -6λ, 4=-12λ ⇒2=λ y-3 , 4-x = -6λ, λ=-13⇒2=-13y-3 , 4-x = -6×-13⇒-6=y-3 , 4-x = 2⇒ y=-3 , x= 2
Q16.
Answer :
(c) 2 AB→
Given: ABCD, a parallelogram with diagonals AC and BD. Then,
AC→=AB→+BC→AD→ = AB→+BD→ ⇒ BD→ = AD→-AB→
∴ AC→ – BD→ = AB→+BC→-AD→+AB→ = 2AB→ [∵ AD→=BC→]
Q17.
Answer :
(d) 12a→-b→
Given a parallelogram OACB such that OC→ = a→, AB→=b→. Then,
OB→+BC→ = OC→⇒ OB→ = OC→-BC→
⇒ OB→ = OC→ – OA→ [∵ BC→=OA→]
⇒OB→= a→-OA→ …1
Therefore,
OA→ + AB→ = OB→⇒ OA→ + b→ = a→ – OA→ Using 1⇒2OA→ = a→-b→⇒ OA→ = 12 a→-b→
Q18.
Answer :
(d) both the vectors a →and b →have the same direction but different magnitudes
If a→ and b→ are collinear vectors, then they are paprallel. Therefore, we have
b→ = λa→ , for some scalar λ.
If λ=±1 ⇒ a→ = ±b→.
If b = b1i^ + b2 j^+ b3 k^ and a→ = a1i^ + a2 j^ + a3 k^. Then,
b→ = λa→.⇒b1i^+ b2 j^ +b3 k^ = λ a1i^+a2 j^+a3k^.⇒b1 i^+b2 j^+b3k^ = λa1i^+λa2j^+λa3k^.⇒ b1=λa1 , b2=λa2 , b3=λa3.⇒ b1a1=b2a2=b3a3 = λ.
Thus, the respective components of a→ and b→ can have different directions. Hence, the statement given in (d) is incorrect.
Q19.
Answer :
(c) AB→+BC→-CA→=0→
We have, LHS = AB→+BC→-CA→ = AC→-CA→ [∵ AB→+BC→ = AC→]
=-CA→-CA→=-2CA→
So, LHS≠RHS
Hence, It is not true.
Page 24.27 Ex. 24.1
Q1.
Answer :
i) We havea→=i∧-2j∧+k∧ and b→=4i∧-j∧+7k∧a→. b→=i∧-2j∧+k∧.4i∧-j∧+7k∧ =14+-2-4+17 =4+8+7 =19
ii) We havea→=j^+2k^=0 i∧+j∧+2k∧ and b→=2i∧+k∧=2i∧+0j∧+k∧a→. b→=0 i∧+j∧+2k∧ . 2i∧+0j∧+k∧ =02+10+21 =0+0+2 =2
iii) We havea→=j∧-k∧=0 i∧+j∧-k∧ and b→=2i∧+3j∧-2k∧a→. b→=0 i∧+j∧-k∧ . 2i∧+3j∧-2k∧ =02+13+-1-2 =3+2 =5
Q2.
Answer :
i) If the vectors a→ and b→ are perpendicular to each other, thena→. b→=0⇒λi∧+2j∧+k∧ . 4i∧-9j∧+2k∧=0⇒4λ-18+2=0⇒4λ-16=0⇒4λ=16⇒λ=4
ii) If the vectors a→ and b→ are perpendicular to each other, thena→. b→=0⇒λi∧+2j∧+k∧ . 5i∧-9j∧+2k∧=0⇒5λ-18+2=0⇒5λ-16=0⇒5λ=16⇒λ=165
iii) If the vectors a→ and b→ are perpendicular to each other, thena→. b→=0⇒2i∧+3j∧+4k∧ . 3i∧+2j∧-λk∧=0⇒6+6-4λ=0⇒12-4λ=0⇒4λ=12⇒λ=3
iv) If the vectors a→ and b→ are perpendicular to each other, thena→. b→=0⇒λi∧+3j∧+2k∧ . i∧-1j∧+3k∧=0⇒λ-3+6=0⇒λ+3=0⇒λ=-3
Q3.
Answer :
Let θ be the angle between a→ and b→.Given thata→ . b→=6⇒a→ b→ cos θ=6⇒43 cos θ=6⇒12 cos θ=6⇒cos θ=612=12⇒θ=cos-1 12=π3
Page 24.28 Ex. 24.1
Q4.
Answer :
We havea→=i∧-j∧ and b→=-j∧+2k∧a→-2b→=i∧-j∧ -2 -j∧+2k∧=i∧-j∧+2j∧-4k∧=i∧+j∧-4k∧a→+b→=i∧-j∧-j∧+2k∧=i∧-2j∧+2k∧a→-2b→ . a→+b→=i∧+j∧-4k∧ . i∧-2j∧+2k∧=1-2-8=-9
Q5.
Answer :
i) Let θ be the angle between a→ and b→.a→=12+-12=2b→=12+12=2a→ . b→=0-1+0=-1cos θ=a→ . b→a→ b→=-122=-12⇒θ=cos-1 -12=2π3
ii) Let θ be the angle between a→ and b→.a→=32+-22+-62=49=7b→=42+-12+82=81=9a→ . b→=12+2-48=-34cos θ=a→ . b→a→ b→=-3479=-3463⇒θ=cos-1 -3463
iii) Let θ be the angle between a→ and b→.a→=22+-12+ 22=9=3b→=42+42+-22=36=6a→ . b→=8-4-4=0cos θ=a→ . b→a→ b→=036=0⇒θ=cos-1 0=π2
iv) Let θ be the angle between a→ and b→.a→=22+-32+ 12=14b→=12+12+-22=6a→ . b→=2-3-2=-3cos θ=a→ . b→a→ b→=-3146=-384⇒θ=cos-1 -384
v) Let θ be the angle between a→ and b→.a→=12+22+ -12=6b→=12+-12+12=3a→ . b→=1-2-1=-2cos θ=a→ . b→a→ b→=-263=-218=-2×22×9=-23⇒θ=cos-1 -23
Q6.
Answer :
Let θ1 be the angle between a→ and x-axis.a→=12+-12+22=4=2b→=i∧(Because i∧ is the unit vector along x-axis)b→=12=1=1a→ . b→=1+0+0=1cos θ1=a→ . b→a→ b→=121=12⇒θ1=cos-1 12=π3Let θ2 be the angle between a→ and y-axis.a→=12+-12+22=4=2b→=j∧(Because j∧ is the unit vector along y-axis)b→=12=1=1a→ . b→=0-1+0=-1cos θ2=a→ . b→a→ b→=-121=-12⇒θ2=cos-1 -12=2π3Let θ3 be the angle between a→ and z-axis.a→=12+-12+22=4=2b→=k∧(Because k∧ is the unit vector along z-axis)b→=12=1=1a→ . b→=0+0+2=2cos θ=a→ . b→a→ b→=221=12⇒θ=cos-1 12=π4
Q7.
Answer :
i) Let ai∧+bj∧+ck∧ be the required vector.Given thatai∧+bj∧+ck∧.i∧+j∧-3k∧=0⇒a+b-3c=0 … 1ai∧+bj∧+ck∧.i∧+3j∧-2k∧=5⇒a+3b-2c=5 … 2ai∧+bj∧+ck∧.2i∧+j∧+4k∧=5⇒2a+b+4c=8 … 3Solving (1), (2) and (3), we geta=1, b=2, c=1So, ai∧+bj∧+ck∧=i∧+2j∧+k∧
ii) Let ai∧+bj∧+ck∧ be the required vector.Given thatai∧+bj∧+ck∧.i∧-j∧+k∧=4⇒a-b+c=4 … 1ai∧+bj∧+ck∧.2i∧+j∧-3k∧=0⇒2a+b-3c=0 … 2ai∧+bj∧+ck∧.i∧+j∧+k∧=2⇒a+b+c=2 … 3Solving (1), (2) and (3), we geta=2; b=-1; c=1So, ai∧+bj∧+ck∧=2i∧-j∧+k∧
Q8.
Answer :
Given that a⏞ and b⏞ are unit vectors.So, a^=1, b^=1We havea^+b^2=a^2+b^2+2 a^.b^ =1+1+2 a^ b^ cos θ =2+2cos θ⇒cosθ=a^+b^2-22 … 1a^-b2=a^2+b^2-2 a^.b^ =1+1-2 a^ b^ cos θ =2-2cos θ⇒cosθ=2-a^-b^22 … 2i Now,cos θ2=1+cos θ2=1+a^+b^2-22 2 From 1=2+a^+b^2-24=a^+b^24=12a^+b^ii sin θ2=1-cos θ2=1-2-a^-b^22 2[From (2)]=2+a^-b^2-24=a^-b^24=12a^-b^Now,tan θ2=sin θ2cos θ2=12a^-b^12a^+b^ =a^-b^a^+b^
Q9.
Answer :
Given that a⏞, b⏞ and a^+b^ are unit vectors.So, a^=1, b^=1 and a^+b^=1We have a^+b^2+a^-b^2=2a^2+b^2⇒ 1+a^-b^2=21+1⇒ 1+a^-b^2=4⇒ a ^-b^2=3⇒ a^-b^=3
Q10.
Answer :
Given that a→, b→ and c→ are unit vectors.So, a→=1, b→=1 and c→=1Since they are mutually perpendicular,a→.b→=b→.c→=c→.a→=0Now,a→+b→+c→2 =a→2+b→2+c→2+2 a→. b→+2 b→.c→+2 c→.a→ =1+1+1+0+0+0 =3∴ a→+b→+c→=3
Q11.
Answer :
We know that a→+b→2+a→-b→2=2a→2+b→2⇒ 602+402=2a→2+462 (Given)⇒ 3600+1600=2a→2+4232⇒ 968=2a→2⇒ a→2=484⇒ a→=22
Q12.
Answer :
Let θ1 be the angle between a→ and x-axis.a→=12+12+12=3b→=i∧(Because i∧ is the unit vector along x-axis)b→=12=1=1a→ . b→=1+0+0=1cos θ1=a→ . b→a→ b→=131=13⇒θ1=cos-1 13…1Let θ2 be the angle between a→ and y-axis.a→=12+12+12=3b→=j∧(Because j∧ is the unit vector along y-axis)b→=12=1=1a→ . b→=0+1+0=1cos θ2=a→ . b→a→ b→=131=13⇒θ2=cos-1 13…2Let θ3 be the angle between a→ and z-axis.a→=12+12+12=3b→=k∧(Because k∧ is the unit vector along z-axis)b→=12=1=1a→ . b→=0+0+1=1cos θ=a→ . b→a→ b→=131=13⇒θ=cos-1 13…3From (1), (2) and (3), the given vector is equally inclined to the coordinate axes
Q13.
Answer :
We havea→=1722+32+62=1749=77=1b→=1732+-62+22=1749=77=1c→=1762+22+-32=1749=77=1Anda→. b→=172i^+3j^+6k^. 173i^-6j^+2k^=1496-18+12=0b→. c→=173i^-6j^+2k^. 176i^+2j^-3k^=14918-12-6=0c→. a→=176i^+2j^-3k^. 172i^+3j^+6k^=14912+6-18=0So, a→=b→=c→=1 and a→. b→=b→. c→=c→. a→=0So, the given vectors are mutually perpendicular unit vectors.
Q14.
Answer :
We havea→+b→ .a→-b→=0⇒a→2-b→2=0⇒a→2=b→2⇒a→=b→
Q15.
Answer :
Given that c→ is perpendicular to both a→ and b→.⇒ c→. a→=0 and c→. b→=0 … 1Now, c→. a→+ b→= c→. a→+ c→. b→=0+0=0 From 1So, c→ is perpendicular to a→+ b→.Again, c→. a→ -b→= c→. a→- c→. b→=0-0=0 From 1So, c→ is perpendicular to a→- b→.
Q16.
Answer :
a→a2-b→b22=a→a22+b→b22-2a→.b→a2b2=a→2a4+b→2b4- 2a→.b→a2b2=a2a4+b2b4- 2a→.b→a2b2(From the given information)=1a2+1b2- 2a→.b→a2b2=b2+a2-2a→.b→a2b2=a2+b2-2a→.b→a2b2=a→2+a→2-2a→.b→a2b2(From the given information)=a→-b→2a2b2=a→-b→ab2
Q17.
Answer :
Given that: d→·a→=0
so, either d→ = 0 or d→⊥a→
similarly, d→·b→=0
so, d→ = 0 or d→⊥b→
Also, d→·c→=0
so, d→ = 0 or d→⊥c→
But d→ cannot be perpendicular to a→, b→, c→ as a→, b→, c→ are non-coplanar.
so, d→=0. d→ is a null vector.
Q18.
Answer :
Given that a→ is perpendicular to b→ and c→.⇒a→. b→=0 and a→. c→=0 … (1)Now, let r→ be any vector in the plane of b→ and c→.Then, r→ is the linear combination of b→ and c→.r→=xb→+yc→, for some x and y.Now,a→. r→=a→. xb→+yc→=x a→. b→+y a→. c→=x0+y0 [From (1)]=0Thus, a→ is perpendicular to r→.That is, a→ is perpendicular to every vector in the plane of b→ and c→ .
Q19.
Answer :
Let ABC be the given triangle and AC→=b→=i^-3j^+5k^CB→=a→=3i^-2j^+k^AB→=c→=2i^+j^-4k^a→. b→=3+6+5=14b→. c→=2-3-20=-21c→. a→=6-2-4=0So, AB→ is perpendicular to CB→.Thus, ∆ABC is a right-angled triangle.
Page 24.29 Ex. 24.1
Q20.
Answer :
Given,a→+b→+c→=0⇒b→+c→=-a→⇒b→+c→2=-a→2⇒b→2+c→2+2b→. c→=a→2⇒2b→. c→=a→2-b→2-c→2⇒2 b→ c→ cos θ=a→2-b→2-c→2∴ cos θ=a→2-b→2-c→22 b→ c→
Q21.
Answer :
Given thatOA→=0i^-1j^-2k^; OB→=3i^+1j^+4k^; OC→=5i^+7j^+1k^AB→=OB→-OA→=3i^+2j^+6k^ ⇒AB→=9+4+36=7BA→=OA→-OB→=-3i^-2j^-6k^ ⇒BA→=9+4+36=7BC→=OC→-OB→=2i^+6j^-3k^⇒BC→=4+36+9=7CB→=OB→-OC→=-2i^-6j^+3k^⇒CB→=4+36+9=7CA→=OA→-OC→=-5i^-8j^-3k^⇒CA→=25+64+9=98=72AC→=OC→-OA→=5i^+8j^+3k^⇒AC→=25+64+9=98=72cos A=AB→. AC→AB→AC→=15+16+18772=49492=12⇒A=cos-112=π4cos B=BA→. BC→BA→BC→=-6-12+1877=049=0⇒B=cos-10=π2cos C=CB→. CA→CB→CA→=10+48-9772=49492=12⇒C=cos-112=π4
Q22.
Answer :
Given thatu→+v→+w→=0⇒u→+v→+w→=0⇒u→+v→+w→2=0⇒u→2+v→2+w→2+2u→. v→+v→. w→+w→. u→=0⇒32+42+52+2u→. v→+v→. w→+w→. u→=0 (Given:u→=3, v→=4 and w→=5)⇒9+16+25+2u→. v→+v→. w→+w→. u→=0⇒50+2u→. v→+v→. w→+w→. u→=0⇒2u→. v→+v→. w→+w→. u→=-50∴ u→. v→+v→. w→+w→. u→=-502=-25
Q23.
Answer :
Given thata→=OA→=4i^-3j^+k^; b→=OB→=2i^-4j^+5k^; c→=OC→=i^-j^+0k^AB→=OB→-OA→=-2i^-j^+4k^ BC→=OC→-OB→=-i^+3j^-5k^CA→=OA→-OC→=3i^-2j^+k^AB→. BC→=2-3-20=-21≠0BC→. CA→=-3-6-5=-14≠0AB→. CA→=-6+2+4=0So, AB→ is perpendicular to CA→.So, ∆ABC is a right-angled triangle.
Q24.
Answer :
Given thatOA→=i^+2j^+3k^; OB→=-1i^+0j^+0k^; OC→=0i^+1j^+2k^AB→=OB→-OA→=-2i^-2j^-3k^ ⇒AB→=4+4+9=17BC→=OC→-OB→=i^+j^+2k^⇒BC→=1+1+4=6CA→=OA→-OC→=i^+j^+k^⇒CA→=1+1+1=3cos ∠ABC=AB→. BC→AB→BC→=-2-2-6176=10102⇒∠ABC=cos-110102
Q25.
Answer :
Given thatOA→=0i^+j^+k^; OB→=3i^+j^+5k^; OC→=0i^+3j^+3k^BC→=OC→-OB→=-3i^+2j^-2k^CA→=OA→-OC→=0i^-2j^-2k^Now,BC→. CA→=0-4+4=0So, BC→ is perpendicular to CA→.So, ∆ABC is right-angled at C.
Q26.
Answer :
We havea→= =x2i⏜+2j^-2k^, b→=i^-j^+k^ and c→=x2i^+5j^-4k^Let θ1 be the angle between a→ and b→ and θ2 be the angle between b→ and c→.Given that θ1 is acute and θ2 is obtuse.⇒cos θ1>0 and cos θ2<0⇒a→.b→a→.b→>o and b→.c→b→.c→<0⇒x2-4×4+4+41+1+1>0 and x2-91+1+1×4+25+16<0⇒x2-4>0 and x2-9<0⇒x∈-∞, -2∪2, ∞ and x∈-3, 3⇒x∈-3, -2 ∪ 2, 3
Q27.
Answer :
We havea→=3i^+xj^-k^ and b→=2i^+j^+yk^It is given that the vectors are perpendicular.⇒a→. b→=0⇒6+x-y=0⇒x-y=-6 … 1Also, it is given thata→=b→⇒9+x2+1=4+1+y2⇒10+x2=5+y2 ⇒10+x2=5+y2 ⇒x2-y2=-5⇒x+yx-y=-5⇒-6 x+y=-5 Using 1⇒x+y=56 … 2(1)+(2) gives2x=-316⇒x=-3112From (1),-3112-y=-6⇒y=-3112+6=4112∴x=-3112 and y=4112
Q28.
Answer :
We havea→+b→=3Squaring both sides, we geta→+b→2=3⇒a→2+b→2+2 a→. b→=3⇒1+1+2 a→. b→=3 (Because a→ and b→ are unit vectors)⇒2+ 2 a→. b→=3⇒2 a→. b→=1⇒2 a→. b→=1⇒ a→. b→=12… 1Now,2a→-5b→.3a→+b→=6a→2+2a→. b→-15 b→. a→-5b→2=6a→2+2a→. b→-15 a→. b→-5b→2 (a→. b→=b→. a)→=6a→2-13a→. b→-5b→2=61-13 12-51 From (1)=1-132=-112
Q29.
Answer :
Given thata→=2, b→=1 and a→. b→=1 … 1Now,3a→-5b→.2a→+7b→=6a→2+21a→. b→-10 b→. a→-35b→2=6a→2+21a→. b→-10 a→. b→-35b→2 (We know that a→. b→=b→. a→)=6a→2+11a→. b→-35b→2=622+11 1-3512 From (1)=24+11-35=0
Q30.
Answer :
Given that a→ is a unit vector.⇒a→=1 … 1i x→-a→.x→+a→=8⇒x→2-a→2=8⇒x→2-12=8 From (1)⇒x→2=9⇒x→=3ii x→-a→.x→+a→=12⇒x→2-a→2=12⇒x→2-12=12 From (1)⇒x→2=13⇒x→=13
Q31.
Answer :
i) Given thata→=2 b→ … 1And a→+b→.a→-b→=12⇒a→2-b→2=12⇒2 b→2-b→2=12 From (1)⇒4 b→2-b→2=12⇒3 b→2=12⇒b→2=4⇒b→=2a→=2 b→=22=4∴a→=4 and b→=2
ii) Given thatAnd a→=8 b→ … 1a→+b→.a→-b→=8⇒a→2-b→2=8⇒8 b→2-b→2=8 From (1)⇒64 b→2-b→2=8⇒63 b→2=8⇒b→2=863⇒b→=863a→=8 b→=8 863=8863∴a→=8863 and b→= 863
iii) Given thata→=2 b→ … 1And a→+b→.a→-b→=3⇒a→2-b→2=3⇒2 b→2-b→2=3 From (1)⇒4 b→2-b→2=3⇒3 b→2=3⇒b→2=1⇒b→=1a→=2 b→=2 1=2∴a→=2 and b→=1
Q32.
Answer :
i) Given thata→=2, b→=5 and a→. b→=8 …1We know thata→-b→2=a→2+b→2-2 a→. b→ =22+52-2 8 Using 1 =4+25-16 =13∴ a→-b→=13
ii) Given thata→=3, b→=4 and a→. b→=1 …1We know thata→-b→2=a→2+b→2-2 a→. b→ =32+42-2 1 Using 1 =9+16-2 =23∴ a→-b→=23
iii) Given thata→=2, b→=3 and a→. b→=4 …1We know thata→-b→2=a→2+b→2-2 a→. b→ =22+32-2 4 Using 1 =4+9-8 =5∴ a→-b→=5
Q33.
Answer :
i) Let θ be the angle between a→ and b→.Given thata→=3, b→=2 and a→. b→=6 …1We know that a→. b→=a→ b→ cos θ⇒6=32 cos θ Using 1⇒cos θ=623=12⇒ θ=cos-112=π4
ii) Let θ be the angle between a→ and b→.Given thata→=3, b→=3 and a→. b→=1 …1We know that a→. b→=a→ b→ cos θ⇒1=33 cos θ Using 1⇒cos θ=133=19⇒ θ=cos-119
Page 24.30 Ex. 24.1
Q34.
Answer :
Given that a→=5i^-2j^+5k^ and b→=3i^+k^Let x→ and y→ be such thata→=x→+y→⇒y→=a→-x→ … 1Since x→ is parallel to b→,⇒x→=t b→ t is constant⇒x→=t 3i^+k^=3t i^+t k^Substituting the values of x→ and a→ in (1), we gety→=5i^-2j^+5k^-3t i^+t k^=5-3t i^-2j^+5-t k^ … 2Since y→ is perpendicular to b→,y→. b→=0⇒5-3t i^-2j^+5-t k^. 3i^+k^=0⇒3 5-3t+0+5-t=0⇒15-9t+5-t=0⇒20-10t=0⇒t=2From (1) and (2), we getx→=6 i^+2 k^y→=- i^-2j^+3 k^
Q35.
Answer :
Given that the angle between a→ and b→ is 300.Also,a→= b→ and a→. b→=3We know that a→. b→=a→ b→ cos θ⇒3=a→a→ cos 30⇒3=a→232⇒ a→2=63=23⇒ a→=23= b→∴ a→=b→=23
Q36.
Answer :
Let a→=2i^-j^+3k^ and b→=2i^+4j^-2k^ and x→ and y→ be such thata→=x→+y→⇒y→=a→-x→ …(1)Since x→ is parallel to b→,x→=t b→⇒x→=t 2i^+4j^-2k^ =2t i^+4t j^-2t k^ …(2)Substituting the values of x→ and a→ in (1),y→=2i^-j^+3k^-2t i^+4t j^-2t k^=2-2t i^+-1-4tj^+3+2t k^ … 3Since y→ is perpendicular to b→,y→. b→=0⇒2-2t i^+-1-4tj^+3+2t k^. 2i^+4j^-2k^ =0⇒2 2-2t+4 -1-4t-2 3+2t=0⇒4-4t-4-16t-6-4t=0⇒-24t=6⇒t=-14From (2) and (3),x→=2-14 i^+4-14 j^-2-14 k^=-12i^-j^+12k^y→=2-2-14 i^+-1-4-14j^+3+2-14 k^ =52i^+52k^=52i^+k^So,a→=x→+y→=-12i^-j^+12k^+52i^+k^
Q37.
Answer :
Let a→=6i^-3j^-6k^ and b→=i^+j^+k^ and x→ and y→ be such thata→=x→+y→⇒y→=a→-x→ … 1Since x→ is parallel to b→,x→=t b→⇒x→=t i^+j^+k^=t i^+t j^+t k^ …(2)Substituting the values of x→ and a→ in (1), we gety→=6i^-3j^-6k^-t i^+t j^+t k^ =6-t i^+-3-tj^+-6-t k^ … 3Since y→ is perpendicular to b→,y→. b→=0⇒6-t i^+-3-tj^+-6-t k^. i^+j^+k^=0⇒1 6-t+1-3-t + 1 -6-t =0⇒-3-3t=0⇒t=-1From (2) and (3), we getx→=-i^-j^-k^y→=7 i^-2j^-5 k^So,a→=x→+y→=-i^-j^-k^+7 i^-2j^-5 k^
Q38.
Answer :
Given thata→=5i^-j^+7k^; b→=i^-j^+λk^∴ a→+b→=5i^-j^+7k^+i^-j^+λk^=6i^-2j^+7+λk^and a→-b→=5i^-j^+7k^-i^-j^+λk^=4i^+0j^+7-λk^Given that a→+b→ is orthogonal to a→-b→.⇒a→+b→. a→-b→=0⇒6i^-2j^+7+λk^.4i^+0j^+7-λk^=0⇒24+0+49-λ2=0⇒λ2=73⇒λ=73
Q39.
Answer :
Given that a→. a→=0⇒a→2=0⇒a→=0 …1Also given thata→. b→=0⇒a→ b→ cos θ=0 (Where θ is the angle between a→ and b→)⇒0 b→ cos θ=0 [From (1)]⇒0=0So, it means that for any vector b→, the given equation a→. b→=0 is satisfied.
Q40.
Answer :
Let a→=a1i^+a2j^+a3k^, where a1, a2 and a3 are components of a→.⇒a12+a22+a32=1 (Because a→ is a unit vector)… 1Now,a→. i^=a1⇒a→i^ cos π4=a1 (Because the angle between a→ and i^ is π4)⇒1 1 12=a1 (Because a→ and i^ are unit vectors)⇒a1=12Again,a→. j^=a2⇒a→i^ cos π3=a2 (Because the angle between a→ and i^ is π3)⇒1 1 12=a2(Because a→ and i^ are unit vectors)⇒a2=12Now from (1),122+122+a32=1⇒12+14+a32=1⇒34+a32=1⇒a32=14⇒a3=12Now,a→. k^=a3⇒a→k^ cos θ=12 (Because the angle between a→ and k^ is θ)⇒1 1 cos θ=12(Because a→ and i^ are unit vectors)⇒θ=cos-112=π3And a→=12i^+12j^+12k^
Q41.
Answer :
Given thata→=5i^-j^-3k^; b→=i^+3j^-5k^∴ a→+b→=5i^-j^-3k^+i^+3j^-5k^=6i^+2j^-8k^And a→-b→=5i^-j^-3k^-i^+3j^-5k^=4i^-4j^+2k^Now,a→+b→. a→-b→=6i^+2j^-8k^.4i^-4j^+2k^=24-8-16=0 So, a→+b→ is orthogonal to a→-b→.
Q42.
Answer :
Given thata→=2i^-2j^+k^b→=i^+2j^-2k^and c→=2i^-j^+4k^∴ b→+c→=i^+2j^-2k^+2i^-j^+4k^=3i^+j^+2k^Projection of b→+c→ on a→ isb→+c→.a→a→=3i^+j^+2k^. 2i^-2j^+k^4+4+1=6-2+23=2
Q43.
Answer :
Given that the angle between a→ and b→ is 300.Also,a→= b→; a→. b→=12We know that a→. b→=a→ b→ cos θ⇒12=a→a→ cos 60⇒12=a→212⇒ a→2=1⇒ a→=1∴ a→= b→=1
Q44.
Answer :
We havea→=2i^+2j^+3k^b→=-i^+2j^+k^andc→=3i^+j^∴ a→+λb→=2i^+2j^+3k^+λ -i^+2j^+k^=2-λ i^+2+2λ j^+3+λ k^Given that a→+λb→ is perpendicular to c→.⇒a→+λb→. c→=0⇒2-λ i^+2+2λ j^+3+λ k^ . 3i^+j^+0k^=0⇒3 2-λ+1 2+2λ+0=0⇒6-3λ+2+2λ=0∴ λ=8
Q45.
Answer :
Let us assume that eithera→=0 or b→=0Then, a→. b→=a→ b→ cos θ=0 (θ is the angle between a→ and b→)Now, let us assume that a→. b→=0⇒a→ b→ cos θ=0But here we cannot say that eithera→=0 or b→=0. (Because even cos θ can be zero)For example, leta→=2i^+j^+3k^ and b→=-3i^+2k^Here, a→=4+1+9=14≠0b→=9+4=13≠0But a→. b→=2i^+j^+3k^ . -3i^+2k^=-6+0+6=0
Q46.
Answer :
Given that α→=3i^+4j^+5k^ and β→=2i^+j^-4k^ Also,β→=β1→+β2→⇒β2→=β→-β→1 … 1Since β→1 is parallel to α→,β1→=t α→⇒β1→=t 3i^+4j^+5k^ =3t i^+4t j^+5t k^ …(2)Substituting the values of β1→ andα→ in (1), we getβ2→=2i^+j^-4k^ -3t i^+4t j^+5t k^=2-3t i^+1-4tj^+-4-5t k^ … 3Since β2→ is perpendicular to α→,β2→. α→=0⇒2-3t i^+1-4tj^+-4-5t k^. 3i^+4j^+5k^=0⇒3 2-3t +4 1-4t+5 -4-5t=0⇒6-9t+4-16t-20-25t=0⇒-50t=10⇒t=-15From (2) and (3), we getβ1→=-15 3i^+4j^+5k^ β2→=135i^+95j^-3k^=1513i^+9j^-15k^
Q47.
Answer :
Given thatp→=5i^+λj^-3k^and q→=i^+3j^-5k^p→+q→=5i^+λj^-3k^+i^+3j^-5k^=6i^+λ+3j^-8k^p→-q→=5i^+λj^-3k^-i^+3j^-5k^=4i^+λ-3j^+2k^Given that p→+q→ is orthogonal to p→-q→.⇒p→+q→. p→-q→=0⇒6i^+λ+3j^-8k^.4i^+λ-3j^+2k^=0⇒24+λ2-9-16=0⇒λ2=1∴ λ=±1
Q48.
Answer :
Given thata→+b→=b→Squaring both sides, we geta→+b→2=b→2⇒a→2+b→2+2 a→. b→=b→2⇒a→2+2 a→. b→=0 … 1Now,a→+2b→.a→=a→.a→+2 b→. a→=a→2+2 a→. b→=0 Using 1So, a→+2b→ is perpendicular to a→.
Page 24.34 (Very Short Answers)
Q1.
Answer :
Let θ be the angle between a→ and b→.Given thata→=2, b→=3 and a→. b→=3We know that a→. b→=a→ b→ cos θ⇒3=23 cos θ⇒cos θ=323⇒cos θ=12⇒ θ=cos-112=π3
Q2.
Answer :
We havea→. b→=6 and b→=4The projection of a→ on b→ isa→. b→b→=64=32
Q3.
Answer :
Let, a→=4i^-3j^+3k^and b→=2i^-j^-k^Let θ be the angle between a→ and b→.a→=42+-32+32=34b→=22+-12+-12=6∴ a→ . b→=8+3-3=8cos θ=a→ . b→a→ b→=8346=8251=451
Q4.
Answer :
It is given that the vectors are othgonal. So, their dot product is zero.3i^+mj^+k^ . 2i^-j^-8k^=0⇒6-m-8=0⇒-m-2=0⇒m=-2
Q5.
Answer :
The given vectors are parallel. ∴ 3i^-2j^-4k^=t 18i^-12j^-mk^⇒3i^-2j^-4k^=18t i^-12t j^-tm k^Comparing both sides, we get 18t=3, -12t=-2, -4=-tm⇒t=16 Substituting the value of m in -4=-tm, we get-4=-m16∴ m=24
Q6.
Answer :
We havea→=b→ …iNow,a→+b→ . a→-b→=a→2-b→2=a→2-a→2 Using i=0
Q7.
Answer :
Given thata→+b→ . a→-b→=0⇒a→2-b→2=0⇒a→2=b→2∴a→=b→
Q8.
Answer :
Given thata→+b→=a→+b→Squaring both sides,we geta→+b→2=a→+b→2⇒a→2+b→2+2 a→. b→=a→2+b→2+2a→ b→⇒a→. b→=a→ b→⇒a→ b→ cos θ=a→ b→ (where θ is the angle between a→ and b→)⇒cos θ=1⇒θ=0o⇒a→ and b→ are parallel.
Q9.
Answer :
Given thata→+b→=a→-b→Squaring both sides, we geta→+b→2=a→-b→2⇒a→2+b→2+2 a→. b→=a→2+b→2-2 a→. b→⇒4a→. b→=0⇒a→. b→=0⇒a→ and b→ are perpendicular.
Q10.
Answer :
Given thata→=b→ and a→ and b→ are inclined at an angle of 60°Also, given thata→. b→=8⇒a→ b→ cos 60°=8⇒a→a→ 12=8⇒a→2=16⇒a→=4
Q11.
Answer :
Given that a→. a→=0⇒a→2=0⇒a→=0 … 1Also, given thata→. b→=0⇒a→ b→ cos θ=0 (where θ is the angle between a→ and b→)⇒0 b→ cos θ=0 [From (1)]⇒0=0So, it means that for any vector b→, the given equation a→. b→=0 is satisfied.
Q12.
Answer :
Given that b→ is a unit vector.∴ b→=1Anda→+b→.a→-b→=8 Given⇒a→2-b→2=8⇒a→2-12=8⇒a→2=9∴ a→=3
Q13.
Answer :
Given that a^ and b^ are unit vectors such that a^+b^ is a unit vector.⇒a^=b^=a^+b^=1 … 1Now,a^+b^=1Squaring both sides, we geta^2+b^2+2a^. b^ =1⇒1+1+2a^. b^ =1 From (1)⇒a^. b^ =-12 … 2Now,a^-b^2=a^2+b^2-2a^. b^ =1+1-2-12=3 From (1) and (2)∴ a^-b^=3
Q14.
Answer :
We havea→=2, b→=5 and a→. b→=2Now,a→-b→2 =a→2+b→2-2 a→. b→ =22+52-2 2 =4+25-4 =25∴ a→-b→=25=5
Q15.
Answer :
We havea→=i^-j^ and b→=-j^+k^The projection of a→ on b→ isa→. b→b→=i^-j^.-j^+k^-j^+k^=0+1+01+1=12
Q16.
Answer :
We havea→+b→2+a→-b→2a→2+b→2=a→2+b→2+2 a→. b→+a→2+b→2-2 a→. b→a→2+b→2=2a→2+b→2a→2+b→2=2
Q17.
Answer :
We haver→=3i^-4j^+12k^Projection of r→ on x-axis = r→. i^i^=31=3Projection of r→ on y-axis = r→. j^j^=-41=-4Projection of r→ on z-axis = r→. k^k^=121=12
Q18.
Answer :
Component of b→ on a→ is a→ . b→aa^=a→. b→a→2a→=a→. b→a→a→2
Q19.
Answer :
Let a→=a1i→+a2j→+a3k→Now,a→. i→ i→+a→. j→ j→+a→. k→ k→=a1i→+a2j→+a3k→=a→
Q20.
Answer :
We havea→=sin θi^+cos θj^andb→=i^-3 j^+2k^It is given that the vectors are perpendicular.⇒a→. b→=0⇒sin θ-3 cos θ=0⇒sin θ=3 cos θ⇒tan θ=3 ⇒θ=π3
Page 24.35 (Very Short Answers)
Q21.
Answer :
Projection of a→ on b→ =a→. b→b→Projection of i→+j→+k→ along j→=i→+j→+k→. j→j→=11=1
Q22.
Answer :
Let a→=a1 i^+a2 j^+a3 k^a→. i^=a1a→. i^+ j^=a1+a2a→. i^+ j^+k^=a1+a2+a3Given thata→. i^=a→. i^+ j^=a→. i^+ j^+k^=1⇒a1=a1+a2=a1+a2+a3=1⇒a1=1;a1+a2=1; a1+a2+a3=1⇒a1=1; 1+a2=1; 1+a2+a3=1⇒a1=1; a2=0; 1+0+a3=1⇒a1=1; a2=0; a3=0So, a→=a1 i^+a2 j^+a3 k^=1 i^+0 j^+0 k^=i^
Q23.
Answer :
We havea→=1 and b→=1 …iNow,a→+b→ . a→-b→=a→2-b→2 =12-12 Using i =0⇒a→+b→ and a→-b→ are perpendicular.∴ Angle between a→+b→ and a→-b→ is 900.
Q24.
Answer :
a→ and b→ are unit vectors and they are perpendicular.⇒a→=b→=1; a→. b→=0 …iNow,a→+b→2=a→2+b→2+2a→. b→ =1+1+2 0 Using i =2 ∴ a→+b→=2
Q25.
Answer :
Given that a→, b→ and c→ are unit vectors.So, a→=1, b→=1 and c→=1 …iSince they are mutually perpendicular, a→.b→=b→.c→=c→.a→=0 …iiNow,a→+b→+c→2 =a→2+b→2+c→2+2 a→. b→+2 b→.c→+2 c→.a→ =1+1+1+0+0+0 Using iand ii =3∴ a→+b→+c→=3
Q26.
Answer :
We havea→=i^-j^+k^ and b→=i+j-k Let θ be the angle between a→ and b→.a→=12+-12+ 12=3b→=12+12+-12=3anda→ . b→=1-1-1=-1Now,cos θ=a→ . b→a→ b→=-133=-13∴ θ=cos-1 -13
Q27.
Answer :
We havea→=2i^+λj^+k^ and b→=i^-2j^+3k^Given that a→ and b→ are perpendicular.⇒a→. b→=0⇒2i^+λj^+k^.i^-2j^+3k^=0⇒2-2λ+3=0⇒5-2λ=0∴ λ=52
Q28.
Answer :
We havea→. b→=8 and b→=2i^+6j^+3k^The projection of a→ on b→ isa→. b→b→=84+36+9=87
Q29.
Answer :
We havea→=3i^+2j^+9k^ and b→= i^+pj^+3k^Given that a→ and b→ are parallel.⇒a→=tb→ for some t.⇒3i^+2j^+9k^=t i^+pj^+3k^⇒3i^+2j^+9k^=t i^+pt j^+3t k^Comparing both sides, we get3=t, 2=pt and 9=3t⇒t=3 and pt=2⇒3t=2∴t=23
Q30.
Answer :
Given: 2i^+λj^+3k^ and 3i+2j-4k are perpendicular to each other.So, their dot product is zero.2i^+λj^+3k^.3i+2j-4k⇒6+2λ-12=0⇒2λ-6=0⇒λ=3
Q31.
Answer :
We havea→=2 and a→. b→=3So,the projection of b→ on a→ isa→. b→a→=32
Q32.
Answer :
Let θ be the angle between a→ and b→.Given,a→=3; b→=2; a→. b→=6We know that a→. b→=a→ b→ cos θ⇒6=32 cos θ⇒cos θ=623=12⇒ θ=cos-112=π4
Q33.
Answer :
The projection of a→ on b→ isa→. b→b→The projection of i^-j^ on i^+j^ is i^-j^ . i^+j^ i^+j^=1-11+1=0
Q34.
Answer :
We havea=λ i^+j^+4k^ and b=2i^+6j^+3k^The projection of a→ on b→ is a→. b→b→Given thata→. b→b→=4⇒λ i^+j^+4k^.2i^+6j^+3k^2i^+6j^+3k^⇒2λ+6+124+36+9=4⇒2λ+187=4⇒2λ+18=28⇒2λ=10∴λ=5
Q35.
Answer :
We havea→=2i^+λ j^+k^ and b→=i^-2j^+3k^Given, a→ and b→ are perpendicular. So, their dot product is zero.⇒2i^+λ j^+k^.i^-2j^+3k^=0⇒2-2λ+3=0⇒-2λ+5=0∴λ=52
Q36.
Answer :
Let a→=7i^+j^-4k^; b→=2i^+6j^+3k^The projection of a→ on b→ isa→. b→b→=7i^+j^-4k^.2i^+6j^+3k^2i^+6j^+3k^=14+6-124+36+9=87
Q37.
Answer :
We havea→=2i^+λj^+k^ and b→=i^-2j^+3k^The given vectors are perpendicular. So, their dot product is zero.2i^+λj^+k^ . i^-2j^+3k^⇒2-2λ+3=0⇒5-2λ=0⇒-2λ=-5⇒λ=52
Q38.
Answer :
Given thata→=2i^-2j^+k^b→=i^+2j^-2k^c→=2i^-j^+4k^b→+c→=i^+2j^-2k^+2i^-j^+4k^=3i^+j^+2k^Projection of b→+c→ on a→ isb→+c→.a→a→=3i^+j^+2k^. 2i^-2j^+k^2i^-2j^+k^=6-2+24+4+1=63=2
Page 24.36 (Multiple Choice Questions)
Q1.
Answer :
(c) cos θ=-45
Given that2a→+b→=p→ … 1a→+2b→=q→ … 2Solving these two we geta→=2p→-q→3, b→=2q→-p→3And we havep→=i^+j^ and q→=i^-j^Substituting the values of p→ and q,→ we geta→=2p→-q→3=2i^+j^-i^-j^3 =i^+3j^3⇒a→=131+9=103b→=2q→-p→3=2i^-j^-i^+j^3=i^-3j^3⇒b→=131+9=103a→. b→=19 1-9=-89We know thata→. b→=a→ b→ cos θ⇒-89=103×103 cos θ⇒-89=109cos θ⇒cos θ=-89×910=-45
Q2.
Answer :
(b) i^
Let a→=a1i^+a2j^+a3k^a→. i^=a1and a→. i^+j^=a1+a2and a→. i^+j^+k^=a1+a2+a3Given,a→. i^=a→. i^+j^=a→. i^+j^+k^=1⇒a1=a1+a2=a1+a2+a3=1⇒a1=1, a2=0, a3=0So, a→=a1i^+a2j^+a3k^=1 i^+0j^+0k^=i^
Q3.
Answer :
(d) π3
Given, a→ =3, b→=5 and c→=7 …iLet θ be the angle between a→and b→. Given thata→+b→+c→=0⇒a→+b→=-c→⇒a→+b→=-c→2⇒a→2+b→2+2a→. b→=c→2⇒2a→. b→=c→2-a→2-b→2⇒2a→. b→=72-32-52 Using i⇒2a→. b→=15⇒2 a→ b→ cos θ=15⇒2 3 5 cos θ=15 Using i⇒cos θ=12∴ θ=π3
Q4.
Answer :
(c) α=2π3
a→ and b→ are unit vectors.⇒a→=b→=1 … 1Now,a→. b→=a→ b→ cos α⇒a→. b→=cos α … 2 Using 1Given that a→+b→=1Squaring both sides, we geta→+b→2=1⇒a→2+b→2+2 a→. b→=1⇒1+1+2 cos α=1 Using 1 and 2⇒2+ 2 cos α=1⇒2 cos α=-1⇒2 cos α=-1⇒cos α=-12⇒α=2π3
Q5.
Answer :
(b) unit vector
Let a→=cos α cos β i^+cos α sin β j^+sin α k^a→=cos2 α cos2 β+cos2 α sin2 β+sin2 α=cos2 α cos2 β+sin2 β+sin2 α=cos2 α1+sin2 α=cos2 α+sin2 α=1=1So, a→ is a unit vector.
Q6.
Answer :
(c) -5162
PQ→=OQ→-OP→=5i^-2j^+4k^-i^+3j^-7k^=4i^-5j^+11k^The unit vector along y-axis is j^.Let θ be the required angle.cos θ=PQ→. j^PQ→j^=-516+25+1211=-5162
Q7.
Answer :
(a) 3
It is given that a→ and b→ are unit vectors.⇒a→=b→=1Now,a→. b→=a→ b→ cos θ=1 1 cos θ=cos θThe range of cos θ is -1, 1. ∴ 3 is not a possible value of cosθ as it is greater than 1.
Q8.
Answer :
(b) an ellipse
Let, a→=i^-2x j^+3y k^ and b→=i^+2x j^-3y k^It is given that the vectors are perpendicular. So, their dot product is zero.a→.b→=0⇒i^-2x j^+3y k^.i^+2x j^-3y k^=0⇒1-4×2-9y2=0⇒4×2+9y2=1Dividing both sides by 36, we getx29+y24=1This is an ellipse.
Q9.
Answer :
(b) a →× b →×a → a →2
The vector component of b→ perpendicular to a→ isa→×b→×a→ a→2
Page 24.37 (Multiple Choice Questions)
Q10.
Answer :
(c) 593
Let ABCD be a parallelogram in which side AB→ = DC →= 5a→+2b→and AD→ = BC→=a→-3b→and diagonals are AC and BD.Now, AC→=AB→+BC→ =5a→+2b→+a→-3b→ =6a→-b→∴ AC→=6a→-b→ =6a→2+b→2-2×6a→×b→cosθ =36a→2+b→2-12×a→×b→cosπ4 =36222+32-12×22×3×12 =288+9-72 =225=15 units BD→= BA→+BD→ =-AB→+BD→ =-5a→+2b→+a→-3b→ =-4a→-5b→∴ BD→=-4a→-5b→ =4a→+5b→ =4a→2+5b→2+2×4a→×5b→cosθ =16a→2+25b→2+40×a→×b→cosπ4 =16222+2532+40×22×3×12 =128+225+240 =593 units Therefore, the larger diagonal=593
Q11.
Answer :
(d) a=1λ
Given thata→=a;Now,λa→=1⇒λ a→=1⇒λa=1⇒a=1λ
Q12.
Answer :
(b) 0≤θ≤π2
a→. b→≥0⇒a→ b→ cos θ≥0⇒cos θ≥0⇒0≤θ≤π2
Q13.
Answer :
(b) 0<x<12
a →=2x2i^+4xj^+k^, b →=7i^-2j^+xk^
Let the angle between vector a and vector b be A.
∴cosA=a →.b →a →b →=2x2i^+4xj^+k^.7i^-2j^+xk^2x2i^+4xj^+k^ 7i^-2j^+xk^ =14×2-8x+x4x4+16×2+149+4+x2 =14×2-7x4x4+16×2+153+x2Now, ∠A is an obtuse angle.∴cosA<0⇒14×2-7x4x4+16×2+153+x2<0⇒14×2-7x<0⇒2×2-x<0⇒x2x-1<0⇒x<0 & 2x-1>0 or x>0 & 2x-1<0⇒x<0 & x>12 or x>0 & x<12⇒x>0 & x<12 As there cannot be any number less than zero and greater than 1/2⇒x∈0, 12 …(i)
Let the equation of the z-axis be zk^.And let the angle between b→ and z-axis be B.∴cosB=7i^-2j^+xk^.zk^7i^-2j^+xk^ zk^ =xzz49+4+x2 =x53+x2Now, angle B is acute and less than π/6.∴0<x53+x2<cosπ6⇒0<x<3253+x2 …(ii)From (i) and (ii) we get0<x<12
Q14.
Answer :
(c) 3a
Given thatSo, a→= b→=c→=a …iSince they are mutually perpendicular,a→.b→=b→.c→=c→.a→=0 …iiNow,a→+b→+c→2 =a→2+b→2+c→2+2 a→. b→+2 b→.c→+2 c→.a→ =a2+a2+a2+0+0+0 Using i and ii =3a2∴ a→+b→+c→=3a
Q15.
Answer :
(c) 14
It is given that vectors 3i^+λj^+k^ and 2i^-j^+8k^ are perpendicular. So, their dot product is zero.3i^+λj^+k^. 2i^-j^+8k^=0⇒6-λ+8=0⇒14-λ=0∴ λ=14
Q16.
Answer :
(a) 1
Let a→=i^+j^+k^ and b→= j^The projection of a→ on b→ isa→. b→b→=i^+j^+k^.j^j^=0+1+01=1
Q17.
Answer :
(b) a = 4, b = 4, c = 5
It is given that vectors 2i^+3j^-4k^ and ai^+bj^+ck^ are perpendicular. So, their dot product is zero.⇒2a+3b-4c=0b a=4; b=4; c=5⇒24+34-45=08+12-20=00=0, which is true.
Q18.
Answer :
(c) 0
Given thata→=a→⇒a→+b→.a→-b→=a→2-b→2 =a→2-a→2 =0
Q19.
Answer :
(a) 2 sinθ2
a→. b→=a→ b→ cos θ =1 ×1 cos θ(Because a→ and b→ are unit vectors) =cos θ …ia→-b→2=a→2+b→2-2 a→. b→ =1+1-2 cos θ Using i =2-2 cos θ =2 1-cos θ =2 2 sin2 θ2 =4 sin2 θ2∴ a→-b→=2 sin θ2
Q20.
Answer :
(c) 4
We have3 a →+b →+ a →-b →=3× a →2+b →2+2a →b →cosθ+ a →2+b →2-2a →b →cosθ=3 × 12+12+2×1×1cosθ+ 12+12-2×1×1 cosθ As a →and b →unit vectors=3 × 2+2 cosθ+ 2-2 cosθ=3 × 21+cosθ+ 21- cosθ=3 × 2×2cos2θ2+ 2×2sin2θ2=23 cosθ2+2sin θ2=23 cosθ2+sin θ2=2×232 cosθ2+12sin θ2=2×2sinπ3 cosθ2+ cosπ3sin θ2=4 sinπ3+ θ2Now, maximum value of sinα=1⇒Maximum value of sinπ3+ θ2=1⇒Maximum value of 4sinπ3+ θ2=4∴Maximum value of 3 a →+b →+ a →-b →=4
Q21.
Answer :
(c) R −[−4, 7]
Let θ be the angle between a→ and b→.cos θ=a→. b→a→ b→=x2-3x-28×2+32+49 x2+x2+42For θ to be acute,cos θ>0⇒x2-3x-28>0⇒x-7x+4>0⇒x∈-∞, -4 ∪7, ∞⇒x∈R–4, 7
Q22.
Answer :
(d) 2π3<θ<π
We have a →+b →<1⇒a →2+b →2+2a →×b → cosθ<1⇒12+12+2×1×1× cosθ<1⇒2+2 cosθ<1⇒21+ cosθ<1⇒2×2cos2θ2<1⇒2cosθ2<1⇒cosθ2<12⇒π3<θ2<2π3⇒2π3<θ<4π3But here θ cannot be more than π.∴2π3<θ<π
Page 24.38 (Multiple Choice Questions)
Q23.
Answer :
(d) −1
Given that a→, b→ and c→ are unit vectors.So, a→=1, b→=1and c→=1.Sincea→ and b→ are mutually perpendicular,a→.b→=0Now,a→+b→+c→=1⇒a→+b→+c→2=1⇒a→2+b→2+c→2+2 a→. b→+2 b→.c→+2 c→.a→=1⇒1+1+1+20+2 a→ b→ cos β+2 c→ a→ cos α=1⇒3+2 cos α+cos β=1⇒2 cos α+cos β=-2⇒cos α+cos β=-1
Q24.
Answer :
(b) a →·b → b → b →2
The orthogonal projection of a→ on b→ isa→. b→ b→b→2
Q25.
Answer :
(d) π3
The given vectors are perpendicular. So, their dot product is zero.sin θ i^+ cos θ j^.i^-3 j^=0⇒sin θ-3 cos θ=0⇒sin θ=3 cos θ⇒tan θ=3⇒θ=π3 (Because θ is acute)
Q26.
Answer :
(d) 2π3
We havea→=1 and b→=1Now, a→+b→=1⇒a→2+b→2+2 a→. b→=1⇒1+1+2 a→ b→ cos θ=1⇒2+2 cos θ=1⇒2 cos θ=-1⇒cos θ=-12⇒θ=2π3
Page 25.23 Ex. 25.1
Q1.
Answer :
Given:a→=i^+3j^-2k^ b→=-i^+0j^+3k^∴ a→×b→=i^j^k^13-2-103 =9+0 i^-3-2 j^+0+3 k^ =9 i ^-j^+3k^⇒a→×b→=92+-12+32 =91
Q2.
Answer :
i) Given: a→=3i^+4j^+0k^ b→=i^+j^+k^∴ a→×b→=i^j^k^340111 =4-0 i^ -3-0 j^ +3-4 k^ =4 i^-3j^-k^⇒a→×b→=16+9+1 =26
ii) Given:a→=2i^+0j^+k^ b→=i^+j^+k^a→×b→=i^j^k^201111 =0-1 i^ -2-1 j^ +2-0 k^ =- i^-j^+2k^⇒a→×b→=-12+-12+22 =6
Q3.
Answer :
i) Given: a→=4i^-j^+3k^ b→=-2i^+j^-2k^∴ a→×b→=i^j^k^4-13-21-2 =2-3 i^ – -8+6 j^ +4-2 k^ =- i^+2j^+2k^⇒a→×b→=1+22+22 =9 =3Unit vector perpendicular to a→ and b→ =a→×b→a→×b→=- i^+2j^+2k^3
ii) Given:a→=2i^+j^+k^ b→=i^+2j^+k^∴ a→×b→=i^j^k^211121 =1-2 i^ -2-1 j^ +4-1k⏜ =-i^-j^+3k^⇒a→×b→=1+1+9 =11Unit vector perpendicular to the plane containing vectors a→ and b→=±a→×b→a→×b→Unit vector perpendicular to the plane containing vectors a→ and b→=±111-i^-j^+3k^
Q4.
Answer :
a→=0i^+4j^+3k^×i^+j^-k^ =i^j^k^04311-1 =i^ -4-3-j^ 0-3+k^ 0-4 =-7i^+3j^-4k^⇒a→=-72+32+-42 =74
Q5.
Answer :
Given:a→=4i^+3j^+k^ 2b→=2i^+0j^-4k^2b→×a→=i^j^k^20-4431 =0+12 i^-2+16 j^+6-0k^ =12i^-18j^+6k^⇒2b→×a→=122+-182+62 =504
Q6.
Answer :
Given:a→=3i^-j^-2k^ b→=2i^+3j^+k^∴ a→+2b→=3i^-j^-2k^+2 2i^+3j^+k^ =7i^+5j^+0k^∴ 2a→-b→=2 3i^-j^-2k^- 2i^+3j^+k^ =4i^-5j^-5k^a→+2b→×2a→-b→=i^j^k^7504-5-5 =i^ -25+0-j^ -35+0+k^ -35-20 =-25i^+35j^-55k^
Q7.
Answer :
i) Given:a→=2i^+3j^+6k^ b→=3i^-6j^+2k^a→×b→=i^j^k^2363-62 =6+36 i^ – 4-18 j^ +-12-9 k^ =42i^+14j^-21k^⇒a→×b→=422+142+-212 =2401 =49Required vector =49×a→×b→a→×b→ =49 ×42i^+14j^-21k^49 =42i^+14j^-21k^
ii) Given:a→=3i^+j^-4k^ b→=6i^+5j^-2k^∴a →×b→=i^j^k^31-465-2 = -2+20 i^–6+24 j^ +15-6 k^ =18i^-18j^+9k^⇒a→×b→=182+-182+92 =729 =27Required vector=3×a→×b→a→×b→ =3×18i^-18j^+9k^27 =32i^-2j^+k^3 =2i^-2j^+k^
Q8.
Answer :
i) Let:a=2i^+0j^+0k^ b→=0i^+3j^+0k^∴ a→×b→=i^j^k^200030 =0-0 i^ -0-0 j^ + 6-0 k^ =0 i^+0j^+6k^Area of the parallelogram=a→×b→ =0+0+62 =6 sq. units
ii) Let: a→ =2i^+j^+3k^ b→=i^-j^+0k^∴ a→×b→=i^j^k^2131-10 =0+3 i^ -0-3 j^ +-2-1 k^ = 3i^+3j^-3k^Area of the parallelogram =a→×b→ =32+32+32 =27 =33 sq. units
iii) Let:a→=3i^+j^-2k^b→=1i^-3j^+4k^a→×b→=i^j^k^31-21-34 =i^ 4-6-j^ 12+2+k^ -9-1 =-2i^-14j^-10k^Area of the parallelogram=a→×b→ =-22+-142+-102 =300 =103 sq. units
iv) Let: a→=i^-3j^+k^ b→=i^+j^+k^a→×b→=i^j^k^1-31111 =-3-1 i^ – 1-1 j^+1+3 k^ =-4i^+0j^+4k^Area of the parallelogram=a→×b→ =-42+0+42 =32 =42 sq. units.
Q9.
Answer :
i) Let:a→=4i^-j^-3k^b→=-2i^+j^-2k^∴ a→×b→=i^j^k^4-1-3-21-2 =2+3 i^ –8-6j^ + 4-2k^ =5i^+14j^+2k^⇒a→×b→=25+196+4 =225 =15Area of the parallelogram = 12a→×b→ =152 sq. units.
ii) Let: a→=2i^+0j^+k^ b→=i^+j^+k^a→×b→=i^j^k^201111 =0-1 i^ -2-1 j^ +2-0 k^ =-i^-j^+2k^⇒a→×b→=-12+-12+2 =6Area of the parallelogram = 12a→×b→ =62 sq. units
iii) Let:a→=3i^+4j^+0k^ b→=i^+j^+k^∴ a→×b→=i^j^k^340111 =4-0 i^ -3-0 j^ +3-4 k^ =4i^-3j^-k^⇒a→×b→=42+-32+-12 =26Area of the parallelogram = 12a→×b→ =262sq. units
iv) Let:a→=2i^+3j^+6k^b→=3i^-6j^+2k^∴ a→×b→=i^j^k^2363-62 = 6+36i^-4-18j^ +-12-9k^ =42i^+14j^-21k^⇒a→×b→=422+142+-212 =2401 =49Area of the parallelogram = 12a→×b→ =492 sq. units
Q10.
Answer :
Given: a→=2i^+5j^-7k^ b→=-3i^+4j^+k^ c→=i^-2j^-3k^∴ a→×b→=i^j^k^25-7-341 =5+28 i^ -2-21 j^ +8+15k^ =33i^+19j^+23k^⇒a→×b→×c→=i^j^k^3319231-2-3 = -57+46i^- -99-23 j^+ -66-19 k^⇒a→×b→×c→ =-11i^+122j^-85k^ …(1)∴ b→×c→=i^j^k^-3411-2-3 = -12+2 i^- 9-1 j^+6-4 k^ =-10i^-8j^+2k^⇒ a→×b→×c→=i^j^k^25-7-10-82 =10-56 i^ -4-70 j^ +-16+50 k^ ⇒ a→×b→×c→=-46i^+66j^+34k^ …(2)From (1) and (2), we geta→×b→×c→≠a→×b→×c→
Q11.
Answer :
We know a→.b→2+a→ ×b→2=a→2b→2⇒a→.b→2+82=22×52 (∵ a→ ×b→=8, a→=2 and b→=5)⇒a→.b→2+64=100⇒a→.b→2=36⇒a→.b→=6
Page 25.24 Ex. 25.1
Q12.
Answer :
Given: a→=17 2i^+3j^+6k^ b→=17 3i^-6j^+2k^ c→=176 i^+2j^-3k^a→×b→=17 17i^j^k^2363-62 =14942 i^+14j^-21k^ =1497 6 i^+2j^-3k^ =176 i^+2j^-3k^ =c→b→×c→=17 17i^j^k^3-6262-3 =14914 i^+21j^+42k^ =1497 2i^+3j^+6k^ =17 2i^+3j^+6k^ =a→c→×a→=17 17i^j^k^62-3236 =14921 i^-42j^+14k^ =1497 3i^-6j^+2k^ =17 3i^-6j^+2k^ =b→a→=174+9+36 =77 =1b→=179+36+4 =77 =1c→=1736+4+9 =77 =1Thus, a→, b→ and c→ form a right handed orthogonal system of unit vectors.
Q13.
Answer :
We know a→.b→2+a→ ×b→2=a→2b→2⇒602+a→ ×b→2=132×52 (∵ a→.b→=60, a→=13 and b→ =5)⇒3600+a→ ×b→2=4225⇒a→ ×b→2=625⇒a→ ×b→=25
Q14.
Answer :
Let θ be the angle between a→and b→.Given:a→×b→=a→. b→⇒a→ b→ sin θ=a→ b→ cos θ⇒sin θ=cos θ⇒tan θ = 1⇒θ=π4
Q15.
Answer :
a→×b→=b→×c→⇒a→×b→=-c→×b→⇒a→×b→+c→×b→=0⇒a→+c→×b→=0 (Using right distributive property)Thus, a→+c→ is parallel to b→.⇔a→+c→=mb→, for some scalar m.
Q16.
Answer :
Let θ be the angle between a→ and b→.a→×b→=3i^+2j^+6k^ (Given)⇒a→×b→=9+4+36 =7We know a→×b→=a→ b→ sin θ⇒7=2 7 sin θ⇒sin θ=12⇒θ=π6
Q17.
Answer :
Given:a→×b→=0→⇒a→=0 b→=0 ∴ a→∥b→ Also,a→.b→=0⇒a→ b→ cos θ=0 ⇒a→=0→ or b→=0→ or, a→⊥b→ But a→ cannot be both perpendicular as well as parallel to b→.∴ a→=0 b→=0
Q18.
Answer :
Given:a→×b→=c→b→×c→=a→c→×a→=b → …(1)Now,a→×b→=c→=1 (∵ c→ is a unit vector)b→×c→=a→=1 (∵ a→ is a unit vector)c→×a→=b→=1 (∵ b→ is a unit vector)∴ a→×b→=b→×c→=c→×a→=1 …(2)From (1) and (2), we know a→, b→ and c→ form an orthonormal right handed triad of unit vectors.
Q19.
Answer :
The vector AB→×AC→ is perpendicular to the vectors AB→ and AC→.∴ Required unit vector =AB→×AC→AB→×AC→Now,AB→ =Position vector of B- Position vector of A =i^-j^-3k^-3i^-j^+2k^ =-2i^+0j^-5kAC → =Position vector of C- Position vector of A =4i^-3j^+k^-3i^-j^+2k^ =i^-2j^-k^∴ AB→×AC→=i^j^k^-20-51-2-1 =0-10 i-2+5 j+4-0 k^ =-10i^-7j^+4k^AB→×BC→=-102+-72+42 =165Unit vector perpendicular to the plane ABC =AB→×AC→AB→×AC→=-10i^-7j^+4k^165
Q20.
Answer :
We haveBC→=a→ CA→=b→AB→=c→a→=ab→=b (∵ Length is always positive)c→=c Now, BC→+CA→+AB→=0→ (Given)⇒a→+b→+c→=0→⇒a→×a→+b→+c→=a→×0→⇒a→×a→+a→×b→+a→×c→=0→⇒0→+a→×b→-c→×a→=0→⇒a→×b→=c→×a→⇒a→ b→sin C=c→ a→ sin B⇒ab sin C=ca sin BDividing both sides by abc, we get⇒sin Cc=sin Bb …(1)Again,BC→+CA→+AB→=0→⇒a→+b→+c→=0→⇒b→×a→+b→+c→=b→×0→⇒b→×a→+b→×b→+b→×c→=0→⇒-a→×b→+0→+b→×c→=0→⇒a→×b→=b→×c→⇒a→ b→ sin C=b→ c→ sin A⇒ab sin C=bc sin ADividing both sides by abc, we get⇒sin Cc=sin Aa …(2)From (1) and (2), we getsin Aa=sin Bb=sin Cc⇒asin A=bsin B=csin C
Q21.
Answer :
Given:a→=i⏜-2j⏜+3k⏜ b→=2i⏜+3j⏜-5k⏜
a→×b→=i^j^k^1-2323-5 =i^+11j^+7k^Now, a→. a→×b→=1-22+21 =0Thus, a→ is perpendicular to a→×b→.
Q22.
Answer :
Given: a→=p^+2q⏜ b→= 2p⏜+q^a→×b→=p→+2q→×2p→+q→=2 p→×p→+p→×q→+4q→×p→+2 q→×q→=20+p→×q→-4 p→×q→+2 0=-3p→×q→Area of the parallelogram=12a→×b→ =12-3p→×q→ =32p→ q→ sin 30o =32 1 1 12 (∵ p→ and q→ are unit vectors) =34sq. units
Q23.
Answer :
RHS=a→. a→a→. b→b→. a→b→. b→ =a→2a→ b→ cos θa→ b→ cos θb→2 =a→2 b→2-a→2 b→2 cos2 θ =a→2 b→2 1-cos2 θ =a→2 b→2 sin2 θ =a→b→ sin θ2 =a→×b→2 =LHSHence proved.
Q24.
Answer :
If a→ and b→ are two non-zero non-parallel vectors, then the vector product denoted by a→×b→ is defined as a→×b→=a→ b→ sin θ η^.Here, θ is the angle between a→ and b→ and η^ is the unit vector perpendicular to the plane of a→ and b→ such that a→, b and η^ form a right handed system.LHS=a→×b→ =a→ b→ sin θ =a→ b→ sin θ ×cos θcos θ =a→ b→ cos θ sin θcos θ =a→ b→ cos θ tan θ =a→. b→ tan θ =RHS Hence proved.
Q25.
Answer :
We knowa→.b→2+a→ ×b→2=a→2b→2⇒a→.b→2+352=262×72 (∵ a→×b→=35, a→=26 and b→ =7)⇒a→.b→2+1225=1274⇒a→.b→2=49⇒a→.b→=7
Q26.
Answer :
Given:OA→ =i^+2j^+3k^OB→=-3i^-2j^+k^ OA→×OB→=i^j^k^123-3-21 =8i^-10j^+4k^OA→×OB→=64+100+16 =180 =65Area of the triangle=12OA→×OB→ =12 65 =3 5 sq. units
Q27.
Answer :
Given:a→=i^+4j^+2k^ b→=3i^-2j^+7k^c→=2i^-j^+4k^Since d is perpendicular to both a and b, it is parallel to a→×b→.Suppose d=λa→×b→ for some scalar λ.d=λ i^j^k^1423-27 =λ 28+4i^-7-6 j^+-2-12k^ =λ 32i^- j^-14k^c.→d→=15 (Given)⇒2i^-j^+4k^.λ 32i^- j^-14k^=15⇒λ64+1-56=15⇒λ=53∴ d→=5332i^- j^-14k^⇒d→=13160i^- 5j^-70k^
Disclaimer: The question should contain
“which is perpendicular to both a→ and b→” instead of “which is perpendicular to both a→ and d→”
Q28.
Answer :
Given: a→=3i^+2j^+2k^b→=i^+2j^-2k^∴ a→+b→=4i^+4j^+0k^ a→-b→=2i^+0j^+4k^a→+b→×a→-b→=i^j^k^440204 =16i^-16j^-8k^∴ a→+b→×a→-b→=256+256+64 =576 =24Unit vector perpendicular to both a→+b→ and a→-b→=a→+b→×a→-b→a→+b→×a→-b→=16i^-16j^-8k^24=8 2i^-2j^-k^24=132i^-2j^-k^
Q29.
Answer :
Let a→, b→ and c→ be the position vectors of A, B and C, respectively. Then,a→=2i^+3j^+5k^b→=3i^+5j^+8k^c→=2i^+7j^+8k^Now, AB→=b→-a→ =i^+2j^+3k^AC→=c→-a→ =0i^+4j^+3k^∴ AB→×AC→=i^j^k^123043 =-6i^-3j^+4k^⇒AB→×AC→=36+9+16 =61Area of triangle ABC=12AB→×AC→ =612sq. units
Page 25.25 Ex. 25.1
Q30.
Answer :
Given: a→=i^+4j^+2k^ b→=3i^-2j^+7k^ c→=2i^-j^+4k^Since d is perpendicular to both a and b, it is parallel to a→×b→.Suppose d=λa→×b→ for some scalar λ.d=λ i^j^k^1423-27 =λ 28+4i^-7-6 j^+-2-12k^ =λ 32i^- j^-14k^c.→d→=15 (Given)⇒2i^-j^+4k^.λ 32i^- j^-14k^=15⇒λ64+1-56=15⇒λ=53∴ d→=5332i^- j^-14k^
Q31.
Answer :
Suppose □ ABCD is the given parallelogram and AC is its diagonal.Let:AB→=2i^-4j^+5k^BC→=i^-2j^-3k^∴ Diagonal AC→=AB→+BC→ =3i^-6j^+2k^⇒AC→=9+36+4 =7Unit vector parallel to AC→=AC→AC→ =3i^-6j^+2k^7Now,AB→×BC→=i^j^k^2-451-2-3 =22i^+11j^+0k^⇒AB→×AC→=484+121 =605 =115Area of triangle ABC=12AB→×AC→ =1152sq. units
Q32.
Answer :
If a→=0→ or b→=0, then a→ b→ sin θ n^=0.→⇒a→×b→=0→But the converse is not true as whenever a→×b→=0→, we cannot be sure that either a→=0→ or b→=0→.For example:a→=i^+2j^+3k^b→=i^+2j^+3k^Here,a→≠0b→≠0But a→×b→=i^j^k^123123 =0i^+0j^+0k^ =0→
Q33.
Answer :
Given:a→=a1i^+a2j^+a3k^b→=b1i^+b2j^+b3k^ c→=c1i^+c2j^+c3k^b→+c→=b1+c1 i^+b2+c2 j^+b3+c3 k^∴ a→×b→+c=i^j^k^a1a2a3b1+c1b2+c2b3+c3 =a2b3+a2c3-a3b2-a3c2i^-a1b3+a1c3-a3b1-a3c1j^+ a1b2+a1c2-a2b1-a2c1k^ …(1)Now, a→×b→=i^j^k^a1a2a3b1b2b3 = a2b3-a3b2i^- a1b3-a3b1j^+ a1b2-a2b1k^a→×c→=i^j^k^a1a2a3c1c2c3 =a2c3-a3c2i^ -a1c3-a3c1j^ +a1c2-a2c1k^ a→×b→+b→×c→= a2b3+a2c3-a3b2-a3c2i^-a1b3+a1c3-a3b1-a3c1 j^ + a1b2+a1c2-a2b1-a2c1k^ …(2)From (1) and (2), we geta→×b→+c=a→×b→+b→×c→
Q34.
Answer :
Let a,→ b→ and c→ be the position vector of A, B and C, respectively. ∴ a→=i^+j^+2k^ b→=2i^+3j^+5k^ c→=i^+5j^+5k^ Area of the triangle=12AB→×AC→AB→=b→-a→ = 2i^+3j^+5k^-i^+j^+2k^ =i^+2j^+3k^AC→=c→-a→ =i+5j+5k-i^+j^+2k^ =0i^+4j^+3k^∴ AB→×AC→=i^j^k^123043 =-6 i^-3j^+4k^⇒AB→×AC→=36+9+16 =61
Area of the triangle =12 AB→×AC→ =612sq. units
Page 25.27 (Very Short Answers)
Q1.
Answer :
If a→ and b→ are two non-zero non-parallel vectors, then the vector product denoted by a→×b→ is defined as a→×b→=a→ b→ sin θ η^.Here, θ is the angle between a→ and b→ and η^ is the unit vector perpendicular to the plane of a→ and b→ such that a→, b→ and η^ form a right handed system.
Q2.
Answer :
i^×j^. k^+i^. j^=k^. k^ +0=k^2+0=12+0 (∵ k=1)=1
Q3.
Answer :
i^. j^×k^+j^. k^×i^+k^. j^×i^=i^. i^+j^. j+k^. -k^=i^2+j^2-k^2 =1+1-1 (∵ i^=1, j^=1 and k^=1)=1
Q4.
Answer :
i^. j^×k^+j^. k^×i^+k^. i^×j^=i^. i^+j^. j+k^. k^=i^2+j^2+k^2=1+1+1=3
Q5.
Answer :
i^× j^+k^+j^× k^+i^+k^× i^+j^=i^× j^+i^× k^+j^× k^+j^× i^+k^× i^+k^× j^=k^-j^+i^-k^+j^-i^=0→
Q6.
Answer :
Given: a→ and b→ are diagonals of a parallelogram.Area of the parallelogram = 12 a→×b→
Q7.
Answer :
a→. b→2+a→×b→2=a→ b→ cos θ2+a→ b→ sin θ2=a→2 b→2 cos2 θ+sin2 θ=a→2 b→2 1=a→2 b→2
Q8.
Answer :
Let θ be the angle between a→and b→.It is given that a→×b→ is a unit vector.⇒a→×b→=1We know a→×b→=a→ b→ sin θ⇒1=3 23 sin θ⇒sin θ=12⇒θ=45o, 135o
Q9.
Answer :
We know a→.b→2+a→ ×b→2=a→2b→2⇒a→.b→2+162=102×22 (∵ a→×b→=16, a→=10 and b→=2)⇒a→.b→2+256=400⇒a→.b→2=144⇒a→.b→=±12
Q10.
Answer :
Let: a→=a1i^+a2j^+a3k^b→=b1i^+b2j^+b3k^b→×a→=i^j^k^b1b2b3a1a2a3 =i^ b2a3-b3a2-j^ b1a3-b3a1+k^ b1a2-b2a1Now,a→. b→×a→=a1i^+a2j^+a3k^. i^ b2a3-b3a2-j^ b1a3-b3a1+k^ b1a2-b2a1=a1b2a3-b3a2-a2 b1a3-b3a1+a3 b1a2-b2a1=a1b2a3-a1b3a2-a2b1a3+a2b3a1+a3b1a2-a3b2a1=0
Q11.
Answer :
a→×b→=3⇒a→ b→ sin θ=3 …(1)a→. b→=1⇒a→ b→ cos θ=1 …(2)Dividing (1) by (2), we geta→ b→ sin θa→ b→ cos θ=3⇒tan θ=3⇒θ=60o
Q12.
Answer :
a→×b→+c→+b→×c→+a→+c→×a→+b→=a→×b→+a→×c→+b→×c→+b→×a→+c→×a→+c→×b→=a→×b→+a→×c→+b→×c→-a→×b→-a→×c→-b→×c→=0→
Q13.
Answer :
Let:a→=a1i^+a2j^+a3k^b→=b1i^+b2j^+b3k^a→×b→=i^j^k^a1a2a3b1b2b3=i^ a2b3-a3b2-j^ a1b3-a3b1+k^ a1b2-a2b1a→×b→. b→=i^ a2b3-a3b2-j^ a1b3-a3b1+k^ a1b2-a2b1 . b1i^+b2j^+b3k^=b1 a2b3-a3b2 -b2 a1b3-a3b1+b3 a1b2-a2b1=a2b1b3-a3b1b2-a1b2b3+a3b1b2+a1b2b3-a2b1b3=0
Q14.
Answer :
i^×j^×k^=i^×i^=0→
Q15.
Answer :
Since a→×b→ is a vector, a→×b→ a→ without any dot or cross product in between is meaningless.
Q16.
Answer :
Let a→=i^+j^+0k^; b→=0i^+j^+k^a→×b→=i^j^k^110011 = i^-j^+k^⇒a→×b→=1+1+1 =3Unit vector perpendicular to a→ and b→ is,a→×b→a→×b→=13i^-j^+k^
Q17.
Answer :
We know a→×b→2+a→. b→2=a→2 b→2⇒144=42 b→2⇒144=16 b→2⇒b→2=9⇒b→=3
Q18.
Answer :
Given: r→=xi^+yj^+zk^Now,i→=i^+0j^+0k^r→×i→=i^j^k^xyz100 =0 i^+zj^-yk^⇒r→×i→=z2+y2⇒r→×i→2=z2+y2
Q19.
Answer :
Let θ be the angle between a→ and b→.Given:a→×b→=1a→=1b→=1We knowa→×b→=a→ b→ sin θ⇒1=1 1 sin θ⇒sin θ=1⇒ θ=π2
Q20.
Answer :
Let θ be the angle between a→ and b→.We know a→×b→=a→ b→ sin θa→. b→=a→ b→ cos θNow,a→×b→=a→. b→ (Given)⇒a→ b→ sin θ=a→ b→ cos θ⇒sin θ=cos θ⇒θ=π4
Q21.
Answer :
It is given that a→ and b→ are unit vectors.⇒a→=b→=1 …(1)Now,a→. b→2+a→×b→2=a→ b→ cos θ2+a→ b→ sin θ2=a→2 b→2 cos2 θ+sin2 θ=a→2 b→2 1=a→2 b→2 =12 12 [From (1)]=1
Q22.
Answer :
We know k^×i^=j^ …(1)Given: a→×i^=j^ …(2) Comparing (1) and (2), we geta→=k^Now,a→. i^=k^. i^ =0
Q23.
Answer :
c→ is a unit vector perpendicular to both a→ and b→.⇒c→=a→×b→a→×b→⇒-c→=b→×a→a→×b→Therefore, -c→ is perpendicular to b→ and a.→Thus,-c→ is another unit vector perpendicular to a→ and b.→
Page 25.28 (Very Short Answers)
Q24.
Answer :
Let θ be the angle between a→ and b→.We know a→×b→=a→ b→ sin θ⇒3=1 2 sin θ⇒sin θ=32⇒θ=π3
Q25.
Answer :
Given: a→×b→ is a unit vector.⇒a→×b→=1 …(1)Let θ be the angle between a→and b→.We know a→×b→=a→ b→ sin θFrom (1), we get1=3 23 sin θ ⇒sin θ=32⇒θ=π3
Q26.
Answer :
Given: i^j^k^26141-λ7=0→⇒i^ 42+14λ-0j^+k^ -2λ-6=0i^+0j^+0k^⇒42+14λ=0; -2λ-6=0⇒λ=-3 (This satisfies the above equations)
Q27.
Answer :
Let:a→=2i^b→=3j^a→×b→=6 i^×j^ =6k^Area of the parallelogram=a→×b→=6 k^=61=6 sq. units
Q28.
Answer :
i^×j^. k^+j^+k^. j^=k^. k^ +j^. j^+k^. j^ (∵ i^×j^= k^) =k^2+j^2+0 (∵ k^. j^=0)=12+12=2
Page 25.28 (Multiple Choice Questions)
Q1.
Answer :
(b) 2a→2
Let a→=a1 i^+a2j^+a3 k^a→×i^=i^j^k^a1a2a3100 =a3j^-a2k^ ⇒a→×i^2=a3j^-a2k^ 2 =a32j^2+a22k^2-2 a3a2 j^. k^ =a32+a22 (∵ j^. k^=0) …(1)∴ a→×j^=i^j^k^a1a2a3010 =-a3i^+a1k^⇒a→×j^2=-a3i^+a1k^ 2 =a32i^2+a12k^2-2 a3a2 i^. k^ =a32+a12 (∵ i^. k^=0) …(2) ∴ a→×k^=i^j^k^a1a2a3001 =a2i^-a1j^⇒a→×k2=a2i^-a1j^2 =a22i^2+a12j2+2 a1a2 i^. j^ =a22+a12 (∵ i^. j^=0) …(3)Adding (1), (2) and (3), we geta→×i^2+a→×j^2+a→×k2=a32+a22+a32+a12+a22+a12 =2 a12+a22+a32 =2 a→2 (∵ a→=a12+a22+a32 )
Q2.
Answer :
(a) b →=c →
a →·b →=a →·c →⇒ a→ ·b →-a →·c →=0⇒ a .→b →-c →=0 Let θ be the angle between a→ and b→-c→ a→b →-c →cos θ …(1)
and a →×b →=a →×c→ ⇒ a →×b →-a →×c→ =0⇒a → ×b →-c→ =0Then , a→ b →-c→ sin θ=0 …(2)Here, it is given that a →≠0Therefore, for eq (1) and eq (2) to be 0We have , b →-c→ cos θ=0 For b →-c→ cos θ=0 , one of b →-c→ or cos θ must be 0Case 1:Let cos θ=0⇒θ=90°⇒sin θ=1& if b →-c→ sin θ=0 and sin θ=1 Then b →-c→ =0⇒b →=c→Case 2:Let b →-c→ =0⇒b →=c→Hence, b →=c→
Q3.
Answer :
(a) 32i^+j^
Let:α→=a1i^+a2j^+a3k^β→=b1i^+b2j^+b3k^Now,b→=3i^+4k^=α→+β→ (Given)⇒3i^+0j^+4k^=a1+b1 i^+a2+b2 j^+a3+b3 k^⇒a1+b1=3; a2+b2=0; a3+b3=4⇒a1+b1=3; a2=-b2; a3+b3=4 …(1)a→=i^+j^ (Given) Also, α→ is parallel to a→.⇒α→×a→=0→⇒i^j^k^a1a2a3110=0→⇒-a3i^+a3j^+a1-a2k^=0i^+0j^+0k^⇒a3=0; a1-a2=0⇒ a3=0; a1=a2 …(2)Since β→ is perpendicular to a→, we get⇒β→. a→=0⇒b1i^+b2j^+b3k^. i^+j^=0⇒b1+b2=0⇒b1=-b2 …(3)Solving (1), (2) and (3), we geta1=32; a2=32; a3=0∴ α→=a1i^+a2j^+a3k^ =32i^+32j^+0k^ =32 i^+j^
Q4.
Answer :
(c) 162i^+j^+k^
The vector PQ→×PR→ is perpendicular to the vectors PQ → and PR→.∴ Required unit vector==PQ→×PR→PQ→×PR→Now, PQ→=P.V. of Q-P.V. of P =i^+j^-3k^PR→=P.V. of R-P.V. of P =-i^+3j^-k^∴ PQ→×PR→=i^j^k^11-3-13-1 =8i^+4j^+4k^ =4 2i^+j^+k^⇒PQ→×PR→=64+16+16 =96 =46Required unit vector=PQ→×PR→PQ→×PR→ =4 2i^+j^+k^46 = 162i^+j^+k^
Page 25.29 (Multiple Choice Questions)
Q5.
Answer :
(b) a →·b →=0
We know that the diagonals in a rhombus (a→ and b→) are perpendicular.Therefore, their dot product is zero.⇒a→. b→=0
Q6.
Answer :
(a) 300
a→+3b→×3a→-b→=3 a→×a→-a→×b→+9 b→×a→-3 b→×b→=3 0-a→×b→-9 a→×b→-3 0=-10 a→×b→Now,a→×3b→×3a→-b→ 2=-10 a→×b→2=100 a→×b→2=100 a→2 b→2 sin2120=100 12 22 322=400 ×34=300
Q7.
Answer :
(a) i^
a→+b→=0i^+3j^+k^b→-c→=0i^-0j^+3k^a→+b→×b→-c→=i^j^k^031003 =9i^a→+b→×b→-c→=9 i^ =91 =9Unit vector perpendicular to both a→+b→ and b→-c→=a→+b→×b→-c→a→+b→×b→-c→=9i^9=i^
Q8.
Answer :
(d) 13i^-j^+k^
Let:a→=i^+j^+0k^ b→=0i^+j^+k^∴ a→×b→=i^j^k^110011 = i^-j^+k^⇒a→×b→=1+1+1 =3Unit vector perpendicular to a→ and b→=a→×b→a→×b→=i^-j^+k^3
Q9.
Answer :
(b) 10i^+3j^+11k^
a→×b→=i^j^k^2-3-114-2 =10 i ^+3j^+11k^
Q10.
Answer :
(b) i^·i^=1
Let us check each option one by one.(a) We knowi^. j^=0 ≠1(b) We knowi^. i^=i^2 =12 =1(c) i^×j^ =k^ ≠1(d) i^ ×j^×k^= i^ ×i^ =0 ≠1
Q11.
Answer :
(b) 27
Let:a→=2i^-2j^+4k^b→=3i^+j^+2k^a→=22+-22+42 =4+4+16 =24 =26 b→=32+12+22 =9+1+4 =14a→×b→=i^j^k^2-24312 =-8i^+8j^+8k^a→×b→=64+64+64 =192 =8 3Let θ be the angle between a→ and b.→a→×b→=a→ b→ sin θ⇒ 8 3=2614 sin θ⇒ sin θ= 8 3421 =27⇒θ=sin-127
Q12.
Answer :
(c) 20
We know a→. b→2+a→×b→2=a→2 b→2 …(1)a→. b→=2 (Given)⇒a→. b→2=a→. b→2From (1), we get22+42=a→2 b→2 ⇒a→2 b→2 =20
Q13.
Answer :
(b) a →2 b →2- a →·b →2
a→. b→2+a→×b→2=a→ b→ cos θ2+a→ b→ sin θ2=a→2 b→2 cos2 θ+sin2 θ=a→2 b→2 1=a→2 b→2 ∴ a→×b→2=a→2 b→2 -a→. b→2Thus, the value of a→×b→2 is a→2 b→2 -a→. b→2.
Q14.
Answer :
(c) 1
i^. j^×k^+j^. i^×k^+k^. i^×j^=i^. i^+j^. -j^+k^. k^=i^2-j^2+k^2=1-1+1=1
Q15.
Answer :
(b) π/4
Let θ be the angle between a→and b→.We know a→×b→=a→ b→ sin θa→. b→=a→ b→ cos θ⇒a→. b→=a→ b→ cos θ=a’→ b→ cos θGiven: a→. b→=a→×b→⇒a→ b→ cos θ=a→ b→ sin θ⇒cos θ=sin θ⇒θ=π4
Page 26.16 Ex. 26.1
Q1.
Answer :
i) We havei^ j^ k^+ j^ k^ i^+ k^ i^ j^= i^ j^ k^+ i^ j^ k^+ i^ j^ k^ ∵ a→ b→ c→=b→ c→ a→=c→ a→ b→=3 i^ j^ k^=3i^×j^. k^ ∵ a→ b→ c→=a→× b→.c→=3 k^. k^=31=3
ii) We have2i^ j^ k^+ i^ k^ j^+ k^ j^ 2i^=2 i^ j^ k^+ i^ k^ j^+2 k^ j^ i^ ∵ la→ mb→ nc→=lmn a→ b→ c→=2i^×j^. k^ +i^× k^. j^+2k^ × j^. i^ ∵ a→ b→ c→=a→× b→.c→=2 k^. k^+- j^. j^+2-i^.i^=21+-1+2-1=2-1-2=-1
Q2.
Answer :
i) Given: a →=2i^-3j^b →=i^+j^-k^ c →=3i^-k^∴ a →×b →=2i^-3j^×i^+j^-k^ =2k^+2j^+3k^+3i^ =3i^+2j^+5k^a→× b→. c→=3i^+2j^+5k^.3i^-k^ =9-5=4 …1Now,a→ b→ c→=a→× b→. c→ =4 Using 1
ii) Given:a →=i^-2j^+3k^b →=2i^+j^-k^ c →=j^+k^∴ a →×b →=i^-2j^+3k^×2i^+j^-k^ =k^+j^+4k^+2i^+6j^-3i^ =-i^+7j^+5k^a→× b→. c→=-i^+7j^+5k^.j^+k^ =7+5=12 …1Now,a→ b→ c→=a→× b→. c→ =12 Using 1
Q3.
Answer :
i) Given:a→=2i^+3j^+4k^b→=i^+2j^-k^ c→=3i^-j^+2k^We know that the volume of a parallelopiped whose three adjacent edges are a→, b→, c→ is equal to a→ b→c→. Here,a→ b→c→ = 2 341 2-13-12 = 2 4-1-32+3+4-1-6 = -37Volume of the parallelopiped = a→ b→c→ = -37 = 37 cubic units
ii) Given:a→=2i^-3j^+4k^b→=i^+2j^-k^ c→=3i^-j^-2k^We know that the volume of a parallelopiped whose three adjacent edges are a→, b→, c→ is equal to a→ b→c→. Here,a→ b→c→=2 -341 2-13-1-2 = 2 -4-1+3-2+3+4-1-6=-35Volume of the parallelopiped = a→ b→c→=-35 = 35 cubic units
iii) Given:a→=11i^b→=2j^ c→=13k^We know that the volume of a parallelopiped whose three adjacent edges are a→, b→, c→ is equal to a→ b→c→. Here,a→ b→c→ = 11 000 200013 = 11 26-0-00-0+00-0 = 286Volume of the parallelopiped = a→ b→c→ = 286 = 286 cubic units
iv) Given:a→=i^+j^+k^b→=i^-j^+k c→=i^+2j-k^We know that the volume of a parallelopiped whose three adjacent edges are a→, b→, c→ is equal to a→ b→c→. Here,a→ b→c→ = 1 111 -1112-1 = 11-2-1-1-1+12+1=4Volume of the parallelopiped = a→ b→c→ = 4 = 4 cubic units
Q4.
Answer :
i) Given: a→=i^+2j^-k^ b→=3i^+2j^+7k^ c→=5i^+6j^+5k^We know that three vectors a→, b→, c→ are coplanar iff their scalar triple product is zero, i.e. a→ b→ c→ = 0Here, a→ b→ c→=12-1327565=1 10-42-215-35-118-10=0Hence, the given vectors are coplanar.
ii) Given: a→=-4i^-6j^-2k^ b→=-i^+4j^+3k^c→=-8i^-j^+3k^We know that three vectors a→, b→, c→ are coplanar iff their scalar triple product is zero, i.e. a→ b→ c→=0.Here, a→ b→ c→ =-4-6-2-143-8-13 =-412+3+6-3+24-21+32=0Hence, the given vectors are coplanar.
iii) Given:a→= i^-2j^+3k^ b→=-2i^+3j^-4k^ c→=i^-3j^+5k^We know that three vectors a→, b→, c→ are coplanar iff their scalar triple product is zero, i.e. a→ b→ c→=0.Here, a→ b→ c→ =1-23-23-41-35=115-12+2-10+4+36-3=0Hence, the given vectors are coplanar.
Q5.
Answer :
i) Given: a→=i^-j^+k^ b→=2i^+j^-k^ c→=λi^-j+λk^We know that vectors a→, b→, c→ are coplanar iff a→ b→ c→=0.It is given that a→, b→, c→ are coplanar.∴ a→ b→ c→ =0⇒1-1121-1λ-1λ =0 ⇒1 λ-1+12λ+λ+1-2-λ = 0⇒λ-1+3λ-2-λ=0⇒3λ – 3 = 0 ⇒λ = 1
ii) Given: a→=2i^-j^+k^ b→=i^+2j^-3k^ c→=λi^+λj+5k^We know that vectors a→, b→, c→ are coplanar iff a→ b→ c→=0.It is given that a→, b→, c→ are coplanar.∴ a→ b→ c→=0⇒2-1112-3λλ5 = 0 ⇒210+3λ+15+3λ+1λ-2λ= 0 ⇒8λ + 25 =0 ⇒λ = -258
iii) Given:a→=i^+2j^-3k^ b→=3i^+λj^+k^ c→=i^+2j^+2k^We know that vectors a→, b→, c→ are coplanar iff a→ b→ c→=0.It is given that a→, b→, c→ are coplanar.∴ a→ b→ c→ = 0⇒ 12-33λ1122=0 ⇒12λ-2-26-1-36-λ= 0⇒5λ-30= 0 ⇒λ = 6
iv) Given: a→=i^+3j^ b→=5k^ c→=λi^-j^We know that vectors a→, b→, c→ are coplanar iff a→ b→ c→ = 0.It is given that a→, b→, c→ are coplanar.∴ a→ b→ c→=0⇒130005λ-10 = 0 ⇒10+5-30-5λ+00-0= 0⇒5 + 15λ = 0 ⇒λ = -13
Page 26.17 Ex. 26.1
Q6.
Answer :
Let A, B, C and D be the given points. These points will be coplanar iff any one of the following triads of vectors are coplanar:AB→, AC→, AD→; AB→, BC→, CD→; BC→, BA→, BD,→ etc.To show that AB→, AC→, AD→ are not coplanar, we have to prove that their scaler triple product,i.e. AB→ AC→ AD→ ≠0Now, PQ→= Position vector of Q – Position vector of PAB→ =16i^-19j^-4k^- 6i^ -7j^ = 10i^ -12j^-4k^AC→ =3j^-6k^- 6i^ -7j^ = -6i^ +10 j^-6k^AD→ = 2i^ +5j^+10k^- 6i^ -7j^ =-4i^+12j^+10k^∴ AB→ AC→ AD→ = 10-12-4-610-6-41210=10100+72+12-60-24-4-72+40 = 840 ≠ 0Thus, the given points are not coplanar.
Q7.
Answer :
The points A, B, C and D will be coplanar iff any one of the following triads of vectors are coplanar: AB→, AC→, AD→; AB→, BC→, CD→; BC→, BA→, BD,→ etc.To show that AB→, AC→, AD→ are coplanar, we have to prove that their scaler triple product,i.e. AB→ AC→ AD→ = 0Now,AB→ =3–1 i^ +2-4j^ + -5–3 k^ =4i ^-2 j^ -2 k^ AC→ =-3–1 i^ + 8-4 j^ + -5–3k^ = -2i^ +4 j^ -2 k^ AD→ = -3–1 i^ + 2-4 j^ + 1–3 k^ = -2 i^-2 j^ + 4 k^∴ AB→ AC→ AD→ = 4-2-2-24-2-2-24= 416-4+2-8-4-24+8 = 0Thus, the given points are coplanar.
Q8.
Answer :
DISCLAIMER: Given points are not coplanar.
Let A, B, C, D be the given points. The given points will be coplanar iff any one ofthe following triads of vectors are coplanar: AB→, AC→, AD→ ; AB→, BC→, CD→ ; BC→, BA→, BD→ etc.In order to show that AB→, AC→, AD→ are coplanar, we will have to show that their scaler tripleproduct i.e. AB→ AC→ AD→ = 0Using, PQ→ =Position vector of Q – Position vector of P, we obtainNow, AB→ =16i^-19j^-4k^-6i^ -7j^ = 10i^-12j^-4k^ AC→= 3i^-6k^-6i^ -7j^ =-3i^+7j^-6k^and, AD→ =2i^-5j^+10k^-6i^ -7j^ = -4i^+2j^+10k^∴ AB→ AC→ AD→ = 10-12-4-37-6-4210= 1070+12+12-30-24-4-6+28 = 84Thus, the given points are not coplanar.
Q9.
Answer :
DISCLAIMER: Given points are not coplanar.
Let A, B, C, D be the given points. The given points will be coplanar iff any one ofthe following triads of vectors are coplanar: AB→, AC→, AD→ ; AB→, BC→, CD→ ; BC→, BA→, BD→ etc.In order to show that AB→, AC→, AD→ are coplanar, we will have to show that their scaler tripleproduct i.e. AB→ AC→ AD→ = 0Using, PQ→ =Position vector of Q – Position vector of P, we obtainNow, AB→ =16i^-19j^-4k^-6i^ -7j^ = 10i^-12j^-4k^ AC→= 3i^-6k^-6i^ -7j^ =-3i^+7j^-6k^and, AD→ =2i^-5j^+10k^-6i^ -7j^ = -4i^+2j^+10k^∴ AB→ AC→ AD→ = 10-12-4-37-6-4210= 1070+12+12-30-24-4-6+28 = 84Thus, the given points are not coplanar.
Q10.
Answer :
We have (a→-b→).(b→-c→) × (c→-a→) =(a→-b→) . ( b→×c→-b→×a→-c→×c→+c→×a→) (By distributive law) = ( a→-b→ ) . ( b¯×c→-b→×a→+c→×a→ ) (∵ c→×c→=0)=( a→-b→ ) . ( b¯×c→+a→×b→+c→×a→ ) = a→.(b→×c→) +a→.(a⇀×b→) +a→.(c→×a→) – b→.(b→×c→) -b→.(a→×b→) – b→.(c→×a→) (By distributive law)=a→b→c→ +a→a→b→ +a→c→a→ -b→b→c→ -b→ a→ b→ -b→c→a→= a→b→c→ +0+0-0-0-a→b→c→ ∵ a→b→c→=b→c→a→ = 0
Q11.
Answer :
We know that if any vector is perpendicular to all three sides of ∆ABC, it must be perpendicular to the plane of ∆ABC.Now,AB→ = b→-a→ , BC→ = c→-b→ , CA→ = a→-c→ Position vectors of A, B and C are a→, b→, c→ We have AB→.( a→×b→ + b→×c→ + c→×a→ )= b→-a→.a→×b→ + b→×c→ + c→×a→ = b→. a→×b→+b→.b→×c→+b→.c→×a→-a→.a→×b→-a→. b→×c→-a→. c→×a→ By distributive law= b→ a→ b→+b→ b→ c→ +b→ c→ a→-a→ a→b→-a→ b→ c→-a→ c→ a→= 0 + 0 + b→ c→ a→ – 0 -a→b→c→ – 0= 0 ∵ b→ c→ a→=a→b→c→ BC→.( a→×b→ + b→×c→ + c→×a→ )= c→-b→.a→×b→ + b→×c→ + c→×a→ = c→. a→×b→+c→.b→×c→+c→.c→×a→-b→.a→×b→-b→. b→×c→-b→. c→×a→ By distributive law= c→ a→ b→+c→ b→ c→ +c→ c→ a→-b→ a→ b→-b→b→c→-b→c→ a→= c→ a→ b→ + 0 + 0 – 0 -0 – b→c→ a→= 0 ∵ c→ a→ b→=b→c→a→ Similarly, CA→.( a→×b→ + b→×c→ + c→×a→ )=a→-c→.a→×b→ + b→×c→ + c→×a→ = a→. a→×b→+a→.b→×c→+a→c→×a→-c→.a→×b→-c→. b→×c→-c→. c→×a→ By distributive law= a→ a→ b→+a→ b→ c→ +a→ c→ a→-c→ a→b→-c→b→c→-c→ c→ a→= 0 + a→ b→ c→ + 0 -c→ a→b→ -0 – 0= 0 ∵ c→ a→ b→=a→b→c→ Hence, vector a→×b→ + b→×c→ + c→×a→ is perpendicular to all sides of ∆ABC and also perpendicular to the plane of ∆ABC.
Q12.
Answer :
i) If c1=1 and c2=2, then a→=i^+j^+k^, b→=i^ and c^=i^+2j^+c3k^.We know that vectors a→, b→, c→ are coplanar iff a→ b→ c=0.It is given that a→, b→, c→ are coplanar.∴ a→ b→ c = 0⇒ 11110012c3=0 ⇒10-0-1c3-o+12-0=0⇒-c3 + 2=0⇒c3=2
ii) If c2=-1 and c3=1, then a→=i^+j^+k^, b→=i^ and c^=c1i^-j^+k.^We know that vectors a→, b→, c→ are coplanar iff a→ b→ c=0.For a→, b→, c→ to be coplanar:⇒a→ b→ c = 0⇒111100c1-11=0 ⇒10-0-11-0+1-1-0=0⇒-1-1=0⇒-2=0But this is never possible, whatever be the value of c1. Thus, no vaue of c1 can make a→, b→ and c→ coplanar.
Q13.
Answer :
The points A, B, C and D will be coplanar iff any one of the following traces of vectors are coplanar:AB→, AC→, AD→; AB→, BC→, CD→; BC→, BA→, BD→, etc.It is given that AB→, AC→, AD→ are coplanar.Thus, their scaler triple product AB→ AC→ AD→ is equal to zero.Now,Direction ratios of the PQ→=Direction ratios of vector Q-Direction ratios of the vector PDirection ratios of vector AB→ = 4-3, λ-2, 5-1, i.e. 1, λ-2, 4Direction ratios of vector AC→ = 4-3, 2-2, -2-1, i.e. 1, 0, -3Direction ratios of vector AD→ = 6-3, 5-2,-1-1, i.e. 3, 3, -2∴ AB→ AC→ AD→=1λ-2410-333-2=10–9-λ-2-2–9+43-0=0 ⇒7λ=35⇒λ=5
Page 26.17 (Very Short Answers)
Q1.
Answer :
We have2i^ 3j^ 4k^=2i^×3j^·4k^ ∵ a→ b→ c→=a→×b→.c→=6k^·4k^ =24
Q2.
Answer :
We havei^+j^ j^+k^ k^ +i^=i^+j^× j^+k^· k^ +i^ ∵ a→ b→ c→=a→×b→.c→ =i^×j^+i^×k^+j^×j^+j^×k^· k^ +i^ =k^ -j^+i^· k^ +i^ =k^·k^+k^·i^-j^·k^-j^·i^+i^·k^+i^·i^ =1+0-0-0+0+1=2
Q3.
Answer :
We havei^-j^ j^-k^ k^-i^=i^-j^× j^-k^· k^-i^ ∵ a→ b→ c→=a→×b→.c→ =i^×j^-i^×k^-j^×j^+j^×k^· k^-i^ =k^+j^+i^· k^-i^ =k^·k^-k^·i^+j^·k^-j^·i^+i^·k^-i^·i^ =1-0+0-0+0-1=0
Q4.
Answer :
Given:α →=i^+2j^+k^β →=ai^+j^+2k^ γ →=i^+2j^+ak^
We know that three vectors α→, β→, γ→ are coplanar iff their scalar product is zero.∴ α→ β→ γ→=0⇒121a1212a=0⇒1a-4-2a2-2+12a-1=0⇒ -2a2+3a-1=0⇒ 2a2-3a+1=0⇒a-12a-1=0⇒a=1, 12
Q5.
Answer :
Let:a→=i^+j^b→=i^+2j^ c→=i^+j^+πk^We know that the volume of a parallelopiped whose three adjecent edges are a→, b→ and c→ is equal to a→ b→ c→.We havea→ b→ c→=11012011π=12π-0-1π-0+01-2=2π-π=π ∴ Volume=a→ b→ c→=π=π cubic units
Page 26.18 (Very Short Answers)
Q6.
Answer :
For any vector r→, we have r→·i^i^+r→·j^j^+r→·k^k^ =r→Replacing r→ by a→×b→, we have a→×b→·i^ i^+ a→×b→·j^ j^+a→×b→·k^ k^=a→×b→ ∴ a→ b→ i^ i^+a→ b→ j^ j^+a→ b→ k^ k^= a→×b→
Q7.
Answer :
Let: a→=sec2Ai^+j^+k^, b→=i^+sec2Bj^+k^ and c→=i^+j^+sec2 Ck^We know that three vectors are coplanar iff their scaler triple product is zero. i.e., a→ b→ c→=0Here, a→ b→ c→=0⇒sec2A111sec2B111sec2 C=0 ⇒sec2Asec2B×sec2 C-1-1sec2 C-1+11-sec2B=0⇒sec2A sec2B sec2C-sec2A-sec2C+1+1-sec2B=0⇒1+tan2A 1+tan2B 1+tan2C-1+tan2A-1+tan2C+1+1-1+tan2B=0
⇒1+tan2A+tan2B+tan2C+tan2A tan2B+tan2B tan2C+tan2C tan2A+tan2A tan2B tan2C-1-tan2A-1-tan2C+1+1-1-tan2B=0⇒tan2A tan2B+tan2B tan2C+tan2C tan2A+tan2A tan2B tan2C=0⇒tan2A tan2B+tan2B tan2C+tan2C tan2A=-tan2A tan2B tan2C⇒tan2A tan2B+tan2B tan2C+tan2C tan2Atan2A tan2B tan2C=-1⇒cot2C+cot2A+cot2B=-1⇒cosec2C-1+cosec2A-1+cosec2B-1=-1∴ cosec2A+cosec2B+cosec2C=2
Q8.
Answer :
We have a→ b→ a→×b→ +a→.b→2= a→×b→.a→×b→ + a→.b→2 By definition of scalar triple product= a→×b→2 + a→.b→2 = a→b→ sinθ 2+a→b→cosθ2= a→b→2sin2θ + a→b→2cos2θ= a→b→2sin2θ +cos2θ= a→b→2 ∵ sin2θ +cos2θ=1 = 3×42 Given: a→=3 and b→=4= 144
Q9.
Answer :
We have3a→+7b→ c→ d→=λ a→ c→ d→+μb→ c→ d→⇒3a→+7b→×c→.d→=λ a→ c→ d→+μb→ c→ d→ By definition of scalar triple product⇒3a→×c→+7b→×c→ .d→=λ a→ c→ d→+μb→ c→ d→ ⇒3a→×c→.d→+7b→×c→.d→=λ a→ c→ d→+μb→ c→ d→ ⇒3a→ c→ d→+ 7b→ c→ d→=λ a→ c→ d→+μb→ c→ d→⇒3 a→ c→ d→+7 b→ c→ d→=λ a→ c→ d→+μb→ c→ d→ ∵ λa→ b→ c→=λa→ b→ c→ for any scalar λComparing both sides, we getλ=3 μ=7∴ λ+ μ=3+7=10
Q10.
Answer :
We have a→.b→×c→c→×a→.b→ +b→.a→×c→c→.a→×b→ =a→ b→ c→c→a→b→ + b→ a→ c→c→ a→ b→ By definition of scalar triple product=a→ b→ c→a→ b→ c→ +-a→ b→ c→a→ b→ c→ Change of cyclic order of vectors changes the sign of the scalar triple product=1-1 =0
Page 26.18 (Multiple Choice Questions)
Q1.
Answer :
(a) a →b →c →=0
If a→ lies in the plane of vectors b→ and c→, then a→, b→, c→ will lie in the same plane, i.e. they will be coplanar.∴ a →b →c→=0
Q2.
Answer :
(a) 0
We have a→-b→, b→-c→, c→-a→=a→-b→×b→-c→.c→-a→ By definition of scalar triple product=a→-b→×b→-a→-b→×c→.c→-a→ =a→×b→-b→×b→-a→×c→+b→×c→.c→-a→ =a→×b→-0-a→×c→+b→×c→.c→-a→ =a→×b→.c→-a→ -a→×c→.c→-a→ +b→×c→.c→-a→ =a→×b→.c→-a→×b→.a→ -a→×c→.c→+a→×c→.a→+b→×c→.c→-b→×c→.a→=a→b→c→-a→b→a→-a→c→c→+a→c→a→+b→c→c→-b→c→a→=a→b→c→-0-0+0+0-a→b→c→ ∵ a→b→c→=b→c→a→=c→a→b→=0
Q3.
Answer :
a±1We have a→b→c→=a→×b→.c→=a→×b→c→cos0° or a→×b→c→cos180° ∵ a→, b, →c→ are perpendicular to each other=a→×b→ or – a→×b→ ∵ c→=1, cos0°=1 and cos180°=-1 =a→b→sin90° or -a→b→sin90° ∵ a→ is perpendicular to b→=1 or -1 ∵ a→=1 and b→=1=± 1
Q4.
Answer :
(c) 0
If r→.a→=0 for some non-zero vector r→, then either a→ is a zero-vector or it is perpendicular to r→. If one of a→, b→, c¯ is zero, then a→b→c→=0 If all a→, b→ and c→ are non-zero, then they must be coplanar as they are perpendicular to vector r→.∴ a→b→c→=0
Q5.
Answer :
(d) none of these
We have a→-b→.b→-c→×c→-a→=a→-b→.b→-c→×c-b→-c→×a→ =a→-b→.b→×c→-c→×c→-b→×a→+c→×a→ =a→-b→.b→×c→-0-b→×a→+c→×a→ =a→-b→.b→×c→-a→-b→.b→×a→+a→-b→.c→×a→ =a→.b→×c→-b.→b→×c→-a→.b→×a→+b→.b→×a→+a→.c→×a→-b→.c→×a→=a→b→c→-0-0+0+0-b→c→a→ ∵ b→b→c→=a→b→a→=b→ b→a→=0=a→b→c→-a→b→c→ ∵ a→b→c→=b→c→a→=c→ a→b→=0
Page 26.19 (Multiple Choice Questions)
Q6.
Answer :
(a) 0
We havea→.b→×c→c→×a→.b→ +b→.a→×c→c→.a→×b→ =a→b→c→c→a→b→ + b→a→c→c→a→b→ By definition of scalar tiple product=a→b→c→a→b→c→ +-a→b→c→a→b→c→ Change in cyclic order of vectors changes the sign of the scalar triple product=1-1 =0
Q7.
Answer :
(c) 14 a →2 b →2
We have a1a2a3b1b2b3c1c2c32=a→×b→.c→2 By definition of scalar triple product= a→×b→c→cos0°2 ∵ a→×b→ is parallel to vector c→ as c→ is perpendicular to both a→ and b→= a→b→sinπ62 ∵ c→=1 and angle between a→ and b→ is π6= a→2b→2122 = 14 a→2b→2
Q8.
Answer :
We havea→ + b→ = 2i^ – 3j^ + 5k^ + 3i^ – 4j^ + 5k^ = 5i^ – 7j^ + 10k^b→ + c→ = 3i^ – 4j^ + 5k^ + 5i^ – 3j^ – 2k^ = 8i^ – 7j^ + 3k^ c→ + a→ = 5i^ – 3j^ – 2k^ + 2i^ – 3j^ + 5k^ = 7i^ -6j^ + 3k^We know that the volume of a parallelopiped whose three adjacent adges are a→ + b→, b→ + c→ and c→ + a→ is equal to a→ + b→ b→ + c→ c→ + a→.We havea→ + b→ b→ + c→ c→ + a→ = 5-7108-737-63 =5-21 + 18 + 724 – 21 + 10-48 + 49 =5 × -3 + 7 × 3 + 10 × 1 =16∴ Volume of parallelopiped =16=16
Q9.
Answer :
(a) 6
We have2a→+4b→ c→ d→=λ a→ c→ d→ + μb→ c→ d→⇒2a→+4b→×c→.d→=λ a→ c→ d→ + μb→ c→ d→ By definition of scalar triple product⇒2a→×c→+4b→×c→ .d→=λ a→ c→ d→ + μb→ c→ d→⇒2a→×c→.d→ + 4b→×c→.d→=λ a→ c→ d→ + μb→ c→ d→⇒2a→ c→ d→ + 4b→ c→ d→=λ a→ c→ d→ + μb→ c→ d→⇒2 a→ c→ d→ +4 b→ c→ d→=λ a→ c→ d→ + μb→ c→ d→ ∵ λa→ b→ c→=λa→ b→ c→ for any scalar λComparing both sides, we getλ=2 μ=4∴ λ+μ =2+4=6
Q10.
Answer :
a a→2b→2We havea→ b→ a→×b→ + a→.b→2=a→×b→ . a→×b→ + a→.b→2=a→×b→2+ a→.b→2= a→b→ sin θ2 + a→ b→ cos θ2=a→2b→2 sin2θ + a→2b→2 cos2θ=a→2b→2sin2θ + cos2θ =a→2b→2
Q11.
Answer :
d 10Let:a→ = 4i^ + 11j^ + mk^ b→ = 7i^ + 2j^ +6k^ c→ = i^ + 5j^ + 4k^We know that vectors a→, b →and c→ are coplanar iff their scalar triple product is zero, i.e. a→ b→ c→=0⇒ 411m726154 = 0 ⇒ 48-30 – 1128-6 + m35-2=0⇒ -88 – 242 + 33m=0⇒ 33m=330 ∴ m=10
Q12.
Answer :
c a→.b→= b→.c→= c→.a→=0We havea→ × b→.c→ = a→ × b→ c→ cosθ= a→ × b→ c→ If θ=0° or 180°, i.e. vectors a→ × b→ and c→ are parallel= a→b→ sin αc→= a→b→c→ If α=90°, i.e. vectors a→ and b→ are perpendicular∴ a→ × b→.c→ = a→b→c→ If vectors a→, b→, c→ are perpendicular to each otherThus, the relation a→ × b→.c→=a→b→c→ holds good if a→.b→= 0 , b→.c→=0 and c→.a→=0.
Q13.
Answer :
d a→ b→ c→ We havea→ + b→.b→ + c→×a→ + b→ +c→= a→ + b→.b→+ c→×a→ +b→ + c→×b→ +b→ + c→×c→= a→ + b→.b→ × a→+c→×a→ + b→×b→ + c→×b→ + b→×c→ + c→×c→= a→ + b→.b→ × a→+ c→×a→ + 0 + c→×b→ + b→×c→ +0 = a→ + b→.b→ × a→+ c→×a→ – b→×c→ + b→×c→ = a→ + b→.b→ × a→+ c→×a→ = a→.b→×a→ + b→.b→×a→ + a→.c→×a→ + b→.c→×a→ = 0 + 0 + 0 + b→ c→ a→ = b→ c→ a→ = a→ b→ c→
Q14.
Answer :
d -a→ b→ c→We havea→+ b→+ c→ . a→+ b→ × a→+ c→=a→+ b→+ c→ . a→+ b→×a→ + a→+ b→×c→ By definition of cross poduct=a→+ b→+ c→ . a→×a→ + b→×a→ + a→×c→ + b→×c→ =a→+ b→+ c→ . 0 + b→×a→ + a→×c→ + b→×c→= a→.b→×a→ + a→.a→×c→ + a→.b→×c→ + b→.b→×a→ +b→.a→×c→ + b→.b→×c→+ c→.b→×a→ + c→.a→×c→ + c→.b→×c→ =a→ b→ a→ + a→ a→ c→ + a→ b→ c→ + b→ b→ a→ + b→ a→ c→ + b→ b→ c→ + c→ b→ a→ + c→ a→ c→ + c→ b→ c→=0 + 0 + a→ b→ c→ + 0 + b→ a→ c→ + 0 + c→ b→ a→ +0 + 0=a→ b→ c→-a→ b→ c→ – a→ b→ c→ ∵ b→ a→ c→ = -c→ a→ b→, b→ a→ c→ =-a→ b→ c→ =-a→ b→ c→
Q15.
Answer :
c 3 a→ b→ c→We havea→ + 2b→ – c→.a→ – b→×a→- b→- c→=a→ + 2b→ – c→.a→ – b→×a→ – a→ – b→×b→ – a→ – b→×c→=a→ + 2b→ – c→.a→×a→ – b→×a→ – a→×b→ + b→× b→- a→ ×c→ + b→×c→=a→ + 2b→ – c→.0 – b→×a→ – a→×b→ + 0 – a→ ×c→ +b→×c→=a→ + 2b→ – c→.- a→ ×c→ + b→×c→ (∵ a→×b→=- b→×a→)=- a→.a→ ×c→ + a→. b→×c→ – 2b→.a→ ×c→ + 2b→.b→×c→ + c→.a→ ×c→ – c→.b→×c→=0 + a→ b→ c→ -2 b→ a→ c→ + 0 + 0 -0 (∵ λa→ b→ c→=λa→ b→ c→ for any scalar λ) =3 a→ b→ c→ (∵ – b→ a→ c→=a→ b→ c→)
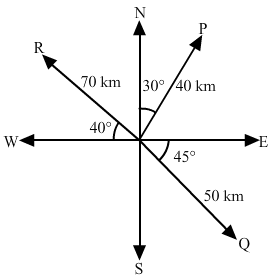
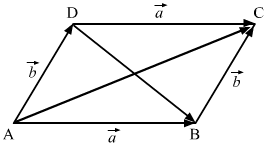
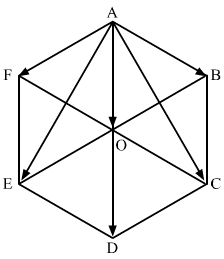
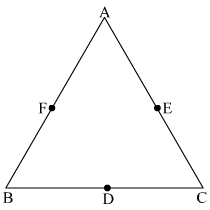
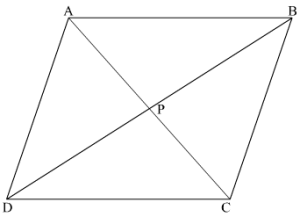
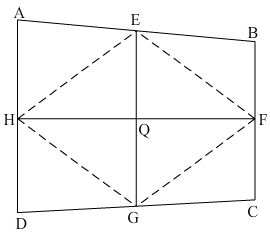
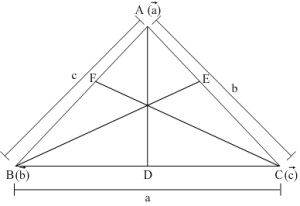
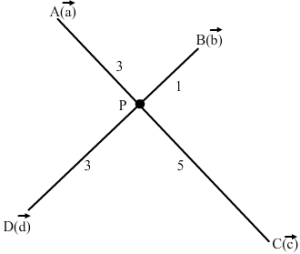
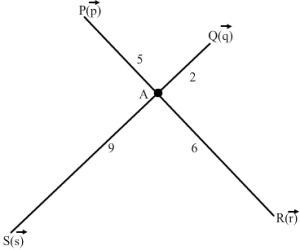
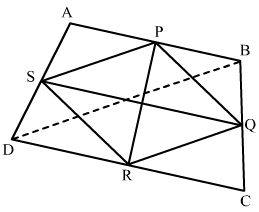
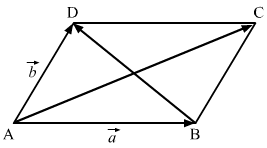
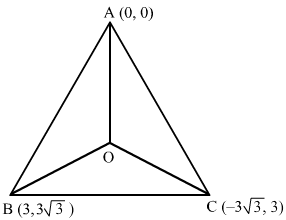
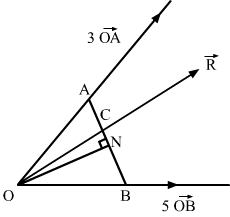
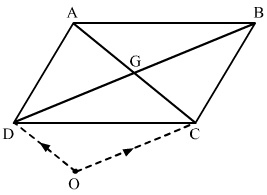
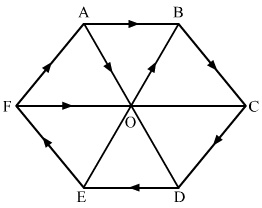

Leave a Reply