Page 9.17 Ex.9.1
Q1.
Answer :
Given:
fx=xx, x≠01, x=0
We observe
(LHL at x = 0) =limx→0-fx = lim h→0f0-h = lim h→0f-h
=limh→0-h-h=limh→0-hh =limh→0-1 =-1
(RHL at x = 0) =limx→0+fx = lim h→0f0+h= lim h→0fh
=limh→0hh=limh→0hh=limh→01=1
∴limx→0+fx ≠limx→0-fx
Hence, fx is discontinuous at the origin.
Q2.
Answer :
Given:
fx=x2-x-6x-3, x≠35, x=3
We observe
(LHL at x = 3) = limx→3-fx = lim h→0f3-h
=limh→03-h2-3-h-63-h-3=limh→09+h2-6h-3+h-6-h=limh→0h2-5h-h=limh→05-h = 5
And, (RHL at x = 3) = limx→3+fx = lim h→0f3+h
=limh→03+h2-3+h-63+h-3=limh→09+h2+6h-3-h-6h=limh→0h2+5hh=limh→05+h = 5
Also, f3=5
∴limx→3+fx =limx→3-fx = f3
Hence, fx is continuous at x=3.
Q3.
Answer :
Given:
fx=x2-9x-3, if x≠36, if x=3
We observe
(LHL at x = 3) = limx→3-fx=limh→0f3-h
= limh→03-h2-93-h-3=limh→032+h2-6h-93-h-3=limh→0h2-6h-h==limh→0hh-6-h=limh→06-h=6
(RHL at x = 3) = limx→3+fx=limh→0f3+h
= limh→03+h2-93+h-3=limh→032+h2+6h-9h=limh→0h2+6hh=limh→0 h6+hh=limh→06+h=6
Given:
f3=6
∴limx→3-fx=limx→3+fx=f3
Hence, fx is continuous at x=3.
Q4.
Answer :
Given:
fx=x2-1x-1, if x≠12, if x=1
We observe
(LHL at x = 1) = limx→1-fx=limh→0f1-h
= limh→01-h2-11-h-1=limh→01+h2-2h-11-h-1=limh→0h2-2h-h=limh→0hh-2-h=limh→02-h=2
(RHL at x = 1) = limx→1+fx=limh→0f1+h
= limh→01+h2-11+h-1=limh→01+h2+2h-11+h-1=limh→0h2+2hh=limh→0hh+2h=limh→02+h=2
Given:
f1=2
∴limx→1-fx=limx→1+fx=f1
Hence, fx is continuous at x=1.
Page 9.18 Ex.9.1
Q5.
Answer :
Given:
fx=sin3xx, when x≠01, when x=0
We observe
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h
= limh→0sin-3h-h=limh→0-sin3h-h=limh→03sin3h3h=3limh→0sin3h3h=3·1=3
(RHL at x = 0) = limx→0+fx=limh→0fh
= limh→0sin3hh=limh→03sin3h3h=3limh→0sin3h3h=3·1=3
Given:
f0=1
It is known that for a function fx to be continuous at x = a,
limx→a-fx=limx→a+fx=fa
But here,
limx→0-fx=limx→0+fx≠f0
Hence, fx is discontinuous at x=0.
Q6.
Answer :
Given:
fx=e1x, if x≠01, if x=0
We observe
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h
= limh→0e-1h=limh→01e1h=1limh→0e1h=0
(RHL at x = 0) = limx→0+fx=limh→0fh
= limh→0e1h=∞
Given:
f0=1
It is known that for a function fx to be continuous at x = a,
limx→a-fx=limx→a+fx=fa
But here,
limx→0-fx≠limx→0+fx
Hence, fx is discontinuous at x=0.
Q7.
Answer :
Given:
fx=1-cosxx2, when x≠01, when x=0
Consider:
limx→0fx=limx→01-cosxx2⇒limx→0fx=limx→02sin2x2x2⇒limx→0fx=limx→02sin2x24x24⇒limx→0fx=limx→02sinx224x22⇒limx→0fx=24limx→0sinx2x22⇒limx→0fx=12·12=12
Given:
f0=1
∴ limx→0fx≠f0
Thus, f(x) is discontinuous at x = 0.
Q8.
Answer :
The given function can be rewritten as:
fx=x-x2, when x>0x+x2, when x<02, when x=0
⇒ fx=0, when x>0x, when x<02, when x=0
We observe
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h=limh→0-h=0
(RHL at x = 0) = limx→0+fx=limh→0f0-h=limh→0fh= limh→00=0
And, f0=2
∴ limx→0-fx =limx→0+fx ≠ f0
Thus, f(x) is discontinuous at x = 0.
Q9.
Answer :
The given function can be rewritten as:
fx=x-ax-a, when x>aa-xx-a, when x<a1, when x=a
⇒ fx=1, when x>a-1, when x<a1, when x=a
⇒ fx=1, when x≥a-1, when x<a
We observe
(LHL at x = a) = limx→a-fx=limh→0fa-h=limh→0-1=-1
(RHL at x = a) = limx→a+fx=limh→0fa+h= limh→01=1
∴ limx→a-fx≠limx→a+fx
Thus, f(x) is discontinuous at x = a.
Q10.
Answer :
(i) Given:
fx=x cos1x, x≠00, x=0
We observe
limx→0 fx=limx→0x cos1x⇒limx→0 fx=limx→0xlimx→0cos1x⇒limx→0 fx=0 ×limx→0cos1x=0
⇒limx→0fx=f0
Hence, f(x) is continuous at x = 0.
(ii) Given:
fx=x2sin1x, x≠00, x=0
We observe
limx→0x2 sin1x=limx→0x2limx→0sin1x=0 ×limx→0sin1x=0
⇒limx→0fx=f0
Hence, f(x) is continuous at x = 0.
(iii) Given:
fx=x-a sin1x-a, x≠a0, x=a
Putting x−a = y, we get
limx→ax-a sin1x-a=limy→0y sin1y=limy→0ylimy→0sin1y=0 × limy→0sin1y=0
⇒limx→afx=fa=0
Hence, f(x) is continuous at x = a.
(iv) Given:
fx=ex-1log1+2x, if x≠07, if x=0
We observe
limx→0fx=limx→0ex-1log1+2x⇒limx→0fx=limx→0ex-12xlog1+2x2x⇒limx→0fx=12limx→0ex-1xlog1+2x2x⇒limx→0fx=12×limx→0ex-1xlimx→0log1+2x2x=12×11=12
And, f0=7
⇒limx→0fx≠f0
Hence, f(x) is discontinuous at x = 0.
(v) Given:
fx=1-xn1-x, x≠1n-1, x=1
Here, f1=n-1
limx→1fx=limx→11-xn1-x⇒limx→1fx=limx→11-xn-1+C1n1-xn-2x+C2n1-xn-3×2+…+Cn-1n1-x0xn-1
⇒limx→1fx=0+0…+1n-1=1≠f1
Thus, fx is discontinuous at x=1.
(vi) Given:
fx=x2-1x-1, x≠12, x=1
⇒fx=x+1, x<-1-x-1, -1≤ x<1x+1, x>12, x=1
We observe
(LHL at x = 1) = limx→1-fx=limh→0f1-h=limh→0-1-h-1=limh→0-2+h=-2
And, f1=2
⇒limx→1-fx≠f1
Hence, f(x) is discontinuous at x = 1.
(vii) Given:
fx=2x+x2x, x≠00, x=0
⇒fx=2x+x2x, x>0-2x+x2x, x<00, x=0
⇒fx=x+2, x>0x-2, x<00, x=0
We observe
(LHL at x = 0) = limx→0-fx=limh→0f-h=limh→0-h-2=-2
(RHL at x = 0) = limx→0+fx=limh→0fh=limh→02+h=2
⇒limx→0-fx≠limx→0+fx
Hence, f(x) is discontinuous at x = 0.
Page 9.19 Ex.9.1
Q11.
Answer :
Given:
fx=1+x2, if 0≤x≤12-x, if x>1
We observe
(LHL at x = 1) = limx→1-fx=limh→0f1-h=limh→01+1-h2=limh→02+h2-2h=2
(RHL at x = 1) = limx→1+fx=limh→0f1+h= =limh→02-1+h=limh→01-h=1
∴ limx→1-fx≠limx→1+fx
Thus, f(x) is discontinuous at x = 1.
Q12.
Answer :
Given:
fx=sin3xtan2x, if x<032, if x=0log1+3xe2x-1, if x>0
We observe
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h
=limh→0sin3-htan2-h=limh→0sin3htan2h=limh→03sin3h3h2tan2h2h=limh→03sin3h3hlimh→02tan2h2h=3limh→0sin3h3h2limh→0tan2h2h=3×12×1=32
(RHL at x = 1) = limx→0+fx=limh→0f0+h=limh→0fh
=limh→0log1+3he2h-1=limh→03hlog1+3h3h2he2h-12h=32limh→0log1+3h3he2h-12h=32limh→0log1+3h3hlimh→0e2h-12h=3×12×1=32
And, f0=32
∴ limx→0-fx=limx→0+fx=f0
Thus, f(x) is continuous at x = 0.
Q13.
Answer :
The given function can be rewritten as:
fx=2x-x, when x>02x+x, when x<00, when x=0
⇒ fx=x, when x>03x, when x<00, when x=0
We observe
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h=limh→0-3h=0
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh= limh→0h=0
And, f0=0
∴ limx→0-fx=limx→0+fx=f0
Thus, f(x) is continuous at x = 0.
Q14.
Answer :
The given function can be rewritten as:
fx=3x-2, x<030-2, x=0x+1, x>0
⇒fx=3x-2, x<0-2, x=0x+1, x>0
We observe
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h = limh→03-h-2=-2
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh = limh→0h+1=1
∴limx→0-fx≠limx→0+fx
Hence, fx is discontinuous at x=0.
Q15.
Answer :
Given:
fx=x, x>01, x=0-x, x<0
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h = limh→0–h=0
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh = limh→0h=0
And, f0=1
∴limx→0-fx=limx→0+fx≠f0
Hence, fx is discontinuous at x=0.
Q16.
Answer :
Given:
fx=x, 0≤x<1212, x=121-x, 12<x≤1
We observe
(LHL at x = 12) = limx→12-fx=limh→0f12-h = limh→012-h=12
(RHL at x = 12) = limx→12+fx=limh→0f12+h = limh→01-12+h=12
Also, f12=12
∴limx→12-fx =limx→12+fx = f12
Hence, fx is continuous at x=12.
Q17.
Answer :
Given:
fx=2x-1, x<02x+1, x≥0
We observe
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h = limh→02-h-1=-1
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh = limh→02h+1=1
∴limx→0-fx≠limx→0+fx
Hence, fx is discontinuous at x = 0.
Q18.
Answer :
Given: fx=x2-1x-1, x≠1k, x=1
If fx is continuous at x = 1, then
limx→1fx = f1
⇒ limx→1×2-1x-1= k
⇒ limx→1x-1x+1x-1= k
⇒ limx→1x+1= k
⇒ k=2
Q19.
Answer :
Given:
fx=x2-3x+2x-1, if x≠1k, if x=1
If fx is continuous at x = 1, then,
limx→1fx = f1
⇒ limx→1×2-3x+2x-1= k
⇒ limx→1x-2x-1x-1= k
⇒ limx→1x-2= k
⇒ k=-1
Page 9.20 Ex.9.1
Q20.
Answer :
Given:
fx=sin5x3x, if x≠0k, if x=0
If fx is continuous at x = 0, then
limx→0fx = f0
⇒ limx→0sin5x3x= k
⇒ limx→05 sin5x3×5x= k
⇒ 53limx→0sin5x5x= k
⇒ 53×1= k
⇒ k=53
Q21.
Answer :
Given:
fx=kx2, if x≤23, if x>2
If fx is continuous at x = 2, then
limx→2-fx =lim x→2+fx= f2 …(1)
Now,
limx→2-fx =limh→0f2-h =limh→0k2-h2 =4k
And, f2=3
From (1), we have
4k=3⇒k=34
Q22.
Answer:
Given:
fx=sin2x5x, if x≠0k, if x=0
If fx is continuous at x = 0, then
limx→0fx = f0
⇒ limx→0sin2x5x= k
⇒ limx→02sin2x5×2x= k
⇒ 25limx→0sin2x2x= k
⇒ 25×1= k
⇒ k=25
Q23.
Answer :
Given:
fx=ax+5, if x≤2x-1, if x>2
We observe
(LHL at x = 2) = limx→2-fx=limh→0f2-h = limh→0a2-h+5=2a+5
(RHL at x = 2) = limx→2+fx=limh→0f2+h = limh→02+h-1 = 1
And, f2=a2+5=2a+5
Since fx is continuous at x = 2, we have
limx→2-fx=limx→2+fx=f2
⇒ 2a+5=1
⇒ 2a=-4
⇒ a=-2
Q24.
Answer :
The given function can be rewritten as:
fx=xx+2×2, x>0-xx-2×2, x<0k, x=0
⇒fx=12x+1, x>012x-1, x<0k, x=0
We observe
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h
=limh→01-2h-1=-1
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh
=limh→012h+1=1
So, limx→0-fx≠limx→0+fx such that limx→0-fx &limx→0+fx are independent of k.
Thus, f(x) is discontinuous at x = 0, regardless of the choice of k.
Q25.
Answer :
Given:
fx=kcosxπ-2x, x≠π23, x=π2
If f(x) is continuous at x = π2, then
limx→π2fx = fπ2
⇒ limx→π2kcosxπ-2x=3 …(1)
Putting π2-x=h, we get
limx→π2k cos xπ-2x=limh→0k cos π2-hπ-2π2-h
From (1), we have
limh→0k cos π2-hπ-2π2-h=3
⇒limh→0k sin h2h=3
⇒limh→0k sin hh=6
⇒k limh→0sin hh=6
⇒k×1=6
⇒k=6
Hence, for k=6 , f(x) is continuous at x = π2.
Q26.
Answer :
The given function can be rewritten as:
fx=sin a+1 x+sin xx, for x<0c , for x=0x+bx2-xbx32 , for x>0
⇒fx=sin a+1x+sin xx, for x<0c , for x=01+bx-1bx , for x>0
We observe
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h
=limh→0-sin a+1h-sin -hh=limh→0-sin a+1hh-sin hh
=-a+1limh→0sin a+1ha+1h-limh→0sin hh=-a-1
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh
=limh→01+bh-1bh=limh→0bhbh1+bh+1=limh→011+bh+1=12
And, f0=c
If fx is continuous at x = 0, then
limx→0-fx=limx→0+fx=f0
⇒-a-1 = 12=c
⇒-a-1 = 12 and c=12
⇒a=-32, c=12
Now, 1+bx-1bx exists only if bx≠0⇒b≠0.
∴ b∈R-0
Q27.
Answer :
Given: fx=1-coskxxsinx, x≠012, x=0
If fx is continuous at x = 0, then
limx→0fx = f0 …(1)
Consider:
limx→0fx=limx→01-cos kxx sin x=limx→02 sin2 kx2x sin x
⇒limx→0fx=limx→02 sin2 kx2x2sin xx
⇒limx→0fx=limx→02k24sin kx22kx22sin xx
⇒limx→0fx=2k24limx→0sinkx22kx22sin xx
⇒limx→0fx=2k24limx→0sin kx22kx22limx→0sin xx
⇒limx→0fx=2k24×1=k22
From equation (1), we have
k22=f0
⇒k22=12⇒k=±1
Q28.
Answer :
Given:
fx=x-4x-4+a, if x<4a+b, if x=4x-4x-4+b, if x>4
We observe
(LHL at x = 4) = limx→4-fx=limh→0f4-h
=limh→04-h-44-h-4+a=limh→0-h-h+a=a-1
(RHL at x = 4) = limx→4+fx=limh→0f4+h
=limh→04+h-44+h-4+b=limh→0hh+b=b+1
And f4=a+b
If f(x) is continuous at x = 4, then
limx→4-fx=limx→4+fx=f4
⇒a-1=b+1=a+b
⇒a-1=a+b, b+1=a+b
⇒b=-1, a=1
Page 9.21 Ex.9.1
Q29.
Answer :
Given: fx=sin2xx, x≠0k, x=0
If f(x) is continuous at x = 0, then
limx→0fx=f0
⇒limx→0sin2xx=k
⇒limx→02sin2x2x=k
⇒2limx→0sin2x2x=k
⇒2×1=k
⇒k=2
Q30.
Answer :
Given: fx=log1+xa-log1-xbx, x≠0
If f(x) is continuous at x = 0, then
limx→0fx=f0
⇒limx→0log1+xa-log1-xbx=f0
⇒limx→0log1+xaaxa-log1-xbbxb=f0
⇒1alimx→0log1+xaxa–1blimx→0log1-xb-xb=f0
⇒1a×1–1b×1=f0 Using: limx→0log1+xx=1⇒1a+1b=f0⇒a+bab=f0
Q31.
Answer :
Given:
fx=2x+2-164x-16, if x≠2k , if x=2
If f(x) is continuous at x = 2, then
limx→2fx=f2⇒limx→22x+2-164x-16=f2⇒limx→242x-42x-42x+4=k⇒limx→242x+4=k⇒422+4=k⇒48=k⇒k=12
Q32.
Answer :
Given:
fx=cos2x-sin2x-1×2+1-1, x≠0k, x=0
If f(x) is continuous at x = 0, then
limx→0fx=f0⇒limx→0cos2x-sin2x-1×2+1-1=k⇒limx→01-sin2x-sin2x-1×2+1-1=k⇒limx→0-2sin2xx2+1-1=k⇒limx→0-2sin2xx2+1+1×2+1-1×2+1+1=k⇒limx→0-2sin2xx2+1+1×2=k⇒-2limx→0sin2xx2+1+1×2=k⇒-2limx→0sinxx2limx→0x2+1+1=k⇒-2×1×1+1=k⇒k=-4
Q33.
Answer :
Given:
fx=1-cos7x-π5x-π2, x=π
If f(x) is continuous at x = π, then
limx→πfx=fπ⇒limx→π1-cos7x-π5x-π2=fπ⇒25limx→πsin27x-π2x-π2=fπ⇒25×494limx→πsin27x-π2494x-π2=fπ⇒25×494limx→πsin27x-π272x-π2=fπ⇒25×494limx→πsin7x-π272x-π2=fπ⇒25×494×1=fπ⇒15×492×1=fπ⇒4910=fπ
Hence, the given function will be continuous at x=π, if fπ=4910.
Q34.
Answer :
Given:
fx=2x+3sinx3x+2sinx, x≠0
If f(x) is continuous at x = 0, then
limx→0fx=f0⇒limx→02x+3sinx3x+2sinx=f0⇒limx→0x2+3sinxxx3+2sinxx=f0⇒limx→02+3sinxx3+2sinxx=f0⇒limx→02+3sinxxlimx→03+2sinxx=f0⇒2+3limx→0sinxx3+2limx→0sinxx=f0⇒2+3×13+2×1=f0⇒55=f0⇒f0=1
Q35.
Answer :
Given: fx=1-cos4x8x2, when x≠0k, when x=0
If f(x) is continuous at x = 0, then
limx→0fx=f0⇒limx→01-cos4x8x2=f0⇒limx→02sin22x8x2=f0⇒22limx→0sin22x4x2=f0⇒22limx→0sin2x2x2=f0⇒1×1=f0⇒k=1 ∵f0=k
Q36.
Answer :
(i) Given:
fx=1-cos 2kxx2, if x≠08 , if x=0
If f(x) is continuous at x = 0, then
limx→0fx=f0⇒limx→01-cos2kxx2=8⇒limx→02k2sin2kxk2x2=8⇒2k2limx→0sinkxkx2=8⇒2k2×1=8⇒k2=4⇒k=±2
(ii) Given:
fx=x-1tanπx2, if x≠1k, if x=1
If f(x) is continuous at x = 1, then
limx→1fx=f1⇒limx→1x-1 tanπx2=k
Putting x-1=y, we get
limy→0 y tanπy+12=k⇒limy→0 y tanπy2+π2=k⇒limy→0 y tanπ2+πy2=k⇒-limy→0 y cotπy2=k⇒-2πlimy→0 πy2cosπy2sinπy2=k⇒-2π limy→0cosπy2limy→0sinπy2πy2=k⇒-2π×11=k⇒k=-2π
(iii) Given:
fx=kx2-2x, if x<0cosx, if x≥0
We have
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h=limh→0kh2+2h=0
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh=limh→0cosh=1
∴limx→0-fx≠limx→0+fx
Thus, no value of k exists for which fx is continuous at x=0.
(iv) Given:
fx=kx+1, if x≤πcosx, if x>π
We have
(LHL at x = π) = limx→π-fx=limh→0fπ-h=limh→0kπ-h+1=kπ+1
(RHL at x = π) = limx→π+fx=limh→0fπ+h=limh→0cosπ+h=cosπ=-1
If f(x) is continuous at x = π, then
limx→π-fx=limx→π+fx
⇒kπ+1=-1⇒k=-2π
(v) Given:
fx=kx+1, if x≤53x-5, if x>5
We have
(LHL at x = 5) = limx→5-fx=limh→0f5-h=limh→0k5-h+1=5k+1
(RHL at x = 5) = limx→5+fx=limh→0f5+h=limh→035+h-5=10
If f(x) is continuous at x = 5, then
limx→5-fx=limx→5+fx⇒5k+1=10⇒k=95
(vi) Given:
fx=x2-25x-5, x≠5k, x=5
⇒fx=x-5x+5x-5, x≠5k, x=5
⇒fx=x+5, x≠5k, x=5
If f(x) is continuous at x = 5, then
limx→5fx=f5⇒limx→5x+5=k⇒k=5+5=10
(vii) Given: fx=kx2, x≥14, x<1
We have
(LHL at x = 1) = limx→1-fx=limh→0f1-h=limh→04=4
(RHL at x = 1) = limx→1+fx=limh→0f1+h=limh→0k1+h2=k
If f(x) is continuous at x = 1, then
limx→1-fx=limx→1+fx⇒k=4
(viii) Given:
fx=kx2+2, if x≤03x+1, if x>0
We have
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0k-h2+2=2k
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→03h+1=1
If f(x) is continuous at x = 0, then
limx→0-fx=limx→0+fx⇒2k=1⇒k=12..
Page 9.22 Ex.9.1
Q37.
Answer :
Given: fx=1, if x≤3ax+b, if 3<x<57, if x≥5
We have
(LHL at x = 3) = limx→3-fx=limh→0f3-h=limh→01=1
(RHL at x = 3) = limx→3+fx=limh→0f3+h=limh→0a3+h+b=3a+b
(LHL at x = 5) = limx→5-fx=limh→0f5-h=limh→0a5-h+b=5a+b
(RHL at x = 5) = limx→5+fx=limh→0f5+h=limh→07=7
If f(x) is continuous at x = 3 and 5, then
∴ limx→3-fx =lim x→3+fx and limx→5-fx =limx→5+fx
⇒1=3a+b …1 and 5a+b=7 …2
On solving eqs. (1) and (2), we get
a=3 and b=-8
Q38.
Answer :
Given: fx=x22, if 0≤x≤12×2-3x+32, if 1<x≤2
We have
(LHL at x = 1) = limx→1-fx=limh→0f1-h=limh→01-h22=12
(RHL at x = 1) = limx→1+fx=limh→0f1+h=limh→021+h2-31+h+32=2-3+32=12
Also, f1=122=12
∴ limx→1-fx =lim x→1+fx =f1
Hence, the given function is continuous at x=1.
Q39.
Answer :
(i) Given: fx=x+x-1
We have
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→00-h+0-h-1=1
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→00+h+0+h-1=1
Also, f0=0+0-1=0+1=1
Now,
(LHL at x = 1) = limx→1-fx=limh→0f1-h=limh→01-h+1-h-1=1+0=1
(RHL at x =1) = limx→1+fx=limh→0f1+h=limh→01+h+1+h-1=1+0=1
Also, f1=1+1-1=1+0=1
∴ limx→0-fx =lim x→0+fx = f0 and lim x→1-fx = lim x→1+fx = f1
Hence, fx is continuous at x=0, 1.
(ii) Given: fx=x-1+x+1
We have
(LHL at x = −1) = limx→-1-fx=limh→0f-1-h=limh→0-1-h-1+-1-h+1=2+0=2
(RHL at x = −1) = limx→-1+fx=limh→0f-1+h=limh→0-1+h-1+-1+h+1=2+0=2
Also, f-1=-1-1+-1+1=-2=2
Now,
(LHL at x = 1) = limx→1-fx=limh→0f1-h=limh→01-h-1+1-h+1=0+2=2
(RHL at x =1) = limx→1+fx=limh→0f1+h=limh→01+h-1+1+h+1=0+2=2
Also, f1=1+1+1-1=2
∴ limx→-1-fx =lim x→-1+fx = f-1 and lim x→1-fx = lim x→1+fx = f1
Hence, fx is continuous at x=-1, 1.
Q40.
Answer :
The given function can be rewritten as
fx=x-xx, when x>0x+xx, when x<02, when x=0
⇒ fx=0, when x>02, when x<02, when x=0
We have
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h=limh→02=2
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh=limh→00=0
∴ limx→0-fx≠limx→0+fx
Thus, f(x) is discontinuous at x = 0.
Q41.
Answer :
The given function can be rewritten as
fx=2×2+k, if x≥0-2×2+k, if x<0
We have
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h=limh→0-2-h2+k=k
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh=limh→02h2+k=k
If fx is continuous at x=0, then
limx→0-fx =limx→0+fx = f0⇒limx→0-fx =limx→0+fx = k
∴ k can be any real number.
Q42.
Answer :
The given function f is
If f is continuous at x = 0, then
Therefore, there is no value of λ for which f(x) is continuous at x = 0.
At x = 1,
f (1) = 4x + 1 = 4 × 1 + 1 = 5
Therefore, for any values of λ, f is continuous at x = 1
At x = -1, we have
f (-1) = λ1+2=3λ
limx→-1λ1+2=3λ∴limx→-1fx=f-1
Therefore, for any values of λ, f is continuous at x = -1
Q43.
Answer :
Given: fx=2x+1, if x<2k, x=23x-1, x>2
We have
(LHL at x = 2) = limx→2-fx=limh→0f2-h=limh→022-h+1=5
(RHL at x = 2) = limx→2+fx=limh→0f2+h=limh→032+h-1=5
Also, f2=k
If f(x) is continuous at x = 2, then
limx→2-fx =lim x→2+fx=f2
⇒ 5=5=k
Hence, for k = 5, fx is continuous at x=2.
Q44.
Answer :
Given: fx=1-sin3x3cos2x, if x<π2a, if x=π2b1-sinxπ-2×2, if x>π2
We have
(LHL at x = π2) = limx→π2-fx=limh→0fπ2-h
=limh→01-sin3π2-h3cos2π2-h=limh→01-cos3h3sin2h=13limh→01-cosh1+cos2h+cosh1-cosh1+cosh=13limh→01+cos2h+cosh1+cosh=131+1+11+1=12
(RHL at x = π2) = limx→π2+fx=limh→0fπ2+h
=limh→0b1-sinπ2+hπ-2π2+h2=limh→0b1-cosh-2h2=limh→02bsin2h24h2=limh→02bsin2h216h24=b8limh→0sinh2h22=b8×1=b8
Also, fπ2=a
If f(x) is continuous at x = π2 , then
limx→π2-fx =lim x→π2+fx = fπ2
⇒12 =b8 = a
⇒a=12 and b=4
Q45.
Answer :
Given: fx=1-cos2x2x2, x<0k, x=0xx, x>0
⇒fx=1-cos2x2x2, x<0k, x=01, x>0
We have
(LHL at x = 0) = limx→0-fx=limh→0f0-h
=limh→01-cos2-h2-h2=limh→01-cos2h2h2=12limh→02sin2hh2=22limh→0sin2hh2=22limh→0sinhh2=1×1=1
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh=limh→01=1
Also, f0=k
If f(x) is continuous at x = 0, then
limx→0-fx =lim x→0+fx=f0
⇒1=1=k
Hence, the required value of k is 1.
Q46.
Answer :
Given: fx=ax+1, if x≤3bx+3, if x>3
We have
(LHL at x = 3) = limx→3-fx=limh→0f3-h=limh→0a3-h+1=3a+1
(RHL at x = 3) = limx→3+fx=limh→0f3+h=limh→0b3+h+3=3b+3
If fx is continuous at x=3, thenlimx→3-fx=limx→3+fx⇒3a+1=3b+3⇒3a-3b=2
Hence, the required relationship between a & b is 3a-3b=2.
Page 9.23 Ex.9.1
Q47.
Answer :
Given: fx=a sin π2x+1, x≤0tan x-sin xx3, x>0
We have
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h=limh→0a sin π2-h+1=a sinπ2=a
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh=limh→0tan h-sin hh3
⇒limx→0+fx=limh→0sin hcos h-sin hh3⇒limx→0+fx=limh→0sin hcos h1-cos hh3⇒limx→0+fx=limh→01-cos htan hh3⇒limx→0+fx=limh→02sin2 h2tan h4h24×h⇒limx→0+fx=24limh→0sin2h2tan hh24×h⇒limx→0+fx=12limh→0sinh2h22limh→0tan hh⇒limx→0+fx=12×1×1⇒limx→0+fx=12
If fx is continuous at x=0, thenlimx→0-fx=limx→0+fx⇒a=12
Page 9.35 Ex.9.2
Q1.
Answer :
When x < 0, we have
fx=sinxx
We know that sin x as well as the identity function x are everywhere continuous.
So, the quotient function sinxx is continuous at each x < 0.
When x > 0, we have fx=x+1, which is a polynomial function.
Therefore, fx is continuous at each x > 0.
Now,
Let us consider the point x = 0.
Given: fx=sinxx, x<0x+1, x≥0
We have
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h=limh→0sin-h-h=limh→0sinhh=1
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh=limh→0h+1=1
Also,
f0=0+1=1
∴ limx→0-fx=limx→0+fx=f0
Thus, fx is continuous at x = 0.
Hence, fx is everywhere continuous.
Q2.
Answer :
Given: fx=xx, x≠00, x=0
x=x, x≥0-x, x<0⇒fx=1, x>0-1, x<00, x=0
We have
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h=limh→0-1=-1
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh=limh→01=1
∴ limx→0-fx≠limx→0+fx
Thus, fx is discontinuous at x = 0.
Q3.
Answer :
(i)
When x ≠1, then
fx=x3-x2+2x-2
We know that a polynomial function is everywhere continuous.
So, fx=x3-x2+2x-2 is continuous at each x ≠1.
At x = 1, we have
(LHL at x = 1) = limx→1-fx=limh→0f1-h=limh→01-h3-1-h2+21-h-2=1-1+2-2=0
(RHL at x = 1) = limx→1+fx=limh→0f1+h=limh→01+h3-1+h2+21+h-2=1-1+2-2=0
Also, f1=4
∴ limx→1-fx=limx→1+fx≠f1
Thus, fx is discontinuous at x = 1.
Hence, the only point of discontinuity for fx is x = 1.
(ii)
Given: fx=x4-16x-2, if x≠216, if x=2
When x ≠2, then
fx=x4-16x-2=x4-24x-2=x2+4x-2x+2x-2=x2+4x+2
We know that a polynomial function is everywhere continuous.
Therefore, the functions x2+4 and x+2 are everywhere continuous.
So, the product function x2+4x+2 is everywhere continuous.
Thus, f(x) is continuous at every x ≠2.
At x = 2, we have
(LHL at x = 2) = limx→2-fx=limh→0f2-h=limh→02-h2+42-h+2=84=32
(RHL at x = 2) = limx→2+fx=limh→0f2+h=limh→02+h2+42+h+2=84=32
Also, f2=16
∴ limx→2-fx=limx→2+fx≠f2
Thus, fx is discontinuous at x = 2.
Hence, the only point of discontinuity for fx is x = 2.
(iii)
When x < 0, then
fx=sinxx
We know that sin x as well as the identity function x are everywhere continuous.
So, the quotient function sinxx is continuous at each x < 0.
When x > 0, then
fx=2x+3, which is a polynomial function.
Therefore, fx is continuous at each x > 0.
Now,
Let us consider the point x = 0.
Given: fx=sinxx, if x<02x+3, if x≥0
We have
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h=limh→0sin-h-h=limh→0sinhh=1
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh=limh→02h+3=3
∴ limx→0-fx≠limx→0+fx
Thus, fx is discontinuous at x = 0.
Hence, the only point of discontinuity for fx is x = 0.
(iv)
When x ≠ 0, then
fx=sin3xx
We know that sin 3x as well as the identity function x are everywhere continuous.
So, the quotient function sin3xx is continuous at each x ≠ 0.
Let us consider the point x = 0.
Given: fx=sin3xx, if x≠04, if x=0
We have
(LHL at x = 0) = limx→0-fx =limh→0f0-h =limh→0f-h =limh→0sin -3h-h =limh→03 sin 3h3h = 3
(RHL at x = 0) = limx→0+fx =limh→0f0+h =limh→0fh =limh→0sin 3hh =limh→03 sin 3h3h = 3
Also, f0=4
∴ limx→0-fx=limx→0+fx≠f0
Thus, fx is discontinuous at x = 0.
Hence, the only point of discontinuity for fx is x = 0.
(v)
When x ≠ 0, then
fx=sinxx+cosx
We know that sin x as well as the identity function x both are everywhere continuous.
So, the quotient function sinxx is continuous at each x ≠ 0.
Also, cos x is everywhere continuous.
Therefore, sin xx+cos x is continuous at each x ≠ 0.
Let us consider the point x = 0.
Given: fx=sinxx+cosx, if x≠05, if x=0
We have
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h=limh→0sin-h-h+cos-h=limh→0sin-h-h+limh→0cos-h=1+1=2
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh=limh→0sinhh+cosh=limh→0sinhh+limh→0cosh=1+1=2
Also, f0=5
∴ limx→0-fx=limx→0+fx≠f0
Thus, fx is discontinuous at x = 0.
Hence, the only point of discontinuity for fx is x = 0.
(vi)
When x ≠ 0, then
fx=x4+x3+2x2tan-1x
We know that x4+x3+2×2 is a polynomial function which is everywhere continuous.
Also, tan-1x is everywhere continuous.
So, the quotient function x4+x3+2x2tan-1x is continuous at each x ≠ 0.
Let us consider the point x = 0.
Given: fx=x4+x3+2x2tan-1x, if x≠010, if x=0
We have
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h=limh→0-h4+-h3+2-h2tan-1-h=limh→0h3-h2+2h-tan-1hh=0-1=0
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh=limh→0h4+h3+2h2tan-1h=limh→0h3+h2+2htan-1hh=01=0
Also, f0=10
∴ limx→0-fx=limx→0+fx≠f0
Thus, fx is discontinuous at x = 0.
Hence, the only point of discontinuity for fx is x = 0.
(vii)
Given: fx=ex-1loge1+2x, if x≠07, if x=0
We have
limx→0fx=limx→0ex-1loge1+2x=limx→0ex-1×2 loge1+2x2x=12×limx→0ex-1xlimx→0loge1+2x2x=12
It is given that f0=7
⇒ limx→0fx≠f0
Hence, the given function is discontinuous at x = 0 and continuous elsewhere.
(viii)
When x > 1, then
fx=x-3
Since modulus function is a continuous function, fx is continuous for each x > 1.
When x < 1, then
fx=x24-3×2+134
Since, x2 & 3x are continuous being polynomial functions, x24 & 3×2 will also be continuous.
Also, 134 is continuous being a polynomial function.
⇒x24-3×2+134 is continuous for each x<1.
⇒fx is continuous for each x < 1.
At x = 1, we have
(LHL at x=1) = lim x→1-fx=lim h→0f1-h=lim h→01-h24-31-h2+134=14-32+134=2
(RHL at x=1) = lim x→1+fx=lim h→0f1+h=lim h→01+h-3=-2=2
Also, f1=1-3=-2=2
Thus, lim x→1-fx=lim x→1+fx=f1
Hence, fx is continuous at x= 1.
Thus, the given function is nowhere discontinuous.
(ix)
At x≤-3, we have
fx=x+3
Since modulus function and constant function are continuous, fx=x+3 is continuous for each x≤-3.
At -3<x<3, we have
fx=-2x
Since polynomial function is continuous and constant function is continuous, fx=-2x is continuous for each-3<x<3.
At x>3, we have
fx=6x+2
Since polynomial function is continuous and constant function is continuous, fx=6x+2 is continuous for each x>3.
Now, we check the continuity of the function at the point x=3.
We have
(LHL at x=3) = limx→3-fx=limh→0f3-h=limh→0-23-h=-6
(RHL at x=3) = limx→3+fx=limh→0f3+h=limh→063+h+2=20
⇒limx→3-fx≠limx→3+fx
Hence, the only point of discontinuity of the given function is x=3
(x)
Given:
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x, such that x < 1
Case II:
If c = 1, then the left hand limit of f at x = 1 is,
The right hand limit of f at x = 1 is,
It is observed that the left and right hand limit of f at x = 1 do not coincide.
Therefore, f is not continuous at x = 1
Case III:
Therefore, f is continuous at all points x, such that x > 1
Thus, from the above observation, it can be concluded that x = 1 is the only point of discontinuity of f.
(xi) The given function is
The given function is defined at all points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x, such that x < 0
Case II:
The left hand limit of f at x = 0 is,
The right hand limit of f at x = 0 is,
Therefore, f is continuous at x = 0
Case III:
Therefore, f is continuous at all points of the interval (0, 1).
Case IV:
The left hand limit of f at x = 1 is,
The right hand limit of f at x = 1 is,
It is observed that the left and right hand limits of f at x = 1 do not coincide.
Therefore, f is not continuous at x = 1
Case V:
Therefore, f is continuous at all points x, such that x > 1
Hence, f is not continuous only at x = 1
(xii)
The given function f is
It is evident that f is defined at all points of the real line.
Let c be a real number.
Case I:
Therefore, f is continuous at all points x, such that x ≠ 0
Case II:
Therefore, f is continuous at x = 0
From the above observations, it can be concluded that f is continuous at every point of the real line.
Thus, f is a continuous function.
(xiii)
The given function f is
The given function is defined at all points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x, such that x < −1
Case II:
The left hand limit of f at x = −1 is,
The right hand limit of f at x = −1 is,
Therefore, f is continuous at x = −1
Case III:
Therefore, f is continuous at all points of the interval (−1, 1).
Case IV:
The left hand limit of f at x = 1 is,
The right hand limit of f at x = 1 is,
Therefore, f is continuous at x = 2
Case V:
Therefore, f is continuous at all points x, such that x > 1
Thus, from the above observations, it can be concluded that f is continuous at all points of the real line.
Page 9.36 Ex.9.2
Q4.
Answer :
(i) Given: fx=sin 2x5x, if x≠03k, if x=0
If fx is continuous at x = 0, then
limx→0fx=f0
⇒limx→0sin 2x5x=f0⇒limx→02sin 2×2×5x=f0⇒25limx→0sin 2x2x=f0⇒25=3k⇒k=215
(ii) Given: fx=kx+5, if x≤2x-1, if x>2
If fx is continuous at x = 2, then
limx→2-fx=limx→2+fx
⇒limh→0f2-h=limh→0f2+h⇒limh→0k2-h+5=limh→02+h-1⇒2k+5=1⇒2k=-4⇒k=-2
(iii) Given: fx=kx2+3x, if x<0cos 2x, if x≥0
If fx is continuous at x = 0, then
limx→0-fx=limx→0+fx
⇒limh→0f-h=limh→0fh⇒limh→0k-h2-3h=limh→0cos 2h⇒0=1 It is not possible
Hence, there does not exist any value of k, which can make the given function continuous.
(iv) Given: fx=2, if x≤3ax+b, if 3<x<59, if x≥5
If fx is continuous at x = 3 and 5, then
limx→3-fx =limx→3+fx and limx→5-fx =limx→5+fx
⇒limh→0f3-h=limh→0f3+h and limh→0f5-h=limh→0f5+h ⇒limh→02=limh→0a3+h+b and limh→0a5-h+b=limh→09⇒2=3a+b and 5a+b=9⇒2=3a+b and 5a+b=9⇒a=72 and b=-172
(v)
Given: fx=4, if x≤-1ax2+b, if -1<x<0cos x, if x≥0
If fx is continuous at x = −1 and 0, then
limx→-1-fx =limx→-1+fx and limx→0-fx =limx→0+fx
⇒limh→0f-1-h =limh→0f-1+h and limh→0f-h =limh→0fh ⇒limh→04 =limh→0a-1+h2+b and limh→0a-h2+b =limh→0cos h⇒4=a+b and b=1⇒a=3 and b=1
(vi)
Given: fx=1+px-1-pxx, if -1≤x<02x+1x-2, if 0≤x≤1
If fx is continuous at x = 0, then
limx→0-fx=limx→0+fx
⇒ limh→0f-h=limh→0fh ⇒limh→01-ph-1+ph-h=limh→02h+1h-2⇒limh→01-ph-1+ph1-ph+1+ph-h1-ph+1+ph=limh→02h+1h-2⇒limh→01-ph-1-ph-h1-ph+1+ph=limh→02h+1h-2⇒limh→0-2ph-h1-ph+1+ph=limh→02h+1h-2⇒limh→02p1-ph+1+ph=limh→02h+1h-2⇒2p2=1-2⇒p=-12
(vii)
Given: fx=5, if x≤2ax+b, if 2<x<1021, if x≥10
If fx is continuous at x = 2 and 10, then
limx→2-fx =limx→2+fx and limx→10-fx =limx→10+fx
⇒ limh→0f2-h =limh→0f2+h and limh→0f10-h =limh→0f10+h⇒ limh→05 =limh→0a2+h+b and limh→0a10-h+b =limh→021⇒ 5=2a+b …1 and 10a+b=21 …2On solving eqs. 1 and 2, we geta=2 and b=1
(viii)
Given: fx=k cos xπ-2x, x<π23 , x=π23 tan 2x2x-π, x>π2
If fx is continuous at x = π2, then
limx→π2-fx=fπ2
⇒limh→0fπ2-h = fπ2⇒limh→0fπ2-h = 3⇒limh→0k cos π2-hπ-2π2-h = 1⇒limh→0k sin hπ-π+2h = 1⇒limh→0k sin h2h = 1⇒k2limh→0sin hh = 1⇒k2 = 1⇒k = 2
Page 9.37 Ex.9.2
Q5.
Answer :
Given: f is continuous on 0,∞
∴ f is continuous at x = 1 and 2
At x = 1, we have
limx→1-fx =limh→0f1-h =limh→01-h2a = 1a
limx→1+fx=limh→0f1+h=limh→0a=a
Also,
At x = 2, we have
limx→2-fx =limh→0f2-h =limh→0a = a
limx→2+fx =limh→0f2+h =limh→02b2-4b2+h2 = 2b2-4b2 = b2-2b
f is continuous at x = 1 and 2
∴ limx→1-fx=limx→1+fx and limx→2-fx=limx→2+fx
⇒1a=a and b2-2b=a⇒a2=1 and b2-2b=a⇒ a=±1 and b2-2b=a …1
If a = 1, then
b2-2b = 1 From eq. (1)⇒b2-2b-1 = 0⇒b = 2±4+42 = 2±222 = 1±2
If a = −1, then
b2-2b = -1 From eq. (1)⇒b2-2b+1 = 0⇒b-12 = 0⇒b = 1
Hence, the most suitable values of a and b are
a = −1, b = 1 or a = 1, b=1±2
Q6.
Answer :
Given: f is continuous on 0, π.
∴ f is continuous at x = π4 and π2
At x = π4, we have
limx→π4-fx =limh→0fπ4-h =limh→0π4-h+a2sin π4-h = π4+a2 sin π4 = π4+a
limx→π4+fx =limh→0fπ4+h =limh→02π4+h cot π4+h+b = π2 cot π4+b = π2+b
At x = π2, we have
limx→π2-fx =limh→0fπ2-h =limh→02π2-h cot π2-h+b = b
limx→π2+fx =limh→0fπ2+h =limh→0a cos 2π2+h-b sin π2+h = -a-b
Since f is continuous at x = π4 and x = π2, we get
limx→π2-fx =limx→π2+fx and limx→π4-fx =limx→π4+fx
⇒-b-a = b and π4+a = π2+b⇒b = -a2 …1 and -π4 = b-a …2⇒ -π4 = -3a2 Substituting the value of b in eq. 2⇒ a = π6⇒ b = -π12 From eq.1
Q7.
Answer :
Given: f is continuous on 0, 8.
∴ f is continuous at x = 2 and x = 4
At x = 2, we have
limx→2-fx =limh→0f2-h =limh→02-h2+a2-h+b = 4+2a+b
limx→2+fx =limh→0f2+h =limh→032+h+2 = 8
Also,
At x = 4, we have
limx→4-fx =limh→0f4-h =limh→034-h+2 = 14
limx→4+fx =limh→0f4+h =limh→02a4+h+5b = 8a+5b
f is continuous at x = 2 and x = 4
∴ limx→2-fx =limx→2+fx and limx→4-fx =limx→4+fx
⇒4+2a+b=8 and 8a+5b=14⇒2a+b=4 …1 and 8a+5b=14 …2
On simplifying eqs. (1) and (2), we get
a=3 and b=-2
Q8.
Answer :
When x≠π4, tan π4-x and cot 2x are continuous in 0, π2.
Thus, the quotient function tan π4-xcot 2x is continuous in 0,π2 for each x≠π4.
So, if fx is continuous at x=π4, then it will be everywhere continuous in 0, π2.
Now,
Let us consider the point x = π4.
Given: fx = tan π4-xcot 2x, x≠π4
We have
(LHL at x = π4) = limx→π4-fx =limh→0fπ4-h =limh→0tanπ4-π4+hcotπ2-2h = limh→0tan htan 2h =limh→0tan hh2 tan 2h2h = 12limh→0tan hhlimh→0tan 2h2h = 12
(RHL at x = π4) = limx→π4+fx =limh→0fπ4+h =limh→0tan π4-π4-hcot π2+2h =limh→0tan -h-tan 2h =limh→0tan htan 2h =limh→0tan hh2 tan 2h2h =12limh→0tan hhlimh→0tan 2h2h = 12
If fx is continuous at x=π4, then
lim x→π4-fx =limx→π4+fx = fπ4
∴ fπ4=12
Hence, for fπ4=12, the function fx will be everywhere continuous in 0, π2.
Q9.
Answer :
When x < 2, we have
fx = 2x-1
We know that a polynomial function is everywhere continuous.
So, fx is continuous for each x < 2.
When x>2, we have
fx=3×2
The functions 3x and 2 are continuous being the polynomial and constant function, respectively.
Thus, the quotient function 3×2 is continuous at each x > 2.
Now,
Let us consider the point x = 2.
Given: fx=2x-1, if x<23×2, if x≥2
We have
(LHL at x = 2) = limx→2-fx =limh→0f2-h =limh→022-h-1 = 4-1 = 3
(RHL at x = 2) = limx→2+fx =limh→0f2+h =limh→03h+22 = 3
Also,
f2=322=3
∴ limx→2-fx=limx→2+fx=f2
Thus, fx is continuous at x = 2.
Hence, fx is everywhere continuous.
Q11.
Answer :
When x < 0, we have
fx=sinxx
We know that sin x as well as the identity function x are everywhere continuous.
So, the quotient function sinxx is continuous at each x < 0.
When x > 0, we have
fx=x+1, which is a polynomial function.
Therefore, fx is continuous at each x > 0.
Now,
Let us consider the point x = 0.
Given: fx = sin xx, x<0x+1, x≥0
We have
(LHL at x = 0) = limx→0-fx =limh→0f0-h =limh→0f-h =limh→0sin -h-h =limh→0sin hh = 1
(RHL at x = 0) = limx→0+fx =limh→0f0+h =limh→0fh =limh→0h+1 = 1
Also,
f0=0+1=1
∴ limx→0-fx=limx→0+fx=f0
Thus, fx is continuous at x = 0.
Hence, fx is everywhere continuous.
Q12.
Answer :
Given:
It is evident that g is defined at all integral points.
Let n∈Z.
Then,
The left hand limit of f at x = n is,
The right hand limit of f at x = n is,
It is observed that the left and right hand limits of f at x = n do not coincide.
i.e. limx→n-gx ≠limx→n+gx
So, f is not continuous at x = n, n∈Z
Hence, g is discontinuous at all integral points.
Page 9.38 Ex.9.2
Q13.
Answer :
It is known that if g and h are two continuous functions, then g+h, g-h and g×h are also continuous.
It has to proved first that g (x) = sin x and h (x) = cos x are continuous functions.
Let g (x) = sin x
It is evident that g (x) = sin x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
So, g is a continuous function.
Let h (x) = cos x
It is evident that h (x) = cos x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
h (c) = cos c
So, h is a continuous function.
Therefore, it can be concluded that
(i) f (x) = g (x) + h (x) = sin x + cos x is a continuous function.
(ii) f (x) = g (x) − h (x) = sin x − cos x is a continuous function.
(iii) f (x) = g (x) × h (x) = sin x cos x is a continuous function.
Q14.
Answer :
Given: f (x) = cos (x2)
This function f is defined for every real number and f can be written as the composition of two functions as
f = g o h, where g (x) = cos x and h (x) = x2
It has to be first proved that g (x) = cos x and h (x) = x2 are continuous functions.
It is evident that g is defined for every real number.
Let c be a real number.
Then, g (c) = cos c
So, g (x) = cos x is a continuous function.
Now,
h (x) = x2
Clearly, h is defined for every real number.
Let k be a real number, then h (k) = k2
So, h is a continuous function.
It is known that for real valued functions g and h, such that (g o h) is defined at x = c, if g is continuous at x = c and if f is continuous at g (c), then, (f o g) is continuous at x = c.
Therefore, is a continuous function.
Q17.
Answer :
The given function f is
It is evident that f is defined at all points of the real line.
Let c be a real number.
Case I:
So, f is continuous at all points x ≠ 0
Case II:
limx→0-fx=limx→0-x2 sin 1x=limx→0x2 sin 1xIt is known that -1≤sin 1x≤1, x≠0.⇒-x2 ≤ x2 sin 1x ≤ x2⇒limx→0-x2 ≤ limx→0x2 sin 1x ≤ limx→0x2⇒0 ≤ limx→0x2 sin 1x ≤ 0⇒limx→0x2 sin 1x = 0⇒limx→0-fx = 0Similarly, limx→0+fx =limx→0+x2 sin 1x =limx→0x2 sin 1x = 0
So, f is continuous at x = 0
From the above observations, it can be concluded that f is continuous at every point of the real line.
Thus, f is a continuous function.
Page 9.38 (Very Short Answers)
Q1.
Answer :
Continuity at a point:
A function fx is said to be continuous at a point x = a of its domain, iff limx→afx=fa.
Thus, fx is continuous at x=a.⇔limx→afx = fa ⇔limx→a-fx =limx→a+fx = fa
Q2.
Answer :
If fx is a function defined in its domain such that limx→afx=fa, then fx becomes continuous at x=a.
Q3.
Answer :
If fxis continuous at x = 0, then limx→0fx=f0 …(1)
Given: fx=x1-1-x
⇒fx = x1+1-x1-1-x1+1-x⇒fx = x1+1-x1-1-x⇒fx = 1+1-x
limx→01+1-x=f0 From eq. (1)
⇒f0=2
So, for f0=2, the function f(x) becomes continuous at x = 0.
Q4.
Answer :
If fx is continuous at x=0, then
limx→0fx=f0
⇒limx→0xsin 3x = k⇒limx→01sin 3xx = k⇒limx→013 sin 3x3x = k⇒131limx→0sin 3x3x = k⇒k = 13
Q5.
Answer :
Given: fx=sin 10xx, x≠0 is continuous at x=0.
limx→0fx=f0
⇒limx→0sin 10xx=f0
⇒limx→010 sin 10x10x=f0⇒10limx→0sin 10x10x=f0⇒f0=10
Page 9.39 (Very Short Answers)
Q6.
Answer :
Given: fx=x2-16x-4, if x≠4k, if x=4
If fx is continuous at x=4, then
limx→4fx=f4
⇒limx→4×2-16x-4=k
⇒limx→4x+4x-4x-4=k⇒limx→4x+4=k⇒k=8
Q7.
Answer :
Given: fx=sin x2x, x≠00, x=0
We have
limx→0fx=limx→0sin x2x =limx→0x sin x2x2 =limx→0sin x2x2 limx→0x =1×0 =0 =f0
∴ limx→0fx=f0
Hence, fx is continuous at x=0.
Q8.
Answer :
Given: fx=1-cos xx2, x≠0k, x=0
If fx is continuous at x=0, then
limx→0fx=f0
⇒limx→01-cos xx2=k⇒limx→02sin x224x22=k⇒12limx→0sinx22x22=k⇒1×12=k⇒k=12
Q9.
Answer :
Given, fx=sin-1xx, x≠0k, x=0
If fx is continuous at x=0, then
limx→0fx=f0
⇒limx→0sin-1xx=f0
⇒limx→0sin-1xx=k⇒k=1 ∵limx→0sin-1xx =1
Q10.
Answer :
Given: fx=5x-4, 0<x≤14×2+3bx, 1<x<2
If fx is continuous at x=1, then
limx→1-fx=limx→1+fx=f1 …(1)
Now,
limx→1-fx=limh→0f1-h=limh→051-h-4=5-4=1
limx→1+fx=limh→0f1+h=limh→041+h2+3b1+h=4+3b
Also, f1=51-4=1
limx→1-fx =limx→1+fx = f1 From eq. (1)⇒1=4+3b=1
⇒1=4+3b⇒-3=3b⇒b=-1
Thus, for b=-1, the function fx is continuous at x=1.
Page 9.39 (Multiple Choice Questions)
Q1.
Answer :
(C) discontinuous exactly at three points
Given: fx=4-x24x-x3⇒fx=4-x2x4-x2⇒fx=1x, x≠0 and 4-x2≠0 or x≠0, ±2
Clearly, fx is defined and continuous for all real numbers except 0, ±2.
Therefore, fx is discontinuous exactly at three points.
Q2.
Answer :
(a) f’a+=ϕa
(b) f’a-=-ϕa
Here, fx=x-a ϕx
f’a+ =limh→0fa+h-fah =limh→0h+a-aϕa+h-a-aϕah =limh→0h ϕa+hh=limh→0ϕa+h=ϕa
Also,
f’a- =limh→0fa-h-fah=limh→0a-h-a ϕa-h-a-a ϕah=limh→0-h ϕa-hh=limh→0-ϕa-h=-ϕa
Q3.
Answer :
(a) f (x) is continuous and f’ (1+) = log10e
(d) f (x) is continuous and f’ (1−) = −log10e
Given: fx = log10 x=loge xloge 10=loge x×log10 e=log10 e loge x
⇒f’1+=limh→0f1+h-f1h= limh→0log10 e loge1+h-log10 e loge 1h=log10 elimh→0loge 1+hh=log10e×1=log10 e
Also,
f’1-=limh→0f1-h-f1h=limh→0log10 e loge 1-h-log10 e loge 1h=-log10 elimh→0loge 1-h-h=-log10 e×1=-log10 e
Q4.
Answer :
c 162 ln2 ln3
Given: fx=36x-9x-4x+12-1+cosx, x≠0k, x=0
If fx is continuous at x=0, then
limx→0fx=f0
⇒limx→036x-9x-4x+12-1+cos x=k⇒limx→09x4x-9x-4x+12-1+cos x=k⇒limx→09x4x-1-14x-12-1+cos x=k⇒limx→09x-14x-12-1+cos x=k⇒limx→09x-14x-12-2cos x2=k⇒limx→09x-14x-121-cos x2=k⇒limx→09x-14x-122sin2x4=k⇒limx→089x-14x-1162x2sin2x4x2=k⇒limx→089x-14x-12x2sin2x4x216=k⇒82limx→09x-14x-1x2sin2x4x42=k⇒82limx→09x-1x limx→04x-1xlimx→0sin x4x42=k⇒82×ln 9×ln 41=k ∵ limx→0ax-1x=a⇒82×2 ln 3×2 ln 21=k ⇒322×ln 3 ln 21=k⇒3222×ln 3 ln 21=k⇒k=162 ln 2 ln 3
Page 9.40 (Multiple Choice Questions)
Q5.
Answer :
(d) x except at x = 0 and x = 1.
Given: fx=x2-xx2-x, x≠0, 11 , x=0-1 , x=1
⇒fx=x x-1xx-1, x≠0, 11 , x=0-1 , x=1
⇒fx=1, x>11, x<0-1, 0<x<11, x=0-1, x=1
⇒fx=1, x>11, x≤0-1, 0<x≤1
So,
limx→0-fx=limh→0f-h=1
Also,
limx→0+fx=limh→0fh=-1
⇒limx→0+fx≠limx→0-fx
Thus, fx is discontinuous at x=0.
Now,
limx→1-fx=limh→0f1-h=-1
limx→1+fx=limh→0f1+h=1
⇒limx→1+fx≠limx→1-fx
So, fx is discontinuous at x=1.
Hence, fx is continuous for all x except at x=0 and x = 1.
Q6.
Answer :
c -164
If fx is continuous at x=π2, then
limx→π2fx=fπ2If π2-x=t, then⇒limt→0 fπ2-t=fπ2⇒limt→01-sin π2-t4t2×log sin π2-tlog1+π2-4ππ2-t+4π2-t2=k⇒limt→01-cos t4t2×log cos tlog1+π2-2π2+4πt+4π24+t2-πt=k⇒limt→01-cos t4t2×log cos tlog1-π2+4πt+π2+4t2-4πt=k⇒limt→01-cos t4t2×log cos tlog 1+4t2=k⇒limt→02 sin2 t216×t24×log cos tlog 1+4t2=k⇒216limt→0sin2 t2t24×log cos t4t2 log 1+4t24t2=k⇒18limt→0sin2 t2t22×log cos t4t2log 1+4t24t2=k⇒18limt→0sin2 t2t22×log 1-sin2 t4t2log1+4t24t2=k⇒18limt→0sin2t2t22×log1-sin2t8t2log1+4t24t2=k⇒164limt→0sin2t2t22×log1-sin2tt2log1+4t24t2=k⇒164lim t→0sint2t22×limt→0log1-sin2tt2limt→0log1+4t24t2=k⇒1641×limt→0-sin2t log 1-sin2tt2-sin2t=k⇒-164limt→0sin2t log 1-sin2tt2-sin2t=k⇒-164limt→0sintt2limt→0log 1-sin2t-sin2t=k⇒-164limt→0sintt2limt→0log1-sin2t-sin2t=k ⇒k=-164 ∵ lim x→0log1-xx=1
Q7.
Answer :
(c) e
Suppose fx is continuous at x=0.
Given: fx=x+1cotx
log fx=cot x log x+1 Taking log on both sides⇒limx→0log fx=limx→0cot x log x+1⇒limx→0log fx=limx→0log x+1tan x⇒limx→0log fx=limx→0log x+1xtan xx⇒limx→0log fx=limx→0log x+1xlimx→0tan xx⇒log limx→0fx=limx→0log x+1xlimx→0tan xx ∵ fx is continuous at x=0⇒log limx→0fx=1⇒limx→0fx=e⇒f0=e ∵ fx is continuous at x=0
Q8.
Answer :
b a+b
Given: fx=log1+ax-log1-bxx, x≠0k, x=0
If f(x) is continuous at x = 0, then
limx→0fx=f0
⇒limx→0log1+ax-log1-bxx=k
⇒limx→0alog1+axax-blog1-bxbx=k⇒alimx→0log1+axax-blimx→0log1-bxbx=k⇒alimx→0log1+axax+blimx→0log1-bx-bx=k⇒a×1+b×1=k ∵ limx→0log1+xx=1⇒k=a+b
Q9.
Answer :
(b) is not continuous at x = 0
Given: fx=e1x-1e1x+1, x≠00, x=0
We have
limx→0fx=limx→0e1x-1e1x+1
If e1x=t, then
x→0, t→∞
limx→0fx=limt→∞t-1t+1=limt→∞1-1t1+1t=1-01+0=1
Also, f0=0
∴ limx→0fx≠f0
Hence, fx is discontinuous at x=0.
Q10.
Answer :
(d) a = 1, b = −1.
Given: fx=x-4x-4+a, if x<4a+b, if x=4x-4x-4+b, if x>4
We have
(LHL at x = 4) = limx→4-fx=limh→0f4-h
=limh→04-h-44-h-4+a=limh→0-h-h+a=a-1
(RHL at x = 4) = limx→4+fx=limh→0f4+h
=limh→04+h-44+h-4+b=limh→0hh+b=b+1
Also,
f4=a+b
If f(x) is continuous at x = 4, then
limx→4-fx=limx→4+fx=f4
⇒a-1=b+1=a+b
⇒a-1=a+b and b+1=a+b
⇒b=-1 and a=1
Q11.
Answer :
(b)
Given: fx=cosx1xk, x=0, x≠0
Iffx is continuous at x=0, then
limx→0fx=f0
⇒limx→0cos x1x=kIf limx→afx=1 and limx→agx=0, then limx→afxgx=elimx→afx-1×gx⇒elimx→0cos x-1x= k⇒e0=k ∵ limx→0cos x-1x=0⇒k=1Q12.
Q12.
Answer :
(a) f (x) is continuous at x = 0, as well as at x = 1
Since modulus function is everywhere continuous , x and x-1 are also everywhere continuous.
Also,
It is known that if f and g are continuous functions, then f + g will also be continuous.
Thus, x+x-1 is everywhere continuous.
Hence, fx is continuous at x=0 and x=1.
Page 9.41 (Multiple Choice Questions)
Q13.
Answer :
(d) R − {1, 2}
Given: fx=x4-5×2+4x-1x-2, x≠1, 26, x=112, x=2
Now,x4-5×2+4=x4-x2-4×2+4=x2x2-1-4×2-1=x2-1×2-4=x-1x+1x-2x+2⇒fx=x-1x+1x-2x+2x-2x-1, x≠1, 26, x=112, x=2
⇒fx=x+1x+2, x<1-x+1x+2, 1<x<2x+1x+2, x>26, x=112, x=2
So,
limx→1-fx=limh→0f1-h=limh→01-h+11-h+2=2×3=6
limx→1+fx=limh→0f1+h=-limh→01+h+11+h+2=-2×3=-6
Also,
limx→2-fx=limh→0f2-h=-limh→02-h+12-h+2=-12
limx→2+fx=limh→0f2+h=limh→02+h+12+h+2=12
Thus, limx→1+fx≠limx→1-fx andlimx→2+fx≠limx→2-fx
Therefore, the only points of discontinuities of the function fx are x=1 and x=2 .
Hence, the given function is continuous on the set R − {1, 2}.
Q14.
Answer :
(c) a = -32, b ∈ R − {0}, c = 12
The given function can be rewritten as
fx=sin a+1 x+x sin xx, for x<0c , for x=0x+bx2-xbx32 , for x>0
⇒fx=sin a+1x+ sin xx, for x<0c , for x=01+bx-1bx , for x>0
We have
(LHL at x = 0) = limx→0-fx =limh→0f0-h =limh→0f-h
=limh→0-sin a+1h- sin -hh=limh→0-sin a+1hh-sin hh
=-a+1limh→0sin a+1ha+1h-lim h→0sin hh=-a-1
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh
=limh→01+bh-1bh=limh→0bhbh1+bh+1=limh→011+bh+1=12
Also, f0=c
If fx is continuous at x = 0, then
limx→0-fx=limx→0+fx=f0
⇒-a-1 = 12=c
⇒-a-1 = 12 and c=12
⇒a=-32, c=12
Now, 1+bx-1bx exists only if bx≠0⇒b≠0.
Thus, b∈R-0.
Q15.
Answer :
(c) n=mπ2n=mπ2
Here,
fπ2=mπ2+1
We have
(LHL at x=π2) = lim x→π2- fx =lim h→0fπ2-h=lim h→0mπ2-h+1=mπ2+1
(RHL at x=π2) = lim x→π2+ fx =lim h→0fπ2+h=lim h→0sinπ2+h+n=n+1
Thus,
If fx is continuous at x=π2, then
lim x→π2- fx =lim x→π2+ fx
⇒mπ2+1=n+1⇒mπ2=n
Q16.
Answer :
(c) -a12
Given: fx=a2-ax+x2-a2+ax+x2a+x-a-x
⇒ fx=a2-ax+x2-a2+ax+x2a2-ax+x2+a2+ax+x2a+x-a-xa2-ax+x2+a2+ax+x2⇒ fx=a2-ax+x2-a2+ax+x2a+x-a-xa2-ax+x2+a2+ax+x2⇒ fx=-2axa+x+a-xa+x-a-xa2-ax+x2+a2+ax+x2a+x+a-x⇒ fx=-2axa+x+a-xa+x-a+xa2-ax+x2+a2+ax+x2⇒ fx=-2axa+x+a-x2xa2-ax+x2+a2+ax+x2⇒ fx=-aa+x+a-xa2-ax+x2+a2+ax+x2
If fx is continuous for all x, then it will be continuous at x = 0 as well.
So, if fx is continuous at x = 0, then
limx→0fx=f0
⇒ limx→0-aa+x+a-xa2-ax+x2+a2+ax+x2=f0⇒ -2aaa2+a2=f0⇒ -2aaa+a=f0⇒ f0=-a
Q17.
Answer :
Given: fx=1, x≥11n2, 1n<x<1n-10, x=0
⇒fx=1, -1≤x≤11n2, 1n<x<1n-10, x=0
Case 1: x>1 or x<-1 and x>1
Here,
fx=1, which is the constant function
So, fx is continuous for all x≥1 or x≤-1 and x≥1.
Case 2: 1n<x<1n-1, n=2, 3, 4, …
Here,
fx=1n2, n=2, 3, 4, … fx=1n2, n=2, 3, 4, …, which is also a constant function.
So, fx is continuous for all 1n<x<1n-1, n=2, 3, 4, ….
Case 3: Consider the points x = -1 and x = 1.
We have
LHL at x=-1=limx→-1-fx=limx→-1-1=1RHL at x=-1=limx→-1+fx=limx→-1+14=14 ∵ fx=14 for -1<x<12, when n=2Clearly, limx→-1-fx≠limx→-1+fx at x=-1So, fx is discontinuous at x=-1.
Similarly, f(x) is discontinuous at x = 1.
Case 4: Consider the point x = 0.
We have
limx→0-fx=limh→0f1n-h=limh→0f1n-h=1n-12
limx→0+fx=limh→0f1n+h=limh→0f1n+h=1n2
limx→0+fx≠limx→0-fx
Thus, fx is discontinuous at x=0.
At x = 0, we have
limx→0-fx≠0=f0
So, fx is discontinuous at x=0.
Case 5: Consider the point x=1n, n=2, 3, 4, …
We have
limx→1n-fx=limh→0f1n-h=limh→0f1n-h=1n-12
limx→1n+fx=limh→0f1n+h=limh→0f1n+h=1n2
limx→1n+fx≠limx→1n-fx
Hence, fx is discontinuous only at x=±1n, n∈Z-0 and x=0.
Q18.
Answer :
(c) 2
For f(x) to be continuous at x = 0, we must have
limx→0fx=f0⇒f0= limx→0fx=limx→027-2×13-39-3243+5×15⇒f0=limx→027-2×13-2713324315-243+5×15=13limx→027-2×13-2713×24315-243+5x15x=-13limx→027-2×13-2713×243+5×15-24315x=215limx→027-2×13-2713-2×243+5×15-243155x=215limx→027-2×13-271327-2x-27243+5×15-24315243+5x-243=215×13×27-2315×243-45=215×13×1272315×124345=2
Page 9.42 (Multiple Choice Questions)
Q19.
Answer :
(d) none of these
Given: fx=2-256-7x185x+3215-2
For fx to be continuous at x = 0, we must have
limx→0fx=f0
⇒f0=limx→0fx=limx→02-256-7x185x+3215-2⇒f0=limx→025618-256-7x185x+3215-3215=-limx→0256-7×18-25618x5x+3215-3215x=-75limx→0256-7×18-256187x5x+3215-32155x=75limx→0256-7×18-25618256-7x-2565x+3215-32155x+32-32=75×18×256-7815×32-45=75×18×2415×27=764
Q20.
Answer :
(b) -12
Given: fx=1+px-1-pxx, if -1≤x<02x+1x-2, if 0≤x≤1
If fx is continuous at x = 0, then
limx→0-fx=limx→0+fx
⇒ limh→0f-h=limh→0fh ⇒limh→01-ph-1+ph-h=limh→02h+1h-2⇒limh→01-ph-1+ph1-ph+1+ph-h1-ph+1+ph=limh→02h+1h-2⇒limh→01-ph-1-ph-h1-ph+1+ph=limh→02h+1h-2⇒limh→0-2ph-h1-ph+1+ph=limh→02h+1h-2⇒limh→02p1-ph+1+ph=limh→02h+1h-2⇒2p2=1-2⇒p=-12
Q21.
Answer :
(c) a = -1, b = 1
Given: fx is continuous for 0 ≤ x < ∞.
This means that fx is continuous for x=1, 2.
Now,
If fx is continuous at x = 1, then
limx→1-fx=f1⇒limh→0f1-h=a⇒1-h2a=a⇒1a=a⇒a2=1⇒a=±1
If fx is continuous at x = 2, then
limx→2-fx=f2⇒limh→0f2-h=2b2-4b2⇒limh→0a=b2-2b⇒a=b2-2b⇒b2-2b-a=0
∴ For a = 1, we have
b2-2b-1=0⇒b=2±4-4-12=1±2
Also,
For a = −1, we have
b2-2b+1=0⇒b-12=0⇒b=1
Thus, a=-1 and b=1
Q22.
Answer :
(a) 18
If fx is continuous at x=π2, then
limx→π2fx=fπ2
limx→π21-sin xπ-2×2=fπ2 …(1)
Suppose π2-x=t, then
limt→01-sin π2-t2t2=fπ2 From eq. (1)⇒limt→01-cos t4t2=fπ2⇒14limt→02 sin2 t2t2=fπ2⇒14limt→024 sin2 t2t24=fπ2⇒18limt→0sin2 t2t24=fπ2⇒18limt→0sin t2t22=fπ2⇒fπ2=λ=18
Q23.
Answer :
(d) none of these
For f(x) to be continuous at x=0, we must have
limx→0fx=f0
limx→04x-13sinxa log1+x23=12log 43
⇒limx→04x-13x3sinxalog1+x23x3=12log 43⇒limx→0a4x-1x3sinxaxalog1+x23x2=12log 43⇒3alimx→04x-1x3sinxaxalog1+x23x23=12log 43⇒3alimx→04x-1x3limx→0sinxaxalimx→0log1+x23x23=12log 43⇒3alog 43=12log 43 ∵ limx→0ax-1x=log a, limx→0log1+xx=1 andlimx→0sin xx=1⇒a=4
Q24.
Answer :
c 2n+1π2: n∈Z
When tan2n+1π2= tannπ+π2=-cotnπ, it is not defined at the integral points. n∈Z
Hence, fx is discontinuous on the set 2n+1π2: n∈Z.
Q25.
Answer :
(b) 6
Given: fx=sin 3xxk2, x=0, x≠0
If fx is continuous at x=0, then
limx→0fx=f0
⇒limx→0sin 3xx=f0⇒3limx→0sin 3x3x=k2⇒3×1=k2⇒k2=3⇒k=6
Q26.
Answer :
(b) 13
Given: fx=2x-sin-1x2x+tan-1x
If f(x) is continuous at x = 0, then
limx→0fx=f0⇒limx→02x-sin-1x2x+tan-1x=f0⇒limx→0x2-sin-1xxx2+tan-1xx=f0⇒limx→02-sin-1xx2+tan-1xx=f0⇒2-limx→0sin-1xx2+limx→0tan-1xx=f0⇒2-12+1=f0⇒f0=13
Page 9.43 (Multiple Choice Questions)
Q27.
Answer :
(a) −1
Given: fx is continuous at every point of its domain. So, it is continuous at x=1.
⇒limx→1+fx=f1⇒limh→0f1+h=f1⇒limh→041+h2+3b1+h=51-4⇒4+3b=1⇒-3=3b⇒b=-1
Q28.
Answer :
(b) {0, 1}
Given: fx=11-x
Clearly, f:R-1→R
Now,
ffx=f11-x=11-11-x=1-x-x=x-1x
∴ fof:R-0, 1→R
Now,
fffx=fx-1x=11-x-1x=x
∴ fofof:R-0, 1→R
Thus, fffx is not defined at x=0, 1.
Hence, fffx is discontinuous at {0, 1}.
Q29.
Answer :
(b) 12
If fx is continuous at x=π4, then
limx→π4fx=fπ4
⇒limx→π4tan π4-xcot 2x=fπ4
If π4-x=y, then x→π4 and y→0.
∴ limy→0tan ycot 2π4-y=fπ4⇒limy→0tanycotπ2-2y=fπ4⇒limy→0tan ytan 2y=fπ4⇒limy→0tan yytan 2yy=fπ4⇒limy→0tan yy2 tan 2y2y=fπ4⇒12limy→0tan yytan 2y2y=fπ4⇒12limy→0tan yylimy→0tan 2y2y=fπ4⇒1211=fπ4⇒fπ4=12
Q30.
Answer :
Here,
x3+x2-16x+20=x3-2×2+3×2-6x-10x+20=x2x-2+3xx-2-10x-2=x-2×2+3x-10=x-2x-2x+5=x-22 x+5
So, the given function can be rewritten as
fx=x-22x+5x-2
⇒fx=x-2x+5
If fx is continuous at x=2, then
limx→2fx=f2
⇒limx→2x-2x+5=f2⇒f2=0
Hence, in order to make fx continuous at x=2, f2 should be defined as 0.
Q31.
Answer :
(a) 12
Given: fx=a sin π2x+1 , x≤0tan x-sin xx3 , x>0
We have
(LHL at x = 0) = limx→0-fx=limh→0f0-h=limh→0f-h=limh→0a sin π2-h+1=a sin π2=a
(RHL at x = 0) = limx→0+fx=limh→0f0+h=limh→0fh=limh→0tan h-sin hh3
=limh→0sin hcos h-sin hh3=limh→0sin hcos h1-cos hh3=limh→01-cos h tan hh3=limh→02 sin2 h2 tan h4×h24×h=24limh→0sin2 h2 tan hh24×h=12limh→0sin h2h22×limh→0tanhh=12×1×1=12
If fx is continuous at x=0, thenlimx→0-fx=limx→0+fx⇒a=12
Q32.
Answer :
(d) (5, 2)
If f(x) is continuous at x = 1, then
limx→1-fx=f1
⇒limh→0f1-h=4 ∵ f1=4⇒limh→0a1-h2+b=4 ⇒a+b=4
Thus, the possible values of (a, b) can be 2, 2, 3, 1, 4, 0. But a, b≠5, 2.
Hence, for a, b=5, 2, fx cannot be continuous at x = 1.
Disclaimer: The question in the book has some error. The solution here is created according to the question given in the book.
Q33.
Answer :
b 5
Given: fx=log 1+3x-log 1-2xx, x≠0k, x=0
If f(x) is continuous at x = 0, thenlimx→0fx=f0.
⇒limx→0log1+3x-log1-2xx=k
⇒limx→03 log 1+3x3x-2 log 1-2x2x=k⇒3limx→0log 1+3x3x-2limx→0log 1-2x2x=k⇒3limx→0log 1+3x3x+2limx→0log 1-2x-2x=k⇒3×1+2×1=k ∵ limx→0log 1+xx=1⇒k=3+2=5
Q34.
Answer :
(b) 50
If fx is continuous at x=0, then
limx→0-fx=f0
⇒limh→0f-h=f0
⇒limh→01-cos -10h-h2=f0⇒limh→01-cos 10hh2=f0⇒limh→02 sin2 5hh2=a⇒limh→02×25sin2 5h25h2=a⇒50limh→0sin2 5h5h2=a⇒50limh→0sin 5h5h2=a⇒a=50
Page 9.44 (Multiple Choice Questions)
Q35.
Answer :
(a) 0
Given: fx=x sin1x, x≠0
Here,
limx→0x sin 1x=limx→0x limx→0sin1x=0×limx→0sin1x=0
If f(x) is continuous at x = 0, thenlimx→0fx=f0.
⇒f0=0
Q36.
Answer :
(d) none of these
If fx is continuous at x=0, then
limx→0fx=f0⇒limx→0sin1x=kBut limx→0sin1x does not exist. Thus, there does not exist any k that makes fx a continuous function.
Q37.
Answer :
c a=log23, b=23, c=1
Given: fx=1+ax1x, x<0b, x=0x+c13-1x+112-1, x>0
If fx is continuous at x=0, then
limx→0-fx=limx→0+fx =f0
⇒limx→0-fx=f0⇒limh→0f-h=f0⇒limh→01-ah-1h=f0⇒limh→0alog 1-ah-ah=log b⇒a×1=log b ∵limx→0log 1+xx=1⇒a=log b
Also,
limx→0+fx =f0
⇒limx→0+fx=f0⇒limh→0fh=f0⇒limh→0h+c13-1h+112-1=f0⇒limh→0h+c13-1h+112-1×h+112+1h+112+1=f0⇒limh→0h+c13-1h×h+112+1=b⇒limh→0h+c13-1h×limh→0h+112+1=b⇒limh→0h+c13-1h×2=b⇒limh→0h+c13-113h+c-c=b2⇒c13-13=b2 ∵ limx→axn-anx-a=nan-1, where c=1⇒13=b2⇒23=b∴ a=log23
Q38.
Answer :
b x=52=5
If 0≤x≤1, then fx=2x.
Since fx=2x is a polynomial function, it is continuous.
Thus, fx is continuous for every 0≤x≤1.
If 1<x<52, then fx=4-2x. Since 2x is a polynomial function and 4 is a constant function, both of them are continuous. So, their difference will also be continuous.
Thus, fx is continuous for every 1<x<52.
If 52≤x≤4, then fx=2x-7. Since 2x is a polynomial function and 7 is continuous function, their difference will also be continuous.
Thus, fx is continuous for every 52≤x≤4.
Now,
Consider the point x=1. Here,
limx→1-fx=limh→0f1-h=limh→021-h=2
limx→1+fx=limh→0f1+h=limh→04-21+h=2
Also, f1=21=2
⇒limx→1-fx=limx→1+fx=f1
Thus, fx is continuous at x=1.
Now,
Consider the point x=52. Here,
limx→52-fx=limh→0f52-h=limh→04-252-h=-1
limx→52+fx=limh→0f52+h=limh→0252-h-7=-2
⇒limx→52+fx ≠limx→52-fx
Thus, fx is discontinuous at x=52.
Q39.
Answer :
(b) a=13 , b=83
Given: fx=1-sin2x3cos2x, if x<π2a, if x=π2b1-sinxπ-2×2, if x>π2
We have
(LHL at x = π2) = limx→π2-fx=limh→0fπ2-h
=limh→01-sin2 π2-h3 cos2 π2-h=limh→01-cos2 h3 sin2 h=13limh→0 sin2 h sin2 h=13
(RHL at x = π2) = limx→π2+fx=limh→0fπ2+h
=limh→0b1-sin π2+hπ-2π2+h2=limh→0b1-cos h-2h2=limh→02b sin2h24h2=limh→02b sin2h216h24=b8limh→0sinh2h22=b8×1=b8
Also, fπ2=a
If f(x) is continuous at x = π2, then
limx→π2-fx =lim x→π2+fx=fπ2
⇒13 =b8 = a
⇒a=13 and b=83
Q40.
Answer :
(b) x = 3
If x≤1, then fx=152×2+3.
Since 2×2+3 is a polynomial function and 15 is a constant function, both of them are continuous. So, their product will also be continuous.
Thus, fx is continuous at x≤1.
If 1<x<3, then fx=6-5x.
Since 5x is a polynomial function and 6 is a constant function, both of them are continuous. So, their difference will also be continuous.
Thus, fx is continuous for every 1<x<3.
If x≥3, then fx=x-3.
Since x-3 is a polynomial function, it is continuous. So, fx is continuous for every x≥3.
Now,
Consider the point x=1. Here,
limx→1-fx=limh→0f1-h=limh→01521-h2+3=1
limx→1+fx=limh→0f1+h=limh→06-51+h=1
Also,
f1=15212+3=1
Thus,
limx→1-fx=limx→1+fx=f1
Hence, fx is continuous at x=1.
Now,
Consider the point x=3. Here,
limx→3-fx=limh→0f3-h=limh→06-53-h=-9
limx→3+fx=limh→0f3+h=limh→03+h-3=0
Also,
f1=15212+3=1
Thus,
limx→3-fx≠limx→3+fx
Hence, fx is discontinuous at x=3.
So, the only point of discontinuity of fx is x=3.
Page 9.45 (Multiple Choice Questions)
Q41.
Answer :
(d) −1
Given: fx=5x-4, if 0<x≤14×2+3ax, if 1<x<2
If fx is continuous in its domain, then it will be continuous at x=1.
Now,
limx→1-fx=limh→0f1-h=limh→051-h-4=5-4=1limx→1+fx=limh→0f1+h=limh→041+h2+3a1+h=4+3a
Since f(x) is continuous at x = 1,
limx→1-fx=limx→1+fx
⇒4+3a=1⇒3a=-3⇒a=-1
Q42.
Answer :
(a) 0
Given: fx=sincos x-cos xπ-2×2, x≠π2k, x=π2
If f(x) is continuous at x=π2, then
limx→π2fx=fπ2
⇒limx→π2sincos x-cos xπ-2×2=k
Now,
π2-x=y
⇒π-2x=2y
Also, x→π2, y→0
⇒limy→0sincosπ2-y-cosπ2-y4y2=k
⇒limy→0sinsin y-siny4y2=k
⇒limy→02 sinsin y-y2 cossin y+y24y2=k ∵ sin C – sin D=2 sinC-D2 cosC+D2⇒12limy→0sinsin y-y2 ycossin y+y2y=k⇒12limy→0sin y-y2 sinsin y-y2 ysin y-y2cossin y+y2y=k⇒12limy→0sin y-y2ysinsin y-y2sin y-y2cossin y+y2y=k⇒12limy→0sin y-y2ylimy→0sinsin y-y2sin y-y2limy→0cossin y+y2y=k⇒14limy→0sin yy-1limy→0sinsin y-y2sin y-y2limy→0cossin y+y2y=k⇒14×0×1×limy→0cossin y+y2y=k⇒0=k
Page 10.9 Ex.10.1
Q1.
Answer :
Given: f(x) = |x-2| = x-2, x≥2-x+2, x<2
Continuity at x=2: We have,
(LHL at x = 2)
=limx→2- f(x) = limh→0 f(2-h) = lim h→0 (-2+h)+2= 0.
(RHL at x = 2)
=lim x→2+f(x) = limh→0 f(2+h) = limh→0 2+h-2 = 0.
and f(2) = 0
Thus, limx→2- f(x) = limx→2+ f(x) = f(2)f(2).
Hence, f(x) is continuous at x=2.
Differentiability at x = 2: We have,
(LHD at x = 2)
=limx→2- f(x) – f(2)x-2 = limx→2 (-x+2) – 0x-2 = limx→2 -(x-2)x-2 = limx→2 (-1) =-1
(RHD at x=2)
= =limx→2+ f(x) – f(2)x-2 = limx→2 (x-2) – 0x-2 = limx→2 1 = 1
Thus, limx→2- f(x) ≠ limx→2+ f(x).
Hence, f(x) is not differentiable at x=2 .
Q2.
Answer :
Disclaimer: It might be a wrong question because f(x) is differentiable at x=0
Given: f(x) = x13.
We have,
(LHD at x = 0)
limx→0- f(x) – f(0)x-0=limh→0 f(0-h) – f(0)0-h-0=limh→0 0-h13-013-h=limh→0 -h13-h=limh→0 -h-23= 0
(RHD at x = 0)
limx→0+ f(x) – f(0)x-0=limh→0 f(0+h) – f(0)0+h-0=limh→0 0+h13-013-h=limh→0 h13h=limh→0 h-23= 0
LHD at (x = 0)= RHD at (x = 0)
Hence, f(x) = x13 is differentiable at x = 0
Q3.
Answer :
Given: f(x) =12x-13, x≤3.2×2 + 5, x>3.
We have to show that the given function is differentiable at x = 3.
We have,
(LHD at x=3) = lim x→3- f(x) – f(3)x-3
= lim x→3 12x-13 – 23x-3= limx→3 12x-36x-3= limx→3 12 (x-3)x-3= limx→3 12 = 12
(RHD at x = 3) = limx→3+ f(x) – f(3)x-3
= limx→3 2×2+5 – 23x-3= limx→3 2×2 -18x-3= limx→3 2 (x2 -9)x-3=limx→3 2(x+3) = 2×6 = 12
Thus, (LHD at x=3) = (RHD at x=3) = 12.
So, f(x) is differentiable at x=3 and f'(3) = 12.
Q4.
Answer :
Given:
f(x) = 3x-2, 0<x≤12×2-x, 1<x≤25x-4, x>2
First , we will show that f(x) is continuos at x=2.
We have,
(LHL at x=2)
=lim x→2- f(x) = lim h→0 f(2-h) = limh→0 2(2-h)2 – (2-h) = limh→0 (8 + 2h2 – 8h – 2 + h) = 6
(RHL at x = 2)
=limx→2+ f(x) = limh→0 f(2+h) = limh→0 5(2+h) – 4 = limh→0 (10 + 5h -4) = 6
and f(2) = 2×4 – 2 = 6.
Thus, limx→2- f(x) = limx→2+ f(x) = f(2).
Hence the function is continuous at x=2.
Now, we will check whether the given function is differentiable at x = 2.
We have,
(LHD at x = 2)
limx→2- f(x) – f(2)x-2 = limh→0 f(2-h) – f(2)-h = limh→0 2h2 -7h + 6 – 6-h =limh→0 -2h + 7 = 7
(RHD at x = 2)
limx→2+ f(x) – f(2)x-2 = limh→0 f(2+h) – f(2)h = limh→0 10 + 5h – 4 -6h= 5
Thus, LHD at x=2 ≠ RHD at x = 2.
Hence, function is not differentiable at x = 2.
Q5.
Answer :
Given:
f(x) = xm sin1x0 x≠0 , x=0
(i) Let m=2, then the function becomes f(x) = x2 sin1x0 , x≠0, x=0
Differentiability at x=0:
limx→0 f(x) – f(0)x-0 = limx→0 f(x)x = limx→0 x sin1x =0.
[ ∵ limx→0 x sin1x = 0 , as x sin1x – 0 = x sin1x = x sin1x ≤x (∵sinθ≤1 for all θ) and hence x sin1x<0 when x-0<εx-0<ε ]
So, f'(0) = 0, which means f is differentiable at x=0.
Hence the given function is differentiable at x=0.
(ii) Let m=12, 0<m<1. Then the function becomes
f(x) = x120sin1x , x≠0 , x=0
Continuity at x=0:
(LHL at x=0) = limx→0- f(x) = limh→0 f(0-h) = limh→0 (-h)12 sin10-h = limh→0 h12 sin1h = limh→0 h32 = 0.
(RHL at x=0) = limx→0+ f(x) = limh→0 f(0+h) = limh→0 h12 sin1h = limh→0 h32 = 0.
and f(0) = 0
LHL at x=0 = RHL at x=0 = limx→0 f(x),
Hence continuous.
Now Differentiabilty at x=0 when 0<m<1.
(LHD at x=0) = limx→0- f(x) – f(0)x-0 = limh→0 f(0-h) – f(0)0-h-0 =limh→0 (-h)12 sin1-h-h
Q6.
Answer :
Given:
f(x) = x2+3x+a, x≤1bx+2, x>1
It is given that the function is differentiable at each x∈R and every differentiable function is continuous.
So, f(x) is continuous at x=1.
Therefore,
limx→1- f(x)=limx→1+ f(x) = f(1)
⇒limx→1 x2+3x+a = limx→1 bx+2 = a+4 Using def. of f(x) ⇒ a+4 = b+2 = a+4 …(i)
Since, f(x) is differentiable at x=1. So,
(LHD at x = 1) = (RHD at x = 1)
limx→1- f(x) – f(1)x-1 = limx→1+ f(x) – f(1)x-1⇒limx→1 x2+3x+a-a-4x-1 = limx→1 bx+2 -4-ax-1 Using def. of f(x)⇒ limx→1 (x+4) (x-1)x-1= limx→1 bx-2-ax-1⇒ limx→1 (x+4) (x-1)x-1= limx→1 bx-bx-1 Using (i) ⇒ limx→1 (x+4) (x-1)x-1 = limx→1 b(x-1)x-1⇒ 5 = b
From (i), we have
a+4 = b+2⇒a+4 = 5+2⇒a = 7-4 ⇒a= 3
Hence, a=3 , b=5.
Q7.
Answer :
Given: f(x) = 2x-3 [x] , x≥1sinπx2, x<1
Continuity at x = 1:
(LHL at x = 1) = limx→1-f(x)=limh→0f(1-h)=limh→0 sinπ (1-h)2=sinπ2=1
(RHL at x = 1) = limx→1+ f(x) = limh→0 f(1+h) = limh→0 2(1+h)-31+h=limh→0 2(1+h)-3=1
Hence, (LHL at x = 1) = (RHL at x = 1)
Differentiability at x = 1:
LHD at x=1=limx→1-fx-f1x-1LHD at x=1=limh→0f1-h-f11-h-1LHD at x=1=limh→0f1-h-f1-hLHD at x=1=limh→0sinπ1-h2-1-hLHD at x=1=limh→0cosπh2-1-hLHD at x=1=-π2limh→0cosπh2-1π2h=0RHD at x=1=limx→1+fx-f1x-1RHD at x=1=limh→0f1+h-f11+h-1RHD at x=1=limh→0f1+h-f1hRHD at x=1=limh→0-21+h-3-1hRHD at x=1=limh→0-2hh=-2
LHD ≠ RHD
Hence, the function is continuous but not differentiable at x = 1.
Q8.
Answer :
Given: f(x) =ax2+b, x<11x, x≥1
⇒ f(x) = -1x , x<-1ax2-b, -1<x<11x, x≥1
It is given that the given function is differentiable at x = 1.
We know every differentiable function is continuous. Therefore it is continuous at x=1. Then,
lim x→1- f(x) = limx→1+ f(x) ⇒limx→1 ax2-b = limx→1 1x⇒ a-b = 1 …(i)
It is also differentiable at x=1. Therefore,
(LHD at x = 1) = (RHD at x = 1)
⇒limx→1-f(x) – f(1)x-1 = limx→1+f(x) – f(1)x-1⇒ limx→1 ax2-b – 1x-1= limx→1 1x – 1x-1 ⇒ limx→1 ax2+1-a-1x-1=limx→1 -(x-1)x-1 Using (i) ⇒ limx→1 a (x+1)= limx→1 -1 ⇒ 2a=-1 ⇒ a =-12
From (i), we have:
a-b = 1⇒-12 – b = 1⇒ b =- 32
Hence, when a=-12 and b=-32 the function is differentiable at x = 1.
Q9.
Answer :
Given: f(x) = x2, x≤cax+b, x>c
It is given that the function is differentiable at x=c.
Every differentiable function is continuous. Therefore, it is continuous at x = c.
Then,
limx→c-f(x) = limx→c+f(x) = f(c)⇒ limx→c x2 = limx→c ax+b = c2⇒ c2 = ac+b ….(i)
Now, f(x) is differentiable at x = c.
(LHD at x=c) = (RHD at x=c)
⇒limx→c-f(x) – f(c)x-c = limx→c+f(x) – f(c)x-c
⇒limx→cx2-c2x-c = limx→cax+b-c2x-c
⇒limx→c (x+c) = limx→cax+b – ac-bx-c [Using (i)]
⇒limx→c (x+c) = limx→c a⇒2c=a
From (i), we have
c2= ac+b⇒c2 = 2c2 + b⇒b =-c2
Hence, when a=2c and b=-c2, the given function is differentiable at x=c.
Q10.
Answer :
The function f(x) = x-0+x-1+x-2+x-3+x-4 is continuous everywhere
but not differentiable at x = 0,1,2,3 and 4
Page 10.15 Ex.10.2
Q1.
Answer :
Given: f(x) = x2.
We know a polynomial function is everywhere differentiable. Therefore f(x) is differentiable at x=2.
f'(2) = limh→0 f(2+h) – f(2)h⇒ f'(2) = limh→0 (2+h)2 – 22h⇒ f'(2) = limh→0 (4+h2+4h) – 4h⇒ f'(2) = limh→0 h (h+4)h⇒ f'(2) = 4
Q2.
Answer :
Given: f(x) = x2-4x+7
Clearly, f(x) being a polynomial function, is everywhere differentiable. The derivative of f at x is given by:
f'(x) = limh→0 f(x+h) – f(x)h⇒ f'(x) = limh→0 x+h2 -4(x+h) +7 – (x2 -4x+7)h⇒ f'(x) = limh→0 x2+h2+2xh -4x-4h+7 -x2+4x-7h⇒ f'(x) = limh→0 h2 +2xh -4hh⇒ f'(x) = limh→0 h(h+2x-4)h⇒ f'(x) = 2x-4
Now,
f'(5) = 2×5 – 4= 6f’72 = 2×72 – 4 = 3
Therefore, f'(5) = 2×3 = 2f’72
Hence proved.
Q3.
Answer :
Given: f(x) = 2×3-9×2+12x+9
Clearly, being a polynomial function, is differentiable everywhere. Therefore the derivative of f at x is given by:
f'(x) = limh→0 f(x+h – f(x)h⇒ f'(x) = limh→0 2(x+h)3-9(x+h)2+12(x+h) + 9 – 2×3+9×2-12x-9h⇒ f'(x) = limh→0 2×3 + 2h3+6x2h +6xh2 -9×2-9h2-18xh+12x+12h+9 -2×3+9×2-12x-9h⇒ f'(x) = limh→0 2h3 +6x2h +6xh2 -9h2 -18xh+12hh⇒ f'(x) = limh→0 h(h2 +6×2+6xh -9h-18x+12)h⇒ f'(x) = 6×2-18x+12
So,
f'(1) = 6×2-3x+2 = 6×(1-3+2) = 0f'(2) = 6×2-3x+2 = 6×(4-6+2) = 0
Hence the derivative at x=1 and x=2 are equal.
Q4.
Answer :
Given: ϕ(x) = λx2+7x-4
Clearly, being a polynomial function, is differentiable everywhere. Therefore the derivative of ϕ at x is given by:
ϕ'(x) = limh→0 ϕ(x+h) – ϕ(x)h⇒ ϕ'(x) =limh→0 λ(x+h)2 +7(x+h) -4 – λx2-7x+4h⇒ ϕ'(x) = limh→0 λx2 +λh2+2λxh+7x+7h-4-λx2-7x+4h⇒ ϕ'(x) = limh→0 λh2 +2λxh+7hh⇒ ϕ'(x) = limh→0 h(λh +2λx+7)h⇒ ϕ'(x) = 2λx+7
It is given ϕ'(5) = 97
Thus,
ϕ'(5) = 10λ + 7 = 97⇒ 10λ+7 =97⇒ 10λ = 90⇒ λ = 9
Q5.
Answer :
Given: f(x) = x3+7×2+8x-9
Clearly, being a polynomial function, is differentiable everywhere. Therefore the derivative of f at x is given by:
f'(x) = limh→0f(x+h) – f(x)h⇒ f'(x) = limh→0 (x+h)3+7(x+h)2+8(x+h)-9 – x3 -7×2-8x+9h⇒ f'(x) = limh→0 x3+h3+3x2h + 3xh2+7×2+7h2+14xh+8x+8h-9-x3-7×2-8x+9h⇒ f'(x) = limh→0 h3+3x2h+3xh2+7h2+14xh+8hh⇒ f'(x) = limh→0 h(h2+3×2+3xh+7h+14x+8)h⇒ f'(x) = limh→0 h2+3×2+3xh+7h+14x+8⇒ f'(x) = 3×2+14x+8
Thus,
f'(4) = 3×42+14×4+8 = 48+56+8 =112
Q6.
Answer :
Given: f(x) = mx+c
Clearly, being a polynomial function, is differentiable everywhere. Therefore the derivative of f at x is given by:
f'(x) = limh→0 f(x+h) – f(x)h⇒ f'(x) = limh→0 m(x+h) +c -mx-ch⇒ f'(x) = limh→0 mx+mh+c-mx-ch⇒ f'(x) = limh→0 mhh ⇒ f'(x) = m
Thus, f'(0) = m
Q7.
Answer :
We have,
f (x) = |log |x||
x=-x -∞<x<-1-x -1<x<0 x 0<x<1 x 1<x<∞log x=log -x -∞<x<-1log -x -1<x<0 log x 0<x<1 log x 1<x<∞log x=log -x -∞<x<-1-log -x -1<x<0 -log x 0<x<1 log x 1<x<∞
LHD at x=-1=limx→-1-fx-f-1x+1 =limx→-1-log -x-0x+1 =limh→0log 1+h-1-h+1 =-limh→0log 1+hh=-1
RHD at x=-1=limx→-1+fx-f-1x+1 =limx→-1+-log -x-0x+1 =limh→0-log 1-h-1+h+1 =limh→0-log 1-hh=1
Here, LHD ≠ RHD
So, function is not differentiable at x = − 1
At 0 function is not defined.
LHD at x=1=limx→1-fx-f1x-1 =limx→1–log x-0x-1 =limh→0-log 1-h1-h-1 =-limh→0log 1-hh=-1
RHD at x=1=limx→1+fx-f1x-1 =limx→1+log x-0x-1 =limh→0log 1+h1+h-1 =limh→0log 1+hh=1
Here, LHD ≠ RHD
So, function is not differentiable at x = 1
Hence, function is not differentiable at x = 0 and ± 1
At 0 function is not defined.
So, at 0 function is not continuous.
LHL at x=-1=limx→-1-fx =limx→-1-log -x =log 1=0RHL at x=-1=limx→-1+fx =limx→-1+-log -x =-log 1=0f-1=0Therefore, fx=log x is continuous at x=-1
LHL at x=1=limx→1-fx =limx→1–log x =-log 1=0RHL at x=1=limx→1+fx =limx→1+log x =log 1=0f1=0Therefore, at x=1, fx=log x is continuous.
Hence, function f (x) = |log |x|| is not continuous at x = 0
Q8.
Answer :
Given: f(x) = ex
⇒ f(x) = ex, x≥0e-x, x<0
Continuity:
(LHL at x = 0)
limx→0- f(x) = limh→0 f(0-h) = limh→0 e-(0-h) = limh→0 eh = 1
(RHL at x = 0)
limx→0+ f(x) = limh→0 f(0+h) = limh→0 e(0+h) = 1
and f(0) = e0 = 1
Thus, limx→0- f(x) = limx→0+ f(x) = f(0)
Hence,function is continuous at x = 0 .
Differentiability at x = 0.
(LHD at x = 0)
limx→0-f(x) – f(0)x-0= limh→0f(0-h) – f(0)0-h-0= limh→0 e-(0-h) – 1-h= limh→0 eh-1-h = -1 ∵ limh→0 eh-1h =1
(RHD at x = 0)
limx→0+f(x) – f(0)x-0= limh→0f(0+h) – f(0)0+h-0= limh→0 e(0+h) – 1h= limh→0 eh-1h = 1 ∵ limh→0 eh-1h =1
LHD at (x = 0)≠RHD at (x = 0)
Hence the function is not differentiable at x = 0.
Q9
Answer :
Given: fx=x-c cos 1x-c,x≠c0 ,x=c
Continuity:
(LHL at x = c)
limx→c- f(x) = limh→0 f(c-h) = limh→0 (c-h-c) cos1c-h-c = limh→0 -h cos1h Since , cos 1h is a bounded function and 0 ×bounded function is 0=0
(RHL at x = c)
limx→c+ f(x) =limh→0 f(c+h) = limh→0 (c+h-c) cos1c+h-c = limh→0 h cos1h Since, cos1h is a bounded function and 0× bounded function is 0=0
and
Differentiability at x = c
(LHD at x = c)
limx→c- f(x) – f(c)x-c = limh→0f(c-h) – f(c)c-h-c = limh→0 -h cos1-h – 0-h ∵0.cos 1c-c=0, as cos function is bounded function.=lim h→0cos1h=A number which oscillates between -1 and 1∴LHD (x=c) does not exist . Similarly , we can show that RHD(x=c) does not exist . Hence , f(x) is not differentiable at x=c
Q10.
Answer :
Let, f(x) = |sin x|
sin x=0, for x=nπ,sin x=-sin x 2m-1π< x<2mπ , where m∈Z sin x 2mπ< x<2m+1π , where m∈Z- sin x 2m+1π< x<2m+1π , where m∈Z
LHD at x=2mπ=limx→2mπ-fx-f2mπx-2mπ =limx→2mπ–sinx-0x-2mπ =limh→0-sin2mπ-h2mπ-h-2mπ =limh→0sinh-h=-1
RHD at x=2mπ=limx→2mπ+fx-f2mπx-2mπ =limx→2mπ+sinx-0x-2mπ =limh→0sin2mπ+h2mπ+h-2mπ =limh→0sinhh=1
Here, LHD ≠ RHD So, function is not differentiable at x=2mπ, where, m∈Z …..1
LHD at x=2m+1π=limx→2m+1π-fx-f2m+1πx-2m+1π =limx→2m+1π-sin x-0x-2m+1π =limh→0sin 2m+1π-h2m+1π-h-2m+1π =limh→0sin h-h=-1
RHD at x=2m+1π=limx→2m+1π+fx-f2m+1πx-2m+1π =limx→2m+1π+-sin x-0x-2m+1π =limh→0-sin 2m+1π+h2m+1π+h-2m+1π =limh→0sin hh=1
Here, LHD ≠ RHD. So, function is not differentiable at x=2m+1π, where, m∈Z …..2
From, 1 and 2, we getfx=sin x is not differentiable at x=nπ
We know that,cos x=cos x For all x∈RAlso we know that cos x is differentiable at all real points.Therefore, cos x is differentiable everywhere.
Page 10.16 (Very Short Answers)
Q1.
Answer :
Let f(x) be a real valued function defined on an open interval (a,b) and let c∈(a,b).
Then f(x) is said to be differentiable or derivable at x=c iff
limx→c f(x) – f(c)x-c exists finitely.
or, f'(c) =limx→c f(x) – f(c)x-c.
Q2.
Answer :
Yes, if a function is differentiable at a point then it is necessary continuous at that point.
Proof :Let a function f(x) be differentiable at x=c . Then, limx→c f(x)-f(c)x-cexists finitely.Let limx→c f(x)-f(c)x-c=f'(c)In order to prove that f(x) is continous at x=c , it is sufficient to show that limx→c f(x)=f(c) limx→c f(x)=limx→c f(x)-f(c)x-cx-c+f(c)⇒ limx→c f(x)=limx→c f(x)-f(c)x-cx-c+f(c)⇒ limx→c f(x)=limx→c f(x)-f(c)x-c. lim x→c x-c+f(c)⇒ limx→c f(x)=f'(c) ×0+f(c)⇒ limx→c f(x)=f(c)Hence, f(x) is continuous at x=c.
Q3.
Answer :
No, function may be continuous at a point but may not be differentiable at that point .
For example: function f(x) = |x| is continuous at x=0 but it is not differentiable at x=0.
Q4.
Answer :
Consider a function, f(x) = x, x>0-x, x≤0
This mod function is continuous at x=0 but not differentiable at x=0.
Continuity at x=0, we have:
(LHL at x = 0)
limx→0- f(x) = limh→0 f(0-h) = limh→0 -(0-h) = 0
(RHL at x = 0)
limx→0+ f(x) = limh→0 f(0+h) = limh→0 (0+h) = 0
and f(0) = 0
Thus, limx→0- f(x) = limx→0+ f(x) = f(0).
Hence, f(x) is continuous at x=0.
Now, we will check the differentiability at x=0, we have:
(LHD at x = 0)
limx→0- f(x) – f(0)x-0 = limh→0 f(0-h) – f(0)0-h-0 = limh→0 -(0-h) – 0-h = -1
(RHD at x = 0)
limx→0+ f(x) – f(0)x-0 = limh→0 f(0+h) – f(0)0+h-0 = limh→0 0+h – 0h = 1
Thus, limx→0- f(x) ≠ limx→0+ f(x)
Hence f(x) is not differentiable at x=0.
Q5.
Answer :
Given: f(x) is differentiable at x=c. Then,
limx→c f(x) – f(c)x-c exists finitely.
or, limx→c f(x) – f(c)x-c = f'(c).
Consider,
limx→c f(x) = limx→c f(x) – f(c)x-c (x-c) + f(c) limx→c f(x) = limx→c f(x) – f(c)x-c (x-c) + f(c)limx→c f(x) = limx→c f(x) – f(c)x-c limx→c (x-c) + f(c)limx→c f(x) = f'(c) × 0 + f(c) = f(c)
Q6.
Answer :
Given: f(x) = x-2 = x-2, x>2-x+2, x≤2
Now,
(LHD at x = 2)
limx→2- f(x) – f(2)x-2 = limh→0 f(2-h) – f(2)2-h-2 = limh→0 (-2+h+2) -0-h = -1
(RHD at x = 2)
limx→2+f(x) – f(2)x-2 = limh→0 f(2+h) – f(2)2+h-2 = limh→0 2+h-2 – 0h=1
Thus, (LHD at x = 2) ≠ (RHD at x = 2)
Hence, limx→2 f(x) – f(2)x-2 = f'(2) does not exist.
Q7.
Answer :
Given: f(x) = logex = -logex, 0<x<1logex, x≥1
Clearly f(x) is differentiable for all x>1 and for all x<1. So, we have to check the differentiability at x=1.
We have,
(LHD at x = 1)
limx→1- f(x) – f(1)x-1
= limx→1- -log x – log 1x-1=- limx→1- log xx-1=- limh→0 log (1-h)1-h-1=-limh→0log (1-h)-h =-1
(RHD at x=1)
= limx→1+ f(x) – f(1)x-1
=limx→1+ log x – log 1x-1=limx→1+ log xx-1= limh→0 log (1+h)1+h-1= limh→0 log (1+h)h=1
Thus, (LHD at x =1) ≠ (RHD at x =1)
So, f(x) is not differentiable at x=1.
Q8.
Answer :
We have,
f (x) = |log |x||
x=-x -∞<x<-1-x -1<x<0 x 0<x<1 x 1<x<∞log x=log -x -∞<x<-1log -x -1<x<0 log x 0<x<1 log x 1<x<∞log x=log -x -∞<x<-1-log -x -1<x<0 -log x 0<x<1 log x 1<x<∞
LHD at x=-1=limx→-1-fx-f-1x+1 =limx→-1-log -x-0x+1 =limh→0log 1+h-1-h+1 =-limh→0log 1+hh=-1
RHD at x=-1=limx→-1+fx-f-1x+1 =limx→-1+-log -x-0x+1 =limh→0-log 1-h-1+h+1 =limh→0-log 1-hh=1
Here, LHD ≠ RHD
So, function is not differentiable at x = − 1
At 0 function is not defined.
LHD at x=1=limx→1-fx-f1x-1 =limx→1–log x-0x-1 =limh→0-log 1-h1-h-1 =-limh→0log 1-hh=-1
RHD at x=1=limx→1+fx-f1x-1 =limx→1+log x-0x-1 =limh→0log 1+h1+h-1 =limh→0log 1+hh=1
Here, LHD ≠ RHD
So, function is not differentiable at x = 1
Hence, function is not differentiable at x = 0 and ± 1
Q9.
Answer :
Given: f(x) = x3 = x3, x≥0-x3, x<0
(LHD at x = 0)
limx→0-f(x) – f(0)x-0= limh→0 f(0-h) – f(0) x= limh→0 h3-h = 0.
(RHD at x = 0)
limx→0+ f(x) – f(0)x-0 = limx→0+ f(0+h) – f(0)x= limh→0 h3 – 0h = 0
and f(0) = 0.
Thus, (LHD at x=0) = (RHD at x = 0) = f(0)
Hence, limx→0f(x) – f(0)x-0 = f'(0) = 0
Q10.
Answer :
Given:
f(x) = x + x-1
⇒f(x) = -x-(x-1), x<0x-(x-1), 0≤x<1x+(x-1), x≥1⇒ f(x) = -2x+1, x<01, 0≤x<12x-1, x≥1
When x<0, we have:
f(x) =-2x+1 which, being a polynomial function is continuous and differentiable.
When 0≤x<1, we have:
f(x) =1 which, being a constant function is continuous and differentiable on (0,1).
When x≥1, we have:
f(x) =2x-1 which, being a polynomial function is continuous and differentiable on x>2.
Thus, the possible points of non- differentiability of f(x) are 0 and 1.
Now,
(LHD at x = 0)
limx→0-f(x) – f(0)x-0
= limx→0 -2x+1 – 1x-0 [∵ f(x) =-2x+1, x<0]
= limx→0 -2xx =-2
(RHD at x = 0)
= limx→0+ f(x) – f(0)x-0
= limx→01-1x-1=0 [∵ f(x)=1, 0≤x<1 ]
Thus, (LHD at x=0) ≠ (RHD at x=0)
Hence f(x) is not differentiable at x=0
Now, f(x) is not differentiable at x=1.
(LHD at x = 1)
limx→1-f(x) – f(1)x-1
= limx→1 1- 1x-1 =0
(RHD at x = 1)
= limx→1+f(x) – f(1)x-1
= limx→1 2x-1 – 1x-1= limx→1 2(x-1)x-1 = 2
Thus, (LHD at x =1) ≠ (RHD at x=1)
.
Hence f(x) is not differentiable at x=1.
Therefore, 0,1 are the points where f(x) is continuous but not differentiable.
Q11.
Answer :
Given: limx→cf(x) – f(c)x-c exists finitely. Then,
limx→c f(x) – f(c)x-c = f'(c).
Now,
limx→c f(x) = lim x→c f(x) – f(c)x-c (x-c) + f(c) = limx→c f(x) – f(c)x-c (x-c) + f(c) = limx→c f(x) – f(c)x-c limx→c (x-c) + f(c) = f'(c)×0 + f(c) = f(c)
Q12.
Answer :
Given: f(x) = x-1 + x-3
⇒ f(x) = -(x-1) -(x-3), x<1x-1 – (x-3), 1≤x<3 (x-1) + (x-3), x≥3
⇒ f(x) = -2x+4, x<12, 1≤x<32x-4, x≥3
We check differentiability at x = 2
(LHD at x = 2)
limx→2- f(x) – f(2)x-2 = limh→0 f(2-h) – f(2)2-h-2 = limh→0 2-2-h =0
Q13.
Answer :
Given: f(x) = x2 + 9
Now,
f(4) = 16+9 = 25 =5
So, f(x) – f(4)x-4 = x2 + 9 – 5x-4
On rationalising the numerator, we get
f(x) – f(4)x-4 = x2+9 -5x-4×x2+9 + 5×2+9 + 5 = x2+9 – 25(x-4) x2+9 + 5 = x2 – 16(x-4) x2+9 + 5 = (x+4)x2+9 + 5
Taking limit x→4, we have
limx→4 f(x) – f(4)x-4 = limx→4 (x+4)x2+9 + 5 = 810 = 45
Page 10.16 (Multiple Choice Questions)
Q1.
Answer :
Option (a) f (x) and g (x) both are continuous at x = 0
Given: fx = x , gx = x3
We know x is continuous at x=0 but not differentiable at x = 0 as (LHD at x = 0) ≠ (RHD at x = 0).
Now, for the function gx = x3 = x3, x≥0-x3, x<0
Continuity at x = 0:
(LHL at x = 0) = limx→0-gx = limh→0 g0-h = limh→0–h3 = limh→0 h3 = 0.
(RHL at x = 0) = limx→0+fx = limh→0f0+h = limh→0 h3 = 0.
and g0 = 0.
Thus, limx→0-gx = limx→0+gx = g0.
Hence, g(x) is continuous at x = 0.
Differentiability at x = 0:
(LHD at x = 0) = limx→0-fx – f0x-0 = limh→0f0-h – f00-h-0 = limh→0h3 -0-h = 0.
(RHD at x = 0) = limx→c+fx – f0x-0 = limh→0f0+h – f00+h-0 = limh→0h3 -0h = limh→0h3h =0
Thus, (LHD at x = 0) = (RHD at x = 0).
Hence, the function gx is differentiable at x = 0.
Q2.
Answer :
(b) continuous at x = 0
Given: f(x) = sin-1cos x.
Continuity at x = 0:
We have,
(LHL at x = 0)
limx→0- f(x) =limh→0 sin-1cos0-h = limh→0 sin-1cos h= sin-11= π2
(RHL at x = 0)
limx→0+ fx= limh→0 sin-1cos0+h= limh→0 sin-1cos h = sin-11 = π2
f(0) = sin-1cos 0 = sin-11 = π2
Differentiability at x = 0:
(LHD at x = 0)
limx→0- fx – f0x-0 = limh→0 sin-1cos0-h – π2-h = limh→0 sin-1cos-h -π2-h = limh→0 sin-1cosh -π2-h= limh→0 sin-1sin π2-h -π2-h= limh→0-h-h=1
RHD at x = 0
limx→0+ fx – f0x-0 = limh→0 sin-1cos0+h-π2h = limh→0 sin-1cosh-π2h = limh→0 sin-1sin π2-h-π2-h= limh→0-hh=-1
∴ LHD≠RHD
Hence, the function is not differentiable at x = 0 but is continuous at x = 0.
Page 10.17 (Multiple Choice Questions)
Q3.
Answer :
(a) -∞, ∞
We have,fx=xx⇒fx=-x2, x<0 0 , x=0 x2, x>0When, x<0, we have fx=-x2 which being a polynomial function is continuous and differentiable in -∞, 0When, x>0, we have fx=x2 which being a polynomial function is continuous and differentiable in 0, ∞Thus possible point of non-differentiability of fx is x=0Now, LHD at x=0 =limx→0- fx- f0x-0 =limx→0–x2- 0x =limh→0–h2-h =limh→0h =0And RHD at x=0 =limx→0+ fx- f0x-0 =limx→0+x2- 0x =limh→0h2h =lim h→0h =0∴LHD at x=0=RHD at x=0So, fx is also differentiable at x=0i.e. fx is differentiable in -∞, ∞
Q4.
Answer :
(b) not continuous at x = − 2
Given:
f(x) = x+2tan-1(x+2) , x≠-2 2 , x=-2
⇒ f(x) = -(x+2)tan-1(x+2), x<-2 (x+2)tan-1(x+2), x>-22 , x=-2
Continuity at x = − 2.
(LHL at x= − 2) = limx→-2-f(x)=limh→0f(-2-h)=limh→0-(-2-h+2)tan-1(-2-h+2)=limh→0htan-1(-h) =-1.
(RHL at x = −2) = limx→-2+f(x=limh→0f(-2+h=limh→0(-2+h+2)tan-1(-2+h+2)=limh→0htan-1(h) =1.
Also f(-2) = 2
Thus, limx→-2-f(x)≠limx→-2+ f(x) ≠ f(-2).
Therefore, given function is not continuous at x = − 2
Q5.
Answer :
(a) f is continuous
(c) f’ is continuous
We have,fx=x+x x =xx+x2 =xx+x2fx=2×2 x≥00 x<0To check continuity of fx at x=0LHL at x=0=limx→0-fx =limx→0-0 =0RHL at x=0=limx→0+fx =limx→0+2×2 =0And f0=0Here, LHL=RHL=f0Therefore, fx is continuous at x=0Hence, fx is continuous everywhere.
To check the differentiability of fx at x=0LHD at x=0=limx→0-fx-f0x-0 =limx→0-0-0x=0RHD at x=0=limx→0+fx-f0x-0 =limx→0-2×2-0x =limx→0-2×2-0x =limx→0-2x=0LHD=RHDTherefore, fx is derivative at x=0Hence, fx is differentiable everywhere.
f’x=4x x≥00 x<0To check continuity of f’x at x=0LHL at x=0=limx→0-f’x =limx→0-0 =0RHL at x=0=limx→0+f’x =limx→0+4x =0And f’0=0Here, LHL=RHL=f’0Therefore, f’x is continuous at x=0Hence, f’x is continuous everywhere.
f”x=4 x≥00 x<0To check continuity of f”x at x=0LHL at x=0=limx→0-f”x =limx→0-0 =0RHL at x=0=limx→0+f”x =limx→0+4 =4Therefore, LHL≠RHL Therefore, f”x is not continuous at x=0Hence, f”x is not continuous everywhere.
Q6.
Answer :
(a) continuous everywhere but not differentiable at x = 0
Given: f(x) = e-x = ex, x ≥0e-x, x<0Continuity :limx→0- f(x) = limh→0 f(0-h) = limh→0 e-(0-h) = limh→0 eh = 1
RHL at x = 0
limx→0+ f(x) = limh→0 f(0+h) = limh→0 e(0+h) = 1
and f(0) = f(0) = e0 = 1
Thus, limx→0- f(x) = limx→0+ f(x) = f
Hence, function is continuous at x = 0
Differentiability at x = 0
(LHD at x = 0)
limx→0-f(x) – f(0)x-0= limh→0f(0-h) – f(0)0-h-0= limh→0 e-(0-h) – 1-h= limh→0 ehh = ∞
Therefore, left hand derivative does not exist.
Hence, the function is not differentiable at x = 0.
Q7.
Answer :
(b) everywhere continuous but not differentiable at (2n + 1) π/2, n ∈ Z
We have,fx=cos x⇒fx=cos x, 2nπ≤x<4n+1π20, x=4n+1π2 -cos x, 4n+1π2<x<4n+3π2 0 , x=4n+3π2 cos x, 4n+3π2< x≤2n+2πWhen, x is in first quadrant, i.e. 2nπ≤x<4n+1π2 , we have fx=cos x which being a trigonometrical function is continuous and differentiable in 2nπ, 4n+1π2When, x is in second quadrant or in third quadrant, i.e., 4n+1π2<x<4n+3π2 , we have fx=-cos x which being a trigonometrical function is continuous and differentiable in 4n+1π2, 4n+3π2When, x is in fourth quadrant, i.e., 4n+3π2< x≤2n+2π , we have fx=cos x which being a trigonometrical function is continuous and differentiable in 4n+3π2, 2n+2πThus possible point of non-differentiability of fx are x=4n+1π2, 4n+3π2Now, LHD at x=4n+1π2 =limx→4n+1π2- fx- f4n+1π2x-4n+1π2 =limx→4n+1π2- cos x- 0x-4n+1π2 =limx→4n+1π2- -sin x1-0 By L’Hospital rule =-1And RHD at x=4n+1π2 =limx→4n+1π2+ fx- f4n+1π2x-4n+1π2 =limx→4n+1π2+ -cos x- 0x-4n+1π2 =limx→4n+1π2+ sin x1-0 By L’Hospital rule =1∴lim x→4n+1π2-fx ≠limx→4n+1π2+fxSo fx is not differentiable at x=4n+1π2Now, LHD at x=4n+3π2 =limx→4n+1π2- fx- f4n+3π2x-4n+3π2 =limx→4n+3π2- -cos x- 0x-4n+3π2 =limx→4n+3π2- sin x1-0 By L’Hospital rule =1And RHD at x=4n+3π2 =limx→4n+3π2+ fx- f4n+3π2x-4n+3π2 =limx→4n+3π2+ cos x- 0x-4n+3π2 =limx→4n+3π2+ -sin x1-0 By L’Hospital rule =-1∴lim x→4n+3π2-fx ≠limx→4n+3π2+fxSo fx is not differentiable at x=4n+3π2Therefore, fx is neither differentiable at 4n+1π2 nor at 4n+3π2i.e. fx is not differentiable at odd multiples of π2i.e. fx is not differentiable at x=2n+1π2Therefore, f(x) is everywhere continuous but not differentiable at 2n+1π2 .
Q8.
Answer :
b continuous on -1,1 and differentiable on -1,0∪0,1
We have,fx=1-1-x2Here, function will be defined for those values of x for which1-x2≥0⇒1≥x2⇒x2≤1⇒x≤1⇒-1≤x≤1Therefore, function is continuous in -1, 1
Now, we need to check the differentiability of fx=1-1-x2 in the interval -1, 1.Now, we will check the differentiability at x=0LHD at x=0=limx→0-fx-f0x-0 =limx→0-1-1-x2-0x =limx→0-1-1-x2x =limh→01-1-0-h20-h =limh→01-1-h2-h=-∞RHD at x=0=limx→0+fx-f0x-0 =limx→0+1-1-x2-0x =limx→0+1-1-x2x =limh→01-1-0+h20+h =limh→01-1-h2h=∞ So, the function is not differentiable at x=0.
Q9.
Answer :
(b) a=0, b=0; c∈R
We have,fx=a sin x+be x+c x3 =a sin x+bex+cx3 0<x<π2-a sin x+be-x-cx3 -π2<x<0Here, fx is differentiable at x=0Therefore, LHD at x=0=RHD at x=0⇒limx→0-fx-f0x-0=limx→0+fx-f0x-0⇒limx→0–a sinx+be-x-cx3-bx=limx→0+a sin x+bex+cx3-bx⇒limh→0-a sin0-h+be-0-h-c0-h3-b0-h=limh→0a sin 0+h+be0+h+c0+h3-b0+h⇒limh→0a sin h+be h+ch3-b-h=limh→0a sin h+beh+ch3-bh⇒limh→0a cos h+beh+3ch2-1=limh→0a cos h+beh+3ch21 By L’Hospital rule⇒-a+b=a+b ⇒-2a+b=0⇒a+b=0This is true for all value of c∴c∈RIn the given options, option b satisfies a+b=0 and c∈R
Q10.
Answer :
(b) is discontinuous
We have,fx=x2+x21+x2+x21+x2+…+x21+x2+….,When x=0 then x2=0 and x21+x2=0∴f0=0+0+0+0…….⇒f0=0When, x≠0Then, x2>0and 1+x2>x2⇒0<x21+x2<1∴limx→0 fx=lim x→0x2+x21+x2+x21+x2+…+x21+x2+…., =limx→0x21+11+x2+11+x2+…+11+x2+…., =limx→0x211-11+x2 Sum of infinite series where, r=11+x2 =limx→0x21+x2x2 =limx→01+x2 =1∴limx→0 fx≠f0∴fx is discontinuous at x=0
Q11.
Answer :
(a) f’ 1+=1 and (b) f’ 1=-1
fx=logex, = – loge x , for 0 < x < 1loge x , for x ≥1Differentiablity at x = 1,we have , (LHD at x = 1 ) =lim x →1- f(x) – f(1)x -1 = lim x →1- -log x – log 1x -1 = -lim x →1- log x x -1 = -lim h →0 log (1 – h) 1 -h – 1 = -lim h →0 log (1 – h) -h = -1
(RHD at x = 1 ) = lim x →1+ f(x) – f(1)x -1 = lim x →1+ log x – log (1)x -1 = lim h → 0 log (1 + h)x -1 = lim h → 0 log (1 + h)h = 1
Q12.
Answer :
(b) f (x) is continuous for all x in its domain but not differentiable at x = ± 1
We have,fx=loge |x|We know that log function is defined for positive value.Here, x is positive for all non zero x.Therefore, domain of function is R-0
And we know that logarithmic function is continuous in its domain.
Therefore, logex is continuous in its domain.
We will check the differentiability at its critical points. logex=loge-x -∞<x<-1-loge-x -1<x<0-logex 0<x<1logex 1<x<∞LHD at x=-1=limx→-1-fx-f-1x–1 =limx→-1-loge-x-0x+1 =limh→0loge–1-h-1-h+1 =limh→0loge1+h-h =-1RHD at x=-1=limx→-1+fx-f-1x–1 =limx→-1+-loge-x-0x+1 =limh→0-loge–1+h-1+h+1 =limh→0-loge1-hh =-limh→0loge1-hh =-1×-1=1Here, LHD≠RHDTherefore, the given function is not differentiable at x=-1.
LHD at x=1=limx→1-fx-f1x-1 =limx→1–logex-0x-1 =limh→0-loge1-h1-h-1 =limh→0loge1-hh =-1RHD at x=1=limx→1+fx-f1x-1 =limx→1+logex-0x-1 =limh→0loge1+h1+h-1 =limh→0loge1+hh =1Here, LHD≠RHDTherefore,the given function is not differentiable at x=1.
Therefore, given function is continuous for all x in its domain but not differentiable at x = ± 1
Page 10.18 (Multiple Choice Questions)
Q13.
Answer :
(b) a=-12, b=32
We have,fx=-1x, x≤-1ax2+b, -1<x<11x, x≥1Given: fx is differentiable and continuous at every point.Consider a point x=1limx→1-fx=limx→1+fx⇒limx→1-ax2+b=limx→1+1x⇒a+b=1 …iIt is also differentiable at x=1limx→1-fx-f1x-1=limx→1+fx-f1x-1⇒limx→1-ax2+b-1x-1=limx→1+1x-1x-1⇒limx→1-ax2-ax-1=limx→1+1-xx-1x Using i⇒limx→1-ax+1=limx→1+-x⇒2a=-1⇒a=-12Plugging a=-12 in i we get,b=32∴a=-12, b=32
Q14.
Answer :
(c) continuous at non-integer points only
We have,fx=x-xConsider n be an integer.fx=x-x=x-n-1 n-1≤x<n0 x=nx-n n≤x<n+1Now,LHL at x=n=limx→n-fx=x-n-1=x-n+1RHL at x=n=limx→n+fx=x-n=x-nAs, LHL≠RHL at x=ni.e., given function is not continuous at n.Now, n is any integer.Therefore, given function is not continuous at integers.
Therefore, given points are continuous at non-integer points only.
Q15.
Answer :
(d) a = 1/2
Given: f(x) = ax2+1, x>1x+12, x≤1
The function is derivable at x = 1, iff left hand derivative and right hand derivative of the function are equal at x = 1.
LHD at x=1=limx→1-fx-f1x-1LHD at x=1=limh→0f1-h-f11-h-1LHD at x=1=limh→0f1-h-f1-hLHD at x=1=limh→01-h+12-32-h=1RHD at x=1=limx→1+fx-f1x-1RHD at x=1=limh→0f1+h-f11+h-1RHD at x=1=limh→0f1+h-f1hRHD at x=1=limh→0a1+h2+1-32hRHD at x=1=limh→0a1+h2+2h-12h∵ LHD=RHD⇒a-12=0⇒a=12
Q16.
Answer :
(b) f (x) is everywhere continuous but not differentiable at x = n π, n ∈ Z
We have,fx=sin x⇒fx=0 , x=2nπ sin x, 2nπ<x<2n+1π0, x=2n+1π-sin x, 2n+1π<x<2n+2πWhen, x is in first or second quadrant, i.e., 2nπ<x<2n+1π , we have fx=sin x which being a trigonometrical function is continuous and differentiable in 2nπ, 2n+1πWhen, x is in third or fourth quadrant, i.e., 2n+1π<x<2n+2π , we have fx=-sin x which being a trigonometrical function is continuous and differentiable in 2n+1π, 2n+2πThus possible point of non-differentiability of fx are x=2nπ and 2n+1πNow, LHD at x=2nπ =limx→2nπ- fx- f2nπx-2nπ =limx→2nπ- -sin x- 0x-2nπ =limx→2nπ- -cos x1-0 By L’Hospital rule =-1And RHD at x=2nπ =limx→2nπ+ fx- f2nπx-2nπ =limx→2nπ+ sin x- 0x-2nπ =limx→2nπ+ cos x1-0 By L’Hospital rule =1∴lim x→2nπ-fx ≠limx→2nπ+fxSo fx is not differentiable at x=2nπNow, LHD at x=2n+1π =limx→2n+1π- fx- f2n+1πx-2n+1π =limx→2n+1π- sin x- 0x-2n+1π =limx→2n+1π- cos x1-0 By L’Hospital rule =-1And RHD at x=2n+1π =limx→2n+1π+ fx- f2n+1πx-2n+1π =limx→2n+1π+ -sin x- 0x-2n+1π =limx→2n+1π+ -cos x1-0 By L’Hospital rule =1∴lim x→2n+1π-fx ≠limx→2n+1π+fxSo fx is not differentiable at x=2n+1πTherefore, fx is neither differentiable at 2nπ nor at 2n+1πi.e.fx is neither differentiable at even multiple of π nor at odd multiple of πi.e. fx is not differentiable at x=nπTherefore, f(x) is everywhere continuous but not differentiable at nπ.
Q17.
Answer :
(c) f (x) is everywhere continuous but not differentiable at x=2n+1π2, n∈Z.
We have,fx=cos x⇒fx=cos x, 2nπ≤x<4n+1π20, x=4n+1π2 -cos x, 4n+1π2<x<4n+3π2 0 , x=4n+3π2 cos x, 4n+3π2< x≤2n+2πWhen, x is in first quadrant, i.e. 2nπ≤x<4n+1π2 , we have fx=cos x which being a trigonometrical function is continuous and differentiable in 2nπ, 4n+1π2When, x is in second quadrant or in third quadrant, i.e., 4n+1π2<x<4n+3π2 , we have fx=-cos x which being a trigonometrical function is continuous and differentiable in 4n+1π2, 4n+3π2When, x is in fourth quadrant, i.e., 4n+3π2< x≤2n+2π , we have fx=cos x which being a trigonometrical function is continuous and differentiable in 4n+3π2, 2n+2πThus possible point of non-differentiability of fx are x=4n+1π2, 4n+3π2Now, LHD at x=4n+1π2 =limx→4n+1π2- fx- f4n+1π2x-4n+1π2 =limx→4n+1π2- cos x- 0x-4n+1π2 =limx→4n+1π2- -sin x1-0 By L’Hospital rule =-1And RHD at x=4n+1π2 =limx→4n+1π2+ fx- f4n+1π2x-4n+1π2 =limx→4n+1π2+ -cos x- 0x-4n+1π2 =limx→4n+1π2+ sin x1-0 By L’Hospital rule =1∴lim x→4n+1π2-fx ≠limx→4n+1π2+fxSo fx is not differentiable at x=4n+1π2Now, LHD at x=4n+3π2 =limx→4n+1π2- fx- f4n+3π2x-4n+3π2 =limx→4n+3π2- -cos x- 0x-4n+3π2 =limx→4n+3π2- sin x1-0 By L’Hospital rule =1And RHD at x=4n+3π2 =limx→4n+3π2+ fx- f4n+3π2x-4n+3π2 =limx→4n+3π2+ cos x- 0x-4n+3π2 =limx→4n+3π2+ -sin x1-0 By L’Hospital rule =-1∴lim x→4n+3π2-fx ≠limx→4n+3π2+fxSo fx is not differentiable at x=4n+3π2Therefore, fx is neither differentiable at 4n+1π2 nor at 4n+3π2i.e. fx is not differentiable at odd multiples of π2i.e. fx is not differentiable at x=2n+1π2Therefore, f(x) is everywhere continuous but not differentiable at 2n+1π2 .
Q18.
Answer :
(b) continuous everywhere
Graph of the function f (x) = 1 + |cos x| is as shown below:
From the graph, we can see that f (x) is everywhere continuous but not differentiable at x=2n+1π2, n∈Z
Q19.
Answer :
(b) continuous but not differentiable at x = (2n + 1) π/2, n ∈ Z
We have,fx=cos x⇒fx=cos x, 2nπ≤x<4n+1π20, x=4n+1π2 -cos x, 4n+1π2<x<4n+3π2 0 , x=4n+3π2 cos x, 4n+3π2< x≤2n+2πWhen, x is in first quadrant, i.e. 2nπ≤x<4n+1π2 , we have fx=cos x which being a trigonometrical function is continuous and differentiable in 2nπ, 4n+1π2When, x is in second quadrant or in third quadrant, i.e., 4n+1π2<x<4n+3π2 , we have fx=-cos x which being a trigonometrical function is continuous and differentiable in 4n+1π2, 4n+3π2When, x is in fourth quadrant, i.e., 4n+3π2< x≤2n+2π , we have fx=cos x which being a trigonometrical function is continuous and differentiable in 4n+3π2, 2n+2πThus possible point of non-differentiability of fx are x=4n+1π2, 4n+3π2Now, LHD at x=4n+1π2 =limx→4n+1π2- fx- f4n+1π2x-4n+1π2 =limx→4n+1π2- cos x- 0x-4n+1π2 =limx→4n+1π2- -sin x1-0 By L’Hospital rule =-1And RHD at x=4n+1π2 =limx→4n+1π2+ fx- f4n+1π2x-4n+1π2 =limx→4n+1π2+ -cos x- 0x-4n+1π2 =limx→4n+1π2+ sin x1-0 By L’Hospital rule =1∴lim x→4n+1π2-fx ≠limx→4n+1π2+fxSo fx is not differentiable at x=4n+1π2Now, LHD at x=4n+3π2 =limx→4n+1π2- fx- f4n+3π2x-4n+3π2 =limx→4n+3π2- -cos x- 0x-4n+3π2 =limx→4n+3π2- sin x1-0 By L’Hospital rule =1And RHD at x=4n+3π2 =limx→4n+3π2+ fx- f4n+3π2x-4n+3π2 =limx→4n+3π2+ cos x- 0x-4n+3π2 =limx→4n+3π2+ -sin x1-0 By L’Hospital rule =-1∴lim x→4n+3π2-fx ≠limx→4n+3π2+fxSo fx is not differentiable at x=4n+3π2Therefore, fx is neither differentiable at 4n+1π2 nor at 4n+3π2i.e. fx is not differentiable at odd multiples of π2i.e. fx is not differentiable at x=2n+1π2Therefore, f(x) is everywhere continuous but not differentiable at 2n+1π2 .
Q20.
Answer :
(a) continuous as well as differentiable for all x ∈ R
Here, fx=sin πx-π4+x2
Since, we know that πx-π=nπ and sinnπ=0.
∵4+x2≠0
∴f(x) = 0 for all x
Thus, f(x) is a constant function and it is continuous and differentiable everywhere.
Page 10.19 (Multiple Choice Questions)
Q21.
(b) b = 0
We have,fx=a+bx+cx4fx=a+bx+cx4 x≥0a-bx+cx4 x<0Here, fx is differentiable at x=0∴ LHD at x=0 = RHD at x=0⇒limx→0-fx-f0x-0=limx→0+fx-f0x-0⇒limx→0-a-bx+cx4-ax=limx→0+a+bx+cx4-ax⇒limh→0a-b0-h+c0-h4-a0-h=limh→0a+b0+h+c0+h4-a0+h⇒limh→0a+bh+ch4-a-h=limh→0a+bh+ch4-ah⇒limh→0bh+ch4-h=limh→0bh+ch4h⇒limh→0-b-ch3=limh→0b+ch3⇒-b=b⇒2b=0⇒b=0
Q22.
Answer :
(d) neither differentiable nor continuous at x = 3
We have,fx=3-x+3+x, where x denotes the least integer greater than or equal to x.fx=3-x+3+3, 2<x<3-3+x+3+4, 3<x<4⇒ fx=-x+9 2<x<3x+4 3<x<4Here,LHL at x=3=limx→3-fx=limx→3–x+9=-3+9=6RHL at x=3=limx→3+fx=limx→3-x+4=3+4=7Since, LHL at x=3≠RHL at x=3Hence, given function is not continuous at x= 3Therefore, the function will also not be differentiable at x=3
Q23.
Answer :
(d) none of these
we have,
(LHL at x = 0 )= limx →0- f(x) = limh →0 f(0 – h) = limh →0 f(- h)= limh →0 11 + e1/-h= limh →0 11 + 1e1/h [limh→01e1/h = 0] = 11 + 0= 1(RHL at x = 0) = limx →0+ f(x) = limh →0 f(0 + h)= limh →0 11 + e1/h= 11 + e1/0 = 11 + e∞ = 11 + ∞
So, f(x) is not continuous at x = 0
Differentiability at x = 0
(LHD at x = 0 ) = limx →0- f(x) – f(0)x – 0= limh→0 f(0 -h) – f(0)0 -h – 0= limh→0 f(-h) – 0 -h= limh→0 11 + e1/ – h -h= limh→0 11 + 1e1/ h -h = limh→0 11 + 0 -h = limh→0 1 -h = -∞(RHD at x = 0) = limx →0+ f(x) – f(0)x – 0= limh →0 f(0 + h) – f(0)0 +h – 0= limh →0 f(h) -0 h = limh→0 11 + e1/ hh = ∞So, f(x) is also not differentiable at x = 0.
Q24.
Answer :
(a) continuous and differentiable
we have,
fx=1-cos xx sin x,x≠012 ,x=0
fx=1-cos xx sin x,x≠012 ,x=0Continuity at x = 0(LHL at x = 0) = limx →0- f(x) = limh →0 f(0 – h) = limh →0 f(- h) = limh →0 1-cos (-h)(-h) sin (-h) = limh →0 1-cos hh sin h = limh →0 1-cosh limh →0 1h sin h = 1 -cos(0) . 10 sin 0 = 0
(RHL at x = 0) = limx →0+ f(x) = limh →0 f(0 + h) = limh →0 f( h) = limh →0 1-cos (h)(h) sin (h) = limh →0 1-cos hh sin h = limh →0 1-cosh limh →0 1h sin h = 1 – cos 0. 10 sin 0 = 0
Hence, f(x)is continuous at x = 0.
For differentiability at x = 0
(LHD at x = 0 ) =limx →0- f(x) – f(0)x -0 = limh→0 f(0 – h) – f(0)0 – h -0 = limh→0 f(- h) -12- h = limh→0 1 – cos(-h)- h sin(-h) -12- h = 1h limh→0 1 – cosh h sin h -limh→0 12 = 12 – 0= 12
RHD at x = 0 ) =limx →0+ f(x) – f(0)x -0 = limh→0 f(0 + h) – f(0)0 – h -0 = limh→0 f( h) -12- h = limh→0 1 – cos(h)- h sin(h) -12- h = -1hlimh→0 1 – cosh h sin h -limh→0 12 = 12 – 0 = 12
Q25.
Answer :
(b) R-3
LHD at x=3=limx→3-fx-f3x-3LHD at x=3=limh→0f3-h-f33-h-3LHD at x=3=limh→0f3-h-f3-hLHD at x=3=limh→03-h-3cos3-h-f3-hLHD at x=3=limh→0hcos3-h-0-h=-cos3RHD at x=3=limx→3+fx-f3x-3RHD at x=3=limh→0f3+h-f33+h-3RHD at x=3=limh→0f3+h-f3hRHD at x=3=limh→03+h-3cos3+h-f3hRHD at x=3=limh→0hcos3+h-0h=cos3
So, f(x) is not differentiable at x = 3.
Also, f(x) is differentiable at all other points because both modulus and cosine functions are differentiable and the product of two differentiable function is differentiable.
Q26.
Answer :
(b) differentiable at x = − 1
fx=1 ,x≤-1x,-1<x<10 ,x≥1
Differentiabilty at x = − 1
(LHD x = − 1)
lim x →- 1- f(x) – f(-1) x + 1=lim x →- 1 f(x) – f(-1) x + 1= lim x →- 1 1 – 1 -1 + 1= 0
(RHD x = − 1)
= limx →-1+f (x) – f(-1)x + 1 = limx →-1f (x) – f(-1)x + 1 = limx →-1f (x) – f(-1)x + 1= limx →-1|x| – |-1|x + 1= 1 – 1|-1 + 1= 0
Page 11.15 Ex.11.1
Q1.
Answer :
Let fx=e-x⇒fx+h=e-x+h ddxfx=limh→0fx+h-fxh =limh→0e-x+h-e-xh =limh→0e-x×e-h-e-xh =limh→0e-xe-h-1-h×-1 =-e-x limh→0e-h-1-h =-e-x ∵limh→0e-h-1-h=1So, ddxe-x=-e-x
Q2.
Answer :
Let fx=e3x⇒fx+h=e3x+hddxfx=limh→0fx+h-fxh =limh→0e3x+h-e3xh =limh→0e3xe3h-e3xh =limh→0e3xe3h-13h×3 =3e3xlimh→0e3h-13h =3e3xHence, ddxe3x=3e3x
Q3.
Answer :
Let fx=eax+b ⇒ fx+h=eax+h+b ∴ ddxfx=limh→0fx+h-fxh =limh→0eax+h+b-eax+bh =limh→0eax+beah-eax+bh =limh→0eax+beah-1ah×a =aeax+blimh→0eah-1ah =aeax+bSo, ddxeax+b=aeax+b
Q4.
Answer :
Let fx=ecosx ⇒ fx+h=ecosx+h ∴ ddxfx=limh→0fx+h-fxh =limh→0ecosx+h-ecosxh =limh→0 ecosxecosx+h-cosx-1h =limh→0 ecosxecosx+h-cosx-1cosx+h cosx×cosx+h-cosxh =ecosxlim h→0 cosx+h-cosxh ×limh→0ecosx+h-cosx-1cosx+h-cosx =ecosxlimh→0 cosx+h-cosxh ∵limh→0ex-1x=1 =ecosxlimh→0 -2sinx+h+x2sinx+h-x2h ∵ cosA-cosB=-2sin A+B2sinA-B2 =ecosxlimh→0-sin2x+h21×sinh2h2 =ecosxlimh→0-sin2x+h21× lim h→0sinh2h2 =ecosxlimh→0-sin2x+h2 ∵ sinxx=1 =ecosx-sinx =-sinxecosxHence, ddxecosx=-sinxecosx
Q5.
Answer :
Let fx=e2x ⇒fx+h=e2x+h ∴ ddxfx=limh→0fx+h-fxh =limh→0e2x+h-e2xh =limh→0 e2xe2x+h-2x-1h =e2xlimh→0 e2x+h-2x-12x+h-2x×limh→02x+h-2xh =e2xlimh→02x+h-2xh ∵ limh→0eh-1h=1 =e2xlimh→0 2x+h-2xh × 2x+h+2x2x+h+2x Rationalising the numerator =e2xlimh→02x+h-2xh2x+h+2x =e2xlimh→02x+2h-2xh2x+h+2x =e2xlimh→02hh2x+h+2x =e2xlimh→022x+h+2x =e2x2xHence, ddxe2x=e2x2x
Q6.
Answer :
Let fx=log cosx⇒fx+h=log cosx+h∴ddxfx=limh→0fx+h=fxh =limh→0log cosx+h-log cosxh =limh→0logcosx+hcosxh ∵logA-logB=logAB =limh→0log1+cosx+hcosx-1h =limh→0log1+cosx+h-cosxcosxcosx+h-cosxcosx×limh→0cosx+h-cosxcosx =1×limh→0cosx+h-cosxcosx × h ∵limx→0log1+xx=1 =limh→0-2sinx+h+x2sinx+h-x2cosx × h =-2limh→0sin2x+h2×sinh22cosx ×h2 =-2sinx2cosx ∵ limx→0sinxx=1 =-tanxSo, ddxlog cosx=-tanx
Q7.
Answer :
i Let fx=ecotx⇒fx+h=ecotx+h∴ ddxfx=limh→0fx+h-fxh =limh→0ecotx+h-ecotxh =limh→0ecotxecotx+h-cotx-1h =ecotxlimh→0ecotx+h-cotx-1cotx+h-cotx×cotx+h-cotxh =ecotxlimh→0cotx+h-cotxh×cotx+h+cotxcotx+h+cotx ∵limx→0ex-1x=1 and rationalizing the numerator =ecotxlimh→0cotx+h-cotxhcotx+h+cotx =ecotxlimh→0cotx+hcotx+1cotx-x-hhcotx+h+cotx ∵cotA-B=cotAcotB+1cotB-cotA =ecotxlimh→0cotx+hcotx+1cot-h×hcotx+h+cotx =-ecotxlimh→0cotx+hcotx+1htanhcotx+h+cotx =ecotx×cot2x+12cotx ∵ limx→0tanxx=1 =-ecotx×cosec2x2cotx ∵ 1+cot2x=cosec2x∴ddxecotx=-ecotx×cosec2x2cotx
ii Let fx=x2ex⇒fx+h=x+h2ex+h =limh→0fx+h-fxh =limh→0x+h2ex+h-x2exh =limh→0x2ex+h-x2exh+2xhex+hh+h2ex+hh =limh→0x2exex+h-x-1h+2xex+h+hex+h =limh→0x2exeh-1h+2xex+h+hex+h =x2ex+2xex+0xex ∵limx→0ex-1x=1∴ddxx2ex=exx2+2x
iii Let fx=log cosecx ⇒ fx+h=log cosecx+h∴ddxfx=limh→0fx+h-fxh =limh→0log cosecx+h-log cosecxh =limh→0logcosecx+hcosecxh =limh→0log1+sinxsinx+h-1h =limh→0log1+sinx-sinx+hsinx+hsinx-sinx+hsinx+hsinx-sinx+hsinx+hh =limh→02cosx+x+h2sinx-x-h2sinx+hh ∵limx→0log1+xx=1 and sinA-sinB=2cosA+B2sinA-B2 =limh→02cos2x+h2sinx+h -2sin-h2-h2 ∵limx→0sinxx=1 =-cotx∴ddxlog cosecx=-cotx
iv Let fx=sin-12x+3 ⇒fx+h=sin-12x+h+3 ⇒fx+h=sin-12x+2h+3∴ ddxfx=limh→0fx+h-fxh =limh→0sin-12x+2h+3-sin-12x+3h =limh→0sin-12x+2h+31-2x+32-2x+31-2x+2h+32h ∵ sin-1x-sin-1y=sin-1×1-y2-y1-x2 =limh→0sin-1zz×zhwhere, z=2x+2h+31-2x+32-2x+31-2x+2h+32 and limh→0sin-1hh=1 =limh→0zh =limh→0 2x+2h+31-2x+32-2x+31-2x+2h+32 h =limh→02x+2h+321-2x+32-2x+321-2x+2h+32h2x+2h+31-2x+32+2x+31-2x+2h+32 Rationalizing numerator =limh→02x+32+4h2+4h2x+31-2x+32-2x+321-2x+32-4h2-4h2x+3h2x+2h+31-2x+32+2x+31-2x+2h+32 =limh→02x+32+4h2+4h2x+3-2x+34-4h22x+32-4h2x+33-2x+32+2x+34+4h22x+32+4h2x+33h2x+2h+31-2x+32+2x+31-2x+2h+32 =limh→04hh+2x+3h2x+2h+31-2x+32+2x+31-2x+2h+32 =42x+32x+31-2x+32+2x+31-2x+32 =42x+322x+31-2x+32 =21-2x+32∴ ddxsin-12x+3=21-2x+32
Page 11.35 Ex.11.2
Q1.
Answer :
Let y=sin3x+5Differentiating y with respect to x we get,dydx=ddxsin3x+5 =cos3x+5ddx3x+5 using chain rule =cos3x+5 ×3 =3cos3x+5So,ddxsin3x+5=3cos3x+5
Q2.
Answer :
Let y=tan2xDifferentiating with respect to x we get,dydx=2 tanxddxtanx using chain rule =2 tanx × sec2x So, ddxtan2x=2 tanxsec2x
Q3.
Answer :
Let, y=tanx°+45°⇒y=tanx+45π180Differentiating it with respect to x we get,dydx=ddxtanx+45π180 =sec2x+45π180×ddxx+45π180 Using chain rule =π180sec2x°+45°So, ddxtanx°+45°=π180sec2x°+45°
Q4.
Answer :
Let y=sinlogxDifferentiate it with respect to x we get,dydx=ddxsinlogx =coslogxddxlogx using chain rule =1xcoslogxSo, ddxsinlogx=1xcoslogx
Q5.
Answer :
Let y=esinxDifferentiate it with respect to x we get,dydx=ddxesinx =esinxddxsinx using chain rule =esinx×cosxddxx using chain rule =esinx×cosx×12x =cosx esinx2xSo, ddxesinx=cosx esinx2x
Q6.
Answer :
Let y=etanxDifferentiate it with respect to x we get,dydx=ddxetanx =etanxddxtanx using chain rule =etanx × sec2xSo, ddxetanx= sec2xetanx
Q7.
Answer :
Let y=sin22x+1Differentiate it with respect to x we get,dydx=ddxsin22x+1 =2sin2x+1ddxsin2x+1 using chain rule =2sin2x+1 cos2x+1 ddx2x+1 using chain rule =4sin2x+1 cos2x+1 =2sin22x+1 ∵ sin2A=2sinAcosA =2 sin4x+2So, ddxsin22x+1=2 sin4x+2
Q8.
Answer :
Let y=log72x-3⇒ y=log2x-3log7 ∵ logab=logblogaDifferentiate it with respect to x we get,dydx=1log7ddxlog2x-3 =1log7×12x-3ddx2x-3 using chain rule =22x-3log7Hence, ddxlog72x-3=22x-3log7
Q9.
Answer :
Let y=tan5x°⇒ y=tan5x×π180Differentiate it with respect to x we get,dydx=ddxtan5x×π180 =sec25x×π180ddx5x×π180 using chain rule =5π180sec25x×π180 =5π180sec25x°Hence, ddxtan5x°=5π180sec25x°
Q10.
Answer :
Let y=2x3Differentiate it with respect to x we get,dydx=ddx2x3 =2×3×loge2ddxx3 using chain rule =3×2 × 2×3×loge2Hence, ddx2x3=3×2 × 2x3loge2
Q11.
Answer :
Let y=3exDifferentiate it with respect to x we get,dydx=ddx3ex =3exlog3ddxex using chain rule =ex×3exlog3So, ddx3ex=ex×3exlog3
Q12.
Answer :
Let y=logx3 ⇒ y=log3logx ∵ logab=logblogaDifferentiate it with respect to x we get,dydx=ddxlog3logx =log3ddxlogx-1 =log3 × -1logx-2ddxlogx using chain rule =-log3logx2×1x =-log3logx2×1x×1log3 =-1xlog3log3x2 ∵logbloga=logabSo, ddxlogx3=-1xlog3log3x2
Q13.
Answer :
Let y=3×2+2xDifferentiate it with respect to x we get,dydx=ddx3x2+2x =3×2+2x × loge3ddxx2+2x using chain rule =2x+23×2+2x loge3So, ddx3x2+2x=2x+23×2+2x loge3
Q14.
Answer :
Let y=a2-x2a2+x2⇒ y=a2-x2a2+x212Differentiate it with respect to x we get,dydx=ddxa2-x2a2+x212 =12a2-x2a2+x212-1×ddxa2-x2a2+x2 Using chain rule =12a2-x2a2+x2-12×a2+x2ddxa2-x2-a2-x2ddxa2+x2a2+x22 =12a2+x2a2-x212-2xa2+x2-2xa2-x2a2+x22 =12a2+x2a2-x212-2xa2-2×3-2xa2+2x3a2+x22 =12a2+x2a2-x212-4xa2a2+x22 =-2xa2a2-x2a2+x232So, ddxa2-x2a2+x2=-2a2xa2-x2a2+x232
Q15.
Answer :
Let y=3x logxDifferentiate it with respect to x we get,dydx=ddx3x logx =3x logx×loge3ddxx logx Using chain rule =3x logx×loge3xddxlogx+logxddxx =3x logx×loge3xx+logx =3x logx1+logx×loge3So, ddx3x logx=3x logx1+logxloge3
Q16.
Answer :
Let y=1+sinx1-sinxDifferentiate it with respect to x we get,dydx=ddx1+sinx1-sinx12 =121+sinx1-sinx12-1ddx1+sinx1-sinx =121-sinx1+sinx121-sinxcosx-1+sinx-cosx1-sinx2 =121-sinx121+sinx12cosx-cosx sinx+cosx+sinx cosx1-sinx2 =12×2cosx1+sinx1-sinx32 =cosx1+sinx1-sinx32 =cosx1+sinx1-sinx1-sinx =cosx1-sin2x×1-sinx =cosxcosx1-sinx Using 1-sin2x=cos2x =11-sinx×1+sinx1+sinx =1+sinx1-sin2x =1+sinxcos2x =1cosx1cosx+sinxcosx =secxsecx+tanxHence, dydx=secxsecx+tanx
Q17.
Answer :
Let y=1-x21+x2⇒ y=1-x21+x212Differentiate it with respect to x we get,dydx=ddx1-x21+x212 =121-x21+x212-1×ddx1-x21+x2 Using chain rule =121-x21+x2-12×1+x2ddx1-x2-1-x2ddx1+x21+x22 =121+x21-x212-2×1+x2-2×1-x21+x22 =121+x21-x212-2x-2×3-2x+2×31+x22 =121+x21-x212-4×1+x22 =-2×1-x21+x232
Q18.
Answer :
Let y=log sinx2Differentiate with respect to x we get,dydx=ddxlog sinx2 =2log sinxddxlog sinx =2log sinx×1sinxddxsinx =2log sinx×1sinx×cosx =2log sinxcotxSo, ddxlog sinx2=2log sinxcotx
Q19.
Answer :
Let y=1+x1-x⇒ y=1+x1-x12Differentiate it with respect to x we get,dydx=ddx1+x1-x12 =121+x1-x12-1×ddx1+x1-x Using chain rule =121+x1-x-12×1-xddx1+x-1+xddx1-x1-x2 Using quotient rule =121-x1+x121-x1-1+x-11-x2 =121-x1+x121-x+1+x1-x2 =121-x121+x12×21-x2 =11+x1-x32So, ddx1+x1-x=11+x1-x32
Q20.
Answer :
Let y=sin1+x21-x2Differentiate it with respect to x we get,dydx=ddxsin1+x21-x2 =cosx1+x21-x2ddx1+x21-x2 Using chain rule =cosx1+x21-x21-x2ddx1+x2-1+x2ddx1-x21-x22 Using quotient rule =cosx1+x21-x21-x22x-1+x2-2×1-x22 =cosx1+x21-x22x-2×3+2x+2×31-x22 =4×1-x22cosx1+x21-x2So,ddxsin1+x21-x2=4×1-x22cosx1+x21-x2
Q21.
Answer :
Let y=e3x cos2xDifferentiate it with respect to x we get,dydx=ddxe3x cos2x =e3x×ddxcos2x+cos2xddxe3x Using product rule =e3x×-sin2xddx2x+cos2xe3xddx3x Using chain rule =-2e3x sin2x+3e3x cos2x =e3x3 cos2x-2 sin2xSo,ddxe3x cos2x=e3x3 cos2x-2 sin2x
Q22.
Answer :
Let y=sinlog sinxDifferentiate it with respect to x we get,dydx=ddxsinlog sinx =coslog sinxddxlog sinx Using chain rule =coslog sinx×1sinxddx sinx Using chain rule =coslog sinxcosxsinx =coslog sinx cotxHence, ddxsinlog sinx=coslog sinx cotx
Page 11.36 Ex.11.2
Q23.
Answer :
Let y=etan3xDifferentiate it with respect to x we get,dydx=ddxetan3x =etan3xddxtan3x =etan3xsec23x ×ddx3x =etan3xsec23x ×3So, ddxetan3x=3etan3xsec23x
Q24.
Answer :
Let y=ecotx⇒ y=ecotx12Differentiate it with respect to x we get,dydx=ddxecotx12 =ecotx12×ddxcotx12 Using chain rule =ecotx×12cotx12-1ddxcotx =-ecotx×cosec2x2cotxSo, ddxecotx=-ecotx×cosec2x2cotx
Q25.
Answer :
Let y=logsinx1+cosxDifferentiate it with respect to x, we getdydx=ddxlogsinx1+cosx =1sinx1+cosx×ddxsinx1+cosx Using chain rule =1+cosxsinx1+cosxddxsinx-sinxddx1+cosx1+cosx2 Using quotient rule =1+cosxsinx1+cosxcosx-sinx-sinx1+cosx2 =1+cosxsinxcosx+cos2x+sin2x1+cosx2 =1+cosxsinx1+cosx1+cosx2 =1sinx =cosecxSo, ddxlogsinx1+cosx=cosecx
Q26.
Answer :
Let y=log1-cosx1+cosx⇒ y=log1-cosx1+cosx12⇒ y=12log1-cosx1+cosx using logab=blogaDifferentiate it with respect to x we get,dydx=ddx12log1-cosx1+cosx =12×11-cosx1+cosx×ddx1-cosx1+cosx Using chain rule =121+cosx1-cosx1+cosxddx1-cosx-1-cosxddx1+cosx1+cosx2 Using quotient rule =121+cosx1-cosx1+cosxsinx-1-cosx-sinx1+cosx2 =121+cosx1-cosxsinx+sinx cosx+sinx-sinx cosx1+cosx2 =121+cosx1-cosx2sinx1+cosx2 =sinx1-cosx1+cosx =sinx1-cos2x =sinxsin2x =1sinx =cosecxSo, ddxlog1-cosx1+cosx=cosecx
Q27.
Answer :
Let y=tanesinxDifferentiate it with respect to x we get, dydx=ddxtanesinx =sec2esinxddxesinx Using chain rule =sec2esinx×esinx×ddxsinx =cosxsec2esinx×esinxSo, ddxtanesinx=cosxsec2esinxesinx
Q28.
Answer :
Let y=logx+x2+1Differentiate with respect to x we get,dydx=ddxlogx+x2+1 =1x+x2+1ddxx+x2+112 Using chain rule =1x+x2+11+12×2+112-1ddxx2+1 =1x+x2+11+12×2+1×2x =1x+x2+1×2+1+xx2+1 =1×2+1So, ddxlogx+x2+1=1×2+1
Q29.
Answer :
Let y=exlogxx2Differentiate with respect to x we get,dydx=x2ddxexlogx-exlogxddxx2x22 Using quotient rule =x2exddxlogx+logxddxex-ex logx×2xx4 Using product rule =x2exx+ex logx-2xex logxx4 =x2ex1+xlogxx-2xex logxx4 =xex1+xlogx-2logxx4 =xexx31x+x logxx-2logxx =exx-21x+logx-2xlogxSo, ddxexlogxx2 = exx-21x+logx-2xlogx
Q30.
Answer :
Let y=log cosecx-cotxDifferentiate it with respect to x we get,dydx=ddxlog cosecx-cotx =1cosecx-cotxddxcosecx-cotx =1cosecx-cotx×-cosecx cotx+cosec2x =cosecxcosecx-cotxcosecx-cotx =cosecxSo,ddxlog cosecx-cotx=cosecx
Q31.
Answer :
Let y=e2x+e-2xe2x-e-2x
Differentiate with respect to x we get,
dydx=ddxe2x+e-2xe2x-e-2x =e2x-e-2xddxe2x+e-2x-e2x+e-2xddxe2x-e-2xe2x-e-2×2 Using quotient rule and chain rule =e2x-e-2xe2xddx2x+e-2xddx-2x-e2x+e-2xe2xddx2x-e-2xddx-2xe2x-e-2×2 =e2x-e-2x2e2x-2e-2x-e2x+e-2x2e2x+2e-2xe2x-e-2×2 =2e2x-e-2×2-2e2x+e-2x2e2x-e-2×2 =2e4x+e-4x-2e2xe-2x-e4x-e-4x-2e2xe-2xe2x-e-2×2 =-8e2x-e-2x2So, ddxe2x+e-2xe2x-e-2x=-8e2x-e-2×2
Q32.
Answer :
Let y=logx2+x+1×2-x+1
Differentiate with respect of x we get,
dydx=ddxlogx2+x+1×2-x+1 =1×2+x+1×2-x+1ddxx2+x+1×2-x+1 Using chain rule and quotient rule =x2-x+1×2+x+1×2-x+1ddxx2+x+1-x2+x+1ddxx2-x+1×2-x+12 =x2-x+1×2+x+1×2-x+12x+1-x2+x+12x-1×2-x+12 =x2-x+1×2+x+12×3-2×2+2x+x2-x+1-2×3-2×2-2x+x2+x+1×2-x+12 =-4×2+2×2+2×2+x+1×2-x+1 =-4×2+2×2+2×2+12-x2 =-2×2-1×4+1+2×2-x2 =-2×2-1×4+x2+1So, ddxlogx2+x+1×2-x+1=-2×2-1×4+x2+1
Q33.
Answer :
Let y=tan-1ex
Differentiate it with respect to x we get,
dydx=ddxtan-1ex =11+ex2ddxex Using chain rule =11+e2x×ex =ex1+e2xSo, ddxtan-1ex=ex1+e2x
Q34.
Answer :
Let y=esin-12x
Differentiate it with respect to x we get,
dydx=ddxesin-12x =esin-12x×ddxsin-12x Using chain rule =esin-12x×11-2x2ddx2x =2esin-12×1-4x2So, ddxesin-12x=2esin-12×1-4×2
Q35.
Answer :
Let y=sin2 sin-1x
Differentiate it with respect to x we get,
dydx=ddxsin2sin-1x =cos2 sin-1xddx2 sin-1x Using chain rule =cos2 sin-1x×211-x2 =2cos2 sin-1×1-x2So,ddxsin2sin-1x=2cos2 sin-1×1-x2
Q36.
Answer :
Let y=etan-1x
Differentiate it with respect to x we get,
dydx=ddxetan-1x =etan-1xddxtan-1x Using chain rule =etan-1x×11+x2ddxx =etan-1×1+x×12x =etan-1x2x1+xSo, ddxetan-1x=etan-1x2x1+x
Q37.
Answer :
Let y=tan-1×2⇒y=tan-1×212
Differentiate it with respect to x we get,
dydx=ddxtan-1×212 =12tan-1×212-1ddxtan-1×2 Using chain rule =12tan-1×2-12×11+x22×ddxx2 =444+x2tan-1×2 =14+x2tan-1x2So, ddxtan-1×2=14+x2tan-1×2
Q38.
Answer :
Let y=logtan-1x
Differentiate it with respect to x we get,
dydx=ddxlogtan-1x =1tan-1x×ddxtan-1x Using chain rule =11+x2tan-1xSo, ddxlogtan-1x=11+x2tan-1x
Q39.
Answer :
Let y=2x cosxx2+32
Differentiate it with respect to x we get,
dydx=ddx2x cosxx2+32 =x2+32ddx2x cosx-2x cosxddxx2+32×2+322 Using quotient rule =x2+322xddxcosx+cosxddx2x-2x cosx2x2+3ddxx2+3×2+34 Using Product rule and chain rule =x2+32-2x sinx+cosx2x loge2-22x cosxx2+32xx2+34 =2xx2+3×2+3cosx loge2-sinx-4x cosxx2+34 =2xx2+32cosx loge2-sinx-4x cosxx2+3So, ddx2x cosxx2+32=2xx2+32cosx loge2-sinx-4x cosxx2+3
Q40.
Answer :
Let y=x sin2x+5x+kk+tan2x3
Differentiate it with respect to x we get,
dydx=ddxx sin2x+5x+kk+tan6x =ddxx sin2x+ddx5x+ddxkk+ddxtan6x =xddxsin2x+sin2xddxx+5x loge5+0+6tan5x×ddxtanx Using product rule and chain rule =x cos2xddx2x+sin2x+5xloge5+6tan5x sec2x =2x cos2x+sin2x+5x loge5+6tan5x sec2xSo, ddxx sin2x+5x+kk+tan2x3=2xcos2x+sin2x+5x loge5+6tan5x sec2x
Q41.
Answer :
Let y=log3x+2-x2log2x-1
Differentiate it with respect to x we get,
dydx=ddxlog3x+2-x2log2x-1 =ddxlog3x+2-ddxx2log2x-1 =13x+2ddx3x+2-x2ddxlog2x-1+log2x-1ddxx2 Using product rule and chain rule =33x+2-2x22x-1-2x log2x-1So, ddxlog3x+2-x2log2x-1=33x+2-2x22x-1-2x log2x-1
Q42.
Answer :
Let y=3×2 sinx7-x2
Differentiate it with respect to x we get,
dydx=ddx3x2 sinx7-x212 =7-x212×ddx3x2 sinx-3×2 sinxddx7-x2127-x2122 Using quotient rule, chain rule and product rule =7-x212× 3x2ddxsinx+sinxddxx2-3x2sinx × 127-x2×ddx7-x27-x2 =7-x2123x2cosx+2x sinx-3×2 sinx × 127-x2-12-2×7-x2 =7-x212× 3×2 cosx+2x sinx7-x2+3x3sinx7-x2-127-x2 =6x sinx+3x2cosx7-x2+3×3 sinx7-x232So, ddx3x2 sinx7-x2=6x sinx+3x2cosx7-x2+3×3 sinx7-x232
Q43.
Answer :
Let y=sin2log2x+3
⇒dydx=ddxsin2log2x+3 =2 sinlog2x+3ddxsinlog2x+3 Using chain rule =2sinlog2x+3 coslog2x+3ddxlog2x+3 =sin2log2x+3×12x+3ddx2x+3 ∵ 2sinA cosA=sin2A =sin2log2x+322x+3So, ddxsin2log2x+3=sin2 log2x+322x+3
Q44.
Answer :
Let y=exlog sin2x
Differentiate it with respect to x we get,
dydx=ddxex log sin2x =exddxlog sin2x+log sin2xddxex Using product rule and chain rule =ex1sin2xddxsin2x+log sin2xex =exsin2xcos2x ddx2x+ex log sin2x =2cos2xexsin2x+ex log sin2x =2excot2x+exlog sin2xSo, ddxex log sin2x=2excot2x+exlog sin2x
Q45.
Answer :
We have, x2+1+x2-1×2+1-x2-1By rationalising we get,x2+1+x2-1×2+1-x2-1×x2+1+x2-1×2+1+x2-1=x2+1+x2-12×2+12-x2-12=x2+12+x2-12+2×2+1×2-1×2+1-x2+1=x2+1+x2-1+2×4-12=2×2+2×4-12=x2+x4-1Now, Let y=x2+x4-1
Differentiate it with respect to x we get,
dydx=ddxx2+x4-1 =2x+12×4-1×ddxx4-1 =2x+12×4-1×4×3 =2x+2x3x4-1
Q46.
Answer :
Let y=logx+2+x2+4x+1
Differentiate it with respect to x we get,
dydx=ddxlogx+2+x2+4x+1 =1x+2+x4+4x+1ddxx+2+x2+4x+112 Using chain rule =1x+2+x4+4x+1×1+0+12×2+4x+1-12ddxx2+4x+1 =1+2x+42×2+4x+1x+2+x4+4x+1 =x2+4x+1+x+2x+2+x2+4x+1×x2+4x+1 =1×2+4x+1So, ddxlogx+2+x2+4x+1=1×2+4x+1
Q47.
Answer :
Let y=sin-1×44
Differentiate it with respect to x we get,
dydx=ddxsin-1×44 =4sin-1x43ddxsin-1×4 Using chain rule =4sin-1×4311-x42ddxx4 Using chain rule =4sin-1x434x31-x8 =16x3sin-1×431-x8So, ddxsin-1×44=16x3sin-1×431-x8
Q48.
Answer :
Let y=sin-1xx2+a2
Differentiate it with respect to x we get,
dydx=ddxsin-1xx2+a2 =11-xx2+a22×ddxxx2+a2 Using chain rule and quotient rule =11-xx2+a22×x2+a212ddxx-xddxx2+a212x2+a2122 =x2+a2x2+a2-x2x2+a2- x2x2+a2ddxx2+a2x2+a2 =x2+a2ax2+a2x2+a2-x2x2+a2×2x =x2+a2ax2+a2x2+a2-x2x2+a2 =a2ax2+a2 =ax2+a2So,ddxsin-1xx2+a2=ax2+a2
Q49.
Answer :
Let y=exsinxx2+23
Differentiate it with respect to x we get,
dydx=x2+23ddxexsinx-exsinxddxx2+23×2+232 Using quotient rule =x2+23excosx+sinxex-ex sinx 3×2+222xx2+26 Using product rule =x2+23excosx+exsinx-6xex sinxx2+22×2+26 =x2+22×2+2excosx+exsinx-6xex sinxx2+26 =x2+2excosx+exsinx-6xex sinxx2+24 =ex sinx+ex cosxx2+23-6xex sinxx2+24So, dydx=ex sinx+ex cosxx2+23-6xex sinxx2+24
Q50.
Answer :
Let y=3e-3x log1+x
Differentiate it with respect to x we get,
dydx=3ddxe-3x log1+x =3e-3×11+x+log1+x-3e-3x Using product rule and chain rule =3e-3×1+x-3e-3xlog1+x =3e-3×11+x-3 log1+xSo, ddx3e-3x log1+x=3e-3×11+x-3 log1+x
Q51.
Answer :
Let y=x2+2cosx
Differentiate it with respect to x we get,
dydx=cosxddxx2+2-x2+2ddxcosxcosx2 Using quotient rule and chain rule =2xcosx-x2+2-12sinxcosxcosx =2xcosx+x2+2sinx2cosxcosx =4x cosx+x2+2sinx2cosx32 =2xcosx+12×2+2sinxcosx32 =1cosx2x+12×2+2sinxcosx =1cosx2x+x2+2tanx2So, ddxx2+2cosx=1cosx2x+x2+2tanx2
Q52.
Answer :
Let y=x21-x23cos 2x
⇒dydx=cos2xddxx21-x23-x21-x23ddxcos2xcos22x =cos2xx2ddx1-x23+1-x23ddxx2-x21-x23-2sin2xcos22x =cos2x-6×31-x22+1-x232x+2×21-x23sin2xcos22x =2×1-x22cos2x-6×31-x22cos2x+2×21-x23sin2xcos22x =2×1-x2sec2x1-4×2+x1-x2tan2xSo, ddxx21-x23cos2x=2×1-x2sec2x1-4×2+x1-x2tan2x
Q53.
Answer :
Let y=log 3x+2-x2 log 2x-1
Differentiating with respect to x,
dydx=ddxlog 3x+2-x2 log2x-1 =33x+2-x2ddxlog 2x-1+log2x-1ddxx2 =33x+2-2x22x-1+2xlog2x-1 =33x+2-2x22x-1-2xlog2x-1So, ddxlog 3x+2-x2 log2x-1=33x+2-2x22x-1-2xlog2x-1
Q54.
Answer :
Let y=eax secx tan2x
Differentiate it with respect to x,
dydx=ddxeax secx tan2x =eaxddxsecx tan2x+secx tan2xddxeax =eaxsecx tanx tan2x+2sec22xsecx+aeax secx tan2x =eaxsecx tanx tan2x+2sec22xsecx+aeax secx tan2x =aeax secx tan2x+eaxsecx tanx tan2x+2eax secxsec22x =eax secxa tan2x+tanx tan2x+2sec22xSo,ddxeax secx tan2x=eax secxa tan2x+tanx tan2x+2sec22x
Q55.
Answer :
Let y=log cosx2
Differentiating with respect to x,
dydx=ddxlogcosx2 = -2x sinx2cosx2 =-2x tanx2So, ddxlogcosx2=-2x tanx2
Q56.
Answer :
Let y=cos log x2
Differentiating with respect to x,
dydx=ddxcoslog x2 =-sinlog x2ddxlog x2 =-sinlog x22logxx =-2logx sinlog x2 xSo, ddxcoslog x2=-2logx sinlog x2 x
Q57.
Answer :
Let y=log x-1x+1⇒ y=log x-1x+112⇒ y=12log x-1x+1⇒ y=12logx-1-logx+1
Differentiate it with respect to x
dydx=12ddxlogx-1-ddxlogx+1 =121x-1-1x+1 =122×2-1 =1×2-1So,dydx=1×2-1
Q58.
Answer :
Here, y=logx-1-x+1
Differentiate it with respect to x we get,
dydx=ddxlogx-1-x+1 =1x-1-x+1ddxx-1-x+1 Using chain rule =1x-1-x+1ddxx-1-ddxx+1 =1x-1-x+112x-1-12-12x+1-12 =121x-1-x+11x-1-1x+1 =121x-1-x+1-x-1-x+1x-1x+1 =-121x-1x+1 =-12×2-1So,dydx=-12×2-1
Q59.
Answer :
We have, y=xx+2
Differentiating with respect to x,
dydx=ddxxx+2⇒dydx=x+2ddxx-xddxx+2x+22 ⇒dydx=x+2-xx+22⇒dydx=x+2x+22-xx+22⇒dydx=1x+2-xy2x2 ∵x+2=xy⇒dydx=yx-y2x⇒dydx=1xy1-y⇒xdydx=1-yy Hence proved
Q60.
Answer :
We have, y=xx+2
Differentiating with respect to x,
dydx=ddxxx+2⇒dydx=x+2ddxx-xddxx+2x+22 ⇒dydx=x+2-xx+22⇒dydx=x+2x+22-xx+22⇒dydx=1x+2-xy2x2 ∵x+2=xy⇒dydx=yx-y2x⇒dydx=1xy1-y⇒xdydx=1-yy Hence proved
Q61.
Answer :
We have, y=logx+1x
Differentiate it with respect to x,
dydx=ddxlogx+1x =1x+1xddxx+1x =xx+112x-12xx =12xx+1x-1xx =x-12xx+1So, dydx=x-12xx+1
Q62.
Answer :
We have, y=1+ex1-ex
Differentiate it with respect to x,
dydx=ddx1+ex1-ex⇒dydx=121+ex1-ex×ddx1+ex1-ex ⇒dydx=12×1-ex1+ex1-exddx1+ex-1+exddx1-ex1-ex2⇒dydx=121-ex1+ex1-exex+1+exex1-ex2⇒dydx=121-ex1+ex×2ex1-ex2⇒dydx=ex1+ex1-ex11-ex⇒dydx=ex1-ex1-e2x
Page 11.37 Ex.11.2
Q63.
Answer :
We have, y=x+1x
Differentiate with respect to x,
⇒dydx=ddxx+1x⇒dydx=ddxx+ddx1x⇒dydx=12x+-12xx⇒dydx=12x-12xx⇒dydx=x-12xx⇒2xdydx=x-1x⇒2xdydx=xx-1x⇒2xdydx=x-1x
Q64.
Answer :
We have, y=x sin-1×1-x2
Differentiating with respect to x,
dydx=ddxx sin-1×1-x2⇒dydx=1-x2ddxx sin-1x-x sin-1xddx1-x21-x22 ⇒dydx=1-x2xddxsin-1x+sin-1xddxx-x sin-1×121-x2ddx1-x21-x2 ⇒dydx=1-x2x1-x2+sin-1x-x sin-1x-2×21-x21-x2⇒dydx=x+1-x2sin-1x+x2sin-1×1-x21-x2⇒1-x2dydx=x+1-x2sin-1×1+x2sin-1×1-x2⇒1-x2dydx=x+1-x2sin-1x+x2sin-1×1-x2⇒1-x2dydx=x+sin-1x-x2 sin-1x+x2sin-1×1-x2⇒1-x2dydx=x+sin-1×1-x2⇒1-x2dydx=x+yx ∵y=x sin-1×1-x2
Q65.
Answer :
We have, y=ex-e-xex+e-x
Differentiating with respect to x,
dydx=ddxex-e-xex+e-x =ex+e-xddxex-e-x-ex-e-xddxex+e-xex+e-x2 =ex+e-xex-e-xddx-x-ex-e-xex+e-xddx-xex+e-x2 =ex+e-xex+e-x-ex-e-xex-e-xex+e-x2 =ex+e-x2-ex-e-x2ex+e-x2 =1-ex-e-x2ex+e-x2 =1-ex-e-xex+e-x2 =1-y2So, dydx=1-y2
Q66.
Answer :
We have, y=x-1 logx-1-x+1 logx+1
Differentiating with respect to x,
dydx=ddxx-1 logx-1-x+1 logx+1 =x-1ddxlogx-1+logx-1ddxx-1-x+1ddxlogx+1+logx+1ddxx+1 =x-1×1x-1ddxx-1+logx-1×1-x+1×1x+1×ddxx+1+logx+11 =1+logx-1-1+logx+1 =logx-1-logx+1 =logx-1x+1 So, dydx=logx-1x+1
Q67.
Answer :
We have, y=ex cosx
Differentiating with respect to x,
dydx=ddxex cosx =exddxcosx+cosxddxex =ex-sinx+excosx =excosx-sinx =2ex cosx2-sinx2 Multiplying and dividing by 2 =2excosπ4cosx-sinπ4sinx =2ex cosx+π4So, dydx=2ex cosx+π4
Q68.
Answer :
We have, y=12log1-cos2x1+cos2x⇒y=12log2sin2x2cos2x ⇒y=12logtan2x⇒y=22log tanx ⇒y=log tanx
Differentiate with respect to x,
dydx=log tanx =1tanx×ddxtanx =sec2xtanx =1cos2x × sinxcosx =1sinx cosx =22sinx cosx =2sin2x So,dydx=2cosec 2x
Q69.
Answer :
We have, y=x sin-1x+1-x2
Differentiate it with respect to x,
dydx=ddxx sin-1x+1-x2 =ddxx sin-1x+ddx1-x2 =x ddxsin-1x+sin-1xddxx+121-x2ddx1-x2 =x1-x2+sin-1x-2×21-x2 =x1-x2+sin-1x-x1-x2 =sin-1x
Q70.
Answer :
We have, y=x2+a2
Squaring both sides we get,
y2=x2+a2⇒2ydydx=ddxx2+a2⇒2ydydx=2x⇒2ydydx=2x⇒ydydx=x⇒ydydx-x=0Hence proved
Q71.
Answer :
We have, y=ex+e-x
Differentiate it with respect to x,
dydx=ddxex+e-x =ddxex+ddxe-x =ex+e-xddx-x Using chain rule =ex+e-x-1 =ex-e-x =ex+e-x2-4ex×e-x ∵a-b=a+b2-4ab =y2-4 ∵ ex+e-x=y
Q72.
Answer :
We have, y=a2-x2
Squaring both sides we get,⇒y2=a2-x2Differentiating both sides w.r.t x, we get,⇒2ydydx=ddxa2-x2⇒2ydydx=0-2x ⇒ydydx=-x⇒ydydx+x=0 Hence proved
Q73.
Answer :
We have, xy=4⇒y=4x
Differentiate it with respect to x,
dydx=ddx4x⇒dydx=4ddxx-1⇒dydx=4-1× x-1-1⇒dydx=4-1×2⇒dydx=-4×2⇒dydx=-44y2 ∵x=4y⇒dydx=-4y216⇒dydx=-y24⇒4dydx=-y2⇒4dydx=3y2-4y2⇒4dydx+4y2=3y2⇒4dydx+y2=3y2
Dividing both side by x,
⇒4xdydx+y2=3y2x⇒ydydx+y2=3y2x ⇒xdydx+y2=3y2y⇒xdydx+y2=3y
Q74.
Answer :
ddxx2a2-x2+a22sin-1xa=a2-x2LHS=ddxx2a2-x2+a22sin-1xa =ddxx2a2-x2+ddxa22sin-1xa =12xddxa2-x2+a2-x2ddxx+a22×11-xa2×ddxxa =12x × 12a2-x2ddxa2-x2+a2-x2+a22×1a2-x2a2×1a =12x-2x2a2-x2+a2-x2+a22aa2-x2×1a =12-2×2+2a2-x22a2-x2+a22a2-x2 =122a2-2x22a2-x2+a22a2-x2 =a2-2x22a2-x2+a22a2-x2 =a2-2×2+a22a2-x2 =2a2-2x22a2-x2 =2a2-x22a2-x2 =a2-x2a2-x2 =a2-x2=RHSHence proved
Q75.
Answer :
Let y=log1+tanx1-tanx⇒y=log1+tanx1-tanx12⇒y=12log1+tanx1-tanx⇒y=12log1+tanx-log1-tanx⇒dydx=12ddxlog1+tanx-ddxlog1-tanx =1211+tanx×ddx1+tanx-11-tanx×ddx1-tanx =1211+tanx0+sec2x-11-tanx0-sec2x =12sec2x1+tanx+sec2x1-tanx =12sec2x1-tanx+1+tanx1-tan2x =12sec2x21-tan2x =sec2x1-tan2x =1+tan2x1-tan2x =11-tan2x1+tan2x =1cos2x =sec2x
Page 11.62 Ex.11.3
Q1.
Answer :
Let, y=cos-12×1-x2Put x=cosθ y=cos-12cosθ1-cos2θ y=cos-12cosθ sinθ y=cos-1sin2θ Since, sin2θ=2sinθcosθ y=cos-1cosπ2-2θ …iNow, 12<x<1⇒12<cosθ<1⇒ 0<θ<π4⇒ 0<2θ<π2⇒ 0>-2θ>-π2⇒π2>π2-2θ>0Hence, from equation iy=π2-2θ Since, cos-1cosθ=θ, if θ∈0,πy=π2-2cos-1x Since, x=cosθ differentiating it with respect to x,dydx=ddxπ2-2ddxcos-1xdydx=0-2-11-x2dydx=21-x2
Q2.
Answer :
Let, y=cos-11+x2Put x=cos2θ y=cos-11+cos 2θ2 y=cos-12cos2θ2 y=cos-1cosθ …iHere, -1<x<1 ⇒ -1<cos2θ<1 ⇒ 0<2θ<π ⇒ 0<θ<π2So, from equation i y=θ since ,cos-1cosθ=θ, ifθ∈0,π⇒ y=12cos-1x Since , x=cos2θDifferentiating it with respect to x,dydx=-121-x2
Q3.
Answer :
Let, y=sin-11-x2Put x=cos 2θ y=sin-11-cos2θ2 y=sin-12 sin2θ2 y=sin-1sinθ …iHere, 0<x<1⇒ 0<cos 2θ<1⇒ 0< 2θ<π2⇒ 0< θ<π4So, from equation i, y=θ Since, sin-1sinθ=θ, if θ∈-π2,π2 y=12cos-1x Since, x=cos 2θDifferentiating it with respect to x,dydx=-121-x2
Q4.
Answer :
Let, y=sin-11-x2Put, x=cos θ y=sin-11-cos2θ y=sin-1sinθ …iHere, 0<x<1⇒ 0<cos θ<1⇒ 0< θ<π2So, from equation i, y=θ Since, sin-1sinθ=θ, if θ∈-π2,π2 y=cos-1x Since, x=cos θDifferentiating it with respect to x,dydx=-11-x2
Q5.
Answer :
Let, y=tan-1xa2-x2Put x=a sinθ y=tan-1a sinθa2-a2sin2θ y=tan-1a sinθa21-sin2θ y=tan-1a sinθa cosθ y=tan-1tanθ …iHere, -a<x<a⇒ -1<xa<1⇒ sin-π2< sinθ<sinπ2 ∵x=a sinθ⇒ -π2< θ<π2So, from equation i, y=θ Since, tan-1tanθ=θ, if θ∈-π2,π2 y=sin-1xa Since, x=a sinθDifferentiating it with respect to x,Using chain rule,dydx=11-xa2ddxxadydx=aa2-x2×1adydx=1a2-x2
Q6.
Answer :
Let, y=sin-1xx2+a2put x=a tanθ⇒ y=sin-1a tanθa2tan2θ+a2⇒ y=sin-1a tanθa2tan2θ+1⇒ y=sin-1a tanθa secθ ⇒ y=sin-1sinθ ⇒ y=θ⇒ y=tan-1xa since, x=a tanθ Differentiating it with respect to x using chain rule, dydx=11+xa2ddxxa⇒dydx=a2a2+x2×1a∴dydx=aa2+x2
Q7.
Answer :
Let, y=sin-12×2-1Put x=cos θ y=sin-12cos2θ-1 y=sin-1cos2θ y=sin-1sinπ2-2θ …i Here, 0<x<1⇒ 0<cos θ<1⇒ 0< θ<π2⇒ 0< 2θ<π⇒ 0> -2θ>-π⇒ π2>π2-2θ>-π2⇒ -π2<π2-2θ<π2So, from equation i, y=π2-2θ Since, sin-1sinθ=θ, if θ∈-π2,π2 ⇒ y=π2-2cos-1x Since, x=cos θDifferentiating it with respect to x, dydx=0-2ddxcos-1x⇒dydx=-2-11-x2∴dydx=21-x2
Q8.
Answer :
Let, y=sin-11-2x2put x=sin θ⇒ y=sin-11-2sin2θ⇒ y=sin-1cos2θ⇒ y=sin-1sinπ2-2θ …i Here, 0<x<1⇒ 0<sin θ<1⇒ 0< θ<π2⇒ 0< 2θ<π⇒ 0> -2θ>-π⇒ π2>π2-2θ>π2-π⇒ π2>π2-2θ>-π2⇒ -π2<π2-2θ<π2So, from equation i, y=π2-2θ Since, sin-1sinθ=θ, if θ∈-π2,π2⇒ y=π2-2sin-1x Since, x=sin θDifferentiating it with respect to x, dydx=0-211-x2∴ dydx=-21-x2
Q9.
Answer :
Let, y=cos-1xx2+a2Put x=a cotθ⇒ y=cos-1a cotθa2cot2θ+a2⇒ y=cos-1a cotθa2cot2θ+1⇒ y=sin-1a cotθa cosecθ⇒ y=cos-1 cosθsinθ1sinθ⇒ y=cos-1cosθ ⇒ y=θ⇒ y=cot-1xa since, x=a cotθ Differentiating it with respect to x using chain rule,dydx=-11+xa2ddxxa⇒dydx=-a2a2+x2×1a∴dydx=-aa2+x2
Q10.
Answer :
Let, y=sin-1sinx+cosx2⇒ y=sin-1sinx12+cosx12⇒ y=sin-1sinx cosπ4+cosx sinπ4⇒ y=sin-1sinx+π4 …iHere, -3π4<x<π4⇒ -3π4+π4<x+π4<π4+π4⇒ -π2<x+π4<π2From i we get,⇒ y= x+π4 Since, sin-1sinθ=θ, if θ∈-π2,π2Differentiating it with respect to x,dydx=1+0∴dydx=1
Q11.
Answer :
Let, y=cos-1cosx+sinx2 y=cos-112cosx+12sinx y=cos-1cosπ4cosx +sinπ4sinx y=cos-1cosπ4-x …iHere, -π4<x<π4⇒ π4>-x>-π4⇒ -π4<-x<π4⇒ -π4+π4<-x+π4< π4+π4⇒ 0<π4-x<π2So, from equation i, y= π4-x Since, cos-1cosθ=θ, if θ∈0, π Differentiating it with respect to x,dydx=0-1dydx=-1
Q12.
Answer :
Let, y=tan-1×1+1-x2Put x=sinθ y=tan-1sinθ1+1-sin2θ y=tan-1 sinθ1+cosθ y=tan-12 sinθ2cosθ22cos2θ2 y=tan-1tan θ2 …iHere, -1<x<1⇒ -1<sinθ<1⇒ -π2< θ<π2⇒ -π4< θ2<π4So, from equation i, y=θ2 Since, tan-1tanθ=θ, if θ∈-π2,π2 y=12sin-1x Since, x= sinθDifferentiating it with respect to x,dydx=121-x2
Q13.
Answer :
Let, y=tan-1xa+a2-x2Put x=a sinθ⇒ y=tan-1a sinθa+a2-a2sin2θ⇒ y=tan-1a sinθa+a21-sin2θ ⇒ y=tan-1 a sinθa+a cosθ⇒ y=tan-1a sinθa1+cosθ ⇒ y=tan-1 sinθ1+cosθ ⇒ y=tan-1 2sinθ2cosθ22 cos2θ2⇒ y=tan-1tan θ2 …i Here, -a<x<a⇒ -1<xa<1⇒ -1< sinθ<1⇒ -π2< θ<π2⇒ -π4< θ2<π4So, from equation i, y=θ2 Since, tan-1tanθ=θ, if θ∈-π2,π2⇒ y=12sin-1xa Since, x=a sinθDifferentiating it with respect to x, dydx=12×11-xa2ddxxa⇒dydx=a2a2-x2×1a∴ dydx=12a2-x2
Q14.
Answer :
Let, y=sin-1x+1-x22putting x=sinθ∴ y=sin-1sinθ+1-sin2θ2⇒ y=sin-1sinθ+cosθ2⇒ y=sin-1sinθ12+cosθ12⇒y=sin-1sinθ cosπ4+cosθ sinπ4⇒y=sin-1sinθ+π4 …..1Here, -1<x<1⇒ -1<sinθ<1 ⇒ -π2<θ<π2 ⇒ -π2+π4< π4+θ <3π4⇒ -π4< π4+θ <3π4So, from 1, y=θ+π4 Since, sin-1sinα=α, if α∈-π2,π2 ⇒ y=sin-1x+π4 Differentiating it with respect to x, dydx=11-x2+0∴dydx=11-x2
Q15.
Answer :
Let y=cos-1x+1-x22Put, x=cosθ y=cos-1cosθ+1-cos2θ2 y=cos-1cosθ+sinθ2 y=cos-1cosθ12+sinθ12 y=cos-1cosθcosπ4+sinθ sinπ4 y=cos-1cosθ-π4 …iHere, -1<x<1⇒ -1<cosθ<1 ⇒ 3π4<θ<5π4 ⇒ 3π4-π4<θ-π4<5π4-π4⇒ π2< θ-π4<πSo, from equation i, y=θ-π4 Since, cos-1cosθ=θ, if θ∈0,π y=cos-1x-π4 Since, x=sinθDifferentiating it with respect to x,dydx=-11-x2+0dydx=-11-x2
Q16.
Answer :
Let, y=tan-14×1-4x2put 2x=tanθ ⇒ y=tan-12 tanθ1-tan2θ ⇒ y=tan-1tan2θ …iHere, -12<x<12⇒ -1<2x<1⇒ -1< tanθ<1⇒ -π4< θ<π4⇒ -π2< 2θ<π2So, from equation i, y=2θ Since, tan-1tanθ=θ, if θ∈-π2,π2 ⇒ y=2tan-12x Since, 2x=tanθDifferentiating it with respect to x,dydx=211+2x2ddx2x⇒dydx=211+4×2×2∴ dydx=41+4×2
Q17.
Answer :
Let, y=tan-12x+11-4xput 2x=tanθ y=tan-12x×21-2×2 y=tan-12 tanθ1-tan2θ y=tan-1tan2θ …iHere, -∞<x<0⇒ 2-∞<2x<2°⇒ 0< 2x<1⇒ 0< θ<π4⇒ 0<2θ<π2So, from equation i, y=2θ Since, tan-1tanθ=θ, if θ∈-π2,π2 y=2 tan-12x Differentiating it with respect to x,dydx=21+2x2ddx2xdydx=2×2x loge21+4xdydx=2x+1 loge21+4x
Q18.
Answer :
Let, y=tan-12ax1-a2xput ax=tanθ ⇒ y=tan-12×ax1-ax2 ⇒ y=tan-12 tanθ1-tan2θ ⇒ y=tan-1tan2θ …iHere, -∞<x<0⇒ a-∞<ax<2°⇒ 0< tanθ<1⇒ 0< θ<π4⇒ 0<2θ<π2So, from equation i, y=2θ Since, tan-1tanθ=θ, if θ∈-π2,π2 ⇒ y=2 tan-1ax Differentiating it with respect to x,dydx=21+ax2ddxax⇒dydx=2×ax logea1+a2x∴dydx=2ax logea1+a2x
Q19.
Answer :
Let, y=sin-11+x+1-x2put x=cos 2θ⇒ y=sin-11+cos 2θ+1-cos 2θ2⇒ y=sin-12cos2θ+2sin2θ2 ⇒ y=sin-12 cosθ+2 sinθ2 ⇒ y=sin-1cosθ12+12sinθ ⇒ y=sin-1 cosθ sinθπ4+cosπ4sinθ ⇒ y=sin-1sinθ+π4 …iHere, 0<x<1⇒ 0<cos 2θ<1 ⇒ 0< 2θ<π2 ⇒ 0< θ<π4⇒ π4< θ+π4<π2So, from equation i, y=θ+π4 Since, sin-1sinθ=θ, if θ∈-π2,π2⇒ y=12cos-1x+π4Differentiate it with respect to x,dydx=12-11-x2+0∴dydx=-121-x2
Q20.
Answer :
Let, y=tan-11+a2x2-1axput ax=tanθ∴ y=tan-11+tan2θ-1tanθ⇒ y=tan-1secθ-1tanθ⇒ y=tan-11-cosθsinθ⇒ y=tan-12sin2θ22θ2θ2⇒ y=tan-1tanθ2⇒ y=θ2⇒ y=12tan-1ax
Differentiate it with respect to x using chain rule,
dydx=12×11+ax2ddxax⇒dydx=121+a2x2a∴dydx=a21+a2x2
Q21.
Answer :
Let fx=tan-1sinx1+cosx
This function is defined for all real numbers where cos x ≠ 1
fx=tan-1sinx1+cosx⇒fx=tan-12 sinx2cosx22 cos2x2⇒fx=tan-1tanx2=x2Thus, f’x=ddxx2=12
Q22.
Answer :
Let, y=sin-111+x2put x=cot θ∴ y=sin-111+cot2θ⇒ y=sin-11cosec2θ⇒ y=sin-1sinθ ⇒ y=θ⇒ y=cot-1x since, cotθ=x
Differentiate it with respect to x,
dydx=-11+x2
Q23.
Answer :
Let, y=cos-11-x2n1+x2nPut xn=tanθ∴ y=cos-11-xn21+xn2⇒ y=cos-11-tan2θ1+tan2θ ⇒ y=cos-1cos 2θ …iHere, 0<x<∞⇒ 0<xn<∞⇒ 0<tanθ<∞⇒ 0<θ<π2⇒ 0<2θ<πSo, from equation i, y=2θ Since, cos-1cos θ=θ, if θ∈0, π ⇒y=2 tan-1xn
Differentiate it with respect to x using chain rule,
dydx=211+xn2ddxxn⇒dydx=21+x2n×nxn-1∴dydx=2nxn-11+x2n
Q24.
Answer :
Let, y=sin-11-x21+x2+sec-11+x21-x2⇒ y=sin-11-x21+x2+cos-11-x21+x2 Since, sec-1x=cos-11x⇒ y=π2 Since, sin-1x+cos-1x=π2
Differentiate it with respect to x,
∴ dydx=0
Q25.
Answer :
Let, y=tan-1a+x1-ax⇒ y=tan-1a+tan-1x Since, tan-1x+tan-1y=tan-1x+y1-xy
Differentiate it with respect to x,
dydx=ddxtan-1a+ddxtan-1x⇒dydx=0+11+x2∴ dydx=11+x2
Q26.
Answer :
Let, y=tan-1x+a1-xa⇒ y=tan-1x+tan-1a Since, tan-1x+tan-1y=tan-1x+y1-xy
Differentiate it with respect to x using chain rule,
dydx=ddxtan-1x+ddxtan-1a⇒dydx=11+x2ddxx+0⇒dydx=11+x12x∴dydx=12×1+x
Q27.
Answer :
Let, y=tan-1a+b tanxb-a tanx⇒ y=tan-1a+b tanxbb-a tanxb⇒ y=tan-1ab+tanx1-abtanx⇒ y=tan-1tantan-1ab+ tanx1-tantan-1ab×tanx⇒ y=tan-1tantan-1ab+x⇒ y=tan-1ab+x
Differentiate it with respect to x,
dydx=0+1∴ dydx=1
Q28.
Answer :
Let, y=tan-1a+bxb-ax⇒ y=tan-1a+bxbb-axb⇒ y=tan-1ab+bxbbb-axb⇒ y=tan-1ab+x1-abx⇒ y=tan-1ab+tan-1x Since, tan-1x+tan-1y=tan-1x+y1-xy
Differentiate it with respect to x,
dydx=0+11+x2⇒dydx=11+x2
Q29.
Answer :
Let, y=tan-1x-ax+a⇒ y=tan-1x-axx+ax⇒ y=tan-1xx-axxx+ax⇒ y=tan-11-ax1+1×ax⇒ y=tan-11-tan-1ax
Differentiate it with respect to x,
dydx=0-11+ax2ddxax⇒ dydx=-x2x2+a2-ax2∴ dydx=aa2+x2
Q30.
Answer :
Let, y=tan-1×1+6×2⇒ y=tan-13x-2×1+3x2x⇒ y=tan-13x-tan-12x Since, tan-1x-tan-1y=tan-1x-y1+xy
Differentiate it with respect to x using chain rule,
dydx=11+3x2ddx3x-11+2x2ddx2x⇒dydx=11+9×23-11+4×22∴dydx=31+9×2-21+4×2
Q31.
Answer :
Let, y=tan-15×1-6×2⇒ y=tan-13x+2×1-3x2x⇒ y=tan-13x+tan-12x Since, tan-1x+tan-1y=tan-1x+y1-xy
Differentiate it with respect to x using chain rule,
dydx=11+3x2ddx3x+11+2x2ddx2x⇒dydx=11+9×2×3+11+4×2×2∴dydx=31+9×2+21+4×2
Q32.
Answer :
Let, y=tan-1cosx+sinxcosx-sinx⇒ y=tan-1cosx+sinxcosxcosx-sinxcosx⇒ y=tan-1cosxcosx+sinxcosxcosxcosx-sinxcosx⇒ y=tan-11+tanx1-tanx⇒ y=tan-1tanπ4+tanx1-tanπ4tanx⇒ y=tan-1tanπ4+x⇒ y=π4+x
Differentiate it with respect to x,
dydx=0+1∴dydx=1
Q33.
Answer :
Let, y=tan-1×13+a131-ax13⇒ y=tan-1×13+tan-1a13 Since, tan-1x+tan-1y=tan-1x+y1-xy
Differentiate it with respect to x using chain rule,
dydx=11+x132×ddxx13+0⇒dydx=13× x13-11+x23∴dydx=13×231+x23
Q34.
Answer :
Let y=sin-1 11+x2Putting x=cot θ ⇒θ=cot-1x∴y=sin-1 11+cot θ2=sin-1 11+cot2 θ=sin-1 1cosec θ=sin-1 sin θ=θ∴ y=cot-1xDiff w.r.t.to x, we getdydx=-11+x2
Q35.
Answer :
Let, y=sin-12×1+x2+sec-11+x21-x2⇒ y=sin-12×1+x2+cos-11-x21+x2Put, x=tanθ∴ y=sin-12 tanθ1+tan2θ+cos-11-tan2θ1+tan2θ ⇒ y=sin-1sin 2θ+cos-1cos 2θ …iHere, 0<x<1⇒ 0<tanθ<1⇒ 0<θ<π4⇒ 0<2θ<π2So, from equation i, y=2θ+2θ Since, sin-1sinθ=θ, if θ∈-π2,π2 cos-1cosθ=θ, if θ∈0,π⇒y=4θ⇒y=4tan-1x Since, x=tanθ
Differentiate it with respect to x,
∴ dydx=41+x2
Page 11.63 Ex.11.3
Q36.
Answer :
Let, y=sin-1×1+x2+cos-111+x2Put x=tanθ∴ y=sin-1 tanθ1+tan2θ+cos-111+tan2θ⇒ y=sin-1sinθcosθsecθ+cos-11secθ⇒ y=sin-1sinθcosθ1cosθ+cos-1cosθ⇒ y=sin-1sin θ+cos-1cos θ …iHere, 0<x<∞⇒ 0<tanθ<∞⇒ 0<θ<π2So, from equation i,y=θ+θ Since, sin-1sinθ=θ, if θ∈-π2,π2 cos-1cosθ=θ, if θ∈0,π⇒y=2θ⇒y=2tan-1x Since, x=tanθ
Differentiate it with respect to x,
∴ dydx=21+x2
Q37.
Answer :
Here, y=tan-11+x2+1-x21+x2-1-x2Put x2=cos2θ⇒ y=tan-11+cos2θ+1-cos2θ1+cos2θ-1-cos2θ⇒ y=tan-12 cos2θ+2 sin2θ2 cos2θ-2 sin2θ⇒ y=tan-12cosθ+sinθ2cosθ-sinθ⇒ y=tan-1cosθ+sinθcosθcosθ-sinθcosθ Dividing numerator and denominator by cosθ⇒ y=tan-1cosθcosθ+sinθcosθcosθcosθ-sinθcosθ⇒ y=tan-11+tanθ1-tanθ⇒ y=tan-1tanπ4+tanθ1+tanπ4+tanθ ⇒ y=tan-1tanπ4+θ ⇒ y=π4+θ⇒ y=π4+12cos-1×2 Using x2=cos 2θ
Differentiate it with respect to x,
dydx=0+12-11-x22×2xdydx=-x1-x4
Q38.
Answer :
Let, y=cot-11+sinx+1-sinx1+sinx-1-sinx …iWe have, 1+sinx+1-sinx1+sinx-1-sinx =1+sinx+1-sinx21+sinx-1-sinx1+sinx+1-sinx =1+sinx+1-sinx+21-sinx1+sinx1+sinx-1-sinx =2+21-sin2x2sinx =1+cosxsinx =2cos2x22sinx2cosx2 =cotx2Therefore, equation i becomes y=cot-1cotx2⇒y=x2∴dydx=12Hence, dydx is independent of x.
Q39.
Answer :
Here, y=tan-12×1-x2+sec-11+x21-x2⇒ y=tan-12×1-x2+cos-11-x21+x2 Put x=tanθ∴ y=tan-12tanθ1-tan2θ+cos-11-tan2θ1+tan2θ ⇒ y=tan-1tan 2θ+cos-1cos 2θ⇒ y=2θ+2θ ⇒ y=4θ⇒ y=4 tan-1x using, x=tanθ
Differentiate it with respect to x,
∴ dydx=41+x2
Q40.
Answer :
Here, y=sec-1x+1x-1+sin-1x-1x+1⇒ y=cos-1x-1x+1+sin-1x-1x+1 Since, sec-1x=cos-11x⇒ y=π2 Since, cos-1α+sin-1α=π2
Differentiate it with respect to x,
∴ dydx=0
Q41.
Answer :
Here, y=sin2 tan-11-x1+xPut x=cos 2θWe have, y=sin2 tan-11-cos 2θ1+cos 2θ =sin2 tan-12 sin2θ2 cos2θ =sin2 tan-1tan2θ =sin2 tan-1tanθ =sin2θ =sin2×12cos-1x Since, x=cos 2θ =sinsin-11-x2 =1-x2
Differentiate it with respect to x using chain rule,
dydx=121-x2ddx1-x2⇒dydx=121-x2-2x∴dydx=-x1-x2
Q42.
Answer :
Here, y=cos-12x+2 cos-11-4x2Put 2x=cosθ∴ y=cos-1cos θ+2 cos-11-cos2θ⇒ y=cos-1cos θ+2 cos-1sinθ⇒ y=cos-1cos θ+2 cos-1cosπ2-θ …iHere, 0<x<12⇒ 0<2x<1⇒ 0<cosθ<1⇒ 0<θ<π2and⇒ 0>-θ>-π2⇒ π2>π2-θ>0⇒ 0<π2-θ<π2So, from equation i, y=θ+2π2-θ Since, cos-1cosθ=θ, if θ∈0,π⇒ y=+π-2θ⇒ y=π-θ⇒ y=π-cos-12x Since, 2x=cosθ
Differentiate it with respect to x using chain rule,
dydx=0–11-2x2ddx2x⇒dydx=11-4×22∴dydx=21-4×2
Q43.
Answer :
Here, ddxtan-1a+bx=1 at x=0⇒ 11+a+bx2ddxa+bxx=0=1⇒ 11+a+bx2×bx=0=1⇒b1+a+02=1⇒ b=1+a2∴1+a2 = b
Q44.
Answer :
Here, y=cos-12x+2 cos-11-4x2Put 2x=cosθ∴ y=cos-1cos θ+2 cos-11-cos2θ⇒ y=cos-1cos θ+2 cos-1sinθ⇒ y=cos-1cos θ+2 cos-1cosπ2-θ …iNow, -12<x<0⇒ -1<2x<0⇒ -1<cosθ<0⇒ π2<θ<πAnd⇒ -π2>-θ>-π⇒ π2-π2>π2-θ>π2-π⇒ 0>π2-θ>-π2⇒ -π2<π2-θ<0So, from equation i,y=θ+2-π2-θ Since, cos-1cosθ=θ, if θ∈0,π cos-1cosθ=-θ, if θ∈-π,0y=θ-2×π2+2θy=-π+3θy=-π+3cos-12x Since, 2x=cosθ
Differentiate it with respect to x using chain rule,
dydx=0+3-11-2x2ddx2x⇒dydx=-31-4×2×2∴dydx=-61-4×2
Q45.
Answer :
Here, y=tan-11+x-1-x1+x+1-xPut x=cos2θ ∴ y=tan-11+cos2θ-1-cos2θ1+cos2θ+1-cos2θ =tan-12 cos2θ-2 sin2θ2 cos2θ+2 sin2θ =tan-12cosθ-sinθ2cosθ+sinθ =tan-1cosθ-sinθcosθcosθ+sinθcosθ Dividing numerator and denominator by cosθ =tan-1cosθcosθ-sinθcosθcosθcosθ+sinθcosθ =tan-11-tanθ1+tanθ
=tan-1tanπ4-tanθ1+tanπ4×tanθ =tan-1tanπ4-θ =π4-θ =π4-12cos-1x Using x=cos2θ
Differentiate it with respect to x,
dydx=0-12-11-x2∴dydx=121-x2
Q46.
Answer :
Let, y=cot-11-x1+xPut x=tanθ ∴ y=cot-11-tanθ1+tanθ =cot-1tanπ4-tanθ1+tanπ4tanθ =cot-1tanπ4-θ =cot-1cotπ2-π4+θ =π4+θ =π4+tan-1x Since, x=tanθ
Differentiate it with respect to x,
dydx=0+11+x2⇒dydx=11+x2
Q47.
Answer :
Let y=cos-12x-31-x213Put, x=cosθ y=cos-12cosθ-31-cos2θ13 y=cos-12cosθ-3sinθ13 y=cos-1cosθ213+sinθ313Let cosϕ=213 and sinϕ=313 y=cos-1cosθcosϕ+sinθ sinϕ y=cos-1cosθ-ϕ …i y=θ-ϕ y=cos-1x-ϕ Differentiating it with respect to x,dydx=-11-x2+0dydx=-11-x2
Q48.
Answer :
i Let, fx=cos-1sinx⇒fx=cos-1cosπ2-x⇒fx=π2-xThus, f’x=ddxπ2-x= -1
ii Let, y=sin-12x+11+4x Put 2x=tanθ ∴ y=sin-12x×21+2×2 ⇒ y=sin-12tanθ1+tan2θ ⇒ y=sin-1sin2θ ⇒ y=2θ Since, sin-1sinθ=θ ⇒ y=2tan-12x Since, 2x=tanθ
Differentiate with respect to x using chain rule,
dydx=21+2x2ddx2x⇒dydx=2×2xlog21+4x∴dydx=2x+11+4xlog2
Page 11.70 Ex.11.4
Q1.
Answer :
We have, xy=c2
Differentiating with respect to x, we get,
ddxxy=ddxc2⇒xdydx+yddxx=0 Using product rule⇒xdydx+y=0⇒xdydx=-y⇒dydx=-yx
Q2.
Answer :
We have, y3-3xy2=x3+3x2y
Differentiating with respect to x, we get,
⇒ddxy3-ddx3xy2=ddxx3+ddx3x2y⇒3y2dydx-3xddxy2+y2ddxx=3×2+3x2ddxy+yddxx2 Using product rule⇒3y2dydx-3x2ydydx+y2=3×2+3x2dydx+y2x⇒3y2dydx-6xydydx-3y2=3×2+3x2dydx+6xy⇒3y2dydx-6xydydx-3x2dydx=3×2+6xy+3y2⇒3dydxy2-2xy-x2=3×2+2xy+y2⇒dydx=3x+y23y2-2xy-x2⇒dydx=x+y2y2-2xy-x2
Q3.
Answer :
We have, x23+y23=a23
Differentiating it with respect to x, we get,
ddxx23+ddxy23=ddxa23⇒23×23-1+23y23-1dydx=0⇒23x-13+23y-13dydx=0⇒23y-13dydx=-23x-13⇒dydx=-23x-13×32y-13⇒dydx=-x-13y-13⇒dydx=-y13x13⇒dydx=-yx13
Q4.
Answer :
We have, 4x+3y= log4x-3y
Differentiating with respect to x, we get,
ddx4x+ddx3y=ddxlog4x-3y⇒4+3dydx=14x-3yddx4x-3y ⇒4+3dydx=14x-3y4-3dydx⇒3dydx+34x-3ydydx=44x-3y-4⇒3dydx1+14x-3y=414x-3y-1⇒3dydx4x-3y+14x-3y=41-4x+3y4x-3y⇒dydx=431-4x+3y4x-3y4x-3y4x-3y+1⇒dydx=431-4x+3y4x-3y+1
Q5.
Answer :
We have, x2a2+y2b2=1
Differentiating with respect to x, we get,
ddxx2a2+y2b2=ddx1⇒ddxx2a2+ddxy2b2=0⇒1a22x+1b22ydydx=0⇒2yb2dydx=-2xa2⇒dydx=-2xa2b22y⇒dydx=-b2xa2y
Q6.
Answer :
We have, x5+y5=5xy
Differentiating with respect to x, we get,
ddxx5+ddxy5=ddx5xy⇒5×4+5y4dydx=5xdydx+yddxx⇒5×4+5y4dydx=5xdydx+y1⇒5×4+5y4dydx=5xdydx+5y⇒5y4dydx-5xdydx=5y-5×4⇒5dydxy4-x=5y-x4⇒dydx=5y-x45y4-x⇒dydx=y-x4y4-x
Q7.
Answer :
We have, x+y2=2axy
Differentiating with respect to x, we get,
⇒ddxx+y2=ddx2axy⇒2x+yddxx+y=2axdydx+yddxx ⇒2x+y1+dydx=2axdydx+y1⇒2x+y+2x+ydydx=2axdydx+2ay⇒dydx2x+y-2ax=2ay-2x+y⇒dydx=2ay-x-y2x+y-ax⇒dydx=ay-x-yx+y-ax
Q8.
Answer :
We have, x2+y2=xy
Differentiating with respect to x, we get,
⇒ddxx2+y22=ddxxy⇒2×2+y2ddxx2+y2=xdydx+yddxx ⇒2×2+y22x+2ydydx=xdydx+y1⇒4xx2+y2+4yx2+y2dydx=xdydx+y⇒4yx2+y2dydx-xdydx=y-4xx2+y2⇒dydx4yx2+y2-x=y-4xx2+y2⇒dydx=y-4xx2+y24yx2+y2-x⇒dydx=4xx2+y2-yx-4yx2+y2
Q9.
Answer :
We have, tan-1×2+y2=a
Differentiate with respect to x, we get,
ddxtan-1×2+y2=ddxa⇒11+x2+y22×ddxx2+y2=0⇒11+x2+y222x+2ydydx=0⇒2x+2ydydx=0⇒x+ydydx=0⇒dydx=-xy
Q10.
Answer :
We have, ex-y=logxy
Differentiate with respect to x,
ddxex-y=ddxlogxy⇒ex-yddxx-y=1xy×ddxxy ⇒ex-y1-dydx=yxyddxx-xdydxy2 ⇒ex-y-ex-ydydx=1xyy1-xdydx⇒ex-y-ex-ydydx=1x-1ydydx⇒1ydydx-ex-ydydx=1x-ex-y⇒dydx1y-ex-y1=1x-ex-y1⇒dydx1-yex-yy=1-xex-yx⇒dydx=yx1-xex-y1-yex-y⇒dydx=-y-xxex-y-1yex-y-1⇒dydx=yxxex-y-1yex-y-1
Q11.
Answer :
We have, sinxy+cosx+y=1
Differentiating with respect to x, we get,
ddxsinxy+ddxcosx+y=ddx1⇒cosxyddxxy-sinx+yddxx+y=0 ⇒cosxyxdydx+yddxx-sinx+y1+dydx=0⇒cosxyxdydx+y1-sinx+y-sinx+ydydx=0⇒xcosxydydx+ycosxy-sinx+y-sinx+ydydx=0⇒xcosxy-sinx+ydydx=sinx+y-ycosxy⇒dydx=sinx+y-y cosxyxcosxy-sinx+y
Q12.
Answer :
We have, 1-x2+1-y2=ax-yLet x=sinA , y=sinB⇒1-sin2A+1-sin2B=asinA-sinB⇒cosA+cosB=asinA-sinB ⇒a=cosA+cosBsinA-sinB⇒a=2 cosA+B2cosA-B22 cosA+B2sinA-B2 ∵sinA-sinB=2 cosA+B2sinA-B2∵cosA+cosB=2 cosA+B2cosA-B2⇒a=cotA-B2⇒cot-1a=A-B2⇒2cot-1a=A-B⇒2cot-1a=sin-1x-sin-1y ∵x=sinA,y=sinB
Differentiating with respect to x, we get,
ddx2cot-1a=ddxsin-1x-ddxsin-1y⇒0=11-x2-11-y2dydx⇒11-y2dydx=11-x2⇒dydx=1-y21-x2⇒dydx=1-y21-x2
Page 11.71 Ex.11.4
Q13.
Answer :
We have, y1-x2+x1-y2=1Let x=sinA , y=sinB⇒sinB1-sin2A+sinA1-sin2B=1⇒sinBcosA+sinAcosB=1 ∵sinx+y=sinx cosy+cosxsiny⇒sinA+B=1⇒A+B=sin-11⇒sin-1x+sin-1y=π2 ∵ x=sinA, y=sinB
Differentiate with respect to x,
⇒ddxsin-1x+ddxsin-1y=ddxπ2⇒11-x2+11-y2dydx=0⇒dydx=-1-y21-x2
Q14.
Answer :
We have, xy=1
Differentiating with respect to x, we get,
ddxxy=ddx1⇒xdydx+yddxx=0 Using product rule⇒xdydx+y1=0⇒dydx=-yx ⇒dydx=-y1y ∵ x=1y⇒dydx=-y2⇒dydx+y2=0
Q15.
Answer :
We have, xy2=1 …i
Differentiating with respect to x, we get,
ddxxy2=ddx1⇒xddxy2+y2ddxx=0 ⇒x2ydydx+y21=0⇒2xydydx=-y2⇒dydx=-y22xy⇒dydx=-y2xput x=1y2 from equation i⇒dydx=-y21y2⇒2dydx=-y3⇒2dydx+y3=0
Q16.
Answer :
We have, x1+y+y1+x=0⇒ x1+y=-y1+xSquaring both sides,we get,⇒ x1+y2=-y1+x2⇒x21+y=y21+x⇒x2+x2y=y2+y2x⇒x2-y2=y2x-x2y⇒x-yx+y=xyy-x⇒x+y=-xy⇒y+xy=-x⇒y1+x=-x⇒y=-x1+x
Differentiating with respect to x, we get,
⇒dydx=-1+xddxx–xddxx+11+x2⇒dydx=-1+x1+x11+x2⇒dydx=-1-x+x1+x2⇒dydx=-11+x2⇒1+x2dydx=-1⇒1+x2dydx+1=0
Q17.
Answer :
We have, logx2+y2=tan-1xy⇒logx2+y212=tan-1yx⇒12logx2+y2=tan-1yx
Differentiate with respect to x, we get,
⇒ 12ddxlogx2+y2=ddxtan-1yx⇒ 121×2+y2ddxx2+y2=11+yx2ddxyx⇒121×2+y22x+2ydydx=x2x2+y2xdydx-yddxxx2⇒1×2+y2x+ydydx=x2x2+y2xdydx-yddxxx2⇒1×2+y2x+ydydx=x2x2+y2xdydx-y1x2⇒ x+ydydx=xdydx-y⇒ydydx-xdydx=-y-x⇒dydxy-x=-y+x⇒dydx=-y+xy-x⇒dydx=x+yx-y
Q18.
Answer :
We have, secx+yx-y=a⇒ x+yx-y=sec-1a
Differentiate with respect to x, we get,
⇒ x-yddxx+y-x+yddxx-yx-y2=0⇒ x-y 1+dydx-x+y 1-dydx=0⇒ x-y+x-ydydx-x+y+x+ydydx=0⇒dydxx-y+x+y=x+y-x+y⇒dydx2x=2y⇒dydx=yx
Q19.
Answer :
We have, tan-1×2-y2x2+y2=a⇒ x2-y2x2+y2=tana⇒ x2-y2=tanax2+y2
Differentiating with respect to x,
⇒ ddxx2-y2=tanaddxx2+y2⇒ 2x-2ydydx=tana2x+2ydydx⇒ 2x-2ydydx=2xtana+2ytanadydx⇒2ytanadydx+2ydydx=2x-2xtana⇒2y1+tanadydx=2×1-tana⇒dydx=xy1-tana1+tana
Hence proved
Q20.
Answer :
We have, xy logx+y=1
Differentiating it with respect to x,
⇒ ddxxy logx+y=ddx1⇒ xyddxlogx+y+x logx+ydydx+y logx+yddxx=0 using chain rule and product rule⇒xy1x+yddxx+y+x logx+ydydx+y logx+y1=0⇒xyx+y 1+dydx+x logx+ydydx+y logx+y=0⇒xyx+ydydx+xyx+y+x1xydydx+y1xy=0 ∵xy logx+y=1⇒dydxxyx+y+1y=-1x+xyx+y⇒ dydxxy2+x+yx+yy=-x+y+x2yxx+y⇒ dydx=-x+y+x2yxx+yyx+yxy2+x+y⇒ dydx=-yxx+y+x2yx+y+xy2
Hence proved
Q21.
Answer :
We have, y=x sina+y
Differentiate with respect to y,
dydx=ddxx sina+y⇒dydx=xddxsina+y+sina+yddxx using product rule and chain rule⇒dydx=x cosa+yddxa+y+sina+y1⇒dydx1-x cosa+y=sina+y⇒dydx=sina+y1-x cosa+y⇒dydx=sina+y1-ysina+y cosa+y∵y=xsina+y ⇒dydx=sin2a+ysin a+y-y cos a+y
Hence proved
Q22.
Answer :
We have, xsina+y+sinacosa+y=0
Differentiate with respect to x,
⇒ddxx sina+y+ddxsin a cosa+y=0⇒xddxsin a+y+sina+yddxx+sin addxcosa+y=0 ⇒x cosa+yddxa+y+sina+y1+sin a-sina+yddxa+y=0⇒x cosa+ydydx+sina+y- sinasina+ydydx=0⇒dydxx cosa+y-sina sina+y=-sina+y⇒dydx-sin acos2a+ysina+y-sin a sina+y=-sina+y ∵x=-sinacosa+ysina+y⇒-dydxsin a cos2a+y+sin a sin2a+ysina+y=-sina+y⇒dydx=sina+ysina+ysinacos2a+y+sin2a+y⇒dydx=sin2a+ysina
Q23.
Answer :
We have, y=x siny
Differentiating with respect to x, we get,
dydx=ddxx siny⇒dydx=xddxsiny+sinyddxx⇒dydx=xcosydydx+siny⇒dydx1-xcosy=siny⇒dydx=siny1-xcosy
Q24.
Answer :
We have, yx2+1=logx2+1-x
Differentiating with respect to x, we get,
⇒ddxyx2+1=ddxlogx2+1-x using product rule and chain rule⇒yddxx2+1+x2+1dydx=1×2+1-x×ddxx2+1-x⇒y2x2+1×ddxx2+1+x2+1dydx=1×2+1-x×12×2+1ddxx2+1-1⇒2xy2x2+1+x2+1dydx=1×2+1-x2x2x2+1-1⇒x2+1dydx=1×2+1-xx-x2+1×2+1-xyx2+1⇒x2+1dydx=-1×2+1-xyx2+1⇒x2+1dydx=-1+xyx2+1⇒x2+1dydx=-1+xy⇒x2+1dydx+1+xy=0
Q25.
Answer :
We have, y=logcosx sinxlogsinx cosx-1+sin-12×1+x2⇒ y=logcosx sinxlogcosx sinx+sin-12×1+x2 ∵logab=logba-1⇒y=log sinxlog cosx2+sin-12×1+x2 ∵logab=logbloga
Differentiating with respect to x,
dydx=ddxlog sinxlog cosx2+ddxsin-12×1+x2⇒dydx=2log sinxlog cosxddxlog sinxlog cosx+11-2×1+x22×ddx2x1+x2 ⇒dydx=2log sinxlog cosxlog cosxddxlog sinx-log sinxddxlog cosxlog cosx2+1+x21+x4-2×21+x22-2x2x1+x22 ⇒dydx=2log sinxlog cosxlog cosx×1sinxddxsinx-log sinx×1cosxddxcosxlog cosx2+1+x21+x4-2×21+x22-2x2x1+x22 ⇒dydx=2log sinxlog cosxlog cosx×cosxsinx+log sinx × sinxcosxlog cosx2+1+x21-x222+2×2-4×21+x22⇒dydx=2log sinxlog cosx3cotx log cosx+tanx log sinx+21+x2put x=π4⇒dydx=2log sinπ4log cosπ43 cotπ4 log cosπ4+tanπ4 log sinπ4+211+π42⇒dydx=21log1221× log12+1× log12+21616+π2 ⇒dydx=2×2log12log122+3216+π2⇒dydx=41log12+3216+π2⇒dydx=41-12log2+ 3216+π2⇒dydx=-8log2+3216+π2So, dydxx=π4=8416+π2-1log2
Q26.
Answer :
We have, sinxy+yx=x2-y2
Differentiating with respect to x, we get,
⇒ddxsin xy+ddxyx=ddxx2-ddxy2⇒cosxyddxxy+xdydx-yddxxx2=2x-2ydydx ⇒cosxyxdydx+yddxx+xdydx-y1x2=2x-2ydydx⇒cosxyxdydx+y1+1x2xdydx-y=2x-2ydydx⇒x cosxydydx+y cosxy+1xdydx-yx2=2x-2ydydx⇒dydxx cosxy+1x+2y=yx2-y cosxy+2x⇒dydxx2cosxy+1+2xyx=1x2y-x2y cosxy+2×3⇒dydx=2×3+y-x2y cosxyxx2 cosxy+1+2xy
Q27.
Answer :
Here, y+x+y-x=c
Differentiating with respect to x,
⇒ddxy+x+ddxy-x=ddxc⇒12y+xddxy+x+12y-xddxy-x=0 ⇒12y+xdydx+1+12y-xdydx-1=0⇒dydx12y+x+dydx12y-x=12y-x-12y+x⇒dydx×121y+x+1y-x=12y+x-y-xy-xy+x⇒dydxy-x+y+xy+xy-x=y+x-y-xy-xy+x⇒dydx=y+x-y-xy+x+y-x×y+x-y-xy+x-y-x rationalizing the denominator⇒dydx=y+x+y-x-2y+xy-xy+x-y+x⇒dydx=2y-2y2-x22x⇒dydx=2y2x-2y2-x22x⇒dydx=yx-y2-x2x2⇒dydx=yx-y2x2-1
Q28.
Answer :
We have, tanx+y+tanx-y=1
Differentiating with respect to x, we get,
⇒ddxtanx+y+ddxtanx-y=ddx1⇒sec2x+yddxx+y+sec2x-yddxx-y=0 ⇒sec2x+y1+dydx+sec2x-y1-dydx=0⇒sec2x+ydydx-sec2x-ydydx=-sec2x+y+sec2x-y⇒dydxsec2x+y-sec2x-y=-sec2x+y+sec2x-y⇒dydx=sec2x+y+sec2x-ysec2x-y-sec2x+y
Q29.
Answer :
We have, ex+ey=ex+y
Differentiating with respect to x, we get
⇒ddxex+ddxey=ddxex+y⇒ex+eydydx=ex+yddxx+y⇒ex+eydydx=ex+y1+dydx⇒eydydx-ex+ydydx=ex+y-ex⇒dydx=ex×ey-exey-ex×ey⇒dydx=exey-1ey1-ex⇒dydx=-exey-1eyex-1
Q30.
Answer :
We have, cos y=x cosa+yDifferentiating with respect to x, we get,ddxcosy=ddxxcosa+y⇒-sinydydx=cosa+yddxx+xddx cosa+y ⇒-sinydydx=cosa+y+x-sina+ydydx⇒xsina+y-sin ydydx=cosa+y ⇒ cosycosa+ysina+y-sin ydydx=cosa+y ∵cosy=x cosa+y⇒x=cosycosa+y ⇒cosysina+y-sinycosa+ydydx=cos2a+y⇒sina+y-ydydx=cos2a+y⇒dydx=cos2a+ysina
Page 11.83 Ex.11.5
Q1.
Answer :
Let y=x1x …i
Taking log on both sides,
log y=log x1x⇒ log y=1xlog x ∵log ab=blog a
Differentiating with respect to x,
⇒1ydydx=1xddxlog x+log xddxx-1 Using product rule⇒1ydydx=1x×1x+log x×-1×2 ⇒1ydydx=1×2-logxx2⇒1ydydx=1-logxx2
⇒dydx=x1x1-log xx [From (i)]
Q2.
Answer :
Let y=xsinx …i
Taking log on both sides,
log y=log xsinx⇒log y=sinx log x ∵log ab=b loga
Differentiating with respect to x, we get,
⇒1ydydx=sinxddxlog x+log xddxsinx using product rule⇒1ydydx=sinx1x+log xcosx⇒dydx=ysinxx+log xcosx
,⇒dydx=xsinxsinxx+log xcosx [From (i)]
Q3.
Answer :
Let y=1+cosxx …i
Taking log on both sides,
log y=log1+cosxx⇒log y=x log1+cosx
Differentiating with respect to x,
1ydydx=xddxlog1+cosx+log1+cosxddxx ⇒1ydydx=x×11+cosxddx1+cosx+log1+cosx1⇒1ydydx=x1+cosx0-sin x+log1+cosx⇒1ydydx=log1+cosx-x sinx1+cosx⇒dydx=ylog1+cosx-x sinx1+cosx⇒dydx=1+cosxxlog1+cosx-x sinx1+cosx using equation i
Q4.
Answer :
Let y=xcos-1x …i
Taking log both sides,
log y=log xcos-1x⇒log y=cos-1x log x
Differentiating with respect to x,
1ydydx=cos-1xddxlog x+log xddxcos-1x ⇒1ydydx=cos-1x1x+log x-11-x2⇒1ydydx=cos-1xx-log x1-x2⇒dydx=ycos-1xx-log x1-x2⇒dydx=xcos-1xcos-1xx-log x1-x2 Using equation i
Q5.
Answer :
Let y=logxx …i
Taking log on both sides,
logy=loglogxx⇒logy=xloglogx
Differentiating with respect to x using chain rule,
1ydydx=xddxloglogx+loglogxddxx⇒1ydydx=x1logxddxlogx+loglogx1⇒1ydydx=xlogx1x+loglogx⇒1ydydx=1logx+loglogx⇒dydx=y1logx+loglogx⇒dydx=logxx1logx+loglogx using equation i
Q6.
Answer :
Let y=logxcosx …i
Taking log on both sides,
logy=loglogxcosx⇒logy=cosx loglogx
Differentiating with respect to x,
⇒1ydydx=cosxddxloglogx+loglogxddxcosx⇒1ydydx=cosxlogxddxlogx+loglogx×-sinx⇒1ydydx=cosxlogx×1x-sinx loglogx⇒dydx=ycosxx logx-sinx loglogx⇒dydx=logxcosxcosxx logx-sinx loglogx using equation i
Q7.
Answer :
Let y=sinxcosx …iTaking log on both sides,logy=logsinxcosx⇒logy=cosx log sinx Differentiating with respect to x,1ydydx=cosxddxlog sinx+log sinxddxcosx ⇒1ydydx=cosx1sinxddxsinx+log sinx-sinx⇒1ydydx=cosxsinxcosx-sinx log sinx⇒dydx=ycosx cotx-sinx log sinx⇒dydx=sinxcosxcosx cotx-sinx log sinx using equation i
Q8.
Answer :
Let y=ex logx Taking log on both sides,logy=xlogxloge⇒logy=x logx Differentiating with respect to x,1ydydx=xddxlogx+logxddxx ⇒1ydydx=x1x+logx1⇒1ydydx=1+logx⇒dydx=y1+logx⇒dydx=exlogx1+logx using equation i⇒dydx=elogxx1+logx ⇒dydx=xx1+logx
Q9.
Answer :
Let y=sinxlogx …iTaking log on both sides,logy=logsinxlogx⇒logy=logx log sinx Differentiating with respect to x,1ydydx=logxddxlog sinx+log sinxddxlogx ⇒1ydydx=logx1sinxddxsinx+log sinx1x⇒1ydydx=logxsinxcosx+ log sinxx⇒dydx=ylogx cotx+log sinxx⇒dydx=sinxlogxlogx cotx+log sinxx using equation i
Q10.
Answer :
Let y=10log sinx …iTaking log on both sides,logy=log10log sinx⇒logy=log sinx log10 Differentiating with respect to x,⇒1ydydx=log10ddxlog sinx ⇒1ydydx=log101sinxddxsinx⇒1ydydx=log101sinxcosx⇒dydx=ylog10×cotx⇒dydx=10log sinx×log1
Q11.
Answer :
Let y=logxlogx ….iTaking log on both sides,logy=loglogxlogx⇒logy=logx log logx Differentiating both side with respect to x,⇒1ydydx=loglogxddxlogx+logx ddxloglogx ⇒dydx=yloglogx1x+logx1logxddxlogx⇒dydx=y1xloglogx+1x∴dydx=logxlogx1+loglogxx using equation i
Q12.
Answer :
Let y=1010x …iTaking log on both sides,logy=loge1010xlogy=10x loge10 Differentiating with respect to x,⇒1ydydx=loge10×10xloge10 ⇒1ydydx=10x×loge102⇒dydx=y10x×loge102 ∴dydx=1010x×10x×loge102 using equation i
Q13.
Answer :
Let y=sin xx ⇒ sin-1y=xx …iTaking log on both sides,logsin-1y=logxx⇒logsin-1y=x logx Differentiating with respect to x,⇒1sin-1ydydxsin-1y=xddxlogx+logxddxx ⇒1sin-1y×11-y2dydx=x1x+logx⇒dydx=sin-1y1-y21+logx⇒dydx=sin-1sin xx1-sin xx21+logx⇒dydx=sin-1sinxx1-sin xx2 1+logx ∴ dydx=xxcosxx1+logx using equation i
Q14.
Answer :
Let y=sin-1xx …iTaking log on both sides,logy=logsin-1xx⇒logy=x logsin-1x Differentiating with respect to x,1ydydx=xddxlog sin-1x+log sin-1xddxx ⇒1ydydx=x1sin-1xddxsin-1x+log sin-1x⇒1ydydx=xsin-1×11-x2+ log sin-1x⇒dydx=ylog sin-1x+xsin-1×1-x2⇒dydx=sin-1xxlog sin-1x+xsin-1×1-x2 using equation i
Q15.
Answer :
Let y=xsin-1x …iTaking log on both sides,logy=logxsin-1x⇒logy=sin-1x logx Differentiating with respect to x,1ydydx=sin-1xddxlogx+logxddxsin-1x ⇒1ydydx=sin-1x1x+logx11-x2⇒dydx=ysin-1xx+logx1-x2⇒dydx=xsin-1xsin-1xx+logx1-x2 using equation i
Q16.
Answer :
Let y=tanx1x …iTaking log on both sides,logy=logtanx1x⇒logy=1xlogtanx Differentiating with respect to x,1ydydx=1xddxlogtanx+logtanxddx1x ⇒1ydydx=1x×1tanxddxtanx+logtanx-1×2⇒1ydydx=1xtanxsec2x-logtanxx2⇒dydx=ysec2xxtanx-logtan xx2⇒dydx=tanx1x sec2xxtanx-logtan xx2 using equation i
Q17.
Answer :
Let y=xtan-1x …iTaking log on both sides,logy=log xtan-1x⇒logy=tan-1x logx Differentiating with respect to x,1ydydx=tan-1xddxlogx+logxddxtan-1x ⇒1ydydx=tan-1x1x+logx11+x2⇒dydx=ytan-1xx+logx1+x2⇒dydx=xtan-1xtan-1xx+logx1+x2 using equation i
Q18.
Answer :
(i)
Let y=xxx …iTaking log on both sides,logy=logxxx⇒logy=logxx+logx12 ⇒logy=x logx+12logx
Differentiating with respect to x,
1ydydx=xddxlogx+logxddxx+12ddxlogx ⇒1ydydx=x1x+logx1+121x⇒1ydydx=1+logx+12x⇒dydx=y1+logx+12x⇒dydx=xxx1+logx+12x using equation i⇒dydx=xx+122x+12x+logx
ii Let y=xsinx-cosx+x2-1×2+1⇒ y=elogxsinx-cosx+x2-1×2+1⇒y=esinx-cosxlogx+x2-1×2+1
Differentiate it with respect to x using chain rule,
dydx=ddxesinx-cosxlogx+ddxx2-1×2+1 =esinx-cosxlogxddxsinx-cosxlogx+x2+1ddxx2-1-x2-1ddxx2+1×2+12 =elogxsinx-cosxsinx-cosxddxlogx+logxddxsinx-cosx+x2+12x-x2-12xx2+12 =xsinx-cosxsinx-cosx1x+logxsinx+cosx+2×3+2x-2×3+2xx2+12 =xsinx-cosxsinx-cosxx+sinx+cosxlogx+4xx2+12
iii Let y=xx cosx+x2+1×2-1Also, Let u=xx cosx and v=x2+1×2-1 ∴ y=u+v⇒dydx=dudx+dvdx …iNow, u=xx cosx⇒log u=logxx cosx⇒log u=x cosx logx
Differentiating both sides with respect to x,
1ududx=cosx logxddxx+xlogxddxcosx+x cosxddxlogx⇒dudx=ucosx logx+x-sinxlogx+x cosx1x⇒dudx=xx cosxcosx logx-x sinx logx+cosx⇒dudx=xx cosxcosx1+logx-x sinx logx …2Again, v=x2+1×2-1⇒log v=logx2+1-logx2-1
Differentiating both sides with respect to x,
1vdvdx=2xx2+1-2xx2-1⇒dvdx=v2xx2-1-2xx2+1×2+1×2-1⇒dvdx=x2+1×2-1-4xx2+1×2-1⇒dvdx=-4xx2-12 …3From i,ii and iii, we obtaindydx=xx cosxcosx1+logx-x sinx logx-4xx2-12
iv Let y=x cosxx+x sinx1x Also, Let u=x cosxx and v=x sinx1x∴ y=u+v⇒dydx=dudx+dvdx …iNow, u=x cosxx⇒log u=logx cosxx⇒log u=x logx cosx⇒log u=xlogx+log cosx⇒log u=xlogx+xlog cosx
Differentiate both sides with respect to x,
1ududx=ddxx logx+ddxx log cosx⇒dudx=ulogxddxx+xddxlogx+log cosxddxx+xddxlog cosx⇒dudx=x cosxxlogx1+x1x+log cosx1+x1cosxddxcosx⇒dudx=x cosxxlogx+1+log cosx+xcosx-sinx⇒dudx=x cosxx1+logx+log cosx-x tanx⇒dudx=x cosxx1-x tanx+logx+log cosx⇒dudx=x cosxx1-x tanx+logx cosx …iiAgain,v=x sinx1x⇒log v=logx sinx1x⇒log v=1xlogx sinx⇒log v=1xlogx+log sinx⇒log v=1xlogx+1xlog sinx
Differentiating both sides with respect to x,
1vdvdx=ddx1xlogx+ddx1xlogsinx⇒1vdvdx=logxddx1x+1xddxlogx+logsinxddx1x+1xddxlogsinx⇒1vdvdx=logx-1×2+1x1x+logsinx-1×2+1x1sinxddxsinx⇒1vdvdx=1×21-logx+-logsinxx2+1x sinxcosx⇒dvdx=x sinx1x1-logxx2+-logsinx+x cotxx2⇒dvdx=x sinx1x1-logx-logsinx+x cotxx2⇒dvdx=x sinx1x1-logxsinx+x cotxx2 …iiiFrom i,ii and iii, we obtaindydx=x cosxx1-x tanx+logx cosx+x sinx1xx cotx+1-logx sinxx2
v Let y=x+1x x+x1+1xAlso, Let u=x+1x x and v=x1+1x∴ y=u +v⇒dydx=dudx+dvdx …iThen, u=x+1x x⇒ log u=logx+1x x⇒log u=x logx+1x
Differentiate both sides with respect to x,
1ududx=logx+1xddxx+xddxlogx+1x⇒1ududx= logx+1x+x1x+1xddxx+1x⇒dudx=ulogx+1x+xx+1x×1-1×2⇒dudx=x+1xxlogx+1x+x-1xx+1x⇒dudx=x+1xxlogx+1x+x2-1×2+1⇒dudx=x+1xxx2-1×2+1+logx+1xAgain, v=x1+1x⇒log v=logx1+1x⇒log v=1+1xlog x
Differentiating both sides with respect to x,
1vdvdx=logxddx1+1x+1+1xddxlogx⇒ 1vdvdx=-1x2logx+1+1x1x⇒ 1vdvdx=-logxx2+1x+1×2⇒dvdx=v-logx+x+1×2⇒dvdx=x1+1xx+1-logxx2 …iiiFrom i,ii and iii, we obtaindydx=x+1xxx2-1×2+1+logx+1x+x1+1xx+1-logxx2
vii Let y=esinx+tanxx⇒ y=esinx+elogtanxx⇒y=esinx+exlogtanx
Differentiating with respect to x,
dydx=ddxesinx+ddxexlogtanx =esinxddxsinx+exlogtanxddxx logtanx =esinxcosx+elogtanxxxddxlogtanx+logtanxddxx =esinxcosx+tanxxxtanxsec2x+logtanx =esinxcosx+tanxxxsecxcosecx+logtanx
viii Let y=cosxx+sinx1x⇒y=elogcosxx+elogsinx1x⇒y=exlogcosx+e1xlogsinx
Differentiating with respect to x,
dydx=ddxex logcosx+ddxe1xlog sinx =ex logcosx×ddxx logcosx+e1xlog sinxddx1xlogsinx =elogcosxx× xddxlogcosx+logcosx × ddxx+elogsinx1x×1xddxlogsinx+logsinxddx1x =cosxxx1cosxddxcosx+logcosx1+sin1x1x×1sinx×ddxsinx+logsinx-1×2 =cosxxx1cosx-sinx+logcosx+sinx1x1x×1sinxcosx-1x2logsinx =cosxxlogcosx-x tanx+sinx1xcotxx-1x2logsinx
ix Let y=xx2-3+x-3×2 Also, let u=xx2-3 and v=x-3×2∴ y=u+v
Differentiate both sides with respect to x,
dydx=dudx+dvdx …iNow, u=xx2-3∴log u=logxx2-3⇒ log u=x2-3 logx
Differentiating with respect to x,
1ududx=logxddxx2-3+x2-3ddxlogx⇒1ududx=logx2x+x2-31x⇒dudx=xx2-3×2-3x+2x logxAlso, v=x-3×2∴log v=logx-3×2⇒log v=x2logx-3
Differentiating both sides with respect to x,
1vdvdx=logx-3ddxx2+x2ddxlogx-3⇒1vdvdx=logx-3 2x+x21x-3ddxx-3⇒dvdx=v2x logx-3+x2x-3×1⇒dvdx=x-3x2x2x-3+2xlogx-3
Substituing the expressions ofdudxand dvdxin equation idydx=xx2-3×2-3x+2x logx+x-3x2x2x-3+2x logx-3
Page 11.84 Ex.11.5
Q19.
Answer :
We have, y=ex+10x+xx⇒ y=ex+10x+elogxx ⇒y=ex+10x+exlogx
Differentiating with respect to x,
dydx=ddxex+ddx10x+ddxexlogx =ex+10x log10+exlogxddxx logx =ex+10x log10+exlogxxddxlogx+logxddxx =ex+10x log10+elogxxx1x+logx =ex+10x log10+xx1+logx =ex+10x log10+xxloge+logx ∵logee=1 =ex+10x log10+xxlogex
Q20.
Answer :
We have, y=xn+nx+xx+nn⇒y=xn+nx+elogxx+nn ⇒y=xn+nx+exlogx+nn
Differentiate with respect to x,
dydx=ddxxn+ddxnx+ddxexlogx+ddxnn =nxn-1+nx logn+elogxxxddxlogx+logxddxx =nxn-1+nx logn+xxx1x+logx =nxn-1+nx logn+xx1+logx =nxn-1+nx logn+xxloge+logx ∵logee=1 and logA+logB=logAB =nxn-1+nx logn+xxlogex
Q21.
Answer :
We have, y=x2-132x-1x-34x-1 …i⇒y=x2-132x-1x-3124x-112
Taking log on both sides,
log y=logx2-132x-1x-3124x-112⇒logy=logx2-13+log2x-1-logx-312-log4x-112⇒logy=3 logx2-1+log2x-1-12logx-3-12log4x-1
Differentiating with respect to x using chain rule,
1ydydx=3ddxlogx2-1+ddxlog2x-1-12ddxlogx-3-12log4x-1⇒1ydydx=31×2-1ddxx2-1+12x-1ddx2x-1-121x-3ddxx-3-1214x-1ddx4x-1⇒1ydydx=31×2-12x+12x-12-121x-31-1214x-14⇒1ydydx=6xx2-1+22x-1-12x-3-24x-1⇒dydx=y6xx2-1+22x-1-12x-3-24x-1⇒dydx=x2-132x-1x-34x-16xx2-1+22x-1-12x-3-24x-1 using equation i
Q22.
Answer :
We have, y=eaxsecx logx1-2x …i⇒y=eaxsecx logx1-2×12
Taking log on both sides,
logy=logeax+logsecx+log logx-12log1-2x ⇒logy=ax+logsecx+loglogx-12log1-2x
Differentiating with respect to x using chain rule,
1ydydx=ddxax+ddxlog secx+ddxlog logx-12log1-2x⇒1ydydx=a+1secxddxsecx+1logxddxlogx-1211-2xddx1-2x⇒1ydydx=a+secx tanxsecx+1logx1x-1211-2x-2⇒dydx=ya+tanx+1x logx+11-2x⇒dydx=eaxsecx logx1-2xa+tanx+1x logx+11-2x Using equation i
Q23.
Answer :
We have, y=e3x× sin4x × 2x …i
Taking log on both sides,
logy=loge3x+logsin4x+log2x ⇒logy=3x loge+logsin4x+x log2 ⇒logy=3x+logsin4x+x log2
Differentiating with respect to x,
1ydydx=ddx3x+ddxlog sin4x+ddxx log2⇒1ydydx=3+1sin4xddxsin4x+log21⇒1ydydx=3+1sin4xcos4xddx4x+log2⇒1ydydx=3+cot4x4+log2⇒1ydydx=3+4cot4x+log2⇒dydx=y3+4cot4x+log2⇒dydx=e3xsin4x2x3+4cot4x+log2 Using equation i
Q24.
Answer :
We have, y=sinx sin2x sin3x sin4x …i
Taking log on both sides,
logy=logsinx sin2x sin3x sin4x⇒logy=logsinx+logsin2x+logsin3x+logsin4x
Differentiating with respect to x using chain rule,
1ydydx=ddxlogsinx+ddxlogsin2x+ddxlogsin3x+ddxlogsin4x⇒1ydydx=1sinxddxsinx+1sin2xddxsin2x+1sin3xddxsin3x+1sin4xddxsin4x⇒1ydydx=1sinxcosx+1sin2xcos2xddx2x+1sin3xcos3xddx3x+1sin4xcos4xddx4x⇒1ydydx=cotx+cot2x2+cot3x3+cot4x4⇒dydx=ycotx+2cot2x+3cot3x+4cot4x⇒dydx=sinx sin2x sin3x sin4xcotx+2cot2x+3cot3x+4cot4x Using equation i
Q25.
Answer :
Let y=xsinx+sinxxAlso, let u=xsinx and v=sinxx∴ y=u+v⇒dydx=dudx+dvdx …iNow, u=xsinxTaking log on both sides,⇒logu=logxsinx⇒logu=sinx logxDifferentiating both sides with respect to x,1ududx=logxddxsinx +sinxddxlogx ⇒dudx=ucosx logx+sinx1x⇒dudx=xsinxcosx logx+sinxx …iiAgain, v=sinxxTaking log on both sides,⇒logv=logsinxx⇒logv=x logsinxDifferentiating both sides with respect to x,1vdvdx=logsinxddxx+xddxlogsinx⇒dvdx=vlogsinx+x1sinxddxsinx⇒dvdx=sinxxlog sinx+xsinxcosx⇒dvdx=sinxxlog sinx+x cotx ..iiiFrom i,iiand iii, we obtaindydx=xsinxcosx logx+sinxx+sinxxlog sinx+x cotx
Q26.
Answer :
We have, y=sinxcosx+cosxsinx⇒y=elogsinxcosx+elogcosxsinx⇒y=ecosx logsinx+esinx logcosxDifferentiating with respect to x,dydx=ddxecosx logsinx+ddxesinx logcosx =ecosx logsinxddxcosx logsinx+esinx logcosxddxsinx logcosx =elogsinxcosxcosxddxlogsinx+logsinxddxcosx+elogcosxsinxsinxddxlogcosx+logcosxddxsinx =sinxcosxcosx1sinxddxsinx+logsinx×-sinx+cosxsinxsinx1cosxddxcosx+logcosx×cosx =sinxcosxcotx cosx-sinx logsinx+cosxsinxtanx-sinx+cosx logcosx =sinxcosxcotx cosx-sinx logsinx+cosxsinxcosx logcosx-sinx tanx
Q27.
Answer :
We have, y=tanxcotx+cotxtanx⇒ y=elogtanxcotx+elogcotxtanx⇒y=ecotx logtanx+etanx logcotx
Differentiating with respect to x using chain rule and product rule,
dydx=ddxecotx logtanx+ddxetanx logcotx =ecotx logtanxddxcotx logtanx+etanx logcotxddxtanx logcotx =elogtanxcotxcotxddxlog tanx+log tanxddxcotx+elogcotxtanxtanxddxlog cotx+logcotxddxtanx =tanxcotxcotx×1tanxddxtanx+log tanx-cosec2x+cotxtanxtanx×1cotxddxcotx+log cotxsec2x =tanxcotxcosec2xsec2xsec2x-cosec2x log tanx+cotxtanxsec2xcosec2x-cosec2x+sec2x log cotx =tanxcotxcosec2x-cosec2x log tanx+cotxtanxsec2x log cotx-sec2x =tanxcotxcosec2x1-log tanx+cotxtanxsec2x log cotx-1
Q28.
Answer :
We have, y=sinxx+sin-1x⇒ y=elogsinxx+sin-1x⇒y=exlog sinx+sin-1x
Differentiating with respect to x using chain rule,
dydx=ddxex log sinx+ddxsin-1x =ex log sinxddxx log sinx+11-x2ddxx =elogsinxxxddxlog sinx+log sinxddxx+11-x×12x =sinxxx1sinxddxsinx+log sinx+12x-x2 =sinxxxsinxcosx+log sinx+12x-x2 =sinxxxcotx+log sinx+12x-x2
Q29.
Answer :
i We have, y=xcosx+sinxtanx⇒y=elogxcosx+elogsinxtanx ⇒y=ecosx logx+etanx log sinx
Differentiating with respect to x using chain rule,
dydx=ddxecosx logx+ddxetanx log sinx =ecosx logxddxcosx logx+etanx log sinxddxtanx log sinx =elogxcosxcosxddxlogx+logxddxcosx+elogsinxtanxtanxddxlog sinx+log sinxddxtanx =xcosxcosx1x+logx-sinx+sinxtanxtanx1sinxddxsinx+log sinxsec2x =xcosxcosxx-sinx logx+sinxtanxtanx1sinxcosx+sec2x log sinx =xcosxcosxx-sinx logx+sinxtanx1+sec2x log sinx
ii We have, y=xx+sinxx⇒y=elogxx+elogsinxx⇒y=ex logx+ex log sinx
Differentiating with respect to x using chain rule and product rule,
dydx=ddxex logx+ddxex log sinx =ex logxddxx logx+ex log sinxddxx log sinx =exlogxxddxlogx+logxddxx+elogsinxxxddxlog sinx+log sinxddxx =xxx1x+logx1+sinxxx1sinxddxsinx+log sinx =xx1+ logx+sinxxx1sinxcosx+ log sinx =xx1+ logx+sinxxx cotx+ log sinx
iii We have, y=sinxx+sin-1x⇒y=elogsinxx+sin-1x⇒y=ex logsinx+sin-1x
Differentiating with respect to x using chain rule and product rule,
dydx=ddxex log sinx+ddxsin-1x =ex log sinxddxx log sinx+11-x2ddxx =elogsinxxxddxlog sinx+log sinxddxx+11-x×12x =sinxxx1sinxddxsinx+log sinx1+12x-x2 =sinxxxsinxcosx+ log sinx+12x-x2 =sinxxx cotx+ log sinx+12x-x2
Q30.
Answer :
We have, y=tanxlogx+cos2π4⇒ y=elogtanxlogx+cos2π4⇒y=elogx log tanx+cos2π4
Differentiating with respect to x using chain rule,
dydx=ddxelogx log tanx+ddxcos2π4 =elogx log tanxddxlogx log tanx+0 =elogtanxlogxlogxddxlog tanx+log tanxddxlogx =tanxlogxlogx1tanxddxtanx+log tanx1x =tanxlogxlogx1tanxsec2x+log tanxx =tanxlogxlogxsec2xtanx+log tanxx
Q31.
Answer :
We have, y=xx+x1x⇒y=elogxx+elogx1x⇒ y=ex logx+e1xlogx
Differentiating with respect to x using chain rule,
dydx=ddxex logx+ddxe1xlogx =ex logxddxx logx+e1xlogxddx1xlogx =elogxxxddxlogx+logxddxx+elogx1x1xddxlogx+logxddx1x =xxx1x+logx1+x1x1x1x+logx-1×2 =xx1+logx+x1x1x2-1x2logx =xx1+logx+x1x1-logxx2
Q32.
Answer :
Let y=xlogx+logxxAlso, let u=logxx and v=xlogx∴y=v+u⇒dydx=dvdx+dudx …iNow, u=logxx⇒logu=loglogxx⇒logu=xloglogx
Differentiating both sides with respect to x,
1ududx=loglogxddxx+xddxloglogx⇒dudx=uoglogx+x1logxddxlogx⇒dudx=logxxloglogx+xlogx×1x⇒dudx=logxxloglogx+1logx …iiAlso, v=xlogx⇒logv=logxlogx⇒logv=logx logx=logx2
Differentiating both sides with respect to x,
1vdvdx=ddxlogx2⇒ 1vdvdx=2logxddxlogx⇒dvdx=2vlogx1x⇒dvdx=2xlogxlogxx⇒dvdx=2xlogxlogxx …iiiFrom i,ii and iii, we obtaindydx=2xlogxlogxx+logxx loglogx+1logx
Q33.
Answer :
We have, x13y7=x+y20
Taking log on both sides,
logx13y7=logx+y20⇒13logx+7logy=20logx+y
Differentiating with respect to x using chain rule,
13ddxlogx+7ddxlogy=20ddxlogx+y⇒13x+7ydydx=20x+yddxx+y⇒13x+7ydydx=20x+y1+dydx⇒7ydydx-20x+ydydx=20x+y-13x⇒dydx7y-20x+y=20x+y-13x⇒dydx7x+y-20yyx+y=20x-13x+yxx+y⇒dydx=20x-13x-13yxx+yyx+y7x+7y-20y⇒dydx=yx7x-13y7x-13y⇒dydx=yx
Q34.
Answer :
We have, x16y9=x2+y17
Taking log on both sides,
logx16y9=logx2+y17⇒16logx+9logy=17logx2+y
Differentiating with respect to x using chain rule,
16ddxlogx+9ddxlogy=17ddxlogx2+y⇒16x+9ydydx=17×2+yddxx2+y⇒16x+9ydydx=17×2+y2x+dydx⇒9ydydx-17×2+ydydx=34xx2+y-16x⇒dydx9y-17×2+y=34xx2+y-16x⇒dydx9x2+y-17yyx2+y=34×2-16×2+yxx2+y⇒dydx9x2+9y-17yyx2+y=34×2-16×2-16yxx2+y⇒dydx9x2-8yyx2+y=18×2-16yxx2+y⇒dydx=yx29x2-8y9x2-8y⇒dydx=2yx⇒xdydx=2y
Q35.
Answer :
Let y=sinxx …iAlso, Let u=xx …iiTaking log on both sides,⇒logu=logxx⇒logu=xlogx
Differentiating both sides with respect to x,
1ududx=ddxx logx⇒ 1ududx=xddxlogx+logxddxx⇒ 1ududx=x1x+logx1⇒ 1ududx=1+logx⇒dudx=u1+logx⇒dudx=xx1+logx …iii using equation iiNow, using equation ii in equation i,y=sinuDifferentiating with respect to x,dydx=ddxsinu⇒dydx=cosududxUsing equation ii and iii,dydx=cosxx× xx1+logx
Q36.
Answer :
We have, xx+yx=1⇒elogxx+elogyx=1⇒ex logx+ex logy=1
Differentiating with respect to x using chain rule,
ddxexlogx+ddxex logy=ddx1⇒ex logxddxx logx+ex logyddxx logy=0⇒ex logxxddxlogx+logxddxx+elogyxxddxlogy+logyddxx=0⇒xxx1x+logx1+yxx1ydydx+logy1=0⇒xx1+logx+yxxydydx+logy=0⇒yx×xydydx=-xx1+logx+yxlogy⇒xyx-1dydx=-xx1+logx+yxlogy⇒dydx=-xx1+logx+yxlogyxyx-1
Q37.
Answer :
We have, xy×yx=1
Taking log on both sides,
logxy×yx=log1⇒ylogx+x logy=log1
Differentiating with respect to x ,
ddxy logx+ddxx logx=ddxlog1⇒yddxlogx+logxdydx+xddxlogy+logyddxx=0⇒y1x+logxdydx+x1ydydx+logy1=0⇒yx+logxdydx+xydydx+logy=0⇒dydxlogx+xy=-logy+yx⇒dydxy logx+xy=-x logy+yx⇒dydx=-yxx logy+yy logx+x
Q38.
Answer :
We have, xy+yx=x+yx+y⇒elogxy+elogyx=elogx+yx+y⇒ey logx+ex logy=ex+y logx+y
Differentiating with respect to x using chain rule and product rule,
⇒ddxey logx+ddxex logy=ddxex+ylogx+y⇒ey logxyddxlogx+logxdydx+ex logyxddxlogy+logyddxx=ex+ylogx+yddxx+ylogx+y⇒elogxyy1x+logxdydx+elogxxydydx+logy1=elogx+yx+yx+yddxlogx+y+logx+yddxx+y⇒xyyx+logxdydx+yxxydydx+logy=x+yx+yx+y1x+yddxx+y+logx+y1+dydx⇒xy×yx+xy logxdydx+yx×xydydx+yxlogy=x+yx+y1×1+dydx+logx+y1+dydx⇒xy-1× y+xylogxdydx+yx-1× xdydx+yxlogy=x+yx+y+x+yx+ydydx+x+yx+ylogx+y+x+yx+ylogx+ydydx⇒dydxxylogx+xyx-1-x+yx+y1+logx+y=x+yx+y1+logx+y-xy-1×y-yxlogy⇒dydx=x+yx+y1+logx+y-yxy-1-yxlogyxylogx+xyx-1-x+yx+y1+logx+y
Q39.
Answer :
We have, xmyn=1
Taking log on both side,
logxmyn=log1⇒m logx+n logy=log1
Differentiating with respect to x,
dydxm logx+ddxn logy=ddxlog1⇒mx+nydydx=0⇒dydx=-mx×yn⇒dydx=-mynx
Q40.
Answer :
We have, yx=ey-x
Taking log on both sides,
logyx=logey-x ⇒xlogy=y-xloge⇒xlogy=y-x …i
Differentiating with respect to x,
ddxx logy=ddxy-x⇒xddxlogy+logyddxx=dydx-1⇒x1ydydx+logy1=dydx-1⇒dydxxy-1=-1-logy⇒dydxy1+logyy-1=-1+logy Using i ⇒dydx1-1-logy1+logy=-1+logy⇒dydx=-1+logy2-logy⇒dydx=1+logy2logy
Q41.
Answer :
We have, sinxy=cosyx
Taking log on both sides,
logsinxy=logcosyx ⇒y logsinx=x logcosy
Differentiating with respect to x,
ddxy log sinx=ddxx logcosy⇒yddxlog sinx+log sinxdydx=xdydxlog cosy+log cosyddxx ⇒y1sinxddxsinx+log sinxdydx=xcosyddxcosy+logcosy1⇒ysinxcosx+log sinxdydx=xcosy-sinydydx+log cosy⇒y cotx+log sinxdydx=-x tanydydx+log cosy⇒dydxlog sinx+x tany=log cosy-y cotx⇒dydx=log cosy-y cotxlog sinx+x tany
Q42.
Answer :
We have, cos xy=tan yx
Taking log on both sides,
logcosxy=logtanyx⇒y log cosx=x log tany
Differentiating it with respect to x using chain,
ddxy log cosx=ddxx log tany⇒yddxlog cosx+log cosxdydx=xddxlog tany+log tanyddxx⇒y1cosxddxcosx+log cosxdydx=x1tanyddxtany+log tany⇒ycosx-sinx+log cosxdydx=xtanysec2ydydx+log tany⇒-ytanx+log cosxdydx=secy cosecy×xdydx+log tany⇒dydxlog cosx-x secy cosecy=log tany+y tanx⇒dydx=log tany+y tanxlog cosx-xsecy cosecy
Q43.
Answer :
We have, ex+ey=ex+y …(1)
Differentiating both sides using chain rule,
ddxex+ddxey=ddxex+y⇒ex+eydydx=ex+yddxx+y⇒ex+eydydx=ex+y1+dydx⇒eydydx-ex+ydydx=ex+y-ex⇒dydx=ex+y-exey-ex+y⇒dydx=ex+y-ex+y+eyex+y-ex-ex+y Using eqn.1⇒dydx=ey-ex⇒dydx=-ey-x⇒dydx+ey-x=0
Page 11.85 Ex.11.5
Q44.
Answer :
We have, ey=yx
Taking log on both sides,
logey=logyx⇒y loge=x logy ⇒y=x logy …i
Differentiating with respect to x,
dydx=ddxx logy⇒dydx=xdydxlogy+logyddxx ⇒dydx=xydydx+logy ⇒dydx1-xy=logy⇒dydxy-xy=logy⇒dydx=y logyy-x⇒dydx=y logyy-ylogy Using equation i⇒dydx=y logylogyy logy-y⇒dydx=y logy2ylogy-1⇒dydx=logy2logy-1
Q45.
Answer :
We have, ex+y-x=0⇒ex+y=x …1
Differentiating with respect to x using chain rule,
ddxex+y=ddxx⇒ex+yddxx+y=1⇒x1+dydx=1 Using equation i⇒1+dydx=1x⇒dydx=1x-1⇒dydx=1-xx
Q46.
Answer :
We have, y=x sina+y
Differentiating with respect to x using chain rule,
dydx=xddxsina+y+sina+yddxx ⇒dydx=x cosa+ydydx+sina+y⇒1-x cosa+ydydx=sina+y⇒dydx=sina+y1-x cosa+y⇒dydx=sina+y1-ysina+ycosa+y ∵ysina+y=x⇒dydx=sin2a+ysina+y-y cosa+y
Q47.
Answer :
We have, x sina+y+sina cosa+y=0
Differentiating with respect to x using chain rule,
ddxx sina+y+sina cosa+y=0⇒xddxsina+y+sina+yddxx+sinaddxcosa+y+cosa+yddxsin a=0⇒x cosa+y0+dydx+sina+y+sina-sina+ydydx+0=0⇒x cosa+y-sina sina+ydydx+sina+y=0⇒dydx=-sina+yx cosa+y-sina sina+y⇒dydx=-sina+y-sina cosa+ysina+ycosa+y-sina sina+y ∵ x=-sina cosa+ysina+y⇒dydx=sin2a+ysinacos2a+y+sinasin2a+y⇒dydx=sin2a+ysinacos2a+y+sin2a+y⇒dydx=sin2a+ysina ∵cos2a+y+sin2a+y=1
Q48.
Answer :
We have, sinxy=x+y
Taking log on both the sides,
logsinxy=logx+y⇒ylogsinx=logx+y
Differentiating with respect to x using chain rule,
ddxy logsinx=ddxlogx+y⇒yddxlog sinx+log sinxdydx=1x+yddxx+y⇒ysinxddxsinx+log sinxdydx=1x+y1+dydx⇒ycosxsinx+log sinxdydx=1x+y+1x+ydydx⇒dydxlog sinx-1x+y=1x+y-y cotx⇒dydxx+ylog sinx-1x+y=1-yx+y cotxx+y⇒dydx=1-yx+ycotxx+ylogsinx-1
Q49.
Answer :
We have, xy logx+y=1 …i
Differentiating with respect to x using chain rule,
dydxxy logx+y=ddx1⇒xyddxlogx+y+x logx+ydydx+y logx+yddxx=0⇒xyx+y1+dydx+xlogx+ydydx+y logx+y1=0⇒xyx+y1+dydx+xlogx+ydydx+y logx+y=0⇒xyx+ydydx+xyx+y+x1xydydx+y1xy=0 Using equation i⇒dydxxyx+y+1y=-1x+xyx+y⇒dydxxy2+x+yx+yy=-x+y+x2yxx+y⇒dydx=-yxx+y+x2yx+y+xy2
Q50.
Answer :
We have, y=x siny …i
Differentiating with respect to x,
dydx=ddxx siny⇒dydx=xddxsiny+sinyddxx ⇒dydx=x cosydydx+siny1⇒dydx-x cosydydx=siny⇒dydx1-x cosy=siny⇒dydx=siny1-x cosy⇒dydx=yx1-x cosy ∵siny=yx
Q51.
Answer :
We have, fx=1+x1+x21+x41+x8Taking log on both sides,log fx=log1+x+log1+x2+log1+x4+log1+x8⇒ddxlog fx=ddxlog1+x+log1+x2+log1+x4+log1+x8⇒1fxf’x=11+x+2×1+x2+4×31+x4+8×71+x8⇒f’x=1+x1+x21+x41+x811+x+2×1+x2+4×31+x4+8×71+x8⇒f’1=1+11+121+141+1811+1+211+12+4131+14+8171+18⇒f’1=2×2×2×212+22+42+82⇒f’1=2×2×2×2×121+2+4+8⇒f’1=8×15=120
Q52.
Answer :
We have, y=logx2+x+1×2-x+1+23tan-13×1-x2
Differentiating with respect to x using chain rule,
dydx=ddxlogx2+x+1×2-x+1+23ddxtan-13×1-x2⇒dydx=1×2+x+1×2-x+1ddxx2+x+1×2-x+1+2311+3×1-x22ddx3x1-x2⇒dydx=x2-x+1×2+x+1×2-x+1ddxx2+x+1-x2+x+1ddxx2-x+1×2-x+12+231-x221+x4-2×2+3×2 1-x2ddx3x-3xddx1-x21-x22⇒dydx=1×2+x+1×2-x+12x+1-x2+x+12x-1×2-x+1+231-x221+x2+x41-x23-3x-2×1-x22⇒dydx=2×3-2×2+2x+x2-x+1-2×3-2×2-2x+x2+x+1×4+2×2+1-x2+233-3×2+23×21+x2+x4⇒dydx=-2×2+2×4+x2+1+23×2+131+x2+x4⇒dydx=21-x2x4+x2+1+2×2+11+x2+x4⇒dydx=21-x2+x2+11+x2+x4⇒dydx=41+x2+x4
Q53.
Answer :
We have, y=sinx-cosxsinx-cosx …(i)
Taking log on both sides,
logy=logsinx-cosxsinx-cosx⇒logy=sinx-cosx logsinx-cosx
⇒1ydydx=logsinx-cosxddxsinx-cosx+sinx-cosxddxlogsinx-cosx using product rule⇒1ydydx=logsinx-cosxcosx+sinx+sinx-cosxsinx-cosxddxsinx-cosx⇒1ydydx=cosx+sinx logsinx-cosx+cosx+sinx⇒1ydydx=cosx+sinx1+logsinx-cosx⇒dydx=ycosx+sinx1+logsinx-cosx⇒dydx=sinx-cosxsinx-cosxcosx+sinx1+logsinx-cosx using equation i
Q54.
Answer :
We have, xy=ex-y
Taking log on both sides,
logxy=logex-y⇒logx+logy=x-yloge⇒logx+logy=x-y×1⇒logx+logy=x-y
⇒ddxlogx+ddxlogy=ddxx-dydx⇒1x+1ydydx=1-dydx⇒1+1ydydx=1-1x⇒y+1ydydx=x-1x⇒dydx=yx-1xy+1
Q55.
Answer :
Given that yx+xy+xx=abPutting u=yx, v=xy and w=xx , we get u+v+w=ab∴dudx+dvdx+dwdx=0 …iNow, u=yx
Taking log on both sides,
log u=x log y
⇒1ududx=xddxlog y+log yddxx using product rule⇒1ududx=x1ydydx+log y×1⇒dudx=uxydydx+log y⇒dudx=yxxydydx+log y …iiAlso, v=xy
Taking log on both sides,
log v=y log x
⇒1vdvdx=yddxlogx+logxdydx⇒1vdvdx=y1x+logxdydx⇒dvdx=vyx+logxdydx⇒dvdx=xyyx+logxdydx …iiiAgain, w=xx
Taking log on both sides,
log w=x log x
⇒1wdwdx=xddxlog x+log xddxx⇒1wdwdx=x1x+logx1⇒dwdx=w1+log x⇒dwdx=xx 1+log x …ivFrom i,ii,iiiand iv, we have yxxydydx+log y+xyyx+log xdydx+xx1+log x=0⇒x.yx-1+xy.log xdydx=-xx1+log x-y.xy-1-yxlog y∴ dydx=-yx log y+y.xy-1+xx 1+log xx.yx-1+xy log x
Page 11.89 Ex.11.6
Q1.
Answer :
We have, y=x+x+x+… to ∞⇒ y=x+ySquaring both sides, we get, y2=x+y⇒ 2y dydx=1+dydx⇒dydx2y-1=1⇒dydx=12y-1
Q2.
Answer :
We have, y=cosx+cosx+cosx+… to ∞⇒y=cosx+ySquaring both sides, we get, y2=cosx+y⇒ 2y dydx=-sinx+dydx⇒dydx2y-1=-sinx⇒dydx=-sinx2y-1⇒dydx=sinx1-2y
Q3.
Answer :
We have,y=logx+logx+logx+… to ∞⇒y=logx+ySquaring both sides,we get,y2=logx+y⇒2y dydx=1x+dydx⇒dydx2y-1=1x
Q4.
Answer :
We have, y=tanx+tanx+tanx+… to ∞⇒y=tanx+ySquaring both sides, we get, y2=tanx+y⇒2y dydx=sec2x+dydx⇒dydx2y-1=sec2x⇒dydx=sec2x2y-1
Q5.
Answer :
We have, y=sinxsinxsinx….∞⇒y=sinxy
Taking log on both sides,
log y=logsinxy⇒log y=y logsinx
⇒1ydydx=yddxlogsinx+log sinxdydx⇒1ydydx=y1sinxddxsinx+log sinxdydx⇒dydx1y-log sinx=ysinxcosx⇒dydx1-y log sinxy=y cotx⇒dydx=y2cotx1-y log sinx
Page 11.90 Ex.11.6
Q6.
Answer :
We have, y=tanxtanxtanx…∞⇒ y=tanxy
Taking log on both sides,
log y=logtanxy⇒log y=y log tanx
Differentiating with respect to x using chain rule ,
1ydydx=yddxlog tanx+log tandydx⇒1ydydx=ytanxddxtanx+log tandydx⇒dydx1y-log tanx=ytanxsec2x⇒dydx=ytanxsec2x×y1-ylog tanxNow, dydxx=π4=y sec2π4tanπ4×y1-y log tanπ4⇒dydxx=π4=y22211-y log tan 1⇒dydxx=π4=2121-0 ∵ yπ4=tanπ4tanπ4tanπ4…∞=1 ⇒dydxx=π4=2
Q7.
Answer :
We have, y=exex+xeex+exxe⇒y=u+v+w⇒dydx=dudx+dvdx+dwdx …iwhere u=exex, v=xeexand w=exxeNow,u=exex …ii
Taking log on both sides,
logu=logexex⇒logu=xexloge⇒logu=xex …iii
Taking log on both sides,
log logu=logxex⇒log logu=ex logx
Differentiating with respect to x,
⇒1loguddxlogu=exddxlogx+logxddxex⇒1logu1ududx=exx+ex logx⇒dudx=uloguexx+ex logx⇒dudx=exex×xexexx+ex logx …A Using equation ii and iiiNow, v=xeex …iv
Taking log on both sides,
log v=log xeex⇒log v=eexlogx
⇒1vdvdx=eexddxlogx+logxddxeex⇒1vdvdx=eex1x+logxeexddxex⇒dvdx=veex1x+logxeexex⇒dvdx=xeex×eex1x+exlogx …B Using equation 4Now, w=exxe …v
Taking log on both sides,
logw=logexxe⇒logw=xxeloge⇒logw=xxe …vi
Taking log on both sides,
log logw=logxxe⇒log logw=xelogx
⇒1logwddxlogw=xeddxlogx+logxddxxe⇒1logw1wdwdx=xe1x+logxexe-1⇒dwdx=w logwxe-1+e logxxe-1⇒dwdx=exxexxexe-11+e logx —-C using equation v,viUsing equation A,B and C in equation i, we getdydx=exexxexexx+exlogx+xeex×eex1x+ex logx+exxexxexe-11+e logx
Q8.
Answer :
We have, y=cosxcosxcosx….∞
⇒y=cosxy
Taking log on both sides,
log y=logcosxy⇒log y=y logcosx
Differentiating with respect to x using chain rule,
1ydydx=yddxlog cosx+log cosxdydx⇒1ydydx=y1cosxddxcosx+log cosxdydx⇒dydx1y-log cosx=ycosx-sinx⇒dydx1-y log cosxy=-y tanx⇒dydx=-y2tanx1-y log cosx
Page 11.93 Ex.11.7
Q1.
Answer :
We have, x=at2 and y=2at⇒dxdt=2at and dydt=2a∴ dydx=dydtdxdt=2a2at=1t
Q2.
Answer :
We have, x=aθ+sinθ and y=a1-cosθ
⇒dxdθ=a1+cosθ and dydθ=a sinθ
∴dydx=dydθdxdθ=a sinθa1+cosθ=2 sinθ2cosθ22cos2θ=tanθ2
Q3.
Answer :
We have, x=a cosθ and y=b sinθ⇒ dxdθ=-a sinθ and dydθ=b cosθ∴dydx=dydθdxdθ=b cosθ-a sinθ=-bacotθ
Q4.
Answer :
We have, x=aeθsinθ-cosθ and y=aeθsinθ+cosθ
⇒dxdθ=aeθddθsinθ-cosθ+sinθ-cosθddθeθ and dydθ=aeθddθsinθ+cosθ+sinθ+cosθddθeθ⇒dxdθ=aeθcosθ+sinθ+sinθ-cosθeθ and dydθ=aeθcosθ-sinθ+sinθ+cosθeθ⇒dxdθ=a2eθ sinθ and dydθ=a2eθ cosθ
∴dydθdxdθ=a2eθcosθa2eθsinθ=cotθ
Q5.
Answer :
We have, x=b sin2θ and y=a cos2θ∴dxdθ=ddθb sin2θ=2b sinθcosθand, dydθ=ddθa cos2θ=-2a cosθsinθ ∴ dydx=dydθdxdθ=-2a cosθsinθ 2b sinθcosθ=-ab
Q6.
Answer :
We have, x=a1-cosθ and y=aθ+sinθ∴ dxdθ=ddθa1-cosθ=asinθand dydθ=ddθaθ+sinθ=a1+cosθ ∴ dydxθ=π2=dydθdxdθθ=π2=a1+cosθasin θθ=π2=a1+0a=1
Q7.
Answer :
We have, x=et+e-t2 and y=et-e-t2
⇒dxdt=12ddtet+ddte-t and dydt=12ddtet-ddte-t⇒dxdt=12et+e-tddt-t and dydt=12et-e-tddte-t⇒dxdt=12et-e-t=y and dydt=12et+e-t=x ∴dydt=dydtdxdt=xy
Q8.
Answer :
We have, x=3at1+t2
Differentiating with respect to t,
dxdt=1+t2ddt3at-3atddt1+t21+t22 using quotient rule⇒dxdt=1+t23a-3at2t1+t22⇒dxdt=3a+3at2-6at21+t22⇒dxdt=3a-3at21-t22⇒dxdt=3a1-t21+t22 …iand, y=3at21+t2
Differentiating it with respect to t,
dxdt=1+t2ddt3at2-3at2ddt1+t21+t22 using quotient rule⇒dxdt=1+t26at-3at22t1+t22⇒dxdt=6at+6at3-6at31+t22⇒dxdt=6at1+t22 …iiDividing equation ii by i,dydtdxdt=6at1+t22×1+t223a1-t2=2t1-t2
Q9.
Answer :
We have, x=acosθ+θ sinθ and y=asinθ-θ cosθ⇒dxdθ =addθcosθ+ddθθ sinθ and dydθ=addθsinθ-ddθθ cosθ⇒dxdθ =a-sinθ+θddθsinθ+sinθddθθ and dydθ=acosθ-θddθcosθ+cosθddθθ⇒ dxdθ =a-sinθ+θ cosθ and dydθ=acosθ+θ sinθ-cosθ⇒dxdθ =aθ cosθ and dydθ=aθ sinθ∴ dydx=dydθdxdθ=aθ sinθaθ cosθ =tanθ
Q10.
Answer :
We have, x=eθθ+1θ
Differentiating it with respect to θ,
dxdθ=eθddθθ+1θ+θ+1θddθeθ using product rule⇒dxdθ=eθ1-1θ2+θ2+1θeθ⇒dxdθ=eθ1-1θ2+θ2+1θ⇒dxdθ=eθθ2-1+θ3+θθ2⇒dxdθ=eθθ3+θ2+θ-1θ2 …iand, y=eθθ-1θ
Differentiating it with respect to θ using chain rule,
dydθ=e-θddθθ-1θ+θ-1θddθe-θ using product rule⇒dydθ=e-θ1+1θ2+θ-1θeθddθ-θ⇒dydθ=e-θ1+1θ2+θ-1θe-θ-1⇒dydθ=e-θ1+1θ2-θ+1θ⇒dydθ=e-θθ2+1-θ3+θθ2⇒dydθ=e-θ-θ3+θ2+θ+1θ2 …iiDividing equation ii by i,dydθdxdθ=e-θθ2-θ3+θ+1θ2×θ2eθθ3+θ2+θ-1 =e-2θθ2-θ3+θ+1θ3+θ2+θ-1
Q11.
Answer :
We have, x=2t1+t2
⇒dxdt=1+t2ddt2t-2tddt1+t21+t22 using quotient rule⇒dxdt=1+t22-2t2t1+t22⇒dxdt=2+2t2-4t21+t22⇒dxdt=2-2t21+t22 …iand,y=1-t21+t2
⇒dydt=1+t2ddt1-t2-1-t2ddt1+t21+t22⇒dydt=1+t2-2t-1-t22t1+t22⇒dydt=-4t1+t22 …iiDividing equation ii by i, we get,dydtdxdt=-4t1+t22×1+t2221-t2⇒dydx=-2t1-t2⇒dydx=-xy ∵xy =2t1+t2×1+t21-t2=2t1-t2
Q12.
Answer :
We have, x=cos-111+t2
⇒dxdt=-11-11+t22ddt11+t2⇒dxdt=-11-11+t2-121+t232ddt1+t2⇒dxdt=1+t2121+t2-1×121+t2322t⇒dxdt=tt2×1+t2⇒dxdt=11+t2 …iNow, y=sin-111+t2
⇒dydt=11-11+t22ddt11+t2⇒dydt=11-11+t2-121+t232ddt1+t2⇒dxdt=1+t2121+t2-1×-121+t2322t⇒dxdt=-12t2×1+t22t⇒dxdt=-11+t2 …iiDividing equation ii by i,dydtdxdt=11+t2×1+t2-1⇒dydx=-1
Q13.
Answer :
We have, y=2t1+t2
⇒dydt=1+t2ddt2t-2tddt1+t21+t22 using quotient rule⇒dydt=1+t22-2t2t1+t22⇒dydt=2+2t2-4t21+t22⇒dydt=2-2t21+t22 …iand,x=1-t21+t2
⇒dxdt=1+t2ddt1-t2-1-t2ddt1+t21+t22⇒dxdt=1+t2-2t-1-t22t1+t22⇒dxdt=-4t1+t22 …iiDividing equation i by ii, we get,dydtdxdt=21-t21+t22×1+t22-4t⇒dydx=21-t2-4t⇒dydx=t2-12t
Q14.
Answer :
We have, x=2 cosθ- cos2θ
⇒dxdθ=2-sinθ–sin2θddθ2θ⇒dxdθ=-2sinθ+2 sin2θ⇒dxdθ=2sin2θ-sinθ …iand,y=2 sinθ-sin2θ
⇒dydθ=2 cosθ-cos2θddθ2θ⇒dydθ=2 cosθ-cos2θ2⇒dydθ=2 cosθ-2 cos2θ⇒dydθ=2cosθ-cos2θ …iiDividing equation ii by equation i,dydθdxdθ=2cosθ-cos2θ2sin2θ-sinθ⇒dydx=cosθ-cos2θsin2θ-sinθ⇒dydx=-2sinθ+2θ2sinθ-2θ22cos2θ+θ2sin2θ-θ2 ∵sinA-sinB=2 cosA+B2sinA-B2and cosA-cosB=-2sinA+B2sinA-B2⇒dydx=-sin3θ2sin-θ2cos3θ2sinθ2⇒dydx=-sin3θ2-sinθ2cos3θ2sinθ2⇒dydx=sin3θ2cos3θ2⇒dydx=tan3θ2
Q15.
Answer :
We have, x=ecos2t and y=esin2t
⇒dxdt=ddtecos2t and dydt=ddtesin2t⇒dxdt=ecos2tddtcos2t and dydt=esin2tddtsin2t⇒dxdt=ecos2t-sin2tddt2t and dydt=esin2tcos2tddt2t ⇒dxdt=-2sin 2tecos2t anddydt=2cos2tesin2t ∵dydtdxdt=2 cos2tesin2t-2sin2tecos2t⇒dydx=-y logxx logy ∵x=ecos2t⇒logx=cos2ty=esin2t⇒logy=sin 2t
Q16.
Answer :
We have, x=cost and y=sin t
⇒dxdt=ddtcos t and dydt=ddtsin t⇒dxdt=-sin t and dydt=cos t ∴dydtdxdt=cos t-sin t=-cot t Now, dydxt=2π3=-cot 2π3=13
Page 11.94 Ex.11.7
Q17.
Answer :
We have, x=at+1t and y=at-1t
⇒dxdt=addtt+1t and dydt=addtt-1t⇒dxdt=a1-1t2 and dydt=a1+1t2 ⇒dxdt=at2-1t2 and dydt=at2+1t2 ∴ dydx = dydtdxdt=at2+1t2×t2at2-1⇒dydx =at2+1t×tat2-1⇒dydx =at+1t×1at-1t⇒ dydx=xy
Q18.
Answer :
We have, x=sin-12t1+t2Put t=tanθ⇒-1<tanθ<1⇒-π4<θ<π4⇒-π2<2θ<π2∴x=sin-12 tanθ1+tan2θ⇒ x=sin-1sin2θ⇒x=2θ ∵-π2<2θ<π2⇒x=2tan-1t ∵t=sinθ
⇒dxdt=21+t2 …iNow, y=tan-12t1-t2put t=tanθ⇒ y=tan-12 tanθ1-tan2θ⇒ y=tan-1tan 2θ ⇒ y=2θ ∵-π2<2θ<π2⇒ y=2 tan-1t ∵ t=tanθ
⇒dydt=21+t2 …iiDividing equation ii by i,dydtdxdt=21+t2×1+t22⇒dydx=1
Q19.
Answer :
We have, x=sin3tcos2t and y=cos3tcos2t⇒dxdt=ddtsin3tcos2t ⇒dxdt=cos2tddtsin3t-sin3tddtcos2tcos2t Using quotient rule⇒dxdt=cos2t3sin2tddtsint-sin3t×12cos2tddtcos 2tcos2t ⇒ dxdt=3cos2tsin2t cost-sin3t2cos2t-2 sin2tcos 2t⇒ dxdt=3cos2t sin2t cost+sin3t sin2tcos2tcos2tNow, dydt=ddtcos3tcos2t ⇒ dydt=cos2tddtcos3t-cos3tddtcos2tcos2t Using quotient rule⇒ dydt=cos2t3cos2tddtcost-cos3t×12cos2tddtcos 2tcos2t ⇒ dydt=3cos2tcos2t -sint-cos3t2cos2t-2 sin2tcos 2t⇒ dydt=-3cos2t cos2t sint+cos3t sin2tcos2tcos2t∴dydx=dydtdxdt=-3cos2t cos2t sint+cos3t sin2tcos2tcos2t×cos2tcos2t3cos2t sin2t cost+sin3t sin2t⇒ dydx=-3cos2t cos2t sint+cos3t sin2t3cos2t sin2t cost+sin3t sin2t⇒ dydx=sint cost-3cos2t cost+2cos3tsint cost3cos2t sint+2sin3t⇒ dydx=-32cos2t-1cost+2cos3t31-2sin2tsint+2sin3t cos2t=2cos2t-1cos2t=1-2sin2t⇒ dydx=-4cos3t+3cost3sint-4sin3t⇒ dydx=-cos3tsin3t cos3t=4cos3t-3costsin3t=3sint-4sin3t∴dydx=-cot3t
Q20.
Answer :
We have, x=t+1ta
⇒dxdt=ddtt+1ta ⇒dxdt=at+1ta-1ddtt+1t⇒dxdt=at+1ta-11-1t2 …i and, y=at+1t
⇒dydt=ddtat+1t ⇒dydt=at+1t× logaddtt+tt⇒dydt=at+1t× loga1-1t2 …iiDividing equation ii by i,dydtdxdt=at+1t× loga1-1t2 at+1ta-11-1t2⇒dydx=at+1t× logaat+1ta-1
Q21.
Answer :
We have, x=a1+t21-t2
⇒dxdt=a1-t2ddt1+t2-1+t2ddt1-t21-t22 Using quotient rule⇒dxdt=a1-t22t-1+t2-2t1-t22⇒dxdt=a2t-2t3+2t+2t31-t22⇒dxdt=4at1-t22 …iand, y=2t1-t2
⇒dydt=21-t2ddtt-tddt1-t21-t22 Using quotient rule⇒dydt=21-t21-t-2t1-t22⇒dydt=21-t2+2t21-t22⇒dydt=21+t21-t22 …iiDividing equation ii by i,dydtdxdt=21+t21-t22 ×1-t224at⇒dydx=1+t22at
Q22.
Answer :
We have, x=10t-sint and y=121-cost⇒dxdt=ddt10t-sint anddydt=ddt121-cost⇒dxdt=10ddtt-sint and dydt=12ddt1-cost⇒dxdt=101-cost and dydt=120–sint=12 sint∴dydx=dydtdxdt=12 sint101-cost⇒dydx=12×2sint2cost210×2sin2t2⇒dydx=65cott2
Q23.
Answer :
We have, x=aθ-sinθ and y=a1+cosθ⇒ dxdθ=ddθaθ-sinθ and dydθ=ddθa1+cosθ⇒dxdθ=a1-cosθ and dydθ=a-sinθ∴ dydx=dydθdxdθ=-a sinθa1-cosθNow, dydxθ=π3=-sinπ31-cosπ3=-321-12=-3
Page 11.100 Ex.11.8
Q1.
Answer :
Let u=x2 and v=x3⇒dudx=2x and dvdx=3×2 ∴dudv=dudxdvdx=2x3x2=23x
Q2.
Answer :
Let u=log1+x2 and v=tan-1x ⇒dudx=11+x2ddx1+x2 =2×1+x2 and dvdx=11+x2 ∴dudv=dudxdvdx=2×1+x2×1+x21=2x
Q3.
Answer :
Let u=logxx
Taking log on both sides,
log u=loglogxx⇒log u=x loglogx
⇒1ududx=xddxloglogx+loglogxddxx⇒1ududx=x1logxddxlogx+loglogx1⇒dudx=uxlogx1x+log logx⇒dudx=logxx1logx+log logx ..iAgain, let v=logx⇒dvdx=1x …iiDividing equation i by ii,we getdudxdvdx=logxx1logx+log logx1x⇒dudv=logxx1+logxlog logxlogx1x⇒dudv=xlogxx-11+logx × log logx
Q4.
Answer :
i Let, u=sin-11-x2Put x=cosθ⇒ u=sin-11-cos2θ⇒ u=sin-1sinθ …iAnd, v=cos-1x …iiNow, x∈0,1⇒ cosθ∈0,1⇒ θ∈0,π2So, from equation i, u=θ Since, sin-1sinθ=θ if θ∈-π2,π2⇒u=cos-1x Since, cosθ=x
Differentiating it with respect to x,
dudx=-11-x2 …iiifrom equation ii,v=cos-1x
Differentiating it with respect to x,
dvdx=-11-x2 …ivDividing equation iii by iv,dudxdvdx=-11-x2×1-x2-1∴dudx=1
ii Let, u=sin-11-x2Put x=cosθ⇒ u=sin-11-cos2θ⇒ u=sin-1sinθ …iAnd, v=cos-1x …iiNow, x∈-1,0⇒ cosθ∈-1,0⇒ θ∈π2,πSo, from equation i, u=π-θ Since, sin-1sinθ=π-θ if θ∈π2,3π2⇒ u=π-cos-1x Since, x=cosθ
Differentiating it with respect to x,
dudx=0–11-x2 ⇒dudx= 11-x2 …iiifrom equation ii,v=cos-1x
Differentiating it with respect to x,
dvdx=-11-x2 …ivDividing equation iii by iv,dudxdvdx=11-x2×1-x2-1∴dudx=-1
Q5.
Answer :
i Let, u=sin-14×1-4×2 put 2x=cosθ ⇒ u=sin-12×cosθ1-cos2θ ⇒ u=sin-12cosθ sinθ ⇒ u=sin-1sin 2θ …i Let, v=1-4×2 …iiHere, x∈-122, 122 ⇒ 2x∈-12, 12 ⇒θ∈π4,3π4So, from equation i, u=π-2θ Since, sin-1sinθ=π-θ ,if θ∈π2, π⇒ u=π-2 cos-12x Since, 2x=cosθ
Differentiating it with respect to x,
dudx=0-2-11-2x2ddx2x⇒dudx=21-4×22⇒dudx=41-4×2 …iiifrom equation iidvdx=-4×1-4x2but, x∈-12,-122dvdx=-4-x1-4-x2⇒dvdx=4×1-4×2 …ivDiferentiating equation ii with respect to x,dvdx=121-4x2ddx1-4×2⇒dvdx=121-4×2-8x⇒dvdx=-4×1-4×2 …vDividing equation iii by vdudxdvdx=41-4×2 ×1-4×2-4x∴dudv=-1x
ii Let, u=sin-14×1-4×2 put 2x=cosθ u=sin-12×cosθ1-cos2θ ⇒ u=sin-12cosθ sinθ ⇒ u=sin-1sin 2θ …i Let, v=1-4×2 …iiHere, x∈122,12 ⇒ 2x∈12,1 ⇒cosθ∈12,1 ⇒θ∈0,π4So, from equation i, u=2θ Since, sin-1sinθ=θ ,if θ∈-π2,π2⇒ u=2 cos-12x Since, 2x=cosθ
Differentiate it with respect to x,
dudx=2-11-2x2ddx2xdudx=-21-4x22dudx=-41-4×2 …iiiDiferentiating equation ii with respect to x,dvdx=121-4x2ddx1-4×2⇒dvdx=121-4×2-8x⇒dvdx=-4×1-4×2 …ivDividing equation iii by ivdudxdvdx=-41-4×2 ×1-4×2-4x∴dudv=1x
iii Let, u=sin-14×1-4×2 put, 2x=cosθ⇒ u=sin-12×cosθ1-cos2θ⇒ u=sin-12cosθ sinθ ⇒ u=sin-1sin 2θ …i Let, v=1-4×2 …iiHere, x∈-12,-122 ⇒ 2x∈-1,-12 ⇒θ∈3π4,πSo, from equation i, u=π-2θ Since, sin-1sinθ=π-θ ,if θ∈π2,3π2⇒ u=π-2 cos-12x Since, 2x=cosθ
Differentiate it with respect to x,
dudx=0-2-11-2x2ddx2x⇒dudx=21-4×22⇒dudx=41-4×2 …iiifrom equation ii,dvdx=-4×1-4x2but, x∈-12,-122∴dvdx=-4-x1-4-x2⇒dvdx=4×1-4×2 …ivDividing equation iii by ivdudxdvdx=41-4×2 ×1-4x24x∴dudv=1x
Q6.
Answer :
Let, u=tan-11+x2-1xput x=tanθ⇒ u=tan-11+tan2θ-1tanθ⇒ u=tan-1secθ-1tanθ ⇒ u=tan-11-cosθsinθ ⇒ u=tan-12sin2θ22sinθ2cosθ2 ⇒ u=tan-1 tanθ2 …iAnd, v=sin-12×1+x2⇒ v=sin-12tanθ1+tan2θ ⇒ v=sin-1sin2θ …iiHere, -1<x<1⇒ -1<tanθ<1 ⇒-π4<θ<π4 …A So, from equation i,u=θ2 Since, tan-1tanθ=θ, if θ∈-π2,π2 ⇒u=12tan-1x since, x=tanθ
Differentiating it with respect to x,
dudx=1211+x2⇒dudx=121+x2 …iNow, from equation ii and A,v=2θ Since, sin-1sinθ=θ, if θ∈-π2,π2⇒v=2tan-1x Since, x=tanθ
Differentiating it with respect to x,
dvdx=211+x2 …ivdividing equation iii by iv,dudxdvdx=121+x2×1+x22∴dudv=14
Q7.
Answer :
i Let, u=sin-12×1-x2 Put x=sinθ ⇒ u=sin-12sinθ1-sin2θ ⇒ u=sin-12 sinθ cosθ ⇒ u=sin-1sin2θ …iAnd, Let v=sec-111-x2⇒ v=sec-111-sin2θ ⇒ v=sec-11cosθ ⇒ v=sec-1secθ ⇒ v=cos-111cosθ Since, sec-1x=cos-11x⇒ v=cos-1cosθ …iiHere, x∈0,12⇒ sinθ∈0,12⇒ θ∈0,π4So, from equation i, u=2θ Since, sin-1sinθ=θ, if θ∈-π2,π2 Let, u=2sin-1x Since, x=sinθ
Differentiating it with respect to x,
dudx=211-x2⇒dudx=21-x2 …iiiAnd, from equation ii,v=θ Since, cos-1cosθ=θ, if θ∈0,π⇒v=sin-1x Since, x=sinθ
Differentiating it with respect to x,
dvdx=11-x2 …ivdividing equation iii by iv,dudxdvdx=21-x2×1-x21∴dudv=2
Q8.
Answer :
Let, u=cosxsinx
Taking log on both sides,
log u=logcosxsinx⇒log u=sinx logcosx
Differentiating it with respect to x using chain rule,
1ududx=sinxddxlog cosx+log cosxddxsinx using product rule⇒1ududx=sinx1cosxddxcosx+log cosxcosx⇒dudx=utanx×-sinx+log logxcosx⇒dudx=cosxsinxcosx logcosx-sinx tanx …iLet, v=sinxcosx
Taking log on both sides,
log v=logsinxcosx⇒log v=cosx logsinx
Differentiating it with respect to x using chain rule,
1vdvdx=cosxddxlogsinx+logsinxddxcosx using product rule⇒1vdvdx=cosx1sinxddxsinx+logsinx-sinx⇒dvdx=vcotxcosx-sinx logsinx⇒dvdx=sinxcosxcotxcosx-sinx logsinxdividing equationi by ii,∴dudv=cosxsinxcosx logcosx-sinx tanxsinxcosxcotxcosx-sinx logsinx
Q9.
Answer :
Let, u=sin-12×1+x2Put x=tanθ⇒ u=sin-12tanθ1+tan2θ⇒ u=sin-1sin2θ …iLet v=cos-11-x21+x2⇒ v=cos-11-tan2θ1+tan2θ⇒ v=cos-1cos2θ …iiHere, 0<x<1⇒ 0<tanθ<1⇒ 0<θ<π4So, from equation i,u=2θ Since, sin-1sinθ=θ , if θ∈-π2,π2⇒u=2tan-1x Since , x=tanθ
Differentiating it with respect to x,
dudx=21+x2 …iiifrom equation ii,v=2θ Since, cos-1cosθ=θ, if θ∈0,π⇒v=2tan-1x Since, x=tanθ
Differentiating it with respect to x,
dvdx=21+x2 …ivDividing equation iii by iv,dudxdvdx=21+x2×1+x22∴dudv=1
Q10.
Answer :
Let, u=tan-11+ax1-axPut ax=tanθ⇒ u=tan-11+tanθ1-tanθ⇒ u=tan-1tanπ4+tanθ1-tanπ4tanθ⇒ u=tan-1tanπ4+θ⇒ u=π4+θ⇒ u=π4+tan-1ax Since, tanθ=ax
Differentiating it with respect to x,
dudx=0+11+ax2ddxax ⇒dudx=a1+a2x2 …i Now,Let, v=1+a2x2
Differentiating it with respect to x,
dvdx=121+a2x2ddx1+a2x2⇒dvdx=121+a2x22a2x⇒dvdx=a2x1+a2x2 …ii Dividing equation i by ii,dudxdvdx=a1+a2x2×1+a2x2a2xdudv=1ax1+a2x2
Q11.
Answer :
Let, u=sin-12×1-x2Put x=sinθ⇒ u=sin-12sinθ1-sin2θ⇒ u=sin-12 sinθcosθ ⇒ u=sin-1sin2θ …iLet v=tan-1×1-x2⇒ v=tan-1sinθ1-sin2θ ⇒ v=tan-1sinθcosθ⇒ v=tan-1tanθ …iiHere, -12<x<12⇒ -12<sinθ<12⇒ -π4<θ<π4So, from equation i,u=2θ Since, sin-1sinθ=θ, if θ∈-π2,π2⇒u=2sin-1x Since, x=sinθ
Differentiating it with respect to x,
dudx=21-x2 …iiifrom equation ii,v=θ Since, tan-1tanθ=θ, if θ∈-π2,π2⇒v=sin-1x Since, x=sinθ
Differentiating it with respect to x,
dvdx=11-x2 …ivDividing equation iii by iv,dudxdvdx=21-x2×1-x21∴dudv=2
Q12.
Answer :
Let, u=tan-12×1-x2Put x=tanθ⇒ u=tan-12tanθ1-tan2θ⇒ u=tan-1tan2θ …ilet, v=cos-11-x21+x2⇒ v=cos-11-tan2θ1+tan2θ ⇒ v=cos-1cos2θ … iiHere, 0<x<1⇒ 0<tanθ<1⇒ 0<θ<π4So, from equation i,u=2θ Since, tan-1tanθ=θ, if θ∈-π2,π2⇒u=2tan-1x Since, x=tanθ
differentiating it with respect to x,
dudx=21+x2 …iiiFrom equation ii,v=θ Since, cos-1cosθ=θ, if θ∈0,π⇒v=2tan-1x Since, x=tanθ
Differentiating it with respect to x,
dvdx=21+x2 …ivDividing equation iii by iv,dudxdvdx=21+x2×1+x22∴dudv=1
Q13.
Answer :
Let, u=tan-1x-1x+1Put x=tanθ⇒ u=tan-1tanθ-1tanθ+1⇒ u=tan-1tanθ-tanπ41+tanθ tanπ4 ⇒ u=tan-1tanθ-π4 …i Here, -12<x<12⇒ -12<tanθ<12⇒ -tan-112<θ<tan-112So, from equation i,u=θ-π4 Since, tan-1tanθ=θ, if θ∈-π2,π2⇒u=tan-1x -π4 Since, x=tanθ
differentiating it with respect to x,
dudx=11+x2-0 ⇒dudx=11+x2 …ii And,Let, v=sin-13x-4x3Put x=sinθ ⇒ v=sin-13sinθ-4sin3θ ⇒ v=sin-1sin3θ …iiiNow, -12<x<12⇒ -12<sinθ<12⇒ -16<θ<π6So, from equation iii,v=3θ Since, sin-1sinθ=θ, if θ∈-π2,π2⇒v=3sin-1x Since, x=sinθ
Differentiating it with respect to x,
dvdx=31-x2 …ivDividing equation iii by iv,dudxdvdx=11+x2×1-x23∴dudv=1-x231+x2
Q14.
Answer :
Let, u=tan-1cosx1+sinx⇒ u=tan-1tanπ4-x2⇒ u=π4-x2
Differentiating it with respect to x,
dudx=0-12dudx=-12 …iLet, v=sec-1x
Differentiating it with respect to x,
dvdx=1xx2-1 …iiDividing equation i by ii,dudxdvdx=-12×xx2-11dudv=-xx2-12
Q15.
Answer :
Let, u=sin-12×1+x2Put x=tanθ ⇒θ=tan-1x,⇒ u=sin-12tanθ1+tan2θ⇒ u=sin-1sin2θ …iLet, v=tan-12×1-x2⇒ v=tan-12tanθ1-tan2θ⇒ v=tan-1tan2θ …iiHere, -1<x<1⇒ -1<tanθ<1⇒ -π4<tanθ<π4So, from equation i,u=2θ Since, sin-1sinθ=θ, if θ∈-π2,π2⇒u=2tan-1x
Differentiating it with respect to x,
dudx=21+x2 …iiifrom equation ii,v=2θ Since, tan-1tanθ=θ , if θ∈-π2,π2⇒v=2tan-1x
Differentiating it with respect to x,
dvdx=21+x2 …ivDividing equation iii by iv,dudxdvdx=21+x2 ×1+x22∴dudv=1
Page 11.101 Ex.11.8
Q16.
Answer :
Let, u=cos-14×3-3xPut, x=cosθ⇒ θ=cos-1xNow, u=cos-14cos3θ-3cosθ⇒ u=cos-1cos3θ …i Let, v=tan-11-x2x ⇒ v=tan-11-cos2θcosθ ⇒ v=tan-1sinθcosθ ⇒ v=tan-1tanθ …iiHere, 12<x<1⇒ 12<cosθ<1⇒ 0<θ<π3So, from equation i,u=3θ Since, cos-1cosθ=θ, if θ∈0,π⇒u=3cos-1x
Differentiating it with respect to x,
dudx=-31-x2 …iiiFrom equation ii,v=θ Since, tan-1tanθ=θ, if θ∈-π2,π2⇒v=cos-1x
Differentiating it with respect to x,
dvdx=-11-x2 …ivDividing equation iii by iv,dudxdvdx=-31-x2-1-x21∴dudv=3
Q17.
Answer :
Let, u=tan-1×1-x2Put x=sinθ⇒ θ=sin-1x ⇒ u=tan-1sinθ1-sin2θ ⇒ u=tan-1sinθcosθ ⇒ u=tan-1tanθ …iAndLet, v=sin-12×1-x2 v=sin-12sinθ1-sin2θ v=sin-12 sinθcosθ v=sin-1sin2θ …iiHere, -12<x<12⇒ -12<sinθ<12⇒ -π4<θ<π4So, from equation i,u=θ Since, tan-1tanθ=θ, if θ∈-π2,π2⇒u=sin-1x
Differentiating it with respect to x,
dudx=11-x2 …iiifrom equation ii,v=2θ Since, sin-1sinθ=θ, if θ∈-π2,π2⇒ v=2sin-1x
Differentiating it with respect to x,
dvdx=21-x2 …ivDividing equation iii by iv,dudxdvdx=11-x21-x22∴dudv=12
Q18.
Answer :
Let, u=sin-11-x2Put x=cosθ⇒ θ=cos-1xWe get, u=sin-1sinθ …i Let, v=cot-1×1-x2 ⇒ v=cot-1cosθ1-cos2θ ⇒ v=cot-1cosθsinθ ⇒ v=cot-1cotθ …iiHere, 0<x<1⇒ 0<cosθ<1⇒ 0<θ<π2So, from equation i,u=θ Since, sin-1sinθ=θ, ifθ∈-π2,π2⇒u=cos-1x
Differentiating it with respect to x,
dudx=-11-x2 …iiiFrom equation ii,v=θ Since, cot-1cotθ=θ, if θ∈0,π⇒v=cos-1x
Differentiating it with respect to x,
dvdx=-11-x2 …ivDividing equation iii by iv,dudxdvdx=-11-x21-x2-1∴dudv=1
Q19.
Answer :
Let, u=sin-12ax1-a2x2Put ax=sinθ ⇒ θ=sin-1ax∴ u=sin-12sinθ1-sin2θ⇒ u=sin-12 sinθcosθ⇒ u=sin-1sin2θ …iAndLet, v=1-a2x2Differentiating it with respect to x,dvdx=121-a2x2 ×ddx1-a2x2 ⇒dvdx=0-2a2x21-a2x2 ⇒dvdx=-a2x1-a2x2 …iiHere, -12<ax<12⇒ -12<sinθ<12⇒ -π4<θ<π4So, from equation i,u=2θ Since, sin-1sinθ=θ, if θ∈-π2,π2⇒u=2sin-1x
Differentiating it with respect to x,
dudx=2×11-ax2ddxax ⇒dudx=21-a2x2a ⇒dudx=2a1-a2x2 …iii
Dividing equation iii by ii,dudxdvdx=2a1-a2x21-a2x2-a2x∴dudv=-2ax
Q20.
Answer :
Let, u=tan-11-x1+xPut x=tanθ⇒ θ=tan-1x⇒ u=tan-11-tanθ1+tanθ⇒ u=tan-1tanπ4-θ …iHere, -1<x<1⇒ -1<tanθ<1⇒ -π4<θ<π4⇒ π4>-θ>π4⇒ -π4<-θ<π4⇒ 0<π4-θ<π2So, from equation i,u=π4-θ Since, tan-1tanθ=θ, if θ∈-π2,π2⇒u=π4-tan-1x
Differentiating it with respect to x,
dudx=0-11+x2⇒dudx=-11+x2 …iiAnd let, v=1-x2
Differentiating it with respect to x,
dvdx=121-x2×ddx1-x2⇒dvdx=121-x2-2x⇒dvdx=-x1-x2 …iiiDividing equation ii by iii,dudxdvdx=-11+x2×1-x2-x∴dudv=1-x2x1+x2
Page 11.104 (Very Short Answers)
Q1.
Answer :
We have, fx=loge logex
Differentiating with respect to x,
f’x=1logexddxlogex ⇒f’x=1logex1x⇒f’e=1logee1e ∵x=e⇒f’e=1e ∵loge e=1
Q2.
Answer :
We have, fx=x+1 Now, fofx=ffx ⇒fofx=fx+1⇒fofx=x+1+1⇒fof=x+2
⇒ddxfofx=ddxx+ddx2⇒ddxfofx=1+0⇒ddxfofx=1
Q3.
Answer :
We have, f’1=2 and y=flogex
Differentiate it with respect to x,
dydx=f’logex×ddxlogex⇒dydx=f’logex1x⇒dydx=f’logee1e ∵ x=e⇒dydx=f’11e ∵ logee=1⇒dydx=2e ∵ f’1=2
Q4.
Answer :
We have, f1=4 and f’1=2Let y=logfex
⇒dydx=ddxlogfex⇒dydx=1fex×ddxfex⇒dydx=1fex×f’ex×ddxex⇒dydx=exf’exfexPutting x=0, we get,dydx=e0f’e0fe0⇒dydx=1f’1f1⇒dydx=24 ∵f’1=2 and f1=4⇒dydx=12
Page 11.105 (Very Short Answers)
Q5.
Answer :
We have, f’x=2×2-1and y=fx2
⇒dydx=ddxfx2⇒dydx=f’x2ddxx2⇒dydx=f’x2× 2x⇒dydx=2xf’x2Putting x=1, we get,dydx=21f’12⇒dydx=2 ×f’1⇒dydx=2 ×1 ∵f’1=212-1=2-1=1⇒dydx=2
Q6.
Answer :
We have, f3=9 ,f’3=9and gx=f-1x⇒gofx=x⇒gfx=x
⇒ddxgfx=1⇒g’fxddxfx=1⇒g’fx × f’x=1Puting x=3, we get,g’f3 × f’3=1⇒g’9 × 9=1 ∵ f3=9 , f’3=9⇒g’9=19
Q7.
Answer :
We have, y=sin-1sinx⇒y=x ∵sin-1sinx=x , if x∈-π2,π2
⇒dydx=ddxx⇒dydx=1
Q8.
Answer :
We have, y=sin-1sinx ⇒ y=π-x ∵sin-1sinx=π-x , if x∈π2,3π2
⇒dydx=ddxπ-x⇒dydx=0-1⇒dydx=-1
Q9.
Answer :
We have, y=cos-1cosx ⇒ y=2π-x ∵cos-1cosx=2π-x , if x∈π,2π
⇒dydx=ddx2π-x⇒dydx=0-1⇒dydx=-1
Q10.
Answer :
We have, y=sin-12×1+x2Putting x=tanθ⇒1<tanθ<∞⇒π4<θ<π2 ⇒π2<2θ<π∴y=sin-1sin2θ ⇒y=sin-1sinπ-2θ ⇒y=π-2θ ⇒y=π-2tan-1x⇒dydx=0-21+x2 ⇒dydx=-21+x2
Q11.
Answer :
We have, f0=f1=0 , f’1=2and,y=fexefx
⇒dydx=ddxfex × efx⇒dydx=fexddxefx+efxddxfex Using product rule⇒dydx=fex × efxddxfx+efx×f’exddxex⇒dydx=fex × efx×f’x+efx×f’ex×exPutting x=0, we get,dydx=fe0 × ef0×f’0+ef0×f’e0×e0⇒dydx=f1ef0×f’0+ef0×f’1×1⇒dydx=0×e0×f’0+e0×2×1 ∵fx=f1=0 and f’1=2⇒dydx=0+1×2×1⇒dydx=2
Q12.
Answer :
We have, y=xx⇒y=x-x ∵x<0⇒y=-x2
⇒dydx=ddx-x2⇒dydx=-2x
Q13.
Answer :
We have, y=sin-1x+cos-1x⇒ y=π2 ∵sin-1x+cos-1x=π2
⇒dydx=0
Q14.
Answer :
We have, x=aθ+sinθ and y=a1+cosθ⇒dxdθ=addθθ+ddθsinθ and dydθ=a0-sinθ⇒dxdθ=a1+cosθ and dydθ=-asinθ ∴dydx=dydθdxdθ=-asinθa1+cosθ=-2sinθ2cosθ22 cos2θ2=-tanθ2
Q15.
Answer :
We have, y=tan-11-cos2x1+cos2x⇒y=tan-12 sin2x2 cos2x⇒y=tan-1tan2x⇒y=tan-1tanx ∵ tan-1tanx=-x , if x∈-π2,0⇒y=-x
⇒dydx=-1
Q16.
Answer :
We have, y=xx …i
Taking log on both sides,
log y=log xx⇒log y=x logx
⇒1ydydx=xddxlogx+logxddxx⇒1ydydx=x1x+logx 1⇒1ydydx=1+logx⇒dydx=y1+logx⇒dydx=xx1+logx using equation iPuting x=e, we get,dydx=ee1+logee⇒dydx=ee1+1 ∵logee=1⇒dydx=2ee
Q17.
Answer :
We have, y=tan-11-x1+x
⇒dydx=11+1-x1+x2ddx1-x1+x⇒dydx=1+x21+x2+2x+1+x2-2×1+xddx1-x-1-xddx1+x1+x2 using quotient rule⇒dydx=1+x22x2+21+x-1-1-x11+x⇒dydx=1+x22x2+1-x-1-1+x1+x2⇒dydx=1+x22x2+1×-21+x2⇒dydx=-1×2+1
Q18.
Answer :
We have, y=logax⇒y=logxloga ∵logab=logbloga
⇒dydx=1logaddxlogx⇒dydx=1loga1x⇒dydx=1x loga
Q19.
Answer :
We have, y=logtanx⇒y=logtanx12⇒y=12log tanx ∵logab=bloga
⇒dydx=12×1tanxddxtanx⇒dydx=12×1tanxsec2x⇒dydx=12sinxcosx×cos2x⇒dydx=12 sinx cosx⇒dydx=1sin2x⇒dydx=cosec2x
Q20.
Answer :
We have, y=sin-1 1-x21+x2+cos-1 1-x21+x2⇒y=π2 ∵sin-1x+cos-1x=π2
⇒dydx=0
Q21.
Answer :
We have, y=sec-1x+1x-1+sin-1x-1x+1 ⇒ y=cos-1x-1x+1+sin-1x-1x+1 ∵sec-1x=cos-11x⇒y=π2 ∵sin-1x+cos-1x=π2
⇒dydx=0
Q22.
Answer :
We have, y=1+x+x2+….to ∞⇒ y=11-x ∵It is a G.P with first term 1and common ratio x
⇒dydx=ddx11-x⇒dydx=-11-x2ddx1-x⇒dydx=-11-x2-1⇒dydx=11-x2
Q23.
Answer :
We have, u=sin-12×1+x2 and v=tan-12×1-x2⇒dudx=21+x2 and dvdx=21+x2 ∴dudv=dudxdvdx=21+x2×1+x22=1
Q24.
Answer :
We have, fx=loguxvxand, u1=v1 , u’1=v’1=2 …i
⇒f’x=ddxloguxvx⇒f’x=1uxvx×ddxuxvx⇒f’x=vxux×vxddxux-uxddxvxvx2 ⇒f’x=vxux×vx×u’x-ux×v’xvx2Putting x=1, we get,f’1=v1u1×v1×u’1-u1×v’1v12⇒f’1=1×u1×2-u1×2u12 Using eqn 1⇒f’1=0u12 ⇒f’1=0
Q25.
Answer :
We have, y=log3x
⇒dydx=ddxlog3x⇒dydx=13xddx3x⇒dydx=13×3⇒dydx=1x
Q26.
Answer :
We have, fx is an even function.⇒f-x=fx
⇒ddxf-x=ddxfx⇒f’-xddx-x=f’x⇒f’-x×-1=f’x⇒-f’-x=f’x⇒f’-x=-f’xThus, f’x is an odd function.
Q27.
Answer :
We have, fx is an odd function.⇒f-x=-fx
⇒ddxf-x=-ddxfx⇒f’-xddx-x=-f’x⇒f’-x×-1=-f’x⇒-f’-x=-f’x⇒f’-x=f’xThus, f’x is an even function.
Page 11.106 (Multiple Choice Questions)
Q1.
Answer :
(d) 1/2 e
We have, fx=logx2logx⇒fx=loglogxlogx2 ⇒fx=loglogx2 logx⇒f’x=12×ddxloglogx logx⇒f’x=12×1logx×1x×logx-loglogxx logx2⇒f’x=12×1x-loglogxx logx2⇒f’e=12×1e-loglogee loge2 Putting x=e⇒f’e=12×1e1⇒f’e=12e
Q2.
Answer :
(c) x log x-1
We have,
fx=log x⇒flogx=loglogx⇒f’logx=1logxddxlogx⇒f’logx=1x logx⇒f’logx=x logx-1
Q3.
Answer :
(a) (2/3)1/2
We have, y=cot-1cos 2x
⇒dydx=-11+cos 2xddxcos 2x⇒dydx=-12 cos2x×12cos 2xddxcos 2x⇒dydx=-12 cos2x×12cos 2x×-2sin 2x⇒dydx=sin2xcos2x × 2cos2x⇒dydx=2 sinx cosxcos2x × 2cos2x⇒dydx=tanxcos2xSo, at x=π6, we getdydxx=π6=tanπ6cos2π6=1312=2312
Q4.
Answer :
(d) x1+x2
We have, y=sectan-1x⇒dydx=sectan-1x tantan-1x×ddxtan-1x⇒dydx=sectan-1x tantan-1x×11+x2⇒dydx=yx1+x2⇒dydx=x1+x2 y
This is the equation of differential equation which have coefficient x1+x2.
Q5.
Answer :
(d) 1/2
Let y=tan-11+sinx1-sinx⇒ y=tan-11-cosπ2+x1+cosπ2+x⇒ y=tan-12 sin2π4+x22 cos2π4+x2 ⇒ y=tan-1tanπ4+x2=π4+x2∴dydx=12
Q6.
Answer :
(a) 1+1xx 1+1x-1x+1
Let y=1+1xxTaking log on both sides,log y=x log1+1x⇒1ydydx=xddxlog1+1x+log1+1xddxx ⇒1ydydx=x11+1xddx1+1x+log1+1x⇒1ydydx=x × xx+1-1×2+log1+1x⇒1ydydx=x2x+1×-1×2+log1+1x⇒1ydydx=-1x+1+log1+1x⇒dydx=y-1x+1+log1+1x⇒dydx=1+1xxlog1+1x-1x+1
Q7.
Answer :
(d) log x1+log x2
We have, xy=ex-yTaking log on both sides we get, ⇒y logx=x-yloge e⇒y logx=x-y⇒y logx+y=x⇒y1+logx=x⇒y=x1+logx
⇒dydx=1+logx × 1-x ×0+1×1+logx2⇒dydx=1+logx -11+logx2⇒dydx=logx1+logx2
Q8.
Answer :
c f-12=f-12We have, fx=4×8⇒f’x=32x7Now, f12=4128=41256=164 f-12=4-128=41256=164f’12=32127=321128=14f’-12=32-127=-321128=-14
Page 11.107 (Multiple Choice Questions)
Q9.
Answer :
(d) sec θ
We have, x=a cos3θ⇒dxdθ=addθcos3θ⇒dxdθ=3acos2θddθcosθ⇒dxdθ=-3acos2θsinθ …1and, y=a sin3θ⇒dydθ=addθsin3θ⇒dydθ=3a sin2θddθsinθ⇒dydθ=3a sin2θ cosθ …2Dividing 2 by 1, we get, dydθdxdθ=3a sin2θ cosθ -3acos2θsinθ⇒dydx=sinθ-cosθ⇒dydx=-tanθNow, 1+dydx2=1+tan2θ=sec2θ=secθ
Q10.
Answer :
(a) -21+x2
Let y=sin-11-x21+x2Differentiating with respect to x using chain rule, we get,dydx=11-1-x21+x22ddx1-x21+x2⇒dydx=1+x21+x22-1-x221+x2ddx1-x2-1-x2ddx1+x21+x22 using quotient rule⇒dydx=1+x21+x22-1-x221+x2-2x-1-x22x1+x22⇒dydx=1+x22x-2x-2×3-2x+2×31+x22⇒dydx=-4x2x1+x2⇒dydx=-21+x2
Q11.
Answer :
(a) does not exist
We know that sec-1α is not defined for α∈-1, 1Here for x=-13, 12×2+1=911∈-1, 1∴ sec-112×2+1 is not defined at x=-13∴ Derivative of sec-112×2+1 does not exist at x=-13
Q12.
Answer :
(c) −1
We have, x+y=1Differentiating with respect to x, we get,12x+12ydydx=0⇒12ydydx=-12x⇒dydx=-12x×2y1⇒dydx=-yxNow, dydx14,14=-1414=-1
Q13.
Answer :
(d) − 1
We have, sinx+y=logx+y⇒cosx+y1+dydx=1x+y1+dydx⇒cosx+y+cosx+ydydx=1x+y+1x+ydydx⇒cosx+ydydx-1x+ydydx=1x+y-cosx+y⇒cosx+y-1x+ydydx=1x+y-cosx+y⇒-1x+y-cosx+ydydx=1x+y-cosx+y⇒dydx=-1
Q14.
Answer :
(d) 1
We have, u=sin-12×1+x2 and v=tan-12×1-x2⇒dudx=21+x2 and dvdx=21+x2
∴dudv=dudxdvdx=21+x2×1+x22=1
Q15.
Answer :
(b) − 1/2
Let u=tan-1cosx1+sinx ⇒ u=tan-1cos2x2-sin2x2cos2x2+sin2x2+2sinx2cosx2 ⇒ u=tan-1cosx2-sinx2cosx2+sinx2cosx2+sinx22 ⇒ u=tan-1cosx2-sinx2cosx2+sinx2⇒ u=tan-11-tanx21+tanx2⇒ u=tan-1tanπ4-tanx21+tanπ4×tanx2⇒ u=tan-1tanπ4-x2⇒ u=π4-x2
⇒dudx=0-12⇒dudx= -12
Q16.
Answer :
(a) x2-1×2-4
Let y=ddxlogexx-2x+234⇒ y=ddxxloge+34logx-2x+2⇒ y=ddxx+34logx-2x+2⇒dydx=1+34x-2x+2×x+2×1-x-2×1x+22⇒dydx=1+3x+24x-2×x+2-x+2x+22⇒dydx=1+3x+24x-2×4x+2⇒dydx=1+3×2-4⇒dydx=x2-4+3×2-4⇒dydx=x2-1×2-4
Q17.
Answer :
(d) cos x2 y-1
We have, y=sinx+ySquaring both sides, we get,y2=sinx+y⇒y2-y=sinx⇒2ydydx-dydx=cosx⇒dydx2y-1=cosx⇒dydx=cosx2y-1
Q18.
Answer :
(a) -yx
We have, 3 sinxy+4 cosxy=5 ⇒ 3 cosxyxdydx+y-4 sinxyxdydx+y=0⇒ xdydx+y3 cosxy-4 sinxy =0⇒ xdydx+y=0⇒ xdydx=-y∴ dydx=-yx
Q19.
Answer :
(b) sin2 a+ysin a
We have, sin y=x sina+y
⇒ddxsin y=ddxx sina+y⇒cos ydydx=sina+yddxx+xddxsina+y⇒cos ydydx=sina+y×1+x cosa+ydydx ⇒cos ydydx=sina+y+x cosa+ydydx⇒cos ydydx-x cosa+ydydx=sina+y⇒cos y-x cos a+ydydx=sina+y⇒cos y-sin ysina+y×cosa+ydydx=sina+y ∵ sin y=2 sinx cosx∴x=sin ysina+y⇒sina+y cos y-sin y cosa+ysina+ydydx=sina+y⇒sina+y-ysina+y×dydx=sina+y ⇒dydx=sin2a+ysina
Page 11.108 (Multiple Choice Questions)
Q20.
Answer :
(a) 2
Let u=cos-12×2-1Put x=cosθ⇒θ=cos-1xdθdx=-11-x2Now, u=cos-1cos2θ⇒u=2θ
⇒dudx=2dθdx⇒dudx=-21-x2 …iand, v=cos-1x⇒v=cos-1cosθ⇒v=θ
dvdx=dθdx⇒dvdx=-11-x2 …iiDividing i by ii, we get,dudxdvdx=-21-x2×1-x2-1⇒dudv=2
Q21.
Answer :
b-1 for x<-3 We have, fx=x2+6x+9 = x+32 =x+3 fx=x+3, x≥-3 -x-3, x<-3 ⇒f’x=1, x≥-3 -1, x<-3 ∴f’x=-1 for x<-3
Q22.
Answer :
c-2x+9 for 4<x<5 We have, fx=x2-9x+20 fx=x2-9x+20, -∞<x≤4-x2-9x+20, 4<x<5×2-9x+20, 5≤x<∞⇒fx=2x-9, -∞<x≤4-2x+9, 4<x<52x-9, 5≤x<∞∴f’x=-2x+9 for 4<x<5
Q23.
Answer :
(d) none of these
We have, fx=x2-10x+25=x-52=x-5 =x-5 for x>5 -x-5 for x<5LHD=limx→5- fx-fax-a =limx→5-x2-10x+25-52-105+25x-5 =limx→5-x-5x-5 =limx→5–x-5x-5 =-1RHD=limx→5+ fx-fax-a =limx→5+x2-10x+25-52-105+25x-5 =limx→5+x-5x-5 =limx→5+x-5x-5 =1Here, LHD≠RHDThus, the functionis not differentiable at x=5
Q24.
Answer :
(c) 0
For, x>10fx=x-3=x-3gx=fof x=x-3-3 =x-3-3 =x-6∴g’x =1
Q25.
Answer :
(b) 0
We have, fx=xlxml+m xmxnm+n xnxln+1
⇒fx=xl-ml+m × xm-nm+n × xn-ln+l⇒fx=xl2-m2 × xm2-n2 × xn2-l2⇒fx=xl2-m2+m2-n2+n2-l2⇒fx=x0⇒fx=1⇒f’x=0
Q26.
Answer :
(c) 0
We have,y=11+xa-b+xc-b+11+xb-c+xa-c+11+xb-a+xc-a=11+xaxb+xcxb+11+xbxc+xaxc+11+xbxa+xcxa=xbxb+xa+xc+xcxc+xb+xa+xaxa+xb+xc=xbxa+xb+xc+xcxa+xb+xc+xaxa+xb+xc=xb+xc+xaxa+xb+xc=xa+xb+xcxa+xb+xc=1∴dydx=ddx1=0
Q27.
Answer :
(a) x2y2 1-y61-x6
We have, 1-x6+1-y6=ax3-y3Putting x3=sinA and y3=sinB⇒1-sin2A+1-sin2B=asinA-sinB⇒ cosA+cosB=asinA-sinB⇒2cosA+B2cosA-B2=2a sinA-B2cosA+B2⇒cotA-B2=a⇒A-B2=cot-1a⇒ A-B=2 cot-1a⇒sin-1×3-sin-1y3=2 cot-1a
⇒11-x6×ddxx3-11-y6×ddxy3=0⇒11-x6×3×2-11-y6×3y2×dydx=0⇒dydx=x2y21-y61-x6
Q28.
Answer :
(b) 1
We have, y=logtanx⇒dydx=1tanx×ddxtanx⇒dydx=1tanx×12tanx×ddxtanx⇒dydx=sec2x2 tanxNow, dydxx=π4=secπ422 tanπ4=22×1=1
Q29.
Answer :
(b) yx
We have, sin-1×2-y2x2+y2=loga⇒ x2-y2x2+y2=sin loga
⇒x2+y22x-2ydydx-x2-y22x+2ydydxx2+y22=0⇒2×3-2x2ydydx+2xy2-2y3dydx-2×3-2x2ydydx+2xy2+2y3dydxx2+y22=0⇒-4x2ydydx+4xy2=0⇒-4x2ydydx=-4xy2⇒dydx=4xy24x2y∴dydx=yx
Q30.
Answer :
(a) cos2 a+ycos a
We have, sin y=x cosa+y
⇒ddxsin y=ddxx cosa+y⇒cos ydydx=1×cosa+y-x sina+yddxa+y⇒cos ydydx=cosa+y-x sina+ydydx⇒cos ydydx+x sina+ydydx=cosa+y⇒cos y+x sina+ydydx=cosa+y⇒cos y+sin ycosa+y×sina+ydydx=cosa+y ∵ sin y=x cosa+y∵x=sin ycosa+y⇒cosa+y cos y+sin y sina+ycosa+ydydx=cosa+y⇒cosa+y-ycosa+y×dydx=cosa+y⇒dydx=cos2a+ycos a
Page 11.109 (Multiple Choice Questions)
Q31.
Answer :
(b) -4×1-x4
We have, y=log1-x21+x2⇒dydx=11-x21+x2ddx1-x21+x2⇒dydx=1+x21-x21+x2-2x-1-x22x1+x22⇒dydx=11-x2-2x-2×3-2x+2×31+x2⇒dydx=-4×1-x4
Q32.
Answer :
(a) cos x2y-1
We have, y=sinx+ySquaring both sides, we get,y2=sinx+y⇒y2-y=sinx⇒2ydydx-dydx=cosx⇒dydx2y-1=cosx⇒dydx=cosx2y-1
Q33.
Answer :
(c) 1
We have, y=tan-1sinx+cosxcosx-sinx⇒dydx=11+sinx+cosxcosx-sinx2ddxsinx+cosxcosx-sinx⇒dydx=cosx-sinx2cosx-sinx2+sinx+cosx2cosx-sinxddxsinx+cosx-sinx+cosxddxcosx-sinxcosx-sinx2⇒dydx=cosx-sinx2cosx-sinx2+sinx+cosx2cosx-sinxcosx-sinx-sinx+cosx-sinx-cosxcosx-sinx2⇒dydx=cosx-sinx2cosx-sinx2+sinx+cosx2cosx-sinxcosx-sinx+sinx+cosxsinx+cosxcosx-sinx2⇒dydx=cosx-sinx2cosx-sinx2+sinx+cosx2×cosx-sinx2+sinx+cosx2cosx-sinx2⇒dydx=1
Q1.
Answer :
(i) We have,
y=x3+tanxDifferentiating w.r.t. x, we getdydx=3×2+sec2xDifferentiating again w.r.t. x, we getd2ydx2=6x+2sec2x tanx
(ii) We have,
y= sinlogxDifferentiating w.r.t. x, we getdydx=coslogx×1xDifferentiating again w.r.t. x, we getd2ydx2=-sinlogx1x×1x+coslogx×-1×2 =-sinlogx+coslogxx2
(iii) We have,
y= logsinxDifferentiating w.r.t. x, we getdydx=1sinx×cosx =cotxDifferentiating again w.r.t. x, we getd2ydx2=-cosec2x
(iv) We have,
y =exsin5xDifferentiating w.r.t. x, we getdydx=ex sin 5x +ex cos 5x×5Differentiating again w.r.t. x, we getd2ydx2=ex sin 5x +ex cos 5x×5+5ex(-sin5x×5)+5ex cos 5x =-24ex sin 5x +10ex cos 5x =2ex5 cos 5x-12 sin 5x
(v) We have,
y= e6x cos 3xDifferentiating w.r.t. x, we getdydx=e6x×6× cos 3x+e6x(-sin 3x×3) =6e6x cos3x-3e6xsin 3xDifferentiating again w.r.t. x, we getd2ydx2=6e6x cos3x × 6 -6e6x sin3x×3- 3×6 e6x sin3x-3e6x×3 cos 3x =27e6x cos3x-36e6x sin3x =9e6x3 cos3x-4 sin3x
(vi) We have,
y = x3 logxDifferentiating w.r.t. x, we getdydx=3×2 logx+x3×1x =3×2 logx+x2Differentiating again w.r.t. x, we getd2ydx2=6x logx+3×2×1x+2x =6x logx +5x
(vii) We have,
y= tan-1xDifferentiating w.r.t. x, we getdydx=11+x2Differentiating again w.r.t. x, we getd2ydx2=-2x×11+x22=-2×1+x22
(viii) We have,
y= x cosxDifferentiating w.r.t. x, we getdydx=cosx -xsinxDifferentiating again w.r.t. x, we getd2ydx2=-sinx-sinx-xcosx =-2sinx+xcosx
(ix) We have,
y= loglogxDifferentiating w.r.t. x, we getdydx=1logx×1x =1xlogxDifferentiating again w.r.t. x, we getd2ydx2=0-logx+1xlogx2=-1+logxxlogx2
Q2.
Answer :
Here,
y=e-x cos xDifferentiating w.r.t. x, we getdydx=-e-x sinx -e-x cos x =-e-x sinx +e-x cos xDifferentiating again w.r.t. x, we getd2ydx2=-e-x cosx -e-x sinx -e-x sinx -e-x cosx =2e-x sinx
Hence proved.
Q3.
Answer :
Here,
y= x+ tanxDifferentiating w.r.t. x, we getdydx=1+sec2xDifferentiating again w.r.t. x, we getd2ydx2=2sec2xtanxDividing both sides by sec2x, we getcos2x d2ydx2=2tanx⇒cos2x d2ydx2=2(y-x) ∵y=x +tanx⇒tanx =y-x⇒cos2x d2ydx2-2y+2x=0
Hence proved.
Q4.
Answer :
Here,
y=x3logxDifferentiating w.r.t. x, we getdydx=3×2 logx +x3×1x =3×2 logx+x2Differentiating again w.r.t. x, we getd2ydx2=6x logx+3×2×1x+2x =6x logx+5xDifferentiating again w.r.t. x, we getd3ydx3=6logx+6x×1x+5 =6 logx+11Differentiating again w.r.t. x, we getd4ydx4=6x
Hence proved.
Q5.
Answer :
Here,
y=logsinxDifferentiating w.r.t. x, we getdydx=1sinx×cosx=cotxDifferentiating again w.r.t. x, we getd2ydx2=-cosec2xDifferentiating again w.r.t. x, we getd3ydx3=-2cosecx ×-cosecx cotx = 2cotx cosec2x = 2cosx cosec3x
Hence proved.
Q6.
Answer :
Here,
y=logxxDifferentiating w.r.t. x, we getdydx=1-logxx2Differentiating again w.r.t. x, we getd2ydx2=-x-2×1-logxx4 =-x-2x+2xlogxx4 =-3+2logxx3 =2logx-3×3
Hence proved.
Q7.
Answer :
Here,
y=logxxDifferentiating w.r.t. x, we getdydx=1-logxx2Differentiating again w.r.t. x, we getd2ydx2=-x-2×1-logxx4 =-x-2x+2xlogxx4 =-3+2logxx3 =2logx-3×3
Hence proved.
Page 12.12 Ex.12.1
Q8.
Answer :
Here,
x=a secθ and y=b tanθDifferentiating w.r.t. θ, we getdxdθ=asecθ tanθ and dydθ=b sec2θ∴dydx=dydθ×dθdx=b sec2θa secθ tanθ=b cosecθaDifferentiating w.r.t. x, we getd2ydx2=b a×-cosecθ cotθ×dθdx =-b a×cosecθ cotθ×1asecθ tanθ =-b a2×cotθ ×1tan2θ =-b a2×1tan3θ =-b4a2y3 ∵y=b tanθ
Hence proved.
Q9.
Answer :
Here,
x= acosθ+θsinθ and y=asinθ-θcosθDifferentiating w.r.t. θ, we getdxdθ=a-sinθ+θcosθ+sinθ=aθcosθ and dydθ=acosθ+θsinθ-cosθ=aθsinθ∴dydx=dydθ×dθdx =aθsinθaθcosθ=tanθ∴ d2ydx2=sec2θ ×dθdx =sec2θ×1aθcosθ ∵dxdθ=aθcosθ =sec3θaθ
Hence proved.
Q10.
Answer :
Here,
y=ex cosx Differentiating w.r.t. x, we getdydx=ex cosx-ex sin x=excosx-sinxDifferentiating again w.r.t. x, we getd2ydx2=ex cosx-sinx+ex -sinx-cosx =excosx-exsinx-exsinx-excosx =-2exsinx =2ex cosx+π2
Hence proved.
Q11.
Answer :
Here,
x=a cosθ and y = b sinθDifferentiating w.r.t. θ, we getdxdθ= -a sinθ and dydθ= b cosθ∴dydx=b cosθ-a sinθ=-bacotθDifferentiating w.r.t. x, we getd2ydx2=-ba×-cosec2θ dθdx =ba×cosec2θ×1-a sinθ =-ba2×1 sin3θ =-ba2×b3y3 ∵y = b sinθ =-b4a2y3
Hence proved.
Q12.
Answer :
Here,
x=a1-cos3θ, y =a sin3θDifferentiating w.r.t. θ, we getdxdθ=3a cos2θ sinθ anddydθ=3a sin2θ cosθ⇒ dydx=3a sin2θ cosθ3a cos2θ sinθ=tanθDifferentiating w.r.t. x, we getd2ydx2=sec2θ dθdx =sec2θ3a cos2θ sinθ =sec4θ3a sinθ∴ d2ydx2 at θ=π6⇒d2ydx2= secπ6 43a sinπ6=3227a
Q13.
Answer :
(i) Here,
x=aθ+sinθ and y=a1+cosθDifferentiating w.r.t. θ, we getdxdθ=a+acosθ and dydθ=-a sinθ∴dydx=-a sinθa+a cosθ=- sinθ1+cosθDifferentiating w.r.t. x, we getd2ydx2=-1+cosθcosθ+ sin2θ1+cosθ2dθdx =-cosθ-cos2θ- sin2θ1+cosθ2×1a+acosθ =-1+cosθa1+cosθ3 =-1a1+cosθ2 =-ay2 ∵ y=a1+cosθ
Hence proved.
(ii) Here,
x=aθ-sinθ and y=a1+cosθDifferentiating w.r.t. θ, we getdxdθ=a-acosθ, dydθ=-a sinθ⇒dydx=-a sinθa-a cosθ=- sinθ1-cosθDifferentiating w.r.t. x, we getd2ydx2=-cosθ+cos2θ+ sin2θ1-cosθ2×dθdx =-cosθ+cos2θ+ sin2θ1-cosθ2×1a-acosθ =1-cosθa1-cosθ3 =1a1-cosθ2
Q14.
Answer :
Here,
x= a1-cosθ and y=aθ+ sinθDifferentiating w.r.t. x, we getdxdθ=a sinθ and dydθ=a+a cosθ∴dydx=a+acosθasinθ=1+cosθsinθDifferentiating w.r.t. x, we getd2ydx2=-sin2θ-1+cosθcosθsin2θdθdx =-1-1+cosθcosθsin2θ1a sinθ∴ d2ydx2 at θ=π2 ⇒d2ydx2θ=π2=1a-1-01=-1a
Hence proved.
Q15.
Answer :
Here,
x=a1+cosθ and y =aθ+sinθDifferentiating w.r.t. θ, we getdxdθ=-asinθ and dydθ=a+a cosθ∴dydx=a+acosθ-asinθ=1+cosθ-sinθDifferentiating w.r.t. x, we getd2ydx2=ddθdydxdθdxd2ydx2=–sin2θ-cosθ-cos2θsin2θdθdx =1+cosθsin2θ×-1a sinθ =-1+cosθasin3θAt θ=π2: d2ydx2=-1+cosπ2a sinπ23=-1a
Q16.
Answer :
Here,
x=a sint -b cost and y=a cost+b sintDifferentiating w.r.t. t, we getdxdt=a cost+b sint and dydt=-a sint+b cost∴dydx=-a sint+b costa cost+b sintDifferentiating w.r.t. x, we getd2ydx2=-a cost+b sint2-a sint-b cost2a cost+b sint2dtdx =-a cost+b sint2-a sint-b cost2a cost+b sint21a cost+b sint =-y2+x2y3
Q17.
Answer :
Here,
x= cosθ and y = sin3θDifferentiating w.r.t. θ, we getdxdθ=-sinθ and dydθ=3sin2θ cosθ∴dydx=3sin2θ cosθ-sinθ=-3sinθ cosθDifferentiating w.r.t. x, we getd2ydx2=-3cos2θ+3 sin2θdθdx=-3cos2θ+3 sin2θ-sinθNow,LHS=yd2ydx2+dydx2 = sin3θ×-3cos2θ+3 sin2θ-sinθ+-3sinθ cosθ2 =3sin2θ cos2θ-3 sin4θ+9sin2θ cos2θ =12sin2θ cos2θ-3 sin4θ =3sin2θ4cos2θ-sin2θ =3sin2θ5cos2θ-1 [∵ cos2+ sin2θ=1] =RHS
Hence proved.
Q18.
Answer :
Here,
y=A sin3x+B cos3xDifferentiating w.r.t. x, we getdydx=3A cos3x-3B sin3xDifferentiating again w.r.t. x, we getd2ydx2=-9A sin3x-9B cos3xNow,d2ydx2+4dydx+3y= 10 cos3x⇒-9A sin3x-9B cos3x+43A cos3x-3B sin3x+3A sin3x+B cos3x=10 cos3x⇒-9A sin3x-9B cos3x+12A cos3x-12B sin3x+3A sin3x+3B cos3x=10 cos3x⇒-6Asin3x-6B cos3x+12A cos3x-12B sin3x=10 cos3x⇒cos3x-6B+12A +sin3x-6A-12B=10 cos3x⇒-6B+12A=10 and -6A-12B=0⇒A=23 and B=-13
Q19.
Answer :
Here,
y= sinsinxDifferentiating w.r.t. x, we getdydx=cossinx cosxDifferentiating again w.r.t. x, we getd2ydx2=-sinsinx cos2x-cossinx sinx⇒d2ydx2=-sinsinx cos2x-cossinx cosxtanx⇒d2ydx2=-y cos2x-tanxdydx⇒d2ydx2+tanxdydx+y cos2x=0
Hence proved.
Q20.
Answer :
Here,
x= sint and y =sinptDifferentiating w.r.t. t, we getdxdt=cost and dydt=p cospt⇒dydx=pcosptcostDifferentiating w.r.t. x, we getd2ydx2=-p2sinpt cost+pcosptsintcos2t×dtdx⇒d2ydx2=-p2sinpt cost+pcosptsintcos3t⇒d2ydx2=-p2sinpt costcos3t+pcosptsintcos3t⇒d2ydx2=-p2ycos2t+xdydxcos2t⇒cos2td2ydx2=-p2y+xdydx⇒1-sin2td2ydx2=-p2y+xdydx⇒1-x2d2ydx2-xdydx+p2y=0.
Hence proved.
Q21.
Answer :
Here,
y=sin-1x2Now,y1=2 sin-1x 11-x2⇒y2=21-x2+2x sin-1×1-x23/2⇒y2=21-x2+2x sin-1×1-x21-x2⇒y2=21-x2+xy11-x2⇒y21-x2=2+xy1⇒y21-x2-xy1-2=0
Hence proved.
Q22.
Answer :
Here,
y= etan-1xDifferentiating w.r.t. x, we getdydx= etan-1x ×11+x2Differentiating again w.r.t. x, we getd2ydx2=etan-1×11+x22+etan-1x-2×1+x22⇒1+x2d2ydx2=etan-1×1+x2-2xetan-1×1+x2⇒1+x2d2ydx2=dydx-2xdydx⇒1+x2d2ydx2+2x-1dydx=0
Hence proved.
Q23.
Answer :
Here,
y=3 coslogx+4 sinlogxDifferentiating w.r.t. x, we gety1=-3sinlogx×1x+4 coslogx×1x =-3sinlogx+4coslogxxDifferentiating again w.r.t. x, we gety2=-3coslogxx-4sinlogxx×x–3sinlogx+4coslogxx2⇒y2=-3coslogx-4sinlogx–3sinlogx+4coslogxx2⇒y2=-3coslogx-4sinlogx–3sinlogx+4coslogxx2⇒y2=-3coslogx-4sinlogxx2–3sinlogx+4coslogxx2⇒y2=-3coslogx+4sinlogxx2–3sinlogx+4coslogxx2⇒y2=-yx2-y1x⇒x2y2=-y-xy1⇒x2y2+y+xy1=0
Hence proved.
Q24.
Answer :
Here,
y=e2xax+bDifferentiating w.r.t. x, we gety1=2e2x ax+b+a e2x⇒y1=2y+a e2x ∵y=e2xax+bDifferentiating again w.r.t. x, we gety2=2y1+2a e2x⇒y2=2y1+2y1-2y ∵y1=2y+a e2x⇒y2=2y1+2y1-4y⇒y2=4y1-4y⇒y2-4y1+4y=0
Hence proved.
Q25.
Answer :
Here,
y= Ae-kt cospt+cDifferentiating w.r.t. t, we getdydt=-kAe-kt cospt+c-pAe-kt sinpt+c⇒dydt=-ky-pAe-kt sinpt+c …1Differentiating again w.r.t. t, we getd2ydt2= -kdydx+pkAe-kt sinpt+c-p2Ae-kt cospt+c⇒d2ydt2=-kdydx+pkAe-kt sinpt+c-p2y⇒d2ydt2=-kdydx+k-ky-dydx-p2y From 1⇒d2ydt2=-kdydx-k2y-kdydx-p2y⇒d2ydt2=-2kdydx-k2+p2y⇒d2ydt2+2kdydx+k2+p2y=0⇒d2ydt2+2kdydx+n2y=0 where n2=k2+p2
Hence proved.
Q26.
Answer :
Here,
y=ax+bcx+dDifferentiating w.r.t. x, we gety1=acx+ad-acx-bccx+d2 =ad-bccx+d2Differentiating again w.r.t. x, we gety2=-2(ad-bc)ccx+d3Differentiating again w.r.t. x, we gety3=6(ad-bc)c2cx+d4⇒y3=6(ad-bc)c2cx+d4×cx+d2cx+d2ad-bcad-bc⇒y3=3-2ad-bcccx+d32×12y1⇒2y1y3=3y22
Hence proved.
Page 12.13 Ex.12.1
Q27.
Answer :
Here,
x= sin1alogy⇒1alogy=sin-1x⇒y=ea sin-1xDifferentiating w.r.t. x, we gety1=ea sin-1x×a1-x2⇒y1=ay1-x2Differentiating again w.r.t. x, we gety2=ay11-x2+xay1-x21-x2⇒y2=ay11-x2+xay1-x21-x2⇒y2=ay11-x2+xay1-x21-x2⇒y2=a2y1-x2+xy11-x2⇒1-x2y2-xy1-a2y=0
Q28.
Answer :
Here,
logy= tan-1xDifferentiating w.r.t. x, we get1y×y1=11+x2⇒1+x2y1=y⇒1+x2y2+2xy1=y1⇒1+x2y2+2xy1-y1=0⇒1+x2y2+2x-1y1=0
Hence proved.
Q29.
Answer :
Here,
y= tan-1xDifferentiating w.r.t. x, we getdydx=11+x2Differentiating again w.r.t. x, we getd2ydx2=-2×1+x22⇒d2ydx2=-2×1+x2×11+x2⇒d2ydx2=-2xdydx1+x2⇒1+x2d2ydx2=-2xdydx⇒1+x2d2ydx2+2xdydx=0
Hence proved.
Q30.
Answer :
Here,
y=logx+x2+12Differentiating w.r.t. x, we getdydx=2logx+x2+1x+x2+1×1+2x2x2+1⇒dydx=2logx+x2+1x+x2+1×x2+1+xx2+1⇒dydx=2logx+x2+1×2+1Differentiating again w.r.t. x, we getd2ydx2=2-2xlogx+x2+1×2+1×2+1⇒d2ydx2=2-xdydxx2+1⇒x2+1d2ydx2=2-xdydx⇒x2+1d2ydx2+xdydx=2
Q31.
Answer :
Here,
y=tan-1x2Differentiating w.r.t. x, we gety1= 2 tan-1×1+x2Differentiating again w.r.t. x, we gety2=2-4x tan-1×1+x22⇒y2=21+x22-2 tan-1x ×2×1+x22⇒y2=21+x22-2xy11+x2⇒1+x22y2=2-2×1+x2y1⇒1+x22y2+2×1+x2y1=2
Hence proved.
Q32.
Answer :
Here,
y= cotxDifferentiating w.r.t. x, we getdydx=-cosec2xDifferentiating again w.r.t. x, we getd2ydx2=-2 cosecx ×- cosec x cotx⇒d2ydx2=2 cosec2x cotx⇒d2ydx2=-2ydydx⇒d2ydx2+2ydydx=0
Hence proved.
Q33.
Answer :
Here,
y=logx2e2Differentiating w.r.t. x, we getdydx=1x2e2×2xe2=2xDifferentiating again w.r.t. x, we getd2ydx2=-2×2
Q34.
Answer :
Here,
y= a e2x+b e-xDifferentiating w.r.t. x, we getdydx=2a e2x-b e-xDifferentiating again w.r.t. x, we getd2ydx2=4a e2x+b e-x⇒d2ydx2=2a e2x-b e-x+2a e2x+b e-x⇒d2ydx2=dydx+2y ⇒d2ydx2-dydx-2y=0
Hence proved.
Q35.
Answer :
Here,
y= exsinx+cosxDifferentiating w.r.t. x, we getdydx=exsinx+cosx+excosx-sinx =2 ex cosxDifferentiating w.r.t. x, we getd2ydx2=2ex cosx-2ex sinxNow, LHS=d2ydx2-2dydx+2y=2ex cosx-2ex sinx-4ex cosx+2 exsinx+cosx=0 = RHS
Hence proved.
Q36.
Answer :
Here,
y= cos-1x Differentiating w.r.t. x, we getdydx=-11-x2Differentiating again w.r.t. x, we getd2ydx2=-2×21-x23/2=-x1-x23/2Now,y = cos-1x⇒x= cosy⇒d2ydx2=-cosy1-cos2y3/2=-cosysin2y3/2= -coty cosec2y
Q37.
Answer :
Here,
y= ea cos-1xDifferentiating w.r.t. x, we getdydx= -ea cos-1x×a1-x2Differentiating again w.r.t. x, we getd2ydx2= ea cos-1x×a21-x2+2xa ea cos-1×21-x232⇒d2ydx2=ea cos-1x×a21-x2+xa ea cos-1×1-x21-x2⇒d2ydx2=y×a21-x2-xdydx1-x2⇒1-x2d2ydx2=a2y-xdydx⇒1-x2d2ydx2+xdydx-a2y=0
Hence proved.
Q38.
Answer :
Here,
y= 500 e7x+600 e-7xDifferentiating w.r.t. x, we getdydx=3500 e7x-4200 e-7x Differentiating again w.r.t. x, we getd2ydx2=24500 e7x+29400 e-7x =49500 e7x+600 e-7x = 49y
Q39.
Answer :
Here,
x= 2 cost -cos2t and y = 2 sint – sin2tDifferentiating w.r.t. t, we getdxdt=-2 sint+2 sin2t and dydt=2 cost-2 cos2t∴ dydx=2 cost-2 cos2t-2 sint+2 sin2t=cost- cos2t- sint+ sin2tDifferentiating w.r.t. x, we getd2ydx2=-sint+2 sin2t- sint+ sin2t- cost- cos2t- cost+2 cos2t- sint+ sin2t2dtdx =-sint+2 sin2t- sint+ sin2t- cost- cos2t- cost+2 cos2t- sint+ sin2t2-2 sint+2 sin2tAt t =π2:d2ydx2=-1+0- 1+0- 0+1- 0-2- 1+ 02-2 +0=1+2-2=-32
Q40.
Answer :
Here,
x= 4z2+5 and y= 6z2+7z+3Differentiating w.r.t. z, we getdxdz=8z and dydz=12z+7∴ dydx=12z+78zDifferentiating w.r.t. x, we getd2ydx2=12×8z-812z+764z2×dzdx =96z-96z-56512z3=-764z3
Q41.
Answer :
Here,
y=log1+cosxDifferentiating w.r.t. x, we getdydx=-sinx1+cosxDifferentiating again w.r.t. x, we getd2ydx2=-cosx-cos2x-sin2x1+cosx2=-cosx+11+cosx=-11+cosxDifferentiating again w.r.t. x, we getd3ydx3=-sinx1+cosx2⇒d3ydx3+sinx1+cosx2=0⇒d3ydx3+-11+cosx-sinx1+cosx=0⇒d3ydx3+d2ydx2×dydx=0
Q42.
Answer :
Here,
y = sinlogxDifferentiating w.r.t. x, we getdydx=coslogxxDifferentiating again w.r.t. x, we getd2ydx2=-sinlogx-coslogxx2⇒d2ydx2=-sinlogxx2-coslogxx2⇒d2ydx2=-yx2-1x×dydx⇒x2d2ydx2+xdydx+y=0
Q43.
Answer :
Here,
y=3e2x+2 e3xDifferentiating w.r.t. x, we getdydx=6 e2x+6 e3xDifferentiating again w.r.t. x, we getd2ydx2=12 e2x+18 e3x⇒d2ydx2=56 e2x+6 e3x-63e2x+2 e3x⇒d2ydx2=5dydx-6y⇒d2ydx2-5dydx+6y=0
Q44.
Answer :
Here,
y= cot-1x2Differentiating w.r.t. x, we gety1=2cot-1x×-11+x2=-2cot-1×1+x2Differentiating again w.r.t. x, we gety2=2+4xcot-1×1+x22⇒y2=21+x22+2x×2cot-1×1+x21+x2⇒y2=21+x22-2xy11+x2⇒1+x22y2=2-2xy11+x2⇒1+x22y2+2xy11+x2=2
Hence proved.
Q45.
Answer :
Here,
y= cosec-1 xDifferentiating w.r.t. x, we getdydx=-1xx2-1Differentiating again w.r.t. x, we getd2ydx2=x2-1+x2x2-1x2x2-1⇒d2ydx2=x2-1+x2x2x2-1×2-1⇒d2ydx2=2×2-1x2x2-1×2-1⇒d2ydx2=2×2-1×2-1-1x2x2-1×2-1⇒x2-1d2ydx2=2×2-1-1x2x2-1⇒x2-1d2ydx2=-2xdydx+1xdydx⇒xx2-1d2ydx2=-2×2-1dydx⇒xx2-1d2ydx2+2×2-1dydx=0
Hence proved.
Page 12.14 (Very Short Answers)
Q1.
Answer :
Here,
y= axn+1+ b x-n and x2d2ydx2=λ yNow,dydx=an+1 xn-bn x-n-1and d2ydx2=ann+1xn-1-bn-n-1 x-n-2Now, x2d2ydx2=λy Given⇒x2ann+1xn-1+bnn+1 x-n-2=λaxn+1+ b x-n⇒ann+1 xn+1+ bnn+1x-n=λaxn+1+ b x-n⇒nn+1axn+1+ b x-n=λaxn+1+ b x-n⇒λ=nn+1
Q2.
Answer :
Here,
x=a cos nt-b sin ntNow,dxdt=- an sin nt-bn cos nt d2xdt2=-an2 cos nt+bn2 sin ntAlso,d2xdt2 =λx Given⇒ -an2 cos nt+bn2 sin nt=λa cos nt-b sin nt⇒ -n2 a cos nt-b sin nt=λa cos nt-b sin nt⇒λ= -n2
Q3.
Answer :
Here,
x=t2 and y = t3⇒dxdt=2t and dydt=3t2∴ dydx=3t2⇒d2ydx2=32dtdx=34t
Q4.
Answer :
Here,
x= 2at and y =at2Differentiating w.r.t. t, we getdxdt=2a and dydt=2at∴dydx=2at2a=tDifferentiating again w.r.t. t, we getd2ydx2=1×dtdx=12aNow, d2ydx2x=12=12a
Q5.
Answer :
Here.
x = f(t) and y = g(t)
⇒dxdt=f’t and dydt=g’t∴dydx=g’tf’t
⇒d2ydx2=ddtg’tf’t×dtdx =f’tg”t-g’tf”tf’t2×1f’t =f’tg”t-g’tf”tf’t3
Q6.
Answer :
Here,
y=1-x+x22! -x33!+x44!+…∞Thus,⇒dydx=-1+2×2!-3×23!+4×34!…∞ =-1+x-x22!+x33!-…∞⇒d2ydx2=1-2×2!+3×23!-4×34!+ … ∞ =1-x+x22! -x33!+…∞ =y
Q7.
Answer :
Here,
y= x+ ex⇒dydx=1+ex⇒dxdy=11+ex⇒d2xdy2=-ex1+ex2dxdy=-ex1+ex3
Q8.
Answer :
Here,
y=x-x2 =x-x2 if 0<x<1-x+x2 if x>1,x<0⇒dydx=1-2x if 0<x<1-1+2x if x>1,x<0⇒d2ydx2=-2 if 0<x<12 if x>1,x<0
Q9.
Answer :
Here,
y=logex =-logex if 0<x<1 logex if x>1Differentiating w.r.t. x, we getdydx=-1x if 0<x<11x if x>1Differentiating again w.r.t. x, we getd2ydx2=1×2 if 0<x<1-1×2 if x>1
Page 12.14 (Multiple Choice Questions)
Q1.
Answer :
(b) −n2x
Here,
x=a cosnt-b sinntDifferentiating w.r.t. t, we getdxdt=-an sinnt-bn cosntDifferentiating again w.r.t. t, we getd2xdt2=-an2 cosnt+bn2 sinnt =-n2acosnt-b sinnt =-n2x
Q2.
Answer :
(d) -12at3
Here,
x=at2 and y=2atDifferentiating w.r.t. t, we getdxdt=2at and dydt=2a∴ dydx=2a2at=1tDifferentiating again w.r.t. t, we getd2ydx2=-1t2dtdx=-12at3
Q3.
Answer :
(b) n(n+1)y
Here,
y=axn+1+bx-n⇒dydx=an+1xn-bn x-n-1⇒d2ydx2=ann+1xn-1+bnn+1x-n-2∴ x2d2ydx2=x2ann+1xn-1+bnn+1x-n-2 =nn+1axn+1+b x-n =nn+1y
Q4.
Answer :
(b) 220(cos2x + 220cos4x)
Here,
y= 2cosx cos3x=cos3x-x+cos3x+x =cos2x+ cos4x⇒dydx=-2 sin2x-4 sin4x=-2sin2x+2 sin4x⇒d2ydx2=-4 cos2x -16 cos4x=-22cos2x+ 22cos4x⇒d3ydx3=23sin2x+23sin4x⇒d4ydx4=232cos2x+4×23cos4x=24cos2x+ 24cos4x∴ d20cos2x+ cos4xdx20=220cos2x+ 220cos4x
Page 12.15 (Multiple Choice Questions)
Q5.
Answer :
(b) 3/4t
Here,
x=t2 and y = t3⇒dxdt=2t and dydt=3t2∴ dydx=3t2⇒d2ydx2=32dtdx=34t
Q6.
Answer :
(b) xd2ydx2=y1
Here,
y= a+bx2⇒y1=2bx⇒y2=2bMultiplying by x on both sides we get, xy2=2bx=y1⇒xd2ydx2=y1
Q7.
Answer :
(c) -nn+122
Here,
fx=cosx+i sinxcos2x+i sin2x … cosnx+i sinnx⇒fx=cosx+i sinxcosx+i sinx2… cosx+i sinxn⇒fx=cosx+i sinx1+2+3………..n⇒fx=cosx+i sinxnn+12⇒fx=cosx+i sinxa where a=nn+12⇒fx=cosax+i sinax …1⇒f1=cosa+i sina⇒1=cosa+i sina …2 ∵f1=1Differentiating eqn.1, we get,f’x=a-sinax+i cosax⇒f”x=a2-cosax-i sinax⇒f”x=-a2cosax+i sinax⇒f”x=-nn+122cosax+i sinax⇒f”1=-nn+122cosa+i sina⇒f”1=-nn+122 Using 2
Q8.
Answer :
(a) −m2y
Here,
y= a sinmx+b cos mx⇒dydx=am cosmx-bm sinmx⇒d2ydx2=-am2 sinmx-bm2 cosmx =-m2a sinmx+b cos mx =-m2y
Q9.
Answer :
(a) 1
Here,
fx=sin-1x 1-x2⇒ 1-x2 fx=sin-1xDiffferentiating w.r.t. x, we get 1-x2f’x-x fx 1-x2=1 1-x2⇒1-x2f’x – xfx=1
DISCLAIMER : In the question instead of (1 − x)2 f ” (x) − xf(x)
it should be (1 − x)2 f ‘ (x) − xf(x)
Q10.
Answer :
(c) 0
y=tan-1 loge e/x2loge ex2+tan-1 3+2 loge x1-6 loge x⇒y=tan-1 1-2logex1+2logex+tan-1 3+2 loge x1-6 loge x⇒y=tan-1 1-2logex1+2logex+3+2 loge x1-6 loge x1-1-2logex1+2logex3+2 loge x1-6 loge x⇒y=tan-1 1-2logex1-6 loge x+3+2 loge x1+2logex1+2logex1-6 loge x-1-2logex3+2 loge x⇒y=tan-1 1-8logex+12logex2+3+8logex+4logex21-4logex-12logex2-3+4logex+4logex2⇒y=tan-1 1-8logex+12logex2+3+8logex+4logex21-4logex-12logex2-3+4logex+4logex2⇒y=tan-1 4+16logex2-2-8logex2⇒y=tan-1 41+4logex2-21+4logex2⇒y=tan-1 -2⇒dydx=0⇒d2ydx2=0
Q11.
Answer :
(a) f”(ex)e2x + f'(ex)ex
Since f(x) is a polynomial,
∴f’ex=f’ex ex⇒f”ex=f”ex (ex)2+f’ex ex =f”ex e2x+f’ex ex
Q12.
Answer :
(c) −y
Here,
y= a coslogex+b sinlogex⇒y1=-asinlogex1x+b coslogex1x⇒y2=-asinlogex+b coslogexx⇒y2=-acoslogex-b sinlogex–asinlogex+b coslogexx2⇒x2y2=-acoslogex+b sinlogex–asinlogex+b coslogex ⇒x2y2=-y-xy1 ⇒x2y2+xy1=-y
Q13.
Answer :
(a) 1/2a
Here,
x= 2at and y =at2Differentiating w.r.t. t, we getdxdt=2a and dydt=2at∴dydx=2at2a=tDifferentiating w.r.t. x, we getd2ydx2=1×dtdx=12aNow, d2ydx2x=12=12a
Q14.
Answer :
(a) f’ g”-g’f”f’3
Here,
x = f(t) and y = g(t)
⇒dxdt=f’t and dydt=g’t∴dydx=g’tf’t
⇒d2ydx2=ddtg’tf’t×dtdx =f’tg”t-g’tf”tf’t2×1f’t =f’tg”t-g’tf”tf’t3
Q15.
Answer :
(c)−m2y
Here,
y= sinmsin-1x⇒y1= cosmsin-1xm1-x2⇒y2=- sinmsin-1xm21-x2+mxcosmsin-1×1-x23/2⇒y2=- sinmsin-1xm21-x2+xmcosmsin-1×1-x2×1-x2⇒y2=- sinmsin-1xm21-x2+xy11-x2⇒1-x2y2=- ym2+xy1⇒1-x2y2-xy1=- m2y
Q16.
Answer :
(a) xy1 + 2
Here,
y=sin-1x2Now,y1=2 sin-1x 11-x2⇒y2=21-x2+2x sin-1×1-x23/2⇒y2=21-x2+2x sin-1×1-x21-x2⇒y2=21-x2+xy11-x2⇒y21-x2=2+xy1
Page 12.16 (Multiple Choice Questions)
Q17.
Answer :
(c) (1 + sin 2x)y1
Here,
y=etanx⇒y1=etanx sec2x⇒y2=etanx sec4x+ etanx ×2secx secx tanx⇒y2=sec2x etanxsec2x+ etanx ×2 tanx⇒cos2xy2=y1+ etanx ×y1sec2x2 tanx⇒cos2xy2=y1+y1×2 sinx cosx⇒cos2xy2=y11+sin2x
Q18.
Answer :
Disclaimer: The question given in the book is wrong.
Q19.
Answer :
(a) 3(xy2 + y1)y2
Here,
y=ax+bx2+c⇒x2+cy=ax+bDiffferentiating w.r.t. x, we get2xy+x2+cdydx=aDiffferentiating w.r.t. x, we get2y+2xy1+2xy1+x2+cy2=0⇒2y+4xy1+x2+cy2=0Diffferentiating again w.r.t. x, we get2y1+4y1+4xy2+x2+cy3+2xy2=0⇒6y1+6xy2+x2+cy3=0⇒6y1+6xy2+-2y-4xy1y2y3=0 ∵2y+4xy1+x2+cy2=0⇒6y1y2+6xy22-2y-4xy1y3=0⇒3y1y2+3xy22-y-2xy1y3=0⇒y1+xy23y2=2xy1+yy3
Q20.
Answer :
(a) (xy1 − y)2
Here,
y=logexa+bxx⇒y=x logexa+bx ⇒y1=logexa+bx+x×a+bxx1a+bx-bxa+bx2⇒y1=logexa+bx+aa+bx …1⇒y1=yx+aa+bx ∵y=x logexa+bx⇒xy1-yx=aa+bx …2Differentiating 1 we get,y2=a+bxxa+bx-bxa+bx2-baa+bx2⇒y2=axa+bx-baa+bx2⇒y2=aa+bx-abxx a+bx2⇒y2=a2x a+bx2⇒y2=xy1-y2x3 Using 2⇒x3 y2=xy1-y2
Q21.
Answer :
(c){f(t) + f”(t)}2
Here,
x= ftcost-f’t sint and y=ft sint+f’tcost⇒dxdt=f’tcost-ftsint-f”tsint-f’tcost and dydt=f’t sint+ftcost+f”tcost-f’t sint⇒dxdt=-ftsint-f”tsint and dydt=ftcost+f”tcostThus,dxdt2+dydt2=-ftsint-f”tsint2+ftcost+f”tcost2 =ftsint+f”tsint2+ftcost+f”tcost2 =sin2tft+f”t2+cos2tft+f”t2 =ft+f”t2sin2t+cos2t =ft+f”t2
Q22.
Answer :
c n2yy1n+y-1n=2xDifferentiating the above equation with respect to x1ny1n-1-1ny-1n-1y1=21nyy1n-y-1ny1=2y1n-y-1ny1=2ny …..1y1n-y-1ny2+y11ny1n-1+1ny-1n-1y1=2ny1nyy1n-y-1ny2+y12y1n+y-1n=2n2yy1Dividing the above equation by y1nyy1y1n-y-1ny2+y1y1n+y-1n=2n2yPutting y1 from equation 1y1n-y-1n22y2+y1y1n+y-1n=2n2y …..2Now,y1n-y-1n2=y1n+y-1n2-4y1n-y-1n2=4×2-4 …..3Putting the value of 3 in 24×2-1y22+2xy1=2n2yx2-1y2+xy1=n2y
Q23.
Answer :
(c) n!n-r!
According to the given equation,
ddxxn-a1 xn-1+a2 xn-2+…+-1n anex=xn ex⇒ddxxn-a1 xn-1+a2 xn-2+…+-1n anex=ddxxn-nxn-1+nn-1xn-2+…+-1n anexComparing the coefficients of the above equation we get,a1=na2=nn-1Similarly,ar=nn-1n-2n-3…n-r+1⇒ar=n!n-r!
Q24.
Answer :
(a) −(n − 1)2 y
Here,
y=xn-1 logx⇒y1=n-1xn-2 logx+xn-1x⇒y1=n-1xn-1 logx+xn-1x⇒xy1=n-1y+xn-1⇒xy2+y1=n-1y1+n-1xn-2⇒xy2+y1=n-1y1+n-1xn-1x⇒x2y2+xy1=xn-1y1+n-1xn-1⇒x2y2+xy1=xn-1y1+n-1xy1-n-1y⇒x2y2+xy1=xn-1y1+n-1xy1-n-12y⇒x2y2+xy1=2xn-1y1-n-12y⇒x2y2+xy1-2xn-1y1=-n-12y⇒x2y2+xy11-2n+2=-n-12y⇒x2y2+3-2nxy1=-n-12y
Q25.
Answer :
(c) 3
Here,
xy-logey=1⇒xy1+y-y1y=0⇒xyy1+y2-y1=0⇒yy1+xy1y1+xyy2+2yy1-y2=0⇒xy12+yy2-y2+3yy1=0∴ λ=3
Q26.
Answer :
(a) a constant
Here,
y2=ax2+bx+cNow,2ydydx=2ax+b⇒2yd2ydx2+2dydx2=2a ⇒yd2ydx2+dydx2=a ⇒yd2ydx2+2ax+b2y2=a ∵2ydydx=2ax+b⇒4y3d2ydx2+2ax+b2=4ay2⇒y3d2ydx2=4ay2-2ax+b24⇒y3d2ydx2=4aax2+bx+c-2ax+b24 ∵y2=ax2+bx+c⇒y3d2ydx2=4a2x2+4abx+4ac-4a2x2-b2-4axb4⇒y3d2ydx2=4ac-b24=a constant
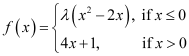
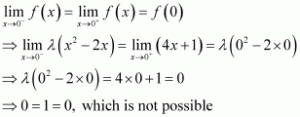
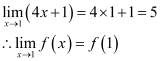
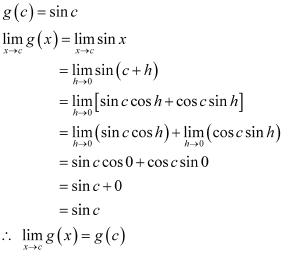
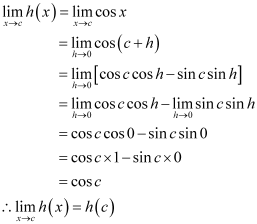
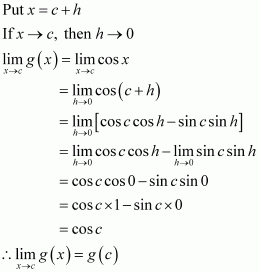
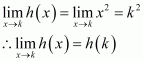
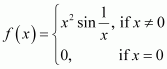
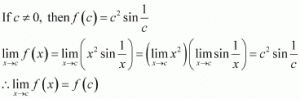
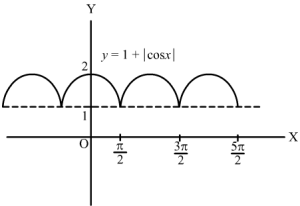

Leave a Reply