Page 13.3 Ex.13.1
Q1.
Answer :
Let T be the total surface area of a cylinder. Then,
T = 2πrr+h
Since the radius varies, we differentiate the total surface area w.r.t. radius r.
Now,
dTdr=ddr2πrr+h⇒dTdr=ddr2πr2+ddr2πrh⇒dTdr=4πr+2πh⇒dTdr=2πr+h
Q2.
Answer :
Let V and r be the volume and diameter of the sphere, respectively. Then,
V = 43πradius3
⇒V=43πr23=16πr3
⇒dVdr=12πr2
Q3.
Answer :
Let V be the volume of the sphere. Then,
V = 43πr3
⇒dVdr=4πr2
Let S be the total surface area of sphere. Then,
S = 4πr2
⇒dSdr=8πr
∴ dVdS=dVdrdSdr⇒dVdS=4πr28πr=r2⇒dVdSr=2 =22 =1 cm
Q4.
Answer :
Let A be the area of the circular disc. Then,
A = πr2
⇒dAdr=2πr
Let C be the circumference of the circular disc. Then,
C = 2πr
⇒dCdr=2π
∴ dAdC=dAdrdCdr⇒dAdC=2πr2π=r⇒dAdCr=3=3 cm
Q5.
Answer :
Let V be the volume of the cone. Then,
V = 13πr2h
⇒dVdr=23πrh
Q6.
Answer :
Let A be area of the circle. Then,
A = πr2
⇒dAdr=2πr
Hence, the rate of change of the area of the circle is 2πr.
When r = 5 cm,
dAdrr=5=2π5 =10π cm2/cm
Q7.
Answer :
Let V be the volume of the spherical ball. Then,
V = 43πr3
⇒dVdr=4πr2
Thus, the rate of change of the volume of the sphere is 4πr2.
When r=2 cm, dVdrr=2=4π22 =16π cm3/cm
Q8.
Answer :
Since the marginal cost is the rate of change of total cost with respect to its output,
Marginal Cost (MC) = dCdxx=ddx0.007×3-0.003×2+15x+4000=0.021×2-0.006x+15
When x = 17,
Marginal Cost (MC) = =0.021172-0.006(17)+15=6.069-0.102+15=Rs 20.967
Q9.
Answer :
Since the marginal revenue is the rate of change of total revenue with respect to its output,
Marginal Revenue (MR) = dRdxx=ddx13x2+26x+15=26x+26
When x = 7,
Marginal Revenue (MR)=26(7)+26=182+26=Rs 208
Page 13.14 Ex.13.2
Q1.
Answer :
Given: A=x2 and dxdt= 4 cm/min Let x be the side of the square and A be its area at any time t. Then,A=x2 ⇒dAdt=2xdxdt⇒dAdt=2×8×4 ∵ x=8 cm and dxdt=4 cm/min⇒dAdt=64 cm2/min
Q2.
Answer :
Let x be the side and V be the volume of the cube at any time t. Then, V=x3⇒dVdt=3x2dxdt⇒dVdt=3×102×3 ∵ x=10 cm and dxdt=3 cm/sec⇒dVdt=900 cm3/sec
Q3.
Answer :
Let x be the side and P be the perimeter of the square at any time t. Then, P=4x⇒dPdt=4dxdt⇒dPdt=4×0.2 ∵ dxdt= 0.2 cm/sec⇒dPdt=0.8 cm/sec
Q4.
Answer :
Let r be the radius and C be the circumference of the circle at any time t. Then, C=2πr⇒dCdt=2πdrdt⇒dCdt=2π×0.7 ∵ drdt=0.7 cm/sec⇒dCdt=1.4π cm/sec
Q5.
Answer :
Let r be the radius and S be the surface area of the spherical ball at any time t. Then, S=4πr2⇒dSdt=8πrdrdt⇒dSdt=8π×7×0.2 ∵ r=7 cm and drdt=0.2 cm/sec⇒dSdt=11.2π cm2/sec
Page 13.15 Ex.13.2
Q6.
Answer :
Let r be the radius and V be the volume of the spherical balloon at any time t. Then, V=43πr3⇒ dVdt=4πr2drdt⇒drdt=14πr2dVdt⇒drdt=9004π152 ∵ r=15 cm and dVdt=900 cm3/sec⇒drdt=900900π⇒drdt=1πcm/sec
Q7.
Answer :
Let r be the radius and V be the volume of the air bubble at any time t. Then,V=43πr3⇒ dVdt=4πr2drdt⇒dVdt=4π12× 0.5 ∵ r=1 cm and drdt=0.5 cm/sec⇒dVdt=2π cm3/sec
Q8.
Answer :
Let AB be the lamp post. Suppose at any time t, the man CD be at a distance of x km from the lamp post and y m be the length of his shadow CE.
Since triangles ABE and CDE are similar,ABCD=AECE⇒62=x+yy⇒3y=x+y⇒x=2y⇒dxdt=2dydt⇒dydt=12dxdt⇒dydt=125 dxdt=5⇒dydt=52 km/hr
Q9.
Answer :
Let r be the radius and A be the area of the circle at any time t. Then, A=πr2⇒dAdt=2πrdrdt⇒dAdt=2π×4×10 ∵ r=4 cm and drdt=10 cm/sec⇒dAdt=80π cm2/sec
Q10.
Answer :
Let AB be the lamp post. Suppose at any time t, the man CD is at a distance of x km from the lamp post and y m is the length of his shadow CE.
Since triangles ABE and CDE are similar,ABCD=AECE⇒61.6=x+yy⇒xy=61.6-1⇒xy=4.41.6⇒y=1644x⇒dydt=1644dxdt⇒dydt=1644×1.1 ∵dxdt=1.1⇒dydt=0.4 m/sec
Q11.
Answer :
Let AB be the lamp post. Suppose at any time t, the man CD is at a distance x km from the lamp post and y m is the length of his shadow CE.
Since triangles ABE and CDE are similar,ABCD=AECE
⇒91.8=x+yy⇒xy=91.8-1⇒xy=7.21.8⇒x=4y⇒dydt=14dxdt⇒dydt=14×2 ∵dxdt=2⇒dydt=0.5 m/sec
Q12.
Answer :
Let the bottom of the ladder be at a distance of x m from the wall and its top be at a height of y m from the ground.
Then,
tan θ=yx and x2+y2=132 ⇒x21+tan2 θ=169⇒sec2 θ=169×2⇒2sec2 θ tan θdθdt=169 -2x3dxdt⇒dθdt=-338×1.51232sec2 θ tan θ …1When x=12, y=169-144=5 mSo, sec θ=1312 and tan θ=125From eq. 1, we getdθdt=-338×1.5123×2×13122 ×512=-338×1.510×169=-0.3 rad/sec
Q13.
Answer :
Here, y=x2+2x⇒dydt=2x+2dxdt⇒2x+2=1 ∵dydt=dxdt⇒2x=-1⇒x=-12Substituting x=-12 in y=x2+2x, we gety=-34Hence, the coordinates of the point are -12,-34.
Q14.
Answer :
Here,y=7x-x3⇒dydx=7x-x3Let s be the slope. Then,s=7-3×2⇒dsdt=-6xdxdt⇒dsdt=-642 ∵ x=2 and dxdt=4 units/sec⇒dsdt=-48
Q15.
Answer :
According to the question,dydt=3dxdtNow, y=x3⇒dydt=3x2dxdt⇒3dxdt=3x2dxdt⇒x2=1⇒x=±1Substituting x=±1 in y=x3, we gety=±1So the points are 1, 1 and -1, -1.
Q16.
Answer :
According to the question,dθdt=2ddtsin θ⇒dθdt=2cos θdθdt⇒2cos θ=1⇒cos θ=12⇒θ=π3
Q17.
Answer :
Let the bottom of the ladder be at a distance of x m from the wall and its top be at a height of y m from the ground.
Here,
x2+y2=36⇒2xdxdt=-2ydydt …1When x=4, y=36-16=25⇒2×4×0.5=-2×25dydt ∵ dxdt=0.5 m/sec⇒dydt=-15m/secFrom eq. (1), we get2xdxdt=-2ydydt ∵ dxdt=dydt ⇒ x=-ySubstituting x=-y in x2+y2=36, we get x2+x2=36⇒x2=18⇒x=32 m
Q18.
Answer :
Let r be the radius of the hemisphere, h be the height and V be the volume of the cone.
Then,H=h+r ⇒H=3r ∵ h=2r ⇒dHdt=3drdtWhen H=9 cm, r=3 cmVolume = 13πr2h+23πr3Substituting h=2r⇒V=23πr3 +23πr3⇒V=43πr3⇒dVdt=4πr2drdt⇒dVdt=4πr23dHdt⇒dVdH=4π323⇒dVdH=12π cm3/sec
Q19.
Answer :
Let r be the radius, h be the height and V be the volume of the cone at any time t.
Then,V=13πr2h⇒dVdt=13πr2dhdt+23πrhdrdtNow, hr=105 or r=h2 anddhdt=2drdt⇒dVdt=13πh22dhdt+23πh2h12dhdt⇒dVdt=π3h24dhdt+h22dhdt⇒dVdt=π3×3h2dh4dt⇒dVdt=πh24dhdt⇒πh24dhdt=π⇒dhdt=4h2⇒dhdt=42.52⇒dhdt=0.64 m/min
Q20.
Answer :
Let AB be the lamp post. Let at any time t, the man CD be at a distance of x km from the lamp post and y m be the length of his shadow CE.
Since triangles ABE and CDE are similar,ABCD=AECE
⇒62=x+yy⇒xy=62-1=2⇒dydt=12dxdt⇒dydt=126⇒dydt=3 km/hr
Q21.
Answer :
Let r be the radius, S be the surface area and V be the volume of the sphere at any time t. Then,S=4πr2⇒dSdt=8πrdrdt⇒drdt=18πrdSdt⇒drdt=28π×6⇒drdt=124π cm/secNow, Volume of sphere=43πr3⇒dVdt=4πr2drdt⇒dVdt=4π6224π⇒dVdt=6 cm3/sec
Q22.
Answer :
Let r be the radius, h be the height and V be the volume of the cylinder at any time t. Then, V=πr2h⇒dVdt=2πrhdrdt+πr2dhdt⇒dVdt=πr2hdrdt+rdhdt⇒dVdt=π×32×5×2+3×-3⇒dVdt=3π20-9⇒dVdt=33π cm3/sec
Page 13.16 Ex.13.2
Q23.
Answer :
Let r1 be the inner radius and r2 be the outer radius and V be the volume of the hollow sphere at any time t. Then,V=43πr13-r23⇒dVdt=4πr12dr1dt-r22dr2dt⇒ r12dr1dt=r22dr2dt ∵dVdt=0⇒42×1=82dr2dt⇒dr2dt=14 cm/sec
Q24.
Answer :
Let r be the radius, h be the height and V be the volume of the conical pile at any time t. Then,V=13πr2h⇒V=13π2h2h ∵ h=r2⇒V=43πh3⇒dVdt=4πh2dhdt⇒50=4πh2dhdt⇒dhdt=504π52⇒dhdt=12π cm/min
Q25.
Answer :
In the right triangle ABC,
Here,AB2+BC2=AC2⇒x2+1202=y2 ⇒2xdxdt=2ydydt⇒dydt=xydxdt⇒dydt=50130×52 ∵ x=1302-1202=50⇒dydt=20 m/sec
Q26.
Answer :
Here, y=23×3+1⇒dydt=2x2dxdt⇒2dxdt=2x2dxdt ∵ dydt=2dxdt⇒x=±1Substituting the value of x=1 and x=-1 in y=23×3+1, we get⇒y=53 and y=13So, the points are 1,53 and -1,13.
Q27.
Answer :
Here, y2=8x …1⇒2ydydt=8dxdt⇒2y=8 ∵ dydt=dxdt⇒y=4⇒x=y28 From eq. 1⇒x=168=2So, the point is 2,4.
Q28.
Answer :
Let x be the side and V be the volume of the cube at any time t. Then,V=x3⇒dVdt=3x2dxdt⇒9=3102dxdt ∵ x=10 cm and dVdt=cm3/sec⇒dxdt=0.03 cm/secLet S be the surface area of the cube at any time t. Then, S=6×2⇒dSdt=12xdxdt⇒dSdt=12×10×0.03 ∵ x=10 cm and dxdt= 0.03 cm/sec⇒dSdt=3.6 cm2/sec
Q29.
Answer :
Let r be the radius and V be the volume of the sphere at any time t. Then, V=43πr3⇒dVdt=4πr2drdt⇒drdt=14πr2dVdt⇒drdt=254π52 ∵ r=5 cm anddVdt=25 cm3/sec⇒drdt=14πcm/secNow, let S be the surface area of the sphere at any time t. Then, S= 4πr2⇒dSdt=8πrdrdt⇒dSdt=8π5×14π ∵ r=5 cm anddrdt=14π cm/sec⇒dSdt=10 cm2/sec
Q30.
Answer :
i Let P be the perimeter of the rectangle at any time t. Then,P=2x+y⇒dPdt=2dxdt+dydt⇒dPdt=2-5+4 ∵ dxdt=-5 cm/min and dydt=4 cm/min⇒dPdt=-2 cm/minii Let A be the area of the rectangle at any time t. Then,A=xy⇒dAdt=xdydt+ydxdt⇒dAdt=84+6-5 ∵ x=8 cm, y=6 cmdxdt=-5 cm/min and dydt=4 cm/min⇒dAdt=32-30⇒dAdt=2 cm2/min
Q31.
Answer :
Let r be the radius and A be the area of the circular disc at any time t. Then, A=πr2⇒dAdt=2πrdrdt⇒dAdt=2π×3.2×0.05 ∵ r=3.2 cm and drdt=0.05 cm/sec⇒dAdt=0.32π cm2/sec
Q32.
Answer :
Distance PQ is given as x=t22-t3⇒x=2t2-t33⇒dxdt=4t-t2⇒dxdt=t4-tNow, the car stops at point Q so, speed of the car at point Q is 0.⇒t4-t=0⇒t=0, t=4So, the car takes 4s to reach point Q.Now, Distance covered by car i.e. PQ=x = t22-t3⇒x=422-43⇒x=16×23⇒x=323m
Page 13.19 (Very Short Answers)
Q1.
Answer :
s=t3-6t2+9t+8⇒dsdt=3t2-12t+9Initial velocity=Velocity at t=0⇒dsdt=302-120+9⇒dsdt=9 units/unit time
Q2.
Answer :
Let r be the radius and V be the volume of the sphere at any time t. Then,V=43πr3⇒dVdt=4πr2drdt⇒drdt=14πr2dVdt⇒drdt=34π22 ∵ r=2 cm and dVdt=3 cm3/sec⇒drdt=316π cm/sec
Q3.
Answer :
Let x be the side and A be the area of the equilateral triangle at any time t. Then, A=34×2⇒dAdt=2×34xdxdt⇒dAdt=32×2×10⇒dAdt=103 cm2/sec
Q4.
Answer :
Let x be the side and P be the perimeter of the square at any time t. Then, P=4x⇒dPdt=4dxdt⇒dPdt=4×0.1 ∵ dxdt=0.1 cm/sec⇒dPdt=0.4 cm/sec
Q5.
Answer :
Let r be the radius and C be the circumference of the circle at any time t. Then, C=2πr⇒dCdt=2πdrdt⇒dCdt=2π×0.5 ∵ drdt=0.5 cm/sec ⇒dCdt=π cm/sec
Q6.
Answer :
Let x be the side and P be the perimeter of the equilateral triangle at any time t. Then, P=3x⇒dPdt=3dxdt⇒dPdt=3×13 ∵ dxdt=13cm/sec⇒dPdt=1 cm/sec
Q7.
Answer :
Let r be the radius and V be the volume of the sphere at any time t. Then,V=43πr3⇒dVdt=4πr2drdt⇒dVdt=4πr2dVdt ∵dVdt=drdt⇒4πr2=1 ⇒Surface area of sphere =1 square unit
Q8.
Answer :
Let r be the radius and V be the volume of the sphere at any time t. Then,V=43πr3⇒dVdt=4πr2drdt⇒4πr2=1 ∵dVdt=drdt⇒r2=14π⇒r=14π⇒r=12π units
Page 13.19 (Multiple Choice Questions)
Q1.
Answer :
(b) 4π
Given: V=43πr3, r=10 and drdt=0.01⇒dVdt=4πr2drdt⇒dVdt=4π102×0.01⇒dVdt=4π
Q2.
Answer :
(b) 4π
Given: V=43πr3, r=10 and drdt=0.01⇒dVdt=4πr2drdt⇒dVdt=4π102×0.01⇒dVdt=4π
Page 13.20 (Multiple Choice Questions)
Q3.
Answer :
(c) 160π cm2/sec
Let r be the radius and S be the surface area of the sphere at any time t. Then,S=4πr2⇒dSdt=8πrdrdt⇒dSdt=8π2000.1⇒dSdt=160π cm2/sec
Q4.
Answer :
(d) 0.002 cm/sec
Let r be the radius, h be the height and V be the volume of the cone at any time t. Then,V=13πr2h⇒V=23πr3 ∵ h=2r⇒dV dt=2×104drdt ∵πr2=1 m2 or 104 cm2 ⇒dr dt=12×104dV dt⇒dr dt=402×104⇒dr dt=0.002 cm/sec
Q5.
Answer :
(a) 1 m/minute
Let r be the radius, h be the height and V be the volume of the cylindrical vessel at any time t. Then, V=πr2h⇒dV dt=πr2dhdt⇒dh dt=1πr2dV dt⇒dh dt=0.25ππ0.52⇒dh dt=0.250.25⇒dh dt=1 m/min
Q6.
Answer :
(b) −42
x=t3-12t2+6t+8⇒dx dt=3t2-24t+6⇒d2x dt2=6t-24⇒6t-24=0 ∵acceleration is zero⇒t=4So, Velocity at t=4⇒dx dt=342-24×4+6⇒dx dt=48-96+6⇒dx dt=-42
Q7.
Answer :
(b) 1603 cm/sec
Let r be the radius, h be the height and α be the semi-vertical angle of the cone.
Then,tan α=rh⇒sec2αdαdt=drh dt⇒dr dt=h×sec2αdαdt⇒dr dt=20×sec230×2 ∵ h=20 cm, α=30° and dαdt=2° per second⇒dr dt=40×232⇒dr dt=1603 cm/sec
Q8.
Answer :
(d) 3, 13
Let y=x3-5×2+5x+8⇒dydt=3×2-10x+5dxdtAccording to the question,⇒2dxdt=3×2-10x+5dxdt⇒3×2-10x+5=2⇒3×2-10x+3=0⇒3×2-9x-x+3=0⇒3xx-3-1x-3=0⇒x-3=0 or 3x-1=0⇒x=3 or x=13
Q9.
Answer :
(a) (3, 16/3)
According to the question,dydt=-dxdt16x2+9y2=400⇒32xdxdt+18ydydt=0⇒32xdxdt=-18ydydt⇒32x=18y⇒x=9y16 …1Now,169y162+9y2=400⇒81y216+9y2=400⇒81y2+144y2=6400⇒225y2=6400⇒y2=6400225⇒y=6400225⇒y=163 or -163So,x=916×163 Using 1 orx=-916×163⇒x=3 or -3So, the required point is 3,163.
Q10.
Answer :
Let r be the radius, h be the height and S be the lateral surface area of the cone at any time t.
Given: drdt=3 cm/min and dhdt=-4 cm/minHere,l2=h2+r2⇒l=242+72⇒l=625⇒l=25S=πrl⇒S2=πrl2⇒S2=π2r2h2+r2⇒S2=π2r4+π2h2r2⇒2SdSdt=4π2r3drdt+2π2r2hdhdt+2π2h2rdrdt⇒2πrldSdt=2π2rh2r2hdrdt +rdhdt+hdrdt⇒25dSdt=24π27224×3 -7×4+24×3 Given: r=7, h=24⇒25dSdt=24π494-28+72⇒25dSdt=24π49+288-1124⇒dSdt=24π225100⇒dSdt=24π2.25⇒dSdt=54π cm2/sec
Q11.
Answer :
(b) 180π cm3/sec
Let r be the radius and V be the volume of the sphere at any time t. Then,V=43πr3⇒dVdt=4πr2drdt⇒dVdt=4π152×0.2⇒dVdt=180π cm3/sec
Q12.
Answer :
(b) 316πcm/sec
Let r be the radius and V be the volume of the sphere at any time t. Then,V=43πr3⇒dVdt=4πr2drdt⇒drdt=14πr2dVdt⇒drdt=34π22⇒drdt=316π cm/sec
Q13.
Answer :
(a) 9 sec
s=45t+11t2-t3⇒dsdt=45+22t-3t2According to the question,3t2-22t-45=0⇒3t2-27t+5t-45=0⇒3tt-9+5t-9=0⇒t-93t +5=0⇒t-9=0 or 3t +5=0As time can’t be negative, t=9 sec
Page 13.21 (Multiple Choice Questions)
Q14.
Answer :
(c) 1/36
Let r be the radius and V be the volume of the sphere at any time t. Then,V=43πr3⇒43πr3=288π⇒r3=288×34⇒r3=216⇒r=6⇒dVdt=4πr2drdt⇒dVdt=4π62drdt ⇒4π=144πdrdt⇒drdt=136
Q15.
Answer :
(d) 12π unit
Let r be the radius and V be the volume of the sphere at any time t. Then,V=43πr3⇒dVdt=433πr2drdt⇒dVdt=4πr2drdt⇒4πr2=1 ∵ dVdt=drdt⇒r2=14π⇒r=14π⇒r=12π unit
Q16.
Answer :
(b) 1π unit
Let r be the radius and Abe the area of the circle at any time t. Then,A = πr2 ⇒A=πD24 ∵ r=D2⇒dAdt=πD2dDdt⇒dDdt=πD2dDdt ∵ dAdt=dDdt⇒D2=1π⇒r=1π units
Q17.
Answer :
(a) 83 cm2/hr
Let x be the side and A be the area of the equilateral triangle at any time t. Then,A=34×2⇒dAdt=32xdxdt⇒dAdt=3228⇒dAdt=83 cm2/hr
Q18.
Answer :
(d) -163 unit/sec
According to the question,s=t3-4t2+5⇒dsdt=3t2-8t⇒d2sdt2=6t-8⇒6t-8=0 As velocity deminishes, thend2sdt2=0 ⇒t=43Now, dsdtt=43=3432-843⇒dsdt=163-323⇒dsdt=-163unit/sec
Q19.
Answer :
(b) π3+3 m/sec
According to the question,s=2t2+sin 2t⇒dsdt=4t+2 cos 2t⇒d2sdt2=4-4 sin 2t⇒4-4 sin 2t=2⇒4 sin 2t=2⇒sin 2t=12⇒2t=π6Now, dsdt=4π12+2 cosπ6⇒ds dt=π3+3 m/sec
Q20.
Answer :
(b) π3+3 m/sec
According to the question,s=2t2+sin 2t⇒dsdt=4t+2 cos 2t⇒d2sdt2=4-4 sin 2t⇒4-4 sin 2t=2⇒4 sin 2t=2⇒sin 2t=12⇒2t=π6Now, dsdt=4π12+2 cosπ6⇒ds dt=π3+3 m/sec
Q21.
Answer :
(c) π2 cm2/sec
Let D be the diameter and A be the area of the circle at any time t. Then,A=πr2 where r is the radius of the cicle⇒A=πD24 ∵ r=D2⇒dAdt=2πD4dDdt⇒dAdt=π2×2π ×1 ∵ dDdt=1 cm/sec⇒dAdt=π2 cm2/sec
Q22.
Answer :
Let AB be the lamp post. Suppose at any time t, the man CD be at a distance of x km from the lamp post and y m be the length of his shadow CE.
Since triangles ABE and CDE are similar,ABCD=AECE
⇒52=x+yy⇒xy=52-1⇒xy=32⇒y=23x⇒dydt=23dxdt⇒dydt=23×4.8⇒dy dt=3.2 km/hr
Q23.
Answer :
(c) 6 ft/sec
Let AB be the lamp post. Suppose at any time t, the man CD be at a distance of x km from the lamp post and y ft be the length of his shadow CE.
Since the triangles ABE and CDE are similar,ABCD=AECE
⇒156=x+yy⇒xy=156-1⇒xy=32⇒y=23x⇒dydt=23dxdt⇒dydt=23×9⇒dydt=6 ft/sec
Page 13.22 (Multiple Choice Questions)
Q24.
Answer :
(c) surface area times the rate of change of radius
Let r be the radius and V be the volume of sphere at any time t. Then,V=43πr3⇒dVdt=433πr2drdt⇒dVdt=4πr2drdtThus, the rate of change of volume is surface area times the rate of change of the radius.
Q25.
Answer :
(d) 8π times the rate of change of radius
Let r be the radius and S be the surface area of the sphere at any time t. Then,S=4πr2⇒dSdt=8πrdrdt∴ The rate of change of surface area is 8π times the rate of change of the radius.
Q26.
Answer :
(a) 1 m/hr
Let r, h and V be the radius, height and volume of the cylinder at any time t. Then, V=πr2h⇒dVdt=πr2dhdt⇒314=3.14 × 102dhdt⇒dhdt=314314⇒dhdt=1 m/hr
Page 14.9 Ex.14.1
Q1.
Answer :
Let: x=π2 x+△x=2214⇒dx=△x=2214-π2=0Now, y=sin x⇒dydx=cos x⇒dydxx=π2= cosπ2=0∴∆y=dydx∆x= 0×0=0⇒△y=0
Hence, there is no change in the value of y.
Q2.
Answer :
Let r be the radius of the sphere. r= 10 cmr+∆r=9.8 cm⇒∆r=10.0-9.8=0.2 cmVolume of the sphere, V=43πr3⇒dVdr=43π×3r2=4πr2⇒dVdrr=10 cm=4π102=400π cm3/cmChange in the volume of the sphere, ∆V=dVdr×dr=400π×0.2=80π cm3
Q3.
Answer :
Let at any time, x be the radius and y be the area of the plate.
Then, y=x2Let ∆x be the change in the radius and △y be the change in the area of the plate. We have∆xx×100=kWhen x=10, we get∆x=10k100=k10Now, y=πx2⇒dydx=2πx⇒dydxx=10 cm=20π cm2/cm∴∆y=dy=dydxdx=20π×k10=2kπ cm2
Hence, the approximate change in the area of the plate is 2kπ cm2 .
Q4.
Answer :
Let x be the edge of the cube and y be the surface area.
y=x2Let ∆x be the error in x and ∆y be the corresponding error in y.We have∆xx×100=1⇒2x=x100 Let dx=∆xNow, y=x2⇒dydx=2x∴ ∆y=dydx×∆x=2x × x100⇒∆y=2×2100⇒∆y=2y100⇒∆yy=2100⇒∆yy×100=2
Hence, the percentage error in calculating the surface area is 2.
Q5.
Answer :
Let x be the radius and y be the volume of the sphere.
y=43πx3Let ∆x be the error in the radius and ∆y be the error in the volume.Then, ∆xx×100=0.1⇒dxx=11000Now, y=43πx3⇒dydx=4πx2⇒dy=4πx2 dx⇒dyy=4πx2 dx43πx3=3xdx⇒dyy=31000⇒∆yy×100=0.3
Hence, the percentage error in the calculation of the volume of the sphere is 0.3.
Q6.
Answer :
We havepv1.4= constant= k sayTaking log on both the sides, we getlog pv1.4=log k⇒log p+1.4 log v= log kDifferentiating both the sides w.r.t. x, we get1pdpdv+1.4v=0⇒dpp=-1.4 dvvNow, dp=dpdvdv=-1.4pvdv⇒dpp×100=-1.4dvv×100 =-1.4×-12=0.7 Since we are given 12% decrease in vHence, the error in pis 0.7%.
Q7.
Answer :
Let h be the height, y be the surface area, V be the volume, l be the slant height and r be the radius of the cone.
Let ∆h be the change in the height, ∆r be the change in the radius of base and ∆l be the change in the slant height.Semi-vertical angle ramaining the same.∴ ∆hh=∆rr=∆llAlso, ∆hh×100=kThen, ∆hh×100=∆rr×100=∆ll×100=k …1i Total surface area of the cone, T=πrl+πr2Differentiating both sides w.r.t. r, we getdTdr=πl+πrdldr+2πr⇒dTdr=πl+πrlr+2πr From 1, dldr=∆l∆r=lr ⇒dTdr=πl+πl+2πr ⇒dTdr=2πl+r∴ ∆T=dTdr∆r=2πl+r×kr100=2krπl+r100∴ ∆TT×100=2krπl+r1002πrl+r×100=2k %Hence, the percentage increase in total surface area of cone is 2k.ii Volume of cone, V=13πr2hDifferentiating both sides w.r.t. h, we getdVdh=13πr2+13πh2rdrdh⇒dVdh=13πr2+13πh2rrh From 1, drdh=∆r∆h=rh⇒dVdh=13πr2+23πr2⇒dVdh=πr2∴ ∆V=dVdhdh=πr2×kh100=kπr2h100∴ ∆VV×100=kπr2h10013πr2h×100=3k %Hence, the percentage increase in the volume of the cone is 3k.
Page 14.10 Ex.14.1
Q8.
Answer :
Let x be the radius of the sphere and y be its volume.
Let ∆x be the error in the radius and ∆V be the approximate error in the volume.y=43πx3⇒dydx=4πx2⇒∆y=dy=dydxdx=4πx2×∆x⇒∆y=3×43πx3×∆xx⇒∆y=3×y×∆xx⇒∆yy=3∆xx
Hence proved.
Q9.
Answer :
(i)
Consider the function y=fx=x.Let: x =25 x+∆x=25.02Then,∆x=0.02For x=25, y=25=5Let: dx=∆x=0.02Now, y=x⇒dydx=12x⇒dydxx=25=110∴ ∆y=dy=dydxdx=110×0.02=0.002⇒∆y=0.002∴ 25.02=y+∆y=5.002
(ii)
Consider the function y=fx=x3.Let: x =0.008x+∆x=0.009Then, ∆x=0.001For x=0.008, y=0.008=0.2Let: dx=∆x=0.001Now, y=x3⇒dydx=13×23⇒dydxx=0.008=13×0.04=10.12∴∆y=dy=dydxdx=10.12×0.001=1120⇒∆y=1120=0.008333∴ 0.00913=y+∆y=0.208333
(iii)
Consider the function y=fx=x.3Let: x =0.008 x+∆x=0.007Then, ∆x=-0.001For x=0.008, y=0.008=0.2Let: dx=∆x=-0.001Now, y=x3⇒dydx=13×23⇒dydxx=0.008=13×0.04=10.12∴ ∆y=dy=dydxdx=10.12×0.001=1120⇒∆y=1120=0.008333∴ 0.00713=y+∆y=0.191667
(iv).
Consider the function y=fx=x.Let: x =400 x+∆x=401Then, ∆x=1For x=400, y=400=20Let: dx=∆x=1Now, y=x⇒dydx=12x⇒dydxx=400=140∴ ∆y=dy=dydxdx=140×1=140⇒∆y=140=0.025∴ 401=y+∆y=20.025
(v)
Consider the function y=fx=x14.Let: x =16 x+∆x=15Then, ∆x=-1For x=16, y=1614=2Let: dx=∆x=-1Now, y=x14⇒dydx=14×34⇒dydxx=16=132∴ ∆y=dy=dydxdx=132×-1=-132⇒∆y=-132=-0.03125∴ 1514=y+∆y=1.96875
(vi)
Consider the function y=fx=x14.Let: x =256x+∆x=255Then, ∆x=-1For x=256, y=25614=4Let: dx=∆x=-1Now, y=x14⇒dydx=14×34⇒dydxx=256=1256∴∆y=dy=dydxdx=1256×-1=-1256⇒∆y=-1256=-0.003906∴ 25514=y+∆y=3.99609≈3.9961
(vii)
Consider the function y=fx=1×2.Let: x =2 x+∆x=2.002Then, ∆x=-0.002For x=2 , y=122=14Let: dx=∆x=0.002Now, y=1×2⇒dydx=2×3⇒dydxx=2=14∴ ∆y=dy=dydxdx=14×-0.002=-0.0005⇒∆y=-0.0005∴ 12.0022=y+∆y=0.2495
(viii)
Consider the function y=fx= logex.Let: x = 4 x+∆x= 4.04Then, ∆x=0.04For x=4, y=loge4=log104log10e=0.60210.4343=1.386368Let: dx=∆x=0.04Now, y=logex⇒dydx=1x⇒dydxx= 4=14∴ ∆y=dy=dydxdx=14×0.04=0.01⇒∆y=0.01∴ loge4.04=y+∆y=1.396368
(ix)
Consider the function y=fx=logex.Let: x =10 x+∆x=10.02Then, ∆x=0.02For x= , y=loge10=2.3026Let: dx=∆x=0.02Now, y=logex⇒dydx=1x⇒dydxx=10=110∴ ∆y=dy=dydxdx=110×0.02=0.002⇒∆y=0.002∴ loge10.02=y+∆y=2.3046
(x)
Consider the function y=fx=log10x.Let: x =10 x+∆x=10.1Then, ∆x=0.1For x= , y=log1010=1Let: dx=∆x=0.1Now, y=log10x=logexloge10⇒dydx=12.3025x⇒dydxx=10=0.04343∴ ∆y=dy=dydxdx=0.04343×0.1=0.004343⇒∆y=0.004343∴ log1010.1=y+∆y=1.004343
(xi)
Consider the function y=fx=cos x°.Let: x =60° x+∆x=61°Then, ∆x=1°=0.01745For x=60°, y=cos 60°=0.5Let: dx=∆x=0.01745Now, y=cos x⇒dydx=-sin x⇒dydxx=60=-0.86603∴ ∆y=dy=dydxdx=-0.86603×0.01745=-0.01511⇒∆y=-0.01511∴ cos 61°=y+∆y=0.48488≈0.48489
(xii)
Consider the function y=fx=1x.Let: x =25 x+∆x=25.1Then, ∆x=0.1For x= , y=125=0.2Let: dx=∆x=0.1Now, y=1x⇒dydx=-12×32⇒dydxx=25=-0.004∴ ∆y=dy=dydxdx=-0.004×0.1=-0.0004⇒∆y=-0.0004∴ 125.1=y+∆y=0.1996
(xiii)
Consider the function y=fx=sin x.Let: x =227 x+∆x=2214Then, ∆x=-2214For x=π, y=sin 227=0Let: dx=∆x=sin -2214=-sin π2=-1Now, y=sin x⇒dydx=cos x⇒dydxx=227=-1∴ ∆y=dy=dydxdx=-1×-1=1⇒∆y=1∴ sin 2214=y+∆y=1
(xiv)
Consider the function y=fx=cos x.Let: x =π3 x+∆x=11π36Then, ∆x=-π36=-5°For x=π3, y=cos π3=0.5Let: dx=∆x=-sin 5°=-0.08716Now, y=cos x⇒dydx=-sin x⇒dydxx=π3=-0.86603∴ ∆y=dy=dydxdx=-0.86603×-0.08716=0.075575⇒∆y=0.075575∴ cos11π36=y+∆y=0.5+0.075575=0.575575
(xv)
Consider the function y=fx=x14.Let: x =81 x+∆x=80Then, ∆x=-1For x=81, y=8114=3Let: dx=∆x=-1Now, y=x14⇒dydx=14×34⇒dydxx=81=1108∴ ∆y=dy=dydxdx=1108×-1=-0.009259⇒∆y=-0.009259∴ 8014=y+∆y=2.99074
(xvi)
Consider the function y=fx=x13.Let: x =27 x+∆x=29Then, ∆x=2For x=27, y=2713=3Let: dx=∆x=2Now, y=x13⇒dydx=13×23⇒dydxx=27=127∴ ∆y=dy=dydxdx=127×2=0.074⇒∆y=0.074∴ 2913=y+∆y=3.074
(xvii)
Consider the function y=fx=x13.Let: x =64 x+∆x=66Then, ∆y=x=2For x=64, y=6413=4Let: dx=∆y=x=2Now, y=x13⇒dydx=13×23⇒dydxx=4=148∴ ∆y=dy=dydxdx=148×2=0.04166⇒∆y=0.04166∴ 6613=y+∆y=4.0416
(xviii)
Consider the function y=fx=x.Let: x =25x+∆x=26Then, ∆x=1For x=25, y=25=5Let: dx=∆x=1Now, y=x1/2⇒dydx=12x⇒dydxx=25=110∴ ∆y=dy=dydxdx=110×1=0.1⇒∆y=0.1∴ 26=y+∆y=5.1
(xix)
Consider the function y=fx=x.Let: x =36 x+∆x=37Then, ∆x=1For x=36, y=36=6Let: dx=∆x=1Now, y=x12⇒dydx=12x⇒dydxx=36=112∴ ∆y=dy=dydxdx=112×1=0.0833⇒∆y=0.0833∴ 37=y+∆y=6.0833
(xx)
Consider the function y=fx=x.Let: x =0.49 x+∆x=0.48Then, ∆x=-0.01For x=0.49, y=0.49=0.7Let: dx=∆x=0.01Now, y=x12⇒dydx=12x⇒dydxx=0.49=11.4∴ ∆y=dy=dydxdx=11.4×-0.01=-0.007143⇒∆y=-0.007143∴ 0.48=y+∆y=0.693
(xxi)
Consider the function y=fx=x14.Let: x =81 x+∆x=82Then, ∆x=1For x=81, y=8114=3Let: dx=∆x=1Now, y=x14⇒dydx=14×34⇒dydxx=81=1108∴ ∆y=dy=dydxdx=1108×1=0.009259⇒∆y=0.009259∴ 8214=y+∆y=3.009259
(xxii)
Consider the function y=fx=x14.Let: x =1681 x+∆x=1781Then, ∆x=181For x=1681, y=168114=23Let: dx=∆x=181Now, y=x14⇒dydx=14×34⇒dydxx=1681=2732∴ ∆y=dy=dydxdx=2732×181=196=0.01042⇒∆y=0.01042∴ 178114=y+∆y=0.6771
(xxiii)
Consider the function y=fx=x15.Let: x =32 x+∆x=33Then, ∆x=1For x=33, y=3215=2Let: dx=∆x=1Now, y=x15⇒dydx=15×45⇒dydxx=32=180∴ ∆y=dy=dydxdx=180×1=0.0125⇒∆y=0.0125∴ 3315=y+∆y=2.0125Disclaimer: This solution has been created according to the question given in the book. However, the solution given in the book is incorrect.
(xxiv)
Consider the function y=fx=x.Let: x =36x+∆x=36.6Then, ∆x=0.6For x=36, y=36=6Let: dx=∆x=0.6Now, y=x12⇒dydx=12x⇒dydxx=36=112∴ ∆y=dy=dydxdx=112×0.6=0.05⇒∆y=0.05∴ 36.6=y+∆y=6.05
(xv)
Consider the function y=fx=x13.Let: x =27 x+∆x=25Then, △x=-2For x=27, y=2713=3Let: dx=∆x=-2Now, y=x13⇒dydx=13×23⇒dydxx=27=127∴ ∆y=dy=dydxdx=127×-2=-0.07407⇒∆y=-0.07407∴ 2513=y+∆y=2.9259
Q10.
Answer :
Let: x=2x+∆x=2.01⇒∆x=0.01fx=4×2+5x+2⇒fx=2=16+10+2=28Now, y=fx⇒dydx=8x+5∴ dy=∆y=dydxdx=8x+5×0.01=16+5×0.01=0.21∴ f2.01=y+∆y=28.21
Q11.
Answer :
Let: x=5 x+∆x=5.001⇒∆x=0.001fx=x3-7×2+15⇒y=fx=3=125-175+15=-35Now, y=fx⇒dydx=3×2-14x∴ dy=∆y=dydxdx=3×2-14x×0.001 =75-70×0.001=0.005∴ f5.001=y+∆y=-35+0.005=-34.995
Q12.
Answer :
Let: y = fx=log10xHere, x=1000, x+∆x=1005⇒∆x=5⇒dx=∆x=5For x=1000, y=log101000=log10103=3Now, y=log10x =logexloge10∴ dydx=0.4343x⇒dydxx=1000=0.43431000=0.0004343 ∆y=dy=dydxdx=0.0004343×5=0.0021715∴ log101005=y+∆y=3.0021715
Q13.
Answer :
Let x be the radius and y be the surface area of the sphere.
Then, x=9 ∆x=0.03 m=3cm⇒x+∆x=9+3=12 cmy=4πx2For x=9, y=4π×92=324πdydx=8πx⇒dydxx=9=72π∴ ∆y=dy=dydxdx=72π×3=216π cm2Therefore, the approximate error in the surface area is 216π cm2.Disclaimer: This solution has been created according to the question given in the book. However, the solution given in the book is incorrect.
Q14.
Answer :
Let y be the surface area of the cube.
y=6 x2We have △xx×100=1Now,dydx=12x⇒△y=dy=dydxdx=12x×x100=0.12 x2 m2Hence, approximate change in the surface area of the cube is 0.12×2 m2.
Q15.
Answer :
Let x be the radius of the sphere and y be its volume.
y=43πx3Let ∆x be the error in the radius.x=7∆x=0.02dydx=4πx2⇒dydxx=7=196π∴ ∆y=dy=dydxdx=196π×0.02 =3.92π Hence, the approximate error in calculating the volume of the sphere is 3.92π m3.
Q16.
Answer :
Volume of the cube, V=x3We have∆x=0.01xdVdx=3×2⇒∆V=dV=dVdxdx=3×2×0.01x=0.03 x3Hence, the approximate change in the value V of the cube is 0.03×3 m3.Disclaimer: This solution has been created according to the question given in the book. However, the solution in the book is incorrect.
Page 14.12(Very Short Answers)
Q1.
Answer :
y=x2 ∆x=0.1 x=10dydx=2x⇒dydxx=10=20⇒∆y=dy=dydxdx=20×0.1=2
Q2.
Answer :
We have
x=3∆x=0.03y=logexFor x=3, y=loge3Also, dydx=1x⇒dydxx=3=13⇒∆y=dy=dydxdx=13 × 0.03=0.01
Q3.
Answer :
Let x be the radius and y be the area of the circular plane.
We have △xx=α and y=x2.⇒dydx=2x⇒△yy=2xydx=2xx2×αx=2αHence, the relative error in the area of the circular plane is 2α.
Q4.
Answer :
Let V be the volume of the sphere.
V=43πx3We have ∆xx×100=α⇒dVdx=4πx2⇒dVV=4πx2Vdx⇒∆VV=4πx243πx3×xα100⇒∆VV×100=3αHence, the the percentage error in the volume is 3α.
Q5.
Answer :
Let x be the side and V be the volume of the cube.
V=x3We have∆xx×100=a∴ dVdx=3×2⇒∆VV=3x2Vdx=3x2x3×ax100⇒∆VV×100=3aHence, the percentage error in the volume is 3a.
Page 14.12(Multiple Choice Questions)
Q1.
Answer :
(a) 1%
Let l be the length if the pendulum and T be the period.
Also, let ∆l be the error in the length and ∆T be the error in the period.We have∆ll×100=2⇒dll×100=2Now, T=2πlgTaking log on both sides, we getlog T=log 2π+12log l-12log gDifferentiating both sides w.r.t. x, we get1TdTdl=12l⇒dTdl=T2l⇒dll×100=2dTT×100⇒dTT×100=22⇒∆TT×100=1Hence, there is an error of 1% in calculating the period of the pendulum.
Q2.
Answer :
(a) 2a%
Let x be the side of the cube and y be its surface area.
∆xx×100=aAlso, y=6×2⇒dydx=12x⇒∆yy=12xy×dx =2x×ax100⇒∆yy×100=2aHence, the error in the surface area is 2a%.
Q3.
Answer :
(b) 3k%
Let x be the radius of the sphere and y be its volume.
Then,
∆xx×100=kAlso, y=43πx3⇒dydx=4πx2⇒∆yy=4πx2ydx=4πx243πx3×kx100 ⇒∆yy×100=3kHence, the error in the volume is 3k%.
Q4.
Answer :
(c) 3αα%Let x be the radius, which is equal to the height of the cylinder. Let y be its volume.
∆xx×100=αAlso, y=πx2x=πx3 Radius = Height of the cylinder⇒dydx=3πx2⇒∆yy=3πx2ydx=3x×αx100⇒∆yy×100=3αHence, the error in the volume of the cylinder is 3α%.
Q5.
Answer :
(b) 2k%
Let x be the side of the triangle and y be its area.
∆xx×100=kAlso, y=34×2⇒dydx=32x⇒∆yy=3x2ydx =2x×kx100⇒∆yy×100=2kHence, the error in the area of the triangle is 2k%.
Page 14.13(Multiple Choice Questions)
Q6.
Answer :
(c) 1.3893
Consider the function y=fx=logex.Let: x=4x+∆x=4.01⇒∆x=0.01For x=4, y=loge4=1.3868y=logex⇒dydx=1x⇒dydxx=4=14⇒∆y=dy=dydxdx=14× 0.01=0.0025∴ loge4.01=y+∆y=1.3893
Q7.
Answer :
(c) 80000 π mm3
Let x be the radius of the sphere and y be its volume.
x=100, x+∆x=98⇒∆x=-2y=43πx3⇒dydx=4πx2⇒dydxx=100=40000π∴ ∆y=dy=dydxdx=40000π×-2=-80000πHence, the decrease in the volume of the sphere is 80000π mm3.
Q8.
Answer :
(c) 3 λ %
Let the radius of the cone be x, the height be 2x and the volume be y.
∆xx=λ%⇒y=13πx2×2x=23πx3⇒dydx=2πx2⇒∆yy=2πx2ydx=3x×λx⇒∆yy=3λ%
Q9.
Answer :
(c) 18 %
We have
△VV=-12%PV14= constant= k sayTaking log on both sides, we getlog PV14=log k⇒log P+14log V=log kDifferentiating both sides w.r.t. x, we get1PdPdV+14V=0⇒dPP=-dV4V=-14×-12=18Hence, the increase in the pressure is 18%.
Q10.
Answer :
(d) n:1
Let ∆xx be the relative error in x and ∆yy be the error in y.Now, y=xn⇒dydx=n xn-1⇒∆yy=n xn-1ydx⇒∆yy=nxn-1xndx =n∆xx⇒∆yy:∆xx=n:1
Q11.
Answer :
(a) 2.0125
Consider the function y= f(x)=x15.
Let: x=32 x+∆x=33⇒∆x=1y=x15For x=32, y=2Also, dydx=15×45⇒dydxx=32=180⇒∆y=dy=dydxdx=180×1=0.0125∴ 3315=y+∆y=2.0125
Q12.
Answer :
(a) 114
Let x be the radius of the circle and y be its circumference.
x=28 cm∆x=0.01 cmx=2πry=πr2=π×x24π2=x24π⇒dydx=x2π⇒∆yy=x2πydx=2x×0.01⇒∆yy×100=2x=114Hence, the percentage error in the area is 114.
Page 15.10 Ex.15.1
Q1.
Answer :
(i) The given function is fx=3+x-223.
Differentiating with respect to x, we get
f’x=23x-223-1⇒f’x=23x-2-13⇒f’x=23x-213
Clearly, we observe that for x=2∈1, 3, f’x does not exist.
Therefore, fx is not derivable on 1, 3.
Hence, Rolle’s theorem is not applicable for the given function.
(ii) The given function is fx=x.
The domain of f is given to be -1, 1.
Let c∈-1, 1 such that c is not an integer.
Then,
limx→cfx=fc
Thus, fx is continuous at x=c.
Now, let c=0.
Then,
limx→0-fx=-1≠0=f0
Thus, f is discontinuous at x = 0.
Therefore, fx is not continuous in -1, 1.
Rolle’s theorem is not applicable for the given function.
(iii) The given function is fx=sin1x.
The domain of f is given to be -1, 1.
It is known that limx→0sin1x does not exist.
Thus, fx is discontinuous at x = 0 on -1, 1.
Hence, Rolle’s theorem is not applicable for the given function.
(iv) The given function is fx=2×2-5x+3 on 1, 3.
The domain of f is given to be 1, 3.
It is a polynomial function.
Thus, it is everywhere derivable and hence continuous.
But
f1=0 and f3=6⇒f3≠f1
Hence, Rolle’s theorem is not applicable for the given function.
(v) The given function is fx=x23 on -1, 1.
The domain of f is given to be -1, 1.
Differentiating fx with respect to x, we get
f’x=23x-13
We observe that at x=0, f’x is not defined.
Hence, Rolle’s theorem is not applicable for the given function.
(vi) The given function is
fx=-4x+5, 0≤x≤12x-3, 1<x≤2
At x = 0, we have
limx→1-fx=limh→0f1-h=limh→0-41-h+5=1
And
limx→1+fx=limh→0f1+h=limh→021+h-3=-1
∴ limx→1-fx≠limx→1+fx
Thus, fx is discontinuous at x=1.
Hence, Rolle’s theorem is not applicable for the given function.
Q2.
Answer :
Given function is fx=xx-42, which can be rewritten as fx=x3-8×2+16x.
We know that a polynomial function is everywhere derivable and hence continuous.
So, being a polynomial function, fx is continuous and derivable on 0, 4.
Also,
f0=f4=0
Thus, all the conditions of Rolle’s theorem are satisfied.
Now, we have to show that there exists c∈0, 4 such that f’c=0.
We have
fx=x3-8×2+16x⇒f’x=3×2-16x+16∴f’x=0 ⇒ 3×2-16x+16=0⇒3×2-12x-4x+16=0⇒3xx-4-4x-4=0⇒x-43x-4⇒x=4, 43
Thus, c=43∈0, 4 such that f’c=0.
Hence, Rolle’s theorem is verified.
Q3.
Answer :
The given function is fx=xx-22, which can be rewritten as fx=x3-4×2+4x.
We know that a polynomial function is everywhere derivable and hence continuous.
So, being a polynomial function, fx is continuous and derivable on 0, 2.
Also,
f0=f2=0
Thus, all the conditions of Rolle’s theorem are satisfied.
Now, we have to show that there exists c∈0, 2 such that f’c=0.
We have
fx=x3-4×2+4x⇒f’x=3×2-8x+4When f’x=0 3×2-8x+4=0⇒3×2-6x-2x+4=0⇒3xx-2-2x-2=0⇒x-23x-2⇒x=2, 23
Thus, c=23∈0, 2 such that f’c=0.
Hence, Rolle’s theorem is verified.
Q4.
Answer :
Given function is fx=x2+5x+6.
We know that a polynomial function is everywhere derivable and hence continuous.
So, being a polynomial function, fx is continuous and derivable on -3, -2.
Also,
f-3=-32+5-3+6=9-15+6=0f-2=-22+5-2+6=4-10+6=0∴ f-3=f-2=0
Thus, all the conditions of the Rolle’s theorem are satisfied.
Now, we have to show that there exists c∈-3, -2 such that f’c=0.
We have
fx=x2+5x+6⇒f’x=2x+5∴ f’x=0 ⇒2x+5=0 ⇒x=-52
Thus, c=-52∈-3, -2 such that f’c=0.
Hence, Rolle’s theorem is verified.
Q5.
Answer :
(i) Given:
fx=x2-8x+12
We know that a polynomial function is everywhere derivable and hence continuous.
So, being a polynomial function, fx is continuous and derivable on 2, 6.
Also,
f2=22-82+12=4-16+12=0f6=62-86+12=36-48+12=0∴ f2=f6=0
Thus, all the conditions of Rolle’s theorem are satisfied.
Now, we have to show that there exists c∈2, 6 such that f’c=0.
We have
fx=x2-8x+12⇒f’x=2x-8∴ f’x=0 ⇒2x-8=0⇒x=4
Thus, c=4∈2, 6 such that f’c=0.
Hence, Rolle’s theorem is verified.
(ii) Given:
fx=x2-4x+ 3
We know that a polynomial function is everywhere derivable and hence continuous.
So, being a polynomial function, fx is continuous and derivable on 1, 3.
Also,
f1=12-41+3=1-4 + 3=0f3=32-43+3=9-12+3=0∴ f1=f3=0
Thus, all the conditions of Rolle’s theorem are satisfied.
Now, we have to show that there exists c∈1, 3 such that f’c=0.
We have
fx=x2-4x+3⇒f’x=2x-4∴ f’x=0 ⇒2x-4=0⇒x=2
Thus, c=2∈1, 3 such that f’c=0.
Hence, Rolle’s theorem is verified.
(iii) Given:
fx=x-1x-22
i.e. fx=x3+4x-4×2-x2-4+4x
i.e. fx=x3-5×2+8x-4
We know that a polynomial function is everywhere derivable and hence continuous.
So, being a polynomial function, fx is continuous and derivable on 1, 2.
Also,
f1=13-512+81-4=0f2=23-522+82-4=0∴ f1=f2=0
Thus, all the conditions of Rolle’s theorem are satisfied.
Now, we have to show that there exists c∈1, 2 such that f’c=0.
We have
fx=x3+8x-5×2-4⇒f’x=3×2+8-10x∴ f’x=0 ⇒3×2-10x+8=0 ⇒3×2-6x-4x+8=0 ⇒3xx-2-4x-2=0 ⇒x-23x-4 ⇒x=2, 43
Thus, c=43∈1, 2 such that f’c=0.
Hence, Rolle’s theorem is verified.
(iv) Given:
fx=xx-12
⇒fx=xx2-2x+1
∴ fx=x3-2×2+x
We know that a polynomial function is everywhere derivable and hence continuous.
So, fx being a polynomial function is continuous and derivable on 0, 1.
Also,
f0=f1=0
Thus, all the conditions of Rolle’s theorem are satisfied.
Now, we have to show that there exists c∈0, 1 such that f’c=0.
We have
fx=x3-2×2+x⇒f’x=3×2-4x+1∴ f’x=0 ⇒3×2-4x+1=0 ⇒3×2-3x-x+1=0 ⇒3xx-1-1x-1=0 ⇒x-1 3x-1=0 ⇒x=1, 13
Thus, c=13∈0, 1 such that f’c=0.
Hence, Rolle’s theorem is verified.
(v) Given:
fx=x2-1x-2
i.e. fx=x3-2×2-x+2
We know that a polynomial function is everywhere derivable and hence continuous.
So, being a polynomial function, fx is continuous and derivable on -1, 2.
Also,
f-1=f2=0
Thus, all the conditions of Rolle’s theorem are satisfied.
Now, we have to show that there exists c∈-1, 2 such that f’c=0.
We have
fx=x3-x-2×2+2⇒f’x=3×2-4x-1∴ f’x=0 ⇒3×2-4x-1=0 ⇒x=–4±-42-4×3×-12×3 ⇒x=4±16+126 ⇒x=4±286 ⇒x=4±276 ⇒x=2±73 ⇒x=132-7, 132+7
Thus, c=132-7, 132+7∈-1, 2 such that f’c=0.
Hence, Rolle’s theorem is verified.
Q6.
Answer :
(i) The given function is fx=cos2x-π4=cos2x-π2=sin2x.
Since sin2x is everywhere continuous and differentiable.
Therefore, sin2x is continuous on 0, π2 and differentiable on 0, π2.
Also,
fπ2=f0=0
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈0, π2 such that f’c=0.
We have
fx=sin2x⇒f’x=2cos2x
∴f’x=0⇒2cos2x=0⇒cos2x=0⇒x=π4
Thus, c=π4∈0, π2 such that f’c=0.
Hence, Rolle’s theorem is verified.
(ii) The given function is fx=sin2x.
Since sin2x is everywhere continuous and differentiable.
Therefore, sin2x is continuous on 0, π2 and differentiable on 0, π2.
Also,
fπ2=f0=0
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈0, π2 such that f’c=0.
We have
fx=sin2x⇒f’x=2cos2x
∴f’x=0⇒2cos2x=0⇒cos2x=0⇒x=π4
Thus, c=π4∈0, π2 such that f’c=0.
Hence, Rolle’s theorem is verified.
(iii)
The given function is fx=cos2x.
Since cos2x is everywhere continuous and differentiable, cos2x is continuous on -π4, π4 and differentiable on -π4, π4.
Also,
fπ4=f-π4=0
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈-π4, π4 such that f’c=0.
We have
fx=cos2x⇒f’x=-2sin2x
∴ f’x=0⇒-2sin2x=0⇒sin2x=0⇒sin2x=0⇒x=0
Since c=0∈-π4, π4 such that f’c=0.
Hence, Rolle’s theorem is verified.
(iv)
The given function is fx=exsinx.
Since sinx & ex are everywhere continuous and differentiable.
Therefore, being a product of these two, fx is continuous on 0, π and differentiable on 0, π.
Also,
fπ=f0=0
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈0, π such that f’c=0.
We have
fx=exsinx⇒f’x=exsinx+cosx
∴ f’x=0⇒exsinx+cosx=0⇒sinx+cosx=0⇒tanx=-1⇒x=π-π4=3π4
Since c=3π4∈0, π such that f’c=0.
Hence, Rolle’s theorem is verified.
(v)
The given function is fx=excosx.
Since cosx & ex are everywhere continuous and differentiable, fx being a product of these two is continuous on -π2, π2 and differentiable on -π2, π2.
Also,
f-π2=fπ2=0
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈-π2, π2 such that f’c=0.
We have
fx=excosx⇒f’x=excosx-sinx
∴ f’x=0⇒excosx-sinx=0⇒sinx-cosx=0⇒tanx=1⇒x=π4
Since c=π4∈-π2, π2 such that f’c=0.
Hence, Rolle’s theorem is verified.
(vi)
The given function isfx=cos2x.
Since cos2x is everywhere continuous and differentiable.
Therefore, fx is continuous on 0, π and differentiable on 0, π.
Also,
fπ=f0=1
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈0, π such that f’c=0.
We have
fx=cos2x⇒f’x=-2sin2x
∴ f’x=0⇒-2sin2x=0⇒sin2x=0⇒2x=π⇒x=π2
Thus, c=π2∈0, π such that f’c=0.
Hence, Rolle’s theorem is verified.
(vii)
The given function is fx=sinxex.
Since cosx and ex are everywhere continuous and differentiable, being the quotient of these two, fx is continuous on 0, π and differentiable on 0, π.
Also,
fπ=f0=0
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈0, π such that f’c=0.
We have
fx=sinxex⇒f’x=cosx-sinxex
∴ f’x=0⇒cosx-sinxex=0⇒cosx-sinx=0⇒tanx=1⇒x=π4
Thus, c=π4∈0, π such that f’c=0.
Hence, Rolle’s theorem is verified.
(viii)
The given function isfx=sin3x.
Since sin3x is everywhere continuous and differentiable, sin3x is continuous on 0, π and differentiable on 0,π.
Also,
fπ=f0=0
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈0, π such that f’c=0.
We have
fx=sin3x⇒f’x=3cos3x
∴f’x=0⇒3cos3x=0⇒cos3x=0⇒3x=π2, 3π2,….⇒x=π6, π2, 5π6
Thus, c=π6, π2, 5π6∈0, π such that f’c=0.
Hence, Rolle’s theorem is verified.
(ix)
The given function isfx=e1-x2.
Since exponential function is everywhere continuous and differentiable, e1-x2 is continuous on -1, 1 and differentiable on -1, 1.
Also,
f1=f-1=1
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈-1, 1 such that f’c=0.
We have
fx=e1-x2⇒f’x=-2xe1-x2
∴f’x=0⇒-2xe1-x2=0⇒x=0
Thus, c=0∈-1, 1 such that f’c=0.
Hence, Rolle’s theorem is verified.
(x)
The given function is fx=logx2+2-log3, which can be rewritten as fx=logx2+23.
Since logarithmic function is differentiable and so continuous in its domain, fx=logx2+23 is continuous on -1, 1 and differentiable on -1, 1.
Also,
f1=f-1=0
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈-1, 1 such that f’c=0.
We have
fx=logx2+23⇒f’x=32xx2+2=6xx2+2
∴f’x=0⇒6xx2+2=0⇒x=0
Thus, c=0∈-1, 1 such that f’c=0.
Hence, Rolle’s theorem is verified.
(xi)
The given function isfx=sinx + cosx.
Since sinx and cosx are everywhere continuous and differentiable, fx=sinx + cosx is continuous on 0, π2 and differentiable on 0, π2.
Also,
fπ2=f0=1
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈0, π2 such that f’c=0.
We have
fx=sinx+cosx⇒f’x=cosx-sinx
∴f’x=0⇒cosx-sinx=0⇒tanx=1⇒x=π4
Thus, c=π4∈0, π2 such that f’c=0.
Hence, Rolle’s theorem is verified.
(xii)
The given function isfx=2sinx +sin2x.
Since sinx & sin2x are everywhere continuous and differentiable, fx is continuous on 0, π and differentiable on 0, π.
Also,
fπ=f0=0
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈0, π such that f’c=0.
We have
fx=2sinx+sin2x⇒f’x=2cosx+2cos2x
∴ f’x=0⇒2cosx+2cos2x=0⇒cosx+cos2x=0⇒cosx+2cos2x-1=0⇒2cos2x+cosx-1=0⇒cosx+1 2cosx-1=0⇒cosx=-1, cosx=12⇒cosx=cosπ, cosx=π3⇒x=π, π3
Thus, c=π3∈0, π such that f’c=0.
Hence, Rolle’s theorem is verified.
(xiii)
The given function isfx=x2-sinπx6.
Since sinx & x2 are everywhere continuous and differentiable, fx is continuous on -1, 0 and differentiable on -1, 0.
Also,
f-1=f0=0
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈-1, 0 such that f’c=0.
We have
fx=x2-sinπx6⇒f’x=12-π6cosπx6
∴ f’x=0⇒12-π6cosπx6=0⇒cosπx6=3π⇒x=-6πcos-13π
Thus, c=-6πcos-13π∈-1, 0 such that f’c=0.
Hence, Rolle’s theorem is verified.
(xiv)
The given function isfx=6xπ-4sin2x.
Since sin2x & x are everywhere continuous and differentiable, fx is continuous on 0, π6 and differentiable on 0, π6.
Also,
fπ6=f0=0
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈0, π6 such that f’c=0.
We have
fx=6xπ-4sin2x⇒f’x=6π-8 sinx cosx
∴ f’x=0⇒6π-8sinxcosx=0⇒sin2x=32π⇒x=12sin-132π
Thus, c=12sin-132π∈0, π6 such that f’c=0.
Hence, Rolle’s theorem is verified.
(xv)
The given function isfx=4sinx.
Since sine function and exponential function are everywhere continuous and differentiable, fx is continuous on 0, π and differentiable on 0, π.
Also,
fπ=f0=1
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈0, π such that f’c=0.
We have
fx=4sinx⇒f’x=4sinxcosxlog4
∴ f’x=0⇒4sinxcosxlog4=0⇒4sinxcosx=0⇒cosx=0⇒x=π2
Thus, c=π2∈0, π such that f’c=0.
Hence, Rolle’s theorem is verified.
(xvi)
According to Rolle’s theorem, if f(x) is a real valued function defined on [a, b] such that it is continuous on [a, b], it is differentiable on (a, b) and f(a) = f(b), then there exists a real number c ∈(a, b) such that f(c) = 0.
Now, f(x) is defined for all x ∈[1, 4].
At each point of [1, 4], the limit of f(x) is equal to the value of the function. Therefore, f(x) is continuous on [1, 4].
Also, exists for all x ∈(1, 4).
So, f(x) is differentiable on (1, 4).
Also,
f(1) = f(4) = 0
Thus, all the three conditions of Rolle’s theorem are satisfied.
Now, we have to show that there exists c ∈(1, 4) such that.
We have
∴f’x=0⇒2x-5=0⇒x=52
[Since ∈(1, 4) such that]
Hence, Rolle’s theorem is verified.
(xvii)
The given function is fx=sin4x + cos4x.
Since sinx and cosx are everywhere continuous and differentiable, fx=sin4x + cos4x is continuous on 0, π2 and differentiable on 0, π2.
Also,
fπ2=f0=1
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈0, π2 such that f’c=0.
We have
fx=sin4x+cos4x⇒f’x=4sin3xcosx-4cos3xsinx
∴f’x=0⇒4sin3xcosx-4cos3xsinx=0⇒sin3xcosx-cos3xsinx=0⇒tan3x-tanx=0⇒tanxtan2x-1=0⇒tanx=0, tan2x=1⇒tanx=0, tanx=±1⇒x=0, x=π4, 3π4
Thus, c=π4∈0, π2 such that f’c=0.
Hence, Rolle’s theorem is verified.
(xviii)
The given function is fx=sinx -sin2x.
Since sinx and sin2x are everywhere continuous and differentiable, fx is continuous on 0, π and differentiable on 0, π.
Also,
fπ=f0=0
Thus, fx satisfies all the conditions of Rolle’s theorem.
Now, we have to show that there exists c∈0, π such that f’c=0.
We have
fx=sinx-sin2x⇒f’x=cosx-2cos2x
∴ f’x=0⇒cosx-2cos2x=0⇒cosx-2cos2x+1=0⇒2cos2x-cosx-1=0⇒cosx-1 2cosx+1=0⇒cosx=1, cosx=-12⇒cosx=cosπ2, cosx=2π3⇒x=π2, 2π3
Thus, c=π2, 2π3∈0, π such that f’c=0.
Hence, Rolle’s theorem is verified.
Page 15.11 Ex.15.1
Q7.
Answer :
The equation of the curve is
y=16-x2. …(1)
Let Px1,y1 be a point on it where the tangent is parallel to the x-axis.
Then,
dydxP=0 …(2)
Differentiating (1) with respect to x, we get
dydx=-2x⇒dydxP=-2×1⇒-2×1=0 from 2⇒x1=0
Px1, y1 lies on the curve y=16-x2.
∴ y1=16-x12
When x1=0,
y1=16
Hence, 0, 16 is the required point.
Q8.
Answer :
(i) Let fx=x2
Since fx is a polynomial function, it is continuous on -2, 2 and differentiable on -2, 2.
Also, f2=f-2=4
Thus, all the conditions of Rolle’s theorem are satisfied.
Consequently, there exists at least one point c∈-2, 2 for which f’c=0.
But f’c=0⇒2c=0⇒c=0
∴ fc=f0=0
By the geometrical interpretation of Rolle’s theorem, 0, 0 is the point on y=x2, where the tangent is parallel to the x-axis.
(ii) Let fx=e1-x2
Since fx is an exponential function, which is continuous and derivable on its domain, fx is continuous on -1, 1 and differentiable on -1, 1.
Also, f1=f-1=1
Thus, all the conditions of Rolle’s theorem are satisfied.
Consequently, there exists at least one point c∈-1, 1 for which f’c=0.
But f’c=0⇒-2ce1-c2=0⇒c=0 ∵ e1-c2≠0
∴ fc=f0=e
By the geometrical interpretation of Rolle’s theorem, 0, e is the point on y=e1-x2 where the tangent is parallel to the x-axis.
(iii) Let fx=12x+1x-2 …(1)
⇒fx=12×2-x-2
⇒fx=12×2-12x-24
Since fx is a polynomial function, fx is continuous on -1, 2 and differentiable on -1, 2.
Also, f2=f-1=0
Thus, all the conditions of Rolle’s theorem are satisfied.
Consequently, there exists at least one point c∈-1, 2 for which f’c=0.
But f’c=0⇒24c-12=0⇒c=12
∴ fc=f12=-123232=-27 (using (1))
By the geometrical interpretation of Rolle’s theorem, 12,-27 is the point on y=12x+1x-2 where the tangent is parallel to the x-axis.
Q9.
Answer :
It is given that is a differentiable function.
Every differentiable function is a continuous function. Thus,
(a) f is continuous in [−5, 5].
(b) f is differentiable in (−5, 5).
Therefore, by the Mean Value Theorem, there exists c ∈ (−5, 5) such that
It is also given that does not vanish anywhere.
Hence proved.
Page 15.19 Ex.15.2
Q1.
Answer :
(i) We have
fx=x2-1
Since a polynomial function is everywhere continuous and differentiable, fx is continuous on 2, 3 and differentiable on 2, 3.
Thus, both conditions of Lagrange’s mean value theorem are satisfied.
So, there must exist at least one real number c∈2, 3 such that
f’c=f3-f23-2
Now, fx=x2-1
⇒f’x=2x , f3=32-1=8 , f2=22-1=3
∴ f’x=f3-f23-2
⇒2x=8-31⇒x=52
Thus, c=52∈2, 3 such that f’c=f3-f23-2.
Hence, Lagrange’s theorem is verified.
(ii) We have,
fx=x3-2×2-x+3=0
Since a polynomial function is everywhere continuous and differentiable.
Therefore, fx is continuous on 0, 1 and differentiable on 0, 1.
Thus, both conditions of Lagrange’s mean value theorem are satisfied.
So, there must exist at least one real number c∈0, 1 such that
f’c=f1-f01-0
Now, fx=x3-2×2-x+3=0
⇒f’x=3×2-4x-1 , f1= 1 , f0=3
∴ f’x=f1-f01-0
⇒3×2-4x-1=1-31⇒3×2-4x-1+2=0⇒3×2-4x+1=0⇒3×2-3x-x+1=0⇒3x-1x-1=0⇒x=13, 1
Thus, c=13∈0, 1 such that f’c=f1-f01-0.
Hence, Lagrange’s theorem is verified.
(iii) We have,
fx=xx-1 which can be rewritten as fx=x2-x
Since a polynomial function is everywhere continuous and differentiable.
Therefore, fx is continuous on 1, 2 and differentiable on 1, 2.
Thus, both conditions of Lagrange’s mean value theorem are satisfied.
So, there must exist at least one real number c∈1, 2 such that
f’c=f2-f12-1
Now, fx=x2-x
⇒f’x=2x-1 , f2= 2 , f1=0
∴ f’x=f2-f12-1
⇒2x-1=2-02-1⇒2x-1-2=0⇒2x=3⇒x=32
Thus, c=32∈1, 2 such that f’c=f2-f12-1.
Hence, Lagrange’s theorem is verified.
(iv) We have,
fx=x2-3x+2
Since a polynomial function is everywhere continuous and differentiable.
Therefore, fx is continuous on -1, 2 and differentiable on -1, 2.
Thus, both conditions of Lagrange’s mean value theorem are satisfied.
So, there must exist at least one real number c∈-1, 2 such that
f’c=f2-f-12+1=f2-f-13
Now, fx=x2-3x+2
⇒f’x=2x-3 , f2=0 , f-1=-12-3-1+2=6
∴ f’x=f2-f-13
⇒2x-3=-2⇒2x-1=0⇒x=12
Thus, c=12∈-1, 2 such that f’c=f2-f-12–1.
Hence, Lagrange’s theorem is verified.
(v) We have,
fx=2×2-3x+1
Since a polynomial function is everywhere continuous and differentiable.
Therefore, fx is continuous on 1, 3 and differentiable on 1, 3.
Thus, both conditions of Lagrange’s mean value theorem are satisfied.
So, there must exist at least one real number c∈1, 3 such that
f’c=f3-f13-1=f3-f12
Now, fx=2×2-3x+1
⇒f’x=4x-3 , f3=10 , f1=212-31+1=0
∴ f’x=f3-f12
⇒4x-3=10-02⇒4x-3-5=0⇒x=2
Thus, c=2∈1, 3 such that f’c=f3-f13-1.
Hence, Lagrange’s theorem is verified.
(vi) We have,
fx=x2-2x+4
Since a polynomial function is everywhere continuous and differentiable.
Therefore, fx is continuous on 1, 5 and differentiable on 1, 5.
Thus, both conditions of Lagrange’s mean value theorem are satisfied.
So, there must exist at least one real number c∈1, 5 such that
f’c=f5-f15-1=f5-f14
Now, fx=x2-2x+4
⇒f’x=2x-2 , f5=25-10+4=19 , f1=1-2+4=3
∴ f’x=f5-f14
⇒2x-2=19-34⇒2x-2-4=0⇒x=62=3
Thus, c=3∈1, 5 such that f’c=f5-f15-1.
Hence, Lagrange’s theorem is verified.
(vii) We have,
fx=2x-x2
Since a polynomial function is everywhere continuous and differentiable.
Therefore, fx is continuous on 0, 1 and differentiable on 0, 1.
Thus, both conditions of Lagrange’s mean value theorem are satisfied.
So, there must exist at least one real number c∈0, 1 such that
f’c=f1-f01-0=f1-f01
Now, fx=2x-x2
⇒f’x=2-2x , f1=2-1=1 , f0=0
∴ f’x=f1-f01
⇒2-2x=1-01⇒-2x=1-2⇒x=12
Thus, c=12∈0, 1 such that f’c=f1-f01-0.
Hence, Lagrange’s theorem is verified.
(viii) We have,
fx=x-1x-2x-3 which can be rewritten as fx=x3-6×2+11x-6
Since a polynomial function is everywhere continuous and differentiable.
Therefore, fx is continuous on 0, 4 and differentiable on 0, 4.
Thus, both conditions of Lagrange’s mean value theorem are satisfied.
So, there must exist at least one real number c∈0, 4 such that
f’c=f4-f04-0=f4-f04
Now, fx=x3-6×2+11x-6
⇒f’x=3×2-12x+11 , f0=-6 , f4=64-96+44-6=6
∴ f’x=f4-f04-0
⇒3×2-12x+11=6+64⇒3×2-12x+8=0⇒x=2-23, 2+23
Thus, c=2±23∈0, 4 such that f’c=f4-f04-0.
Hence, Lagrange’s theorem is verified.
(ix) We have,
fx=25-x2
Here, fx will exist,
if
25-x2≥0⇒x2≤25⇒-5≤x≤5
Since for each x∈-3, 4, the function fx attains a unique definite value.
So, fx is continuous on -3, 4
Also, f’x=1225-x2-2x=-x25-x2 exists for all x∈-3, 4
So, fx is differentiable on -3, 4.
Thus, both the conditions of lagrange’s theorem are satisfied.
Consequently, there exists some c∈-3, 4 such that
f’c=f4-f-34+3=f4-f-37
Now, fx=25-x2
f’x=-x25-x2 , f-3=4 , f4=3
∴ f’x=f4-f-34+3
⇒-x25-x2=3-47⇒49×2=25-x2⇒x=±12
Thus, c=±12∈-3, 4 such that f’c=f4-f-34–3.
Hence, Lagrange’s theorem is verified.
(x) We have,
fx=tan-1x
Clearly, fx is continuous on 0, 1 and derivable on 0,1
Thus, both the conditions of lagrange’s theorem are satisfied.
Consequently, there exists some c∈-3, 4 such that
f’c=f1-f01-0=f1-f01
Now, fx=tan-1x
f’x=11+x2 , f1=π4 , f0=0
∴ f’x=f1-f01-0
⇒11+x2=π4-0⇒4π-1=x2⇒x=±4-ππ
Thus, c=4-ππ∈0, 1 such that f’c=f1-f01-0.
Hence, Lagrange’s theorem is verified.
(xi) We have,
fx=x+1x=x2+1x
Clearly, fx is continuous on 1, 3 and derivable on 1, 3
Thus, both the conditions of lagrange’s theorem are satisfied.
Consequently, there exists some c∈1, 3 such that
f’c=f3-f13-1=f3-f12
Now, fx=x2+1x
f’x=x2-1×2 , f1=2 , f3=103
∴ f’x=f3-f12
⇒x2-1×2=46⇒x2-1×2=23⇒3×2-3=2×2⇒x=±3
Thus, c=3∈1, 3 such that f’c=f3-f13-1.
Hence, Lagrange’s theorem is verified.
(xii) We have,
fx=xx+42=xx2+16+8x=x3+8×2+16x
Since fx is a polynomial function which is everywhere continuous and differentiable.
Therefore, fx is continuous on 0, 4 and derivable on 0,4
Thus, both the conditions of lagrange’s theorem are satisfied.
Consequently, there exists some c∈0, 4 such that
f’c=f4-f04-0=f4-f04
Now, fx=x3+8×2+16x
f’x=3×2+16x+16 , f4=64+128+64=256 , f0=0
∴ f’x=f4-f04-0
⇒3×2+16x+16=2564⇒3×2+16x-48=0⇒x=-432+13, 4313-2
Thus, c=-8+4133∈0, 4 such that f’c=f4-f04-0.
Hence, Lagrange’s theorem is verified.
(xiii) We have,
fx=x2-4
Here, fx will exist,
if
x2-4≥0⇒x≤-2 or x≥2
Since for each x∈2, 4, the function fx attains a unique definite value.
So, fx is continuous on 2, 4
Also, f’x=12×2-42x=xx2-4 exists for all x∈2, 4
So, fx is differentiable on 2, 4.
Thus, both the conditions of lagrange’s theorem are satisfied.
Consequently, there exists some c∈2, 4 such that
f’c=f4-f24-2=f4-f22
Now, fx=x2-4
f’x=xx2-4 , f4=23 , f2=0
∴ f’x=f4-f24-2
⇒xx2-4=232⇒xx2-4=3⇒x2x2-4=3 ⇒x2=3×2-12⇒x2=6⇒x=±6
Thus, c=6∈2, 4 such that f’c=f4-f24-2.
Hence, Lagrange’s theorem is verified.
(xiv) We have,
fx=x2+x-1
Since polynomial function is everywhere continuous and differentiable.
Therefore, fx is continuous on 0, 4 and differentiable on 0, 4
Thus, both the conditions of lagrange’s theorem are satisfied.
Consequently, there exists some c∈0, 4 such that
f’c=f4-f04-0=f4-f04
Now, fx=x2+x-1
f’x=2x+1 , f4=19 , f0=-1
∴ f’x=f4-f04-0
⇒2x+1=204⇒2x+1=5⇒2x=4 ⇒x=2
Thus, c=2∈0, 4 such that f’c=f4-f04-0.
Hence, Lagrange’s theorem is verified.
(xv) We have,
fx=sinx-sin2x-x
Since sinx, sin2x & x are everywhere continuous and differentiable
Therefore, fx is continuous on 0,π and differentiable on 0, π
Thus, both the conditions of lagrange’s theorem are satisfied.
Consequently, there exists some c∈0, π such that
f’c=fπ-f0π-0=fπ-f0π
Now, fx=sinx-sin2x-x
f’x=cosx-2cos2x-1 , fπ=-π , f0=0
∴ f’x=fπ-f0π-0
⇒cosx-2cos2x-1=-1⇒cosx-2cos2x=0⇒cosx-4cos2x=-2 ⇒4cos2x-cosx-2=0⇒cosx=181±33⇒x=cos-1181±33
Thus, c=cos-11±338∈0, π such that f’c=fπ-f0π-0.
Hence, Lagrange’s theorem is verified.
(xvi) We have,
fx=x3-5×2-3x
Since polynomial function is everywhere continuous and differentiable
Therefore, fx is continuous on 1, 3 and differentiable on 1, 3
Thus, both the conditions of lagrange’s theorem are satisfied.
Consequently, there exists some c∈1, 3 such that
f’c=f3-f13-1=f3-f12
Now, fx=x3-5×2-3x
f’x=3×2-10x-3 , f3=-27 , f1=-7
∴ f’x=f3-f12
⇒3×2-10x-3=-202⇒3×2-10x+7=0⇒x=1, 73
Thus, c=73∈1, 3 such that f’c=f3-f13-1.
Hence, Lagrange’s theorem is verified.
Q2.
Answer :
Given:
fx=x
If Lagrange’s theorem is applicable for the given function, then fx is continuous on -1, 1 and differentiable on -1, 1.
But it is known that fx=x is not differentiable at x=0∈-1, 1.
Thus, our supposition is wrong.
Therefore, Lagrange’s theorem is not applicable for the given function.
Q3.
Answer :
Given:
fx=1x
Clearly, fx does not exist for x = 0
Thus, the given function is discontinuous on -1, 1.
Hence, Lagrange’s mean value theorem is not applicable for the given function on -1, 1.1x
Q4.
Answer :
The given function is fx=14x-1.
Since for each x∈1, 4, the function attains a unique definite value, fx is continuous on 1, 4.
Also, f’x=-44x-12 exists for all x∈1, 4
Thus, both the conditions of Lagrange’s mean value theorem are satisfied.
Consequently, there exists some c∈1, 4 such that
f’c=f4-f14-1=f4-f13
Now,
fx=14x-1⇒f’x=-44x-12, f4=115, f1=13
∴ f’x=f4-f14-1
⇒f’x=115-134-1=-445⇒-44x-12=-445⇒4x-12=45⇒16×2-8x-44=0⇒4×2-2x-11=0⇒x=141±35
Thus, c=141+35∈1, 4 such that f’c=f4-f14-1.
Hence, Lagrange’s theorem is verified.
Q5.
Answer :
Let:
fx=x-42=x2-8x+16
The tangent to the curve is parallel to the chord joining the points 4, 0 and 5, 1.
Assume that the chord joins the points a, fa and b, fb.
∴ a=4, b=5
The polynomial function is everywhere continuous and differentiable.
So, x2-8x+16 is continuous on 4, 5 and differentiable on 4, 5.
Thus, both the conditions of Lagrange’s theorem are satisfied.
Consequently, there exists c∈4, 5 such that f’c=f5-f45-4.
Now,
fx=x2-8x+16⇒f’x=2x-8, f5=1, f4=0
∴f’x=f5-f45-4⇒2x-8=11⇒2x=9⇒x=92
Thus, c=92∈4, 5 such that f’c=f5-f45-4.
Clearly,
fc=92-42=14
Thus, c, fc, i.e. 92,14, is a point on the given curve where the tangent is parallel to the chord joining the points (4, 0) and (5, 1).
Q6.
Answer :
Let:
fx=x2+x
The tangent to the curve is parallel to the chord joining the points 0, 0 and 1, 2.
Assume that the chord joins the points a, fa and b, fb.
∴ a=0, b=1
The polynomial function is everywhere continuous and differentiable.
So, fx=x2+x is continuous on 0, 1 and differentiable on 0, 1.
Thus, both the conditions of Lagrange’s theorem are satisfied.
Consequently, there exists c∈0, 1 such that f’c=f1-f01-0.
Now,
fx=x2+x⇒f’x=2x+1, f1=2, f0=0
∴f’x=f1-f01-0⇒2x+1=2-01-0⇒2x=1⇒x=12
Thus, c=12∈0,1 such that f’c=f1-f01-0.
Clearly,
fc=122+12=34.
Thus, c, fc, i.e. 12, 34, is a point on the given curve where the tangent is parallel to the chord joining the points (4, 0) and (5, 1).
Q7.
Answer :
Let:
fx=x-32=x2-6x+9
The tangent to the curve is parallel to the chord joining the points 3, 0 and 4, 1.
Assume that the chord joins the points a, fa and b, fb.
∴ a=3, b=4
The polynomial function is everywhere continuous and differentiable.
So, fx=x2-6x+9 is continuous on 3, 4 and differentiable on 3, 4.
Thus, both the conditions of Lagrange’s theorem are satisfied.
Consequently, there exists c∈3, 4 such that f’c=f4-f34-3.
Now,
fx=x2-6x+9⇒f’x=2x-6, f3=0, f4=1
∴f’x=f4-f34-3⇒2x-6=1-04-3⇒2x=7⇒x=72
Thus, c=72∈3, 4 such that f’c=f4-f34-3.
Clearly,
fc=72-32=14
Thus, c, fc, i.e. 72, 14, is a point on the given curve where the tangent is parallel to the chord joining the points 3, 0 and 4, 1.
Q8.
Answer :
Let:
fx=x3-3x
The tangent to the curve is parallel to the chord joining the points 1, -2 and 2, 2.
Assume that the chord joins the points a, fa and b, fb.
∴ a=1, b=2
The polynomial function is everywhere continuous and differentiable.
So, fx=x3-3x is continuous on 1, 2 and differentiable on 1, 2.
Thus, both the conditions of Lagrange’s theorem are satisfied.
Consequently, there exists c∈1, 2 such that f’c=f2-f12-1.
Now,
fx=x3-3x⇒f’x=3×2-3, f1=-2, f2=2
∴f’x=f2-f12-1⇒3×2-3=2+22-1⇒3×2=7⇒x=±73
Thus, c=±73 such that f’c=f2-f12-1.
Clearly,
f73=7332-373=7373-3=73-23=-2373 and f-73=2373
∴ fc=∓2373
Thus, c, fc, i.e. ±73, ∓2373, are points on the given curve where the tangent is parallel to the chord joining the points 1, -2 and 2, 2.
Q9.
Answer :
Let:
fx=x3+1
The tangent to the curve is parallel to the chord joining the points 1, 2 and 3, 28.
Assume that the chord joins the points a, fa and b, fb.
∴ a=1, b=3
The polynomial function is everywhere continuous and differentiable.
So, fx=x3+1 is continuous on 1, 3 and differentiable on 1, 3.
Thus, both the conditions of Lagrange’s theorem are satisfied.
Consequently, there exists c∈1, 3 such that f’c=f3-f13-1.
Now,
fx=x3+1⇒f’x=3×2, f1=2, f3=28
∴f’x=f3-f13-1⇒3×2=262⇒3×2=13⇒x=±133
Thus, c=133 such that f’c=f3-f13-1.
Clearly,
fc=13332+1
Thus, c, fc, i.e. 133, 1+13332, is a point on the given curve where the tangent is parallel to the chord joining the points 1, 2 and 3, 28.
Q10.
Answer :
Consider, the function
fx=tanx, x∈a, b, 0<a<b<π2
Clearly, fx is continuous on a, b and derivable on a, b.
Thus, both the conditions of Lagrange’s theorem are satisfied.
Consequently, c∈a, b such that f’c=fb-fab-a.
Now,
fx=tanx ⇒ f’x=sec2x, fa=tana, fb=tanb
∴ f’c=fb-fab-a ⇒ sec2c=tanb-tanab-a …1
Now,
c∈a, b⇒a<c<b⇒sec2a<sec2c<sec2b ∵sec2x is increasing in 0, π2⇒sec2a<tanb-tanab-a<sec2b from 1⇒b-asec2a<tanb-tana<b-asec2b
Hence proved.
Page 15.20 (Very Short Answers)
Q1.
Answer :
We have
fx=Ax2+Bx+C
Differentiating the given function with respect to x, we get
f’x=2Ax+B
⇒f’c=2Ac+B
∴ f’c=0 ⇒2Ac+B=0⇒c=-B2A …1
∵fa=fb∴ Aa2+Ba+C=Ab2+bB+C⇒ Aa2+Ba=Ab2+bB⇒ Aa2-b2+Ba-b=0⇒ Aa-ba+b+Ba-b=0⇒ a-bAa+b+B=0⇒ a=b, A=-Ba+b⇒ a+b=-BA ∵a≠b
From (1), we have
c=a+b2
Q2.
Answer :
Rolle’s Theorem:
Let f be a real valued function defined on the closed interval a,b such that
(i) it is continuous on the closed interval a,b,
(ii) it is differentiable on the open interval a, b, and
(iii) fa=fb
Then, there exists a real number c∈a,b such that f’c=0.
Q3.
Answer :
Lagrange’s Mean Value Theorem:
Let fx be a function defined on a,b such that
(i) it is continuous on a,b and
(ii) it is differentiable on a,b.
Then, there exists a real number c∈a,b such that f’c=fb-fab-a.
Q4.
Answer :
We have
fx=2xx-3n
Differentiating the given function with respect to x, we get
f’x=2xnx-3n-1+x-3n⇒f’x=2x-3nxnx-3+1⇒f’c=2c-3ncnc-3+1
Given:
f’34=0
∴ 2-94n34n-94+1=0⇒ 2-94n-n3+1=0⇒-n3+1=0⇒-n+3=0⇒n=3
Q5.
Answer :
We have
fx=x2-4
Here, fx will exist, if
x2-4≥0⇒x≤-2 or x≥2
Since for each x∈2, 3, the function fx attains a unique definite value, fx is continuous on 2, 3.
Also, f’x=12×2-42x=xx2-4 exists for all x∈2, 3.
So, fx is differentiable on 2, 3.
Thus, both the conditions of lagrange’s theorem are satisfied.
Consequently, there exists c∈2, 3 such that
f’c=f3-f23-2=f3-f21
Now,
fx=x2-4
f’x=xx2-4 , f3=5 , f2=0
∴ f’x=f3-f23-2
⇒xx2-4=5⇒x2x2-4=5 ⇒x2=5×2-20⇒4×2=20⇒x=±5
Thus, c=5∈2, 3 such that f’c=f3-f23-2.
Hence, Lagrange’s theorem is verified.
Page 15.20 (Multiple Choice Questions)
Q1.
Answer :
(c) at least one root
We observe that, nanxn-1+n-1an-1xn-2+…+a1=0 is the derivative of the
polynomial anxn+an-1xn-1+an-2xn-2+…+a2x2+a1x+a0=0
Polynomial function is continuous every where in R and consequently derivative in R
Therefore, anxn+an-1xn-1+an-2xn-2+…+a2x2+a1x+a0 is continuous on α, β and derivative on α, β.
Hence, it satisfies the both the conditions of Rolle’s theorem.
By algebraic interpretation of Rolle’s theorem, we know that between any two roots of a function fx, there exists at least one root of its derivative.
Hence, the equation nanxn-1+n-1an-1xn-2+…+a1=0 will have at least one root between α and β.
Q2.
Answer :
(c) (0, 2)
Letfx=ax3+bx2+cx+d …..1f0=df2=8a+4b+2c+d =24a+2b+c+d =d ∵4a+2b+c=0
f is continuous in the closed interval [0, 2] and f is derivable in the open interval (0, 2).
Also, f(0) = f(2)
By Rolle’s Theorem,
f’α=0 for 0<α<2Now, f’x=3ax2+2bx+c⇒f’α=3aα2+2bα+c=0Equation 1 has atleast one root in the interval 0, 2.Thus, f’x must have root in the interval 0, 2.
Q3.
Answer :
(b)3
We have
fx=x+1x=x2+1x
Clearly, fx is continuous on 1, 3 and derivable on 1, 3.
Thus, both the conditions of Lagrange’s theorem are satisfied.
Consequently, there exists c∈1, 3 such that
f’c=f3-f13-1=f3-f12
Now, fx=x2+1x
f’x=x2-1×2 , f1=2 , f3=103
∴ f’x=f3-f12
⇒x2-1×2=46⇒x2-1×2=23⇒3×2-3=2×2⇒x=±3
Thus, c=3∈1, 3 such that f’c=f3-f13-1.
Page 15.21 (Multiple Choice Questions)
Q4.
Answer :
(c) a < x1 < b
In the Lagrange’s mean value theorem, c∈a, b such that f’c=fb-fab-a.
So, if there is x1 such that f’x1=fb-fab-a, then x1∈a, b.
⇒a<x1<b
Q5.
Answer :
(b) the interval [0, π]1−5√2
The given function is ϕx=asinx, where a > 0.
Differentiating the given function with respect to x, we get
f’x=loga cosx asinx
⇒ f’c=loga cosc asinc
Let f’c=0 ⇒loga cosc asinc=0⇒ cosc asinc=0⇒ cosc=0⇒c=π2
∴ c∈0, π
Also, the given function is derivable and hence continuous on the interval 0, π.
Hence, the Rolle’s theorem is applicable on the given function in the interval 0, π.
Q6.
Answer :
(a) 2
Given:
fx=2×3-5×2-4x+3
Differentiating the given function with respect to x, we get
f’x=6×2-10x-4⇒f’c=6c2-10c-4∴f’c=0 ⇒ 3c2-5c-2=0⇒ 3c2-6c+c-2=0⇒ 3cc-2+c-2=0⇒ 3c+1c-2=0⇒ c=2, -13∴ c=2∈13, 3
Thus, c=2∈13,3 for which Rolle’s theorem holds.
Hence, the required value of c is 2.
Q7.
Answer :
(a) e1/1−e
Given:
y=fx=xlogx
Differentiating the given function with respect to x, we get
f’x=1+logx
⇒ Slope of the tangent to the curve = 1+logx
Also,
Slope of the chord joining the points 1, 0 and e, e, (m) = ee-1
The tangent to the curve is parallel to the chord joining the points 1, 0 and e, e.
∴ m=1+logx
Q8.
Answer :
(c) 1-521−5√2
Given:
fx=xx+1ex
Differentiating the given function with respect to x, we get
f’x=ex2x+1-xx+1exex2⇒f’x=2x+1-xx+1ex⇒f’x=2x+1-x2-xex ⇒f’x=-x2+x+1ex⇒f’c=-c2+c+1ec∴ f’c=0 ⇒ -c2+c+1ec=0⇒ c2-c-1=0⇒ c=1-52, 1+52∴ c=1-52∈-1, 0
Hence, the required value of c is 1-52.
Q9.
Answer :
(d)32
We have
f (x) = x (x − 2)
It can be rewritten as fx=x2-2x.
We know that a polynomial function is everywhere continuous and differentiable.
Since fx is a polynomial , it is continuous on 1, 2 and differentiable on 1, 2.
Thus, fx satisfies both the conditions of Lagrange’s theorem on 1, 2.
So, there must exist at least one real number c ∈1, 2 such that
f’c=f2-f12-1=f2-f11
Now, fx=x2-2x
⇒f’x=2x-2,
and f1=-1, f2=0
∴ f’x=f2-f12-1
⇒f’x=0+11⇒2x-2=1⇒x=32
∴ c=32∈1, 2
Q10.
Answer :
(a) 1
The given function is fx=x3-3x.
This is a polynomial function, which is continuous and derivable in R.
Therefore, the function is continuous on [0, 3] and derivable on (0, 3 ).
Differentiating the given function with respect to x, we get
f’x=3×2-3⇒f’c=3c2-3∴ f’c=0 ⇒ 3c2-3=0⇒c2=1⇒c=±1
Thus, c=1∈0, 3 for which Rolle’s theorem holds.
Hence, the required value of c is 1.
Q11.
Answer :
(d) 3π/4
The given function is fx=exsinx.
Differentiating the given function with respect to x, we get
f’x=excosx+sinxex⇒f’c=eccosc+sincecNow , excosx is continuous and derivable in R.Therefore, it is continuous on 0, π and derivable on 0, π.∴ f’c=0 ⇒ eccosc+sinc=0⇒ cosc+sinc=0 ∵ ec≠0⇒ tanc=-1⇒ c=3π4, 7π4, …∴ c=3π4∈0, π
Thus, c=3π4∈0,π for which Rolle’s theorem holds.
Hence, the required value of c is 3π/4.
Page 16.10 Ex.16.1
Q1.
Answer :
i) y=x3=x32⇒dydx=32×12=32xWhen x=4, y=x3=64=8Now,Slope of the tangent=dydx4, 8=324=3Slope of the normal=-1dydx4, 8=-13
ii) y=x=x12⇒dydx=12x-12=12xWhen x=9, y=x=9=3Now,Slope of the tangent=dydx9, 3=129=16Slope of the normal=-1dydx9, 3=-116=-6
iii) y=x3-x⇒dydx=3×2-1When x=2, y=x3-x=23-2=6Now,Slope of the tangent=dydx2, 6=322-1=11Slope of the normal=-1dydx2, 6=-111
iv) y=2×2+3 sin x⇒dydx=4x+3 cos xWhen x=0, y=2×2+3 sin x=202+3 sin 0=0Now,Slope of the tangent=dydx0, 0=40+ 3 cos 0=3Slope of the normal=-1dydx0, 0=-13
v) x=aθ-sin θ⇒dxdθ=a1-cos θ y=a1+cos θ ⇒dydθ=a-sin θ∴ dydx=dydθdxdθ=a-sin θa1-cos θ=-2 sin θ2 cos θ22 sin2θ2=-cot θ2Now,Slope of the tangent=dydxθ=-π2=-cot -π22=-cot -π4=1Slope of the normal=-1dydxθ=-π2=-11=-1
vi) x=a cos3 θ⇒dxdθ=-3a cos2 θ sin θy=a sin3 θ⇒ dydθ=3a sin2 θ cos θ∴ dydx=dydθdxdθ=3a sin2 θ cos θ-3a cos2 θ sin θ=-tan θNow,Slope of the tangent=dydxθ=π4=-tan π4=-1Slope of the normal=-1dydxθ=π4=-1-1=1
vii) x=aθ-sin θ⇒dxdθ=a1-cos θ y=a1-cos θ⇒ dydθ=asin θ∴ dydx=dydθdxdθ=asin θa1-cos θ=2 sin θ2 cos θ22 sin2θ2=cot θ2Now,Slope of the tangent=dydxθ=π2=cot π22=cot π4=1Slope of the normal=-1dydxθ=π2=-11=-1
viii) y=sin 2x+cot x+22⇒dydx=2 sin 2x+cot x+2 2cos 2x-cosec2xNow,Slope of the tangent=dydxx=π2=2 sin 2π2+cot π2+2 2cos 2π2-cosec2 π2=2 0+0+2 -2-1=-12Slope of the normal=-1dydxx=π2=-1-12=112
ix) x2+3y+y2=5On differentiating both sides w.r.t. x, we get2x+3dydx+2y dydx=0⇒dydx3+2y=-2x⇒dydx=-2×3+2yNow,Slope of the tangent=dydx1, 1=-2×3+2y=-23+2=-25Slope of the normal=-1dydx1, 1=-1-25=52
x) xy=6On differentiating both sides w.r.t. x, we getxdydx+y=0⇒xdydx=-y⇒dydx=-yxNow,Slope of the tangent=dydx1, 6=-yx=-61=-6Slope of the normal=-1dydx1, 6=-1-6=16
Q2.
Answer :
Given:xy+ax+by=2 … 1On differentiating both sides w.r.t. x, we getxdydx+y+a+bdydx=0⇒dydxx+b=-a-y⇒dydx=-a-yx+bNow,dydx1, 1=2⇒-a-11+b=2⇒-a-1=2+2b⇒-a=3+2b⇒a=-3+2bOn substituting a=-3+2b, x=1 and y=1 in eq. (1), we get1-3+2b+b=2⇒1-3-2b+b=2⇒b=-4and a=-3+2b=-3-8=5∴ a=5 and b=-4
Q3.
Answer :
Given: x-y+5=0⇒y=x+5⇒dydx=1Now, y=x3+ax+b …1⇒dydx=3×2+aSlope of the tangent at 1, -6 = Slope of the given line⇒dydx1, -6=1⇒3+a=1⇒a=-2On substituting a=-2, x=1 and y=-6 in eq. (1), we get-6=1-2+b⇒b=-5∴ a=-2 and b=-5
Q4.
Answer :
Let (x1, y1) be the required point.
Slope of the chord=y2-y1x2-x1=2+22-1=4y=x3-3x⇒dydx=3×2-3 …1Slope of the tangent=dydxx1, y1=3×12-3It is given that the tangent and the chord are parallel.∴ Slope of the tangent = Slope of the chord⇒3×12-3=4⇒3×12=7⇒x12=73⇒x1=±73=73 or -73Case 1When x1=73On substituting this in eq. (1), we get y1=73 3-373 =7373 -373 =-2373 ∴ x1, y1=73, -2373 Case 2When x1=-73On substituting this in eq. (1), we get y1=-73 3-3-73 =-7373 +373 =2373 ∴ x1, y1=-73, 2373
Q5.
Answer :
Let (x1, y1) be the required point.
Given:
y=2x-3∴ Slope of the line= dydx=2y=x3-2×2-2xSince x1y1 lies on curve, y1=x13-2×12-2×1 …1⇒dydxx1,y1=3×12-4×1-2It is given that the tangent and the given line are parallel.∴ Slope of the tangent = Slope of the given line3x12-4×1-2=2⇒3×12-4×1-4=0⇒3×12-6×1+2×1-4=0⇒3×1 x1-2 +2 x1-2=0⇒x1-2 3×1+2=0⇒x1=2 or x1=-23Case 1When x1=2On substituting the value of x1 in eq. (1), we get y1=8-8-4=-4∴ x1, y1=2, -4 Case 2When x1=-23On substituting the value of x1 in eq. (1), we get y1=-827-89+43=-8-24+3627=427∴ x1, y1=-23, 427
Q6.
Answer :
Let (x1, y1) be the required point.
Given:
y2=2×3 Since x1y1 lies on a curve, y12=2×13 ….1⇒2ydydx=6×2⇒dydx=6x22y=3x2ySlope of the tangent at x, y=3x12y1Slope of the tangent=3 [Given]∴ 3x12y1=3 ….2⇒y1=x12On substituting the value of y1 in eq. (1), we getx14=2×13⇒x13 x1-2=0⇒x1=0, 2Case 1 When x1=0, y1=x2=0. Thus, we get the point 0, 0. But, it does not satisfy eq. (2). So, we can ignore (0, 0).Case 2 When x1=2, y1=x12=4. Thus, we get the point 2, 4.
Q7.
Answer :
Let the required point be (x1, y1).
Slope of the tangent at this point = tan 45° = 1
Given:
xy+4=0 … 1Since the point satisfies the above equation,x1y1+4=0 …2On differentiating equation 2 both sides with respect to x, we get xdydx+y=0⇒dydx=-yxSlope of the tangent at x1, y1 = dydxx, y=-y1x1Slope of the tangent =1 [Given]∴ -y1x1=1⇒x1=-y1On substituting the value of x1 in eq. (2), we get-y12+4=0⇒y12=4⇒y1=±2Case 1When y1=2, x1=-y1=-2∴ (x1, y1) = (-2, 2)Case 2When y1=-2, x1=-y1=2∴ x1, y1 = (2, -2)
Q8.
Answer :
Let the required point be (x1, y1).
Given:
y=x2Point x1, y1 lies on a curve.∴ y1=x12 …1Now,y=x2⇒ dydx=2xSlope of the tangent at x1, y1 = dydxx1, y1=2x1Slope of the tangent =x coordinate of the point [Given]∴ 2×1=x1This happens only when x1= 0.On putting x1=0 in eq. 1, we gety1=x12=02=0Thus, t
Q9.
Answer :
Let the required point be (x1, y1).
We know that the slope of the x-axis is 0.
Given:
x2+y2-2x-4y+1=0 x1,y1 lies on a curve.∴ x12+y12-2×1-4y1+1=0 …1Now, x2+y2-2x-4y+1=0 ⇒2x+2y dydx-2-4dydx=0⇒dydx 2y-4=2-2x⇒dydx=2-2x2y-4=1-xy-2Slope of the tangent at x1, y1=dydxx1, y1= 1-x1y1-2 …(2)Slope of the tangent = 0 [Given]∴1-x1y1-2=0⇒1-x1=0⇒x1=1On substituting the value of x1 in eq. (1), we get1+y12-2-4y1+1=0⇒y12-4y1=0⇒y1y1-4=0⇒y1=0, 4Thus, the required points are (1, 0) and (1, 4).
Q10.
Answer :
Let the required point be (x1, y1).
The tangent makes an angle of 45o with the x-axis.
∴ Slope of the tangent = tan 45o = 1
Since, the point lies on the curve.Hence, y12=x1Now, y2=x⇒2ydydx=1⇒dydx=12ySlope of the tangent = dydxx1, y1=12y1Given:12y1=1⇒2y1=1⇒y1=12Now,x1=y12=122=14∴x1, y1=14, 12
Q11.
Answer :
Let (x1, y1) be the required point.
It is given that the tangent at this point is equally inclined to the axes. It means that the angle made by the tangent with the x-axis is ±45°.
∴ Slope of the tangent = tan (±45) = ± 1 …(1)
Since, the point lies on the curve.Hence, y1=3×12-9×1+8 Now, y=3×2-9x+8⇒dydx=6x-9Slope of the tangent at x1, y1=dydxx1, y1=6×1-9 …(2)From eq. (1) and eq. (2), we get6x1-9=±1⇒6×1-9=1 or 6×1-9=-1⇒6×1=10 or 6×1=8⇒x1=106=53 or x1=86=43Also,y1=3532-953+8 or y1=3432-943+8⇒y1=253-453+8 or y1=163-363+8⇒y1=43 or y1=43Thus, the required points are 53, 43 and 43, 43.
Q12.
Answer :
Let (x1, y1) be the required point.
The slope of line y = 3x + 4 is 3.
Since, the point lies on the curve.Hence, y1=2×12-x1+1Now, y=2×2-x+1dydx=4x-1Now,Slope of the tangent at x1, y1=dydxx1, y1=4×1-1Slope of the tangent at x1, y1= Slope of the given line [Given]∴ 4×1-1=3⇒4×1=4⇒x1=1andy1=2×12-x1+1=2-1+1=2Thus, the required point is 1, 2.
Q13.
Answer :
Let (x1, y1) be the required point.
Slope of the given line = -16
∴ Slope of the line perpendicular to it = 6
Since, the point lies on the curve.Hence, y1=3×12+4Now, y=3×2+4∴ dydx=6xNow,Slope of the tangent at x1, y1=dydxx1, y1=6x1Slope of the tangent at x1, y1= Slope of the given line [Given]∴ 6×1=6⇒x1=1andy1=3×12+4=3+4=7Thus, the required point is 1, 7.
Q14.
Answer :
Let (x1, y1) represent the required point.
The slope of line 2x + 3y = 7 is -23.
Since, the point lies on the curve.Hence, x12+y12=13 …1Now, x2+y2=13On differentiating both sides w.r.t. x, we get2x+2ydydx=0⇒dydx=-xySlope of the tangent at x1, y1=dydxx1, y1=-x1y1Slope of the tangent at x1, y1= Slope of the given line [Given]⇒-x1y1=-23⇒x1=2y13 …2From eq. (1), we get2y132+y12=13⇒13y129=13⇒y12=9⇒y1=±3⇒y1=3 or y1=-3andx1=2 or x1=-2 [From eq. (2)]Thus, the required points are 2, 3 and -2, -3.
Q15.
Answer :
Let (x1, y1) represent the required points.
The slope of the x-axis is 0.
Here,
2a2y=x3-3ax2 Since, the point lies on the curve.Hence, 2a2y1=x13-3ax12 …1Now, 2a2y=x3-3ax2 On differentiating both sides w.r.t. x, we get2a2dydx=3×2-6ax⇒dydx=3×2-6ax2a2Slope of the tangent at x1, y1=dydxx1, y1=3×12-6ax12a2Given:Slope of the tangent at x1, y1= Slope of the x-axis⇒3×12-6ax12a2=0⇒3×12-6ax1=0⇒x1 3×1-6a=0⇒x1=0 or x1= 2aAlso,2a2y1=0 or 2a2y1=8a3-12a3 [From eq. (1)]⇒y1=0 or y1=-2aThus, the required points are 0, 0 and 2a, -2a.
Q16.
Answer :
Let (x1, y1) be the required point.
Slope of the given line = -12
Slope of the line perpendicular to this line = 2
Since, the point lies on the curve.Hence, y1=x12-4×1+5 …1Now, y=x2-4x+5 ∴dydx=2x-4Now,Slope of the tangent at x1, y1=dydxx1, y1=2×1-4Slope of the tangent at x1, y1=Slope of the given line [Given]∴2×1-4=2⇒2×1=6⇒x1=3Also,y1=9-12+5=2 [From eq. (1)]Thus, the required point is 3, 2.
Q17.
Answer :
(i) The slope of the x-axis is 0.
Now, let (x1, y1) be the required point.
Since, the point lies on the curve.Hence, x124+y1225=1 …1 Now, x24+y225=1 ∴ 2×4+2y25dydx=0⇒2y25dydx=-x2⇒dydx=-25x4yNow,Slope of the tangent at x1, y1=dydxx1, y1=-25x14y1Slope of the tangent at x1, y1=Slope of the x-axis [Given]∴ -25x14y1=0⇒x1=0Also,0+y1225=1 [From eq. (1)]⇒y12=25⇒y1=±5Thus, the required points are 0, 5 and 0, -5.
(ii) The slope of the y-axis is ∞.
Now, let (x1, y1) be the required point.
Since, the point lies on the curve.Hence, x124+y1225=1 …1Now, x24+y225=1 ∴ 2×4+2y25dydx=0⇒2y25dydx=-x2⇒dydx=-25x4yNow,Slope of the tangent at x1, y1=dydxx1, y1=-25x14y1Slope of the tangent at x1, y1=Slope of the y-axis [Given]∴ -25x14y1=∞⇒4y1-25×1=0⇒y1=0Also,x124=1 [From eq. (1)]⇒x12=4⇒x1=±2Thus, the required points are 2, 0 and -2, 0.
Page 16.11 Ex.16.1
Q18.
Answer :
Let (x1, y1) be the required point.
Since the point lie on the curve.Hence x12+y12-2×1-3=0 …1Now, x2+y2-2x-3=0 ⇒2x+2y dydx-2=0∴dydx=2-2x2y=1-xyNow,Slope of the tangent = dydxx1, y1= 1-x1y1Slope of the tangent = 0 (Given)∴1-x1y1=0⇒1-x1=0⇒x1=1From (1), we getx12+y12-2×1-3=0⇒1+y12-2-3=0⇒y12-4=0⇒y1=±2Hence, the points are 1, 2 and 1, -2.
Q19.
Answer :
(i) The slope of the x-axis is 0.
Now, let (x1, y1) be the required point.
Since, the point lies on the curve.Hence, x129+y1216=1 …1Now, x29+y216=1 ⇒ 2×9+2y16dydx=0⇒y16dydx=-x9⇒dydx=-16x9yNow,Slope of the tangent at x, y=dydxx1, y1=-16x19y1Slope of the tangent at x, y= Slope of the x-axis [Given]∴ -16x19y1=0⇒x1=00+y1216=1 [From eq. (1)]Also,y12=16y1=±4Thus, the required points are 0, 4 and 0, -4.
(ii) The slope of the y-axis is ∞.
Let (x1, y1) be the required point.
Given:
Since, the point lies on the curve.Hence, x129+y1216=1 …1×29+y216=1 ⇒ 2×9+2y16dydx=0⇒y16dydx=-x9⇒dydx=-16x9yNow,Slope of the tangent at x, y=dydxx1, y1=-16x19y1Slope of the tangent at x1, y1 = Slope of the y-axis [Given]∴-16x19y1=∞⇒9y1-16×1=0⇒y1=0⇒x129+0=1 [From eq. (1)]⇒x12=9⇒x1=±3Thus, the required points are 3, 0 and -3, 0.
Q20.
Answer :
Given: y=7×3+11∴ dydx=21x2Now,Slope of the tangent at (x=2) = dydxx=2=21 22=84Slope of the tangent at (x=-2) = dydxx=-2=21 -22=84
Both slopes are the same. Hence, the tangents at points x = 2 and x = −2 are parallel.
Q21.
Answer :
Let (x1, y1) be the required point.
x coordinate of the point is x1.
Since, the point lies on the curve.Hence, y1=x13 … 1Now, y=x3⇒dydx=3x2Slope of tangent at x, y=dydxx1, y1=3x12Given thatSlope of tangent at x1, y1= x co-ordinate of the point⇒3×12=x1⇒x1 3×1-1=0⇒x1=0 or x1=13⇒y1=03 or y1=133 (From (1))⇒y1=0 or y1=127So, the points are x1, y1= 0, 0, 13, 127
Page 16.28 Ex.16.2
Q1.
Answer :
x+y=aDifferentiating both sides w.r.t. x,⇒12x+12ydydx=0⇒dydx=-yxGiven x1, y1=a24, a24Slope of tangent, m = dydxa24, a24=-a24a24=-1Equation of tangent is,y-y1=m x-x1⇒y-a24=-1x-a24⇒y-a24=-x+a24⇒x+y=a22
Q2.
Answer :
y=2×3-x2+3Differentiating both sides w.r.t. x,dydx=6×2-2xSlope of tangent = dydx1, 4=6 12-2 1=4Slope of normal = -1Slope of tangent=-14Given x1, y1=1, 4Equation of normal is,y-y1=m x-x1⇒y-4=-14 x-1⇒4y-16=-x+1⇒x+4y=17
Q3.
Answer :
(i)
y=x4-bx3+13×2-10x+5Differentiating both sides w.r.t. x,dydx=4×3-3bx2+26x-10Slope of tangent, m = dydx0, 5=-10Given x1, y1=0, 5Equation of tangent is,y-y1=m x-x1⇒y-5=-10x-0⇒y-5=-10x⇒y+10x-5=0
Equation of normal is,y-y1=-1m x-x1⇒y-5=110 x-0⇒10y-50=x⇒x-10y+50=0
(ii)
y=x4-6×3+13×2-10x+5When x=1 , y=1-6+13-10+5=3So, x1, y1=1, 3Now, y=x4-6×3+13×2-10x+5Differentiating both sides w.r.t. x,dydx=4×3-18×2+26x-10Slope of tangent, m = dydx1,3=4-18+26-10=2Equation of tangent is,y-y1=2 x-x1⇒y-3=2x-1⇒y-3=2x-2⇒2x-y+1=0
Equation of normal is,y-y1=-1m x-x1⇒y-3=-12 x-1⇒3y-6=-x+1⇒x+3y-7=0
(iii)
y=x2Differentiating both sides w.r.t. x,dydx=2xGiven x1, y1=0, 0Slope of tangent, m = dydx0, 0=2 0=0Equation of tangent is,y-y1=mx-x1⇒y-0=0 x-0⇒y=0
Equation of normal is,⇒y-y1=-1m x-x1⇒y-0=-10 x-0⇒x=0
(iv)
y=2×2-3x-1Differentiating both sides w.r.t. x,dydx=4x-3Given x1, y1=1, -2Slope of tangent, m = dydx1, -2=4-3=1Equation of tangent is,y-y1=mx-x1⇒y+2=1 x-1⇒y+2=x-1⇒x-y-3=0
Equation of normal is,y-y1=-1m x-x1⇒y+2=-1 x-1⇒y+2=-x+1⇒x+y+1=0
(v)
y2=x34-xDifferentiating both sides w.r.t. x,2y dydx=4-x3x2-x3-14-x2=12×2-3×3+x34-x2=12×2-2×34-x2dydx=12×2-2x32y 4-x2Given x1, y1=2, -2Slope of tangent, m = dydx2, -2=48-16-16=-2Equation of tangent is,y-y1=mx-x1⇒y+2=-2 x-2⇒y+2=-2x+4⇒2x+y-2=0
Equation of normal is,y-y1=-1m x-x1⇒y+2=12 x-2⇒2y+4=x-2⇒x-2y-6=0
(vi)
y=x2+4x+1Differentiating both sides w.r.t. x,dydx=2x+4When x =3, y=9+12+1=22 So, x1, y1=3, 22Slope of tangent, m = dydxx=3=10Equation of tangent is,y-y1=m x-x1⇒y-22=10x-3⇒y-22=10x-30⇒10x-y-8=0
Equation of normal is,y-y1=-1m x-x1⇒y-22=-110 x-3⇒10y-220=-x+3⇒x+10y-223=0
(vii)
x2a2+y2b2=1Differentiating both sides w.r.t. x,⇒2xa2+2yb2dydx=0⇒2yb2dydx=-2xa2⇒dydx=-xb2ya2Slope of tangent, m = dydxa cos θ, b sin θ=-a cos θ b2b sin θ a2=-b cos θa sin θGiven x1, y1=a cos θ, b sin θEquation of tangent is,y-y1=m x-x1⇒y-b sin θ=-b cos θa sin θx-a cos θ⇒ay sin θ-ab sin2 θ=-bx cos θ+ab cos2 θ⇒bx cos θ+ay sin θ=abDividing by ab,⇒xacos θ +ybsin θ=1
Equation of normal is,y-y1=-1m x-x1⇒y-b sin θ=a sin θb cos θx-a cos θ⇒by cos θ-b2sin θ cos θ=ax sin θ-a2sin θ cos θ⇒ax sin θ-by cos θ=a2-b2sin θ cos θDividing by sin θ cos θ,ax sec θ-by cosec θ=a2-b2
(viii)
x2a2-y2b2=1Differentiating both sides w.r.t. x,⇒2xa2-2yb2dydx=0⇒2yb2dydx=2xa2⇒dydx=xb2ya2Slope of tangent, m = dydxa sec θ, b tan θ=a sec θ b2b tan θ a2=b a sin θGiven x1, y1=a sec θ, b tan θEquation of tangent is,y-y1=m x-x1⇒y-b tan θ=b a sin θx-a sec θ⇒ay sin θ -ab sin2θcos θ=bx-abcos θ⇒ay sin θ cos θ-ab sin2θcos θ=bx cos θ -abcos θ⇒ay sin θ cos θ-ab sin2θ=bx cos θ -ab⇒bx cos θ-ay sin θ cos θ=ab 1-sin2 θ ⇒bx cos θ-ay sin θ cos θ=ab cos2θDividing by ab cos2 θ,⇒xasec θ -ybtan θ=1
Equation of normal is,y-y1=-1m x-x1⇒y-b tan θ=-a sin θbx-a sec θ⇒yb-b2tan θ=-ax sin θ+a2 tanθ⇒ax sin θ+by=a2+b2tan θDividing by tan θ,ax cos θ+by cot θ=a2+b2
(ix)
y2=4axDifferentiating both sides w.r.t. x,2y dydx=4a⇒dydx=2ayGiven x1, y1=am2, 2amSlope of tangent = dydxam2, 2am=2a2am=mEquation of tangent is,y-y1=m x-x1⇒y-2am=m x-am2⇒my-2am=mm2x-am2⇒my-2a=m2x-a⇒m2x-my+a=0
Equation of normal is,y-y1=1Slope of tangent x-x1⇒y-2am=-1mx-am2⇒my-2am=-1mm2x-am2⇒m3y-2am2=-m2x+a⇒m2x+m3y-2am2-a=0
(x)
c2x2+y2=x2y2Differentiating both sides w.r.t. x,⇒2x c2+2y c2dydx=x2 2y dydx+2xy2⇒dydx2y c2-2x2y=2xy2-2xc2⇒dydx=xy2-xc2yc2-x2ySlope of tangent, m = dydxccos θ, csin θ=c3cos θ sin2θ -c3cos θc3sinθ-c3cos2θ sinθ=1-sin2θcosθ sin2θcos2θ-1cos2θ sinθ=cos2θcos θ sin2θ×cos2θ sinθ-sin2θ=-cos3θsin3θGiven x1, y1=ccos θ, csin θEquation of tangent is,y-y1=m x-x1⇒y-csin θ=-cos3θsin3θ x-ccos θ⇒ysinθ-csinθ=-cos3θsin3θx cosθ-ccosθ⇒sin2θy sinθ -c=-cos2θxcosθ-c⇒ysin3θ-csin2θ=-xcos3θ+ccos2θ⇒xcos3θ+ysin3θ=csin2θ+cos2θ⇒xcos3θ+ysin3θ=c
Equation of normal is,y-y1=-1m x-x1⇒y-csin θ=sin3θcos3θx-ccos θ⇒cos3θy-csin θ=sin3θx-ccos θ⇒ycos3θ-c cos3θsinθ=xsin3θ-c sin3θcosθ⇒xsin3θ-ycos3θ=c sin3θcosθ-c cos3θsinθ⇒xsin3θ-ycos3θ=csin4θ-cos4θcosθ sinθ⇒xsin3θ-ycos3θ=csin2θ+cos2θsin2θ-cos2θcosθ sinθ⇒sin3θ-ycos3θ=2c-cos2θ-sin2θ2cosθ sinθ⇒sin3θ-ycos3θ=2c-cos 2θsin2θ⇒sin3θ-ycos3θ=-2c cot2θ⇒sin3θ-ycos3θ+2c cot2θ=0
(xi)
xy=c2Differentiating both sides w.r.t. x,xdydx+y=0⇒dydx=-yxGiven x1, y1=ct, ctSlope of tangent, m = dydxct, ct=-ctct=-1t2Equation of tangent is,y-y1=m x-x1⇒y-ct=-1t2 x-ct⇒yt-ct=-1t2 x-ct⇒yt2-ct=-x+ct⇒x+yt2=2ct
Equation of normal is,y-y1=-1m x-x1⇒y-ct=t2x-ct⇒yt-c=t3x-ct4⇒xt3-yt=ct4-c
(xii)
x2a2+y2b2=1Differentiating both sides w.r.t. x,2xa2+2yb2dydx=0⇒2yb2dydx=-2xa2⇒dydx=-xb2ya2Slope of tangent, m = dydxx1, y1=-x1b2y1a2Equation of tangent is,y-y1=m x-x1⇒y-y1=-x1b2y1a2x-x1⇒yy1a2-y12a2=-xx1b2+x12b2⇒xx1b2+yy1a2=x12b2+y12a2 … 1Since x1, y1 lies on the given curve.Therefore,x12a2+y12b2=1⇒x12b2+y12a2a2b2=1⇒x12b2+y12a2=a2b2Substituting this in (1), we getxx1b2+yy1a2=a2b2Dividing this by a2b2,xx1a2+yy1b2=1
Equation of normal is,y-y1=m x-x1⇒y-y1=y1a2x1b2x-x1⇒yx1b2-x1y1b2=xy1a2-x1y1a2⇒xy1a2-yx1b2=x1y1a2-x1y1b2⇒xy1a2-yx1b2=x1y1a2-b2Dividing by x1y1a2xx1-b2yy1=a2-b2
(xiii)
x2a2-y2b2=1Differentiating both sides w.r.t. x,2xa2-2yb2dydx=0⇒2yb2dydx=2xa2⇒dydx=xb2ya2Slope of tangent, m = dydxx0, y0=x0b2y0a2Equation of tangent is,y-y1=m x-x1⇒y-y0=x0b2y0a2x-x0⇒yy0a2-y02a2=xx0b2-x02b2xx0b2-yy0a2=x02b2-y02a2 … 1Since x0, y0 lies on the given curve,⇒x02a2-y02b2=1⇒x02b2-y02a2=a2b2Substituting this in (1), we get⇒xx0b2-yy0a2=a2b2Dividing this by a2b2xx0a2-yy0b2=1
Equation of normal is,y-y1=m x-x1⇒y-y0=-y0a2x0b2x-x0⇒yx0b2-x0y0b2=-xy0a2+x0y0a2⇒xy0a2+yx0b2=x0y0a2+x0y0b2⇒xy0a2+yx0b2=x0y0a2+b2Dividing by x0y0a2xx0+b2yy0=a2+b2
(xiv)
x23+y23=2Differentiating both sides w.r.t. x,23x-13+23y-13dydx=0⇒dydx=-x-13y-13=-y13x13Slope of tangent, m = dydx1, 1= -11=-1Given x1, y1=1, 1Equation of tangent is,y-y1=m x-x1⇒y-1=-1x-1⇒y-1=-x+1⇒x+y-2=0
Equation of normal is,y-y1=-1m x-x1⇒y-1=1x-1⇒y-1=x-1⇒y-x=0
(xv)
x2=4yDifferentiating both sides w.r.t. x,2x=4dydx⇒dydx=x2Slope of tangent, m = dydx2, 1=22=1Given x1, y1=2, 1Equation of tangent is,y-y1=m x-x1⇒y-1=1x-2⇒y-1=x-2⇒x-y-1=0
Equation of normal is,y-y1=-1m x-x1⇒y-1=-1x-2⇒y-1=-x+2⇒x+y-3=0
(xvi)
y2=4xDifferentiating both sides w.r.t. x,2y dydx=4⇒dydx=2ySlope of tangent, m = dydx1, 2=22=1Given x1, y1=1, 2Equation of tangent is,y-y1=m x-x1⇒y-2=1x-1⇒y-2=x-1⇒x-y+1=0
Equation of normal is,y-y1=-1m x-x1⇒y-2=-1x-1⇒y-2=-x+1⇒x+y-3=0
(xvii) Equation of tangent:
4×2+9y2=36Differentiating both sides w.r.t. x,8x+18y dydx=0⇒18y dydx=-8x⇒dydx=-8x18y=-4x9ySlope of tangent, m = dydx3 cosθ, 2 sinθ=-12cosθ18sinθ=-2 cosθ3 sinθGiven x1, y1=3 cosθ, 2 sinθEquation of tangent is,y-y1=m x-x1⇒y-2 sinθ=-2 cosθ3 sinθx-3 cosθ⇒3y sinθ-6sin2θ=-2x cosθ+6cos2θ⇒2x cosθ+3y sinθ=6cos2θ+sin2θ⇒2x cosθ+3y sinθ=6
Equation of normal is,y-y1=-1m x-x1⇒y-2 sinθ=3 sinθ2 cosθx-3 cosθ⇒2y cosθ-4 sinθ cosθ=3x sinθ-9 sinθ cosθ⇒3x sinθ-2y cosθ-5sinθ cosθ=0
Q4.
Answer :
x=θ+sin θ and y=1+cos θdxdθ=1+cos θ and dydθ=-sin θ∴dydx=dydθdxdθ=-sin θ1+cos θSlope of tangent=dydxθ=π4=-sin π41+cos π4=-121+12=-12+1=-12+1×2-12-1=1-2×1, y1=π4+sinπ4, 1+cos π4=π4+12, 1+12Equation of tangent is,y-y1=mx-x1⇒y-1+12=1-2x-π4+12⇒y-1-12=1-2x-π4-12
Q5.
Answer :
(i)
x=θ+sinθ and y=1+cosθdxdθ=1+cosθ and dydθ=-sinθ∴dydx=dydθdxdθ=-sinθ1+cosθSlope of tangent, m = dydxθ=π2=-sinπ21+cosπ2=-11+0=-1Now, x1, y1=π2+sinπ2, 1+cosπ2=π2+1, 1Equation of tangent is,y-y1=m x-x1⇒y-1=-1x-π2-1⇒2y-2=-2x+π+2⇒2x+2y-π-4=0
Equation of normal is,y-y1=-1m x-x1⇒y-1=1 x-π2-1⇒2y-2=2x-π-2⇒2x-2y=π
(ii) Equation of tangent:
x=2at21+t2 and y=2at31+t2dxdt=1+t24at-2at22t1+t22=4at1+t22 anddydt=1+t26at2-2at32t1+t22=6at2+2at41+t22dydx=dydtdxdt=6at2+2at41+t224at1+t22=6at2+2at44atSlope of tangent, m = dydxt=12=3a2+a82a=12a+a82a=13a8×12a=1316Now, x1, y1=2at21+t2,2at31+t2 =a21+14, a41+14=a254, a454=2a5, a5Equation of tangent is,y-y1=m x-x1⇒y-a5=1316x-2a5⇒5y-a5=13165x-2a5⇒5y-a=13165x-2a⇒80y-16a=65x-26a⇒65x-80y-10a=0⇒13x-16y-2a=0
Equation of normal is,y-y1=-1m x-x1⇒y-a5=-1613 x-2a5⇒5y-a5=-16135x-2a5⇒5y-a=-16135x-2a⇒65y-13a=-80x+32a⇒80x+65y-45a=0⇒16x+13y-9a=0
(iii)
x=at2 and y=2atdxdt=2at and dydt=2a∴dydx=dydtdxdt=2a2at=1tSlope of tangent, m = dydxt=1=11=1Now, x1, y1=a, 2aEquation of tangent is,y-y1=m x-x1⇒y-2a=1x-a⇒y-2a=x-a⇒x-y+a=0
Equation of normal:
Equation of normal is,y-y1=m x-x1⇒y-2a=-1 x-a⇒y-2a=-x+a⇒x+y=3a
(iv)
x=a sec t and y=b tan tdxdt=a sec t tan t and dydt=b sec2t∴dydx=dydtdxdt=b sec2ta sec t tan t=bacosec tSlope of tangent, m = dydxt=t=bacosec tNow, x1, y1=a sec t, b tan tEquation of tangent is,y-y1=m x-x1⇒y- b tan t=bacosec tx-a sec t⇒y-b sin tcos t=ba sin tx-acos t⇒y cos t-b sin tcos t=ba sin tx cos t-acos t⇒y cos t-b sin t=ba sin tx cos t-a⇒ay sin t cos t-ab sin2t=bx cos t-ab⇒bx cos t-ay sin t cos t-ab1-sin2t=0⇒bx cos t-ay sin t cos t=ab cos2tDividing by cos2t,bx sec t-ay tan t=ab
Equation of normal is,y-y1=m x-x1⇒y- b tan t=-absin tx-a sec t⇒y- b sin tcos t=-absin tx-acos t⇒y cos t-b sin tcos t=-absin tx cos t-acos t⇒y cos t-b sin t=-absin tx cos t-a⇒by cos t-b2sin t=-ax sin t cos t+a2sin t⇒ax sin t cos t+by cos t=a2+b2sin tDividing both sides by sin t,ax cos t+by cot t=a2+b2
(v)
x=aθ+sinθ and y=a1-cosθdxdθ=a1+cosθ and dydθ=asinθ∴dydx=dydθdxdθ=asinθa1+cosθ=sinθ1+cosθ=2sinθ2cosθ22cos2θ2=tanθ2 …1Slope of tangent, m = dydxθ=tanθ2Now, x1, y1=aθ+sinθ, a1-cosθ Equation of tangent is,y-y1=m x-x1⇒y-a1-cosθ=tanθ2x-aθ+sinθ⇒y-a2 sin2θ2=xtanθ2-aθtanθ2-atanθ2sinθ⇒y-a2 sin2θ2=xtanθ2-aθtanθ2-a2sinθ2cosθ22cos2θ22sinθ2cosθ2 (From (1))⇒y-2a sin2θ2=x-aθtanθ2-2a sin2θ2⇒y=x-aθtanθ2
Equation of normal is,y-a1-cosθ=-cotθ2x-aθ+sinθ⇒tan θ2y-a2 sin2θ2=-x+aθ+asinθ⇒tan θ2y-a2 1-cos2θ2=-x+aθ+asinθ⇒tan θ2y-2a+a 2 sin θ2 cos θ2=-x+aθ+asinθ⇒tan θ2y-2a+asinθ=-x+aθ+asinθ⇒tan θ2y-2a=-x+aθ⇒tan θ2y-2a+x-aθ=0
Q6.
Answer :
Abscissa means the horizontal co-ordiante of a point.
Given that abscissa = 2.
i.e., x = 2
x2+2y2-4x-6y+8=0 … 1Differentiating both sides w.r.t. x,2x+4ydydx-4-6dydx=0⇒dydx4y-6=4-2x⇒dydx=4-2x4y-6=2-x2y-3When x=2, from (1), we get4+2y2-8-6y+8=0⇒2y2-6y+4=0⇒y2-3y+2=0⇒y-1y-2=0⇒y=1 or y=2Case-1: y=1Slope of tangent = dydx2, 1=0-1=0x1, y1=2, 1Equation of normal is,y-y1=-1m x-x1⇒y-1=-10 x-2⇒x-2=0⇒x=2Case-2: y=2Slope of tangent = dydx2, 2=01=0x1, y1=2, 2Equation of normal is,y-y1=-1m x-x1⇒y-2=-10 x-2⇒x-2=0⇒x=2
In both cases, the equation of normal is x = 2
Q7.
Answer :
ay2=x3Differentiating both sides w.r.t. x,2ay dydx=3×2⇒dydx=3x22aySlope of tangent = dydxam2, am3=3a2m42a2m3=3m2Given x1, y1=am2, am3Equation of normal is,y-y1=-1m x-x1⇒y-am3=-23m x-am2⇒3my-3am4=-2x+2am2⇒2x+3my-am22+3m2=0
Q8.
Answer :
The slope of the given line y = 4x − 5 is 4
y2=ax3+b … 12y dydx=3ax2⇒dydx=3ax22ySlope of tangent=dydx2, 3=12a6=2aGiven thatSlope of tangent= slope of given line2a=4⇒a=2Substituting this and x = 2, y = 3 in (1), we get9=16+b⇒b=-7Hence, a=2 and b=-7
Page 16.29 Ex.16.2
Q9.
Answer :
Let (x0, y0) be the point of intersection of both the curve and the tangent.
y=x2+4x-16Since, x0,y0 lies on curve. Thereforey0=x02+4×0-16 … 1Now, y=x2+4x-16⇒dydx=2x+4Slope of tangent = dydxx0, y0=2×0+4Given that The tangent is parallel to the line So,Slope of tangent=slope of the given line2x0+4=3⇒2×0=-1⇒x0=-12From (1),y0=14-2-16=-714Now, slope of tangent, m =3×0, y0=-12, -714Equation of tangent isy-y0=m x-x0⇒y+714=3x+12⇒4y+714=32x+12⇒4y+71=12x+6⇒12x-4y-65=0
Q10.
Answer :
Let (x1, y1) be a point on the curve where we need to find the normal.
Slope of the given line = -114
Since, the point lies on the curve.Hence, y1=x13+2×1+6 Now, y=x3+2x+6⇒dydx=3×2+2Slope of the tangent=dydxx1, y1=3×12+2Slope of the normal=-1slope of the tangent==-13×12+2Given that,slope of the normal=slope of the given line⇒-13×12+2=-114⇒3×12+2=14⇒3×12=12⇒x12=4⇒x1=±2Case-1: x1=2y1=x13+2×1+6=8+4+6=18∴x1, y1=2, 18Slope of the normal, m=-114Equation of normal is,y-y1=m x-x1⇒y-18=-114x-2⇒14y-252=-x+2⇒x+14y-254=0Case-2: x1=-2y1=x13+2×1+6=-8-4+6=-6∴x1, y1=-2, -6Slope of the normal, m=-114Equation of normal is,y-y1=m x-x1⇒y+6=-114x+2⇒14y+84=-x-2⇒x+14y+86=0
Q11.
Answer :
Let (x1, y1) be a point on the curve where we need to find the tangent(s).
Slope of the given line = -19
Since, tangent is perpendicular to the given line,
Slope of the tangent = -1-19=9
Let x1, y1 be the point where the tangent is drawn to this curve.Since, the point lies on the curve.Hence, y1=4×13-3×1+5 Now, y=4×3-3x+5⇒dydx=12×2-3Slope of the tangent=dydxx1, y1=12×12-3Given that,slope of the tangent=slope of the perpendicular line⇒12×12-3=9⇒12×12=12⇒x12=1⇒x1=±1Case-1: x1=1y1=4×13-3×1+5=4-3+5=6∴ x1, y1=1, 6Slope of the tangent=9Equation of tangent is,y-y1=m x-x1⇒y-6=9x-1⇒y-6=9x-9⇒9x-y-3=0Case-2: x1=-1y1=4×13-3×1+5=-4+3+5=4∴x1, y1=-1, 4Slope of the tangent=9Equation of tangent is,y-y1=m x-x1⇒y-4=9x+1⇒y-4=9x+9⇒9x-y+13=0
Q12.
Answer :
Slope of the given line is 1
Let x1, y1 be the point where the tangent is drawn to the curve.Since, the point lies on the curve.Hence, y1= x1 loge x1 … 1Now, y= x loge x ⇒dydx=x×1x+loge x 1=1+loge xSlope of tangent=1+loge x1Slope of normal = -1Slope of tangent=-11+loge x1Given thatSlope of normal = slope of the given line-11+loge x1=1⇒-1=1+loge x1⇒-2=loge x1⇒x1=e-2=1e2Now, y1= e-2-2=-2e2 From (1)∴x1, y1=1e2, -2e2Equation of normal is,y+2e2=1 x-1e2⇒y+2e2=x-1e2⇒x-y=3e2⇒x-y=3e-2
Q13.
Answer :
(i) Slope of the given line is 2
Let x1, y1 be the point where the tangent is drawn to the curve y=x2-2x+7 Since, the point lies on the curve.Hence, y1=x12-2×1+7 … 1Now, y=x2-2x+7⇒dydx=2x-2Slope of tangent at point x1, y1=2×1-2Given thatSlope of tangent= Slope of the given line⇒2×1-2=2⇒2×1=4⇒x1=2Now, y1= 4-4+7=7∴x1, y1=2, 7Equation of tangent is,y-y1=m x-x1⇒y-7=2 x-2⇒y-7=2x-4⇒2x-y+3=0
(ii) Slope of the given line is 3
Slope of the line perpendicular to this line = -13
Let x1, y1 be the point where the tangent is drawn to the curve.Since, the point lies on the curve.Hence, y1=x12-2×1+7 … 1Now, y=x2-2x+7⇒dydx=2x-2Slope of tangent at x1, y1=2×1-2Given thatSlope of tangent at x1, y1= Slope of the perpendicular line⇒2×1-2=-13⇒6×1-6=-1⇒6×1=5⇒x1=56Now, y1=2536-106+7=25-60+25236=21736∴x1, y1=56,21736Equation of tangent is,y-21736=-13 x-56⇒36y-21736=-6x+518⇒36y-217=-12x+10⇒12x+36y-227=0
Q14.
Answer :
Slope of given tangent = 2
Let x1, y1 be the point where the tangent is drawn to this curve.Since, the point lies on the curve.Hence, y1=1×1-3Now, y=1x-3⇒dydx=-1x-32Slope of tangent = dydx=-1×1-32Given that Slope of the tangent = 2⇒-1×1-32=2⇒x1-32=-2⇒x1-3=-2, which does not exist because 2 is negative.
So, there does not exist any such tangent.
Q15.
Answer :
Slope of the given tangent is 0.
Let x1,y1be a point where the tangent is drawn to the curve (1).Since, the point lies on the curve.Hence, y1=1×12-2×1+3… 1 Now, y=1×2-2x+3⇒dydx=x2-2x+30-2x-21×2-2x+32=-2x+2×2-2x+32Slope of tangent=-2×1+2×12-2×1+32Given thatSlope of tangent = slope of the given line⇒-2×1+2×12-2×1+32=0⇒-2×1+2=0⇒2×1=2⇒x1=1Now, y= 11-2+3=12 From1∴x1, y1=1, 12Equation of tangent is,y-y1=m x-x1⇒y-12=0 x-1⇒y=12
Q16.
Answer :
Slope of the given line is 2
Let x1,y1be the point where the tangent is drawn to the curve y=3x-2Since, the point lies on the curve.Hence, y1=3×1-2 … 1Now, y=3x-2⇒dydx=323x-2Slope of tangent at x1,y1 =323×1-2Given thatSlope of tangent = slope of the given line⇒323×1-2=2⇒3=43×1-2⇒9=163×1-2⇒916=3×1-2⇒3×1=916+2=9+3216=4116⇒x1=4148Now, y1=12348-2=2748=916=34 From (1)∴x1, y1=4148, 34Equation of tangent is,y-y1=m x-x1⇒y-34=2 x-4148⇒4y-34=248x-4148⇒24y-18=48x-41⇒48x-24y-23=0
Q17.
Answer :
Suppose (x1, y1) be the point of contact of tangent.
We can find the slope of the given line by differentiating the equation w.r.t x
So, Slope of the line = 4
Since,x1, y1 lies on the curve.Therefore, x12+3y1-3=0 … 1Now, x2+3y-3=0⇒2x+3dydx=0⇒dydx=-2x3Slope of tangent, m=dydxx1, y1=-2x13Given that tangent is parallel to the line, SoSlope of tangent, m = slope of the given line-2×13=4⇒x1=-636+3y1-3=0(From (1))⇒3y1=-33⇒y1=-11×1, y1=-6, -11Equation of tangent is,y-y1=m x-x1⇒y+11=4 x+6⇒y+11=4x+24⇒4x-y+13=0
Q18.
Answer :
Now, xan+ybn=2na xan-1+nbybn-1dydx=0nbybn-1dydx=-na xan-1dydx=-na xan-1×bnbyn-1=-babxayn-1Slope of tangent=dydxa, b=-bab*aa*bn-1=-ba … (2)The equation of tangent isy-b=-bax-a⇒ya-ab=-xb+ab⇒xb+ya=2ab⇒xa+yb=2
So, the given line touches the given curve at the given point.
Q19.
Answer :
x=sin 3t and y=cos 2tdxdt=3 cos 3t and dydt=-2 sin 2t∴dydx=dydtdxdt=-2 sin 2t3 cos 3tSlope of tangent, m = dydxt=π4=–2 sin π23 cos 3π4=-2-32=223×1=sin 3×π4=12 and y1=cos 2×π4=0So, x1, y1=12, 0Equation of tangent is,y-y1=m x-x1⇒y-0=223x-12⇒3y=22x-2⇒22x-3y-2=0
Q20.
Answer :
Slope of x – axis is 0
Let (x1, y1) be the required point.
y=2×3-15×2+36x-21Sincex1,y1 lies on the curve.Therefore y1=2×13-15×12+36×1-21 … 1Now, y=2×3-15×2+36x-21⇒dydx=6×2-30x+36Slope of tangent at x1, y1=dydxx1, y1= 6×12-30×1+36Given thatSlope of tangent at x, y= slope of the x-axis6x12-30×1+36=0⇒x12-5×1+6=0⇒x1-2×1-3=0⇒x1=2 or x1=3Case-1: x1=2y1=16-60+72-21=7 (From (1))x1, y1=2, 7Equation of tangent is,y-y1=mx-x1⇒y-7=0x-2⇒y=7Case-2: x1=3y1=54-135+108-21=6 (From (1))x1, y1=3, 6Equation of tangent is,y-y1=mx-x1⇒y-6=0x-3⇒y=6
Page 16.36 Ex.16.3
Q1.
Answer :
i) Given curves are,y2=x … 1×2=y … 2From these two equations, we getx22=x⇒x4-x=0⇒x x3-1=0⇒x=0 or x = 1Substituting the values of x in 2 we get,y=0 or y=1 ∴x, y = 0, 0 or 1, 1Differenntiating (1) w.r.t. x,2y dydx=1⇒dydx=12y …3Differenntiating (2) w.r.t. x,2x = dydx …4Case -1: x, y = 0, 0The tangent to curve is parallel to x-axis.Hence, the angle between the tangents to two curve at 0, 0 is a right angle.∴θ=π2Case -2: x, y = 1, 1From 3 we have, m1=12From 4 we have, m2=2 1=2Now,tan θ=m1-m21+m1m2=12-21+12×2=34⇒θ=tan-1 34
ii) Given curves are,y=x2 … 1×2+y2=20 … 2From these two equations we get y+y2=20⇒y2+y-20=0⇒y+5y-4=0⇒y=-5 or y=4Substituting the values of y in 1 we get,x2=-5 or x2=4 ⇒x=±2 and x2 = -5 has no real solutionSo, x, y=2, 4 or -2, 4Differenntiating (1) w.r.t. x,dydx=2x …3Differenntiating (2) w.r.t. x,2x +2y dydx=0⇒dydx=-xy …4Case -1: x, y = 2, 4From 3 we have, m1=22=4From 4 we have, m2=-24=-12Now, tan θ=m1-m21+m1m2=4+121+4 -12=92⇒θ=tan-1 92Case -2: x, y = -2, 4From 3 we have, m1=2-2=-4From 4 we have, m2=24=12Now, tan θ=m1-m21+m1m2=-4-121-4 12=92⇒θ=tan-1 92
iii) Given curves are,2y2=x3 … 1y2=32x … 2 From these two equations we get232x=x3⇒64x=x3⇒xx2-64=0⇒x=0, 8 , -8Substituting the value of x in 2 we get, y1=0, 16, -16∴x1, y1 = 0, 0, 8, 16 or 8, -16 Differentiating (1) w.r.t. x,4y dydx=3×2⇒dydx=3x24y …3Differenntiating (2) w.r.t. x,2ydydx=32⇒dydx=16y …4Case – 1: x, y = 0, 0From 3 we have, m1=00 ∴We cannot determine θ in this case.Case – 2: x, y = 8, 16From 3 we have, m1=19264=3From 4 we have, m2=1616=1Now,tan θ=m1-m21+m1m2=3-11+3=24=12⇒θ=tan-1 12Case- 3: x1, y1 = 8, -16From 3 we have, m1=192-64=-3From 4 we have, m2=16-16=-1Now, tan θ=m1-m21+m1m2=-3+11+3=24=12⇒θ=tan-1 12
iv) Given curves are,x2+y2-4x-1=0 … 1×2+y2-2y-9=0 … 2From (3) we getx2+y2=4x+1Substituting this in (2),4x+1-2y-9=0⇒4x-2y=8⇒2x-y=4⇒y=2x-4 … 3Substituting this in (1),x2+2x-42-4x-1=0⇒x2+4×2+16-16x-4x-1=0⇒5×2-20x+15=0⇒x2-4x+3=0⇒x-3x-1=0⇒x=3 or x=1Substituting the values of x in 3, we get,y=2 or y=-2 ∴x, y = 3, 2, 1, -2Differentiating (1) w.r.t. x,2x+2y dydx-4=0⇒dydx=4-2x2y=2-xy … 4Differenntiating (2) w.r.t. x,2x+2y dydx-2dydx=0⇒dydx2y-2=-2x⇒dydx=2×2-2y=x1-y … 5Case – 1: x, y = 3, 2From 4, we get, m1=2-32=-12From 5, we get, m2=31-2=-3Now,tan θ=m1-m21+m1m2=-12+31+32=1⇒θ=tan-1 1=π4Case – 2: x, y = 1, – 2From 4, we get, m1=2-1-2=-12From 5, we get, m2=11+2=13Now,tan θ=m1-m21+m1m2=-12-131-16=1⇒θ=tan-1 1=π4
v) Given curves are,x2a2+y2b2=1 … 1×2+y2=ab … 2Multiplying (2) by 1a2,x2a2+y2a2=ba … 3Subtracting (1) from (3), we gety2a2- y2b2=ba-1⇒y2b2-a2a2b2=b-aa⇒y2=b-aa×a2b2b+ab-a=ab2b+a⇒y=±bab+aSubstituting this in (3),x2a2+ab2b+aa2=ba⇒a+bx2+ab2=ab2+a2b⇒x2=a2ba+b⇒x=±aba+b∴x, y = ±aba+b, ±bab+aNow, x, y = aba+b, bab+aDifferentiating (1) w.r.t. x, we get,2xa2+2yb2dydx=0⇒dydx=-xb2a2y⇒m1=-ab2ba+ba2bab+a =-bbaaDifferenntiating (2) w.r.t. x, we get,2x+2ydydx=0⇒dydx=-xy⇒m2=-aba+b bab+a=-abbaWe have,tan θ=m1-m21+m1m2=-bbaa+abba1+bbaaabba=-b2ab+a2aba2ba2b+ab2a2b=aba+ba-ba2b×a2baba+b=a-bab⇒θ=tan-1 a-babSimilarly, we can prove that θ=tan-1 a-bab for all possibilities of x, y
vi) Given curves are,x2+4y2=8 … 1×2-2y2=2 … 2From (1) and (2) we get 6y2=6⇒y=1 or y1=-1Substituting the values of y in 1x=2, -2 or x=2, -2 So, x, y=2, 1, 2, -1, -2, 1, -2, -1Differenntiating (1) w.r.t. x,2x+8y dydx=0⇒dydx=-x4y …3Differenntiating (2) w.r.t. x,2x-4y dydx=0⇒dydx=x2y …4 Case -1: x, y = 2, 1 From 3, we get, m1=-12From 4, we get, m2=1We have,tan θ=m1-m21+m1m2=-12-11-12=3⇒θ=tan-1 3Case -2: x, y = 2, -1 From 3, we get, m1=12From 4, we get, m2=-1We have,tan θ=m1-m21+m1m2=12+11-12=3⇒θ=tan-1 3Case -3: x, y= -2, 1 From 3, we get, m1=12From 4, we get, m2=-1We have,tan θ=m1-m21+m1m2=12+11-12=3⇒θ=tan-1 3Case -4: x, y= -2, -1 From 3, we get, m1=-12From 4, we get, m2=1We have,tan θ=m1-m21+m1m2=-12-11-12=3⇒θ=tan-1 3
vii) Given curves are,x2=27y … 1y2=8x … 2From (2) we getx=y28 Substituting this in (1),y282=27y⇒y4=1728y⇒y y3-123=0⇒y=0 or y=12Substituting the values of y in (2), we get, ⇒x=0 or x=18⇒x, y = 0, 0, 18, 12Differentiating (1) w.r.t. x,2x=27dydx⇒dydx=2×27 … 3Differenntiating (2) w.r.t. x,2y dydx=8⇒dydx=4y … 4Case – 1: x, y = 0, 0From 4 we have, m2 is undefined∴ We cannot find θCase – 2: x, y = 18, 12From 3 we have, m1=3627=43From 4 we have, m2=412=13Now, tan θ=m1-m21+m1m2=43-131+49=913⇒θ=tan-1 913
viii) Given curves are,x2+y2=2x … 1y2=x … 2From these two equations we get x2+x=2x⇒x2-x=0⇒x x-1=0⇒x=0 or x=1Substituting the values of x in 2 we get,y=0 or y=±1 ∴ x,y =0, 0, 1, 1, 1, -1Differenntiating (1) w.r.t. x,we get,2x+2ydydx=2⇒dydx=1-xy … 3Differenntiating (2) w.r.t. x,we get,2y dydx=1⇒dydx=12y … 4Case -1: x, y = 0, 0From 3 we get, m1 is undefined. ∴We can not find θCase -2: Let x, y = 1, 1From 3 we get, m1=0From 4 we get, m2=12Now, tan θ=m1-m21+m1m2=0-121+0=12⇒θ=tan-112Case -3: Let x, y = 1, -1From 3 we get, m1=0From 4 we get, m2=-12Now, tan θ=m1-m21+m1m2=0+121=12⇒θ=tan-112
Q2.
Answer :
i) y=x3… 16y=7-x2 … 2From (1) and (2) we get6x3=7-x2⇒6×3+x2-7=0x=1 satisfies this.Dividing this by x-1 ,we get6x2+7x+7=0, Discriminant = 72-467=-119<0So, this has no real roots.When x=1, y=x3=1 (From (1))So, x, y = 1, 1Differentiating (1) w.r.t. x,dydx=3×2⇒m1=dydx1, 1=3Differenntiating (2) w.r.t. x,6dxdx=-2x⇒dxdx=-2×6=-x3⇒m2=dydx1, 1=-13Now, m1×m2=3×-13⇒m1×m2=-1Since, m1×m2 = -1
So, the given curves intersect orthogonally.
ii) Let the given curves intersect at x1, y1x3-3xy2=-2… 13x2y-y3=2 … 2Differentiating (1) w.r.t. x,3×2-3y2-6xydydx=0⇒dydx=3×2-3y26xy=x2-y22xy⇒m1=dydxx1, y1=x12-y122x1y1Differenntiating (2) w.r.t. x,3x2dydx+6xy-3y2dydx=0⇒dydx3x2-3y2=-6xy⇒dydx=-6xy3x2-3y2=-2xyx2-y2⇒m2=dydxx1, y1=-2x1y1x12-y12Now, m1×m2=x12-y122x1y1×-2x1y1x12-y12⇒ m1×m2=-1Since, m1×m2=-1
So, the given curves intersect orthogonally.
iii) x2+4y2=8 … 1×2-2y2=4 … 2From (1) and (2) we get6y2=4⇒y2=23⇒y=23 or y=-23From (1),x2+83=8⇒x2=163⇒x=±43So, x, y=43, 23, 43, -23,-43, 23, -43, -23Consider point x1, y1=43, 23Differentiating (1) w.r.t. x,2x+8ydydx=0⇒dydx=-x4y⇒m1=dydx43, 23=-43423=-12Differenntiating (2) w.r.t. x,2x-4ydydx=0⇒dydx=x2y⇒m2=dydx43, 23=43223=2Now, m1×m2=-12×2⇒ m1×m2=-1Since, m1×m2=-1Hence,, the curves are orthogonal at 43, 23.Similarly, we can see that the curves are orthogonal in each possibility of x1, y1.
Page 16.37 Ex.16.3
Q3.
Answer :
i) x2=4y… 14y+x2=8 … 2Given point is 2, 1Differentiating (1) w.r.t. x,2x=4dydx⇒dydx=x2⇒m1=dydx2,1=22=1Differenntiating (2) w.r.t. x,4dydx+2x=0⇒dydx=-x2⇒m2=dydx2,1=-22=-1Since, m1×m2=-1
Hence, the given curves intersect orthogonally at the given point.
ii) x2=y… 1×3+6y=7 … 2Given point is 1, 1Differentiating (1) w.r.t. x,2x=dydx⇒m1=dydx1,1=21=2Differenntiating (2) w.r.t. x,3×2+6dydx=0⇒dydx=-x22⇒m2=dydx1,1=-12Since, m1×m2=-1
Hence, the given curves intersect orthogonally at the given point.
iii) y2=8x… 12×2+y2=10 … 2Given point is 1, 22Differentiating (1) w.r.t. x,2ydydx=8⇒dydx=4y⇒m1=dydx1, 22=422=2Differenntiating (2) w.r.t. x,4x+2ydydx=0⇒dydx=-2xy⇒m2=dydx1, 22=-222=-12Since, m1×m2=-1
Hence, the given curves intersect orthogonally at the given point.
Q4.
Answer :
(i) x2a2-y2b2=1 …1xy=c2 …2Let the curves intersect orthogonally at x1, y1.On differentiating (1) on both sides w.r.t. x, we get2xa2-2yb2dydx=0⇒dydx=xb2a2y⇒m1=dydxx1, y1=x1b2a2y1On differentiating (2) on both sides w.r.t. x, we getxdydx+y=0⇒dydx=-yx⇒m2=dydxx1, y1=-y1x1It is given that the curves intersect orhtogonally at x1, y1.∴m1×m2=-1⇒x1b2a2y1×-y1x1=-1⇒a2=b2
(ii) The condition for the curves ax2+by2=1 and a’x2+b’y2=1 to intersect orthogonally is given below:
1a-1b=1a’-1b’So, the condition for the curves x2a2+y2b2=1 and x2A2-y2B2=1 to intersect orthogonally is11a2-11b2=11A2-1-1B2⇒a2-b2=A2+B2
Q5.
Answer :
We have, x2a2+λ1+y2b2+λ1=1 …1and x2a2+λ2+y2b2+λ2=1 …2Now we can find the slope of both the curve by differentiating w.r.t x⇒2xa2+λ1+2ydydxb2+λ1=0 and 2xa2+λ2+2ydydxb2+λ2=0⇒dydx=-xy×b2+λ1a2+λ1 and dydx=-xy×b2+λ2a2+λ2⇒m1=-xy×b2+λ1a2+λ1 and m2=-xy×b2+λ2a2+λ2Subtracting 2 from 1, we get,x21a2+λ1-1a2+λ2+y21b2+λ1-1b2+λ2=0⇒x2y2=λ2-λ1b2+λ1b2+λ2×1λ1-λ2a2+λ1a2+λ2Now,m1××m2=x2y2×b2+λ1a2+λ1×b2+λ2a2+λ2 =λ2-λ1b2+λ1b2+λ2×a2+λ1a2+λ2λ1-λ2×b2+λ1a2+λ1×b2+λ2a2+λ2 =-1hence, 1 and 2 cuts orthogonally.
Q6.
Answer :
Given:4x=y2 …14xy=k …2From (1) and (2), we gety3=k⇒y=k13From (1), we get4x=k23⇒x=k234On differentiating (1) w.r.t. x, we get4=2ydydx⇒ dydx=2y⇒m1=dydxk234, k13=2k13=2k-13On differentiating (2) w.r.t. x, we get4xdydx+4y=0⇒dydx=-yx⇒m2=dydxk234, k13=-k13k234=-4k-13It is given that the curves intersect at right angles.∴m1×m2=-1⇒2k-13×-4k-13=-1⇒8k-23=1⇒k-23=18⇒k23=8Cubing on both sides, we getk2=512
Q7.
Answer :
Given:2x=y2 …12xy=k …2From (1) and (2), we gety3=k⇒y=k13From (1), we get2x=k2 3⇒x=k232On differentiating (1) w.r.t. x, we get2=2ydydx⇒ dydx=1y⇒m1=dydxk232, k13=1k13=k-13On differentiating (2) w.r.t. x, we get2xdydx+2y=0⇒dydx=-yx⇒m2=dydxk232, k13=-k13k232=-2k-13It is given that the curves intersect orthogonally.∴m1×m2=-1⇒k-13×-2k-13=-1⇒2k-23=1⇒k-23=12⇒k23=2Cubing on both sides, we getk2=8
Page 16.37 (Very Short Answers)
Q1.
Answer :
The slope of the x-axis is 0.
Now, let (x1, y1) be the required point.
Here,
Since, the point lies on the curve.Hence, y1=x12-2×1+3 … 1Now, y=x2-2x+3dydx=2x-2Slope of the tangent at x, y=dydxx1, y1=2×1-2Given:Slope of the tangent at x1, y1=Slope of the x-axis=2×1-2=0⇒x1=1andy1=1-2+3=2 [From (1)]∴Required point=x1, y1=1, 2
Q2.
Answer :
Here,x=t2+3t-8 and y=2t2-2t-5dxdt=2t+3 and dydt=4t-2∴dydx=dydtdxdt=4t-22t+3Now,Slope of the tangent=dydxt=2=8-24+3=67
Q3.
Answer :
The slope of the x-axis is 0.
Also, the tangent at a point (x, y) on the curve y = f(x) is parallel to the x-axis.
∴ Slope of the tangent dydx= Slope of the x-axis = 0
Q4.
Answer :
The slope of the y-axis is ∞.
Also, the normal at (x, y) on the curve y = f(x) is parallel to the y-axis.
∴ Slope of the normal = Slope of the y-axis = ∞
⇒ dydx=Slope of the tangent=-1Slope of the normal=-1∞=0
Q5.
Answer :
Because the tangent to the curve at (x, y) is equally inclined to the coordinate axes, the angle made by the tangent with the axes can be ±45°.
∴dydx=Slope of the tangent=tan ±45=±1
Q6.
Answer :
Slope of the y-axis is ∞.
Also, the tangent at (x, y) on the curve y = f(x) is parallel to the y-axis,
∴ Slope of the tangent, dydx = Slope of the y-axis = ∞
dxdy=1dydx=1∞=0
Page 16.38 (Very Short Answers)
Q7.
Answer :
Here,x=1t and y=tdxdt=-1t2and dydt=1∴dydx=dydtdxdt=1-1t2=-t2Now,Slope of the tangent=dydx=-t2Slope of the normal=-1 Slope of the tangent=-1-t2=1t2
Q8.
Answer :
Let the required point be (x1, y1).
The tangent makes an angle of 45o with the x-axis.
∴ Slope of the tangent = tan 45o = 1
Since, the point lies on the curve.Hence, y12=x1Now, y2=x⇒2ydydx=1⇒dydx=12ySlope of the tangent = dydxx1, y1=12y1Given:12y1=1⇒2y1=1⇒y1=12Now,x1=y12=122=14∴x1, y1=14, 12
Q9.
Answer :
Here,x=et cos t and y=et sin tdxdt=et cos t-et sin t anddydt=et sin t+et cos t∴dydx=dydtdxdt=et sin t+et cos tet cos t-et sin t=sin t+cos tcos t-sin tNow,Slope of the tangent =dydxt=π4=sin π4+cos π4cos π4-sin π4=12+1212-12=220=∞Let θ be the angle made by the tangent with the x-axis.∴tan θ=∞⇒θ=π2
Q10.
Answer :
Here,y=x+sin x cos xOn differentiating both sides w.r.t. x, we getdydx=1+cos2 x-sin2xNow,Slope of the tangent = dydxx=π2= 1+cos2π2-sin2π2= 1-1=0When x=π2, y=π2+sin π2cosπ2=π2∴x1, y1=π2, π2Equation of the normal=y-y1=-1Slope of the tangentx-x1⇒y-π2=-10x-π2⇒x=π2⇒2x=π
Q11.
Answer :
Let (x1, y1) be the required point.
Slope of the given line = -2
Since, the point lies on the curve.Hence, y12=3-4×1 …1Now, y2=3-4x⇒2ydydx=-4∴dydx=-42y=-2ySlope of the tangent = dydxx1, y1=-2y1Given:Slope of the tangent = Slope of the line⇒-2y1=-2⇒y1=1From (1), we get1=3-4×1⇒-2=-4×1⇒x1=12∴x1, y1=12, 1
Q12.
Answer :
When the curve crosses the y-axis, the point on the curve is of the form (0, y).
Here,
y=x2-x+2⇒y=0-0+2=2So, the point where the curve crosses the y-axis is (0, 2).Now, y=x2-x+2⇒dydx=2x-1Slope of the tangent, m = dydx0, 2=20-1=-1∴x1, y1=0, 2andEquation of tangent=y-y1=mx-x1⇒y-2=-1x-0⇒y-2=-x⇒x+y-2=0
Q13.
Answer :
Given:y2=4x …1×2=2y-3 …2On differentiating (1) w.r.t. x, we get2ydydx=4⇒dydx=2y⇒m1=dydx1, 2=22=1On differentiating (2) w.r.t. x, we get2x=2dydx⇒dydx=x⇒m2=dydx1, 2=1Thus, we gettan θ=m1-m21+m1m2⇒tan θ=1-11+1⇒tan θ=0⇒θ=0o
Q14.
Answer :
Given:y=e-x …1y=ex …2On substituting the value of y in (1), we gete-x=ex⇒x=0andy=1 [From (2)]On differentiating (1) w.r.t. x,we getdydx=-e-x⇒m1=dydx0, 1=-1On differentiating (2) w.r.t. x, we getdydx=ex⇒m2=dydx0, 1=1∵m1×m2=-1Since the multiplication of the slopes is -1 so the slopes are perpendicular to each other.∴Required angle=π2
Q15.
Answer :
Given:y=1xOn differentiating both sides w.r.t. x, we getdydx=-1x2Now,Slope of the tangent = dydx3, 13=-19Slope of the normal = -1Slope of tangent=-1-19= 9
Q16.
Answer :
Let (x1, y1) be the required point.
Slope of the given line = 3
Since, the point lies on the curve.Hence, y1=2×12-x1+1 …1 Now, y=2×2-x+1 ∴dydx=4x-1Now,Slope of the tangent = dydxx1, y1= 4×1-1Given:Slope of the tangent = Slope of line∴4×1-1=3⇒x1=1From (1), we gety1=2-1+1=2∴x1, y1=1, 2
Q17.
Answer :
Given:y=cos xOn differentiating both sides w.r.t. x, we getdydx=-sin xNow,Slope of the tangent=dydx0, 1=-sin 0=0andEquation of the normal=y-y1=-1mx-x1⇒y-1=-10x-0⇒x=0
Page 16.38 (Multiple Choice Questions)
Q1.
Answer :
(c) x + y = 0
Given:y=sin xOn differentiating both sides w.r.t. x, we getdydx=cos xSlope of the tangent = dydx0, 0= cos 0 =1Slope of the normal, m = -11=-1Given:x1, y1=0, 0∴Equation of the normal=y-y1=mx-x1⇒y-0=-1x-0⇒y=-x⇒x+y=0
Q2.
Answer :
(d) 2x = π
Given:y=x+sin x cosxOn differentiating both sides w.r.t. x, we getdydx=1+cos2 x-sin2 xSlope of the tangent=dydxx=π2=1+cos 2π2-sin2π2=1-1=0Slope of the normal, m=-10When x=π2, y=π2+cos π2 sin π2=π2Now, x1, y1=π2, π2∴Equation of the normal=y-y1=mx-x1⇒y-π2=-10x-π2⇒x=π2⇒2x=π
Q3.
Answer :
(a) x − 2y = 2
Here,y=x2-x=2x-x2⇒dydx=2-2xSlope of the tangent=dydx2, 0=2-4=-2Slope of the normal, m=-1-2=12Given:x1, y1=2, 0∴Equation of the normal=y-y1=mx-x1⇒y-0=12x-2⇒2y=x-2⇒x-2y=2
Q4.
Answer :
(b) (1/4, 1/2)
Let the required point be (x1, y1).
The tangent makes an angle of 45o with the x-axis.
∴ Slope of the tangent = tan 45o = 1
Since, the point lies on the curve.Hence, y12=x1Now, y2=x⇒2ydydx=1⇒dydx=12ySlope of the tangent = dydxx1, y1=12y1Given:12y1=1⇒2y1=1⇒y1=12Now,x1=y12=122=14∴x1, y1=14, 12
Q5.
Answer :
(c) (0, 0)
Let the required point be (x1, y1).
Since, the point lies on the curve.Hence, x1=at2 and y1=2atNow, x=at2 and y=2at⇒dxdt=2at and dydt=2a⇒dydx=dydtdxdt=2a2at=1t=2aySlope of the tangent = dydxx1, y1=2ay1It is given that the tangent is perpendicular to the y-axis.It means that it is parallel to the x-axis.∴ Slope of the tangent = Slope of the x-axis2ay1=0⇒a=0Now, x1=at2=0 and y1=2at=0∴x1, y1=0, 0
Page 16.39 (Multiple Choice Questions)
Q6.
Answer :
(b) (1, 0)
y = x
⇒dydx=1
Let x1, y1 be the required point.Since, the point lies on the curve,Hence, y1=x12-3×1+2Now, y=x2-3x+2∴dydx=2x-3Slope of the tangent=dydxx1, y1=2×1-3
The tangent is perpendicular to this line.
∴Slope of the tangent = -1Slope of the line=-11=-1
Now,
2×1-3=-1⇒2×1=2⇒x1=1andy1=x12-3×1+2=1-3+2=0∴x1, y1=1, 0
Q7.
Answer :
(b) (1/4, 1/2)
Let the required point be (x1, y1).
The tangent makes an angle of 45o with the x-axis.
∴ Slope of the tangent = tan 45o = 1
Since, the point lies on the curve.Hence, y12=x1Now, y2=x⇒2ydydx=1⇒dydx=12ySlope of the tangent = dydxx1, y1=12y1Given:12y1=1⇒2y1=1⇒y1=12Now,x1=y12=122=14∴x1, y1=14, 12
Q8.
Answer :
(d) none of these
Let x1, y1 be the required point.Since, the point lies on the curve,Hence, y1=12×1-x12Now,y=12x-x2⇒dydx=12-2xSlope of the tangent = dydxx1, y1=12-2x1Given:Slope of the tangent=012-2×1=0⇒x1=6Now,y1=12×1-x12=72-36=36∴x1, y1=6, 36
Q9.
Answer :
(b) tan-1 34
Given:y2=x …1×2=y …2Point=1, 1On differentiating (1) w.r.t. x, we get2y dydx=1⇒dydx=12y⇒m1=12On differentiating (2) w.r.t. x, we get2x = dydx⇒m2=21=2Now,tan θ=m1-m21+m1m2=12-21+12×2=34⇒θ=tan-1 34
Q10.
Answer :
(c) x + 3y ± 8 = 0
The slope of line x + 3y = 8 is -13.
Since the normal is parallel to the given line, the equation of normal will be of the given form.x+3y=k 3×2-y2=8 Let x1, y1 be the point of intersection of the two curves.Then, x1+3y1=k …13×12-y12=8 …2Now, 3×2-y2=8 On differentiating both sides w.r.t. x, we get6x-2ydydx=0⇒dydx=6x2y=3xySlope of the tangent = dydxx1, y1=3x1y1Slope of the normal, m = -13xy=-y13x1Given:Slope of the normal = Slope of the given line⇒-y13x1=-13⇒y1=x1 …3From (2), we get3x12-x12=8⇒2×12=8⇒x12=4⇒x1=±2Case 1:When x1=2 From (3), we gety1=x1=2∴x1, y=2, 2From (1), we get2+32=k⇒2+6=k⇒k=8∴Equation of the normal from (1)⇒x+3y=8⇒x+3y-8=0Case 2:When x1=-2 From (3), we gety1=x1=-2,∴x1, y=-2, -2From (1), we get-2+3-2=k⇒-2-6=k⇒k=-8∴Equation of the normal from (1)⇒x+3y=-8⇒x+3y+8=0From both the cases, we get the equation of the normal as:x+3y±8=0
Q11.
Answer :
(b) x + y − 1 = 0 = x − y − 2
Let the tangent meet the x-axis at point (x, 0).
Now,
y=x2-3x+2⇒dydx=2x-3The tangent passes through point (x, 0).∴0=x2-3x+2⇒x-2x-1=0⇒x=2 or x=1Case 1: When x=2:Slope of the tangent, m=dydx2, 0=4-3=1∴x1, y1=2, 0Equation of the tangent:y-y1=m x-x1⇒y-0=1 x-2⇒x-y-2=0Case 2: When x=1:Slope of the tangent, m=dydx2, 0=2-3=-1∴x1, y1=1, 0Equation of the tangent:y-y1=m x-x1⇒y-0=-1 x-1⇒x+y-1=0
Q12.
Answer :
(b) 6/7
x=t2+3t-8 and y=2t2-2t-5dxdt=2t+3 and dydt=4t-2∴dydx=dydtdxdt=4t-22t+3The given point is (2, -1).∴ x=2 and y=-1Now,t2+3t-8=2 and 2t2-2t-5=-1Let us solve one of these to get the value of t.t2+3t-10=0 and 2t2-2t-4=0⇒t+5t-2=0 and 2t+2t-2=0⇒t=-5 or t= 2 and t=-1 or t=2These two have t=2 as a common solution.∴Slope of the tangent = dydxt=2= 8-24+3=67
Q13.
Answer :
(d) (1, 2), (1, −2)
Let (x1, y1) be the required point.
Since, the point lie on the curve.Hence, x12+y12-2×1-3=0 …1Now, x2+y2-2x-3=0 ⇒2x+2y dydx-2=0∴dydx=2-2x2y=1-xyNow,Slope of the tangent = dydxx1, y1= 1-x1y1Slope of the tangent=0 (Given)∴1-x1y1=0⇒1-x1=0⇒x1=1From (1), we getx12+y12-2×1-3=0⇒1+y12-2-3=0⇒y12-4=0⇒y1=±2So, the points are 1, 2 and 1, -2.
Q14.
Answer :
(c) 90°
Given:xy=a2 …1×2-y2=2a2 …2Let x1, y1 be the point of intersection.On differentiating (1) w.r.t. x, we getxdydx+y=0⇒dydx=-yx⇒m1=dydxx1, y1=-y1x1On differentiating (2) w.r.t. x, we get2x -2y dydx=0⇒dydx=xy⇒m2=dydxx1, y1=x1y1Now, m1×m2=-y1x1×x1y1⇒ m1×m2=-1∵m1×m =-1So, the angle between the curves is 90°.
Q15.
Answer :
(c) 6
Given:ay+x2=7 …1×3=y …2Point=1, 1On differentiating (1) w.r.t. x, we getadydx+2x=0⇒dydx=-2xa⇒m1=dydx1, 1=-2aAgain, on differentiating (2) w.r.t. x, we get3x2=dydx⇒m2=dydx1, 1=3It is given that the curves are orthogonal at the given point.∴m1×m2=-1⇒-2a×3=-1⇒a=6
Q16.
Answer :
(b) b = −1, c = 1
We can find the slope of the line by differentiating w.r.t. x.
Slope of the given line = 1
Now,
y=x2+bx+c …1⇒dydx=2x+bSlope of the tangent= dydx1, 1=2+bGiven:Slope of the tangent = 1⇒2+b=1⇒b=-1On substituting b=-1, x=1 and y=1 in (1), we get⇒1=1-1+c⇒c=1
Q17.
Answer :
(b) 0
Given:x=3t2+1 y=t3-1x=1Now,3t2+1=1⇒3t2=0⇒t=0dxdt=6t and dydt=3t2∴dydx=dydtdxdt=3t26t=t2Thus, we getSlope of the tangent=dydxt=0=02=0
Q18.
Answer :
(c) ab = 1
Given:y=aex …1y=be-x …2Let the point of intersection of these two curves be x1, y1.Now,On differentiating (1) w.r.t. x, we getdydx=aex⇒m1=dydx x1, y1 =aex1Again, on differentiating (2) w.r.t. x, we getdydx=-be-x⇒m2=dydx x1, y1=-be-x1It is given that the curves cut orthogonally.∴m1×m2=-1⇒aex1×-be-x1=-1⇒ab=1
Q19.
Answer :
(c) x = y
Here,x=a cos3 θ and y=a sin3 θdxdθ=-3a cos2 θ sin θ and dydθ=3a sin2 θ cos θ∴dydx=dydθdxdθ=3a sin2 θ cos θ-3a cos2 θ sin θ=-tan θNow,Slope of the tangent = dydxθ=π4=-tan π4=-1×1, y1=a cos3 π4, a sin3 π4=a22, a22∴Equation of the normal=y-y1=-1m x-x1⇒y-a22=1 x-a22⇒x=y
Q20.
Answer :
(a) 1/2
Given:y=2ex …1y=ae-x …2Let the point of intersection of these curves be x1, y1.On differentiating (1) w.r.t. x, we getdydx=2ex⇒m1=dydx x1, y1=2ex1Now, on differentiating (2) w.r.t. x, we getdydx=-ae-x⇒m2=dydx x1, y1=-ae-x1It is given that the curves are orthogonal.∴m1×m2=-1⇒2ex1×-ae-x1=-1⇒2a=1⇒a=12
Page 16.40 (Multiple Choice Questions)
Q21.
Answer :
(b) (3, 9)
Let (x1, y1) be the point where the given curve intersect the given line at the given angle.
Since, the point lie on the curve.Hence, y1=6×1-x12Now, y=6x-x2⇒dydx=6-2x⇒m1=6-2x1andx+y=0⇒1+dydx=0 ⇒dydx=-1⇒m2=-1It is given that the angle between them is π4.∴tan θ=m1-m21+m1m2⇒tan π4=6-2×1+11-6+2×1⇒1=7-2x12x1-5⇒7-2x12x1-5=±1⇒7-2x12x1-5=1 or 7-2x12x1-5=-1⇒7-2×1=2×1-5 or 7-2×1=-2×1+5⇒4×1=12 or 2 = 0 (It is not true.)⇒x1=3andy1=6×1-x12=18-9=9∴x1, y1=3, 9
Q22.
Answer :
(c) π/2
Given:y2=4ax …1×2=4ay …2Point = 0, 0On differentiating (1) w.r.t. x, we get2y dydx=4a⇒dydx=2ay⇒m1=∞Now, on differentiating (2) w.r.t. x, we get2x=4adydx⇒dydx=x2a=0∴tan θ=m1-m21+m1m2=∞1+0=∞⇒θ=tan-1∞=π2
Q23.
Answer :
(c) π/3
Given:x=π6Now,y=2sin2x⇒dydx=4sinx cosx⇒dydx=2 sin 2x⇒m1=dydxx=π6=2×32=3Also,y=cos 2x⇒dydx=-2 sin2x⇒m2=dydxx=π6=-2 ×32=-3∴tan θ=m1-m21+m1m2=3+31-33=23-2=3⇒θ=tan-13=π3
Q24.
Answer :
(c) makes an acute angle with x-axis
We have, y = 2×7 + 3x + 5
dydx=14×6+3⇒dydx>3 ∵x6 is always positive for any real value of x⇒dydx>0So, tanθ>0Hence, θ lies in first quadrant.Thus, the tangent to the curve makes an acute angle with x-axis
Q25.
Answer :
(a) 4, 83 and (c) 4, -83
Let (x1, y1) be the required point.
Since, x1,y1 lies on the given curve∴9y12=x13 …1Now, 9y2=x3 18y dydx=3×2⇒dydx=3x218y=x26ySlope of the tangent = dydxx1, y1=x126y1Slope of the normal = -1x126y1=-6y1x12It is given that the normal makes equal intercepts with the axes.∴ Slope of the normal = ±1Now,-6y1x12=±1⇒-6y1x12=1 or -6y1x12=-1⇒y1=-x126 or y1=x126 …2Case 1: When y1=-x126From (1), we have9x1436=x13⇒x14=4×13⇒x14-4×13=0⇒x13x1-4=0⇒x1=0, 4Putting x1=0 in 1, we get,9y12=0⇒y1=0Putting x1=4 in 1, we get,9y12=43⇒y1=±83But, the line making the equal intercepts with the coordinate axes can not pass through the origin.So, the points are 4, ±83
Q26.
Answer :
(b) 67
Given:
x = t2 + 3t − 8 and y = 2t2 − 2t − 5
⇒dxdt=2t+3 and dydt=4t-2∴dydx=dydtdxdt=4t-22t+3The given point is (2, -1).∴ x = 2 and y = -1Now,t2+3t-8=2 and 2t2-2t-5=-1⇒t2+3t-10=0 and t2-t-2=0⇒t+5t-2=0 and t+1t-2=0⇒t=-5, 2 and t=-1, 2We can see that t=2 satisfies both of these.∴Slope of the tangent = dydxt=2= 8-24+3=67
Thus, the correct option is (b).
Q27.
Answer :
(a) 1
Let (x1, y1) be the required point.
The slope of the given line is m.
We have
y2=4x⇒2y dydx=4⇒dydx=42y=2ySlope of the tangent =dydx x1, y1=2y1Given:Slope of the tangent = mNow,2y1=m …1
Because the given line is a tangent to the given curve at point (x1, y1), this point lies on both the line and the curve.
∴y1=mx1+1 and y12=4×1⇒x1=y1-1m and x1=y124So, y1-1m=y124⇒y1-12y1=y124 [From (1)]⇒y1y1-12=y124⇒2y12-2y1=y12⇒y12-2y1=0⇒y12-2y1=0⇒y1y1-2=0⇒y1=0, 2So, For y1=0, m=20=∞For y1=2, m=22=1
Q28.
Answer :
(b) x − y = 0
Given:2y+x2=3⇒2dydx+2x=0⇒dydx=-2×2=-xSlope of the tangent = dydx1, 1=-1Slope of the normal, m = -1Slope of the tangent = -1-1=1Now,x1, y1=1, 1∴Equation of the normal=y-y1=m x-x1⇒y-1=1 x-1⇒x-y=0
Q29.
Answer :
Disclaimer: None of the given options is correct.
Given:x2=4y⇒2x=4dydx⇒dydx=2×4=x2Slope of the tangent = dydx1, 2=12Slope of the normal, m = -1Slope of the tangent=-112=-2Also,x1, y1=1, 2∴Equation of the normal=y-y1=m x-x1⇒y-2=-2 x-1⇒y-2=-2x+2⇒2x+y=4
Q30.
Answer :
(a) 4, ±83
Let (x1, y1) be the required point.
Since x1,y1 lies on the given curve∴9y12=x13 …1Now, 9y2=x3 18y dydx=3×2⇒dydx=3x218y=x26ySlope of the tangent = dydxx1, y1=x126y1Slope of the normal = -1x126y1=-6y1x12It is given that the normal makes equal intercepts with the axes.∴ Slope of the normal = ±1Now,-6y1x12=±1⇒-6y1x12=1 or -6y1x12=-1⇒y1=-x126 or y1=x126 …2Case 1: When y1=-x126From (1), we have9x1436=x13⇒x14=4×13⇒x14-4×13=0⇒x13x1-4=0⇒x1=0, 4Putting x1=0 in 1, we get,9y12=0⇒y1=0Putting x1=4 in 1, we get,9y12=43⇒y1=±83But, the line making the equal intercepts with the coordinate axes can not pass through the origin.Hence, the points are 4, ±83.
Page 17.11 Ex.17.1
Q1.
Answer :
Let x1, x2 ∈0, ∞ such that x1<x2. Then, x1<x2⇒loge x1<loge x2⇒fx1<fx2∴ x1<x2⇒fx1<fx2, ∀ x1, x2 ∈0, ∞So, fx is increasing on 0, ∞.
Q2.
Answer :
fx=loga xLet x1, x2 ∈0, ∞ such that x1<x2.Case 1: Let a>1Here, x1<x2⇒loga x1<loga x2⇒fx1<fx2∴ x1<x2⇒fx1<fx2, ∀ x1, x2 ∈0, ∞So, fx is increasing on 0, ∞.Case 2: Let 0<a<1Here, x1<x2⇒loga x1>loga x2⇒fx1>fx2∴ x1<x2⇒fx1>fx2, ∀ x1, x2 ∈0, ∞So, fx is decreasing on 0, ∞.
Q3.
Answer :
Here,fx=ax+bLet x1, x2 ∈R such that x1<x2. Then, x1<x2⇒a x1<a x2 ∵ a >0⇒a x1+b<a x2+b⇒fx1<fx2∴ x1<x2⇒fx1<fx2, ∀ x1, x2 ∈R So, fx is increasing on R.
Q4.
Answer :
fx=ax+bLet x1, x2 ∈R such that x1<x2.Then, x1<x2⇒a x1>a x2 (∵ a <0)⇒a x1+b>a x2+b⇒fx1>fx2Thus, x1<x2⇒fx1>fx2, ∀ x1, x2 ∈RSo, fx is decreasing on R.
Q5.
Answer :
Here,fx=1xLet x1, x2 ∈0, ∞ such that x1<x2. Then, x1<x2⇒1×1>1×2⇒fx1>fx2∴ x1<x2⇒fx1>fx2, ∀ x1, x2 ∈0, ∞So, fx is decreasing on 0, ∞.
Q6.
Answer :
Here,fx=11+x2Case 1: Let x1, x2 ∈0, ∞ such that x1<x2. Then, x1<x2⇒x12<x22⇒1+x12<1+x22⇒11+x12>11+x22⇒fx1>fx2 ∀ x1, x2 ∈0, ∞So, fx is decreasing on 0, ∞.Case 2: Let x1, x2 ∈(-∞, 0] such that x1<x2. Then, x1<x2⇒x12>x22⇒1+x12>1+x22⇒11+x12<11+x22⇒fx1<fx2⇒fx1<fx2, ∀ x1, x2 ∈(-∞, 0]So, fx is increasing on (-∞, 0].
Q7.
Answer :
fx=11+x2R can be divided into two intervals 0, ∞ and (-∞, 0].Case1: Let x1, x2 ∈0, ∞ such that x1<x2. Then, x1<x2⇒x12<x22⇒1+x12<1+x22⇒11+x12>11+x22⇒fx1>fx2∀ x1, x2 ∈0, ∞So, fx is decreasing on 0, ∞.Case 2: Let x1, x2 ∈(-∞, 0] such that x1<x2. Then, x1<x2⇒x12>x22⇒1+x12>1+x22⇒11+x12<11+x22⇒fx1<fx2 ∀ x1, x2 ∈(-∞, 0]So, fx is increasing on (-∞, 0].Here, fx is decreasing on 0, ∞ and increasing on (-∞, 0].Thus, fx is neither increasing nor decreasing on R.
Q8.
Answer :
Here,fx=x(a) Let x1, x2 ∈0, ∞ such that x1<x2. Then, x1<x2⇒x1<x2⇒fx1<fx2∴ x1<x2⇒fx1<fx2, ∀ x1, x2 ∈0, ∞So, fx is increasing on 0, ∞.(b) Let x1, x2 ∈ (-∞, 0]. such that x1<x2. Then, x1<x2⇒x1>x2⇒fx1>fx2∴ x1<x2⇒fx1>fx2, ∀ x1, x2∈ (-∞, 0].So, fx is decreasing on (-∞, 0].
Q9.
Answer :
Here,fx=7x-3Let x1, x2 ∈R such that x1<x2. Then, x1<x2⇒7 x1<7 x2 ∵ 7 >0⇒7 x1-3<7 x2-3⇒fx1<fx2∴ x1<x2⇒fx1<fx2, ∀ x1, x2 ∈RSo, fx is strictly increasing on R.
Page 17.36 Ex.17.2
Q2.
Answer :
Here,fx=x2-6x+9f’x=2x-6For f(x) to be increasing, we must havef’x>0⇒2x-6>0⇒2x>6⇒x>3⇒x∈3, ∞So, f(x) is increasing on 3, ∞.For f(x) to be decreasing, we must havef’x<0⇒2x-6<0⇒2x<6⇒x<3⇒x∈-∞, 3So, f(x) is decreasing on -∞, 3.
Let (x, y) be the coordinates on the given curve where the normal to the curve is parallel to the given line.
Slope of the given line = 1
Slope of tangent = dydxx, y= 2x-6Slope of normal = -1Slope of tangent=-12x-6Now,Slope of normal = Slope of the given line-12x-6=1-1=2x-62x=5x=52Given curve isy=x2-6x+9 =254-15+9 =14x, y=52, 14Hence, the coordinates are 52, 14.
Q3.
Answer :
fx=sin x – cos x, x∈0, 2πf’x=cos x + sin xFor f(x) to be increasin, we must havef’x>0⇒cos x + sin x>0⇒sin x>-cos x⇒tan x>-1⇒x∈0, 3π4∪7π4, 2πSo, f(x) is increasing on 0, 3π4∪7π4, 2π.
For f(x) to be decreasing we must have,f’x<0⇒cos x + sin x<0⇒sin x<-cos x⇒tan x<-1⇒x∈3π4, 7π4So, f(x) is decreasing on 3π4, 7π4.
Q4.
Answer :
fx=e2xf’x=2e2xNow, x∈RSince the value of e2x is always positive for any real value of x, e2x>0.⇒2e2x>0⇒f’x>0So, f(x) is increasing on R.
Q5.
Answer :
fx=e1xf’x=e1xddx1x =e1x-1×2 =-e1xx2Here, e1x>0 and x2>0, for any real value of x ≠ 0.∴ f’x=-e1xx2<0,∀x∈R, x≠ 0So, f(x) is a decreasing function.
Q6.
Answer :
fx=loga x =log xlog af’x=1x log aSince 0<a<1 and x>0, f’x=1x log a<0.So, fx is decreasing for all x>0.
Q7.
Answer :
Here,fx=sin xDomain of sin x is 0, π.f’x=cos xFor x∈0, π2, cos x>0 ∵ cos x is positive in first quadrant f’x>0So, f(x) is increasing for 0, π2.For x∈π2, π, cos x<0 ∵ cos x is negative in second quadrant So, f(x) is decreasing for π2, π.Since f(x) is increasing on 0, π2 and d
Q8.
Answer :
Here,fx=log sin xDomain of log sin x is 0, π.f’x=1sin xcos x =cot xFor x∈0, π2, cot x>0 ∵ Cot function is positive in first quadrant⇒f’x>0 So, f(x) is increasing on 0, π2.For x∈π2, π, cot x<0 ∵ Cot function is negative in second quadrant ⇒f’x<0 So, f(x) is decreasing on π2, π.
Q9.
Answer :
fx=x-sin xf’x=1-cos xFor f(x) to be increasing, we must havef’x>0⇒1-cos x>0⇒f'(x)⩾0 for all x∈R ∵ Cos x⩽1So, f(x) is increasing for all x∈R.
Q10.
Answer :
fx=x3-15×2+75x-50f’x=3×2-30x+75 =3 x2-10x+25 =3x-52>0, ∀x∈R ∵ Square of any function is always greater than zero So, f(x)is an increasing function for all x∈R.
Q11.
Answer :
fx=cos2xf’x=2 cos x -sin x⇒f’x=-sin 2x …1Now,0<x<π2⇒0<2x<π ⇒sin 2x>0 ∵ Sine fuction is positive in first and second quadrant ⇒-sin 2x<0⇒f’x<0 From eq. (1)So, f(x) is decreasing on 0, π2.
Q12.
Answer :
fx=sin xf’x=cos x>0 ∀x∈-π2, π2 ∵ Cos function is positive in first and fourth quadrant So, fx is increasing on -π2, π2.
Q13.
Answer :
Here,fx=cos xDomain of cos x is -π, π.⇒f’x=-sin xFor x∈-π, 0, sin x<0 ∵ sine function is negative in third and fourth quadrant ⇒- sin x>0⇒f’x>0So, cos x is increasing in -π,0.For x∈0, π), sin x>0 ∵ sine function is positive in first and second quadrant ⇒-sin x<0⇒f’x<0So, f(x) is decreasing on 0, π.Thus, f(x) is neither increasing nor decreasing in -π, π.
Q14.
Answer :
fx=tan xf’x=sec2 xHere,-π2<x<π2⇒sec x>0 ∵ Sec function is positive in first and fourth quadrant ⇒sec2 x>0⇒f’x>0, ∀x∈-π2, π2So, f(x) is increasing on -π2, π2.
Q15.
Answer :
fx=tan-1sin x+cos xf’x=11+sin x+cos x2cosx-sinx =11+1+2 sin x cos xcosx-sinx =cosx-sinx2+sin 2xHere,π4<x<π2⇒π2<2x<π⇒sin 2x>0⇒2+sin 2x>0 …1Also,π4<x<π2cos x<sin x⇒cos x-sin x<0 …2f’x=cos x-sin x2+sin 2x<0, ∀x∈π4, π2 From eqs. (1) and (2)So, fx is decreasing on π4, π2.
Q16.
Answer :
fx=sin 2x+π4f’x=2 cos 2x+π4Here,3π8<x<5π8⇒3π4<2x<5π4⇒π<2x+π4<3π2⇒cos 2x+π4<0 ∵ Cos function is negative in third quadrant⇒2 cos 2x+π4<0⇒f’x<0, ∀x∈3π8, 5π8So, fx is decreasing on 3π8, 5π8.
Q17.
Answer :
fx=tan x-4xf’x=sec2x-4 =1cos2x-4 =1-4cos2xcos2x =sec2x 1-4cos2x =4sec2x 14-cos2x =4sec2x12-cosx12+cos xHere,-π3<x<π3cos x>12⇒-cosx<-12⇒12-cosx<0 …1Also,-π3<x<π3⇒cos x>12⇒12+cosx>1⇒12+cosx>0 …24 sec2 x >0 ∵ a2>0Now,f’x=4sec2x12-cos x12+cos x<0, ∀∈-π3, π3 From eqs. (1) and (2)So, fx is decreasing on -π3, π3.
Q18.
Answer :
fx=x-1 ex+1f’x=x-1 ex+ex =xex-ex+ex =xexGiven: x>0 We know, ex>0⇒ xex>0⇒f’x>0, ∀x>0So, f(x) is increasing on for all x>0.
Q19.
Answer :
fx=x2-x+1f’x=2x-1For f(x) to be increasing, we must havef’x>0⇒2x-1>0⇒2x>1⇒x>12⇒x∈12, 1So, f(x) is increasing on 12, 1.For f(x) to be decreasing, we must havef’x<0⇒2x-1<0⇒2x<1⇒x<12⇒x∈0, 12So, f(x) is decreasing on 0, 12.Since f(x) is increasing on 12, 1 and decreasing on 0, 12, fx is neither increasing nor decreasing on (0, 1).
Q20.
Answer :
fx=x9+4×7+11f’x=9×8+28×6≥0, ∀x∈R ∵ x8, x6≥0, for ∀x∈RSo, f(x) is increasing on R.
Q21.
Answer :
fx=x3-6×2+12x-18f’x=3×2-12x+12 =3×2-4x+4 =3x-22≥0, ∀x∈R ∵ 3>0 & x-22≥0So, f(x) is increasing on R.
Q22.
Answer :
A function f(x) is said to be increasing on a, b if it is increasing at x=a and x=b.Here,fx=x2-6x+3f’x=2x-6⇒f’x=2x-3Now, f’4=24-3 = 2∴ f’4>0 So, f(x) is increasing on x=4 &, f’6=26-3 =6∴ f’6>0 So, f(x) is increasing on x=6 Hence, fx is increasing on [4, 6].
Q23.
Answer :
fx=x2-x sin xf’x=2x-x cos x-sin xHere,0<x<π2⇒0<sin x<1 and 0<cos x<1⇒2x-x cos x-sin x>0⇒f’x>0, ∀x∈0, π2So, fx is increasing on 0, π2.
Q24.
Answer :
fx=x3-axf’x=3×2-aGiven: fx is increasing on R.⇒f’x≥0 ∀ x∈R⇒3×2-a≥0 ∀ x∈R⇒a≤3×2∀ x∈RThe least value of 3×2 is 0.∴ a≤0
Page 17.37 Ex.17.2
Q25.
Answer :
fx=sin x-bx+cf’x=cos x-bGiven: fx is decreasing on R.f’x<0, ∀x∈R⇒cos x-b<0, ∀x∈R⇒cos x-b<0,∀x∈R ⇒cos x<b, ∀x∈R⇒ b⩾1 ∵ -1⩽cos x⩽1
Q26.
Answer :
fx=x+cos x-af’x=1-sin xWe know,sin x≤1, ∀x∈R⇒-sin x≥-1, ∀x∈R⇒1-sin x≥0, ∀x∈R⇒f’x≥0, ∀x∈RHence, fx is increasing on R for all values of a.
Q27.
Answer :
fx=sin x-cos xf’x=cos x+sin x =cos x1+sin xcos x =cos x1+cot xHere,-π4<x<π4⇒cos x>0 … 1Also,-π4<x<π4⇒-1<cot x<1⇒0<1+cot x<2⇒1+cot x>0 … 2cos x1+cot x>0, ∀x∈-π4, π4 From eqs. (1) and (2) ⇒f’x>0, ∀x∈-π4, π4So, fx is increasing on -π4, π4.
Q28.
Answer :
fx=tan-1x-xf’x=11+x2-1 =1-1-x21+x2 =-x21+x2We know,x2≥0, 1+x2>0, ∀ x∈R∴ -x21+x2<0, ∀ x∈R⇒f’x<0, ∀ x∈RSo, fx is decreasing on R.
Q29.
Answer :
fx=-x2+sin xf’x=-12+cos xHere, -π3<x<π3⇒cos x>12⇒-12+cos x>0⇒f’x>0, ∀x∈-π3, π3So, fx is increasing on -π3, π3.
Q30.
Answer :
fx=log 1+x-x1+xDomain of fx is -1, ∞.f’x=11+x-1+x-x1+x2 =11+x-11+x2 =x1+x2For f(x) to be increasing, we must havef’x>0⇒x1+x2>0⇒x>0 ∵ 1+x2>0, Domain: -1, ∞⇒x∈0, ∞So, f(x) is increasing on 0, ∞.For f(x) to be decreasing, we must havef’x<0⇒x1+x2<0⇒x<0 ∵1+x2>0, Domain: -1, ∞⇒x∈-1, 0So, f(x) is decreasing on -1, 0.
Q31.
Answer :
fx=x+2 e-xf’x=-e-xx+2+e-x =-xe-x-2e-x+e-x =-xe-x-e-x =e-x-x-1For f(x) to be increasing, we must havef’x>0⇒e-x-x-1>0⇒-x-1>0 ∵ e-x>0, ∀x∈R⇒-x>1⇒x<-1⇒x∈-∞, -1So, f(x) is increasing on -∞, -1.For f(x) to be decreasing, we must havef’x<0⇒e-x-x-1<0⇒-x-1<0 ∵ e-x>0, ∀x∈R⇒-x<1⇒x>-1⇒x∈-1, ∞So, f(x) is decreasing on -1, ∞.
Q32.
Answer :
fx=10xf’x=10x log 10>0, ∀x∈RSo, f(x) is increasing for all x∈R.
Q33.
Answer :
fx=x-xLet x1, x2 ∈0, 1 such that x1<x2. Then,x1=x2= 0 …(1)Now, x1<x2⇒x1-x1<x2-x2 From eq. (1)⇒fx1<fx2∴ x1<x2⇒fx1<fx2, ∀ x1, x2 ∈0, 1So, fx is increasing on 0, 1.
Q34.
Answer :
fx=3×5+40×3+240xf’x=15×4+120×2+240 =15 x4+8×2+16 =15 x2+42>0, ∀x∈R ∵ 15>0 and x2+42>0So, f(x) is increasing on R.
Q35.
Answer :
If a function is continuous and differentiable and f(0) = f(1) in given domain x ∈ [0, 1],
then by Rolle’s Theorem;
f'(x) = 0 for some x ∈ [0, 1]
Given: |f”(x)| ≤ 1
On integrating both sides we get,
|f'(x)| ≤ x
Now, within interval x ∈ [0, 1]
We get, |f’ (x)| < 1.
Q36.
Answer :
fx=log cos xf’x=1cos x-sin x =-tan xNow, x∈-π2, 0⇒tan x<0⇒-tan x>0 ⇒f'(x)>0So, f(x) is strictly increasing on -π2, 0.Now, x∈0,π2⇒tan x>0⇒-tan x<0 ⇒f'(x)<0So, f(x) is strictly decreasing on 0, π2.
Q37.
Answer :
fx=x3-3×2+4xf’x=3×2-6x+4 =3×2-2x+4 =3×2-2x+1-3+4 =3x-12+1>0, ∀x∈RHence, f(x) is strictly increasing on R.
Q38.
Answer :
fx=cos xf’x=-sin xi Here,0<x<π⇒sin x>0 ∵ Sine function is positive in first and second quadrant⇒-sin x<0⇒f’x<0, ∀x∈0, πSo, f(x) is strictly decreasing on 0, π.ii Here,π<x<2π⇒sin x<0 ∵ Sine function is negative in third and fourth quadrant⇒-sin x>0⇒f’x>0, ∀x∈π, 2πSo, f(x) is strictly increasing on π, 2π.iii From eqs. (1) and (2), we get f(x) is strictly decreasing on 0, π and is strictly increasing on π, 2π.So, fx is neither increasing nor decreasing on 0, 2π.
Page 17.40 (Very Short Answers)
Q1.
Answer :
fx=axf’x=ax log aGiven: f(x) is increasing on R.⇒f’x>0⇒ax log a>0Logarithmic function is defined for positive values of a.⇒a>0⇒ax>0We know, ax log a>0It can be possible when ax>0 and log a>0 or ax<0 and log a<0. ⇒log a>0⇒a>1So, f(x) is increasing when a > 1.
Q2.
Answer :
fx=axf’x=axlog aGiven: fx is decreasing on R.⇒f’x<0,∀x∈R⇒axlog a<0,∀x∈RHere, logaritmic function is not defined for negative values of a.⇒ax>0 ∴ axlog a<0 can be possible when log a<0,∀x∈R. ⇒0<a<1
Q3.
Answer :
fx=loga xLet x1, x2 ∈0, ∞ such that x1<x2.Since given function is logarithmic, either a>1 or 0<a<1.Case 1: Let a>1Here, x1<x2⇒loga x1<loga x2⇒fx1<fx2∴ x1<x2⇒fx1<fx2, ∀ x1, x2 ∈0, ∞So, fx is increasing on 0, ∞.Case 2: Let 0<a<1Here, x1<x2⇒loga x1>loga x2⇒fx1>fx2∴ x1<x2⇒fx1>fx2, ∀ x1, x2 ∈0, ∞Thus, for a>1, f(x) is increasing in its domain.
Q4.
Answer :
Given: fx=loga xDomain of the given function is 0, ∞.Let x1, x2 ∈0, ∞ such that x1<x2.Since the given function is logarithmic, either a>1 or 0<a<1.Case 1: Let a>1Here,x1<x2⇒loga x1<loga x2⇒fx1<fx2∴ x1<x2⇒fx1<fx2, ∀ x1, x2 ∈0, ∞So, fx is increasing on 0, ∞.Case 2: Let 0<a<1Here, x1<x2⇒loga x1>loga x2⇒fx1>fx2∴ x1<x2⇒fx1>fx2, ∀ x1, x2 ∈0, ∞So, fx is decreasing on 0, ∞Thus, for 0<a<1, fx is decreasing in its domain.
Q5.
Answer :
fx=a x+sin x+af’x=a 1+cos xFor f(x) to be increasing, we must havef’x>0⇒a 1+cos x>0 … 1We know, -1≤cos x≤1, ∀x∈R⇒0≤1+cos x≤2, ∀x∈R
∴ a>0 From eq. 1⇒a∈0, ∞
Q6.
Answer :
fx=sin x-ax+4f’x=cosx-aGiven: f(x) is increasing on R.⇒f’x>0⇒cosx-a>0⇒cosx>a We know, cosx≥-1, ∀x∈R ⇒a<-1⇒a∈-∞, -1
Q7.
Answer :
fx=bx+cos x+4f’x=b1-sin xGiven: f(x) is decreasing on R.⇒f’x<0⇒b1-sin x<0 … 1We know,sin x≤1⇒1-sin x≥0⇒b<0 Since 1-sin x≥0, b1-sin x<0⇒b<0⇒b∈-∞,0
Q8.
Answer :
fx=x+cos x+ax+bf’x=1-sin x+aFor f(x) to be increasing, we must havef’x>0⇒1-sin x+a>0⇒sin x<1+aWe know that the maximum value of sin x is 1.⇒1+a>1⇒a>0⇒a∈0, ∞
Q9.
Answer :
fx=kx-sin xf’x=k-cos xFor f(x) to be increasing, we must havef’x>0⇒k-cos x>0⇒cos x<kWe know that the maximum value of cos x is 1.Since cos x < k, the minimum value of k is 1.⇒ k∈1, ∞
Q10.
Answer :
Given: gx is decreasing on R.⇒x1<x2⇒gx1>gx2Applying tan-1 on both sides, we get⇒tan-1gx1>tan-1gx2⇒fx1>fx2Thus, x1<x2 ⇒fx1>fx2So, fx is decreasing on R.
Q11.
Answer :
fx=ax+bf’x=aFor f(x) to be decreasing, we must havef’x<0⇒a<0⇒a∈-∞, 0
Q12.
Answer :
fx=sin x+cos x, x∈0, π2f’x=cos x-sin xFor f(x) to be increasing, we must havef’x>0⇒cos x-sin x>0⇒sin x<cos x⇒sin xcos x<1⇒tan x<1⇒x∈ [0, π4)
Q13.
Answer :
fx=tan x-xf’x=sec2x-1 =tan2 x⩾0, ∀x∈0,2πSo, f(x) is increasing in its domain.
Q14.
Answer :
fx=cos x+a2x+bf’x=a2-sinxGiven: f(x) is strictly increasing on R.⇒f’x>0, ∀x∈R⇒a2-sin x>0, ∀x∈R⇒a2>sin x, ∀x∈RWe know that the maximum value of sin x is 1.Since a2>sin x, a2 is always greater than 1.⇒a2>1⇒a2-1>0⇒a+1a-1>0⇒a∈(-∞, -1)∪(1, ∞)
Page 17.41 (Multiple Choice Questions)
Q1.
Answer :
(b) (−∞, 0)
fx=x-ex+tan2π7f’x=1-exFor f(x) to be increasing, we must havef’x>0⇒1-ex>0⇒ex<1⇒x<0⇒x∈-∞, 0So, f(x) is increasing on -∞, 0.
Q2.
Answer :
(c) (−∞, ∞)
fx=cot-1x+xf’x=-11+x2+1 =-1+1+x21+x2 =x21+x2≥0, ∀x∈RSo, f(x) is increasing on -∞, ∞.
Q3.
Answer :
(c) (0, 1/e)
Given: fx=xxApplying log with base e on both sides, we getlog fx=x loge xf’xfx=1+loge xf’x=fx1+loge x=xx1+loge xFor f(x) to be decreasing, we must havef’x<0⇒xx1+loge x<0Here, logaritmic function is defined for positive values of x.⇒xx>0⇒1+loge x<0 Since xx>0, xx1+loge x<0⇒1+loge x<0 ⇒loge x<-1⇒x<e-1 ∵ logax<N⇒x<aN for a>1 Here, e>1⇒logex<-1⇒x<e-1⇒x∈0, e-1So, f(x) is decreasing on 0, 1e.
Q4.
Answer :
(b) (2, 3)
Given: fx=2 log x-2-x2+4x+1Domain of fx is 2, ∞.f’x=2x-2-2x+4 =2-2×2+4x+4x-8x-2 =-2×2+8x-6x-2 =-2 x2-4x+3x-2For f(x) to be increasing, we must havef’x>0⇒-2 x2-4x+3x-2>0⇒x2-4x+3+<0 ∵ x-2>0 & -2<0⇒x-1x-3<0⇒1<x<3⇒x∈1, 3Also, the domain of fx is 2, ∞.⇒x∈1, 3∩2, ∞⇒x∈2, 3
Q5.
Answer :
(a) (−∞, 4)
fx=2×2-kx+5f’x=4x-kFor f(x) to be increasing, we must havef’x>0⇒4x-k>0⇒k<4xSince x∈1, 2, 4x∈4, 8.So, the minimum value of 4x is 4.Since k<4x, k<4.⇒k∈-∞, 4
Q6.
Answer :
(c) a2 − 3b + 15 < 0 fx=x3+ax2+bx+5sin2xf’x=3×2+2ax+b+5 sin 2xGiven: fx is increasing on R.⇒f’x>0, ∀x∈R⇒3×2+2ax+b+5 sin 2x>0, ∀x∈R Since this quadratic function is >0, its discriminant is <0.⇒2a2-43b+5 sin 2x<0⇒4a2-12b-60 sin 2x<0⇒a2-3b-15 sin 2x
Q7.
Answer :
(b) odd and increasing
f(x) =logex3+x6+1⇒f(-x)=loge-x3+x6+1 =loge-x3+x6+1×3+x6+1×3+x6+1 =logex6+1-x6x3+x6+1 =loge1x3+x6+1 =-logex3+x6+1 =-f(x) Hence, f(-x)=-f(x)Therefore, it is an odd function.
f(x)=logex3+x6+1ddxf(x)=1×3+x6+1×3×2+12×6+1×6×5 =1×3+x6+1×6x2x6+1+6x52x6+1 =1×3+x6+1×6x2x6+1+x32x6+1 =6x22x6+1>0Therefore, given function is an increasing function.
Q8.
Answer :
f(x)= 2 tan x+2a+1logesec x+a-2 xWhen sec x>0⇒sec x=sec xddxfx=2sec2x+2a+11sec x×sec x tan x+a-2 =2sec2x+2a+1tan x+a-2 For f(x) to be increasing, 2sec2x+2a+1tan x+a-2⩾0⇒2+2 tan2x+2a+1tan x+a-2⩾0⇒2 tan2x+2a+1tan x+a⩾0Its discriminant ⩽0 ∵ax2+bx+c⩾0⇒b2-4ac⩽0⇒2a+12-4.2.a⩽0⇒4a2-4a+1⩽0⇒2a-12⩽02a-12<0 cannot be possible .∴ 2a-12=0⇒a=12When sec x<0⇒sec x=-sec xddxfx=2sec2x+2a+11-sec x×sec x tan x+a-2 =2sec2x-2a+1tan x+a-2 For f(x) to be increasing, 2sec2x-2a+1tan x+a-2⩾0⇒2+2 tan2x-2a+1tan x+a-2⩾0⇒2 tan2x-2a+1tan x+a⩾0 Its discriminant ⩽0 ∵ax2+bx+c⩾0⇒b2-4ac⩽0⇒-2a+12-4.2.a⩽0⇒4a2-4a+1⩽0⇒2a-12⩽02a-12<0 cannot be possible .∴ 2a-12=0⇒a=12
Q9.
Answer :
(a) increasing on (0, π/2)
Given: gx is increasing on 0, π2. Then,x1<x2, ∀ x1, x2∈0, π2⇒gx1<gx2Taking tan-1 on both the sides, we gettan-1gx1<tan-1gx2⇒fx1<fx2, ∀ x1, x2∈0, π2So, fx is increasing on 0, π2.
Q10.
Answer :
(c) f(x) is invertible
f(x) =x3 − 6x2 + 15x + 3
f'(x) =3×2-12x+15 =3×2-4x+5 =3×2-4x+4+1 =3x-22+13>0Therefore, f(x) is strictly increasing function.⇒ f-1(x) exists.Hence, f(x) is an invertible function.
Q11.
Answer :
(b) 0 < x < 2
fx=x2e-xf’x=2xe-x-x2e-x =e-x x2-xFor f(x) to be monotonic increasing, we must havef’x>0⇒e-x x2-x>0 ∵ e-x>0⇒ x2-x>0⇒ xx-2<0⇒0<x<2
Q12.
Answer :
(a) λ > 1/2
fx=cos x-2 λ xf’x=-sin x-2 λ For f(x) to be decreasing, we must havef’x<0⇒-sin x-2 λ <0⇒sin x+2 λ>0 ⇒2 λ>-sin xWe know that the maximum value of -sin x is 1.⇒2 λ>1⇒λ>12
Q13.
Answer :
(b) monotonically decreasing
If 1<x<2, then x>1 and x<2.⇒x-1>0 and x-2<0⇒x-1=x-1 and x-2=-x-2Now,fx=2 x-1+3 x-2=2x-1-3x-2=2x-2-3x+6=-x+4f’x=-1<0, ∀x∈1, 2So, fx is monotonically decreasing.
Page 17.42 (Multiple Choice Questions)
Q14.
Answer :
(d) | x | ≥ 3
fx=x3-27x+5f’x=3×2-27 =3 x2-9For f(x) to be increasing, we must havef’x>0⇒3 x2-9>0⇒x2-9>0 Since 3>0, 3 x2-9>0⇒x2-9>0|⇒x+3x-3>0⇒x<-3 or x>3⇒x>3
Q15.
Answer :
(d) 1 < x < 2
fx=2×3-9×2+12x+29f’x=6×2-18x+12 =6 x2-3x+2 =6x-1x-2For f(x) to be decreasing, we must havef’x<0⇒6x-1x-2<0 ⇒x-1x-2<0 Since 6>0, 6x-1x-2<0⇒x-1x-2<0⇒1<x<2So, f(x) is decreasing for 1<x<2.
Q16.
Answer :
(c) k > 3
fx=kx3-9×2+9x+3f’x=3kx2-18x+9 =3 kx2-6x+3Given: f(x) is monotonically increasing in every interval. ⇒f’x>0⇒3 kx2-6x+3>0⇒kx2-6x+3>0⇒k>0 and -62-4k3<0 ∵ ax2+bx+c>0⇒a>0 and Disc<0 ⇒k>0 and -62-4k3<0⇒k>0 and 36-12k<0⇒k>0 and 12k>36⇒k>0 and k>3⇒k>3
Q17.
Answer :
(c) x ∈ R
Given: fx=2x-tan-1x-log x+x2+1f’x=2-11+x2-1x+x2+11+12×2+1.2x =2-11+x2-1x+x2+11+xx2+1 =2-11+x2-1x+x2+1x+x2+1×2+1 =2-11+x2-1×2+1 =2+2×2-1-x2+11+x2 =1+2×2-x2+11+x2For f(x) to be monotonically increasing, f’x>0.⇒1+2×2-x2+11+x2>0 ⇒1+2×2-x2+1>0 ∵ 1+x2>0⇒1+2×2>x2+1⇒1+2×22>x2+1⇒1+4×4+4×2>x2+1⇒4×4+3×2>0Thus, f(x) is monotonically increasing for x∈R.
Q18.
Answer :
(d) 0 < x < 1
fx=x-x-1Case 1: Let x<0 If x<0 , then x=-x⇒ x-1=-x-1Now, fx=x-x-1 =-x–x+1 =-x+x-1 =-1f’x=0So, fx is not monotonically increasing when x < 0.Case 2: Let 0<x<1Here,x=x⇒ x-1=-x-1Now, fx=x-x-1 =x+x-1 =2x-1f’x=2>0So, fx is monotonically increasing when 0<x<1.Case 3: Let x>1 If x>0, then x=x⇒ x-1=x-1Now, fx=x-x-1 =x-x+1 =1f’x=0So, fx is not monotonicallyincreasing when x >1.Thus, fx is monotonically increasing when 0<x<1.
Q19.
Answer :
(a) monotonic function
We know that “every invertible function is a monotonic function”.
Q20.
Answer :
(b) decreasing
Given: fx=2x-1+3x-2If 1<x<2, then x-1=x-1.⇒x-2=-x-2Now, fx=2x-1+3x-2 =2 x-1+3 -x+2 =2x-2-3x+6 =-x+4f’x=-1<0So, fx is decreasing when 1<x<2.
Q21.
Answer :
(c)
a≤-12 Given: fx=cos x-2ax+bNow, x=x , x≥0 -x, x<0and cos x=cosx , x≥0 cos-x=cosx, x<0∴cosx=cos x ,∀x∈R∴ fx=cos x-2ax+b⇒f’x=-sin x-2aIt is given that f(x) is increasing.⇒f’x≥0⇒-sin x-2a≥0⇒sin x+2a≤0⇒2a ≤-sin xThe least value of -sin x is -1.⇒2a≤-1⇒a≤-12
Q22.
Answer :
(a) strictly increasing
fx=x1+xCase 1: When x>0, x=xfx=x1+x =x1+x⇒f’x=1+x1-x11+x2 =11+x2>0, ∀x∈RSo, fx is strictly increasing when x > 0.Case 2: When x<0, x=-xfx=x1+x =x1-x⇒f’x=1-x1-x-11-x2 =11-x2>0, ∀x∈RSo, fx is strictly increasing when x < 0.Thus, fx is strictly increasing on R.
Q23.
Answer :
(d) λ > 2
fx=λ sin x+2 cos xsin x+cos xf’x=sin x+cos xλ cos x-2 sin x+λ sin x+2 cos xcos x-sin xsin x+cos x2=λcos x sin x+λcos2x-2 sin2x-2 sinx cos x-λsinx cos x-2cos2x+λ sin2x+2 cosx sinx sin x+cos x2=-2 sin2x+cos2x+λ sin2x+cos2xsin x+cos x2=-2 +λ sin x+cos x2For f(x) to be increasing, we must havef’x>0⇒-2 +λ sin x+cos x2>0 ⇒λ -2>0 ∵sin x+cos x2>0⇒λ >2
Q24.
Answer :
(d) a > 1
fx=axf’x=ax log aGiven: f(x) is increasing on R.⇒f’x>0⇒ax log a>0⇒ax>0 Logarithmic function is defined for positive values of aWe know,ax log a>0It can be possible when ax>0 and log a>0 or ax<0 and log a<0 Not possible, logarithmic function is defined for positive values of a⇒log a>0⇒a>1So, f(x) is increasing when a > 1.
Q25.
Answer :
(b) a > 1
fx=loga x=log xlog af’x=1x log aGiven: f(x) is increasing on R.⇒f’x>0, ∀x∈R⇒1x log a>0, ∀x∈R⇒a>1
Q26.
Answer :
Given: ϕ(x) = f(x) + f(2a − x)
Differentiating above equation with respect to x we get,
ϕ'(x) = f'(x) − f(2a − x) …..(1)
Since, f”(x) > 0, f'(x) is an increasing function.
Now,
when
x∈0, a
x≤2a-xf’x≤f2a-x …..2
Considering equation (1) and (2) we get,
ϕ'(x) ≤ 0
⇒ ϕ'(x) is decreasing in [0, a]
Q27.
Answer :
(d) k ∈ (−∞, 4)
fx=x2-kx+5f’x=2x-kGiven: f(x) is increasing on[2, 4].⇒ f’x>0⇒2x-k>0⇒k<2x∵ x∈2, 4, maximum value of k is 4, k < 4.∴ k∈-∞, 4
Page 17.43 (Multiple Choice Questions)
Q28.
Answer :
f(x) =-x2+sin x defined on -π3,π3∴ f'(x)=-12+cos x ⇒ f'(x)⩾0 ∀x∈-π3,π3∵ for x∈-π3,π3 , cos x⩾12
Hence, the given function is increasing .
Q29.
Answer :
(a)
fx=x3-9kx2+27x+30f’x=3×2-18kx+27 =3 x2-6kx+9Given: f(x) is increasing on R.⇒f’x>0 for all x∈R⇒3 x2-6kx+9>0 for all x∈R⇒x2-6kx+9>0 for all x∈R⇒-6k2-419<0 ∵ ax2+bx+c>0 for all x∈R⇒a>0 and Disc<0⇒36k2-36<0⇒k2-1<0⇒k+1k-1<0It can be possible when k+1<0 and k-1>0.⇒k<-1 and k>1 (Not possible)or k+1>0 and k-1<0⇒k>-1 and k<1⇒-1<k<1Disclaimer: (a) part should be −1< k < 1 instead of −1 ≤ k < 1.
Q30.
Answer :
(a) R
fx=x9+3×7+64f’x=9×8+21×6>0, ∀x∈RSo, f(x) is increasing on R.
Page 18.7 Ex.18.1
Q1.
Answer :
Given: f(x) = 4x2 − 4x + 4
⇒f(x) = (4x2 − 4x + 1)+3
⇒f(x) = (2x − 1)2 + 3
Now,
(2x − 1)2 ≥ 0 for all x ∈ R
⇒f(x) = (2x − 1)2 + 3 ≥ 3 for all x ∈ R
⇒f(x) ≥ 3 for all x ∈ R
The minimum value of f is attained when (x − 1) = 0.
(2x − 1) = 0
⇒ x = 12
Thus, the minimum value of f (x) at x = 12 is 3.
Since f(x) can be enlarged, the maximum value does not exist, which is evident in the graph also.
Hence, function f does not have a maximum value.
Q2.
Answer :
Given: f(x) = − (x − 1)2 + 2
Now,
(x − 1)2 ≥ 0 for all x ∈ R
⇒f(x) = − (x − 1)2 + 2 ≤ 2 for all x ∈ R
The maximum value of f(x) is attained when (x − 1) = 0.
(x − 1) = 0
⇒ x = 1
Therefore, the maximum value of f (x) = 2
Since f(x) can be reduced, the minimum value does not exist, which is evident in the graph also.
Hence, function f does not have a minimum value.
Q3.
Answer :
Given: f(x) = x+2
Now,
x+2≥0 for all x ∈ R
Thus, f(x) ≥0 for all x ∈ R
Therefore, the minimum value of f at x = -2 is 0.
Since f(x) can be enlarged, the maximum value does not exist, which is evident in the graph also.
Hence, the function f does not have a maximum value.
Q4.
Answer :
Given: f(x) = sin 2x + 5
We know that − 1 ≤ sin 2x ≤ 1.
⇒ − 1 + 5 ≤ sin 2x + 5 ≤ 1 + 5
⇒ 4 ≤ sin 2x + 5 ≤ 6
⇒ 4 ≤ f(x) ≤ 6
Hence, the maximum and minimum values of f are 6 and 4, respectively.
Q5.
Answer :
Given: f(x) =sin 4x+3
We know that −1 ≤ sin 4x ≤ 1.
⇒ 2 ≤ sin 4x + 3 ≤ 4
⇒ 2 ≤ sin 4x+3 ≤ 4
⇒ 2 ≤ f(x) ≤ 4
Hence, the maximum and minimum values of f are 4 and 2, respectively.
Q6.
Answer :
We can observe that f(x) increases when the values of x are increased and f(x) decreases when the values of x are decreased. Also, f(x) can be reduced by giving small values of x.
Similarly, f(x) can be enlarged by giving large values of x.
So, f(x) does not have a minimum or maximum value.
Q7.
Answer :
Given: f(x) =-x+1 + 3
Now,
-x+1≤0 for all x ∈ R
⇒f(x) = -x+1 + 3≤ 3 for all x ∈ R
⇒f(x) ≤ 3 for all x ∈ R
The maximum value of f is attained when x+1=0.⇒x=-1
Therefore, the maximum value of f at x = -1 is 3.
Since f(x) can be reduced, the minimum value does not exist, which is evident in the graph also.
Hence, the function f does not have a minimum value.
Q8.
Answer :
Given: f(x) = 16x2 − 16x + 28
⇒f(x) = 4(4x2 – 4x + 1) + 24
⇒f(x) = 4(2x − 1)2 + 24
Now,
4(2x − 1)2 ≥ 0 for all x ∈ R
⇒f(x) = 4(2x − 1)2 + 24 ≥ 24 for all x ∈ R
⇒f(x) ≥ 24 for all x ∈ R
The minimum value of f is attained when (2x − 1) = 0.
(2x − 1) = 0
⇒ x = 12
Therefore, the minimum value of f at x = 12 is 24.
Since f(x) can be enlarged, the maximum value does not exist, which is evident in the graph also.
Hence, the function f does not have a maximum value.
Q9.
Answer :
Given: f(x) = sin 2x + 5
We know that − 1 ≤ sin 2x ≤ 1.
⇒ − 1 + 5 ≤ sin 2x + 5 ≤ 1 + 5
⇒ 4 ≤ sin 2x + 5 ≤ 6
⇒ 4 ≤ f(x) ≤ 6
Hence, the maximum and minimum values of f are 6 and 4, respectively.
Q10.
We can observe that f(x) increases when the values of x increase and f(x) decreases when the values of x decrease. Also, f(x) can be reduced by giving smaller values of x.
Similarly, f(x) can be enlarged by giving larger values of x.
So, f(x) does not have a minimum or maximum value.
Page 18.15 Ex.18.2
Q1.
Answer :
Given: fx=x-54⇒f’x=4x-53For a local maximum or a local minimum, we must havef’x=0⇒4x-53=0⇒x=5
Since f ‘(x) changes from negative to positive when x increases through 5, x = 5 is the point of local minima.
The local minimum value of f (x) at x = 5 is given by
5-54=0
Q2.
Answer :
Given: fx=x3-3x⇒f’x=3×2-3For a local maximum or a local minimum, we must havef’x=0⇒3×2-3=0⇒x2-1=0⇒x=±1
Since f ‘(x) changes from negative to positive as x increases through 1, x = 1 is the point of local minima.
The local minimum value of f (x) at x = 1 is given by
13-31=-2
Since f ‘(x) changes from positive to negative when x increases through -1, x = -1 is the point of local maxima.
The local maximum value of f (x) at x = -1 is given by
-13-3-1=2
Q3.
Answer :
Given: fx=x3x-12⇒f’x=3x2x-12+2x3x-1For a local maximum or a local minimum, we must have f’x=0⇒3x2x-12+2x3x-1=0⇒x2x-13x-3+2x=0⇒x2x-15x-3=0⇒x=0, 1, 35
Since f ‘(x) changes from negative to positive when x increases through 1, x = 1 is the point of local minima.
The local minimum value of f (x) at x = 1 is given by
131-12=0
Since f ‘(x) changes from positive to negative when x increases through 35, x = 35 is the point of local maxima.
The local minimum value of f (x) at x = 35 is given by
35335-12=27125×425=1083125
Since f ‘(x) does not change from positive as x increases through 0, x = 0 is a point of inflexion.
Disclaimer: The solution in the book is incorrect. The solution here is created according to the question given in the book.
Q4.
Answer :
Given: fx=x-1x+22⇒f’x=x+22+2x+2x-1For a local maximum or a local minimum, we must havef’x=0⇒x+22+2x+2x-1=0⇒x+2x+2+2x-2=0⇒x+23x=0⇒x=0, -2
Since f ‘(x) changes from negative to positive when x increases through 0, x = 0 is the point of local minima.
The local minimum value of f (x) at x = 0 is given by
0-10+22=-4
Since f ‘(x) changes sign from positive to negative when x increases through -2, x = -2 is the point of local maxima.
The local maximum value of f (x) at x = -2 is given by
-2-1-2+22=0
Q5.
Answer :
Given: fx=x-13x+12⇒f’x=3x-12x+12+2x-13x+1For a local maximum or a local minimum, we must have f’x=0⇒3x-12x+12+2x-13x+1=0⇒x+1x-123x+3+2x-2=0⇒x+1x-125x+1=0⇒x=-1, 1 and -15
Since f ‘(x) changes from negative to positive when x increases through -15, x = -15 is the point of local minima.
The local minimum value of f (x) at x = -15 is given by
-15-13-15+12=-34563125
Since f ‘(x) changes from positive to negative when x increases through -1, x = -1 is the point of local maxima.
The local maximum value of f (x) at x = -1 is given by
-1-13-1+12=0
Q6.
Answer :
Given: fx=x3-6×2+9x+15⇒f’x=3×2-12x+9For a local maximum or a local minimum, we must havef’x=0⇒3×2-12x+9=0⇒x2-4x+3=0⇒x-1x-3=0⇒x=1 or 3
Since f ‘(x) changes from negative to positive when x increases through 3, x = 3 is the point of local minima.
The local minimum value of f (x) at x = 3 is given by
33-632+93+15=27-54+27+15=15
Since f ‘(x) changes from positive to negative when x increases through 1, x = 1 is the point of local maxima.
The local maximum value of f (x) at x = 1 is given by
13-612+91+15=1-6+9+15=19
Q7.
Answer :
Given: fx=sin 2x⇒f’x=2 cos 2xFor a local maximum or a local minimum, we must havef’x=0⇒2 cos 2x=0⇒cos 2x=0⇒x=π4 or 3π4
Since f ‘(x) changes from positive to negative when x increases through π4, x = π4 is the point of maxima.
The local maximum value of f (x) at x = π4 is given by
sinπ2=1
Since f ‘(x) changes from negative to positive when x increases through 3π4, x = 3π4 is the point of minima.
The local minimum value of f (x) at x = 3π4 is given by
sin3π2=-1
Q8.
Answer :
Given: fx=sin x-cos x⇒f’x=cos x+sin xFor a local maximum or a local minimum, we must havef’x=0⇒cos x+sin x=0⇒cos x=-sin x⇒tan x=-1⇒x=3π4 or 7π4
Since f ‘(x) changes from positive to negative when x increases through 3π4, x = 3π4 is the point of local maxima.
The local maximum value of f (x) at x = 3π4 is given by
sin3π4-cos3π4=2
Since f ‘(x) changes from negative to positive when x increases through 7π4, x = 7π4 is the point of local minima.
The local minimum value of f (x) at x = 7π4 is given by
sin7π4-cos7π4=-2
Q9.
Answer :
Given: fx=cos x⇒f’x=-sin xFor a local maximum or a local minimum, we must havef’x=0⇒-sin x=0⇒sin x=0⇒x=0 or π.
Since 0<x<π, none is in the interval 0, π.
Q10.
Answer :
Given: fx=sin 2x-x⇒f’x=2 cos 2x-1For a local maximum or a local minimum, we must havef’x=0⇒2 cos 2x-1=0⇒cos 2x=12⇒x=-π6 or π6.
Since f ‘(x) changes from positive to negative when x increases through π6, x = π6 is the point of local maxima.
The local maximum value of f (x) at x = π6 is given by
sin π3-π6=32-π6
Since f ‘(x) changes from negative to positive when x increases through -π6, x = -π6 is the point of local minima.
The local minimum value of f (x) at x = -π6 is given by
sin -π3+π6=π6-32
Q11.
Answer :
Given: fx=2 sin x-x⇒f’x=2 cos x-1For a local maximum or a local minimum, we must have f’x=0⇒2 cos x-1=0⇒cos x=12⇒x=π3 or -π3
Since f ‘(x) changes from positive to negative when x increases through π3, x = π3 is the point of local maxima.
The local maximum value of f (x) at x = π3 is given by
2 sin π3-π3=3-π3
Since f ‘(x) changes from negative to positive when x increases through -π3, x = -π3 is the point of local minima.
The local minimum value of f (x) at x = -π3 is given by
2 sin -π3+π3=π3-3
Q12.
Answer :
Given: fx=x1-x⇒f’x=1-x-x21-x=2-3×21-xFor the local maxima or minima, we must havef’x=0⇒2-3×21-x=0⇒x=23
Since, f ‘(x) changes from positive to negative when x increases through 23, x = 23 is a point of maxima.
The local maximum value of f (x) at x = 23 is given by
231-23=233=239
Q13.
Answer :
Given: fx=x32x-13⇒f’x=3x22x-13+6x32x-12For the local maxima or minima, we must have f’x=0⇒3x22x-13+6x32x-12=0⇒3x22x-122x-1+2x=0⇒x22x-124x-1=0⇒x=0, 12 and 14
Since f ‘(x) changes from negative to positive when x increases through 14, x = 14 is a point of local minima.
The local minimum value of f (x) at x = 14 is given by
14312-13=-1512
Q14.
Answer :
Given: fx=x2+2x⇒f’x=12-2x2For the local maxima or minima, we must havef’x=0⇒12-2×2=0⇒12=2×2⇒x2=±2
Since x > 0, f ‘(x) changes from negative to positive when x increases through 2. So, x = 2 is a point of local minima.
The local minimum value of f (x) at x = 2 is given by
22+22=2
Q15.
Answer :
Given: fx=1×2+2⇒ f’x=-2xx2+22For the local maxima or minima, we must have f’x=0⇒-2xx2+22=0⇒x=0
Now, for values close to x = 0 and to the left of 0, f’x>0.
Also, for values close to x = 0 and to the right of 0, f’x<0.
Therefore, by first derivative test, x = 0 is a point of local maxima and the local maximum value of fx is 12.
Page 18.28 Ex.18.3
Q1.
Answer :
i) Given: fx = x4-62×2+120x+9⇒f’x = 4×3-124x+120For the local maxima or minima, we must have f’x=0⇒4×3-124x+120=0⇒x3-31x+30=0⇒x-1×2+x-30=0⇒x-1x+6x-5=0⇒x=1, 5 and -6Thus, x=1, x=5 and x=-6 are the possible points of local maxima or local minima.Now,f”x=12×2-124At x=1: f”1 = 1212-124=-112<0So, x=1 is the point of local maximum.The local maximum value is given byf1 = 14-6212+120×1+9=68At x=5: f”5 = 1252-124=176>0So, x=5 is the point of local minimum.The local minimum value is given byf5 = 54-6252+120×5+9=-316At x=-6: f”-6 = 12-62-124=308>0So, x=-6 is the point of local maximum.The local minimum value is given by f-6 =-64-62-62+120×-6+9=-1647
ii) Given: fx = x3-6×2+9x+15⇒f’x = 3×2-12x+9For the local maxima or minima, we must have f’x=0⇒ 3×2-12x+9=0⇒ x2-4x+3=0⇒x-1x-3=0⇒x=1 and 3Thus, x=1 and x=3 are the possible points of local maxima or local minima.Now, f”x = 6x-12At x=1: f”1 = 61-12=-6<0So, x=1 is the point of local maximum.The local maximum value is given byf1 = 13-612+9×1+15=19At x=3: f”3 = 63-12=6>0So, x=3 is the point of local minimum.The local minimum value is given byf3 =33-632+9×3+15=15
iii) Given: fx =x-1x+22=x-1×2+4x+4=x3+4×2+4x-x2-4x-4=x3+3×2-4⇒f’x = 3×2+6xFor the local maxima or minima, we must have f’x=0⇒ 3×2+6x=0⇒3xx+2=0⇒x=0 and-2Thus, x=0 and x=-2 are the possible points of local maxima or local minima.Now, f”x = 6x+6At x=0: f”0 = 60+6=6>0So, x=0 is the point of local minimum.The local minimum value is given byf0 = 0-10+22=-4At x=-2: f”-2 = 6-2+6=-6<0So, x=-2 is the point of local maximum.The local maximum value is given by f-2 =-2-1-2+22=0
iv) Given: fx = 2x-2×2=2x-1-2x-2⇒f’x =-2x-2+4x-3=4×3-2x2For the local maxima or minima, we must have f’x=0⇒4×3-2×2=0⇒4-2x=0⇒x=2Thus, x=2 is the possible point of local maxima or local minima.Now, f”x = -12×4+4x3At x=2: f”2 =-1216+48 =-12+816=-14<0So, x=2 is the point of local maximum.The local maximum value is given byf2 = 22-222=1-12=12
v) Given: fx = xex⇒f’x = ex+xexFor the local maxima or minima, we must have f’x=0⇒ex+xex=0⇒ex1+x=0⇒ex≠0 , x=-1⇒x=-1Thus, x=-1 is the possible point of local maxima or local minima.Now,f”x = ex+ex+xexAt x=-1: f”-1 =e-1+e-1-e-1 =e-1>0So, x=-1 is the point of local minimum.The local minimum value is given byf-1 = -e-1=-1e
vi) Given: fx = x2+2x⇒f’x = 12-2x2For the local maxima or minima, we must have f’x=0⇒12-2×2=0⇒x2=4⇒x=2 and-2Thus, x=2 and x=-2 are the possible points of local maxima or a local minima.Since x>0, x=2Now, f”x = 4x3At x=2: f”2 =423 =12>0So, x=2 is the point of local minimum.The local minimum value is given by f2 = x2+2x =1+1=2
vii) Given: fx =x+1x+213⇒f’x =x+213+13x+1x+2-23For the local maxima or minima, we must have f’x=0⇒ x+213+13x+1x+2-23=0⇒13x+1=-x+213×x+223⇒13x+1=-x+2⇒x+1=-3x-6⇒x=-74Thus, x=-74 is the possible point of local maxima or local minima.Now, f”-74 =23x+2-23-29x+1x+2-53At x=-74: f”-74 =23-74+2-23-29-74+1-74+2-53=2314-23+11814-52>0So, x=-74 is the point of local minimum.The local minimum value is given byf-74 = -74+1-74+213=-341413=-3443
viii) Given: fx = x32-x2⇒f’x = 32-x2-x232-x2For the local maxima or minima, we must have f’x=0⇒32-x2-x232-x2=0⇒32-x2=x32-x2⇒32-x2 =x2 ⇒x2=16 ⇒x=±4 Thus, x=4 and x=-4 are the possible points of local maxima or local minima.Now, f”x =-x32-x2 -2×32-x2+x332-x232-x2=-x32-x2 -2×32-x2+x332-x232-x2At x=4: f”4 = -432-42 -832-42+4332-4232-42 =-1-19264=-3<0So, x=4 is the point of local maximum.The local maximum value is given by f4 = 432-42 =16At x=-4: f”-4 = 432-42 +832-42-4332-4232-42 =1+2=3>0So, x=-4 is the point of local minimum.The local minimum value is given by f-4 = -432-42 =-16
ix) fx = x3-2ax2+a2x⇒f’x = 3×2-4ax+a2For the local maxima or minima, we must have f’x=0⇒3×2-4ax+a2=0⇒ 3×2-3ax-ax+a2=0⇒3xx-a-ax-a=0⇒3x-ax-a=0⇒x=a and a3Thus, x=a and x=a3 are the possible points of local maxima or local minima.Now, f”x = 6x-4aAt x=a: f”a = 6a-4a=2a>0So, x=a is the point of local minimum.The local minimum value is given byfa = a3-2aa2+a2a=0At x=a3: f”a3 = 6a3-4a=-2a<0So, x=a3 is the point of local maximum.The local maximum value is given byfa3 =a33 -2aa32 +a2a3 =a327-2a39+a33=4a327
x) Given: fx = x+a2x⇒f’x = 1-a2x2For the local maxima or minima, we must havef’x=0⇒ 1-a2x2=0⇒x2=a2⇒x=±a Thus, x=a and x=-a are the possible points of local maxima or local minima.Now, f”x = a2x3At x=a: f”a =a2a3 =1a>0So, x=a is the point of local minimum.The local minimum value is given byfa=x+a2x=a+a=2aAt x=-a: f”a =a2-a3 =-1a<0So, x=-a is the point of local maximum.The local maximum value is given byf-a = x+a2x =-a-a=-2a
xi) Given: fx = x2-x2⇒f’x = 2-x2-x22-x2For the local maxima or minima, we must have f’x=0⇒2-x2-x22-x2=0⇒2-x2=x2-x2⇒2-x2 =x2 ⇒x2=1 ⇒x=±1 Thus, x=1 and x=-1 are the possible points of local maxima or local minima.Now, f”x =-x2-x2 -2×2-x2+x32-x22-x2=-x2-x2 -2×2-x2+x32-x22-x2At x=1: f”1 = -12-12 -22-12+132-122-12 =-12-32=-2<0So, x=1 is the point of local maximum.The local maximum value is given byf4 = 12-12 =1At x=-1: f”-1 = 12-12 +22-12-132-122-12 =1+1=2>0So, x=-1 is the point of local minimum.The local minimum value is given byf-1 = -12-12 =-1
xii) Given: fx = x+1-x⇒f’x = 1-121-xFor the local maxima or minima, we must have f’x=0⇒1-121-x=0⇒1-x=12⇒1-x=14 ⇒x=34 Thus, x=34 is the possible point of local maxima or local minima.Now, f”x = -141-x41-xAt x=34: f”34 = -141-3441-34 =-12<0So, x=34 is the point of local maximum.The local maximum value is given byf34 = 34+1-34 =54
Page 18.29 Ex.18.3
Q2.
Answer :
i) Given: fx=x-1x-22=x-1×2-4x+4=x3-4×2+4x-x2+4x-4=x3-5×2+8x-4⇒f’x= 3×2-10x+8For the local maxima or minima, we must have f’x=0⇒ 3×2-10x+8=0⇒3×2-6x-4x+8=0⇒x-23x-4=0⇒x=2 and43Thus, x=2 and x=43 are the possible points of local maxima or local minima.Now, f”x = 6x-10At x=2: f”2 = 62-10=2>0So, x=2 is the point of local minimum.The local minimum value is given byf2 = 2-12-22=0At x=43: f”43 = 643-10=-2<0So, x=4 3is the point of local maximum.The local maximum value is given byf4 3 =4 3-14 3-22=13×49=427
ii) Given: fx = x1-x⇒f’x = 1-x-x21-xFor the local maxima or minima, we must have f’x=0⇒1-x-x21-x=0⇒1-x=x21-x⇒2-2x=x⇒3x=2 ⇒x=23 Thus, x=23 is the possible point of local maxima or local minima.Now, f”x =-11-x -121-x+x21-x1-x=-11-x -122-x1-x1-xAt x=23: f”23 = -11-23 -122-231-231-23 =-3-4313×3=-3-43<0So, x=23 is the point of local maximum.The local maximum value is given byf23 = 231-23 =233
iii) Given: fx =-x-13x+12⇒f’x =- 3x-12x+12+2x+1x-13For the local maxima or minima, we must have f’x=0⇒ -3x-12x+12-2x+1x-13=0⇒x-12x+1-3x+1-2x-1=0⇒x-12x+1-3x-3-2x+2=0⇒x-12x+1-5x-1=0⇒x=1, -1 and -15Thus, x=1, x=-1 and x=-15 are the possible points of local maxima or local minima.Now, f”x = – 32x-1x+12+2x+1x-12+2x-13+3x-12x+1 = -6x-1x+12+6x+1x-12-2x-13-6x-12x+1At x=1: f”1 =-61-11+12+61+11-12-21-13-61-121+1=0So, it is a point of inflexion.At x=-1: f”-1 =-6-1-1-1+12+6-1+1-1-12-2-1-13-6-1-12-1+1=16>0So, x=-1 is the point of local minimum.The local minimum value is given by f-1 =-1-13-1+12=0At x=-15: f”-15 =-6-15-1-15+12+6-15+1-15-12+2-15-13-6-15-12-15+1=576125+384125-432125-864125=-336125<0So, x=-15 is the point of local maximum.The local maximum value is given by f-15 =–15-13-15+12=–2161251625=34653125
Q3.
Answer :
Given: fx=y=a log x+bx2+x⇒f’x=ax+2bx+1Since, f’x has extreme values at x=1 and x=2, f’1=0.⇒a1+2b1+1=0⇒a=-1-2b …1f’2=0⇒a2+2b2+1=0⇒a+8b=-2 ⇒a=-2-8b …2From eqs. 1 and 2, we get-2-8b=-1-2b⇒6b=-1⇒b=-16Substituting b=-16 in eq. 1, we geta=-1+13=-23
Q4.
Answer :
Here,fx = log xx⇒f’x = 1-log xx2For the local maxima or minima, we must have f’x=0⇒1-log xx2=0⇒1=log x⇒log e=log x⇒x=eNow, f”x = x2-1x-2×1-log xx4=-3+2 log xx3⇒f”e = -3+2 log ee3=-1e3<0So, x=e is the point of local maximum.
Q5.
Answer :
Given: fx = 4x+2+x⇒f’x = -4x+22+1For a local maxima or a local minima, we must have f’x=0⇒-4x+22+1=0⇒-4x+22=-1⇒x+22=4⇒x+2=±2⇒x=0 and -4Thus, x=0 and x=-4 are the possible points of local maxima or local minima.Now, f”x = 8x+23At x=0: f”0 =823 =1>0So, x=0 is a point of local minimum.The local minimum value is given byf0 = 40+2+0 =2At x=-4: f”-4 =8-43 =-18<0So, x=-4 is a point of local minimum.The local maximum value is given byf-4 = 4-4+2-4 =-6
Q6.
Answer :
Given: fx =y=tan x-2x⇒f’x =sec2 x-2For a local maxima or local minima, we must have f’x=0⇒sec2 x-2=0⇒sec2 x=2⇒sec x=±2⇒x=π4 and 3π4Thus, x=π4 and x=3π4 are the possible points of local maxima or a local minima.Now,f”x = 2 sec2 x tan xAt x=π4: f”π4 =2 sec2 π4 tan π4 = 4>0So, x=π4 is a point of local minimum.The local minimum value is given byfπ4 =tanπ4-2×π4 =1-π2At x=3π4: f”3π4 =2 sec2 3π4 tan 3π4 =-4<0So, x=3π4 is a point of local maximum.The local maximum value is given byf3π4 =tan 3π4-2×3π4 =-1-3π2
Page 18.34 Ex.18.4
Q1.
Answer :
i) Given: fx=4x-x22⇒f’x=4-xFor a local maximum or a local minimum, we must havef’x=0⇒4-x=0⇒x=4Thus, the critical points of f are -2, 4 and 4.5.Now,f-2=4-2–222=-8-2=-10f4=44-422=16-8=8f4.5=44.5-4.522=18-10.125=7.875Hence, the absolute maximum value when x=4 is 8 and the absolute minimum value when x=-2 is -10.
ii) Given: fx=x-12+3⇒f’x=2x-1For a local maximum or a local minimum, we must have f’x=0⇒2x-1=0⇒x=1Thus, the critical points of f are -3 and 1.Now,f-3=-3-12+3=16+3=19f1=1-12+3=3Hence, the absolute maximum value when x=-3 is 19 and the absolute minimum value when x=1 is 3.
iii) Given: fx=3×4-8×3+12×2-48x+25⇒f’x=12×3-24×2+24x-48For a local maximum or a local minimum, we must havef’x=0⇒12×3-24×2+24x-48=0⇒x3-2×2+2x-4=0⇒x2x-2+2x-2=0⇒x-2×2+2=0⇒x-2=0 or x2+2=0 ⇒x=2 No real root exists for x2+2=0. Thus, the critical points of f are 0, 2 and 3.Now,f0=304-803+1202-480+25=25f2=324-823+1222-482+25=-39f3=334-833+1232-483+25=16Hence, the absolute maximum value when x=0 is 25 and the absolute minimum value when x=2 is -39.
iv) Given: fx=x-2x-1⇒f’x=x-1+x-22x-1For a local maximum or a local minimum, we must havef’x=0⇒x-1+x-22x-1=0⇒2x-1+x-2=0⇒2x-2+x-2=0⇒3x-4=0⇒3x=4 ⇒x=43 Thus, the critical points of f are 1, 43 and 9.Now, f1=1-21-1=0 f43=43-243-1=-23×13=-233 f9=9-29-1=142Hence, the absolute maximum value when x=9 is 142 and the absolute minimum value when x=43 is -233.Disclaimer: The solution given in the book is incorrect. The solution here is created according to the question given in the book.
Q2.
Answer :
Given: fx=2×3-24x+107⇒f’x=6×2-24For a local maximum or a local minimum, we must havef’x=0⇒6×2-24=0⇒6×2=24⇒x2=4⇒x=±2Thus, the critical points of f in the interval 1, 3 are 1, 2 and 3. Now, f1=213-241+107=85f2=223-242+107=75f3=233-243+107=89Hence, the absolute maximum value when x=3 in the interval 1, 3 is 89.Again, the critical points of f in the interval -3, -1 are -1, -2 and-3. So, f-3=2-33-24-3+107=125f-2=2-23-24-2+107=139f-1=2-13-24-1+107=129Hence, the absolute maximum value when x=-2 is 139.
Q3.
Answer :
Given: fx=cos2 x+sin x⇒f’x=2 cos x-sin x+cos x=-2 sin x cos x+cos xFor a local maximum or a local minimum, we must have f’x=0⇒-2 sin x cos x+cos x=0⇒cos x 2 sin x-1=0⇒sin x=12 or cos x=0⇒x=π6 or π2 ∵ x∈0, πThus, the critical points of f are 0, π6, π2 and π.Now,f0=cos2 0+sin 0=1fπ6=cos2 π6+sin π6=54fπ2=cos2 π2+sin π2=1fπ=cos2 π+sin π=1Hence, the absolute maximum value when x=π6 is 54 and the absolute minimum value when x=0, π2, π is 1.
Q4.
Answer :
Given: fx=12×43-6×13⇒f’x=16×13-2x-23=28x-1x23For a local maximum or a local minimum, we must havef’x=0⇒28x-1×23=0⇒8x-1=0⇒x=18Thus, the critical points of f are -1, 18 and 1.Now,f-1=12-143-6-113=18f18=121843-61813=-94f1=12143-6113=6Hence, the absolute maximum value when x=-1 is 18 and the absolute minimum value when x=18is -94.
Q5.
Answer :
Given: fx=2×3-15×2+36x+1⇒f’x=6×2-30x+36For a local maximum or a local minimum, we have f’x=0⇒6×2-30x+36=0⇒x2-5x+6=0⇒x-3x-2=0⇒x=2 and x=3 Thus, the critical points of f are 1, 2, 3 and 5.Now,f1=213-1512+361+1=24f2=223-1522+362+1=29f3=233-1532+363+1=28f5=253-1552+365+1=56Hence, the absolute maximum value when x=5 is 56 and the absolute minimum value when x=1 is 24.
Page 18.61 Ex.18.5
Q1.
Answer :
Let the two positive numbers be x and y. Then,x+y=15 …1Now,z=x2+y2⇒z=x2+15-x2 From eq. 1⇒z=x2+x2+225-30x⇒z=2×2+225-30x⇒dzdx=4x-30For maximum or minimum values of z, we must havedzdx=0⇒4x-30=0⇒x=152d2zdx2= 4 > 0Substituting x=152 in 1, we get y=152Thus, z is minimum when x=y=152.
Q2.
Answer :
Suppose 64 is divided into two parts x and 64-x. Then,z=x3+64-x3⇒dzdx=3×2+364-x2For maximum or minimum values of z, we must havedzdx=0⇒3×2+364-x2=0⇒3×2=364-x2⇒x2=x2+4096-128x⇒x=4096128⇒x=32Now, d2zdx2=6x+664-x ⇒d2zdx2=384>0Thus, z is minimum when 64 is divided into two equal parts, 32 and 32..
Q3.
Answer :
Let the two numbers be x and y. Then,x, y >-2 and x+y=12 …(1)Now,z=x +y3⇒z=x+12-x3 From eq. 1⇒dzdx=1+312-x2For maximum or minimum values of z, we must havedzdx=0⇒1+312-x2=0⇒12-x2=13⇒12-x=±13⇒x=12±13d2zdx2=612-x⇒d2zdx2=3-6xAt x=12±13:d2zdx2=3-612+13⇒-63<0Thus, z is maximum when x= 12+13.At x=12-13:d2zdx2=3-612-13⇒63>0Thus, z is minimum when x= 12-13.x+y=12Substituting the value of x in eq. 1, we gety=-12+13+12y=13So, the required two numbers are 12-13 and 13.
Q4.
Answer :
Let the two numbers be x and y. Then,x+y=15 …(1)Now, z=x2y3⇒z=x215-x3 From eq. 1⇒dzdx=2×15-x3-3×215-x2For maximum or minimum values of z, we must havedzdx=0⇒2×15-x3-3×215-x2=0⇒2×15-x=3×2⇒30x-2×2=3×2⇒30x=5×2⇒x=6 and y =9d2zdx2=215-x3-6×15-x2-6×15-x2+6×215-xAt x=6:d2zdx2=293-3692-3692+6369⇒d2zdx2=-2430<0Thus, z is maximum when x= 6 and y =9.So, the required two parts into which 15 should be divided are 6 and 9.
Q5.
Answer :
Let r and h be the radius and height of the cylinder, respectively. Then, VolumeV of the cylinder =πr2h⇒100=πr2h⇒h=100πr2Surface area S of the cylinder=2πr2+2πrh=2πr2+2πr×100πr2⇒S=2πr2+200r∴dSdr=4πr-200r2 For the maximum or minimum, we must have dSdr=0⇒4πr-200r2=0⇒4πr3=200⇒r=50π13Now, d2Sdr2=4π+400r3⇒ d2Sdr2>0 when r=50π13Thus, the surface area is minimum when r=50π13.At r=50π13:h=100π50π23 =250π13
Q6.
Answer :
Suppose the wire, which is to be made into a square and a circle, is cut into two pieces of length x m and y m, respectively. Then,x+y=25 …1Perimeter of square, 4Side=x⇒Side=x4Area of square=x42=x216Circumference of circle, 2πr=y⇒r=y2πArea of circle=πr2=πy2π2=y24πNow,z=Area of square+Area of circle ⇒z=x216+y24π⇒z=x216+25-x24π⇒dzdx=2×16-225-x4πFor the maximum or minimum values of z, we must havedzdx=0⇒2×16-225-x4π=0 ⇒x4=25-xπ⇒xπ4+x=25⇒xπ4+1=25⇒x=25π4+1⇒x=100π+4⇒y=25-100π+4 From eq. 1⇒y=25ππ+4 d2zdx2=18+12π>0Thus, z is minimum when x=100π+4 and y =25ππ+4.So, the wire of length 25 m should be cut into two pieces of lengths 100π+4 m and 25ππ+4 m.
Q7.
Answer :
Suppose the wire, which is to be made into a square and a circle, is cut into two pieces of length x m and y m, respectively. Then,x+y=28 …1Perimeter of square, 4side=x⇒Side=x4⇒Area of square=x42=x216Circumference of circle, 2πr=y⇒r=y2πArea of circle=πr2=πy2π2=y24πNow,z=Area of square+Area of circle ⇒z=x216+y24π⇒z=x216+28-x24π⇒dzdx=2×16-228-x4πFor maximum or minimum values of z, we must havedzdx=0⇒2×16-228-x4π=0 From eq. 1⇒x4=28-xπ⇒xπ4+x=28⇒xπ4+1=28⇒x=28π4+1⇒x=112π+4⇒y=28-112π+4 From eq. 1⇒y=28ππ+4 d2zdx2=18+12π>0Thus, z is minimum when x=112π+4 and y =28ππ+4.Hence, the length of the two pieces of wire are 112π+4 m and 28ππ+4 m respectively.
Q8.
Answer :
Suppose the wire, which is to be made into a square and a triangle, is cut into two pieces of length x and y, respectively. Then,x+y=20 …1Perimeter of square, 4Side=x⇒Side=x4Area of square=x42=x216Perimeter of triangle, 3Side=y⇒Side=y3Area of triangle=34×Side2=34×y32=3y236Now,z=Area of square+Area of triangle⇒z=x216+3y236⇒z=x216+320-x236 From eq. 1⇒dzdx=2×16-2320-x36For maximum or minimum values of z, we must havedzdx=0⇒2×16-320-x18=0⇒9×4=320-x⇒9×4+x3=203⇒x94+3=203⇒x=20394+3⇒x=8039+43⇒y=20-8039+43 From eq. 1⇒y=1809+43 d2zdx2=18+318>0Thus, z is minimum when x=8039+43 and y =1809+43.Hence, the wire of length 20 cm should be cut into two pieces of lengths 8039+43 m and 1809+43 m.Disclaimer: The solution given in the book is incorrrect. The solution here is created according to the question given in the book.
Q9.
Answer :
Let the length of a side of the square and radius of the circle be x and r, respectively. It is given that the sum of the perimeters of square and circle is constant. ⇒4x+2πr=K Where K is some constant⇒x=K-2πr4 …1Now,A=x2+πr2⇒A=K-2πr216+πr2 From eq. 1⇒dAdr=K-2πr216+πr2⇒dAdr=2K-2πr-2π16+2πr⇒dAdr=K-2πr-π4+2πr⇒K-2πr-π4+2πr=0⇒K-2πrπ4=2πr⇒K-2πr=8r …2d2Adx2=π22+2π>0So, the sum of the areas, A is least when K-2πr=8r.From eqs. 1 and 2, we getx=K-2πr4⇒x=8r4⇒x=2r∴ Side of the square=Diameter of the circle
Page 18.62 Ex.18.5
Q10.
Answer :
Let the side of the square to be cut off be x cm.
Then, the length and the breadth of the box will be (18 − 2x) cm each and height of the box will be x cm.
Volume of the box, V(x) = x(18 − 2x)2
V’x=18-2×2-4×18-2x =18-2×18-2x-4x =18-2×18-6x =129-x3-xV”x=12-9-x-3-x =-129-x+3-x =-246-x
For maximum and minimum values of V, we must have V’x=0
⇒x = 9 or x = 3
If x = 9, then length and breadth will become 0.
x ≠ 9
x = 3
Now,
V”3=-246-3=-72<0
x = 3 is the point of maxima.
Vx=318-62=3×144=432 cm3
Hence, if we remove a square of side 3 cm from each corner of the square tin and make a box from the remaining sheet, then the volume of the box so obtained would be the largest, i.e. 432 cm3.
Q11.
Answer :
Suppose square of side measuring x cm is cut off.Then, the length, breadth and height of the box will be 45-x, 24-2x and x, respectively. ⇒Volume of the box, V=45-2×24-2xx⇒dVdx= 45-2×24-2x- 2×45-2x-2×24-2xFor maximum or minimum values of V, we must havedVdx=0⇒45-2×24-2x- 2×45-2x-2×24-2x=0⇒4×2+1080-138x-48x+4×2+4×2-90x=0⇒12×2-276x+1080=0⇒x2-23x+90=0⇒x2-18x-5x+90=0⇒xx-18-5x-18=0⇒x-18=0 or x-5=0⇒x=18 or x=5Now,d2Vdx2=24x-276d2Vdx2x=5=120-276=-156<0 d2Vdx2x=18=432-276=156>0Thus, volume of the box is maximum when x=5 cm.Hence, the side of the square to be cut off measures 5 cm.
Q12.
Answer :
Let l, h, V and S be the length, height, volume and surface area of the tank to be constructed.Since volume, V is constant,l2h=V⇒h=Vl2 …1Surface area, S=l2+4lh⇒S=l2+4Vl From eq. 1⇒dSdl=2l-4Vl2For S to be maximum or minimum, we must havedSdl=0⇒2l-4Vl2=0⇒2l3-4V=0⇒2l3=4V⇒l3=2VNow, d2Sdl2=2+8Vl3⇒d2Sdl2=2+8V2V=6>0Here, surface area is minimum.h=Vl2Substituting the value of V=l32 in eq. 1, we geth=l32l2⇒h=l2Hence proved.
Q13.
Answer :
Let l, b and h be the length, breadth and height of the box, respectively.Volume of the box=c Given: l=2b …1⇒c=lbh⇒c=2b2h⇒h=c2b2 … 2Let cost of the material required for bottom be K/m2.Cost of the material required for 4 walls and top = Rs 3K/m2Total cost, T= Klb+3k2lh+2bh+lb⇒T=2Kb2+3K4bc2b2+2bc2b2+2b2 From eqs. 1 and 2 ⇒dTdb=4Kb+3K-3cb2+4bFor maximum or minimum values of T, we must havedTdb=0⇒4kb+3K-3cb2+4b=0⇒4b=33cb2-4b⇒4b=9cb2-12b⇒4b=9c-12b3b2⇒4b3=9c-12b3⇒16b3=9c⇒b=9c1613Now, d2Tdb2=4K+3K6cb3+4⇒d2Tdb2=4K+3K6c9c×16+4⇒K4+3×443⇒48K>0∴ Cost is minimum when b=9c1613.Substituting b = 9c1613in eq. 1 and eq. 2⇒l=29c1613h=c2b2⇒h=c29c1623⇒h=32c8113Thus, the most economic dimensions of the box are l=29c1613, b=9c1613 and h=32c8113.
Q14.
Answer :
Let l, b and h be the length, breadth and height of the tank, respectively.
Height, h = 2 m
Volume of the tank = 8 m3
Volume of the tank = l × b × h
∴ l × b × 2 = 8
⇒lb=4⇒b=4l
Area of the base = lb = 4 m2
Area of the 4 walls, A= 2h (l + b)
∴A=4l+4l⇒dAdl=41-4l2For maximum or minimum values of A, we must havedAdl=0⇒41-4l2=0⇒l=±2
However, the length cannot be negative.
Thus,
l = 2 m
∴ b=42=2 mNow, d2Adl2=32l3At l=2:d2Adl2=328=4>0
Thus, the area is the minimum when l = 2 m
We have
l = b = h = 2 m
∴ Cost of building the base = Rs 70 × (lb) = Rs 70 × 4 = Rs 280
Cost of building the walls = Rs 2h (l + b) × 45 = Rs 90 (2) (2 + 2)= Rs 8 (90) = Rs 720
Total cost = Rs (280 + 720) = Rs 1000
Hence, the total cost of the tank will be Rs 1000.
Disclaimer: The solution given in the book is incorrect. The solution here is created according to the question given in the book.
Q15.
Answer :
Let the dimensions of the rectangular part be x and y. Radius of semi-circle =x2Total perimeter=10⇒x+2y+πx2=10⇒2y=10-x-πx2⇒y=1210-x1+π2 …1Now, Area, A=π2×22+xy⇒A=πx28+x210-x1+π2 From eq. 1⇒A=πx28+10×2-x221+π2⇒dAdx=πx4+102-2×21+π2For maximum or minimum values of A, we must havedAdx=0⇒πx4+102-2×21+π2=0⇒xπ4-1-π2=-5⇒x=-5-4-π4⇒x=20π+4Substituting the value of x in eq. 1, we gety=1210-20π+41+π2⇒y=5-10π+22π+4⇒y=5π+20-5π-10π+4⇒y=10π+4 d2Adx2=π4-π2-1⇒d2Adx2=π-2π-44⇒d2Adx2=-π-44<0Thus, the area is maximum when x=20π+4 and y=10π+4. So, the required dimensions are given below:Length=20π+4 m Breadth=10π+4 m
Q16.
Answer :
Let the dimensions of the rectangle be x and y.Perimeter of the window=x+y+x+x+y=12⇒3x+2y=12⇒y=12-3×2 …1Area of the window =xy +34×2⇒A=x12-3×2 +34×2⇒A=6x-3×22+34×2⇒dAdx=6-6×2+234x⇒dAdx=6-3x+32x⇒dAdx=6-x3-32For maximum or a minimum values of A, we must havedAdx=0⇒6=x3-32⇒x= 126-3Substituting the value of x in eq. 1, we gety=12-3126-32⇒y=18-636-3Now, d2Adx2=-3+32<0Thus, the area is maximum when x=126-3 and y=18-636-3.
Q17.
Answer :
Let the height and radius of the base of the cylinder be h and r, respectively. Then,h24+r2=R2⇒h=2R2-r2 …1Volume of cylinder, V=πr2hSquaring both sides, we get⇒V2=π2r4h2⇒V2=4π2r4R2-r2 From eq. 1Now,Z=4π2r4R2-r6⇒dZdr=4π24r3R2-6r5For maximum or minimum values of Z, we must havedZdr=0⇒4π24r3R2-6r5=0⇒4r3R2=6r5⇒6r2=4R2⇒r2=4R26⇒r=2R6Substituting the value of r in eq. 1, we get ⇒h=2R2-2R62⇒h=26R2-4R26⇒h=2R23⇒h=2R3Now, d2Zdr2=4π212r2R2-30r4⇒d2Zdr2=4π2122R62R2-302R64⇒d2Zdr2=4π28R4-80R46⇒d2Zdr2=4π248R4-80R46⇒d2Zdr2=4π2-16R43<0So, volume of the cylinder is maximum when h=2R3.Hence proved.
Q18.
Answer :
Let the dimensions of the rectangle be x and y. Then,x24+y2=r2⇒x2+4y2=4r2⇒x2=4r2-y2 …1Area of rectangle=xy⇒A=xySquaring both sides, we get⇒A2=x2y2⇒Z=4y2r2-y2 From eq. 1⇒dZdy=8yr2-16y3For the maximum or minimum values of Z, we must havedZdy=0⇒8yr2-16y3=0⇒8r2=16y2⇒y2=r22⇒y=r2Substituting the value of y in eq. 1, we get⇒x2=4r2-r22⇒x2=4r2-r22⇒x2=4r22⇒x2=2r2⇒x=r2Now, d2Zdy2=8r2-48y2⇒d2Zdy2=8r2-48r22⇒d2Zdy2=-16r2<0So, the area is maximum when x= r2 and y =r2.Area =xy⇒A=r2×r2⇒A=r2
Q19.
Answer :
Let the surface area of conical tent be S = πrr2+h2Let the volume of the conical tent V = 13πr2h⇒h=3Vπr2∴S=πrr2+3Vπr22⇒S=1rπ2r6+9V6Now differentiating with respect to r we get,dSdr=ddr1rπ2r6+9V6 =1r6π2r52π2r6+9V6-π2r6+9V6r2For minima putting dSdr=0 we get,3π2r4π2r6+9V6=π2r6+9V6r2⇒3π2r6=π2r6+9V6⇒2π2r6= 9V6Substitutting the value of V we get,2π2r6= 913πr2h2⇒2π2r6= π2r4h2⇒2r2=h2∴h=2 r
Q20.
Answer :
Let h, r and R be the height, radius of base of the cone and radius of the sphere, respectively. Then,h=R+R2-r2⇒h-R2=R2-r2⇒h2+R2-2hr=R2-r2⇒r2=2hR-h2 …1Volume of cone =13πr2h⇒V=13πh2hR-h2 From eq. 1⇒V=13π2h2R-h3⇒dVdh=π34hR-3h2For maximum or minimum values of V, we must havedVdh=0⇒π34hR-3h2=0⇒4hR=3h2⇒h=4R3Substituting the value of y in eq. 1, we get x2=4r2-r22⇒x2=4r2-r22⇒x2=4r22⇒x2=2r2⇒x=r2Now, d2Vdh2=π34R-6h⇒d2Vdh2=π34R-6×4R3⇒d2Vdh2=-4πR3<0So, the volume is maximum when h= 4R3.⇒h=23Diameter of sphereHence proved.
Page 18.63 Ex.18.5
Q21.
Answer :
Let r be the radius of the sphere, x be the side of the cube and S be the sum of the surface area of both. Then,
S=4πr2+6×2
⇒x=S-4πr2612 …(1)
Sum of volumes, V= 43πr3+x3
⇒V = 4πr33+S-4πr2632 [From eq. (1)]
⇒dVdr=4πr2-2πrS-4πr2612
For the minimum or maximum values of V, we must have
dVdr=0 …(2)
⇒4πr2-2πrS-4πr2612=0 From eq. 2⇒4πr2=2πrS-4πr2612⇒4πr2=2πrx From eq. 1 ⇒x=2r
Now,
d2Vdr2=8πr-2πS-4πr2612-2πr2S-4πr26-12-8πr6⇒d2Vdr2=8πr-2πS-4πr2612+43π2r26S-4πr212⇒d2Vdr2=8πr-2πx+43π2r21x=8πr-4πr+23π2r⇒d2Vdr2=4πr+23π2r>0
So, volume is minimum when x = 2r.
Q22.
Answer :
Volume, V=12πlD22⇒V=πD2l8⇒l=8VπD2 …1Total surface area=πD24+lD+πDl2⇒S=πD24+8VπD+8V2D From eq. 1⇒dSdD=πD2-8VπD2-8V2D2For maximum or minimum values of S, we must havedSdD=0⇒πD2-8VπD2-8V2D2=0⇒πD2=8VD21π+12⇒D3=16Vπ1π+12Now, d2SdD2=π2+16VD31π+12⇒d2SdD2=π2+π>0l=8VπD2⇒l=8πD2πD3162ππ+2⇒l=Dππ+2⇒lD=ππ+2Hence proved.
Q23.
Answer :
Let l, b and V be the length, breadth and volume of the rectangle, respectively. Then, 2l+b=36⇒l=18-b …1Volume of the cylinder when revolved about the breadth, V=πl2b⇒V=π18-b2b From eq.1⇒V=π324b+b3-36b2⇒dVdb=π324+3b2-72bFor the maximum or minimum values of V, we must havedVdb=0⇒π324+3b2-72b=0⇒324+3b2-72b=0⇒b2-24b+108=0⇒b2-6b-18b+108=0⇒b-6b-18=0⇒b=6, 18Now, d2Vdb2=π6b-72At b=6:d2Vdb2=π6×6-72⇒d2Vdb2=-36π<0At b=18:d2Vdb2=π6×18-72⇒d2Vdb2=36π>0Substituting the value of b in eq. 1, we getl=18-6=12So, the volume is maximum when l=12 cm and b=6 cm.
Q24.
Answer :
Let the breadth, height and strength of the beam be b, h and S, respectively.a2=h2+b24⇒4a2-b2=h2 …1Here,Strength of beam, S=Kbh2 Where K is some constant⇒S=kb4R2-b2 From eq. 1⇒S=kb4a2-b3⇒dSdb=k4a2-3b2For maximum or minimum values of S, we must havedSdb=0⇒k4a2-3b2=0⇒4a2-3b2=0⇒4a2=3b2⇒b=2a3Substituting the value of b in eq. 1, we get⇒4a2-2a32=h2⇒12a2-4a23=h2⇒h=223aNow, d2Sdb2=-6Kb⇒d2Sdb2=-6K2a3⇒d2Sdb2=-12Ka3<0So, the strength of beam is maximum when b=2a3 and h=223a.
Q25.
Answer :
Let the height, radius of the base and surface area of the cylinder be h, r and S, respectively. Then,Volume =πr2h⇒2156=πr2h⇒2156=227r2h⇒h=2156×722r2⇒h=686r2 …1Surface area=2πrh+2πr2⇒S=4312r+44r27 From eq. 1⇒dSdr=4312-r2+88r7For maximum or minimum values of S, we must havedSdr=0⇒4312-r2+88r7=0⇒4312r2=88r7⇒r3=4312×788⇒r3=343⇒r=7 cmNow, d2sdr2=8624r3+887⇒d2sdr2=8624343+887⇒d2sdr2=1767>0So, the surface area is minimum when r=7 cm.
Q26.
Answer :
Let the base, height and area of a right angled triangle respectively be b, h and A. Then,b2=25-h2 … 1Area, A=12bh⇒A=12h25-h2 Using 1On squaring both side, we get⇒A2=1425-h2h2⇒A2=25h24-h44Let Z=A2=25h24-h44⇒dZdh=50h4-h3For maximum or minimum values of Z, we must havedZdh=0⇒50h4-h3=0⇒50h4=h3⇒4h2=50⇒h=52So, b2=25-522=252⇒b=52Now, d2Zdh2=252-3h2⇒d2Zdh2=252-752=-25<0So, area is maximum for h=b=52Maximum area=12bh=12×52×52=254 cm2
Q27.
Answer :
Let A be the area of the triangle. Then,Area of the triangle=12ab sin θdAdθ=12ab cos θFor maximum or minimum values of A, we must havedAdθ=0⇒12ab cos θ=0⇒cos θ=0⇒θ=π2Now,d2Adθ2=-12ab sin θ⇒d2Adθ2=-12ab<0So, area is maximum when θ=π2.∴ Maximum area=12ab sin π2=12ab
Q28.
Answer :
Let the height, radius of base and volume of a cylinder be h, r and V, respectively. Then,h24+r2=R2⇒h2=4R2-r2⇒r2=R2-h24 …1Now, V=πr2h⇒V=πhR2-h34 From eq. 1⇒dVdh=πR2-3h24For maximum or minimum values of V, we must havedVdh=0⇒πR2-3h24=0⇒R2-3h24=0⇒R2=3h24⇒h=2R3d2Vdh2=-3πh2d2Vdh2=-3π2×2R3⇒d2Vdh2=-3πR3<0So, the volume is maximum when h=2R3.Maximum volume=πhR2-h24=π×2R3R2-4R212=2πR38R212=4πR333=4π53333=500π cm3
Q29.
Answer :
Let the height, radius of base and volume of the cone be h, r and V, respectively. Then,h=R+R2-r2⇒h-R=R2-r2Squaring both the sides, we geth2+R2-2hR=R2-r2⇒r2=2hR-h2 …1Now, V=13πr2h⇒V=π32h2R-h3 From eq. 1⇒dVdh=π34hR-3h2For maximum or minimum values of V, we must havedVdh=0⇒π34hR-3h2=0⇒4hR=3h2⇒h=4R3Now, d2Vdh2=π34R-6h⇒π34R-8R=0⇒-4πR3<0So, the volume is maximum when h=4R3.⇒h=4×123=16 cm
Q30.
Answer :
Here,x2+y2=r2⇒y=r2-x2 …1Now,Z=x+y⇒Z=x+r2-x2 From eq. 1⇒dZdx=1 +-2x2r2-x2For maximum or minimum values of Z, we must havedZdx=0⇒1 +-2x2r2-x2=0⇒2x=2r2-x2⇒x=r2-x2Squaring both the sides, we get⇒x2=r2-x2⇒2×2=r2⇒x=r2Substituting the value of x in eq. 1, we gety=r2-x2⇒y=r2-r22⇒y=r2d2zdx2=-r2-x2+x-xr2-x2r2-x2⇒d2zdx2=-r2+x2-x2r2-x232⇒d2zdx2=-r2r3×22⇒d2zdx2=-22r<0So, z=x+y is maximum when x=y=r2.Hence proved.
Q31.
Answer :
Let the point x, y on the curve x2=4y be nearest to 0, 5. Then,x2=4y⇒y=x24 … 1Also,d2=x2+y-52 Using distance formulaNow,Z=d2=x2+y-52⇒Z=x2+x24-52 Using eq. 1⇒Z=x2+x416+25-5×22⇒dZdy=2x+4×316-5xFor maximum or minimum values of Z, we must havedZdy=0⇒2x+4×316-5x=0⇒4×316=3x⇒x3=12x⇒x2=12⇒x=±23Substituting the value of x in eq. 1, we gety=3Now,d2Zdy2=2+12×216-5⇒d2Zdy2=9-3=6>0So, the required nearest point is ±23, 3 .
Q32.
Answer :
Let point x, y be the nearest to the point 2, -8. Then,y2=4x⇒x=y24 … 1d2=x-22+y+82 Using distance formulaNow,Z=d2=x-22+y+82⇒Z=y24-22+y+82 From eq. 1⇒Z=y416+4-y2+y2+64+16y⇒dZdy=4y316+16For maximum or minimum values of Z, we must havedZdy=0⇒4y316+16=0⇒4y316=-16⇒y3=-64⇒y=-4Substituting the value of x in eq. 1, we getx=4Now, d2Zdy2=12y216⇒d2Zdy2=12>0So, the nearest point is 4,-4.
Q33.
Answer :
Let x, y be nearest to the point 2, 4. Then,x2=8y⇒y=x28 …1d2=x-22+y-42 Using distance formulaNow,Z=d2=x-22+y-42⇒Z=x-22+x28-42 From eq. 1⇒Z=x2+4-4x+x464+16-x2⇒dZdy=-4+4x364For maximum or minimum values of Z, we must havedZdy=0⇒-4+4×364=0⇒x316=4⇒x3=64⇒x=4Substituting the value of x in eq. 1, we gety=2Now,d2Zdy2=12×264⇒d2Zdy2=3>0So, the nearest point is 4, 2.
Q34.
Answer :
Let the required point be x, y. Then,x2=2y⇒y=x22 …1The distance between points x, y and 0, 5 is given byd2=x2+y-52Now,d2=Z⇒Z=x2+x22-52⇒Z=x2+x44+25-5×2⇒dZdy=2x+x3-10xFor maximum or a minimum values of Z, we must havedZdy=0⇒x3-8x=0⇒x2=8⇒x=±22Substituting the value of x in eq. 1, we gety=4d2Zdy2=3×2-8⇒d2Zdy2=24-8=16>0So, the nearest point is ±22, 4.
Q35.
Answer :
Let coordinates of the point on the parabola be x, y. Then,y=x2+7x+2 … 1Let the distance of a point x, x2+7x+2 from the line y=3x-3 be S. Then,S=-3x+x2+7x+2 +310⇒dSdt=-3+2x+710For maximum or minimum values of S, we must havedSdt=0⇒-3+2x+710=0⇒2x=-4⇒x=-2Now, d2Sdt2=210>0So, the nearest point is x, x2+7x+2 .⇒-2, 4-14+2⇒-2, -8
Q36.
Answer :
Suppose a point x, y on the curve y2=2x is nearest to the point 1, 4. Then,y2=2x⇒x=y22 …1d2=x-12+y-42 Using distance formulaNow,Z=d2=x-12+y-42⇒Z=y22-12+y-42 From eq. 1⇒Z=y44+1-y2+y2+16-8y⇒dZdy=y3-8For maximum or minimum values of Z, we must havedZdy=0⇒y3-8=0⇒y3=8⇒y=2Substituting the value of y in 1, we getx=2Now,d2Zdy2=3y2⇒d2Zdy2=12>0So, the required nearest point is 2, 2.
Q37.
Answer :
Given: y=-x3+3×2+2x-27 …1Slope= dydx=-3×2+6x+2Now,M=-3×2+6x+2⇒dMdx=-6x+6For maximum or minimum values of M, we must havedMdx=0⇒-6x+6=0⇒6x=6⇒x=1Substituing the value of x in eq. 1, we gety=-13+3×12+2×1-27=-23d2Mdx2=-6<0So, the slope is maximum when x=1 and y=-23.∴ At 1, -23: Maximum slope=-312+61+2=-3+6+2=5
Q38.
Answer :
The equation of line passing through 1, 4 with slope m is given by y-4=mx-1 …1Substituting y=0, we get0-4=mx-1⇒-4m=x-1⇒x=m-4mSubstituting x=0, we get y-4=m0-1⇒y=-m+4⇒x=-m-4So, the intercepts on coordinate axes are m-4m and -m-4.Let S be the sum of the intercepts. Then,S=m-4m-m-4⇒dSdm=4m2-1For maximum or minimum values of S, we must have dSdm=0⇒4m2-1=0⇒4m2=1⇒m2=4⇒m=±2Now, d2Sdm2=-8m3d2Sdm2m=2=-823=-1<0So, the sum is minimum at m=2.d2Sdm2m=-2=-8-23=1>0So, the sum is maximum at m=-2.Thus, the minimum value is given byS=-2-4-2–2-4=3+6=9
Q39.
Answer :
Let x and y be the length and breadth of the rectangular page, respectively. Then,Area of the page =150⇒xy=150⇒y=150x …1Area of the printed matter= x-3y-2⇒A=xy-2x-3y+6⇒A=150-2x-450x+6⇒dAdx=-2+450x2For maximum or minimum values of A, we must havedAdx=0⇒-2+450×2=0⇒2×2=450⇒x=15Substituting the value of x in 1, we gety=10Now,d2Adx2=-900×3⇒d2Adx2=-900153⇒d2Adx2=-9003375<0So, area of the printed matter is maximum when x=15 and y=10.
Q40.
Answer :
Given: s=t5-40t3+30t2+80t-250⇒dsdt=5t4-120t2+60t+80Acceleration, a=d2sdt2=20t3-240t+60⇒dadt=60t2-240For maximum or minimum values of a, we must havedadt=0⇒60t2-240=0⇒60t2=240⇒t=2Now,d2adt2=120t⇒d2adt2=240>0So, acceleration is minimum at t= 2.⇒amin=2023-2402+60=160-480+60=-260∴ At t=2:a=-260
Q41.
Answer :
Given: s=t44-2t3+4t2-7⇒v=dsdt=t3-6t2+8t⇒a=dvdt=3t2-12t+8For maximum or minimum values of v, we must havedvdt=0⇒3t2-12t+8=0On solving the equation, we gett=2±23Now,d2vdt2=6t-12At t=2-23:d2vdt2=62-23-12⇒-123<0So, velocity is maximum at t=2-23.Again,dadt=6t-12For maximum or minimum values of a, we must havedadt=0⇒6t-12=0⇒t=2Now,d2adt2=6>0So, acceleration is minimum at t=2.
Page 18.64 Ex.18.5
Q42.
Answer :
Profit =S.P. – C.P.⇒P=x50-x2-x24+35x+25⇒P=50x-x22-x24-35x-25⇒dPdx=50-x-x2-35For maximum or minimum values of P, we must havedPdx=0⇒15-3×2=0⇒15=3×2⇒x=303⇒x=10Now, d2Pdx2=-32<0So, profit is maximum if daily output is 10 items.
Q43.
Answer :
Profit =S.P. – C.P.⇒P=x5-x100-500+x5⇒P=5x-x2100-500-x5⇒dPdx=5-x50-15For maximum or minimum values of P, we must havedPdx=0⇒5-x50-15=0⇒245=x50⇒x=24×505⇒x=240Now, d2Pdx2=-150<0So, the profit is maximum if 240 items are sold.
Q44.
Answer :
i) Given: M=WL2x-W2x2⇒dMdx=WL2-2×Wx2⇒dMdx=WL2-WxFor maximum or minimum values of M, we must havedMdx=0⇒WL2-Wx=0⇒WL2=Wx⇒x=L2Now,d2Mdx2=-W <0So, M is maximum at x=L2.
ii) Given: M=Wx3-Wx33L2⇒dMdx=W3-3×Wx23L2⇒dMdx=W3-Wx2L2For maximum or minimum values of M, we must havedMdx=0⇒W3-Wx2L2=0⇒W3=Wx2L2⇒x=L3Now,d2Mdx2=-2WxL2 <0So, M is maximum at x=L3.
Q45.
Answer :
Given: y=x3+ax2+bx+c⇒dydx=3×2+2ax+bSince fx is at maximum at x=-1 and minimum at x=3, x=-1 and x=3 are the critical points. At x=-1:dydx=3-12+2a-1+b=0 ⇒3-2a+b=0⇒2a-b=3 … 1At x=3:dydx=332+2a3+b=0⇒27+6a+b=0⇒-6a-b=27 … 2From eqs. 1 and 2, we geta=-3, b=-9 and c∈R
Page 18.65 (Very Short Answers)
Q1.
Answer :
We know that at the extreme points of a function f(x), the first order derivative of the function is equal to zero, i.e.
f ‘(x) = 0 at x = c
⇒f ‘(c) = 0
Q2.
Answer :
We know that at the extreme points of a function f(x), the first order derivative of the function is equal to zero, i.e.
f ‘(x) = 0 at x = c
⇒f ‘(c) = 0
Also, at the point of local maximum, the second order derivative of the function at the given point must be less than zero, i.e.
f ”(c) < 0
Q3.
Answer :
If f(x) attains a local minimum at x = c, then the first order derivative of the function at the given point must be equal to zero, i.e.
f ‘(x) = 0 at x = c
⇒f ‘(c) = 0
The second order derivative of the function at the given point must be greater than zero, i.e.
f ”(c) > 0
Q4.
Answer :
Given: fx = x+1x⇒f’x = 1-1x2For a local maxima or a local minima, we must have f’x=0⇒1-1×2=0⇒x2=1⇒x=1, -1But x>0⇒x=1Now,f”x = 1x3At x=1: f”1 =213 =2>0So, x=1 is a point of local minimum.Thus, the local minimum value is given byf1 = 1+11 =1+1=2
Q5.
Answer :
Given: fx = x+1x⇒f’x = 1-1x2For a local maxima or a local minima, we must have f’x=0⇒1-1×2=0⇒x2=1⇒x=1, -1But x<0⇒x=-1Now,f”x = 1x3At x=-1: f”-1 =2-13 =-2<0So, x=-1 is a point of local maximum.Thus, the local maximum value is given byf-1 = -1+1-1 =-1-1=-2
Q6.
Answer :
Given: fx = x loge x⇒f’x = loge x+1For a local maxima or a local minima, we must havef’x=0⇒loge x+1=0⇒loge x=-1⇒x=1e⇒f1e = 1e loge 1e=-1eNow,f”x = 1xAt x=1e:f”1e =11e =e>0So, 1e, -1e is a point of local minimum..
Q7.
Answer :
We have,fx = ax+bx⇒f’x =a-bx2For a local maxima or a local minima, we must havef’x=0⇒a-bx2=0⇒x2=ba⇒x=ba, -baBut, x>0 ⇒x=baNow,f”x = 2bx3At x=ba f”ba =2bba3 =2a32b12>0 ∵a>0 and b>0So, x=ba is a point of local minimum.Hence, the least value isfba = aba+bba =ab+ab=2ab
Q8.
Answer :
Given: fx = xxTaking log on both sides, we getlog fx=x log xDifferentiating w.r.t. x, we get1fx f’x=log x+1⇒f’x=fx log x+1⇒f’x=xx log x+1 ….1For a local maxima or a local minima, we must have f’x=0⇒xx log x+1=0⇒log x=-1⇒x=1eNow,f”x =xx log x+12+xx×1x=xx log x+12+xx-1At x=1e:f”1e =1e1elog1e+12+1e1e-1=1e1e-1>0So, x=1e is a point of local minimum.Thus, the minimum value is given byf1e = 1e1e=e-1e
Q9.
Answer :
Given: fx = x1xTaking log on both sides, we getlog fx=1xlog xDifferentiating w.r.t. x, we get1fxf’x=-1x2log x+1×2⇒f’x=fx1x21-log x⇒f’x=x1x1x2-1x2log x …1⇒f’x=x1x-21-log x For a local maxima or a local minima, we must havef’x=0⇒x1x-21-log x=0⇒log x=1⇒x=eNow, f”x =x1x1x2-1x2log x2+x1x-2×3+2x3log x-1×3=x1x1x2-1x2log x2+x1x-3×3+2x3log xAt x=ef”e =e1e1e2-1e2log e2+e1e-3e3+2e3log e=-e1e1e3<0So, x=e is a point of local maximum.Thus, the maximum value is given byfe = e1e
Q10.
Answer :
Given: fx =log xx⇒f’x = 1-log xx2For a local maxima or a local minima, we must have f’x=0⇒1-log xx2=0⇒1-log x=0⇒log x=1⇒log x=log e⇒x=eNow, f”x = -x-2×1-log xx4=-3x-2x log xx4At x=e:f”e =-3e-2e log ee4 =-5e3<0So, x=e is a point of local maximum.Thus, the local maximum value is given byfe =log ee=1e.
Page 18.66 (Multiple Choice Questions)
Q1.
Answer :
(a) e1e
Given: fx = x1xTaking log on both sides, we getlog fx=1xlog xDifferentiating w.r.t. x, we get1fxf’x=-1x2log x+1×2⇒f’x=fx1x21-log x⇒f’x=x1x1x2-1x2log x …1⇒f’x=x1x-21-log x For a local maxima or a local minima, we must havef’x=0⇒x1x-21-log x=0⇒log x=1⇒x=eNow, f”x =x1x1x2-1x2log x2+x1x-2×3+2x3log x-1×3=x1x1x2-1x2log x2+x1x-3×3+2x3log xAt x=e:f”e =e1e1e2-1e2log e2+e1e-3e3+2e3log e=-e1e1e3<0So, x=e is a point of local maxima.∴ Maximum value=fe = e1e
Disclaimer: The answer given in the book is incorrect. The solution provided here is according to the question.
Q2.
Answer :
(b) ab≥c24Given: ax+bx≥cMinimum value of ax+bx=cNow,fx=ax+bx⇒f’x=a-bx2For a local maxima or a local minima, we must havef’x=0⇒a-bx2=0⇒ax2-b=0⇒ax2=b⇒x2=ba⇒x=±baf”x=2bx3⇒f”x=2bba3⇒f”x=2b a32b32>0So, x=ba is a local minima.∴ fba=aba+bba≥c=aaba+bbba≥c=ab+ab≥c⇒2ab≥c⇒c2≤ab⇒c24≤ab
Q3.
Answer :
(a) e Given: fx= xloge x⇒f’x=loge x-1loge x2For a local maxima or a local minima, we must have f’x=0⇒loge x-1loge x2=0⇒loge x-1=0⇒loge x=1⇒x=eNow, f”x=-1xloge x2+2xloge x3⇒ f”e=-1e+2e=1e>0So, x=e is a local minima.∴ Minimum value of fx=eloge e=e
Q4.
Answer :
(d) maximum value < minimum valueGiven: fx= x+1x⇒f’x=1-1x2For a local maxima or a local minima, we must have f’x=0⇒1-1×2=0⇒x2-1=0⇒x2=1⇒x=±1Now, f”x=2×3⇒f”1=21=2>0So, x=1 is a local minima.Also,f”-1=-2<0So, x=-1 is a local maxima.The local minimum value is given byf1=2The local maximum value is given byf-1=-2∴ Maximum value<Minimum value
Q5.
Answer :
(b) a minimum at x=1Given: fx= x3+3×2-9x+2⇒f’x=3×2+6x-9For a local maxima or a local minima, we must have f’x=0⇒3×2+6x-9=0⇒x2+2x-3=0⇒x+3x-1=0⇒x=-3, 1Now, f”x=6x+6⇒f”1=6+6=12>0So, x=1 is a local minima.Also, f”-3=-18+6=-12<0So, x=-3 is a local maxima.
Q6.
Answer :
(b) 4Given: fx= x4-x2-2x+6⇒f’x=4×3-2x-2⇒f’x=x-14×2+4x+2For a local maxima or a local minima, we must have f’x=0⇒x-14×2+4x+2=0⇒x-1=0⇒x=1Now, f”x=12×2-2⇒f”1=12-2=10>0So, x=1 is a local minima.The local minimum value is given byf1=1-1-2+6=4
Q7.
Answer :
(a) 12Let the required number be x. Then,fx=x-x2 ⇒f’x=1-2xFor a local maxima or a local minima, we must have f’x=0⇒1-2x=0⇒2x=1⇒x=12Now, f”x=-2<0So, x=12 is a local maxima.Hence, the required number is 12.
Q8.
Answer :
(a) a+b+c3Given: fx= x-a2+x-b2+x-c2⇒f’x= 2x-a+2x-b+2x-cFor a local maxima or a local minima, we must have f’x=0⇒2x-a+2x-b+2x-c=0⇒2x-2a+2x-2b+2x-2c=0⇒6x=2a+b+c⇒x=a+b+c3Now, f”x=2+2+2=6>0So, x=a+b+c3 is a local minima.
Q9.
Answer :
(b) 12Let the two non-zero numbers be x and y. Then,x+y=8⇒y=8-x … 1Now,fx=1x+1y⇒fx=1x+18-x From eq. 1⇒f’x=-1×2+18-x2For a local minima or a local maxima, we must have f’x=0⇒-1×2+18-x2=0⇒-8-x2+x2x28-x2=0⇒-64-x2+16x+x2=0⇒16x-64=0⇒x=4f”x=2×3-28-x3⇒f”4=243-28-43⇒f”4=264-264=0∴ Minimum value=14+14=12
Q10.
Answer :
(c) 3Given: fx= ∑r=15x-r2⇒fx=x-12+x-22+x-32+x-42+x-52⇒f’x=2x-1+x-2+x-3+x-4+x-5⇒f’x=25x-15For a local maxima and a local minima, we must havef’x=0⇒25x-15=0⇒5x-15=0⇒5x=15⇒x=3Now, f”x=10f”x=10>0So, x=3 is a local minima.
Q11.
Answer :
(d) none of these
Given: fx=2 sin 3x+3 cos 3x⇒f’x=6 cos 3x-9 sin 3xFor a local minima or a local maxima, we must have f’x=0⇒6 cos 3x-9 sin 3x=0⇒6 cos 3x=9 sin 3x⇒sin 3xcos 3x=23⇒tan 3x=23 …1At x=5π6: tan 3x=tan 5π2⇒tan 3x=tan π2So, tan 3x is not defined. tan 3x≠23 is not satisfying eq. 1Thus, x=5π6 is not a critical point.
Page 18.67 (Multiple Choice Questions)
Q12.
Answer :
(c) 1Given: fx= x2+x+1⇒f’x=2x+1For a local maxima or a local minima, we must have f’x=0⇒2x+1=0⇒2x=-1⇒x=-12∉0, 1At extreme points: f0=0f1=1+1+1=3>0So, x=1 is a local minima.
Q13.
Answer :
(d) 0Given: fx= x3-18×2+96x⇒f’x=3×2-36x+96For a local maxima or a local minima, we must have f’x=0⇒3×2-36x+96=0⇒x2-12x+32=0⇒x-4x-8=0⇒x=4, 8So,f8=83-1882+968=512-1152+768=128f4=43-1842+964=64-288+384=160f0=03-1802+960=0f9=93-1892+969=729-1458+864=135Hence, 0 is the minimum value in the range 0, 9.
Q14.
Answer :
Given: fx= x4-x+x2⇒f’x=4-x+x2-x-1+2×4-x+x22For a local maxima or a local minima, we must have f’x=0⇒4-x+x2-x-1+2×4-x+x22=0⇒4-x+x2-x-1+2x=0⇒4-x+x2+x-2×2=0⇒x2=4⇒x=±2 ∉-1, 1So,f-1=-14–1+-12=-16f1=14-1+12=14Hence, the maximum value is 14.
Q15.
Answer :
(b) 1, 2Let the required point be x, y. Then, y2=4x⇒x=y24 … 1Now, d=x-22+y-12Squaring both sides, we get⇒d2=x-22+y-12⇒d2=y24-22+y-12⇒d2=y416+4-y2+y2+1-2y From eq. 1Now,Z=d2=y416+4-y2+y2+1-2y⇒dZdy=y34-2y+2y-2⇒dZdy=y34-2⇒y34-2=0⇒y3=8⇒y=2Substituting the value of y in 1, we getx=1Now, d2Zdy2=3y24⇒d2Zdy2=3224=3>0So, the nearest point is 1, 2.
Q16.
Answer :
(b) 16Given: x+y=8⇒y=8-x … 1Let fx be xy.⇒ fx= x8-x From eq. 1⇒f’x=8-2xFor a local maxima or a local minima, we must have f’x=0⇒8-2x=0⇒8=2x⇒x=4⇒y=8-4=4 From eq. 1Now, f”x=-2⇒f”4=-2<0So, x=4 is a local maxima.Hence, the local maximum value is given byf4=4×4=16
Q17.
Answer :
Given: fx= x3-6×2+9x⇒f’x=3×2-12x+9For a local maxima or a local minima, we must have f’x=0⇒3×2-12x+9=0⇒x2-4x+3=0⇒x-1x-3=0⇒x=1, 3Now,f0= 03-602+90=0f1= 13-612+91=1-6+9=4f3= 33-632+93=27-54+27=0f6= 63-662+96=216-216+54=54
The least and greatest values of f(x) = x3- 6×2+9x in [0, 6] are 0 and 54, respectively.
Q18.
Answer :
(c) π6Given: fx= sin x +3 cos x⇒f’x=cosx-3 sin xFor a local maxima or a local minima, we must have f’x=0⇒cos x-3 sin x=0⇒cos x=3 sin x⇒tan x=13⇒x=π6Now, f”x=-sin x-3 cos x⇒⇒f”π2=-sinπ2-3 cosπ2-12-32=-2<0So, x= π2 is a local maxima.
Q19.
Answer :
(d) 23
Let h, r, V and R be the height, radius of the base, volume of the cone and the radius of the sphere, respectively. Given: h=R+R2-r2⇒h-R=R2-r2Squaring both side, we geth2+R2-2hR=R2-r2⇒r2=2hr-h2 … 1Now, Volume =13πr2h⇒V=π32h2R-h3 From eq. 1⇒dVdh=π34hR-3h2For maximum or minimum values of V, we must havedVdh=0⇒π34hR-3h2=0⇒4hR-3h2=0⇒4hR=3h2⇒h=4R3Now, d2Vdh2=π34R-6h=π34R-6×4R3=-4πR3<0So, volume is maximum when h=4R3.⇒h=22R3⇒h2R=23∴ HeightDiameter of sphere=23
Q20.
Answer :
(a) 75
Given: fx= x2+250x⇒f’x=2x-250x2For a local maxima or a local minima, we must have f’x=0⇒2x-250×2=0⇒2×3-250=0⇒x3=125⇒x=5Now, f”x=2+500×3⇒f”5=2+50053=750125=6>0So, x=5 is a local minima.∴ f’xmin= 52+2505=3755=75
Q21.
Answer :
(d) none of these
Given: fx= x+1x⇒f’x=1-1x2For a local maxima or a local minima, we must have f’x=0⇒1-1×2=0⇒x2-1=0⇒x2=1⇒x=±1⇒x=1 Given: x>0Now, f”x=2×3⇒f”1=2>0So, x=1 is a local minima.
Q22.
Answer :
(a) 43
Maximum value of 14×2+2x+1= Minimum value of 4×2+2x+1
Now, fx= 4×2+2x+1⇒f’x=8x+2For a local maxima or a local minima, we must have f’x=0⇒8x+2=0⇒8x=-2⇒x=-14Now, f”x=8⇒f”1=8>0So, x=-14 is a local minima.Thus, 14×2+2x+1is maximum at x=-14.⇒Maximum value of 14×2+2x+1 =14-142+2-14+1 =1416-12+1=1612=43
Q23.
Answer :
(b) 2
Given: xy=1⇒y=1xfx= x+1x⇒f’x= 1-1x2For a local maxima or a local minima, we must have f’x=0⇒1-1×2=0⇒x2-1=0⇒x2=1⇒x=±1⇒x=1 Given: x>1⇒y=1Now, f”x=2×3⇒f”1=2>0So, x=1 is a local minima.∴ Minimum value of fx=f1=1+1=2
Q24.
Answer :
d none of theseGiven: fx= x+1x⇒f’x=1-1x2For a local maxima or a local minima, we must have f’x=0⇒1-1×2=0⇒x2-1=0⇒x2=1⇒x=±1⇒x=1 Given: x>0Now, f”x=2×3⇒f”1=2>0So, x=1 is a local minima.
Q25.
Answer :
(d) 2
Given: fx= 2×3-15×2+36x+4⇒f’x=6×2-30x+36For a local maxima or a local minima, we must have f’x=0⇒6×2-30x+36=0⇒x2-5x+6=0⇒x-2x-3=0⇒x=2, 3Now, f”x=12x-30⇒f”2=24-30=-6<0So, x=1 is a local maxima.Also, f”3=36-30=6>0So, x=2 is a local maxima.
Q26.
Answer :
(c) 16
Given: fx= x4+x+x2⇒f’x=4+x+x2-x1+2×4+x+x22For a local maxima or a local minima, we must have f’x=0⇒4+x+x2-x1+2×4+x+x22=0⇒4+x+x2-x1+2x=0⇒4-x2=0⇒x=±2∉-1,1The values of fx at extreme points are given byf1=14+1+12=16f-1=-14-1+-12=-14Thus, 16 is the maximum value.
Page 18.68 (Multiple Choice Questions)
Q27.
Answer :
(c) 2
Given: fx= 2×3-3×2-12x+5⇒f’x=6×2-6x-12For a local maxima or a local minima, we must have f’x=0⇒6×2-6x-12=0⇒x2-x-2=0⇒x-2x+1=0⇒x=2, -1Now, f”x=12x-6⇒f”-1=-12-6=-18<0So, x=1 is a local maxima.Also, f”2=24-6=18>0So, x=2 is a local minima.
Q28.
Answer :
(c) -1eHere, fx= x loge x⇒f’x=loge x +1For a local maxima or a local minima, we must have f’x=0⇒loge x +1=0⇒loge x =-1⇒x=e-1Now, f”x=1x⇒f”e-1=e>0So, x=e-1 is a local minima.Hence, the minimum value of fx=fe-1.⇒e-1 loge e-1 =-e-1=-1e
Q29.
Answer :
(a)-128
Given: fx= 2×3-21×2+36x-20⇒f’x=6×2-42x+36For a local maxima or a local minima, we must have f’x=0⇒6×2-42x+36=0⇒x2-7x+6=0⇒x-1x-6=0⇒x=1, 6Now, f”x=12x-42⇒f”1=12-42=-30<0So, x=1 is a local maxima.Also, f”6=72-42=30>0So, x=6 is a local miniima.The local minimum value is given byf6==263-2162+366-20=-128
Q30.
Answer :
(a) Minimum at x=π2Given: fx=1+2 sin x+3 cos2 x⇒f’x=2 cos x-6 cos x sin x⇒f’x=2 cos x1-3 sin xFor a local maxima or a local minima, we must have f’x=0⇒2 cos x1-3 sin x=0⇒2 cos x=0 or 1-3 sin x=0⇒cos x=0 or sin x=13⇒x=π2 or x=sin-113Now, f”x=-2 sin x-6 cos 2x⇒f”π2=-2 sin π2-6 cos 2×π2=-2+6=4>0So, x=π2 is a local minima.Also, f”sin-113=-2 sin sin-113-6 cos sin-113=-23-6×223=-23+42<0So, x=sin-113 is a local maxima.
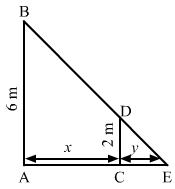
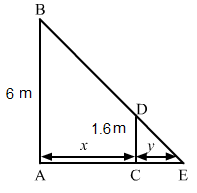
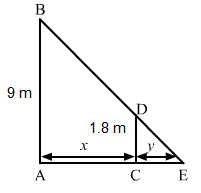
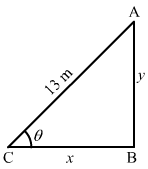
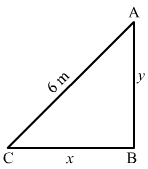
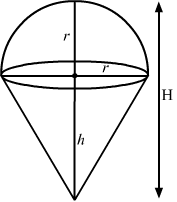
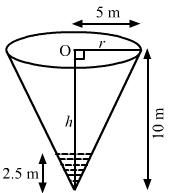
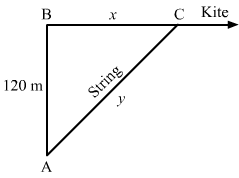
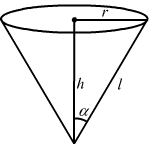
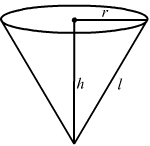
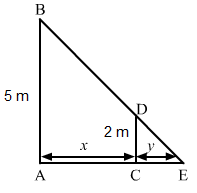
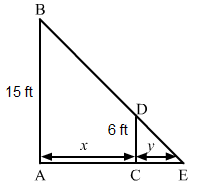
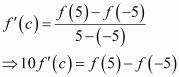
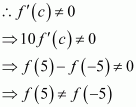
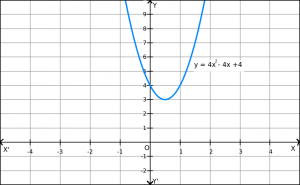
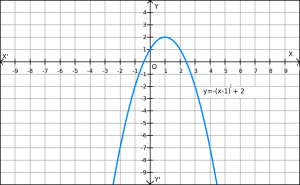
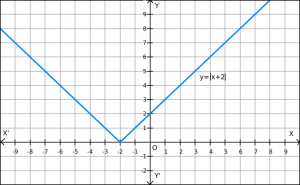
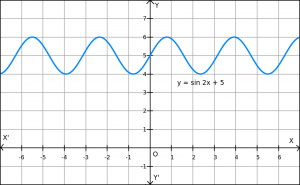
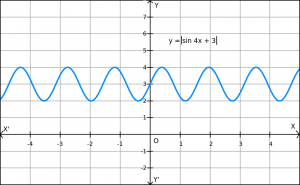
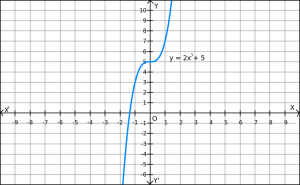
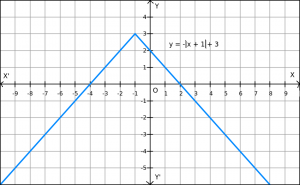
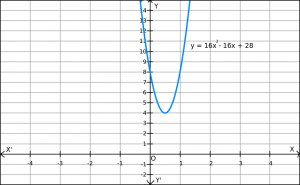
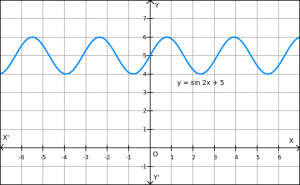
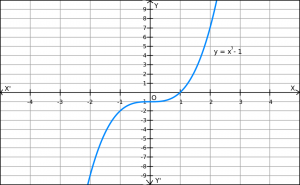
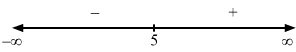

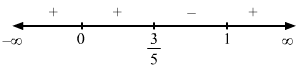

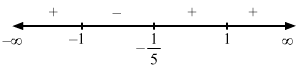



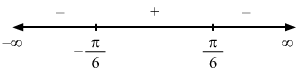
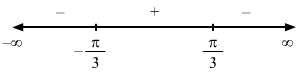
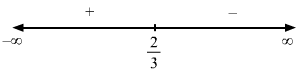
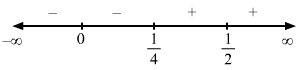
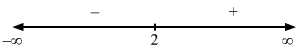

Leave a Reply